Примерная программа учебного курса (учебной дисциплины) Программа курса

Вид материала

Примерная программа

Содержание Термодинамика и молекулярная физика Докторов Александр Борисович Цели освоения дисциплины (курса) Место дисциплины в структуре образовательной программы 4. Структура и содержание дисциплины Формы текущего контроля успеваемости Самостоятельная работа студентов (в т.ч. время, предусмотренное на сдачу семестровых домашних заданий) Экзамен проводится только после полной сдачи заданий. 5. Образовательные технологии Домашние задания по курсу «Термодинамика и молекулярная физика» T. Найти теплоемкость системы при постоянном давлении. 7. Серебряная проволока диаметром d H от дна установлена перегородка. Между перегородкой и поршнем находится жидкость массы M P1, которое из–за поверхностного натяжения в капле больше давления P N, попавших на экран за постоянное время t R , вращающейся с угловой скоростью ω 1-я контрольная работа по термодинамике и молекулярной физике 7. Учебно-методическое и информационное обеспечение дисциплины

Подобный материал:

• Приказ № от. 09. 2010 г. Рабочая программа учебного предмета (учебного курса, учебной, 1190.63kb.
• Примерная программа учебной дисциплины фармакология название учебной дисциплины 2010, 648.57kb.
• Примерная программа основного общего образования по литературе для образовательных, 445.11kb.
• Программа учебной дисциплины «Информатика и программирование» Программа дисциплины, 135.24kb.
• Примерная программа учебной дисциплины «Основы банковского дела», 132.65kb.
• Примерная программа учебной дисциплины «Основы алгоритмизации и программирования», 217.7kb.
• Примерная программа учебной дисциплины "Бухгалтерский учет", 533.34kb.
• Примерная программа учебной дисциплины "Экономика отрасли", 257.63kb.
• Примерная программа учебной дисциплины «Разработка и эксплуатация удаленных баз данных», 189.07kb.
• Примерная программа учебной дисциплины "Анализ финансово-хозяйствен­ной деятельности", 185.61kb.

Учебный курс «Термодинамика и молекулярная физика» является частью профессионального цикла подготовки бакалавра физики. Дисциплина изучается студентами первого курса физического факультета. Программа подготовлена в соответствии с требованиями образовательного стандарта третьего поколения.

Цели курса – дать представление об основных методах и подходах, а также базовых понятиях классической равновесной термодинамики и молекулярной физики, научить решать широкий класс задач, подготовить понятийную базу для освоения различных курсов теоретической физики, сформировать общекультурные и профессиональные навыки. Односеместровый курс «Термодинамика и молекулярная физика» состоит из лекционных и практических занятий, сопровождаемых регулярной индивидуальной работой преподавателя со студентами в процессе сдачи семестровых домашних заданий, а также самостоятельной работы. Курс завершается экзаменом.

Общая трудоемкость дисциплины составляет 3 зачетные единицы, 136 академических часа (из них 96 аудиторных). Программой дисциплины предусмотрены 32 часа лекционных и 64 часа практических занятий, а также 40 часов самостоятельной работы.


Авторы

докт. физ.-мат. наук, проф. А. Б. Докторов,

канд. физ.-мат. наук, доц. В. П. Замураев


Программа учебного курса подготовлена в рамках реализации Программы развития НИУ-НГУ на 2009–2018 г. г.


 Новосибирский государственный

университет, 2011

Приложение № 2.


Примерная программа учебного курса (учебной дисциплины)


Программа курса « Термодинамика и молекулярная физика» составлена в соответствии с требованиями к обязательному минимуму содержания и уровню подготовки дипломированного специалиста бакалавра по профессиональному циклу дисциплин (Б.3) по направлению «011200 Физика», а также задачами, стоящими перед Новосибирским государственным университетом по реализации Программы развития НГУ.


Авторы Докторов Александр Борисович, доктор физико-математических наук, профессор,

Замураев Владимир Павлович, кандидат физико-математических наук, доцент

Факультет: физический

Кафедра: общей физики

1. Цели освоения дисциплины (курса)
   

Курс «Термодинамика и молекулярная физика» предназначен для обучения студентов-физиков, для которых классическая равновесная термодинамика и молекулярная физика являются основой для понимания физических процессов, связанных с молекулярными представлениями о строении вещества. Развиваемые в этой главе методы и идеи оказываются важными для значительной части разделов физики.

Как и в подавляющем числе теоретических курсов для студентов первого года обучения мы осуществляем постепенное вхождение в сложные разделы классической термодинамики и молекулярной физики, с тем, чтобы не потерять связь со слушателями. Курс начинается с изучения классической термодинамики, где в начале повторяются частично известные ещё со школы понятия теплоты и работы и термодинамических переменных, фигурирующих в термическом уравнении состояния на примере газов (температуры, давления, объёма). Даются ясные физические представления о функциях состояния и функциях процесса, которые органически увязываются с известными из математических курсов первого семестра понятиями полного дифференциала функций двух переменных. На этой основе в связи с изучением теоретических основ работы тепловых машин затем осуществляется введение дополнительного термодинамического параметра   энтропии (функции состояния) и формулируются основные термодинамические принципы, составляющие суть второго начала термодинамики. Даются основы построения термодинамики произвольных термодинамических систем, целью которых является обучить студентов рассматривать любые термодинамические процессы для широкого круга термодинамических систем.

Мы надеемся, что такой подход позволяет проще и быстрее освоить новые понятия термодинамики равновесных (обратимых) процессов, а также неравновесных процессов, протекающих между исходным и конечным равновесными состояниями. Далее в этой части курса читались уже устоявшиеся традиционные разделы равновесной термодинамики, такие как охлаждение газов и фазовое равновесие. Такие важные разделы как основы статистической и неравновесной термодинамики, должны, по нашему мнению, быть предметами отдельных дополнительных курсов.

Во второй части курса рассматриваются молекулярные представления в описании идеальных газов. Как и в первой части курса рассмотрение разделов построено на постепенном усложнении материала. Целью этой части курса является научить уверенному владению молекулярными распределениями (распределение Максвелла по скоростям в сосуде и молекулярном потоке, распределение Больцмана и каноническое распределение Гиббса), применяемых в рамках курса к рассмотрению диэлектрических свойств газов и их теплоёмкости. Особенностью этой части курса является рассмотрение молекулярных систем с дискретным энергетическим спектром, что на наш взгляд помогает не только глубже понять смысл статистических распределений и температурную зависимость теплоёмкости, но и заложить начальное понимание квантовой природы атомно-молекулярных систем, которая более подробно будет изучаться в соответствующих курсах. В курсе даны также простейшие элементы физической кинетики, такие как столкновения в газах и связанные с ними явления переноса (теплопроводность, вязкость, диффузия, ионная и электронная электропроводность).

Курс в целом даёт достаточно цельное представление о протекании физических процессов, связанных с молекулярной структурой вещества и его знание необходимо для изучения статистической физики, физической кинетики и других разделов физики.

2. Место дисциплины в структуре образовательной программы
   

Курс «Термодинамика и молекулярная физика» читается в весеннем семестре 1 курса.

Необходимыми предпосылками для успешного освоения курса являются следующее.

В цикле математических дисциплин: простейшие понятия теории вероятности, знание основ линейной алгебры и математического анализа, умение грамотно оперировать с функциями двух и трёх переменных, решать простые дифференциальные уравнения, умение применять эти знания при решении задач.

В цикле общефизических дисциплин необходимыми предпосылками являются знание и умение применять основные простейшие законы классической механики в рамках курса общей физики. Предполагается, что студенты уже знакомы с такими понятиями, как сила, масса, импульс и момент импульса, уравнения Ньютона, кинетическая и потенциальная энергии, колебания одномерных систем, движение заряда в электрическом поле.


С другой стороны, такие разделы данного курса как первое, второе и третье начало термодинамики, физические принципы работы тепловых и охлаждающих машин, фазовое равновесие, молекулярные распределения и основы кинетической теории являются той основой, без знания которой невозможно глубокое понимание окружающих нас основных природных и техногенных процессов и дальнейшее более глубокое изучение статистической физики и термодинамики и физической кинетики.


3. Компетенции обучающегося, формируемые в результате освоения дисциплины

«Термодинамика и молекулярная физика»

• общекультурные компетенции: ОК-1, ОК-5, ОК-17, ОК-18, ОК-20, ОК-21;
  
• профессиональные компетенции: ПК-1 –ПК-4 , ПК-5, ПК-10.
  

В результате освоения дисциплины обучающийся должен:

• Знать: первое, второе и третье начала термодинамики, глубоко понимать принципы термодинамики и физические основы работы тепловых и охлаждающих машин, понимать смысл термодинамических потенциалов и условия равновесия фаз, знать основные молекулярные распределения и физические средние, природу теплоёмкости и молекулярные основы явлений переноса в плотных и разреженных газах.
  
• Уметь: рассчитывать уравнения и физические характеристики (коэффициент полезного действия и холодильный коэффициент, теплоёмкости) различных термодинамических процессов для различных термодинамических систем; использовать различные молекулярные распределения для расчёта равновесных и кинетических параметров молекулярных систем.
  
• Владеть: техникой расчета уравнений и физических характеристик (коэффициент полезного действия и холодильный коэффициент, теплоёмкости) различных термодинамических процессов для различных термодинамических систем; техникой расчёта равновесных и кинетических параметров молекулярных систем на основе молекулярных распределений.
  

4. Структура и содержание дисциплины курса «Термодинамика и молекулярная физика»

Общая трудоемкость дисциплины составляет 3 зачетных единиц, 136 часов.

№ п/п	Раздел дисциплины	Семестр	Неделя семестра	Виды учебной работы, включая самостоятельную работу студентов и трудоемкость (в часах)			Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам)
1	Сведения из математики (дифференциал функций двух переменных в термодинамике, якобиан преобразования). Уравнение состояния. Идеальный газ и газ Ван-дер-Ваальса. Термодинамические коэффициенты уравнения состояния. Основное термодинамическое тождество. Тепло и работа, их эквивалентность.	2-й	1-я	Лекции, 2 часа	Практические занятия, 4 часа	Самостоятельная работа студентов (в т.ч. время, предусмотренное на сдачу семестровых домашних заданий), 2,5 часа	В начале каждого очередного занятия проверка задач, заданных на дом.
2	Изобарическое расширение идеального газа. Теплоёкость, соотношение Майера. Понятие внутренней энергии системы. Первое начало термодинамики. Термодинамика идеального газа: необратимое адиабатическое расширение, калорическое уравнение состояния, обратимые изотермическое и адиабатическое расширения газов, политропический процесс.		2-я	2 часа лекций	4 часа семинаров	2,5 часа
3	Циклические процессы. КПД тепловых машин. Цикл Карно. Принцип Карно. Теорема о приведённых теплотах. Энтропия. Удобство использования энтропии. Калибровочная инвариантность. Второе начало термодинамики для обратимых процессов. Эквивалентность различных формулировок второго начала термодинамики. Второе начало термодинамики для неравновесных процессов. Тепловые насосы.		3-я	2 часа лекций	4 часа семинаров	2,5 часа
4	Термодинамика произвольных систем. Метод термодинамических коэффициентов. Термодинамические функции и потенциалы: внутренняя энергия и адиабатический потенциал; энтальпия; свободная энергия и изотермический потенциал, уравнение Гиббса–Гельмгольца; термодинамический потенциал Гиббса. Естественные переменные, соотношения взаимности.		4-я	2 часа лекций	4 часа семинаров.	2,5 часа
5	Третье начало термодинамики (принцип Нернста) и его следствия. Невозможность достижения абсолютного нуля температур. Расширение газов. Процессы Гей–Люссака и Джоуля–Томсона. Изоэнтальпическое расширение газа Ван-дер-Ваальса. Кривая инверсии. Температура инверсии и температура Бойля для газа Ван-дер-Ваальса.		5-я	2 часа лекций	4 часа семинаров	2,5 часа
6	Термодинамика различных систем (равновесное излучение, поверхностное натяжение). Системы с переменным числом частиц. Рост энтропии в процессах смешения газов. Парадокс Гиббса. Открытые системы. Химический потенциал.		6-я	2 часа лекций	4 часа семинаров	2.5 часа
7	Фазовые переходы первого рода. Условие равновесия фаз. Правило Максвелла. Диаграммы состояния. Кривая сосуществования. Уравнение Клапейрона–Клаузиуса. Давление насыщающих паров. Расчёт термодинамических коэффициентов при равновесии фаз. Термодинамическое понятие о фазовых переходах второго рода.		7-я	2 часа лекций	4 часа семинаров	2.5 часа	Контрольная работа.
8	Давление идеального газа. Вероятность и функция распределения, статистическое среднее, средняя скорость молекул. Функция распределения по проекциям скорости. Уравнение состояния идеального газа.		8-я	2 часа лекций	4 часа семинаров	2.5 часа	Разбор контрольной работы.
9	Распределение Максвелла по проекциям скорости. Распределение по абсолютной величине скорости и по кинетической энергии молекул. Статистический вес. Наиболее вероятные и средние величины. Опыт Штерна. Молекулярный поток и уравнение неразрывности.		9-я	2 часа лекций	4 часа семинаров	2,5 часа
10	Плотности потока частиц и энергии и распределение по скоростям и энергиям в потоке. Вес газа. Барометрическая формула. Распределение Больцмана. Центрифугирование.		10-я	2 часа лекций	4 часа семинаров	2,5 часа
11	Максвелл   Больцмановское распределение. Каноническое распределение Гиббса. Поляризуемость газов и формула Ланжевена.		11-я	2 часа лекций	4 часа семинаров	2,5 часа
12	Классическая теория теплоёмкостей. Закон равнораспределения энергии по степеням свободы и исключения из него. Температурные аномалии.		12-я	2 часа лекций	4 часа семинаров	2,5 часа
13	Квантование гармонического осциллятора. Высокотемпературный предел. Правило квантования Бора. Вымораживание тепловых движений. Квантовая статистика. Парамагнетизм газов.		13-я	2 часов лекций	4 часа семинаров	2,5 часа
14	Релаксация. Столкновения в газе. Столкновения при движении с заданной скоростью. Средняя частота столкновений. Длина свободного пробега.		14-я	2 часа лекций	4 часа семинаров	2,5 часа
15	Явления переноса в плотных газах (теплопроводность, вязкость, диффузия). Соотношения между кинетическими коэффициентами. Уточнение расчётов. Термодиффузия. Теплопередача.
16	Явления переноса в ультраразреженном газе. Ток в газе. Ионная и электронная проводимости.						Экзамен.
Итого				32 часа	64 часа	40 часов

Экзамен проводится только после полной сдачи заданий.


Примерный план семинарских занятий

(номера задач даются по ссылке [3] из списка литературы, см. раздел 7 настоящей Программы)


Часть 1. Термодинамика

1. Уравнение состояния реального газа (1 час)
   

Задачи: № 1.1—1.2.

2. Работа и количество теплоты. Внутренняя энергия системы. Первое начало термодинамики. (4 часа)
   

Задачи:

Для одного моля идеального газа рассмотреть следующие равновесные процессы: изохорический, изобарический, изотермический, адиабатический и политропический. Получить уравнение каждого процесса в переменных p, V. Вычислить: работу A, совершенную газом; количество теплоты Q, полученное им; изменение внутренней энергии DU и энтропии DS; теплоемкость C. Получить соотношение Майера. Считать молярные теплоемкости C_p и C_V известными и постоянными.


№ 1.10, 1.12—1.14, 1.17, 1.20, 1.22.


В сосуде с поршнем находится 1 моль идеального одноатомного газа. Поршень удерживается пружиной. Найти теплоемкость газа. Объемом газа при ненапряженной пружине пренебречь.

Ответ. C = 2R.

3. Циклические процессы. Цикл Карно. Неравенство Клаузиуса. Метод циклов. (5 часов)
   

Задачи: № 1.23, 1.25, 1.27, 1.29—1.31, 1.33, 1.35.


Помещение может отапливаться либо путем непосредственного сжигания дров в печке (при этом выделяется количество тепла Q₀), либо с помощью холодильной машины, которая работает по обратимому циклу Карно и приводится в действие тепловой машиной, потребляющей то же количество дров, что и печка, и работающей (также по циклу Карно) между температурами t₁ = 100 ˚C и t₂ = 10 ˚C. Во сколько раз количество тепла Q₁, передаваемое помещению холодильной машиной, больше величины Q₀? В помещении поддерживается температура t₀ = 20 ˚C. Температура наружного воздуха равна t₂ (= 10 ˚C).

Ответ. Q₁/Q₀ = (T₁ – T₂)T₀/(T₀ – T₂)/T₁ ≈ 7,1.


№ 1.41, 1.42.

4. Энтропия системы. Второе начало термодинамики. (4 часа)
   

Задачи: № 1.43—1.45, 1.47, 1.51, 1.52.

5. Термодинамические функции. Уравнения Гиббса – Гельмгольца. (3 часа)
   

Задачи: № 1.53, 1.54, 1.57—1.59.

6. Термодинамические коэффициенты. Процесс Джоуля – Томсона. (4 часа)
   

Задачи: № 1.64, 1.70, 1.65, 1.66, 1.68.


Рассмотреть процесс Джоуля – Томсона. Показать, что энтальпия в этом процессе сохраняется. Доказать, что данный процесс неравновесный. Найти коэффициент Джоуля – Томсона, считая известными термическое уравнение состояния и теплоемкость при постоянном давлении.


№ 1.62, 1.63.

7. Термодинамика различных систем. (5 часов)
   

Задачи: № 1.77, 1.79, 1.81, 1.84, 1.86, 1.88, 4.19.


Считая известным термическое уравнение состояния фотонного газа и, что плотность его энергии зависит только от температуры, найти вид этой зависимости.

8. Химический потенциал. Равновесие фаз. (4 часа)
   

Задачи: № 1.99—1.101, 1.103, 1.108, 1.109.

9. Поверхностное натяжение. (2 часа)
   

Задачи: № 1.113, 1.116, 1.117, 1.121—1.123.


Часть 2. Молекулярная физика

10. Элементы теории вероятности. (1 час)
    

Задачи: № 2.1, 2.2, 2.4.

11. Распределение Максвелла по скоростям и по энергиям. Средние значения скорости и энергии молекул. Доля молекул, скорости которых больше заданной. (3 часа)
    

Задачи: № 2.6—2.8, 2.10, 2.13.


Построить графики функций распределения молекул компоненте скорости v_x и по абсолютной величине скорости.

12. Распределение молекул в потоке. Средняя скорость потока частиц. Силовое воздействие на экран молекулярного потока. (4 часа)
    

Задачи: № 2.15, 2.18—2.20, 2.24, 2.28, 2.29.

13. Распределение Больцмана. (4 часа)
    

Задачи:

Найти распределение газа в “толстой” изотермической атмосфере планеты. Исследовать предельный случай тонкой атмосферы.


№ 2.36, 2.40, 2.43, 2.44, 2.48.

14. Теплоемкость одноатомного и двухатомного газов в классическом приближении. Квантование гармонического осциллятора и жесткого ротатора; их энергии и теплоемкости. (6 часов)
    

Задачи: № 2.53, 2.55, 2.61, 2.63, 2.64, 2.67, 2.69, 2.70.


Вычислить среднюю энергию и молярную теплоемкость линейного гармонического осциллятора.

15. Электрические и магнитные свойства газов. (2 часа)
    

Задачи: № 2.74—2.76.


Часть 3. Физическая кинетика

16. Столкновение молекул. Длина свободного пробега. (3 часа)
    

Задачи: № 3.2, 3.3, 3.5.

17. Явления переноса в плотном газе: диффузия, теплопроводность, вязкость. (4 часа)
    

Задачи: № 3.8, 3.12, 3.13, 3.15, 3.16, 3.18, 3.22.

18. Явления переноса в ультраразреженном газе. (5 часов)
    

Задачи: № 3.25, 3.26, 3.28, 3.34—3.36, 3.38.


5. Образовательные технологии


Всюду, где это допускается уровнем знаний и подготовки студентов, материал лекционного курса увязывается с современными исследованиями. Там, где есть возможность достаточно просто провести аналогии или сопоставления со статистической механикой или квантовой механикой, это делается.


В термодинамике при изучении второго начала рассматриваются различные термодинамические циклы, в том числе те, которые являются идеализированными циклами для работы двигателей внутреннего сгорания (карбюраторных и дизельных), на что мы обращаем внимание.


При рассмотрении холодильных машин мы обращаем внимание на то, что они могут использоваться как тепловые насосы, являющиеся достаточно эффективными и экономичными обогревателями.


Рассказывая об электронной проводимости, мы увязываем этот материал с работой радиоламп и ламп дневного света.


Все семинарские занятия проводятся в интерактивной форме. Помимо семинаров, существует система заданий: каждый студент должен самостоятельно решить примерно 15 задач. Задание сдается в форме беседы с преподавателем в специально отведенное время (прием заданий).


6. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов


Домашние задания по курсу «Термодинамика и молекулярная физика»

Замечания

Оценка на экзамене по курсу «Термодинамика и молекулярная физика» выставляется после устного ответа с учетом решения экзаменационной задачи и предварительной отметки:

• оценки, выставляемой преподавателем за работу в семестре с учетом своевременной сдачи заданий, активности на семинарах и результатов двух контрольных работ и коллоквиума.
  

При проверке задач на всех этапах существенными будут следующие факторы:

• понимание физической сущности задач, области применимости решения, контроль получения решения по размерности, с помощью предельных или частных случаев, где найти решение особенно просто;
  
• рациональное использование математического аппарата, нахождение наилучшего из возможных путей к решению с указанием вариантов решения;
  
• получение как точного результата, так и, в необходимом случае, оценки;
  

умение довести решение до конца, грамотно и разумно использовать системы единиц.


Задание № 1

(сдать до 6 марта)


1. Теплоизолированный сосуд разделен перегородкой на две части объемом V₁ и V₂. В объеме V₁ находится идеальный газ при температуре T₀, имеющий показатель адиабаты γ. В объеме V₂ вакуум. В перегородке образовалось малое по сравнению с размерами сосуда (но большое по сравнению с длиной свободного пробега) отверстие. В результате газ занял весь объем сосуда. Определить температуры T₁ и T₂ газа в объемах V₁ и V₂ сразу после выравнивания давления. Перегородкатепло не проводит.

2. Идеальный газ сжимается под поршнем в цилиндре так, что уходящее в окружающую среду тепло равно изменению внутренней энергии газа. Определить работу, затраченную на сжатие моля газа при изменении объема в два раза. Чему равна теплоемкость в этом процессе? Начальная температура газа T₀.

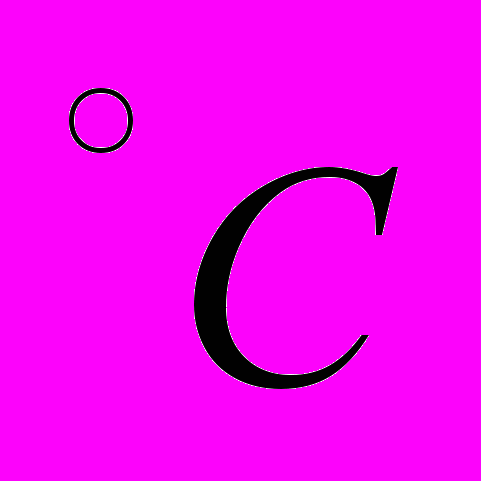3. Один моль H₂O с температурой 25охлаждается до 0и замерзает. Все тепло, полученное охлаждающей машиной, работающей с максимальной теоретически допустимой эффективностью, передается другому молю H₂O при 25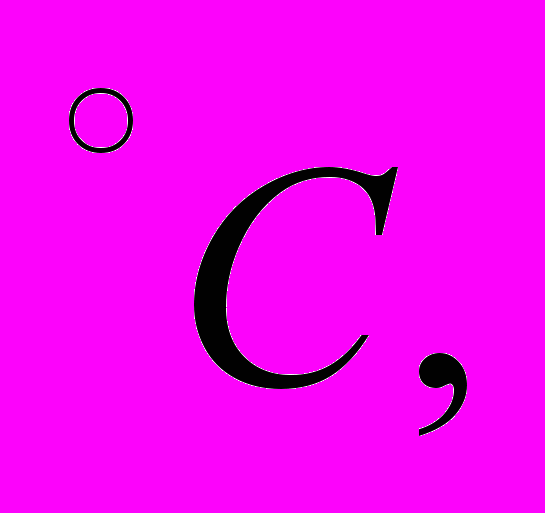в результате чего его температура повышается до 100 Сколько молей H₂O переходит в пар при 100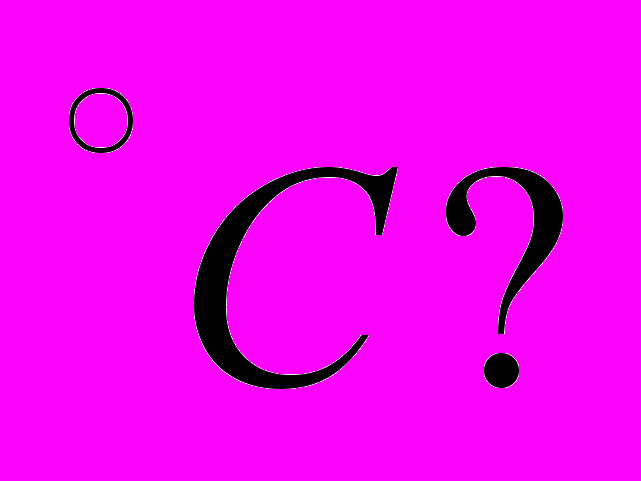Теплота испарения при 100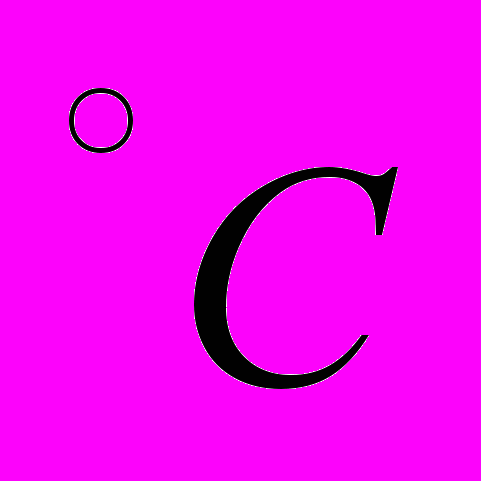равна 9730 кал/моль. Теплота плавления льда при 0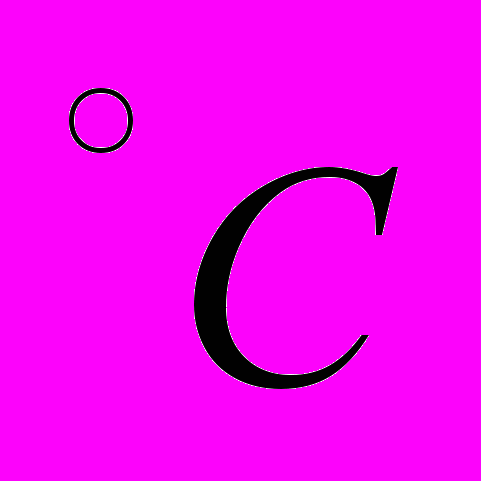равна 1438 кал/моль.

4. Идея динамического отопления, высказанная В. Томсоном (1852 г.), заключается в следующем. Тепловой двигатель, в топке которого сжигается уголь, приводит в действие холодильную машину. Холодильная машина отнимает теплоту от природного резервуара воды (например, от грунтовой воды) и отдает ее воде в отопительной системе. Одновременно вода в отопительной системе служит холодильником теплового двигателя. Определить теоретическое количество тепла, которое получает отапливаемое помещение от сжигания 1 кг каменного угля. Удельная теплота сгорания угля q = 8000 ккал/кг, температура в котле паровой машины t₁ = 210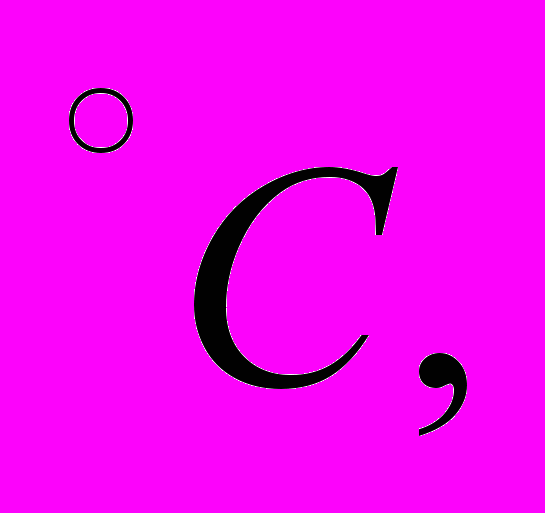температура воды в отопительной системе t₂ = 60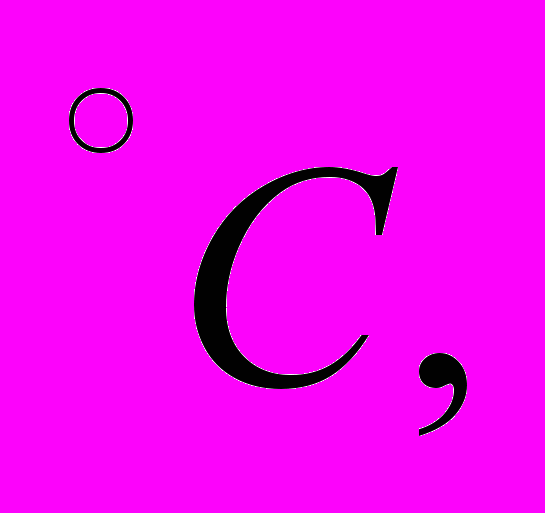а грунтовой воды t₃ = 15

5. Теплоизолированный цилиндрический сосуд разделен поршнем пренебрежимо малой массы на две равные части. По одну сторону поршня находится идеальный газ с массой , молекулярным весом μ и молярными теплоемкостями и 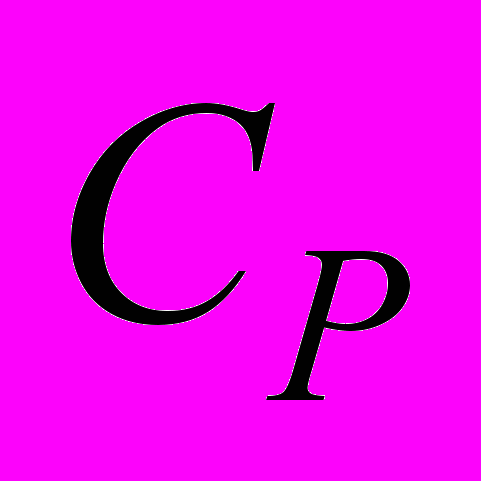_, не зависящими от температуры, а по другую сторону поршня создан высокий вакуум. Начальная температура и давление газа T₀ и P₀. Поршень отпускают, и он, свободно двигаясь, дает возможность газу заполнить весь объем цилиндра. После этого, постепенно увеличивая давление на поршень, медленно доводят объем газа до первоначальной величины. Найти изменение внутренней энергии и энтропии газа при таком процессе.

Задание № 2

(сдать до 31 марта)


6. В объеме V находятся в равновесии один моль идеального газа с постоянной теплоемкостью и фотонный газ. Температура этой системы T. Найти теплоемкость системы при постоянном давлении.

7. Серебряная проволока диаметром d = 1 мм адиабатически нагружается при комнатной температуре силой F = 10 Н. Полагая, что удельная теплоемкость C = 234 Дж/(К × кг), плотность r = 10 г/см³, а температурный коэффициент линейного расширения a = 1,9 ×10^– 5 К^–1, определить изменение температуры проволоки.

8. Уравнение состояния сверхплотного вещества звезд типа белых карликов P = a · n^5/3 + b · T² · n^1/3, где a и b – постоянные, n – число молей в единице объема, а теплоемкость C_V моля обращается в нуль при n → ∞. Найти теплоемкость, энтропию, внутреннюю энергию, свободную энергию моля вещества.

9. Определить точку кипения воды на вершине холма высотой 300 м над уровнем моря. Изменением температуры с высотой пренебречь. Удельная теплота парообразования при нормальных условиях равна 540 кал/г. Пар подчиняется уравнению состояния идеального газа.

10. Теплота плавления льда при 0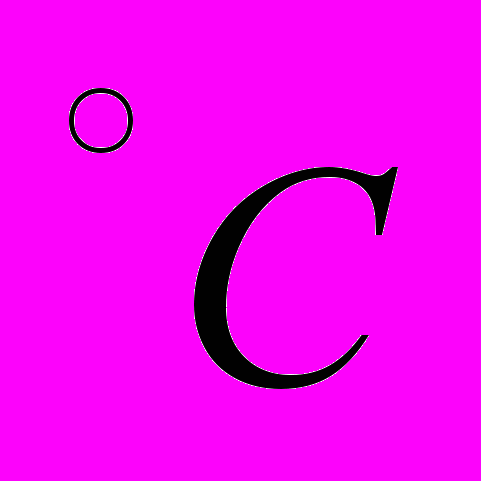и давлении 1 атм равна 80 кал/г, а отношение удельного объема воды к удельному объему льда равно 1:1,091. Давление насыщенного пара и теплоты парообразования при 0 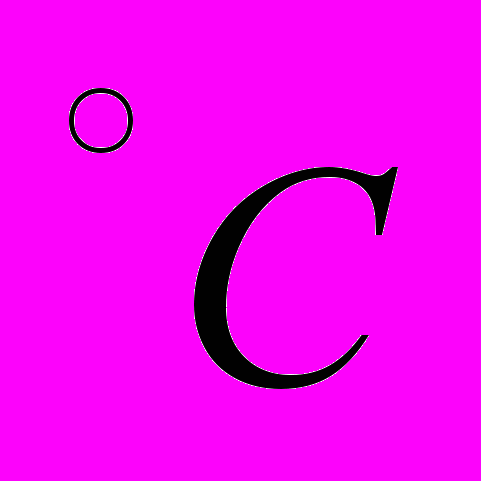составляет 4,58 мм рт. ст. и 600 кал/г. По приведенным данным оценить температуру тройной точки.

11. В цилиндре с поршнем на высоте H от дна установлена перегородка. Между перегородкой и поршнем находится жидкость массы M с очень тонким слоем насыщенного пара при температуре T. Ниже перегородки вакуум. Система полностью теплоизолирована. После того как через отверстие в перегородке жидкость сливается вниз, поршень поднимается на высоту h. Определить массу образовавшегося насыщенного пара, если удельная теплота парообразования жидкости λ, ее молярная масса μ, ускорение свободного падения g. Пар считать идеальным газом.

12. Капля жидкости находится в равновесии с паром при давлении P₁, которое из–за поверхностного натяжения в капле больше давления P₂ насыщенного пара над плоской поверхностью при той же температуре. Найти критический (равновесный) радиус капли в предположении |P₁ – P₂| << P₂. Известны T – температура системы, s – коэффициент поверхностного натяжения, m – молярная масса вещества, r – плотность жидкости. Пар считать идеальным газом и пренебречь молярным объемом жидкости по сравнению с молярным объемом пара.


Задание № 3

(сдать до 30 апреля)


13. Пленки некоторых нерастворимых органических кислот и спиртов можно моделировать идеальным двумерным газом. Считая, что такой идеальный газ находится в неравновесном состоянии, в котором все молекулы имеют одинаковые по модулю скорости v и изотропно распределены по направлениям движения в плоскости пленки, найти распределение для проекций скоростей на некоторую ось в плоскости пленки. С его помощью рассчитать давление газа и число ударов молекул о единичный отрезок границы пленки. Концентрация газа n, масса молекулы m.

14. В эксперименте с молекулярным пучком ртути получена следующая зависимость числа частиц Δ N, попавших на экран за постоянное время t >> 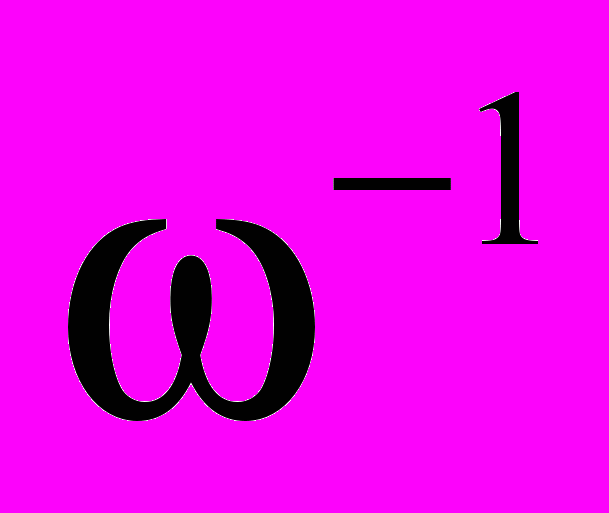, от скорости (определяемой как v = ω l/α):

v м/с = 150  200  250  300  350  400  450 500 550 600  650 700.

ΔN 10^-9 = 61  195  415  664  856  915  835 663 417 287  155 70.

П
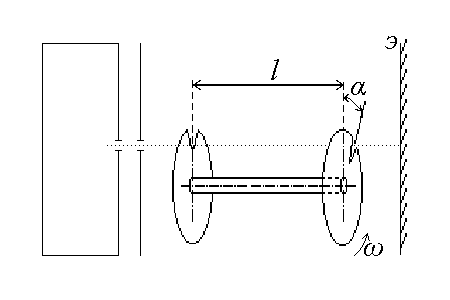
остроить график распределения молекул ртути по скоростям в печке. Какова приблизительно температура паров ртути в печке? В процессе измерений ω = const, l = const. Обратите внимание на то, что интервал скоростей молекул, проходящих через вертушку, не остается постоянным.

15. На расстоянии l от малого отверстия площадью S, через которое происходит молекулярное истечение (эффузия) газа, расположен экран. Найти распределение давления по экрану, создаваемое пучком. Температура газа в сосуде T, давление P₀, m – масса молекулы.

16. Из сосуда объемом V газ истекает в вакуум через малые отверстия общей площадью S. Как во времени нужно подводить тепло к газу, чтобы его температура оставалась неизменной? Как будет изменяться температура газа в адиабатически изолированном сосуде? Начальная плотность газа n₀.

17. Два полых цилиндра с поперечными сечениями S и 2S и одинаковой высоты h соединены встык и образуют замкнутый сосуд. В его объем закачан идеальный газ при температуре T. Найти относительное изменение давления в нижней части сосуда при его переворачивании, возникающее при учете неравномерности распределения газа по высоте. Оценить его для условий Земли.

18. В центрифуге радиуса R , вращающейся с угловой скоростью ω, находится смесь двух газов с молекулярными весами μ₁ и μ₂ и количеством молекул N₁ и N₂. Найти отношение плотностей газов у внешней стенки и на оси центрифуги. Сделать оценки для смесей H₂ ¾ D₂ и U²³⁵ ¾ U²³⁸; R =10 см, ω = 10⁴ .


Задание № 4

(сдать до 21 мая)


19. Рассчитать распределение по скоростям точечных частиц после упругого столкновения с бесконечно тяжелой сферой. До столкновения все частицы имеют одинаковую скорость

20. Молекулы реального газа взаимодействуют друг с другом по закону u = – а/r ⁶ при r  > d, где d – эффективный диаметр молекулы. Найти зависимость сечения соударений s от температуры (поправка Сезерленда), считая соударением соприкосновение частиц.

21. Оценить время испарения воды из трубки длиной 10 см, запаянной с одного конца. Температура комнатная. Первоначально вода заполняла трубку наполовину. Относительная влажность воздуха 50 %, давление насыщенных паров 27 мм рт. ст. Длина свободного пробега молекул в системе воздух–пар порядка 10^–5 см. Пар у поверхности воды считать насыщенным, капиллярными явлениями пренебречь.

22. Определить, на какой угол φ повернется диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см вращается второй такой же диск с угловой скоростью ω = 50 с ^– 1. Радиусы дисков R = 10 см, модуль кручения нити f  = 100 дин·см/рад. Между дисками находится аргон (газокинетический диаметр атома 3,6 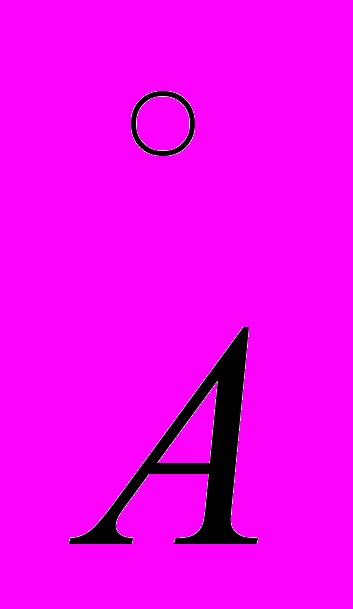). Рассмотреть случаи различных давлений и построить график зависимости угла поворота φ от давления P.

23. Для измерения теплопроводности газа им заполняется пространство между двумя длинными коаксиальными цилиндрами радиуса r₁ и r₂. Заполнение производится при невысоком давлении (~ 10 мм рт. ст.), чтобы исключить конвекцию. Внутренний цилиндр нагревается источником тепла с удельной мощностью Q, установившиеся температуры цилиндров t₁ и t₂ измеряются. Рассчитать коэффициент теплопроводности и газокинетический диаметр молекулы для азота, если r₁ = 0,5 см, r₂ = 2 см, Q = 0,038 вт/см, t₁ = 93 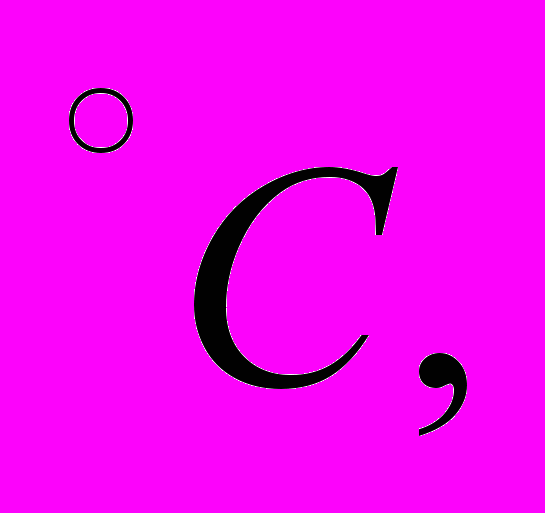t₂ = 0

24. В сферическом реакторе радиуса R, заполненном газообразной смесью реагентов, идет химическая реакция. Тепловой эффект реакции в расчете на единичный объем равен Q. Какой поток тепла следует снимать с поверхности реактора, если ее температура поддерживается равной T₀? Найти распределение температуры в реакторе. Учесть зависимость коэффициента теплопроводности от температуры.


1-я контрольная работа по термодинамике и молекулярной физике


2-я контрольная работа по термодинамике и молекулярной физике

1. 
   ..
   

7. Учебно-методическое и информационное обеспечение дисциплины


а) основная литература:

1. 
   Докторов А.Б., Бурштейн А.И. Термодинамика и молекулярная физика. Курс лекций. Новосибирск: РИЦ НГУ, 2010.
   
2. Замураев В.П., Калинина А.П. Термодинамика и молекулярная физика // Новосибирск. Изд. НГУ. 2007.
   
3. Замураев В.П., Калинина А.П. Задачи по термодинамике и молекулярной физике. Новосибирск: Изд. НГУ, 2003.
   
4. Замураев В. П., Калинина А. П. Задачи с решениями по термодинамике и молекулярной физике. Новосибирск: Изд. НГУ, 2008.
   

б) дополнительная литература:

5. Зоммерфельд А. Термодинамика и молекулярная физика. М.: Наука, 1955.
   
6. Бурштейн А.И. Молекулярная физика. Новосибирск: Наука, 1986.
   
7. Румер Ю.Б., Рывкин М.Ш. Термодинамика, статистическая физика и кинетика: Учебное пособие для вузов. М.: Наука, 1972.
   
8. Сивухин Д.В. Общий курс физики. М.: Наука, 1979.
   
9. Кубо Р. Статистическая механика. М.: Мир, 1967.
   
10. Киттель Ч. Элементарная статистическая физика. М.: Иностр. лит., 1960.
    

8. Материально-техническое обеспечение дисциплины


Требуется большая аудитория, большая доска и хороший мел.


Рецензент (ы) _________________________


Программа одобрена на заседании ____________________________________________

(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)

от ___________ года.