Вторая тема. Лекция. 5
| Вид материала | Лекция |
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- 1 11 Тема 2 12 тема 3 13 Тема 4 14 Тема 5 15 Тема 6 17 Тема 7 20 Тема 8 22 Тема, 284.17kb.
- Коррекции мозговой деятельности, т е., в частности профилактика инсульта и вторая тема, 213.38kb.
- Курс: История политических и правовых учений Тема Политические и правовые идеи в государствах, 742.92kb.
- Лекция №25 Тема: золотой век Екатерины, 275.85kb.
- Лекции оглавление, 3095.45kb.
- Лекции оглавление, 3056.94kb.
- Лекция «Исследование качественных и количественных характеристик транскриптома», 240.64kb.
- Т. А. доцент кафедры Индустрии моды исмд владивостокский государственный университет, 284.47kb.
- Тема Лекция, 34.13kb.
Вторая тема.
ЛЕКЦИЯ.5
Типы физических исследовательских программ, имевших место в ходе развития естествознания.
Выделяют 4 исследовательских программы в истории развития науки:
- механистическая; 2.релятивисткая; 3. квантово – полевая; 4.единая теория поля.
Механистическая исследовательская программа.
Основой этой программы является механика Ньютона. Базой, на которой построена Ньютоновская механика, выступают атомы (корпускулы) и пустота, а так же абсолютное время и абсолютное пространство.
Ньютон ввел математическую символику для описания фундаментальных понятий физики и создал фундаментальную теорию – механику материальной точки. (Фундаментальный от слова фундамент. Это значит основной, базовый).
Понятие материальной точки ввел в физику Эйлер. Он же продолжает деятельность Ньютона и рассматривает большое число задач движения свободной точки ( в пустоте, в среде с сопротивлением, движение системы связанных точек). Это приводит к созданию фундаментальной теории твердого тела.
Далее, Лагранж находит общий аналитический метод решения различных механических задач появляется фундаментальная теория – аналитическая механика. В дальнейшем, развиваясь, она приводит к формированию таких фундаментальных теорий как механика небесных тел, гидродинамика, аэродинамика, механика твердого тела, теория упругости и т.д.
Однако, возникли теории, которые не могли быть интерпретированы в рамках механистической теории – это термодинамика и электродинамика. Это привело к возникновению новой физической программы.
Релятивисткая исследовательская программа
Своим возникновением она обязана попытке построения простой теории, свободной от противоречий электродинамики движущихся тел. Это построение было успешно осуществлено А. Эйнштейном в специальной теории относительности (СТО). Теория относительности базируется на новом взгляде на природу пространства и времени
На смену трехмерного пространства Евклида в СТО приходит четырехмерное псевдоевклидово пространство Минковского, в котором время по своему месту в физических уравнениях эквивалентно трем пространственным координатам. В СТО пространство и время не могут быть рассмотрены независимо друг от друга, а речь идет о четырехмерном пространстве-времени. Это позволило создать математический аппарат для обобщенного описания специальной теории относительности. Все фундаментальные физические теории в последствии были переформулированы в четырехмерном формализме.
Стремление распространить принцип относительности на любые типы движения приводит Эйнштейна к созданию общей теории относительности. ОТО лежит в основе космологии – науки о происхождении и эволюции вселенной. На сегодняшний день она рассматривается как классическая теория гравитации.
Следующая, квантово – полевая исследовательская программа.
Гениальная идея высказанная Максом Планком, о дискретном (прерывистом) характере излучения, о корпускулярной теории света привела к возникновения квантовой механики. Квантовая механика – фундаментальная теория, позволяющая описывать поведение объектов в микромире. Основополагающей в квантовой механике является идея о том, что корпускулярно-волновая двойственность свойств, установленная для света, имеет универсальный характер и распространяется на все объекты микромира. Синтез релятивисткой исследовательской программы и квантовой теории привел к созданию квантовой электродинамики – фундаментальной теории, описывающей любые взаимодействия микрочастиц – электромагнитные, сильные, слабые.
И последняя: единая теория поля.
На современном этапе предпринята попытка построения единой теории поля – новой физической исследовательской программы, в которой удалось бы объединить известные четыре типа физических взаимодействий – гравитационное, электромагнитное, сильное и слабое в единое суперсимметричное поле.
В рамках данной программы предполагается рассмотрение эволюции Вселенной из этого суперсимметричного состояния, в котором материя представлена только физическим вакуумом. Спонтанное нарушение симметрии вакуума в процессе расширения Вселенной и приводит к многообразию физического мира.
ЛЕКЦИЯ 6
Макромир. Концепции классического естествознания. Механистическая исследовательская программа).
Физика – наука о природе , изучающая простейшие и вместе с тем наиболее общие свойства материального мира.
Формирование научных взглядов на строение материи относится к 16 веку, когда Галилеем была заложена основа первой в истории науки физической картины мира – механистической.
Ньютон, опираясь на труды Галилея, Декарта и Гюйгенса разработал строгую научную теорию механики, описывающую и движения небесных тел. Механика изучает движения тел и их деформации. Основной задачей механики является определение траектории движения тела, то есть установление строгой причинной зависимости координат (положение тела в пространстве) в зависимости от времени.
Существенными характеристиками ньютоновского мира было трехмерное евклидово пространство. Это пространство абсолютно постоянно и всегда пребывает в покое. Время представлялось как величина не зависящая ни от пространства, ни от материи. Движение рассматривалось, как перемещение в пространстве по непрерывным траекториям по законам механики. Траектория – это линия, по которой движется тело в пространстве.
В своих работах Ньютон отводил математике более значительную роль, чем это делали его предшественники. Таким образом, концепцией естествознания становится концепция математического обоснования явлений природы. Были написаны уравнения движения тела с помощью которых, зная начальные условия, можно получить полное описание движения тела. То есть, зная координату тела в начальный момент времени, его начальную скорость и время, в течение которого тело совершало движение, с помощью уравнений движения можно определить, где окажется тело через данный промежуток времени и какая скорость у него будет в этой конечной точке. С помощью уравнений движения можно определить скорость движения тела в каждой точке траектории движения тела. Или наоборот, с помощью уравнений движения можно определить траекторию движения тела.
Во времена Ньютона в основу строения вещества становится атом Демокрита, который рассматривается как экспериментально исследуемая частица. Атом рассматривается как первичный « кирпичик» вещества, который неделим, неизменен и вечен. Атомистическая (корпускулярная) концепция содержит в себе представление о дискретной структуре вещества, т. е. Вещество состоит из атомов и пустоты между ними. Наличие пустоты обязательное условие для перемещения атомов в пространстве. (Дискретный значит прерывистый).
Корпускула в переводе на русский – частица.
Основания механики Ньютона составляют три закона и два положения относительно пространства и времени.
Три закона Ньютона:
- Тело движется прямолинейно равномерно, если на него не действуют никакие силы или действие сил со стороны других тел уравновешенны.
- Величина силы, действующей на тело прямо пропорциональна ускорению этого тела.
F = m a
m – коэффициент пропорциональности – масса характеризует свойства конкретного тела – мера инертности.
Два тела действуют друг на друга с силами F1 и F2 , которые численно равны и направлены в противоположные стороны. Или действие равно противодействию.
F1 = - F2
Сила – это векторная величина, мера действия одного тела на другое. Ньютон определял силу следующим образом : «Приложенная сила есть действие, производимое на тело для изменения его состояния покоя или равномерного прямолинейного движения».
Под массой Ньютон понимал количество материи. Однако, с развитием науки представление о физических свойствах материи изменяется. С точки зрения современной науки масса – это величина, определяющая инертные свойства тел. Масса – мера инертности тела. Т.е. масса определяет, какое ускорение приобретет тело, если мы на него подействуем волне определенной, известной по величине силой. Инертность – это свойство тела изменять скорость своего движения при воздействии на это тело силой.
Например, если столкнуться два тела разной массы, то после соударения одно из тел приобретет большее ускорение, другое – меньшее. То тело, которое приобретет меньшее ускорение, называют более инертным и его масса больше.
Два положения, составляющие основу механики:
По Ньютону, истинное время абсолютно, ни от чего не зависит, протекает равномерно и направленно в одну сторону.
Пространство тоже однородно, везде является одним и тем же ( изотропно – все направления в нем равноправны).
Законы Ньютона выполняются не во всех, а только в инерциальных системах отсчета. Система отсчета – это точка в пространстве и связанная с ней система координат, относительно которых рассматривается движение интересующего нас тела. Задачей механики является вычисление скорости, ускорения или координаты рассматриваемого тела в тот или иной момент времени. Определить эти величины мы можем только относительно других тел. И если какое-либо тело неподвижно или движется по прямой и без ускорения, то с этим телом мы можем связать инерциальную систему координат и отсчитывать относительно этого тела скорость или ускорение или определять координату изучаемого тела.
Инерциальными системами отсчета называются все системы отсчета, которые движутся прямолинейно равномерно или находятся в покое. То есть, которые не подвергаются не уравновешивающим друг друга силам.
ПРИМЕР
Примером инерциальной системы отсчета будет вагон, движущийся равномерно прямолинейно, в котором сидит наблюдатель. Или наблюдатель, стоящий на платформе мимо которой движущийся прямолинейно равномерно вагон. Как только, под действием силы тяги локомотива вагон начинает тормозить или ускоряться, вагон перестает быть инерциальной системой отсчета. Это замечает наблюдатель, который стоит на платформе. А наблюдатель в вагоне чувствует, как он начинает отклоняться под действием ему невидимой силы.
Все происходящее в вагоне, объясняется появлением новой силы – силы инерции. Причем в полном соответствии с законами Ньютона.
Принцип относительности Галилиея.
Галилей установил, что в инерциальной системе отсчета никакими механическими опытами невозможно установить движется система или покоится. Или по другому: во всех инерциальных системах отсчета все физические явления происходят одинаково.
Таково содержание принципа относительности Галилея.
В механике Ньютона учитываются два фактора
- Зависимость координат и скорости от выбранной системы координат.
- Одинаковость (инвариантность) законов механики во всех инерциальных системах координат.
Преобразования Галилея показывает наглядно, как работают эти два положения.
Преобразования Галилея – это переход из одной системы координат в другую. При таком переходе одни физические величины меняются, другие остаются постоянными. Рассмотрим это на примере, который нам наглядно покажет справедливость двух факторов, указанных выше.
Рассмотрим две инерциальные системы координат L и L‛ , при этом L‛ движется относительно L вдоль оси х с постоянной скоростью U
Например: представим себе, что L – это неподвижный наблюдатель на платформе, L' – это наблюдатель, который идет по платформе с постоянной скоростью U – относительно платформы. Пусть точка А – это поезд, который движется вдоль платформы. Обозначим буквой t – время. В начальный момент времени, когда мы начинаем свой мысленный эксперимент, t = 0, координата поезда (или точки А) относительно системы координат L (или неподвижного наблюдателя) равна нулю: XA =0, Координата поезда относительно подвижного наблюдателя тоже равна нулю: X'A = 0, И, наконец, координата самого подвижного наблюдателя L' относительно наблюдателя, спокойно стоящего на платформе тоже в начальный момент равна нулю: XL' = 0. (см. рис 1) XA – координата поезда относительно неподвижной системы координат L (неподвижный наблюдатель на платформе), X'A -координата поезда относительно подвижной системы координат L' (наблюдатель, который прогуливается по платформе с постоянной скоростью U). XL' – координата подвижной системы (прогуливающегося наблюдателя) относительно неподвижно стоящего на платформе наблюдателя.
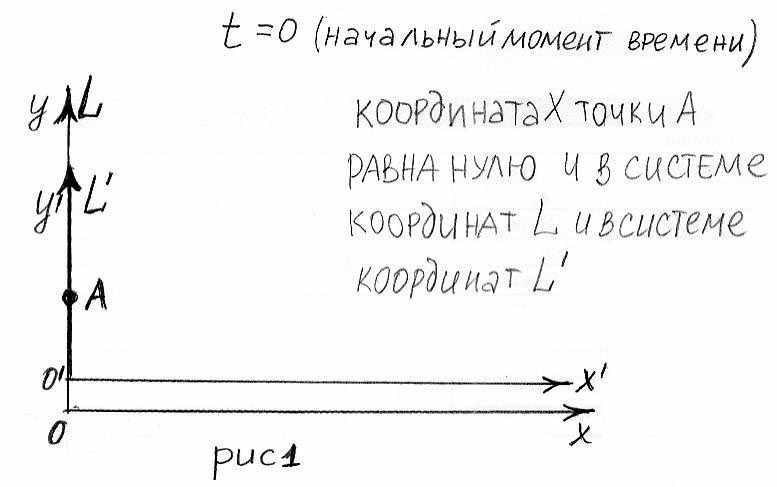
Через какое то время – t – наблюдатель L' отошел от наблюдателя L на расстояние l которое вычисляется по формуле: l=U·t (см рис 2.) Точка А (поезд) за это же время, как видно из рисунка, относительно неподвижного наблюдателя переместится на расстояние – X, а относительно подвижного наблюдателя (подвижной системы координат) на расстояние X' и тогда очевидно, что: X=X'+U·t. Из этой формулы мы видим, что в одной системе координат координата точки А (расстояние которое прошел поезд) не равна координате этой же точки в другой системе координат. То есть X≠X'.

Иными словами, обращаясь к нашим наблюдателям и поездам, относительно неподвижного наблюдателя поезд прошел большее расстояние, чем относительно подвижного (если конечно наблюдатель двигался в ту же сторону, что и поезд). – Первое положение подтвердилось – координата точки зависит от выбранной системы координат.
Теперь продифференцируем левую и правую части этого уравнения X=X'+U·t. Вы помните, что производная координаты по времени, есть скорость движения точки (dX/dt = V). В результате получим: dX/dt = dX'/dt + dU·t/dt или V = V' + U где V - скорость поезда (точки) относительно стоящего на платформе наблюдателя (неподвижной системы координат), а V' – скорость поезда относительно идущего по платформе наблюдателя (подвижной системы координат).
Итак, мы видим, что скорость тоже зависит от выбранной системы координат. Первое положение полностью подтвердилось. (Напомним первое положение: зависимость координаты и скорости от выбранной системы координат).
Теперь займемся доказательством справедливости второго положения:
Продифференцируем еще раз последнее уравнение по времени. Из школьного курса вы знаете, что производная скорости по времени – есть ускорение (dV/dt = a).
dV/dt = dV'/dt + dU/dt . dU/dt=0 т.к. U- величина постоянная. (Из школьного курса математики вы должны знать, что производная постоянной величины равна нулю). В результате дифференцирования мы получаем: a=a' Видим, что ускорение не меняется при переходе из одной системы координат к другой. Ускорение поезда одинаково и для неподвижного наблюдателя и для прогуливающегося…При переходе из одной системы координат к другой постоянной остается и сила F . В нашем случае это сила тяги локомотива. Поэтому второй закон Ньютона F=m·a- тоже не меняется при переходе от неподвижной системе координат к подвижной. Т.е. во всех инерциальных системах координат законы Ньютона (или законы движения тел) выполняются. Уравнение F = m a остается неизменным (инвариантным) при преобразованиях Галилея.
Так как при переходе из одной системы координат к другой F и m остаются постоянными и, ускорение тоже не зависит от системы координат, то и тот факт, что ускорение и сила остаются ивариантными относительно обеих систем отсчета, позволяет сделать выводы, о том, что законы механики одинаковы во всех инерциальных системах отсчета. Это и составляет суть принципа относительности. Второе положение подтвердилось.
Оптика в механистической картине мира.
Разрабатывая оптику, Ньютон, следуя логике своей теории, считал свет потоком материальных частиц – корпускул. В корпускулярной теории света утверждалось, что светящиеся тела испускают мельчайшие частицы, которые движутся в согласии с законами механики и вызывают ощущение света, попадая в глаза. На базе этой теории Ньютон дал объяснение законов преломления и отражения света.
Основной задачей классической механики является определение параметров, характеризующих состояния механической системы и ее эволюцию во времени. Этими параметрами являются совокупность всех координат и скоростей
(импульсов) материальных точек, составляющих эту систему.
Итак, основная задача динамики состоит в том, чтобы зная начальные состояния системы и законы движения ( законы Ньютона), однозначно определить состояние системы во все последующие моменты времени, то есть однозначно определить траектории движения материальных объектов.. Траектории движения получаются при интегрировании дифференциальных уравнений движения и дают полное описание движения объектов в прошлом, будущем и настоящем.
