Методические указания ф со пгу 18. 2/05 Министерство образования и науки

Вид материала

Методические указания

Содержание Область применения 75% от общего числа применяемых оптимизационных методов приходится на ЛП Пример задачи ЛП Постановка задачи Графическое решение задачи линейного программирования Моделирование непрерывных случайных величин. Моделирования дискретных случайных величин. М/М/1 имеют следующий вид: вероятность того, что обслуживающий прибор свободен, Р

Подобный материал:

• Методические указания Форма ф со пгу 18. 2/05 Министерство образования и науки Республики, 98.43kb.
• Методические указания ф со пгу 18. 2/05 Министерство науки и образования Республики, 126.96kb.
• Методические указания Форма ф со пгу 18. 2/05 Министерство образования и науки Республики, 121.19kb.
• Методические указания ф со пгу 18. 2/05 Министерство науки и образования Республики, 268.47kb.
• Методические указания Форма ф со пгу 18. 2/06 Министерство образования и науки Республики, 317.33kb.
• Методические указания Форма ф со пгу 18. 2/08 Министерство образования и науки Республики, 347.35kb.
• Методические указания Форма ф со пгу 18. 2/05 Министерство образования и науки Республики, 907.44kb.
• Методические указания Форма ф со пгу 18. 2/05 Министерство образования и науки Республики, 152.27kb.
• Методические указания Форма ф со пгу 18. 2/07 Министерство образования и науки Республики, 178.18kb.
• Методические указания Форма ф со пгу 18. 2/07 Министерство образования и науки Республики, 249.4kb.

Область применения

Задачами линейного программирования (ЛП) называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств и для которых методы математического анализа оказываются непригодными. ЛП представляет собой наиболее часто используемый метод оптимизации. К задачам, решаемым с помощью методов ЛП относятся, например, следующие:

• рациональное использование сырья и материалов;
  
• задачи оптимизации раскроя;
  
• оптимизации производственной программы предприятий;
  
• оптимального размещения и концентрации производства;
  
• на составление оптимального плана перевозок, работы транспорта;
  
• управления производственными запасами;
  
• и многие другие, принадлежащие сфере оптимального планирования.
  

Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на ЛП. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач ЛП и их многочисленных модификаций.

Пример задачи ЛП

Лесничество имеет 24 га свободной земли под паром и заинтересовано извлечь из нее доход. Оно может выращивать саженцы быстрорастущего гибрида новогодней ели, которые достигают спелости за один год, или бычков, отведя часть земли под пастбище. Деревья выращиваются и продаются в партиях по 1000 штук. Требуется 1.5 га для выращивания одной партии деревьев и 4 га для вскармливания одного бычка. Лесничество может потратить только 200 ч. в год на свое побочное производство. Практика показывает, что требуется 20 ч. для культивации, подрезания, вырубки и пакетирования одной партии деревьев. Для ухода за одним бычком также требуется 20 ч. Лесничество имеет возможность израсходовать на эти цели 6 тыс. руб. Годовые издержки на одну партию деревьев выливаются в 150 руб. и 1,2 тыс. руб. на одного бычка. Уже заключен контракт на поставку 2 бычков. По сложившимся ценам, одна новогодняя ель принесет чистый доход в 2,5 руб., один бычок - 5 тыс. руб.

Постановка задачи

1. В качестве показателя эффективности целесообразно взять доход за операцию (годовой чистый доход с земли в рублях).

2. В качестве управляемых переменных задачи следует взять:

x₁ - количество откармливаемых бычков в год;

x₂ - количество выращиваемых партий быстрорастущих новогодних елей по 1000 шт. каждая в год.

3. Целевая функция:

W=5000 x₁ + 2500 x₂ 

где

5000- чистый доход от одного бычка, руб.;

2500 - чистый доход от одной партии деревьев (1000 шт. по 2,5 руб.).

4. Ограничения:

4.1. По использованию земли, га:

4 x₁ + 1,5 x₂ <=24.

4.2. По бюджету, руб.:

1200 x₁ + 150 x₂<= 6000.

4.3. По трудовым ресурсам, ч:

20 x₁ + 20 x₂ <= 200.

4.4. Обязательства по контракту, шт.:

x₁ >= 2.

4.5. Областные ограничения:

x₁ >= 0, x₂ >= 0.

Графическое решение задачи линейного программирования

Задачи ЛП с двумя переменными поддаются решению графическим способом. Продемонстрируем данный способ на примере 1 "Оптимизация размещения побочного производства лесничества":

5000 x₁ + 2500 x₂ max,

4 x₁ + 1,5 x₂ <= 24;

1200 x₁ + 150 x₂ <= 6000;

20 x₁ + 20 x₂ <= 200;

x₁ >= 2;

x₁ >= 0; x₂ >= 0.

На первом шаге следует определить все возможные неотрицательные значения переменных x₁ и x₂, которые удовлетворяют ограничениям. С этой целью в декартовой системе координат (рис.1) наносим линии, соответствующие уравнениям прямых:

4 x₁ + 1,5 x₂ = 24;

1200 x₁ + 150 x₂ = 6000;

20 x₁ + 20 x₂ = 200;

x₁ = 2; x₂ = 0,

и
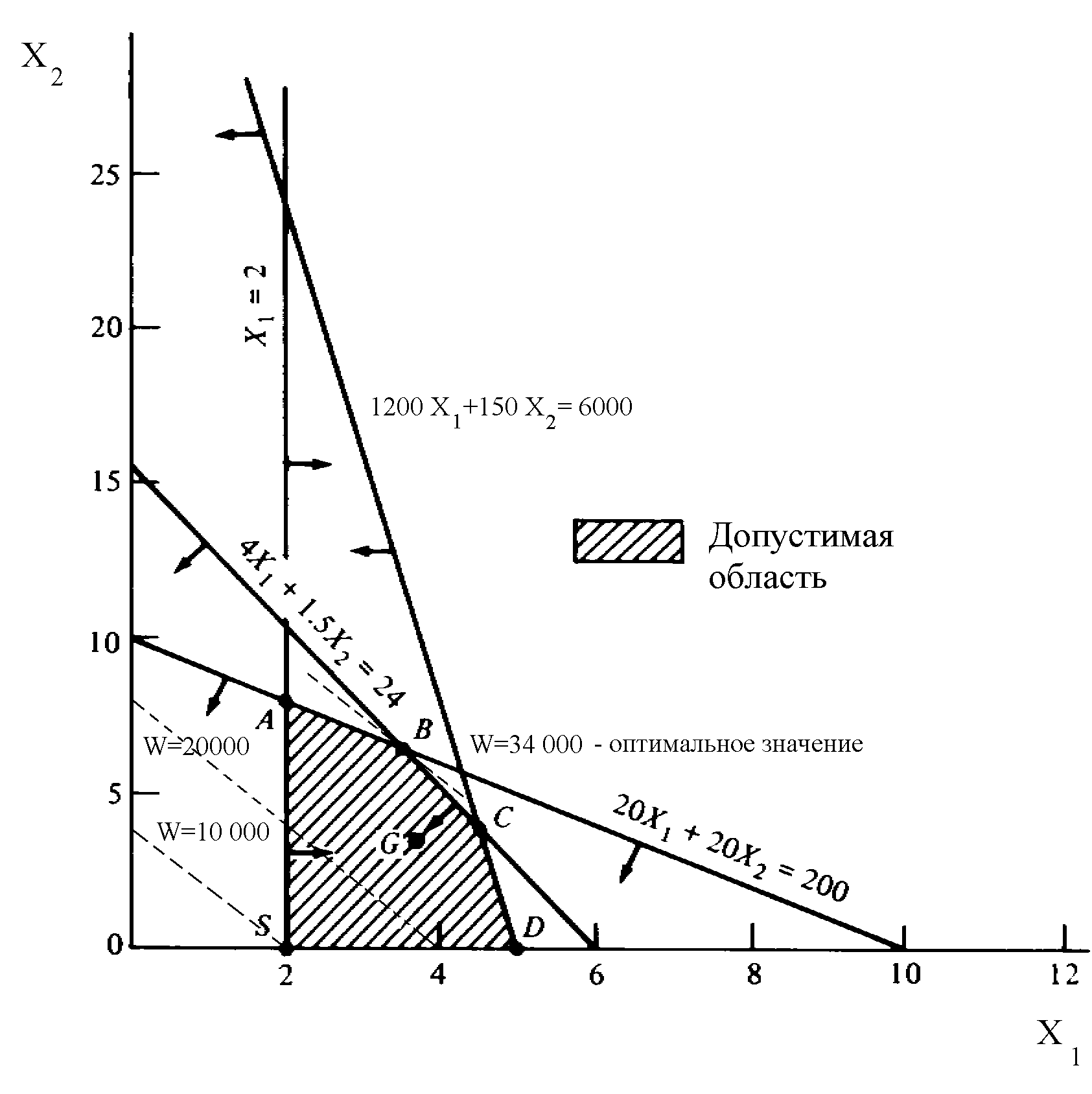
заштриховываем область, в точках которой выполняются все ограничения. Каждая такая точка называется допустимым решением, а множество всех допустимых решений называется допустимой областью. Очевидно, что решение задачи ЛП состоит в отыскании наилучшего решения в допустимой области, которое, в свою очередь, называется оптимальным. В рассматриваемом примере оптимальное решение представляет собой допустимое решение, максимизирующее функцию 5000 x₁ + 2500 x₂. Значение целевой функции, соответствующее оптимальному решению, называется оптимальным значением задачи ЛП. В нашем случае, для нахождения оптимального решения достаточно через любую из вершин допустимой области провести прямую целевой функции и, вслед за этим, путем параллельного переноса полученной прямой найти такие вершины, в которых происходит только касание с допустимой областью.


Максимальный доход в размере 34 тыс. руб. лесничество может извлечь придерживаясь следующей стратегии - выращивая 3,6 бычка и 6,4 партии новогодних елей. Однако окончательное решение должно быть представлено в целочисленной форме. Как правило, на практике полученные результаты округляют до ближайших целых, что может привести к достаточно грубым ошибкам. В разбираемом примере округление даст x₁=3 и x₂=6, что приводит к доходу в 30 тыс. руб. Однако достаточно удаленная от оптимального решения стратегия x₁=4 и x₂=5 приводит к более оптимистичному результату в 32,5 тыс. руб. Более того, как будет показано далее, еще более далекая точка x₁=3 и x₂=7 приводит к аналогичному результату. Поэтому расчеты необходимо продолжить с использованием методов целочисленного программирования, которые нами будут обсуждаться ниже.


Графический метод ввиду большой размерности реальных практических задач ЛП достаточно редко применяется, однако он позволяет ясно уяснить одно из основных свойств ЛП - если в задаче ЛП существует оптимальное решение, то по крайней мере одна из вершин допустимой области представляет собой оптимальное решение. Несмотря на то, что допустимая область задачи ЛП состоит из бесконечного числа точек, оптимальное решение всегда можно найти путем целенаправленного перебора конечного числа ее вершин. Рассматриваемый далее симплекс-метод решения задачи ЛП основывается на этом фундаментальном свойстве. Прежде чем перейти к непосредственному применению симплекс-метода, всякая практическая задача должна быть сведена к стандартной форме.

3. Моделирование непрерывных случайных величин. Классификация методов моделирования непрерывных случайных величин. Метод обратной функции. Метод исключения Дж.Неймана. Метод предельных теорем. Метод композиций. Моделирование специальных непрерывных распределений.
   

Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.

В теории систем массового обслуживания (в дальнейшем просто -CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.

Совокупность однотипных обслуживающих устройств называется обслуживающими устройствами. Такими системами могут быть телефонные станции, аэродромы, билетные кассы, ремонтные мастерские, склады и базы снабженческо-сбытовых организаций и т.д.

В теории СМО рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных процессов .

Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.

СМО классифицируются на разные группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дисциплины обслуживания требований.

По составу СМО бывают одноканальные(с одним обслуживающим устройством) и многоканальными (с большим числом обслуживающих устройств). Многоканальные системы могут состоять из обслуживающих устройств как одинаковой, так и разной производительности.

По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:

1) с неограниченным временем ожидания (с ожиданием),

2) с отказами;

3) смешанного типа.

В СМО с неограниченным временем ожидания очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.

В системах с отказами поступившее требование, застав все устройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.

В системах смешанного типа поступившее требование, застав все (устройства занятыми, становятся в очередь и ожидают обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установленное время, требование покидает систему.

В системах с определенной дисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в очередь.

Основными элементами СМО являются: входящий поток требований, очередь требований, обслуживающие устройства,(каналы)и выходящий поток требований.

Изучение СМО начинается с анализа входящего потока требований.

Входящий поток требований представляет собой совокупность требований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания.

В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также интервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными.

Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований и определяется следующим соотношением:

[pic]

где Т - среднее значение интервала между поступлением очередных требований.

Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона. Такой поток называется простейшим.

Простейший поток обладает такими важными свойствами:

1)Свойством стационарности, которое выражает неизменность

вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.

2)Отсутствия последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени.

Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.

3) Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).

При простейшем потоке требований распределение требований, поступающих в систему подчиняются закону распределения Пуассона:

вероятность [pic] того, что в обслуживающую систему за время t

поступит именно k требований:

[pic]

где[pic]. - среднее число требований, поступивших на обслуживание в единицу времени.

На практике условия простейшего потока не всегда строго выполняются.

4. Моделирования дискретных случайных величин. Основной метод моделирования дискретных случайных величин. Моделирование геометрического закона распределения. Моделирование закона распределения Пуассона.
   

С системами массового обслуживания (СМО) мы встречаемся повседневно. Любому из нас приходилось когда-то ждать обслуживания в очереди (например, в магазине, на авто заправке, в библиотеке, кафе и т. д.). Аналогичные ситуации возникают при потребности воспользоваться телефонной связью или выполнить свою программу на компьютере. Более того, любое производство можно представить как последовательность систем обслуживания. К типичным системам обслуживания относят также ремонтные и медицинские службы, транспортные системы, аэропорты, вокзалы и другие.

Особое значение приобрели такие системы при изучении процессов в информатике. Это, прежде всего, компьютерные системы, сети передачи информации, ОС, базы и банки данных. Системы обслуживания играют значительную роль в повседневной жизни. Опыт моделирования разных типов дискретных событийных систем свидетельствует о том, что приблизительно 80% этих моделей основаны на СМО.

Что же характеризует эти системы как СМО? Такие системы можно описать, если задать:

1) входящий поток требований или заявок, которые поступают на обслуживание;

2) дисциплину постановки в очередь и выбор из нее;

3) правило, по которому осуществляется обслуживание;

4) выходящий поток требований;

5) режимы работы.

Входящий поток. Для задания входящего потока требований необходимо описать моменты времени их поступления в систему (закон поступления) и количество требований, которое поступило одновременно. Закон поступления может быть детерминированный (например, одно требование поступает каждые 5 мин) или вероятностный (требования могут появляться с равной вероятностью в интервале 5::i:2 мин). В общем случае входящий поток требований описывается распределением вероятностей интервалов времени между соседними требованиями. Часто предполагают, что эти интервалы времени независимые и имеют одинаковое распределение случайных величин, которые образуют стационарный входящий поток требований. Классическая теория массового обслуживания рассматривает так называемый пуассоновский (простейший) поток требований. Для этого потока число требований k для любого интервала времени распределено по закону Пуассона.

На практике обоснованием того, что входящий поток требований имеет распределение Пуассона, является то, что требования поступают от большого числа независимых источников за определенный интервал времени. Примерами могут быть вызовы абонентов в телефонной сети, запросы к распределенной базе данных от абонентов сети за некоторое время и другие. Для того, чтобы при моделировании задать пуассоновский поток требований в систему, достаточно задать экспоненциальное распределение интервалов времени поступление для соседних требований.

Дисциплины постановки в очередь и выбора из нее определяют порядок постановки требований в очередь, если заняты устройства обслуживания, и порядок выбора из очереди, если освобождается обслуживающее устройство. Простейшая дисциплина допускает постановку в очередь в порядке поступления требований. Такую дисциплину называют «раньше поступил – раньше отслужился» (РПРО, в англоязычной литературе FIFO ~ First In-First Out), например, очередь к телефону-автомату.

Организация очереди по правилу «последний поступил -' первый отслужился» (ПППО, в англоязычной литературе LIFО - Last InFirst Out) допускает, что на обслуживание выбираются последние требования из очереди. Это правило также называется «стеком» или «магазином» .

Правило выбора из очереди может быть случайным (RANDOM).

Возможна также организация выбора из очереди по параметрам (например, мужчины в очереди пропускают женщин вперед). На очередь могут накладываться ограничения по длине очереди или по времени пребывания в ней. Например, если в очереди находится более трех требований, то новое требование, которое поступило, покидает систему; или, если время пребывания в очереди более двух минут, то требование покидает систему.

Очередь может быть с ограниченным количеством мест ожидания в ней - это так называемый буфер (например, бункер, в который поступают заготовки раньше, чем они будут обработаны станком).

Для ускорения работы компьютеров используются буферы при об, мене информацией между быстрыми и медленными устройствами (буферы ввода-вывода). Информация заранее размещается в буфере, а потом считывается из него. В сетях ЭВМ буферы используются для организации очередей сообщений или пакетов, если линия связи занята.

Правила обслуживания характеризуются длительностью обслуживания (распределением времени обслуживание), количеством требований, которые обслуживаются одновременно и дисциплиной обслуживания. Время обслуживания бывает детерминированным или заданным вероятностным законом распределения. Обслуживание может организовываться с помощью одного устройства - это так называемые системы с одним устройством (каналом) обслуживания - или с несколькими идентичными устройствами обслуживания, например, если установлено несколько кабин с телефонами-автоматами. Системы с идентичными устройствами обслуживания называют многоканальным системами. Устройства обслуживания могут быть объединены в последовательную цепочку. Это многофазные системы обслуживания, в которых требования последовательно проходят несколько фаз обслуживания, перед тем

Очереди как элементы упорядочения процессов в производстве, сбыте и потреблении товаров имеют место во всех сферах маркетинговой деятельности. Основные параметры очереди характеризуются свойствами входящего потока требований, потока обслуживания и дисциплины очереди. Расчеты систем обслуживания производятся с целью уменьшения нагрузок на обслуживающие приборы, уменьшения длины очередей, снижения затрат на обслуживание, увеличения пропускной способности системы и т. п. Основные показатели работы систем: длина очереди, время нахождения требования в системе, доля времени, в течение которого прибор бывает свободен.

Наиболее универсальной моделью системы массового обслуживания является модель с пуассоновским входящим потоком и экспоненциальным распределением времени обслуживания.

Распределение Пуассона – распределение вероятностей случайных величин x_i, принимающих целые неотрицательные значения k = 0,1,2,…,n с вероятностями [3, 4, 9, 20]

(5.1)

где λ > 0 – параметр.

Математическое ожидание, дисперсия и моменты более высоких порядков равны λ. Сумма независимых случайных величин X_i, имеющих распределение Пуассона с параметрами λ_i, подчиняется также распределению Пуассона с параметрами ∑λ_i. Это предельное распределение безгранично делимо: если сумма случайных величин имеет распределение Пуассона, то каждое слагаемое можно представить как распределенное по закону Пуассона.

Поток событий – это последовательность событий, происхо-дящих одно за другим в случайные моменты времени.

Поток называют стационарным, если вероятность появления некоторого числа событий в какой-то промежуток времени зависит только от величины временного промежутка.

Поток событий называют потоком без последействия, если для любых не перекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

Поток событий называют ординарным, если вероятность попадания на элементарный участок Δt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Если поток обладает всеми тремя свойствами, он называется простейшим (пуассоновским).

Время обслуживания (как и время между поступлениями в систему обслуживания), когда поток обслуживания (или поступления в систему) обладает этими тремя свойствами, распределено по экспоненциальному закону

g(t) = μe^–μt, (5.2)

где μ – параметр, величина, обратная среднему времени обслуживания одной заявки: μ = 1/m_{t обсл}.

Величина λ должна быть меньше, чем μ, иначе очередь будет расти до бесконечности по геометрической прогрессии.

Когда входящий поток – пуассоновский, а время обслуживания распределено по экспоненциальному закону, при одном приборе обслуживания, система обозначается М/М/1. Буква G в обозначении системы массового обслуживания означает произвольное распределение, E_k – распределение Эрланга порядка k, D – детерминированный поток (равные промежутки времени между поступлениями требований в систему или применительно к прибору обслуживания – неслучайное и одинаковое время обслуживания для всех требований). Например, E₃/G /2 означает, что входящий поток системы – эрланговский третьего порядка, поток обслуживания имеет произвольное распределение времени обслуживания, число обслуживающих приборов равно двум.

При формулировании задачи важную роль играет дисциплина очереди, здесь рассматривается следующая: требование приходит в систему и дожидается обслуживания, а например, не уходит, если очередь велика, и, кроме того, каждое требование обслуживается в свою очередь без каких-либо приоритетов.

Отношение λ/μ = ρ – загрузка системы (коэффициент загрузки).

Расчетные формулы для системы М/М/1 имеют следующий вид:

вероятность того, что обслуживающий прибор свободен,

Р₀ =1 – ρ. (5.3)

среднее число требований в системе (находящихся в очереди и на обслуживании)

E(n) = ρ/(1 – ρ); (5.4)

среднее время ожидания обслуживания

E(t) = ρ/[μ(1 – ρ)]; (5.5)

средняя длина очереди, ожидающей обслуживания,

E(n_o) = ρ²/(1 – ρ); (5.6)

среднее время, проведенное требованием в системе,

E(t_c) = 1/[μ(1 – ρ)]. (5.7)

Пример 1. Требования поступают на обслуживающее устройство (в кассу магазина для оплаты покупок) случайно, причем средний промежуток времени между поступлениями требований равен 1,0 мин, среднее время обслуживания – 0,8 мин. Определить: среднее число требований в системе; среднее время ожидания обслуживания; среднюю длину очереди, ожидающей обслуживания; среднее время; проведенное требованием в системе; вероятность отсутствия требований в системе, если она состоит из одного прибора и имеет пуассоновский входящий поток и экспоненциальное время обслуживания (М/М/1).

Решение. Так как средний промежуток времени между поступлениями требований известен: m_{t пост} = 1 мин, то среднее число покупателей, приходящих к кассе для расчета за покупки в течение 1 мин,

λ = 1/m_{t пост}; λ = 1/1 = 1 покупатель/мин.

Поскольку среднее время обслуживания m_{t обсл} = 0,8 мин, то среднее число покупателей, обслуживаемых в 1 мин,

μ = 1/m_tобсл ; μ = 1/0,8 = 1,25,

т. е. в среднем кассир обслуживает более одного покупателя в минуту.

Тогда вероятность простоя системы (в данном случае кассы и кассира)

Р₀ = 1 – ρ; Р₀ = 1 – 0,8 = 0,2,

т. е. 20 % рабочего времени система простаивает.

Среднее число покупателей в системе (стоят в очереди плюс один рассчитывается за покупку)

E(n) = ρ/(1 – ρ); E(n) = 0,8/(1 – 0,8) = 4 покупателя.

Среднее время ожидания в очереди

E(t) = ρ/μ(1 – ρ); E(t) = 0,8/(1,25·0,2) =3,2 мин.

Средняя длина очереди, ожидающей обслуживания,

E(n₀) = ρ²/(1 – ρ); E(n) = 0,8²/ (1 – 0,8) = 3,2 покупателя.

т. е., как правило, немногим больше трех покупателей стоят в очереди.

Среднее время, проведенное покупателем в системе, ожидая сначала в очереди, а потом и собственно своего обслуживания кассиром,

E(t_c) = 1/μ(1 – ρ); E(t_c) = 1/[1,25·(1 – 0,8)] = 4 мин.

Пример 2. При этих же условиях задачи рассматривается ситуация: добавлен еще один кассовый аппарат с кассиром при тех же условиях: все покупатели стоят в одной очереди и, как только один из кассиров освобождается, первый из стоящих в очереди поступает к нему на обслуживание (т. е. имеет место система М/М/2). Как изменятся первые три основных показателя?

Решение. Вероятность простоя системы

Р₀ = (2 – ρ)/ (2 + ρ); P₀ = (2 – 0,8)/(2 + 0,8) = 0,43,

т. е. 43 % рабочего времени кассиры будут простаивать.

Среднее число требований в системе

E(n) = 2ρ/(4 – ρ²); E(n) = 2·0,8/(4 – 0,8²) = 0,48,

т. е. практически очереди нет.

Среднее время ожидания обслуживания

E(t) = ρ²/[μ(4 – ρ²)]; E(t) = 0,8²/ 1,25(4 – 0,8²) = 0,15 мин.

При увеличении числа обслуживающих приборов на единицу практически не стало очереди и покупателям не приходится терять время в ней.

Модели М/М/m (здесь m – число обслуживающих приборов) можно использовать в любых случаях, нужно только помнить, что они дают завышенные показатели при одних и тех же значениях λ и μ, когда законы распределения величин, формирующих случайные потоки, более упорядочены.