«Применение пакета Mathematica 0 для расчета экстракционных равновесий в аналитической химии»
| Вид материала | Реферат |
- «Применение пакета Mathematica для математических вычислений», 261.66kb.
- Программа по аналитической химии, 184.24kb.
- План лекций по аналитической химии на III семестр для студентов, 86.94kb.
- План лекций по аналитической химии в iii семестре для студентов II курса фарм факультета, 175.67kb.
- Темы лекций по аналитической химии: Общие положения и принципы аналитической химии, 23.35kb.
- «Применение методов информатики для решения химических задач», 200.25kb.
- Программа курса «аналитическая химия», 26.7kb.
- Элективный курс «Основы аналитической химии», 41.7kb.
- Секция №1 теория и моделирование экстракционных процессов председатели – Кизим Н. Ф.,, 706.84kb.
- Утверждаю, 69.43kb.
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Выпускная работа по
«Основам информационных технологий»
Магистрант
кафедры аналитической химии
Кащей Сергей Леонидович
Руководители:
д.х.н. Гулевич Александр Львович
ассистент Шешко Сергей Михайлович
Минск 2008 г.
Оглавление
Список обозначений 4
Введение 6
1.Описание возможностей Mathematica 5.0 7
2.Применение Mathemathica 5.0 на практике 9
ПРИМЕР 1 9
ПРИМЕР 2 11
ПРИМЕР 3 12
Заключение 17
Список литературы 18
Предметный указатель
19
19
Интернет - источники в предметной области
20
Личный сайт
22
Граф научных интересов 23
Список источников 24
Приложение 26
Список обозначений
СКМ – система компьютерной математики
АК – аминокислота
pH – водородный показатель
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Реферат
«Применение пакета Mathematica 5.0 для расчета экстракционных равновесий в аналитической химии»
Магистрант
кафедры аналитической химии
Кащей Сергей Леонидович
Руководители:
д.х.н. Гулевич Александр Львович
ассистент Шешко Сергей Михайлович
Минск 2008 г.
Введение
Экстракция, как процесс разделения веществ между двумя фазами, была описана еще в 19 веке. Однако, бурное развитие экстракции началось в 50-е годы двадцатого столетия. В это время при помощи экстракции были решены важные научно-технические задачи атомной энергетики: в частности, вопросы переработки ядерного топлива, очистки и выделения многих радиоактивных элементов. Эти достижения вызвали бурный рост исследований по теории экстракционных процессов, что в свою очередь, привело к появлению новых аспектов практического применения, в том числе и в аналитической химии.
Основываясь на константах распределения, экстракции, ионного обмена, а также зная кислотно-основные характеристики разделяемых веществ можно оптимизировать экстракционные системы и проводить целенаправленную экстракцию одних веществ в присутствии других.
В современной аналитической химии исследователю, занимающемуся экстракционным разделением веществ и разработкой условий оптимизации экстракции, приходится иметь дело со сложными системами математических уравнений. Решение такого рода задач вручную весьма затруднительно, особенно когда результаты расчетов должны быть получены несколько раз в процессе проведения опыта. Для решения этой проблемы применяются системы компьютерной математики.
Применение данных систем позволяет решать в аналитическом и численном виде системы сложных алгебраических и дифференциальных уравнений,позволяет решать различные задачи в области графики и геометрии. Наиболее распространены следующие системы компьютерной математики – Mathematica, Maple, Mathcad, Matlab.
Предметом моего детального рассмотрения явилось применение в расчетах экстракционных процессов и оптимизации экстракции СКМ Mathematica 5.0
1.Описание возможностей Mathematica 5.0
Mathematica 5.0 состоит из двух основных частей - ядра (kernel), производящего вычисления по заданным командам, и интерфейсного процессора (front end), задающего внешнее оформление и характер взаимодействия с пользователем и системой. Вся работа осуществляется в окне рабочего документа - блокнота (notebook), - внешний вид которого зависит от типа платформы и определяется интерфейсным процессором, своим для каждой платформы. Блокнот может содержать различные математические и специальные символы, графические объекты, однако внутреннее представление документа, с которым работает ядро программы, - всегда неформатированный текст. Это позволяет легко переносить документы с одной платформы на другую. Более того, возможен вариант работы, когда интерфейсный процессор запускается на одной машине, а вычисляющее ядро на более мощном компьютере.
Применение программы Mathemathica 5.0 позволяет осуществлять следующие операции математического анализа
- Вычисление сумм
- Вычисление сумм в аналитическом виде
- Вычисление сумм в численном виде
- Вычисление сумм в аналитическом виде
- Вычисление произведений
- Вычисление произведений в аналитическом виде
- Вычисление произведений в численном виде
- Вычисление произведений в аналитическом виде
- Вычисление производных
- Вычисление интегралов
- Вычисление интегралов в символьном виде
- Вычисление определенных интегралов
- Вычисление кратных интегралов
- Особые случаи вычисления интегралов
- Численное интегрирование
- Вычисление интегралов в символьном виде
- Вычисление пределов функций
- Уравнения и системы уравнений
- Решение уравнений
- Решение систем нелинейных уравнений в символьном виде
- Численное решение уравнений
- Поиск корней уравнений
- Графическая иллюстрация и выбор метода решения уравнений
- Получение неизвестных в явном виде
- Решение уравнений
- Дифференциальные уравнения
- Решение дифференциальных уравнений в символьном виде
- Решение дифференциальных уравнений в численном виде
- Решение дифференциальных уравнений в символьном виде
- Оптимизационные задачи
- Поиск максимального и минимального чисел в списке
- Поиск локального минимума аналитической функции
- Поиск глобального максимума и минимума аналитической функции
- Решение задач линейного программирования
- Поиск максимального и минимального чисел в списке
Таким образом, как видно из приведенного выше списка, применение Mathemathica 5.0 позволяет решать любые математические задачи, с которыми приходится иметь дело химику-аналитику при расчетах.
2.Применение Mathemathica 5.0 на практике
Для более наглядной демонстрации возможностей использования программы я счел необходимым привести ряд аналитических задач, решенных с помощью Mathemathica 5.0 с соответствующими комментариями.
ПРИМЕР 1
Рассчитать численные значения мольных долей различных форм лейцина при заданном значении pH водной фазы.
(pKa=9,74;, pKb=11,67).
Теория. Аминокислоты (АК) в водных растворах присутствуют в виде цвиттер-ионов (АК)
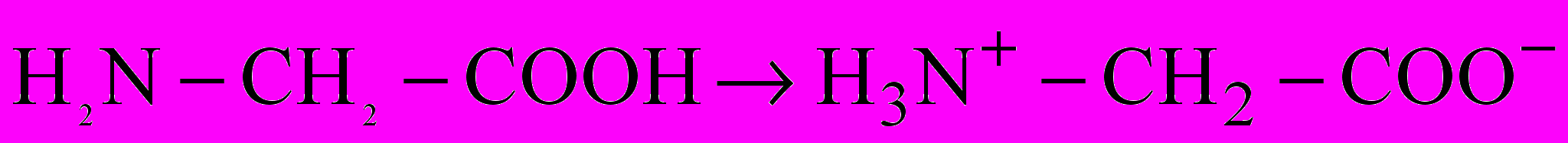 , (1)
, (1)которые обладают как кислотными, так и основными свойствами и характеризуются соответствующими константами кислотной (Ka) и основной (Kb) ионизации.
Равновесие кислотной ионизации АК имеет вид
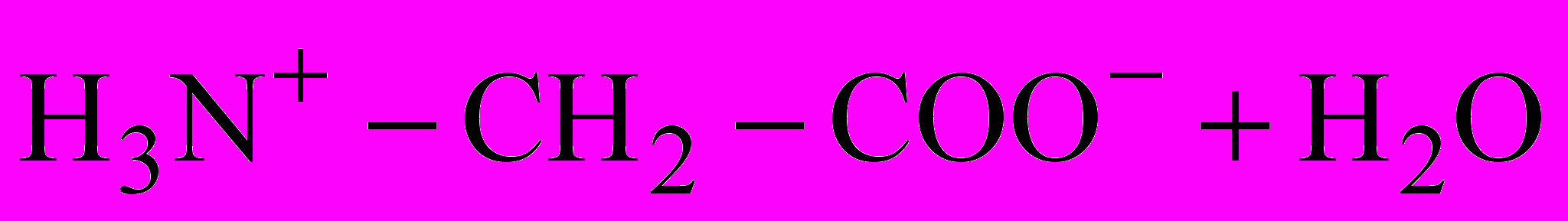
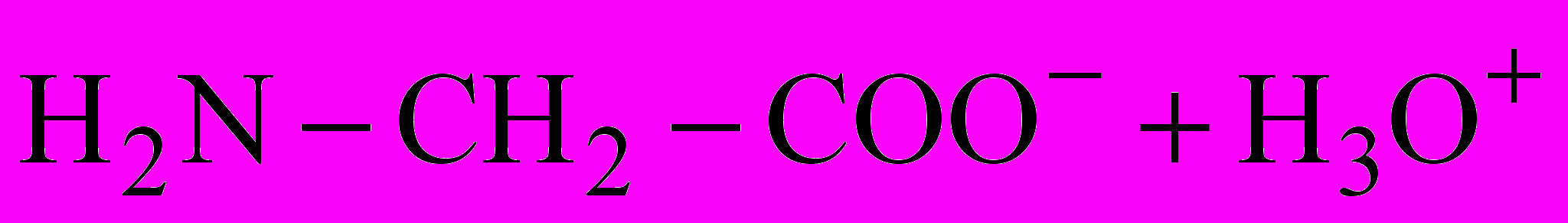 (2)
(2)и характеризуется константой кислотной ионизации
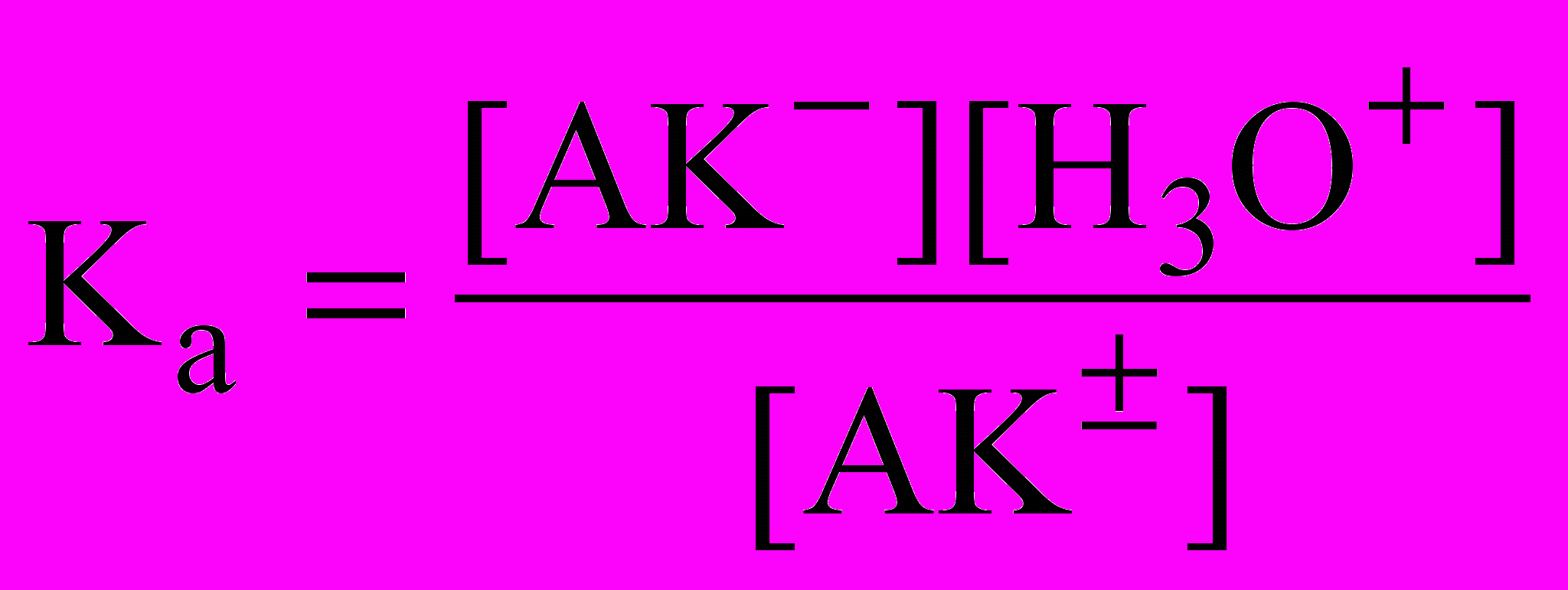 . (3)
. (3)Равновесие ионизации АК по основному типу имеет вид
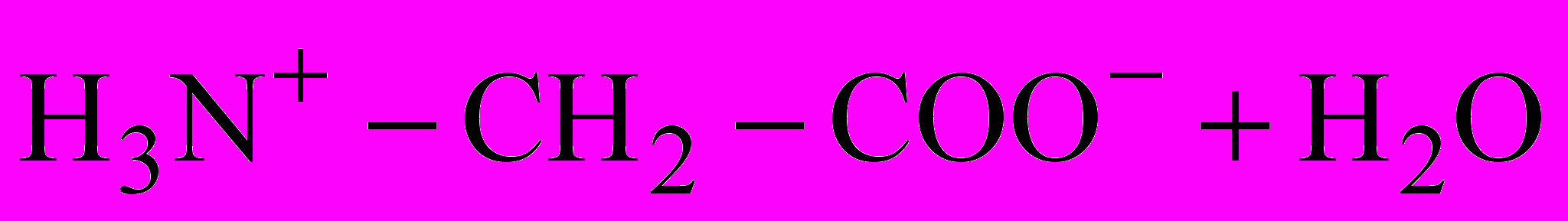
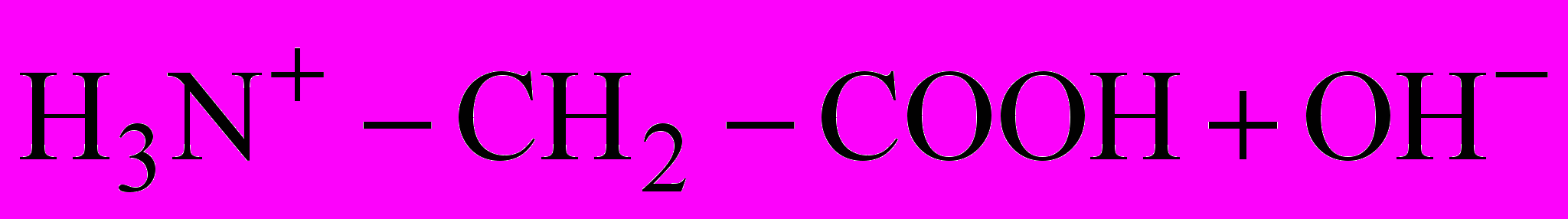 (4)
(4)и описывается константой основной ионизации
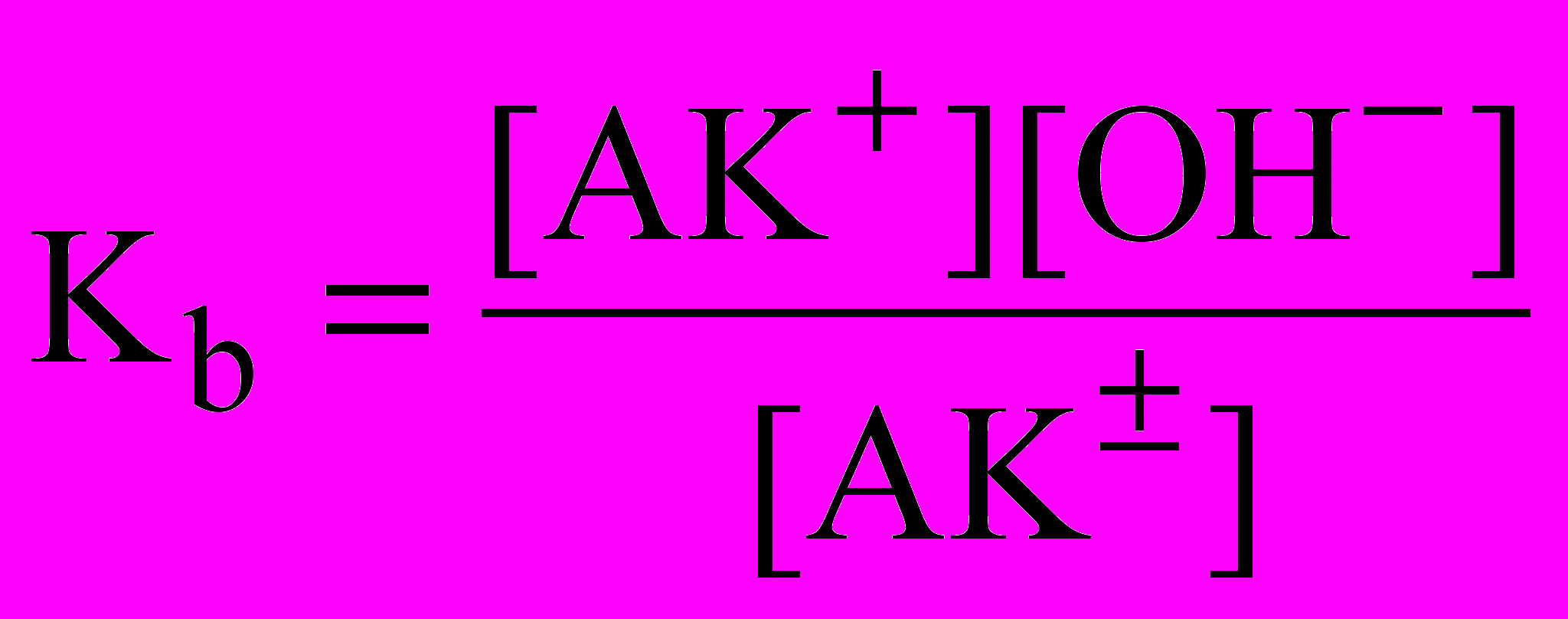 (5)
(5)Уравнение материального баланса по аминокислоте может быть представлено в виде
C0,AK = [AK] + [AK] + [AK-]. (6)
Используя (3), (5) и (6), можно найти аналитические выражения для мольных долей всех трех форм аминокислоты:
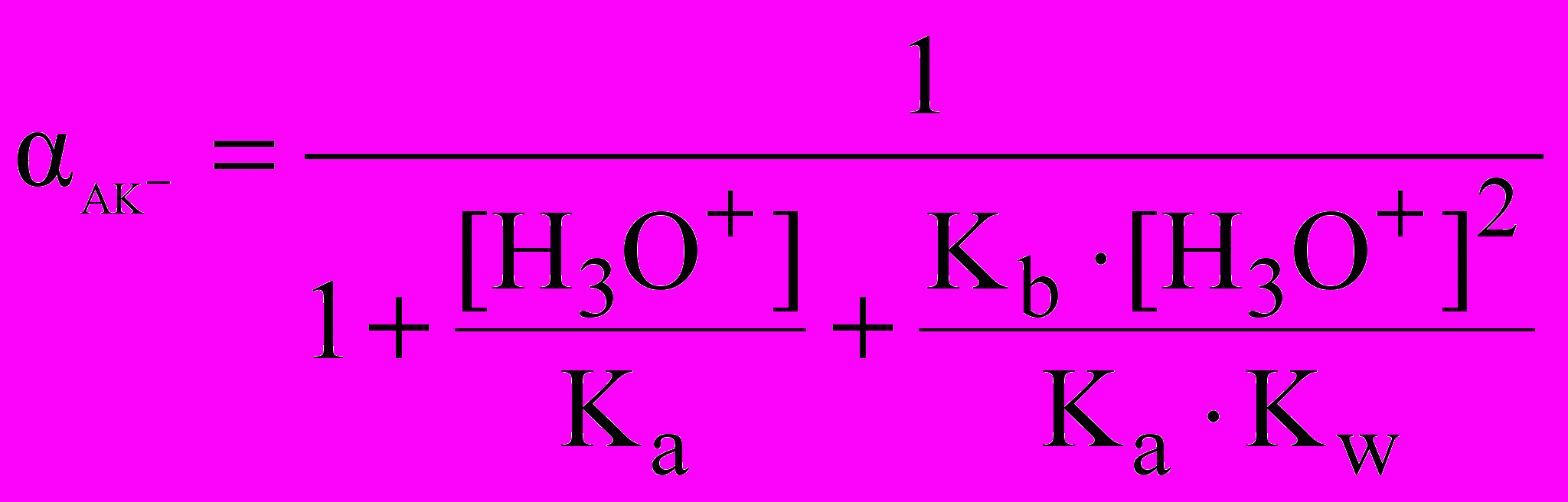 (7)
(7)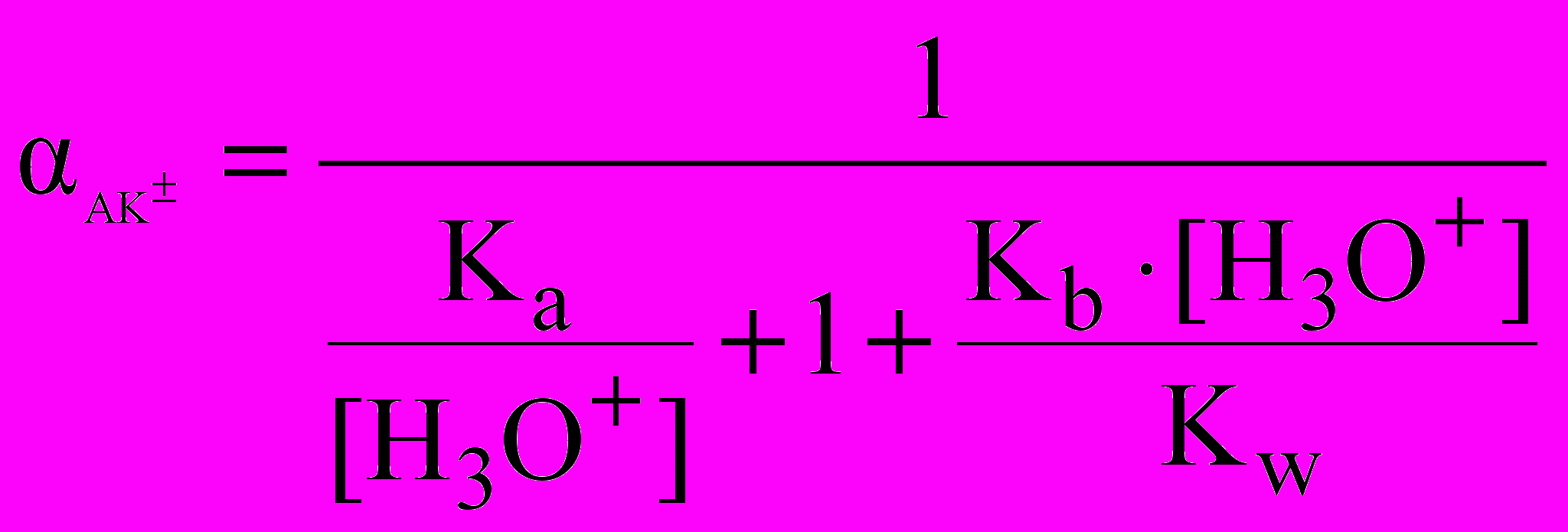 (8)
(8)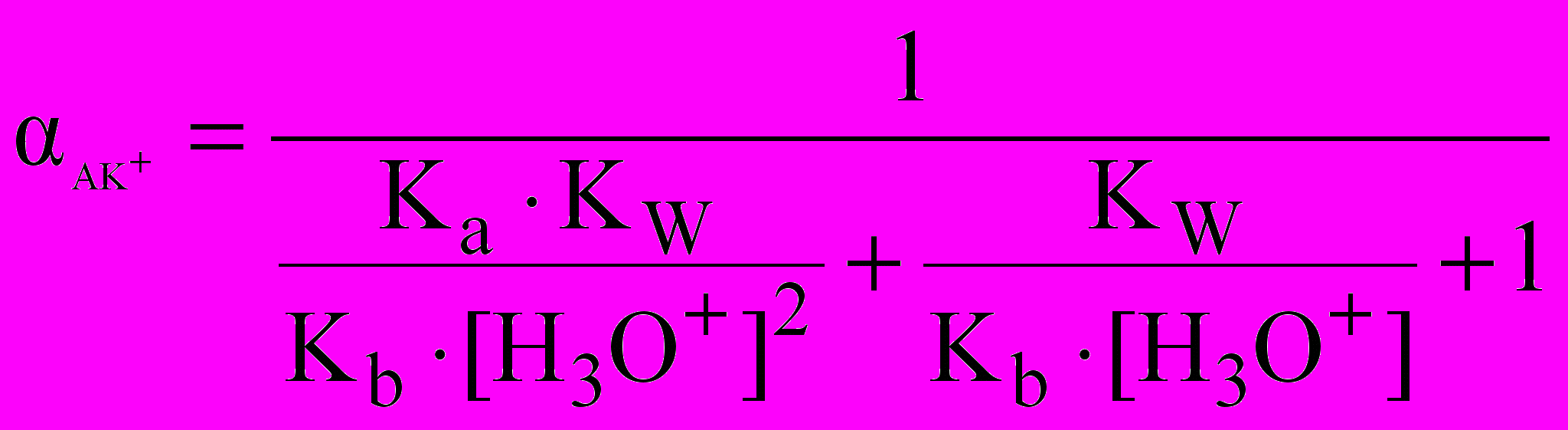 (9)
(9)Программа 1.
Clear[h,pH,alfa1,alfa2,alfa3];
Ka=10-9.74;
Kb=10-11.67;
Kw=10-14;
pH=1;
h=10-pH;
alfa1=1/(1+h/Ka+Kb*h2/Kw/Ka)
alfa2=1/(Ka/h+1+Kb*h/Kw)
alfa3=1/(Ka*Kw/Kb/h2+Kw/h/Kb+1)
Вывод.
После выполнения программы появляется результат вычислений в виде:
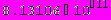
0.0446835
0.955316
Комментарии.
- Строка 1: происходит обнуление переменных.
- Строки 2-4: задаются численные значения констант.
- Строка 5: задается конкретное численное значение рН, для которого необходимо рассчитать численные значения мольных долей лейцина.
- Строка 6: по заданному значению рН рассчитывается концентрация катионов гидроксония.
- Строки 7-9: рассчитываются значения мольных долей анионной (alfa1), цвиттер-ионной (alfa2) и анионной (alfa3) форм лейцина.
- Точка с запятой в конце строки предотвращает вывод результата вычисления этой строки на экран монитора.
- Вычисления запускают комбинацией клавиш: Shift+Enter.
- По умолчанию ответ выводится с шестью значащими цифрами.
ПРИМЕР 2
Построить графические зависимости αi - рН в заданном
диапазоне рН для всех форм глицина.
Программа 2.
Clear[h,pH,alfa1,alfa2,alfa3];
Ka=10-9.74;
Kb=10-11.67;
Kw=10-14;
h=10-pH;
alfa1=1/(1+h/Ka+Kb*h2/Kw/Ka);
alfa2=1/(Ka/h+1+Kb*h/Kw);
alfa3=1/(Ka*Kw/Kb/h2+Kw/h/Kb+1);
Plot[{alfa1,alfa2,alfa3},{pH,0,14}]
Вывод.
После выполнения программы появляется график зависимости мольных долей анионной, катионной и цвиттер-ионной форм глицина от рН:
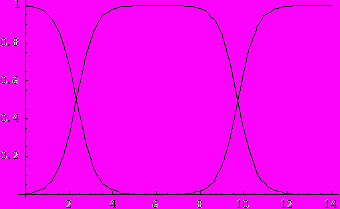
Комментарии.
- Программа 2 аналогична программе 1, за исключением последней строки. Для вывода графиков используется машинная функция Plot. В первых фигурных скобках задается список функций, которые надо прорисовать, а во вторых фигурных скобках – наименование переменной по оси ОХ, а также минимальное и максимальное ее значение.
- Координаты любой точки на графике можно определить, нажав Ctrl и щелкнув левой клавишей мышки на интересующей точке графика. Координаты этой точки появляются в нижнем левом углу окна.
- Используя различные опции функции Plot, можно прорисовать кривые различными цветами, сместить начало координат в любую точку, подписать оси и еще многое другое. Для использования опций необходимо обратиться к пункту меню Help.
ПРИМЕР 3
Рассчитать оптимальную концентрацию Cl-ионов, обеспечивающую максимальное значение коэффициента распределения
нейтрального комплекса InCl3.
(lgK1=1,0; lgK1,2=1,5; lgK1,2,3=1,55; lgK1,2,3,4=1,35).
Теория. Константа распределения нейтрального комплекса InCl3 и коэффициент распределения индия (3) связаны соотношением:
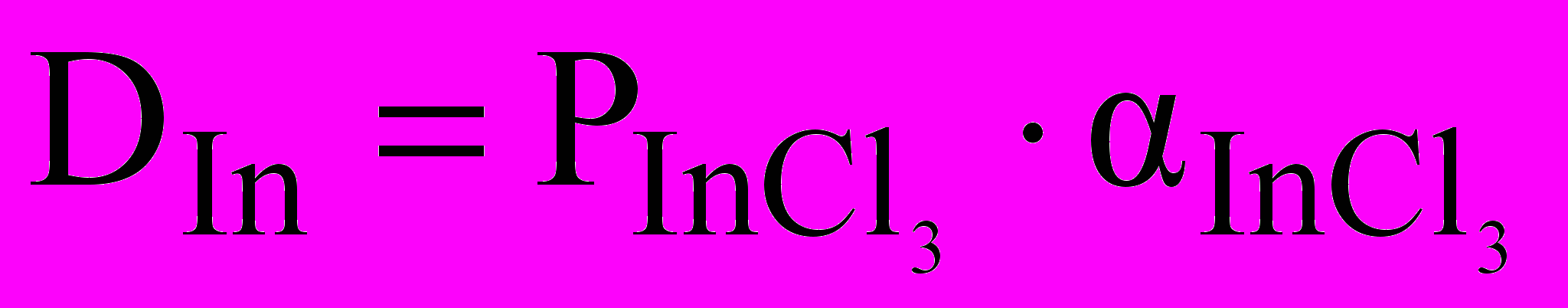 . (10)
. (10)Мольная доля нейтрального комплекса InCl3 , выраженная через полные константы устойчивости определяется выражением:
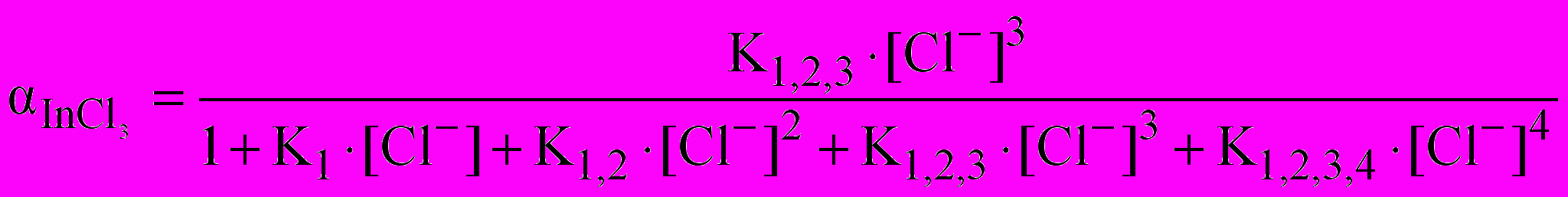 (11)
(11)где полные константы устойчивости являются произведением ступенчатых констант устойчивости: K1,2=K1∙K2 и т.д.
Для нахождения оптимальной концентрации хлорид-ионов необходимо продифференцировать (11) по концентрации хлорид-ионов, приравнять полученное выражение к нулю и решить его относительно [Cl-].
С целью упрощения дальнейшего дифференцирования необходимо (11) видоизменить, оставив 1 в числителе:
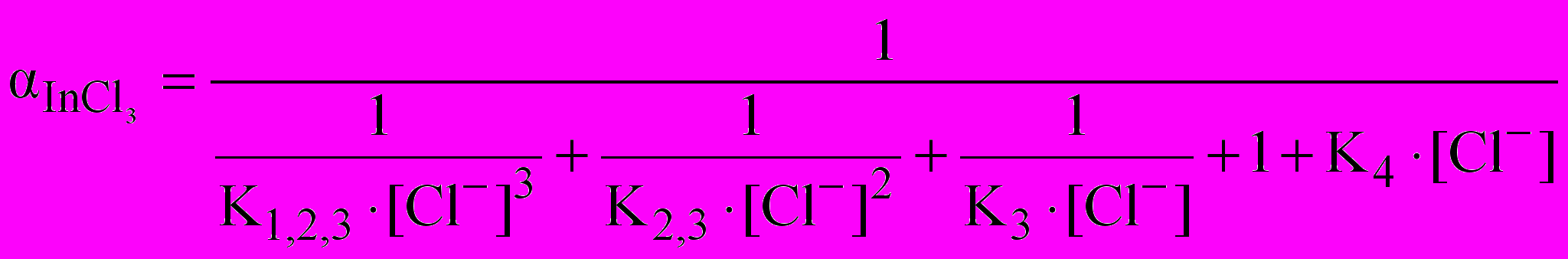 (12)
(12)При такой форме представления
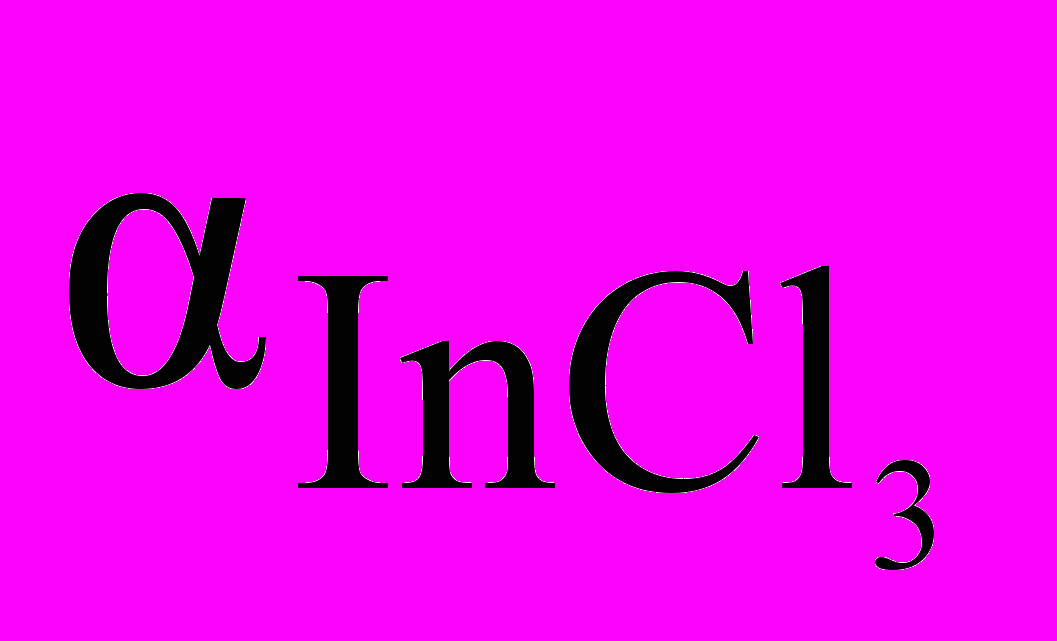 проще продифференцировать обратную ей величину
проще продифференцировать обратную ей величину 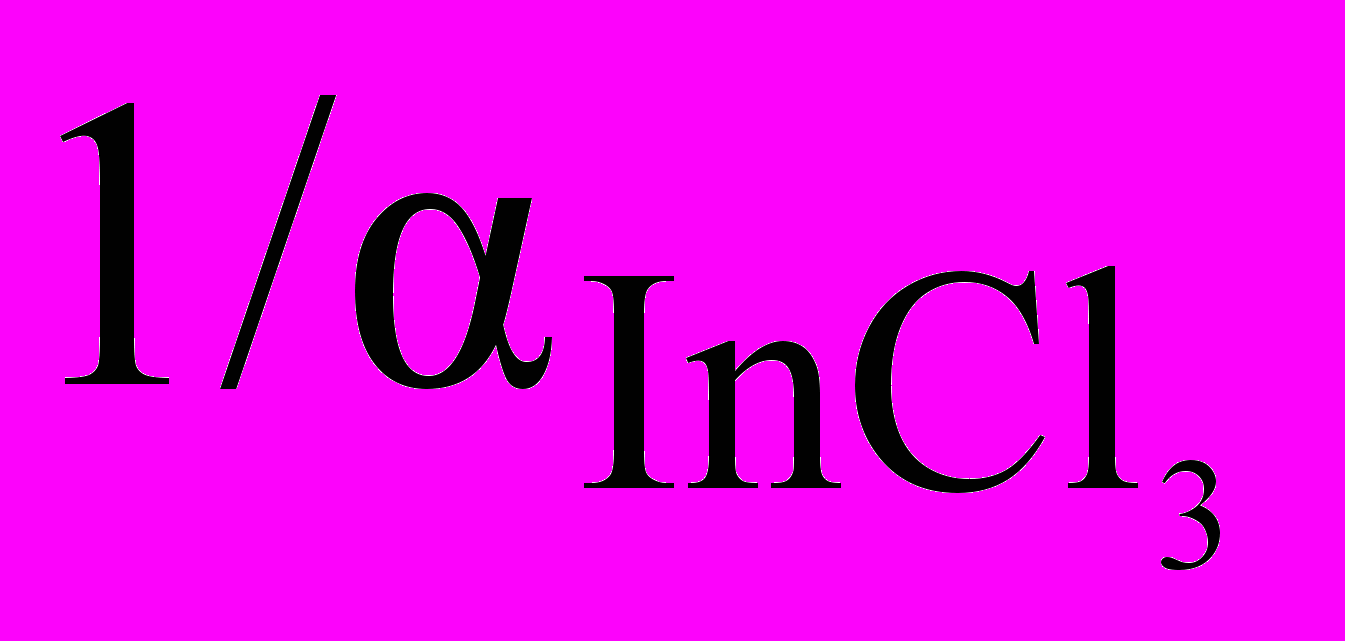 и приравнять ее к нулю:
и приравнять ее к нулю: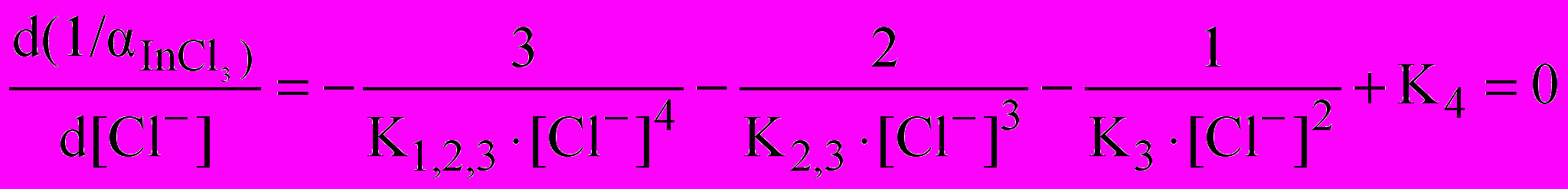 (13)
(13)Это уравнение 4-й степени, которое можно решить при помощи СКМ.
Программа 3а.
K1=101;
K2=10(1.5-1);
K3=10(1.55-1.5);
K4=10(1.35-1.55);
NSolve[-3/K1/K2/K3/Cl4-2/K2/K3/Cl3-1/K3/Cl2+K40,Cl]
Вывод.
После выполнения программы появляется результат вычислений в виде:
{Cl1.44704},{Cl-0.607734+0.174846},
{Cl-0.607734-0.174846},{Cl-0.231568}
Комментарии.
1. В программе 3 используется функция численного решения уравнения NSolve. Особенностью синтаксиса этой функции является двойное написание знака = = в уравнении.
2. При выводе результатов индицируются все корни уравнения, в том числе отрицательные и мнимые. Поэтому необходимо выбрать только положительное решение: 1,44704. Т.е., при концентрации хлорид-инов 1,45 моль/л доля нейтрального комплекса InCl3 будет максимальна.
В ряде случаев при решении такого рода задач выражения, которые необходимо продифференцировать, настолько сложны, что сделать это вручную затруднительно. СКМ Mathematica 5.0 легко справляется с дифференцированием практически сколь угодно сложных функций.
Продифференцируем знаменатель выражения (12), используя функцию дифференцирования D.
Программа 3б.
Clear [K1,K2,K3,K4]
f=K1*K2*K3/(Cl)3+K2*K3/(Cl)2+K3/Cl+1+Cl/K4;
D[f,Cl]
Вывод.
После выполнения программы появляется результат дифференцирования в виде:
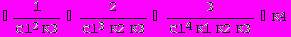
Комментарии.
1. Как видно из результатов машинного дифференцирования, полученное выражение полностью идентично выражению (13), полученному вручную.
2. Знаменатель (12) в программе обозначен через f.
СКМ Mathematica 5.0 позволяет совместить и дифференцирование, и решение получающегося нелинейного уравнения. Это значительно упрощает решение такого рода задач по оптимизации концентрации лиганда при экстракции металлокомплексов.
Программа 3в.
Clear[K1,K2,K3,K4,alfa,Cl];
K1=101;
K2=10(1.5-1);
K3=10(1.55-1.5);
K4=10(1.35-1.55);
alfa=K1*K2*K3*Cl3/(1+K1*Cl+K1*K2*Cl2+K1*K2*K3*Cl3+K1*K2*K3*K4*Cl4);
NSolve[D[alfa,Cl]0,Cl];
Cases[%,{(__?Positive)...}];
NumberForm[%,3]
Вывод.
После выполнения программы появляется результат вычислений в виде:
Cl1.45
Комментарии.
1. В программе 3в совмещены операции дифференцирования и решения уравнения 4-й степени.
2. Для вывода только положительных корней использована функция Cases.
3. Для ограничения количества значащих цифр в ответе использована функция NumberForm.
4. Символ % означает обращение к результату вычислений, полученных в предыдущей строке программы.
Заключение
Таким образом, использование системы компьютерной математики Mathematica 5.0 при расчетах различных параметров экстракционного разделения и оптимизации процесса экстракции позволяет достаточно просто и быстро решить возникающие задачи в наиболее удобном для исследователя виде (в численном или графическом). В силу этих причин изучение систем компьютерной математики и в частности Mathematica 5.0 проводится в БГУ в рамках курса аналитической химии. Это позволяет выработать у студентов навыки системного мышления и позволяет им в дальнейшим самостоятельно разрабатывать алгоритмы решения любых, даже самых сложных ,аналитических задач
Список литературы
- Кулешов А.А., Земсков С.В., Позняк Ю.В. Система Mathematica 5.0. Опыт использования в математике и программировании// ссылка скрыта
- А.Л.Гулевич, С.М.Лещев, Е.М.Рахманько Экстракционные методы разделения и концентрирования веществ./ А.Л.Гулевич, С.М.Лещев, Е.М.Рахманько – Минск: изд.БГУ 2008г. стр.158-165
- Болохонов, А.П. Microsoft Office 2003: Краткие инструкции для новичков / А.П. Болохонов. – Москва: Аквариум, 2004. – 128 с.
- Гультяев, А.К. MS Office XP 2003. Word, Excel, Access, Outlook, PowerPoint, FrontPage / А.К. Гультяев. – Москва: КОРОНА-Век, 2006. – 64 с.
- Я. К. Шмидский Mathematica 5./ Самоучитель. М.: Диалектика. 2004.
- Microsoft PowerPoint 2003: самоучитель / М.В.Спека. – Москва, Санкт-Петербург, Киев: Диалектика, 2004. – 363 с.
- Microsoft Word 2003 в теории и на практике / С.Бондаренко, Бондаренко. – Минск: Новое знание, 2004. – 336 с., ил.
Предметный указатель
M
Mathemathica 7, 8, 9
а
анализ 19
к
константа
констант 11, 13
концентрацию
концентрация 12
С
СКМ 4, 7, 14, 15
Э
Экстракция 6
Экстракции 6
Интернет - источники в предметной области
- cedirect.com;
Сайт издательства Elsevier. Содержит резюме всех статей различных журналов данного издательства.
- ier.com
Сайт издательства Elsevier. Отличается системой каталогизации и спецификой направленности. Доступ к полнотекстовым документам можно получить в библиотеке Академии наук.
- rary.com;
Множество полезных статей в основном на английском языке. Доступ предоставляется только зарегистрированным пользователям. Наиболее полный доступ можно получить в библиотеке Академии Наук.
- s.com/scopus/home.url
Самый мощный поисковик резюме. Кроме этого выдается ссылка на полнотекстовую версию файла или номер и название журнала, в котором приведена статья.
Поисковик и научной информации. Охватывается широкий спектр иностранных журналов, однако не очень хорошо налажена систематизация.
- ac.ru/Chemistry/Soft/
Незаменимый сайт для химиков. Приведены описания большого количества химических программ, а самое главное – ссылки сайтов, с которых их можно скачать.
- t.chat.ru/
Сайт, на котором выложено множество программ, Полезных для химиков. Предоставляется возможность их прямого скачивания, что, безусловно, экономит время и деньги.
Сайт создан доцентом кафедры общей химии и методики преподавания химии Белорусского государственного университета А.А. Рагойшей. Тут размещается каталог бесплатных журналов по химии, биохимии и другим областям. Включает две части: постоянно доступные химические журналы и ознакомительные временно доступные химические журналы. В каталоге собрана информация об известных химических научных журналах, предоставляющих бесплатный доступ к полным текстам опубликованных статей.
Сайт Высшей аттестационной комиссии Республики Беларусь. Тут можно найти информацию о подготовке научных кадров, присуждении ученых степеней и званий, кратких паспортам специальностей и програмах-минимум кандидатских экзаменов по специальности. В разделе «Каталог файлов» представлены доступные для скачивания файлы нормативных документов с приложениями и шаблоны регистрационных документов.
Самый главный поисковик для любого поиска. Позволяет производить простой поиск по ключевым словам, возможен вариант расширенного поиска по группам, особым признакам (определение, тип файла) и т.д.
Портал одного из крупнейших в мире поставщиков химических реактивов и лабораторного оборудования. Огромное множество соединений, предлагаемых на продажу.
Интернет-портал химиков-аналитиков.
Личный сайт
ссылка скрыта
Граф научных интересов
магистранта химического факультета Кащея С.Л.
Специальность: аналитическая химия
| Смежные специальности
| Основная специальность
| Сопутствующие специальности
|
Список источников
- Кулешов А.А., Земсков С.В., Позняк Ю.В. Система Mathematica 5.0. Опыт использования в математике и программировании// ссылка скрыта
- А.Л.Гулевич, С.М.Лещев, Е.М.Рахманько Экстракционные методы разделения и концентрирования веществ./ А.Л.Гулевич,
- С.М.Лещев, Е.М.Рахманько – Минск: изд.БГУ 2008г. стр.158-165
- Болохонов, А.П. Microsoft Office 2003: Краткие инструкции для новичков / А.П. Болохонов. – Москва: Аквариум, 2004. – 128 с.
- Гультяев, А.К. MS Office XP 2003. Word, Excel, Access, Outlook, PowerPoint, FrontPage / А.К. Гультяев. – Москва: КОРОНА-Век, 2006. – 64 с.
- Я. К. Шмидский Mathematica 5./ Самоучитель. М.: Диалектика. 2004.
- Microsoft PowerPoint 2003: самоучитель / М.В.Спека. – Москва, Санкт-Петербург, Киев: Диалектика, 2004. – 363 с.
- Microsoft Word 2003 в теории и на практике / С.Бондаренко, М.Бондаренко. – Минск: Новое знание, 2004. – 336 с., ил.
- Володько В.В. Powerpoint для чайников/Володько В.В.- М.:Вагриус,2006, стр.94
- Ольшук Д.И. Оптимизация экстракционных равновесий с участием жидких анионообменников/Киев,2003,стр. 56
- Шпак А.В. Электрофоретические методы определения аминокислот / А.В. Шпак, А.В. Пирогов, О.А. Шпигун // Международный форум «Аналитика и аналитики»: Каталог рефератов и статей. Т. 1. Воронеж, 2–6 июля 2003 г. – Воронеж, 2003. – С. 192.
- Лисовская А.Г. Веб-дизайн — просто о сложном/Лисовская А.Г. Москва: Аквариум, 2004. – 56. ,ил.
Приложение



