Данная лекция может содержать ошибки (как логические, так и грамматические)

Вид материала

Лекция

Содержание I задано как множество атрибутов пикселей, пусть после применения к I 1.Run Length Encoding (RLE) 1.1.RLE — битовый уровень 1.2.RLE — байтовый уровень Алгоритм декодирования 2.Кодирование одинаковых подстрок 2.1.LZ77 (Lempel, Ziv) Алгоритм декодирования 2.2.LZW (Lempel, Ziv, Welch) Алгоритм кодирования Утв. По выходной последовательности реконструируется и словарь, и входная последовательность.Алгоритм декодирования 3.Алгоритмы, учитывающие частоту вхождения символов 3.1.Алфавитное кодирование 3.2.Метод Хаффмана 3.3.Арифметическое кодирование Построение двоичной дроби.

Подобный материал:

• Правила и ошибки возможные при определении. Деление как логическая операция. Виды деления, 23.4kb.
• Методика работы над орфографическим и пунктуационным правилом. Творческие уроки русского, 19.9kb.
• Время, требуемое для выполнения проекта 7 недель, 14 часов, 8.75kb.
• Философия Древней Индии и Китая (по желанию студентов). Только в тех группах, где семинар, 316.52kb.
• Старо-новогодняя сказка 2000, 81.41kb.
• Н. В. Демидов творческое наследие Искусство актера Н. В. Демидов книга, 5224.17kb.
• Создание Web-страниц. Изучение языка html, 186.84kb.
• Грамматические ошибки, 54.38kb.
• Петр Валентинович Турчин один из сильнейших специалистов в мире по популяционной динамике,, 156.73kb.
• «Парадоксы» общей теории относительности, 129.98kb.

Lecture 10: Сжатие изображений

Данная лекция может содержать ошибки (как логические, так и грамматические). Авторы будут признательны за любые сообщения об ошибках, неточностях, а также за любые комментарии и дополнения, присланные по адресу Denis@fit.com.ru (Денису Иванову).

План лекции

1. Необходимость сжатия изображений
   
   • Сжатие без потерь
     
   • Сжатие с потерями
     
   • Не существует алгоритма, сжимающего все
     
2. Run Length Encoding (RLE)
   
   • RLE битового уровня
     
   • RLE байтового уровня
     
3. Кодирование одинаковых подстрок
   
   • LZ77 (Lempel, Ziv)
     
   • LZW (Lempel, Ziv, Welch)
     
4. Учет частоты вхождения символов
   
   • Алфавитное кодирование
     
   • Метод Хаффмана
     
   • Арифметическое кодирование
     

Типичное изображение, полученное цифровой фотокамерой, имеет размер 2048×1024, для передачи цвета обычно используется 24 бита/пиксель. Следовательно, такая картинка занимает 6 мегабайт, это при том, что при таком разрешении изображение получается хуже, чем на обычной фотографии 10×15. Реально же требуется в 5-6 раз лучшее разрешение. Поэтому очень актуальными являются алгоритмы сжатия изображений.


Существуют две основные тенденции развития таких алгоритмов:

1. Сжатие без потерь: пусть изображение I задано как множество атрибутов пикселей, пусть после применения к I алгоритма A мы получили набор данных I₁, тогда существует алгоритм A ¹: . Т.е. можно реконструировать I. (Сжатие без потерь применяется в PCX, PING, GIF, …)
   
2. Сжатие с потерями, т.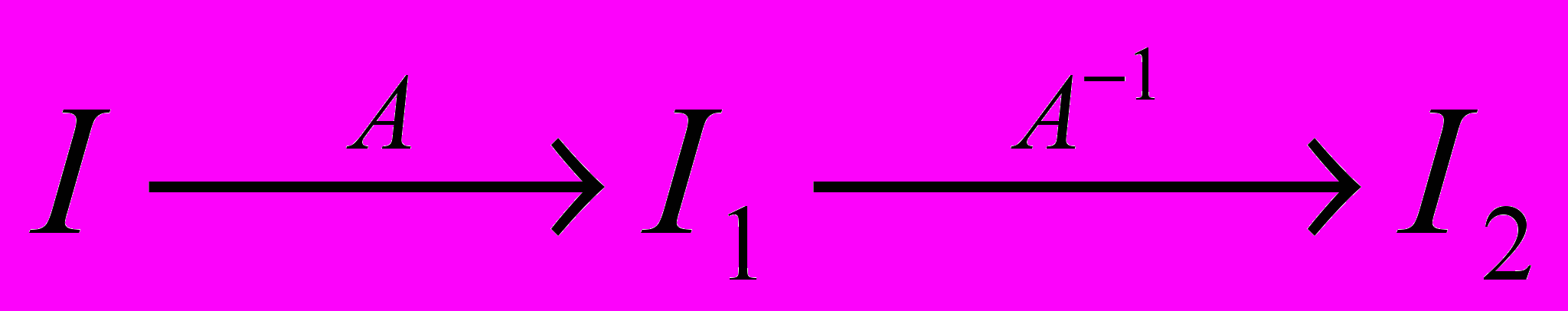е. , где . При этом возникает вопрос, насколько велико визуальное отличие I₂ от I, и как его оценивать. (JPEG)
   

Эта лекция посвящена сжатию без потерь, что требуется в случаях, когда информация была получена большой ценой (например, медицинские изображения или снимки со спутников).


Утверждение. Не существует алгоритма, который сжимал бы без потерь любой набор данных.

□ Существует 2^N изображений 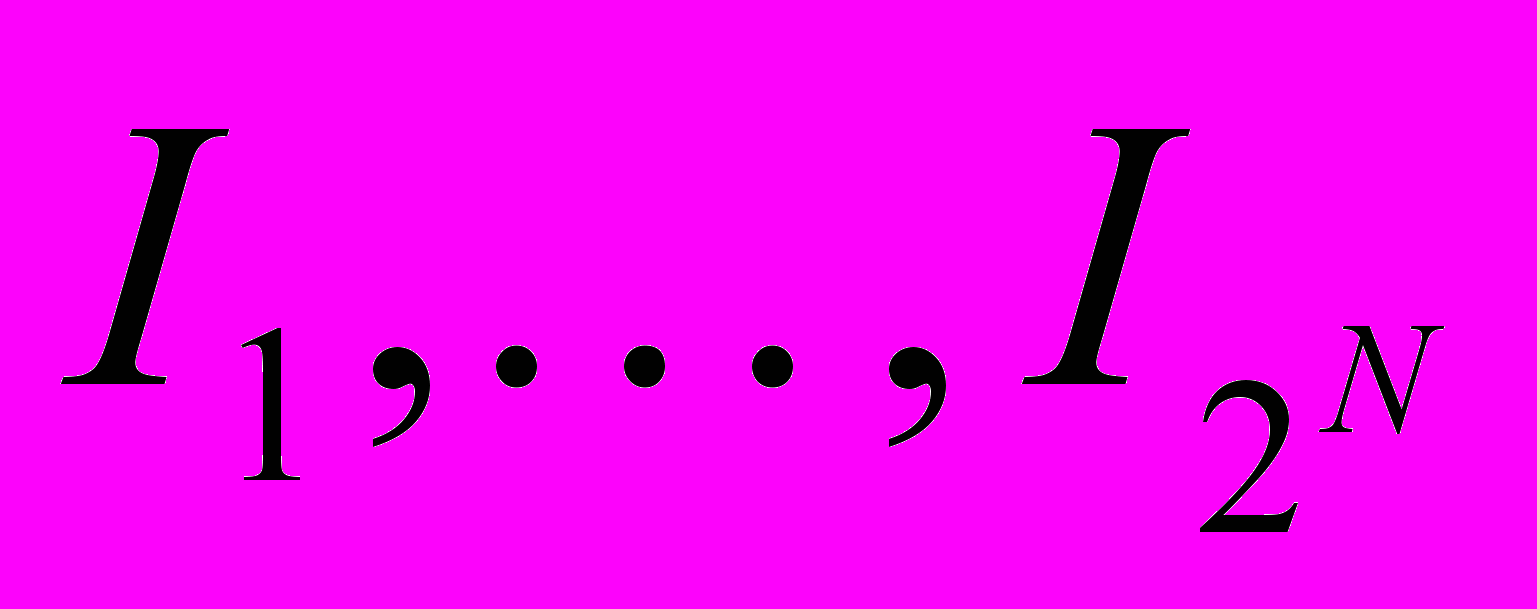размера N битов (будем рассматривать бит как минимальный носитель информации). Пусть найдется алгоритм 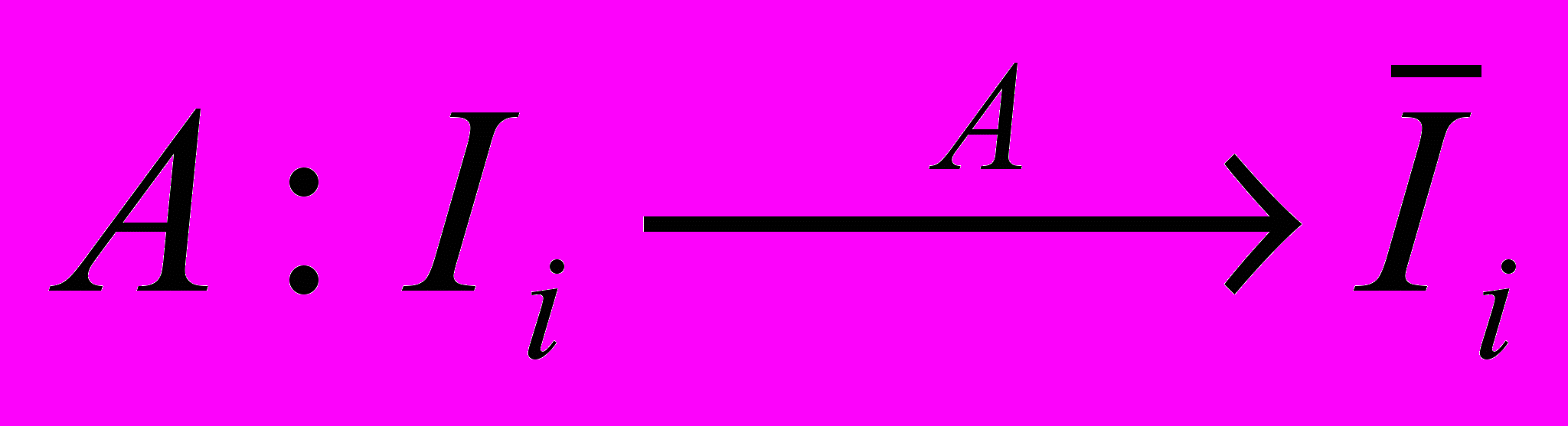так, что 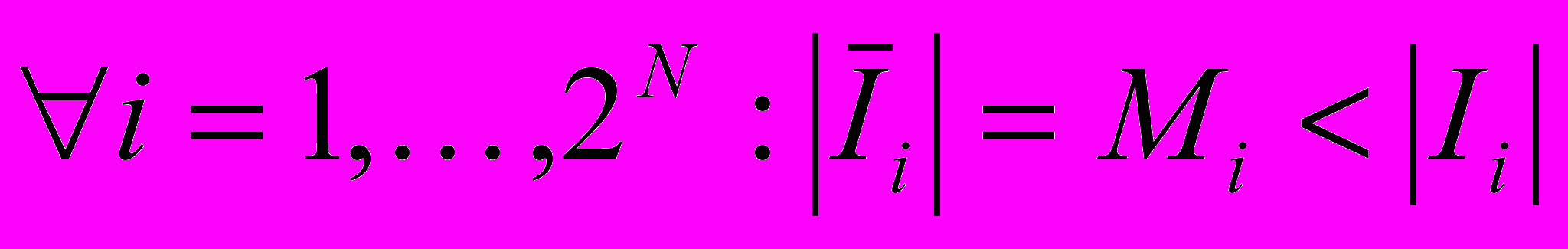, где 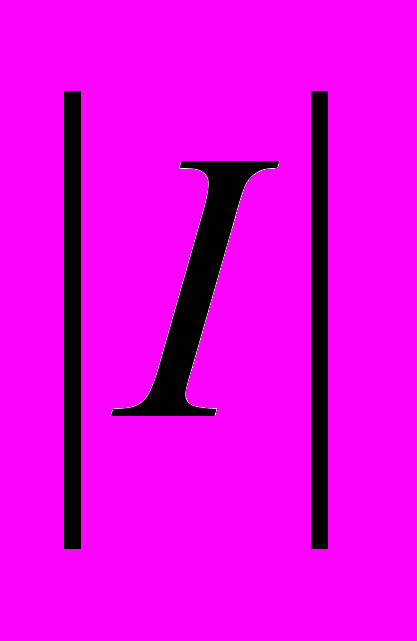— длина I в битах. M = max M_i, M < N. Но существует лишь 2¹ + 2² + … + 2^M (< 2^N) изображений с размером, меньшим M.■


Поэтому каждый алгоритм оптимизируется, чтобы сжимать некоторый подкласс в множестве всех изображений.


Категории алгоритмов

1.Run Length Encoding (RLE)

1.1.RLE — битовый уровень

Рассмотрим черно-белое изображение, на входе — последовательность битов, где 0 и 1 чередуются (все изображение разбивается на строки, которые выстраиваются друг за другом). Подряд обычно идет несколько 0 или 1, и можно помнить лишь количество идущих подряд одинаковых цифр. Т.е. последовательности

0000 11111 000 11111111111

соответствует набор чисел 4 5 3 11. Возникает следующий нюанс: числа, соответствующие входной последовательности, также надо кодировать битами. Можно считать, что каждое число изменяется от 0 до 7, тогда последовательности 11111111111 можно сопоставить, например, числа 7 0 4, т.е. 7 единиц, 0 нулей, 4 единицы.

Идея этого метода используется при передаче факсов.

1.2.RLE — байтовый уровень

Предположим, что на вход подается полутоновое изображение, где на цвет пикселя отводится 1 байт. Ясно, что по сравнению с черно-белым растром ожидание длинной цепочки одинаковых битов существенно снижается.

Будем разбивать входной поток на байты (буквы) и кодировать повторяющиеся буквы парой (счетчик, буква).

Т.е. AABBBCDAA кодируем (2A) (3B) (1C) (1D) (2A). Однако могут быть длинные отрезки данных, где ничего не повторяется, а мы кодируем каждую букву парой цифра-буква.

Пусть у нас есть фиксированное число M (от 0 до 255). Тогда одиночную букву 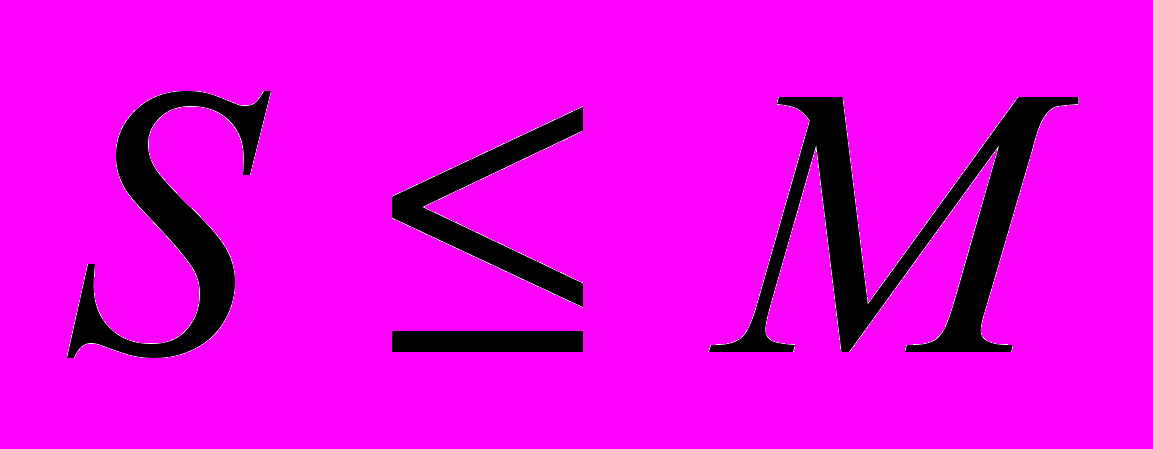можно закодировать ею самою — выход = S, одиночную букву от M до 255 — парой (1S), причем, если надо сказать, что подряд несколько букв S, то выход = CS, где 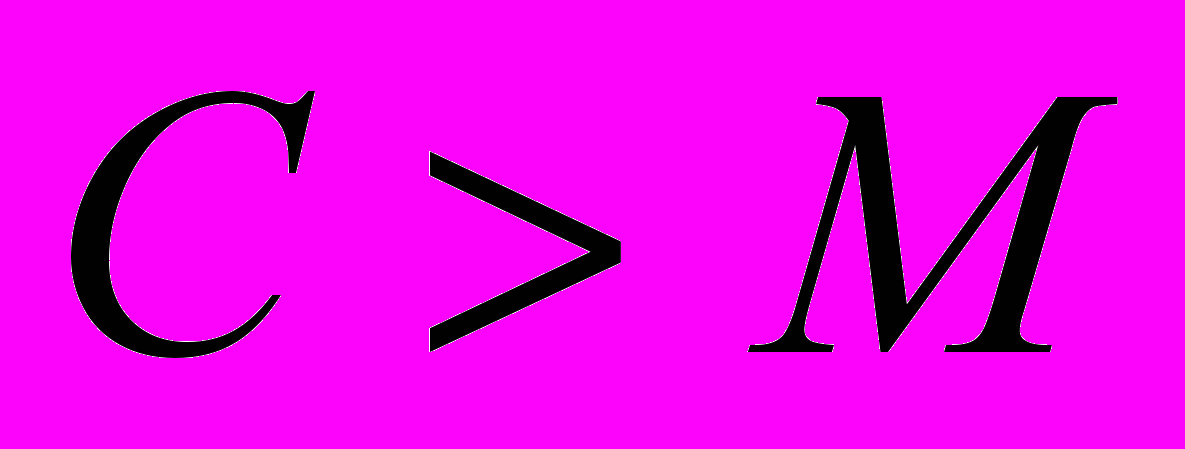, а 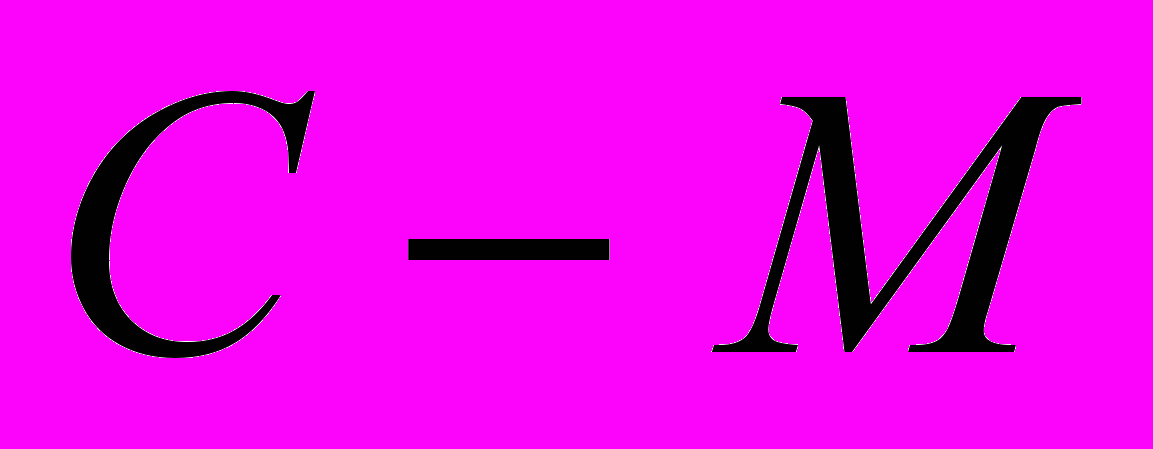— количество идущих подряд букв S. Тогда алгоритм декодирования будет выглядеть так:


Алгоритм декодирования

C = считать следующий символ.

если (C > M) то

C-M — счетчик,

следующий в последовательности — символ,

который надо повторить C-M раз

иначе

C — символ, надо вывести C

конец алгоритма


Встает вопрос, как выбрать M, в PCX считается, если первые два бита — 11, то остальное — счетчик.

Кроме как в PCX, этот алгоритм используется также в JPG.


Легко представить пример, когда изложенные алгоритмы не приводят к уменьшению объема информации. Рассмотрим камеру слежения, из-за различных наводок возникает много шумов, следовательно, одинаковые подряд идущие биты редки.

2.Кодирование одинаковых подстрок

2.1.LZ77 (Lempel, Ziv)

Рассмотрим алгоритм декодирования. Пусть входной поток байтов 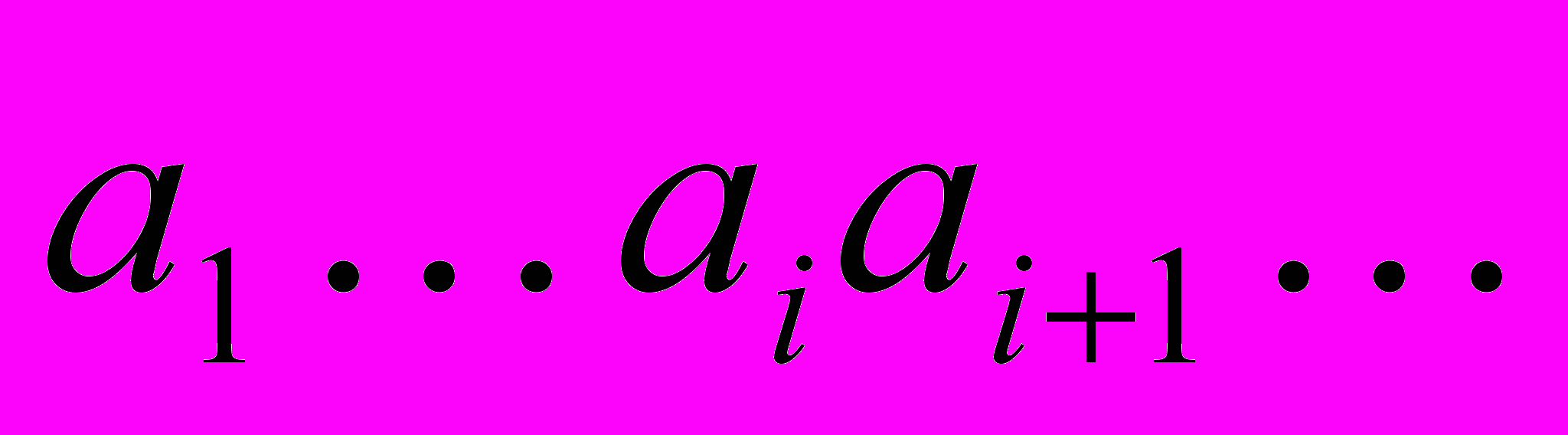был закодирован в последовательность байтов .

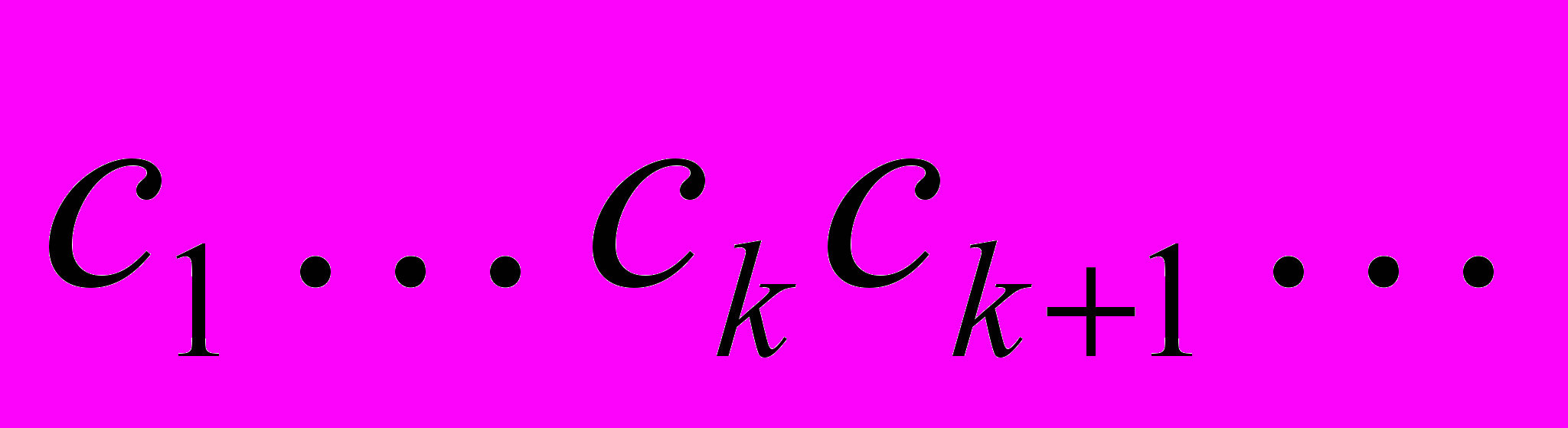Алгоритм декодирования

пусть по c₁ … c_k-1 уже восстановили a₁ … a_i-1,

читаем c_k

если (первый бит c_k = 0) то //(см. пример на рис.1)

рассмотреть остальные биты c_k как двоичную запись числа n

следующие n символов c_k+1 … c_k+n просто скопировать на выход

если (первый бит c_k = 1) то //(см. пример на рис.2)

рассмотреть остальные биты c_k как двоичную запись числа n;

считать c_k+1 — смещение назад;

скопировать на выход ;

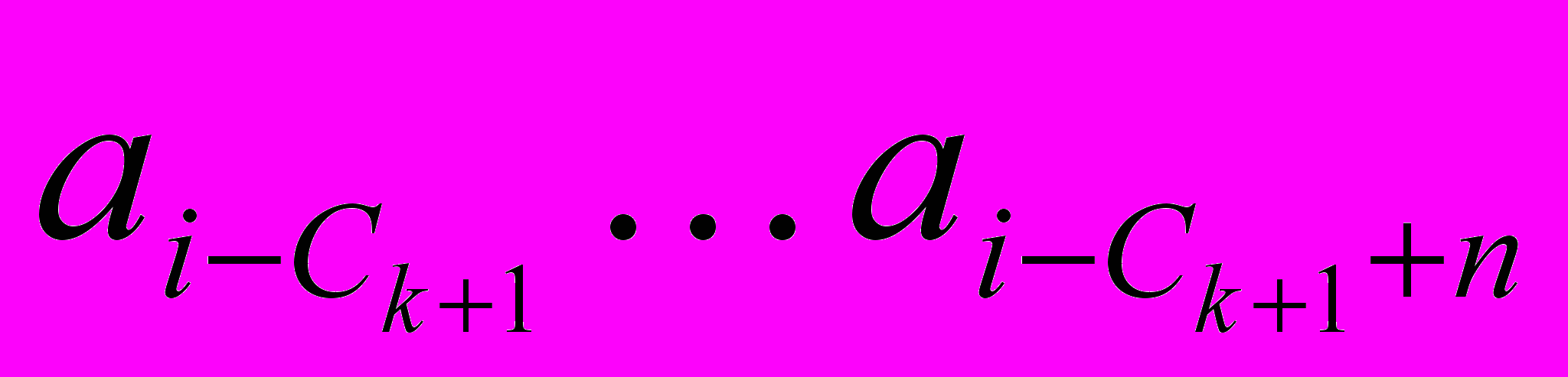конец алгоритма




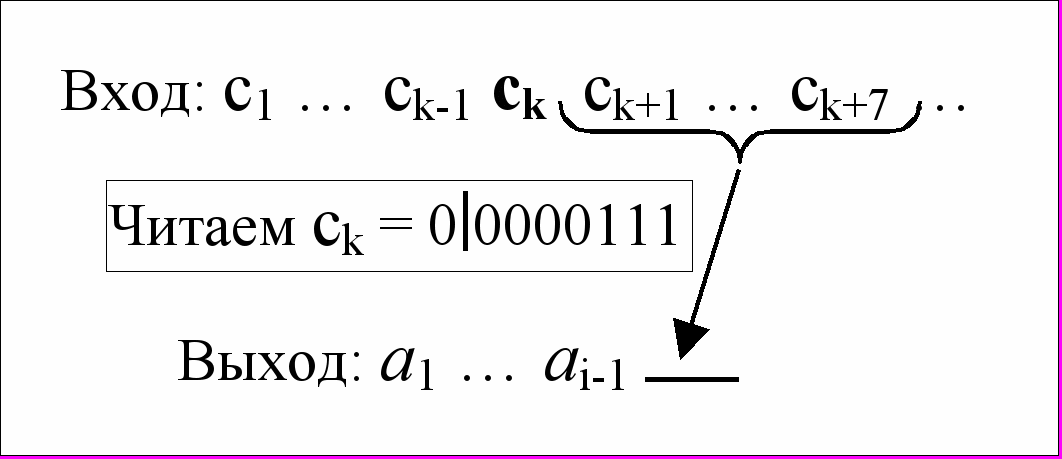
рис.1




рис.2


«Минусы» LZ77:

c_j ограничены (~ 16 бит), следовательно, смещение назад ограничено, т.е. кодировщик «забывает» начало входного потока;

долгий процесс кодирования.

2.2.LZW (Lempel, Ziv, Welch)

Пусть на вход подаются символы a, b, c, … (256 различных символов по 8 бит). Идея в том, что часто встречающиеся слова (т.е. последовательности символов) будем хранить в “словаре”.

Алгоритм кодирования (Пример работы алгоритма см. на рис.3)

Кладем в словарь символы a, b, c, … под номерами 0 .. 255, соответственно.

строка = пустая

пока (поток не пуст) //смотрим входной поток

строка += след.элемент

если (строка есть в словаре) то продолжить;

иначе

// код(строка0) — код, соответствующий строке0 в словаре

вывести код(строка – последний элемент)

добавить_в_словарь(строка)

строка = последний_элемент(строка)

конец если

конец пока

конец алгоритма




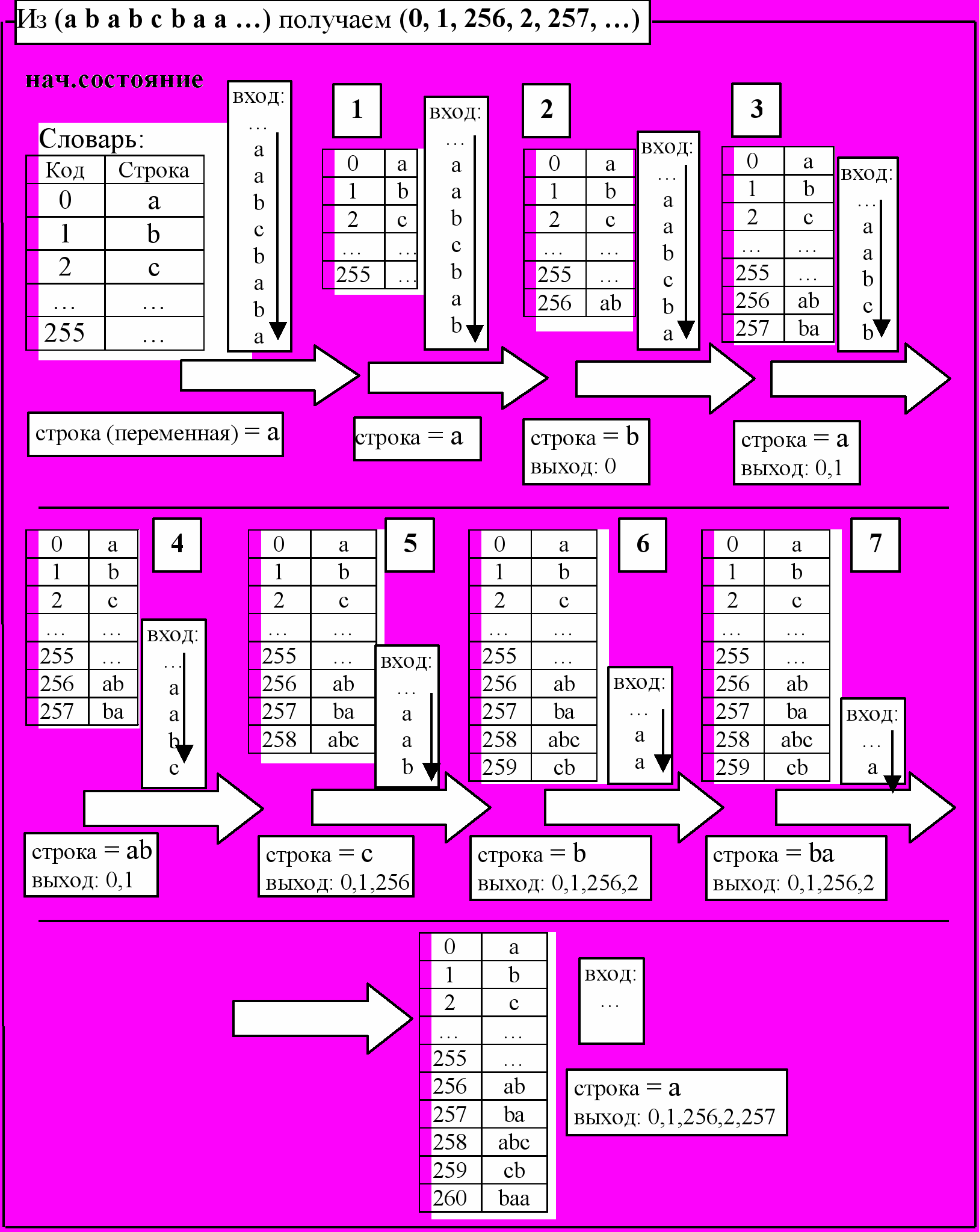
рис.3. Работа кодировщика LZW


Утв. По выходной последовательности реконструируется и словарь, и входная последовательность.


Алгоритм декодирования

Кладем в словарь символы a, b, c, … под номерами 0 .. 255, соответственно.

пока (поток не пуст)

код = следующий код из потока

1если (в словаре есть слово для кода) (рис.4)

вывести содержимое_словаря(по коду)

добавить в словарь(содерж_словаря(по прошлому_коду) +

+ перв_символ(содерж_словаря(по коду)) )

2иначе

строка = содерж_словаря(по прошлому_коду) +

+ перв_символ(содерж_словаря(по прошлому_коду))

вывести(строка)

добавить в словарь(строка)

конец если

конец пока

конец алгоритма




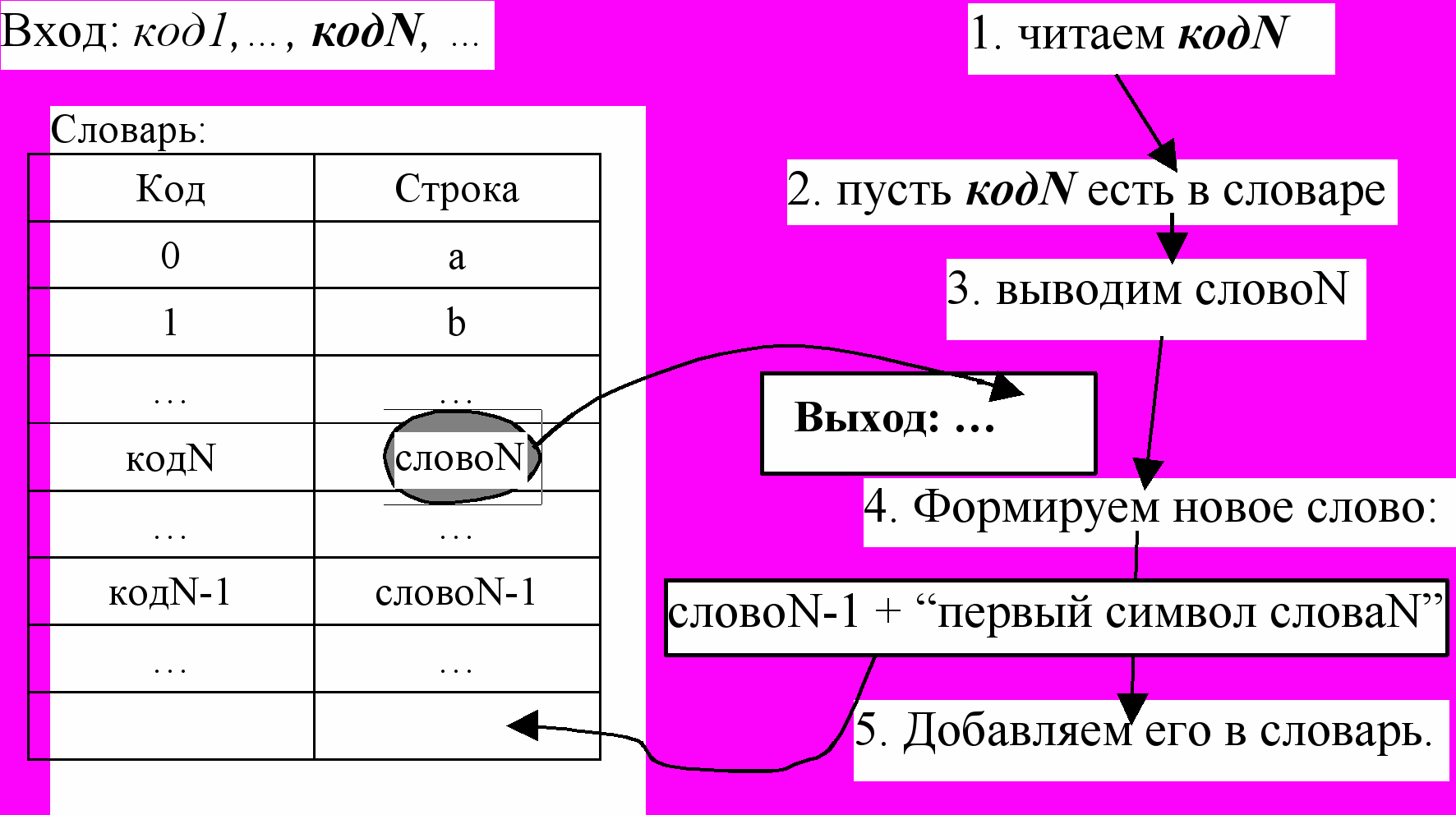
рис.4. Шаг работы декодировщика LZW в случае 1


Возникают следующие вопросы.

1. Пока в словарь добавили мало слов, на представление кода можно отводить меньше бит: до 512 слов — 9 бит на код, от 512 до 1024 — 10 бит и т.д. Изменение длины кодов должны контролировать и кодировщик, и декодировщик.

2. Если словарь кончится: обнуляем словарь (главное, это должны знать и кодировщик, и декодировщик).

3. Чтобы поиск последовательности в словаре занимал меньше времени можно организовать словарь в виде бинарного дерева поиска.


LZW используется в GIF, PING, ZIP, …

3.Алгоритмы, учитывающие частоту вхождения символов

3.1.Алфавитное кодирование

Пусть

a₁ a₂ … a_N — буквы входного потока,

b₁ b₂ … b_M — буквы выходного потока,

последовательность букв есть слово: 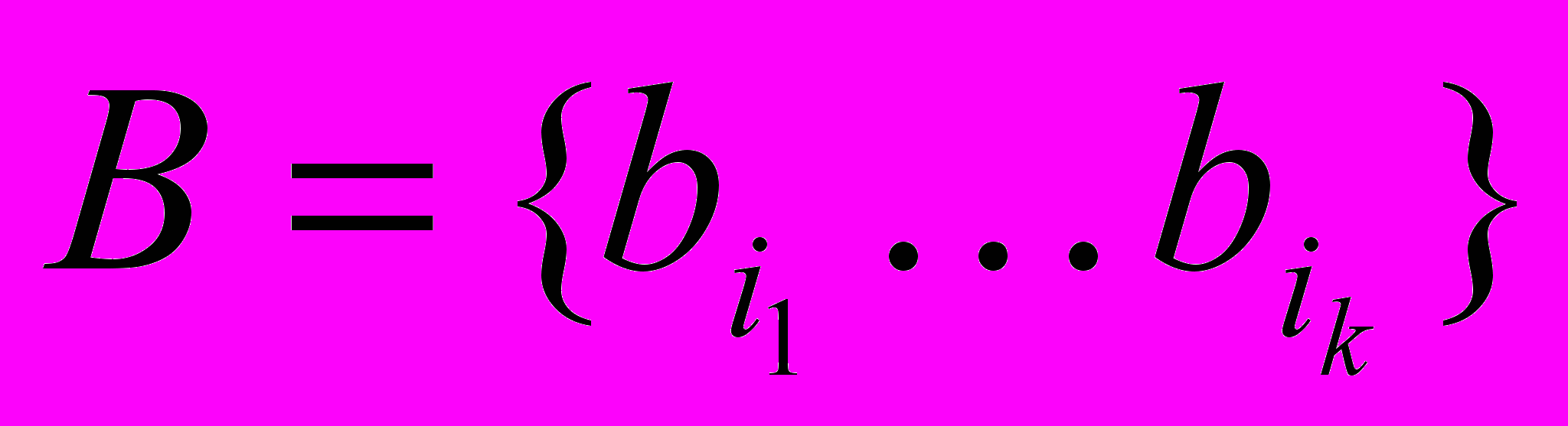— слово.

Рассмотрим следующую схему кодирования.

Каждому a_i сопоставим B_i.

Выполняется свойство префикса, т.е. 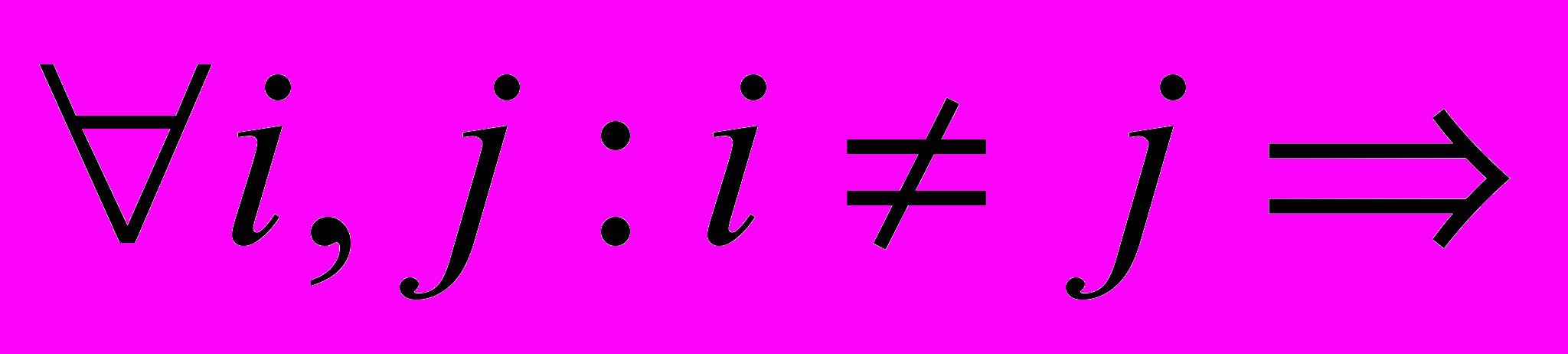B_i не есть начало B_j (значит, возможно однозначное декодирование).

Если на вход подавались 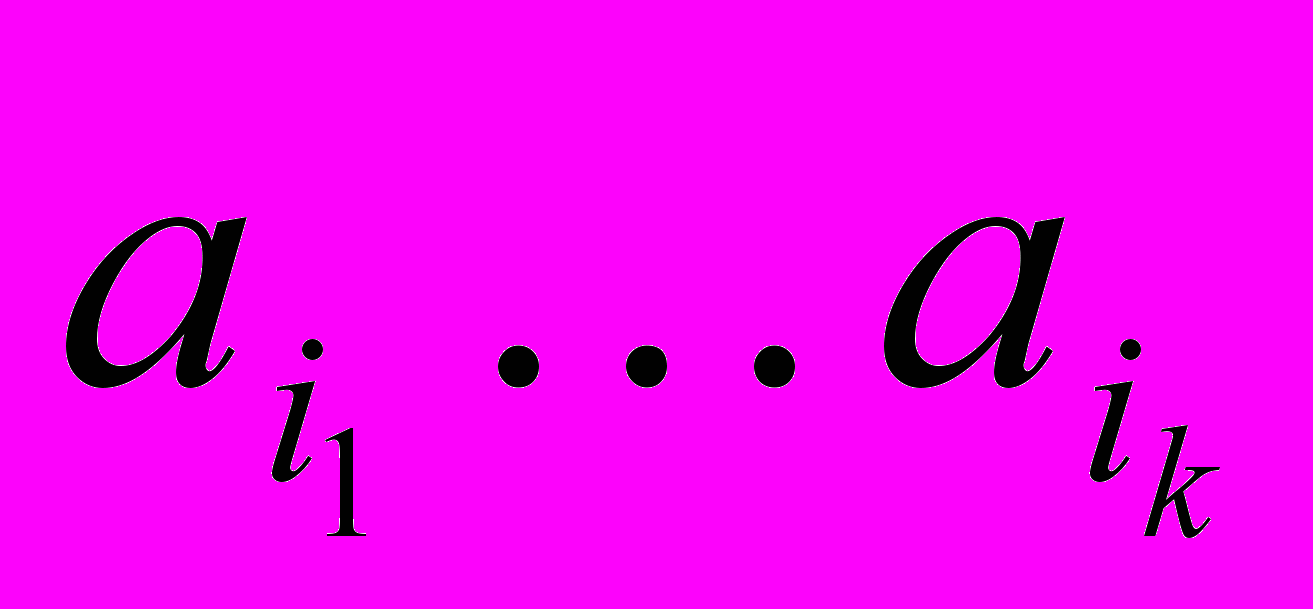и какая-то буква встречается чаще, чем остальные, то кодируем ее меньшим числом бит, чем другие буквы (т.е. в процессе кодирования строим гистограмму частот входных букв).

Остается вопрос, какой код приписать a_i.

3.2.Метод Хаффмана

{a₁, a₂, …, a_N} — алфавит входного потока;

{0, 1} — алфавит выходного потока.

Пусть у нас буквы a, b, c, d расположены в терминальных вершинах дерева:

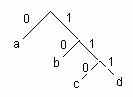рис.5.

Каждой букве мы можем приписать путь до нее от корня дерева, считая, например, передвижение по ветви влево — 0, вправо — 1:

a ~ 0, b ~ 10, c ~ 110, d ~ 111.

Разберем на примере процедуру построения дерева по входной последовательности, состоящей из a₁, a₂, a₃, a₄, a₅.

Пусть a₁, a₂, a₃, a₄, a₅ встретились 5, 3, 10, 1 и 4 раза соответственно. Строим гистограмму частот этих символов.

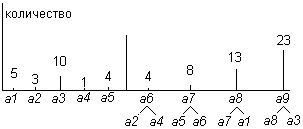рис.6.

1. Берем две самые редкие буквы: a₂ и a₄, создаем временный узел a₆, для которого a₂ и a₄ — нижние листья, (частота a₆) = (частота a₂) + (частота a₄) = 4. a₂ и a₄ в дальнейшем не рассматриваем.


2. Из a₁, a₃, a₅, a₆ выбираем две самые редкие буквы: a₅ и a₆, создаем временный узел a₇ с частотой 4 + 4 = 8, для которого a₅ и a₆ — нижние листья. a₅ и a₆ в дальнейшем не рассматриваем.


3. Из a₁, a₃, a₇ выбираем две самые редкие буквы: a₁ и a₇, создаем a₈ с частотой 13, для которого a₁ и a₇ — нижние листья. a₁ и a₇ в дальнейшем не рассматриваем.


4. Создаем a₉, с нижними листьями a₃, a₈.


Получаем дерево:

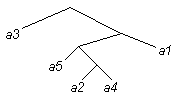рис.7.

Свойства метода Хаффмана:

1. Код Хаффмана оптимален (в смысле результата наименьшей длины в пределе) в классе алгоритмов, использующих префиксный код.
   
2. Таблицу частот символов можно или строить для каждой входной последовательности свою, или использовать фиксированную таблицу кодов, или строить ее динамически по имеющимся на каждый момент данным.
   

Кодирование Хаффмана используется, например, в JPG.

3.3.Арифметическое кодирование

Строим гистограмму частот символов входной последовательности: a₁, a₂, a₃, … — с частотами p₁, p₂, p₃, …. Рассматриваем отрезок [0, 1]. Разбиваем его на отрезки 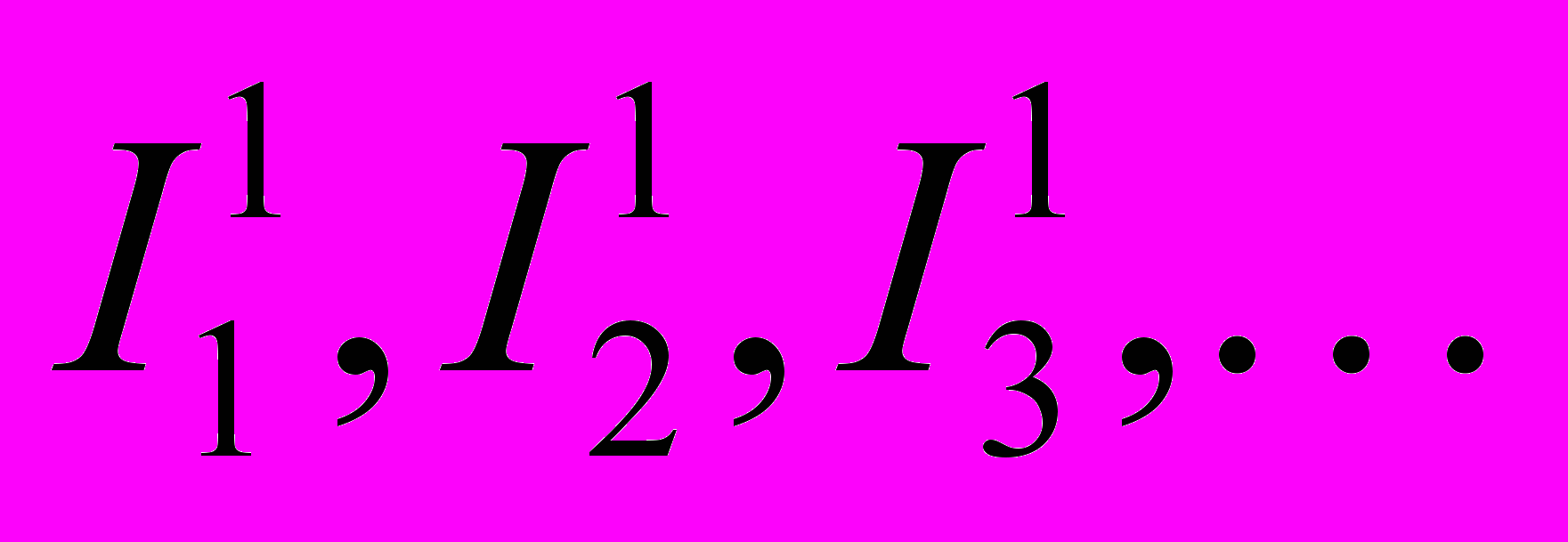с длинами, пропорциональными p₁, p₂, p₃, …. Далее, вся входная последовательность кодируется одним числом из [0, 1]. Пусть первый символ — a_i, тогда разбиваем отрезок 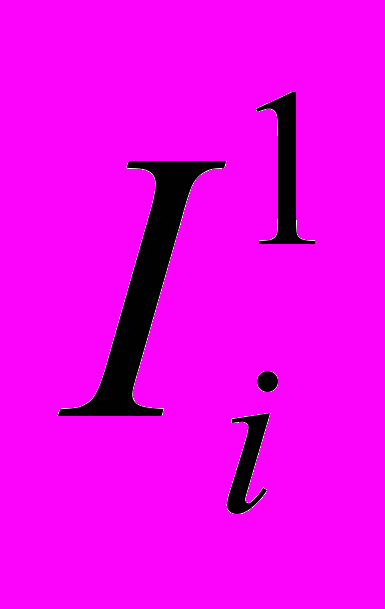, на 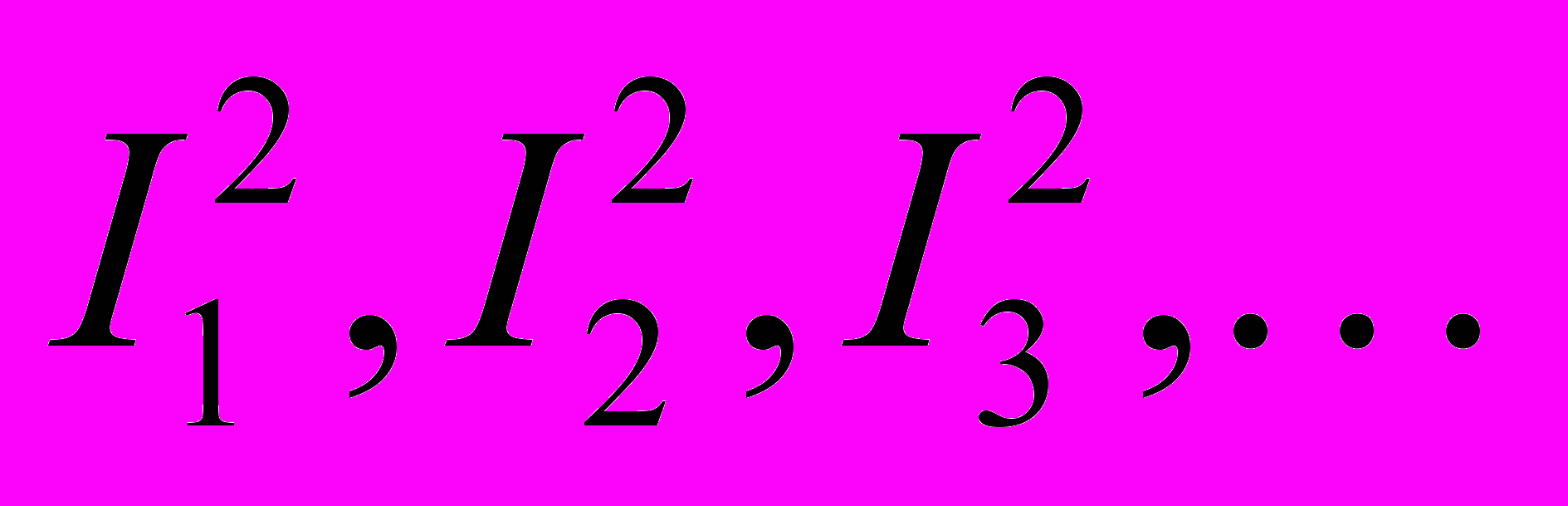с длинами, пропорциональными p₁, p₂, p₃, …. Пусть второй символ на входе — a_j, тогда разбиваем отрезок 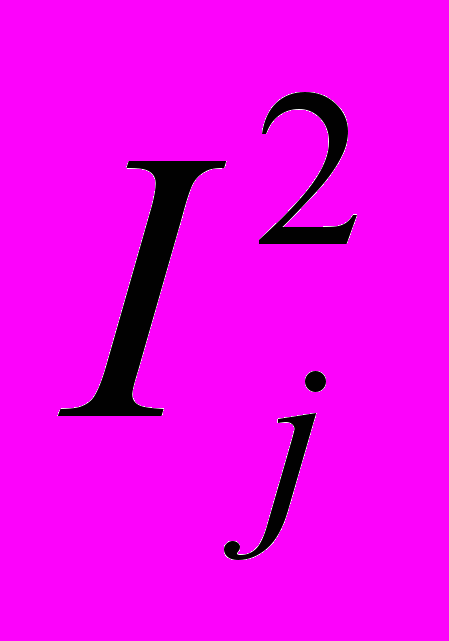, на 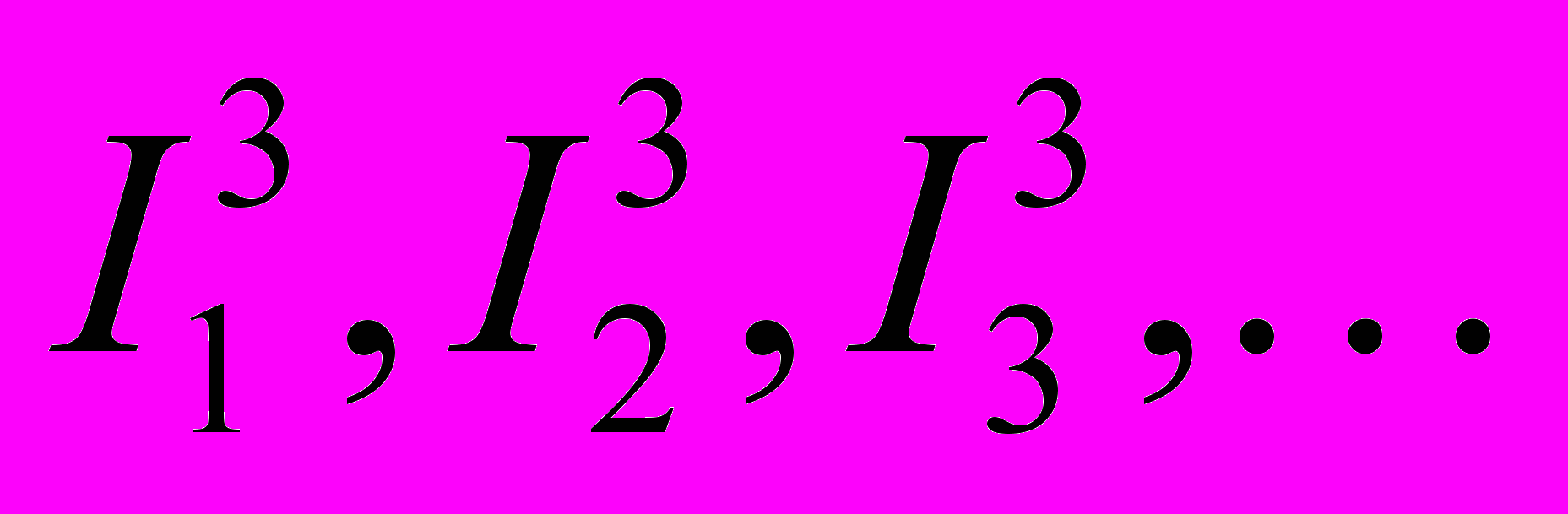с длинами, пропорциональными p₁, p₂, p₃, …. И т.д. Пусть последний символ попал в отрезок 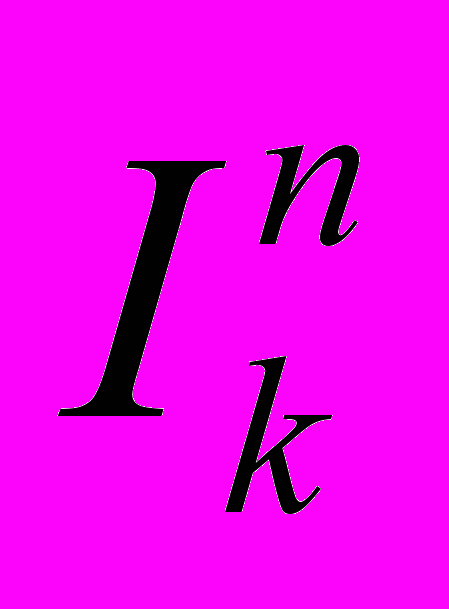, тогда вся последовательность кодируется каким-нибудь числом (его можно записать в двоичном виде) из 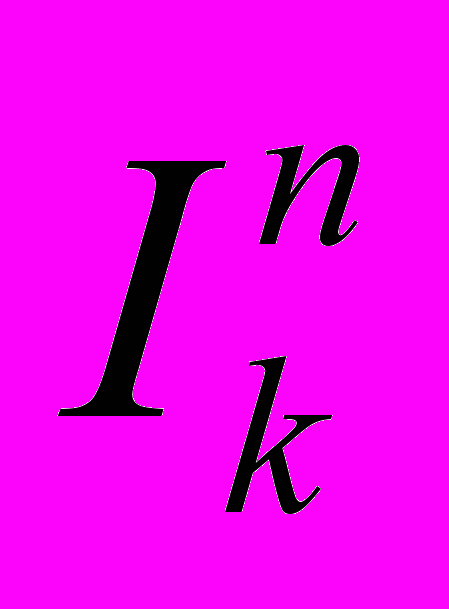, при этом, конечно, надо или хранить таблицу частот входных символов, или использовать фиксированную, или строить ее динамически по имеющимся на каждый момент данным.

Арифметическое кодирование также в пределе оптимально.


Построение двоичной дроби.

Пусть результирующий отрезок 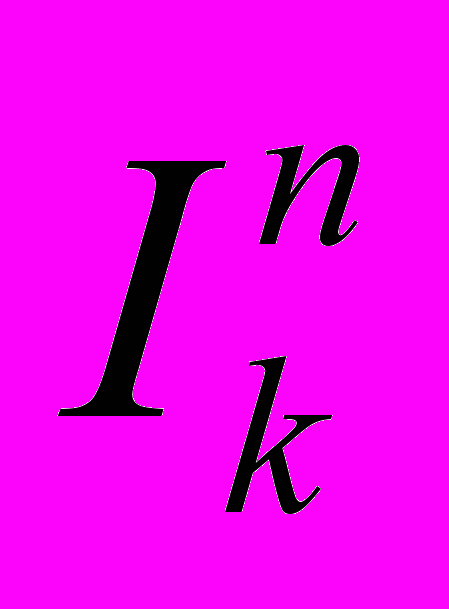= [x, y]. Чтобы получить кодирующую дробь нам достаточно получить двоичную запись какого-нибудь числа, отстоящего от z = (x + y)/2 меньше чем на d = (y – x)/2. Это можно сделать, например, так:

алгоритм

a = 0, b = 1

строка = пустая

пока( (z – a > d) или (b – z > d) )

c = (a + b)/2

если (z <= c)

строка += “0”

b = c

иначе

строка += “1”

a = c

конец пока

ответ = строка

конец алгоритма

В итоге: [a,b] лежит внутри [x,y], число, двоичная запись которого хранится в переменной строка, лежит внутри [a,b], значит, это число можно использовать для кодирования.


Пример.

На вход подаются символы a, b, c с частотами p_a, p_b, p_c.

Последовательность начинается с abc….

Это начало кодируется так:







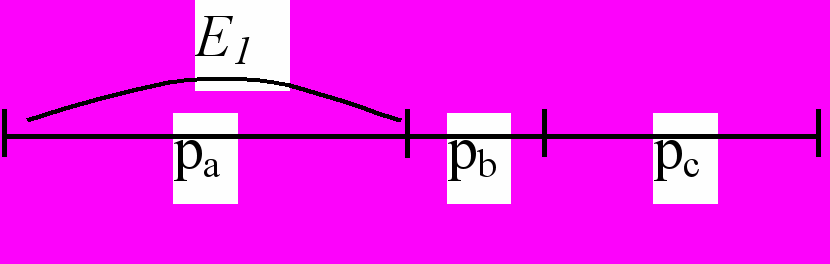
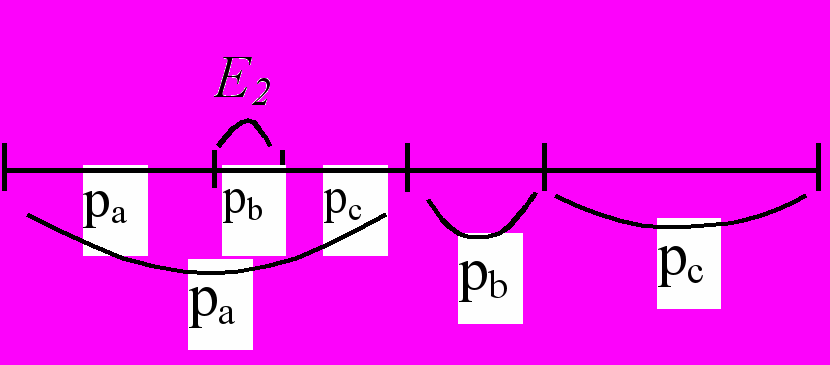
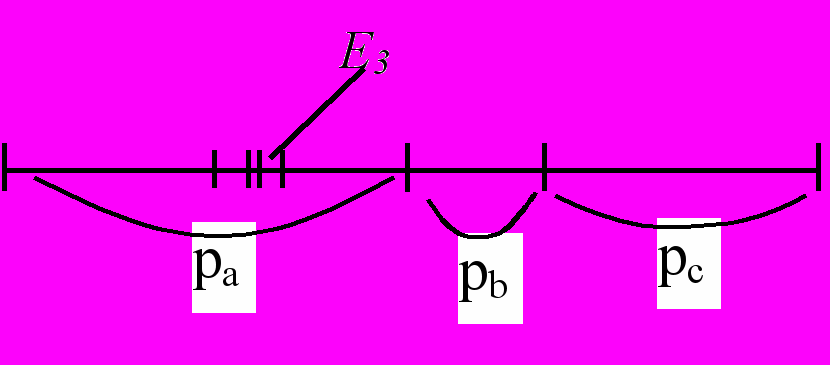
отрезок E₁ ~ a, отрезок E₂ ~ ab, отрезок E₃ ~ abc.