Симетрические разностные схемы метода совместной аппроксимации для решения линейного уравнения переноса
| Вид материала | Литература |
- Теория разностных схем, 25.48kb.
- Решение уравнения теплопроводности Постановка задачи, 83.2kb.
- Синявская средняя общеобразовательная школа, 63.47kb.
- Вдокладе представлен сравнительный анализ метода конечных объёмов и метода Галёркина, 27.76kb.
- Тема: Уравнение с двумя переменными. Цели урока, 251.03kb.
- Реализация алгоритмов решения задач газовой динамики на многопроцессорных вычислительных, 9.14kb.
- Выносимых на итоговый государственный экзамен, 118.84kb.
- Лекции 34 час. Для специальности «Математика. Прикладная Практ занятия 51 математика», 21.96kb.
- Лекция №8, 45.41kb.
- Библиотека нейтронных констант программы mcu-fcp, предназначенной для решения уравнения, 109.99kb.
УДК 519.6
СИМЕТРИЧЕСКИЕ РАЗНОСТНЫЕ СХЕМЫ МЕТОДА СОВМЕСТНОЙ АППРОКСИМАЦИИ ДЛЯ РЕШЕНИЯ ЛИНЕЙНОГО УРАВНЕНИЯ ПЕРЕНОСА
к. т. н., доц. В. Л. Бучарский, Днепропетровский национальный университет им. О. Гончара
инж.-констр. Е. М. Калинчук КБ «Южное», smileliz@mail.ru
На сегодняшний день существует множество подходов к построению разностных схем для решения линейных уравнений в частных производных. Ранее автором был предложен метод совместной аппроксимации [1, 2], позволяющий получать разностные схемы более высокого порядка точности, чем классические подходы.
В работах [1, 2] для построения разностных схем использовались несимметричные противопоточные шаблоны. Это не давало возможности проводить расчеты при отрицательных значениях скорости переноса. В настоящей работе приведены результаты применения данного метода к построению симметричных разностных схем для решения линейного уравнения переноса.
При построении использовались трёхточечные, пятиточечные и семиточечные шаблоны. Были получены разностные схемы от второго до восьмого порядка точности для нестационарного линейного гиперболического уравнение первого порядка.
Было проведено исследование устойчивости полученных разностных схем. Показано, что полученные разностные схемы позволяют проводить устойчивые расчеты при любых знаках скорости переноса.
Для подтверждения теоретических выкладок был проведен ряд тестовых расчетов. Работоспособность схем была проверена на решении уравнения переноса пр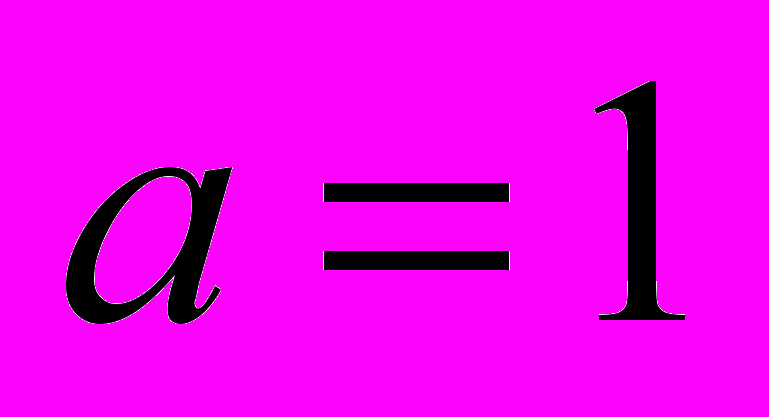и
и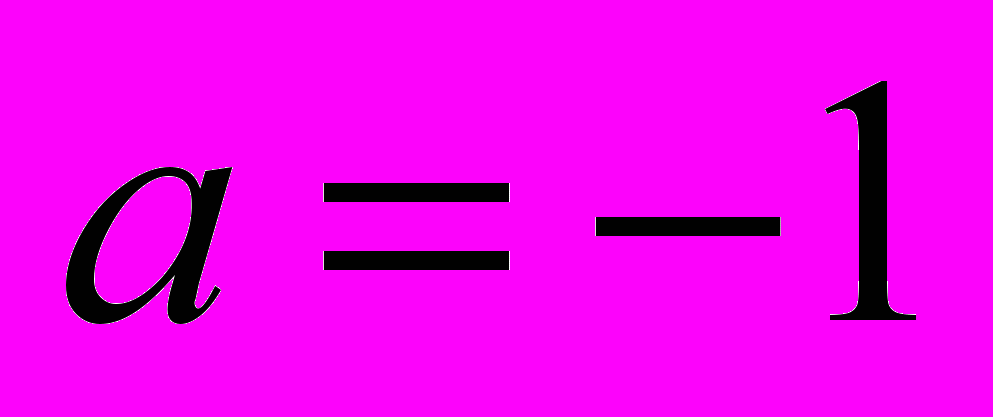 
с периодическими граничными условиями.Литература
- Бучарский В. Л. Метод совместной аппроксимации построения разностных схем для решения уравнений в частных производных // Техническая механика. – 2007. – №1 – С. 50–57.
- Бучарский В. Л. Разностная схема метода совместной аппроксимации для решения квазилинейных гиперболических уравнений // Проблеми обчислювальної механіки і міцності конструкцій. – 2008. – Вип. 12. – С. 12–19.