Решение транспортных задач с использованием комбинированного генетического алгоритма*

Вид материала

Решение

Содержание Постановка задачи V – количество идентичных автомобилей грузоподъемностью q C – множество клиентов. Ограничение (3) – это ограничение по времени; прибытие автомобиля к клиенту должно быть в пределах време 2. Структура генетического алгоритма Оператор инициализации Оператор кроссинговера. Операторы мутации. 3. Результаты экспериментов Список литературы

Подобный материал:

• Isbn 978-5-7262-1377 нейроинформатика 2011, 136.96kb.
• План урока Организационный момент(1 мин) Проверка материала прошлого урока(10 мин.), 53.54kb.
• Блох Илья Игоревич, Дураков Андрей Викторович пгниу, ул. Букирева, 15 Аннотация Вданной, 97.49kb.
• Т. С. Скворцова Рязанский государственный радиотехнический университет, 39.64kb.
• Литература: [1,8-11,16,18], 419.3kb.
• Е. И. Коняева Рязанский государственный радиотехнический университет, 38.53kb.
• Рассматривается применение генетических алгоритмов для задачи составления расписания, 27.38kb.
• Титов Д. В., Кобак В. Г. Анализ подходов к улучшению результатов работы генетического, 82.51kb.
• Доклад на тему: "Модели эволюций и генетические алгоритмы", 155.74kb.
• Д. С. Осипенко Понятие алгоритма. Примеры алгоритмов. Свойства алгоритмов. Способы, 96.46kb.

РЕШЕНИЕ ТРАНСПОРТНЫХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ КОМБИНИРОВАННОГО ГЕНЕТИЧЕСКОГО АЛГОРИТМА^*


Т.С. Емельянова, В. М. Курейчик¹.

Представлен новый генетический алгоритм для решения транспортных задач с ограничением по времени (VRPTW - Vehicle Routing Problems with Time Windows) большой размерности.

Введение

Транспортные задачи (ТЗ) с ограничением по времени широко распространенный класс задач маршрутизации автотранспорта (VRP – Vehicle Routing Problem) [Babb, 2005]. Точные методы, основанные на методах направленного перебора, не позволяют эффективно решать данные задачи большой размерности. Эвристические и метаэвристические методы, к которым относятся генетические алгоритмы (ГА), дают в этом случае лучшие результаты. В данной статье описывается новый ГА, который позволяет эффективно решать ТЗ с ограничением по времени. Операторы инициализации и кроссинговера данного ГА построены на комбинации известных методов решения ТЗ с ограничением по времени. В первой части статьи дана постановка задачи, во второй описание ГА и всех его операторов, в третьей результаты решения тестовых задач с использованием данного ГА и выводы по результатам экспериментов.

1. Постановка задачи
   

ТЗ с ограничением по времени можно описать следующим образом. Имеется некоторое количество автотранспорта, один склад (депо) и некоторое количество клиентов. Для каждого транспортного средства требуется составить маршрут, на протяжении которого транспортное средство посещает ряд клиентов (например, с целью доставки какого-либо груза). На маршрут каждого транспортного средства накладывается ряд ограничений. Основные ограничения представлены формулами (1)-(3).

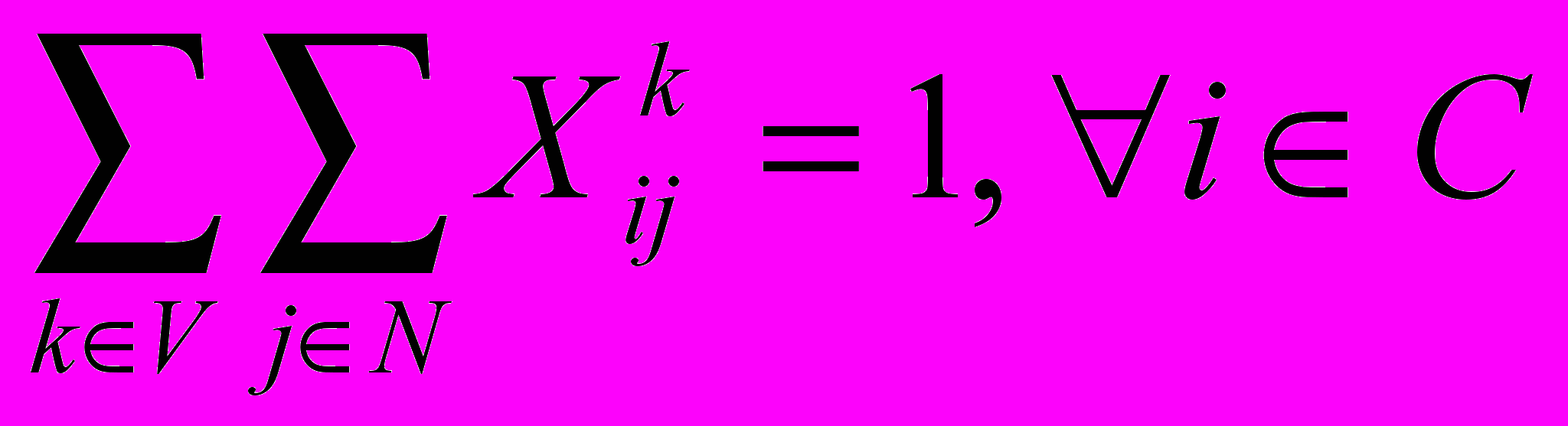(1)

(2)

(3)

Ограничение (1) полагает, что каждый клиент обслуживается только одним транспортным средством и только один раз. Переменные X_ij^k принимают значения {0, 1}, 1 означает, что автомобиль движется от вершины i к вершине j, 0 обратное. Верхним индексом k обозначаться соответствующий автомобиль, где , V – количество идентичных автомобилей грузоподъемностью q. Ограничение (2) определяет, что транспортное средство не может обслужить больше клиентов, чем позволяет его грузоподъемность. d_i, – спрос соответствующего клиента, C – множество клиентов. Ограничение (3) – это ограничение по времени; прибытие автомобиля к клиенту должно быть в пределах временного окна, где S_i^k – это время прибытия соответствующего автомобиля к определенному клиенту, а [a_i, b_i] промежуток времени, так называемое “временное окно” (time window) в течении которого должен быть обслужен клиент. Для данной задачи формулируются следующие цели (целевые функции): первичная цель – минимизировать общее количество транспортных средств, необходимых для обслуживания всех клиентов; вторичные – минимизировать общее время обслуживания всех клиентов и общее расстояние, пройденное всеми транспортными средствами [Cordeau, 2001].

2. Структура генетического алгоритма

ГА являются случайно направленными поисковыми методами и успешно применялись для решения задач транспортного типа [Емельянова, 2006], [Емельянова, 2007]. В общем случае структура ГА состоит из следующих операторов: инициализации, селекции, кроссинговера и мутации [Курейчик, 2004]. Далее будут подробно описаны данные операторы, т. к. они являются основой представляемого ГА.

Оператор инициализации построен на основе метода конструирования маршрутов – метод Соломона [Bräysy, 2001], [Tan, 2000]. Преимущество данного оператора в том, что он позволяет не только строить новые решения при инициализации популяции решений, но и достраивать решения (решения в которых часть клиентов обслужена, а часть еще нет), это особенность будет использоваться в описанных ниже операторах.

Оператор кроссинговера. Данный оператор кроссинговера реализован по аналогии с адаптивной памятью в методе поиска с запретами [Taillard, 1997]. Количество родителей, участвующих в скрещивании определяется числом N, увеличение N позволяет более эффективно передавать свойства (маршруты) родителей потомкам, сходимость алгоритма увеличивается, но это грозит опасностью попадания в локальный минимум. При уменьшении N растет разнообразие в популяции. Эксперименты показали, что алгоритм дает наилучшие результаты при N от 2 до 4.

1. Выбираем число N – количество решений (особей) участвующих в кроссинговере.
   
2. Выбираем N решений из популяции. Для этого применяем оператор Селекции.
   
3. Маршруты из выбранных решений объединяем в одно решение. Данное решение назовем объединенным решением.
   
4. Пока в объединенном решении есть маршруты, делаем следующее: выбираем маршрут и вставляем его в новое решение, для этого берем случайное число в пределах от 0 до количества маршрутов в объединенном решении, данное число и будет указывать номер маршрута в объединенном решении; удаляем выбранный маршрут в объединенном решении; удаляем в объединенном решении все маршруты, в которых есть клиенты из выбранного решения;
   
5. Вставляем не обслуженных клиентов в новое решение с использованием оператора Инициализации
   

Новое решение является потомков выбранных N решений родителей. Рис.1 иллюстрирует данный оператор кроссинговера.

Рис. 1. Оператор кроссинговера

Операторы мутации. В данном ГА применяются два оператора мутации. Разные операторы мутации и комбинации этих операторов применяются на разных этапах поиска. Основным для применения является оператор мутации ОМ_1, оператор мутации OM_2 применяются для дополнительного стимулирования процесса поиска. ОМ_1 наименее затратный по временным ресурсам оператор мутации. При применении данного оператора из решения удаляются маршруты целиком, затем клиенты с удаленных маршрутов заново вставляются в решение, рис. 2.

Рис. 2 Оператор мутации ОМ_1	Рис. 3 Оператор мутации ОМ_2

При применении оператора мутации ОМ_2 из решения удаляются отдельные клиенты, и затем заново вставляются в маршрут, рис. 3. В результате применения операторов мутации мы получаем новое решение, которое расширяет область поиска за счет нового набора маршрутов.

3. Результаты экспериментов

Проверка эффективности алгоритма осуществлялась решением тестовых задач Соломона [Gendreau, 2003]. Тестовые задачи Соломона делятся на шесть классов R1 (12 задач), R2 (11  задач), С1 (9  задач), С2 (8 задач), RС1 (8 ), RС2 (8 задач). В задачах класса R клиенты географически распределены равномерно вероятностным образом, в задачах класса С клиенты расположены группами, в задачах класса RC часть клиентов расположена группами, а остальная часть распределена равномерно вероятностным образом. В каждой задаче 100 клиентов и одно депо, задачи в пределах одного класса имеют одинаковые координаты клиентов и максимальную грузоподъемность машины, но различаются по временным ограничениям обслуживания клиентов. В Таблице сравниваются решения, полученные с использованием данного ГА, с лучшими решениями тестовых задач. Решения полученные в классах С1 и С2 не показаны, т. к. они совпадают с с лучшими известными результатами. Параметры ГА следующие P_к = 30%, P_м = 80%, размер популяции – 300, (*) означает, что максимальное кол-во итераций – 500,(**) – максимальное кол-во итераций 1000

Таблица

Название задачи	Исторически лучшие решения	Решение полученное данным ГА	Название задачи	Исторически лучшие решения	Решение полученное данным ГА
R101	19/1645.79	19/1653.53(*)	R201	4/1252.37	4/1302.94(*)
R102	17/1486.12	17/1487.31(*)	R202	3/1191.70	4/1096.39(**)
R103	13/1292.68	13/1307.25(*)	R203	3/939.54	3/1015.96(*)
R104	9/1007.24	10/990.85(*)	R204	2/825.52	3/769.86(*)
R105	14/1377.11	14/1402.76(*)	R205	3/994.42	3/1062.04(*)
R106	12/1251.98	12/1271.89(*)	R206	3/906.14	3/991.73(*)
R107	10/1104.66	10/1146.2(*)	R207	2/893.33	3/845.87(*)
R108	9/960.88	10/976.23(*)	R208	2/726.75	2/789.25(*)
R109	11/1194.73	12/1157.13(*)	R209	3/909.16	3/993.07(*)
R110	10/1118.59	11/1162.34(*)	R210	3/939.34	3/973.96(*)
R111	10/1096.72	11/1081.30(*)	R211	2/892.71	3/837.35(*)
R112	9/982.14	10/1024.14(*)	RC201	4/1406.91	4/1451.66(*)
RC101	14/1696.94	15/1642.99(*)	RC202	3/1367.09	4/1239.44(*)
RC102	12 /1554.75	13/1489.92(*)	RC203	3/1049.62	3/1138.46(*)
RC103	11/1261.67	11/1297.85(*)	RC204	3/798.41	3/843.79(*)
RC104	10/1135.48	10/1146.37(**)	RC205	4/1297.19	4/1378.34(*)
RC105	13/1629.44	14/1552.05(**)	RC206	3/1146.32	3/1269.23 (*)
RC106	11/1424.73	12/ 1400.83(**)	RC207	3/1061.14	3 /1145.06(*)
RC107	11/1230.48	11/1239.01(**)	RC208	3/828.14	3/889.80(*)
RC108	10/1139.82	10/1187.61(**)

На рис.4-5 показаны графики зависимости ЦФ лучших решений и решений полученных с помощью описанного ГА от номера задачи. ЦФ определялась по формуле ЦФ = Кол-во машин * 1000 + Общее пройденное расстояние. Данные графики наглядно показывают результаты испытаний для тестовых задач класса R1 и RC1.

Рис. 4 Зависимость ЦФ лучших решений от номера задачи в группе R1.	Рис. 5 Зависимость ЦФ лучших решений от номера задачи в группе RС1.

Из результатов экспериментов представленных в Таблице и на рис. 4-5, следует вывод, что в некоторых задачах: группы R и группы RC количество требуемых машин больше на одну машину, чем количество машин лучших результатов, но увеличенное количество машин компенсируется уменьшением общего пройденного расстояния. Во всех остальных задачах количество машин равно количеству машин лучших результатов. Следовательно, данный алгоритм позволяет эффективно решать ТЗ с ограничением по времени. Общее пройденное расстояние, в каждой отдельной задаче близко к лучшему, а в задачах группы С совпадает с лучшим значением. Применение дополнительного оператора мутации повышает эффективность ГА и качество получаемого решения в смысле ЦФ.

Список литературы

[Babb, 2005] Tobias Babb. Pickup and Delivery Problem with Time Windows, Coordinated Transportation Systems: The State of the Art. Department of Computer Science University of Central Florida Orlando, Florida, 2005.

[Cordeau, 2001] J.-F. Cordeau, Guy Desaulniers, Jacques Gesrosiers, Marius M. Solomon, Francois Soumis. The VRP with Time Windows. Chapter 7, Paolo Toth and Daniel Vigo (eds), SIAM, Monographs on Discrete Mathematics and Applications, 2001.

[Емельянова, 2006] T. C. Емельянова. Применение генетических алгоритмов для решения транспортной задачи линейного программирования. // Перспективные информационные технологии и интеллектуальные системы Таганрог, №3(27), 15 – 29, 2006.

[Емельянова, 2007] T. C. Емельянова. Об одном генетическом алгоритме решения транспортной задачи. // Известия ТРТУ. – Таганрог, №1(73), 65 – 70, 2007.

[Курейчик, 2004] Генетические алгоритмы: Учебное пособие. Под ред. В. М. Курейчика. – Ростов-на-Дону: OOO «Ростиздат», 2004.

[Bräysy, 2001] Olli Bräysy, Michel Gendreau. Route Construction and Local Search Algorithms for the Vehicle Routing Problem with Time Windows. Internal Report STF42 A01024, SINTEF Applied Mathematics, 2001.

[Taillard, 1997] EricTaillard, Philippe Badeau, Michel Gendreau, Francois Guertin and Jean-Yves Potvin. A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows. Transportation Science 31, 170 – 186, 1997.

[Tan, 2000] K. C. Tan, L. H. Lee, K. Q. Zhu. Heuristic Methods for Vehicle Routing Problem with Time Windows. Proceedings of the 6^th Internayional Symposium on Artifical Intelligence & Mathematics, Ft. Lauderdale, Florida, 2000.

[Gendreau, 2003] Michel Gendreau, Olli Bräysy. Metaheuristic Approaches for the Vehicle Routing Problem with Time Windows: A Survey. MIC2003: The Fifth Metaheuristics International Conference, Kyoto, Japan, August 25-28, 2003.