Кандидат в члены-корреспонденты ран

Вид материала

Документы

Содержание Список литературы

Подобный материал:

• Академии Лауреаты Ленинской и Государственной премий, академики и члены-корреспонденты, 49.21kb.
• Академики в п. Волгин (председатель),, 12468.59kb.
• Регламент Конференции, 98.98kb.
• Альные педагогические мыслители, органично сочетающие незаурядный профессионализм, 125.4kb.
• Сибирское отделение ран центр общественных связей, 41.06kb.
• Ж. Т. Тощенко "О понятийном аппарате социологии" (№9). Вчтениях участвовали члены редколлегии,, 117.96kb.
• Доклад на Всероссийской научной конференции «От СССР к рф: 20 лет итоги и уроки», 140.15kb.
• Ганопольский В. И., Безносиков Е. Я., Булатов, 4124.25kb.
• Туризм и спортивное ориентирование, 3876.34kb.
• Номер: за 1994 год, 300.09kb.

Кандидат в члены-корреспонденты РАН

по Отделению энергетики, машиностроения, механики

и процессов управления РАН

по специальности «наномеханика и прочность материалов»


ПОБЕДРЯ Борис Ефимович

Заведующий кафедрой механики композитов механико-математического факультета Московского государственного университета им. М.В.Ломоносова, 1937 года рождения, доктор физико-математических наук, заслуженный профессор МГУ, лауреат Государственной премии СССР и Ломоносовской премии, заслуженный деятель науки РФ, член Национального Комитета РФ по теоретической и прикладной механике.

Победря Б.Е. – специалист в области механики деформируемого твёрдого тела, наномеханики и прочности материалов. Автор более 180 публикаций, в том числе 9 монографий и учебных пособий.

Основные научные результаты Победри Б.Е.:

- разработаны основы линейной и нелинейной термовязкоупругости с учётом тепловыделения при деформировании, созданы основы вычислительной механики композитов и нанокомпозитов для определения с любой наперёд заданной точностью микронапряжений и микротемпературы в физико-химически взаимодействующих между собой компонентах композита с учётом эволюционной деструкции, взаимодиффузии и фазовых переходов;

- предложена адекватная теория термовязкоупругости и общая теория процессов деформирования для анизотропных материалов, описаны алгоритмы решения краевых задач и решены важные прикладные задачи механики композитов;

- дан численный анализ известной прочностной задачи о «закладных элементах», найдены явные выражения для эффективных характеристик слоистых и однонаправленных волокнистых композитов и нанокомпозитов;

- предложены критерии прочности анизотропных и композиционных материалов, в том числе и термодинамические;

- дана принципиально новая постановка задачи механики деформируемого твёрдого тела в напряжениях, за которую ему присуждена Ломоносовская премия;

• решены задачи об идентификации слоистых нанокомпозитов.
  

- на основе асимптотической техники осреднения он предложил методику определения микронапряжений в каждом компоненте упругих, вязкоупругих и упругопластических композитов и нанокомпозитов, построил точные аналитические выражения приведённых механических и теплофизических характеристик слоистых и однонаправленных волокнистых композитов с упругими, вязкоупругими и упруго-пластическими компонентами, предложил критерии прочности композитов, в том числе термодинамические.

В последнее время Победря Б.Е. получил существенные результаты в механике резинокордных композитов, в механике слоистых нанокомпозитов, нелинейной теории вязкоупругости, в постановке задачи «в напряжениях» для полярных сред и разработке идентификации нанокомпозитов. В течение последних лет научно-исследовательской темой кафедры механики композитов является «микро - и наномеханика композитов». Победря создал оригинальные учебные программы для студентов и аспирантов основанной им кафедры механики композитов и факультета наук о материалах МГУ, подготовил и прочитал на механико-математическом факультете и факультете наук о материалах МГУ более 60 основных и специальных курсов. Среди них курсы «Механика нанокомпозитов» и «Механика вязкоупругих нанокомпозитов».

Победря Б.Е. с 1980 по 2000 г.г. – научный консультант ЦНИИСМ. Под его руководством защищены 49 кандидатских и 9 докторских диссертаций.

Многие из его разработок внедрены в промышленность. За работы по созданию методов расчёта конструкций из композиционных материалов Победря Б.Е. был удостоен Государственной премии СССР.

Как известно, механические и физико-химические характеристики вещества или материала инвариантны относительно его количества или размера. Однако это утверждение справедливо только до определенных пределов, а именно когда хотя бы в одном измерении протяжённость изучаемого объекта становится меньше 100 нм, его свойства перестают быть инвариантными, а становятся размернозави­симыми. Последний признак принципиально важен для корректного определения таких терминов, как “наночастица”, “нанопроволока”, “наноплёнка”. Механики используют фе­номенологический подход, и часто нанокомпозитами называют накроконструкции, в ко­торых отдельные компоненты по своим размерам на порядки меньше других компонентов композита. Естественным образом компоненты композита можно подразделить на макрокомпоненты и нанокомпоненты. При этом должна быть феноменологически учтена размернозависимость нанокомпонентов. Этого можно достичь путём введения многоуровневого (по крайней мере, двухуровневого) континуума [1].

Примером нанокомпозитов могут служить системы «подложка-покры­тие», которые бывают и многослойными. Различают «жёсткие» покрытия (когда их механические характеристики жёстче характеристик подложки) и «мягкие» (когда их механические характеристики мягче характеристик подложки). Термомеханическое поведение «жёстких» и «мягких» покрытий резко отличаются друг от друга. Их поведение также существенно зависит от технологии нанесения покрытия.

Из-за того, что во многих случаях толщина этих нанопокрытий на несколько порядков меньше толщины подложки, экспериментально определить их механические свойства очень трудно, а в большинстве случаев невозможно. На помощь приходят методы численного моделирования. Один из таких методов обсуждён в работе [2].

Рассмотрим для простоты композит с упругими однородными компонентами [3]. Обозначим тензоры четвёртого ранга модулей упругости каждого компонента 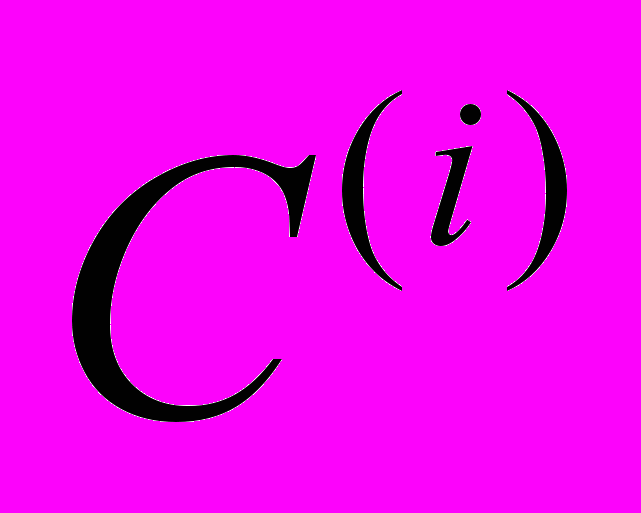, где i – номер компонента. Пусть имеется макрокомпонентов и 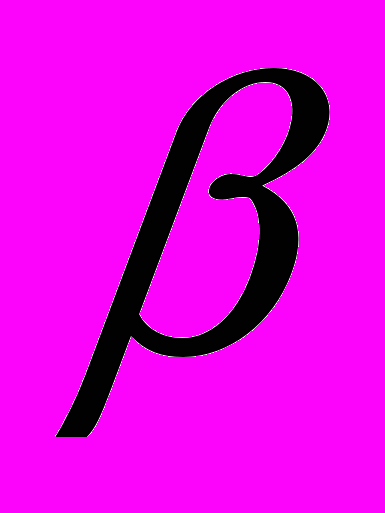нанокомпонентов композита. Для макрокомпонентов будем считать известными все тензоры модулей упругости, которые инвариантны относительно некоторых групп преобразований [4]. Для нанокомпонентов будем считать также известными эти группы преобразований, но неизвестными численные значения этих модулей.

Используя метод осреднения, подробно описанный в работе [3], можно аналитически или численно найти выражения тензора эффективных модулей упругости h, инвариантного относительно группы преобразований, определяемой группами преобразований тензоров .

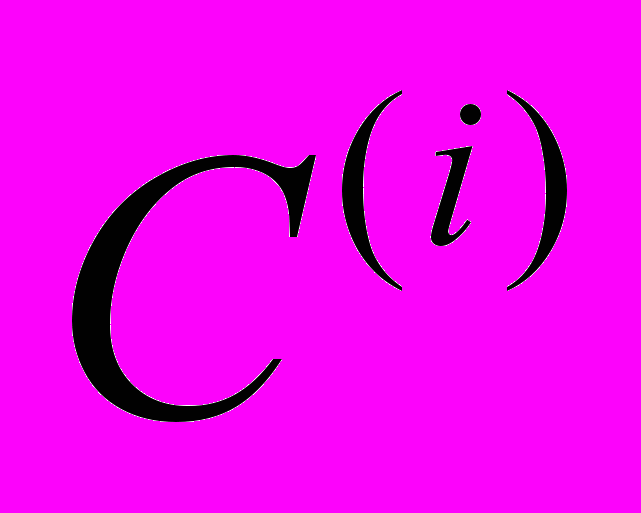Запишем условно этот тензор эффективных модулей упругости h в виде тензорной функции

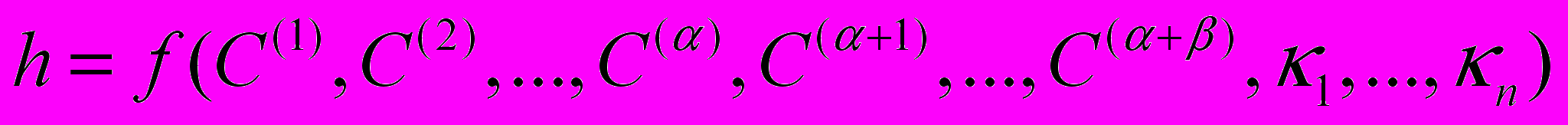(1)

где 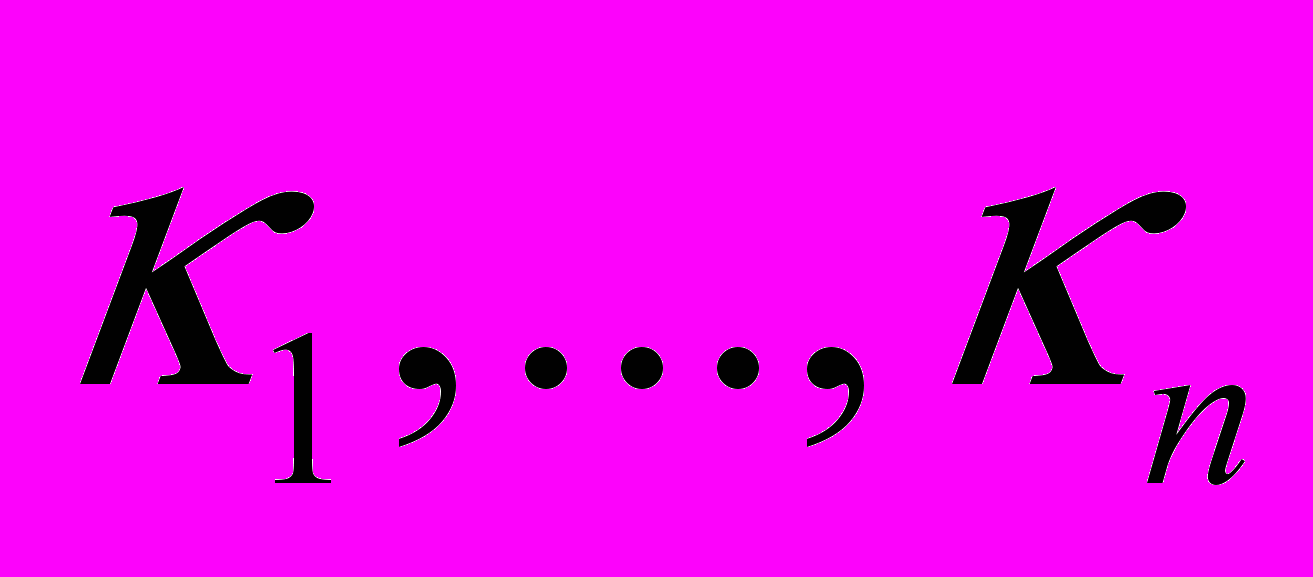- некоторые постоянные, определяющие структуру исследуемого композита.

Образуем какой-либо инвариант 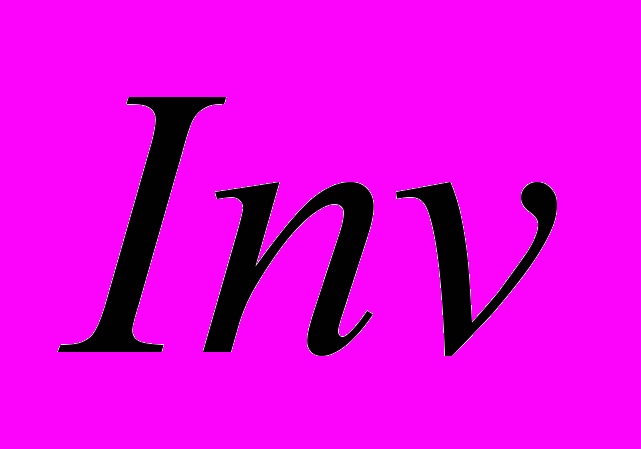тензора h, например, его определитель. Обозначим этот инвариант через

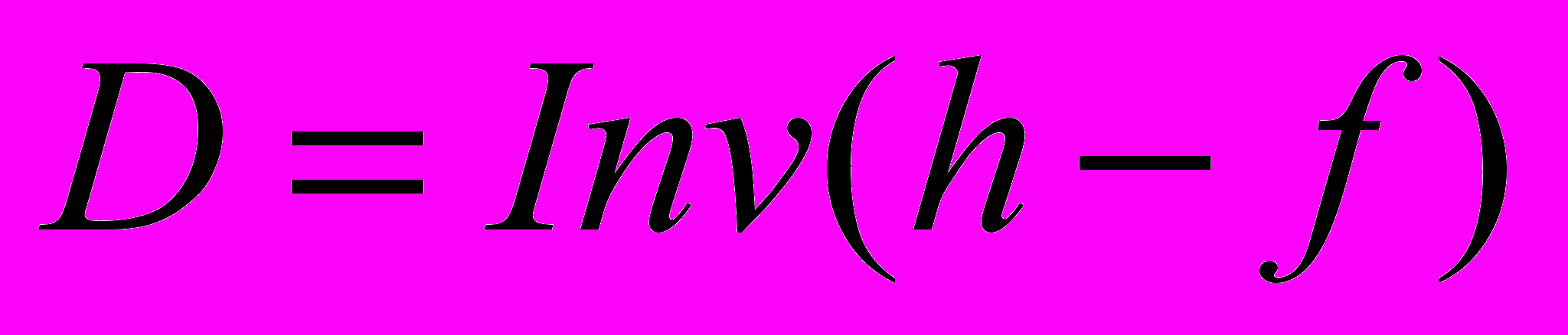(2)

Пусть число независимых компонент тензора модулей упругости 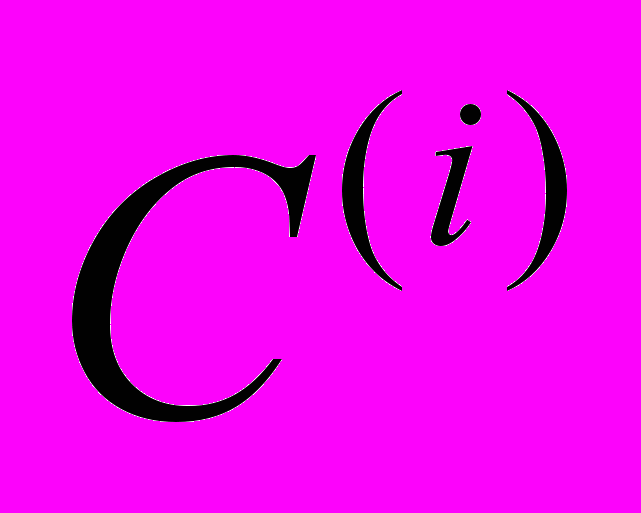нанокомпонента 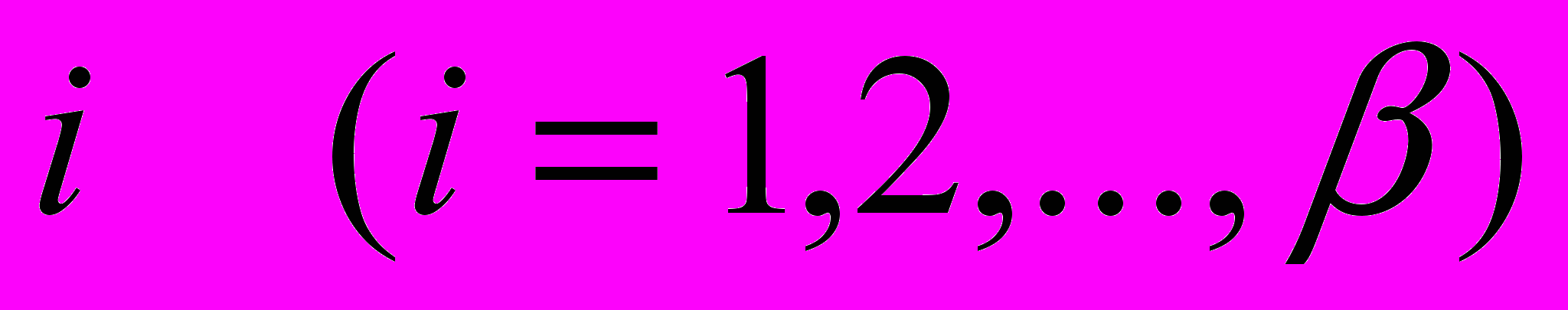равно 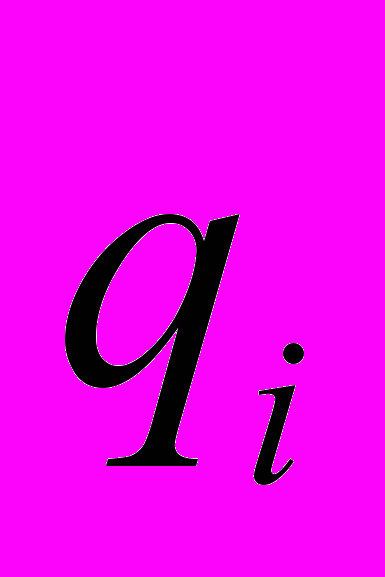(обычно слово «компонент» композита – мужского рода, а «компонента» вектора или тензора – женского).

Составим теперь систему 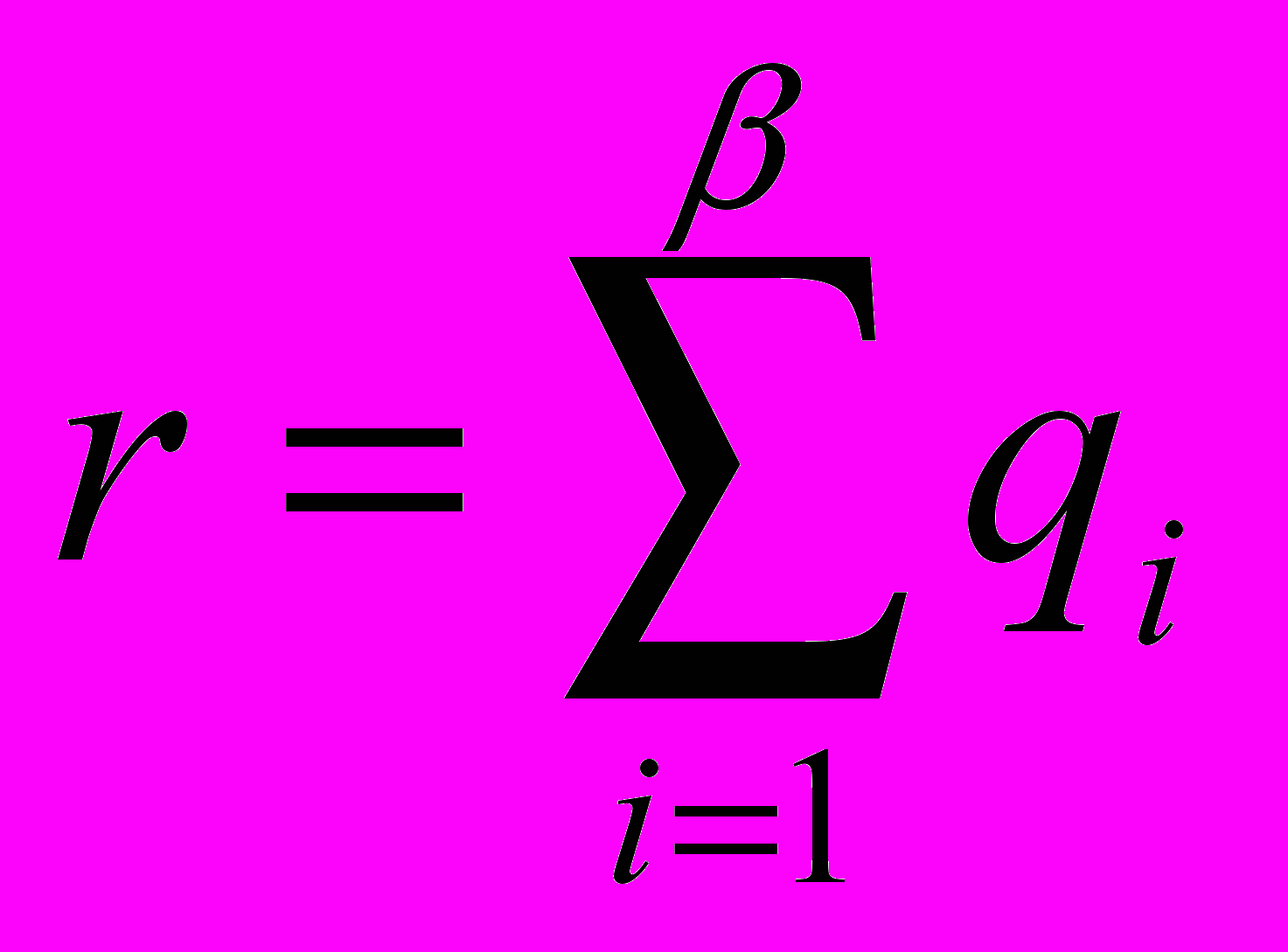нелинейных алгебраических уравнений

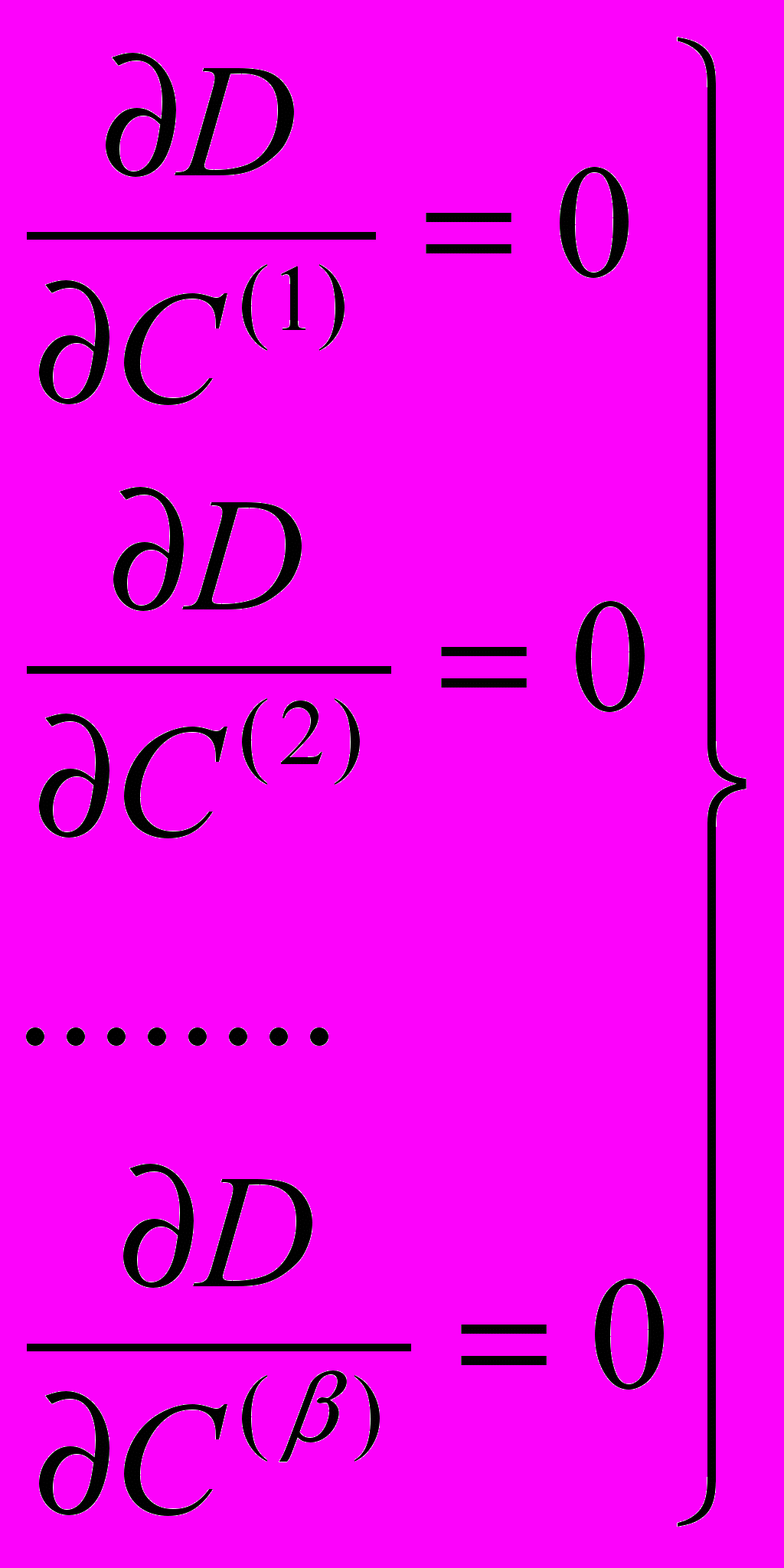(3)

относительно r неизвестных. Эти уравнения можно решить любым пригодным для этой цели методом [5].

Заметим, что конструкции, используемые в системах «подложка-покрытие», имеют самое разнообразное применение. Примером могут служить искусственные кожи, сопла ракетных двигателей, бронематериалы, влаго- и теплозащитные покрытия и т.п. В настоящее время также интенсивно развивается использование полимерных плёнок с нанесённым на них тонким, порядка 0,1-0,5 микрон, покрытием [6]. Подобные плёнки используются в электронике (например, при производстве жидкокристаллических дисплеев), в пищевой промышленности, в фармацевтике – процессы диффузии; разделение смесей; фильтрация; распространяется применение покрытий, обладающих принципиально разными свойствами: светочувствительными, вкусовыми, запахом и т.д. и т.п. Как правило, конструкции перечисленных типов при эксплуатации подвергаются различным температурно-силовым воздействиям, которые приводят к растрескиванию тонких покрытий, к их отслоению от подложки, то есть, в конечном итоге, к прочностным нарушениям, к потере работоспособности или товарного вида [7].

Поэтому для практики очень большое значение имеет проблема создания адекватной реальной математической модели, позволяющей понять механизм разрушения слоёв при эксплуатационных нагрузках, а также с той или иной точностью описать поведение системы «подложка-покрытие». Трещиностойкость нанокомпозитов описывается введением феноменологических параметров многоуровневого континуума. Рассмотрено несколько таких приёмов. Разъясняются причины зарождения трещин для некоторых нанопокрытий и предлагаются методы их предотвращения [8].


Победря Б.Е. – член редколлегий журналов «Известия РАН. Механика твёрдого тела», «Вестник Московского университета. Сер. Математика. Механика», «Механика композитных материалов», член Учёного совета механико-математического факультета МГУ, председатель специализированного докторского совета на механико-математическом факультете МГУ, член Президиумов Научных советов РАН по механике деформируемого твёрдого тела и по механике конструкций из композиционных материалов.

Победря Б.Е. выдвинут кандидатом в члены-корреспонденты РАН по специальности «наномеханика и прочность материалов» Учёным советом механико-математического факультета МГУ.


СПИСОК ЛИТЕРАТУРЫ

1. 
   Победря Б.Е. Элементы структурной механики деформируемого твёрдого тела. Математическое моделирование систем и процессов. ПГТУ. Пермь, 1996, с. 66-73.
   
2. Победря Б.Е., Курочкина Ю.В., Об идентификации в механике нанокомпозитов. Изв. РАН. МТТ. 2007, №3, с.6-17.
   

3. Победря Б.Е. Механика композиционных материалов. М.: Изд-во Моск. Ун-та, 1984. 336 с.

4. Победря Б.Е. Лекции по тензорному анализу. М.: Изд-во Моск. Ун-та, 1986. с.264.

5. Победря Б.Е. Численные методы в теории упругости и пластичности. М.: Изд-во Моск. Ун-та, 1995. 336 с.
   
6. Победря Б.Е. Проблемы механики нанокомпозитов. Труды международной конференции «Неклассические задачи механики». Том 1. Кутаиси. 2007, с. 68-71.
   
7. Победря Б.Е., Курочкина Ю.В. Об особенностях слоистых нанокомпозитов. Зимняя школа по МСС (пятнадцатая). Сб. статей, ч.2, Пермь. 2007, с. 284-289.
   
8. Победря Б.Е. О термодинамических критериях прочности в механике композитов. Проблемы механики твёрдых деформируемых тел. Сборник статей к 75-летию Е.И.Шемякина. М. Физматлит. 2006, с.548-565.