Программный моделирующий комплекс для расчета статических и динамических режимов миниээс произвольной конфигурации В. М. Винокур, Б. В. Кавалеров

Вид материала

Документы

Содержание H - вектор, определяющий воздействие на элемент со стороны средств регулирования электрических параметров. Компоненты вектора H Y - блочная матрица проводимостей ветвей (элементов), образующих систему; H

Подобный материал:

• Приложение 2 Перечень измерений при обращении нефти и продуктов ее переработки, 174.13kb.
• А. Н. Медведков научный руководитель Н. П. Васильев,, 36.29kb.
• «Исследование асинхронного конденсаторного двигателя», 34.15kb.
• А. Л. Сафонов Применение современных методов расчета тепловых режимов работы электрических, 165.32kb.
• Математическое моделирование динамических процессов на горных склонах (снежные лавины,, 9.02kb.
• Удк 621. 362 Метод расчета на ЭВМ установившихся режимов энергосистемы, 78.08kb.
• Сорбция ионов железа и марганца окисленными углеродными волокнами в статических и динамических, 27.56kb.
• M. 13. O. программный Комплекс для исследования статистических характеристик шумовых, 126.35kb.
• А. С. Раутиан палеонтология как источник сведений о закон, 642.22kb.
• Курсовой проект на тему, 427.02kb.

Программный моделирующий комплекс для расчета статических и динамических режимов миниЭЭС произвольной конфигурации

В.М.Винокур, Б.В.Кавалеров

Пермский государственный технический университет,

614000, Россия, Пермь, Комсомольский пр. 29, каб. 349

Тел.: (3422) 128753, Факс: (3422) 128753, Email: kbv@pstu.ru

В статье рассматриваются и обосновываются задачи математического моделирования установившихся режимов и переходных процессов в мини-энергосистемах произвольной конфигурации. Особое внимание уделяется мини-энергосистемам, построенным на базе автономных мини-электростанций: газотурбинных, дизельных, карбюраторных и др. Представлены математические модели, алгоритмический аппарат программного моделирующего комплекса «МЭЭС». Пермский государственный технических университет предлагает потенциальным заказчикам различные варианты компоновки программных комплексов в зависимости от характера решаемых задач.


В настоящее время актуализировались задачи исследования мини-электроэнергетических систем (миниЭЭС) в связи с необходимостью обеспечения их надежности, устойчивости, для оперативного диспетчерского управления в нештатных ситуациях, с целью поиска оптимальной топологии системы, разработки систем автоматического управления энергетических модулей и всей миниЭЭС в целом. Особое внимание уделяется миниЭЭС, создаваемым на базе автономных мини-электростанций: газотурбинных, газопоршневых, дизельных и др. Формируемые в этом случае миниЭЭС должны обеспечивать требуемые показатели в различных режимах: автономная и параллельная работа, работа на мощную сеть, установившиеся, переходные и несимметричные режимы работы. Решение перечисленных задач возможно только при использовании соответствующих компьютерных программ. С этой целью в Пермском государственном техническом университете был разработан универсальный программный моделирующий комплекс «МЭЭС» (расшифровывается: «мини-электроэнергетическая система»). Основу комплекса составляет алгоритмическая база «МЭЭС» для формирования математических моделей миниЭЭС произвольной конфигурации и состава структурных элементов. В зависимости от потребностей исследователей, требований заказчика алгоритмическая база «МЭЭС» позволяет создавать компьютерные программы различного назначения. Перечислим лишь некоторые из них:

- расчет установившегося режима (узловые напряжения и токи ветвей);

- расчет переходных процессов (в генераторах, линиях связи, нагрузках);

- расчет несимметричных режимов работы;

- автоматизация управления миниЭЭС в нормальных эксплутационных и аварийных режимах работы;

- синтез САУ энергоблоков, генераторов и первичных двигателей;

- расчет ввода резерва и вывода электрооборудования в ремонт;

- решение задачи оперативного диспетчерского управления в нештатных ситуациях;

- расчет различных оптимизационных задач.

Инструментальные программные средства дают разработчику весь необходимый арсенал методов и средств, реализованный в соответствии с форматом заказчика и основанный на строго обоснованных критериях практической эксплуатации в условиях промышленного производства. Алгоритмическая база «МЭЭС» формирует гибкую систему, которая может автоматически настраиваться на конкретные потребности заказчика и модифицировать свою структуру в соответствии с текущими ситуациями. Сегодня мы имеем несколько форматов, которые предложили заказчики, данные форматы легли в основу поля возможностей, формируемого при создании инструментальных средств и расширяемого по мере развития алгоритмической базы. Одним из главных требований являются адаптируемость и возможность к дальнейшему развитию, к расширению класса используемых методов и их свободному включению в инструментарий.

Среди особенностей, присущих электроэнергетическим объектам, в первую очередь следует отметить значительную сложность большинства из них, которая проявляется в многоэлементности и иерархичности структуры, обилии степеней свободы, разнообразии параметров, характеризующих состояние [1]. Наличие у электроэнергетических объектов указанных признаков позволяет причислить их к объектам кибернетического типа [2]. Кроме того, необходимо отметить, что стандартные технические решения, обычно применяемые для электростанций больших и средних мощностей, оказываются неприемлемыми для малых (мини-электростанции). В то же время, каких-либо специальных норм технологического проектирования для них не существует, что требует от проектировщика творческого подхода к решению возникающих технических проблем [3]. В связи с этим задачи, которые необходимо решать при эксплуатации существующих, а также при создании новых образцов, оказываются весьма сложными. Решение таких задач на интуитивном уровне недопустимо.

Принятие оптимальных решений возможно только при наличии полной информации о свойствах объекта, получаемой путем всестороннего его анализа. Проведение такого анализа с помощью прямого экспериментирования в энергосистемах практически полностью исключено.

Изучение свойств сложных электроэнергетических объектов возможно либо с помощью регистрации процессов, либо с помощью математических моделей, на которых расчетным путем моделируются различные процессы, возникающие в электроэнергетических объектах. Очевидно, что первый путь не всегда бывает удовлетворительным, а в ряде случаев, например при создании нового, уникального объекта (электростанции), он полностью исключен.

На основании вышеизложенного можно сделать вывод, что путь исследования, состоящий в изучении свойств имитационных моделей, является наиболее перспективным, а подчас и единственно возможным.

Мини-энергосистема является сложной системой, поскольку сложность определяется глубиной рассмотрения процессов в системе.

Основными отличительными признаками сложной системы при этом являются следующие признаки [4].

1) Наличие большого количества взаимно связанных и взаимодействующих между собой элементов.

2) Сложность функций, выполняемых системой и направленных на достижение заданной цели функционирования.

3) Возможность разбиения системы на подсистемы, цели функционирования которых подчинены общей цели функционирования всей системы.

4) Наличие управления.

Процесс функционирования сложной системы можно представить как совокупность действий и элементов, подчиненных единой цели.

Математическая модель сложной системы состоит из математических моделей элементов и математической модели взаимодействия между элементами [4].

Исходя из этого, процесс создания математической модели миниЭЭС рассматривается как последовательность двух этапов: создание моделей отдельных элементов и создание модели их взаимодействия.

Под элементами будем понимать подсистемы, не подлежащие дальнейшему расчленению, внутренние процессы в которых не рассматриваются.

Перейдем к решению задачи структурной декомпозиции. Выбор уровня декомпозиции осуществим, исходя из следующих соображений. Целесообразно, как уже отмечалось, получить по возможности наиболее универсальную математическую модель, ориентированную на широкий класс электроэнергетических объектов. Возможность получения такой модели обусловлена тем, что электроэнергетические объекты состоят в основном из ограниченного набора типовых элементов. К их числу относятся вращающиеся электрические машины, трансформаторы, линии электропередачи, реакторы, батареи конденсаторов и т.п. Таким образом, наиболее целесообразным и естественным представляется выбрать в качестве структурных элементов мини-энергосистем вышеперечисленные наиболее распространенные типовые элементы электрических систем и сетей.

Главным условием, которое необходимо выполнить при разработке математических моделей элементов, является следующее условие: математические модели структурных элементов должны быть получены в такой форме, которая должна допускать их непосредственное включение в модель миниЭЭС. Следовательно, математические модели всех элементов должны быть представлены в единой универсальной форме записи.

Рассмотрим общую форму записи уравнений электрически взаимодействующих элементов (электрических машин, статической нагрузки, линий связи). Уравнения моментов для вращающихся машин здесь не рассматриваются, механическое взаимодействие рассматривается отдельно. Взаимодействие электрически связанных элементов наиболее естественно организовать посредством таких электрических параметров режима как токи и напряжения. С учетом сказанного систему уравнений структурного элемента миниЭЭС относительно внешних переменных можно представить в общем виде следующим векторным уравнением:

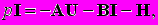(1)

где: I, pI - вектор токов и вектор производных токов элемента;

U - вектор напряжений, приложенных между внешними зажимами элемента;

A, B - матрицы, размерность которых зависит от системы координат в которых моделируется структурный элемент (d,q или a,b,c), а также от того полные это уравнения или упрощенные;

H - вектор, определяющий воздействие на элемент со стороны средств регулирования электрических параметров.

Компоненты вектора H для пассивных элементов электрической системы - нулевые, для синхронных машин при отсутствии РВ (регулирования возбуждения) - постоянные, при наличии РВ - меняются на каждом шаге расчета.

Уравнения (1) решаются на каждом шаге расчета методом численного интегрирования относительно внешних токов структурного элемента. При этом следует отметить, что для пассивных элементов выражение (1) содержит всю систему дифференциальных уравнений элемента. Для электрических машин уравнения (1) следует интегрировать совместно с уравнениями роторных контуров и уравнениями, описывающими механическое состояние элемента. Таким образом, для электрических машин вектора I и pI не совпадают по размерности: вектор I содержит не только внешние, но и внутренние (роторные) токи, расчет которых производится на каждом шаге численного интегрирования полной системы дифференциальных уравнений электрической машины. Знаки при слагаемых уравнения (1) соответствуют нормальному направлению токов в электрических машинах (от генератора к узлу).

После приведения математических моделей всех элементов к единой обобщенной форме записи (1) строится математическая модель взаимодействия структурных элементов.

Электрическую систему будем изображать в виде совокупности соединенных между собой двухполюсников (ветвей), т.е. элементов с двумя зажимами. Наиболее общим понятием, соответствующим представлению системы в виде соединения ветвей, является понятие графа [5]. Представление системы миниЭЭС в виде схемы является полным, т.е. дает достаточную информацию для решения задачи моделирования, если оно содержит как соединения входящих в нее элементов, так и характеристики этих элементов. Характеристики элементов записываются в форме (1). Способ соединения элементов в систему будем отражать в виде графа.

На основании анализа возможных методов моделирования взаимодействия элементов выбор был сделан в пользу методов, основанных на решении уравнений связи.

Для построения алгоритма решения уравнений связи и автоматизации построения расчетных схем электрических систем используется матрично-топологическое направление теории цепей.

Запишем уравнения связи электрически взаимодействующих элементов. Принцип формирования систем уравнений связи, как отмечается в [2], базируется на условии инвариантности граничных переменных, согласно которому в общем для элементов узле в произвольный момент времени каждая скалярная граничная переменная, определяемая в одном элементе, тождественно равна себе самой, определенной в любом другом из этих элементов, а алгебраическая сумма векторных граничных переменных при тех же условиях равны нулю. При этом скалярной является переменная, не имеющая направления (в нашем случае - потенциал), а векторной - граничная переменная, характеризующаяся направлением (в нашем случае - ток). Уравнения связи могут быть составлены как баланс активной и реактивной мощностей в узловой точке [6]:

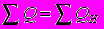, , (2)

что равноценно уравнению 1-го закона Кирхгофа для узловой точки.

Для системы, представленной на рис. уравнения связи в соответствии со сказанным будут иметь следующий вид:

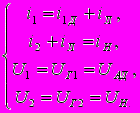(3)

Аналогично составляются уравнения связи и для более сложных структурных схем.





На основании системы уравнений (3) формируется векторно-матричное уравнение для расчета узловых напряжений для каждого шага расчета:

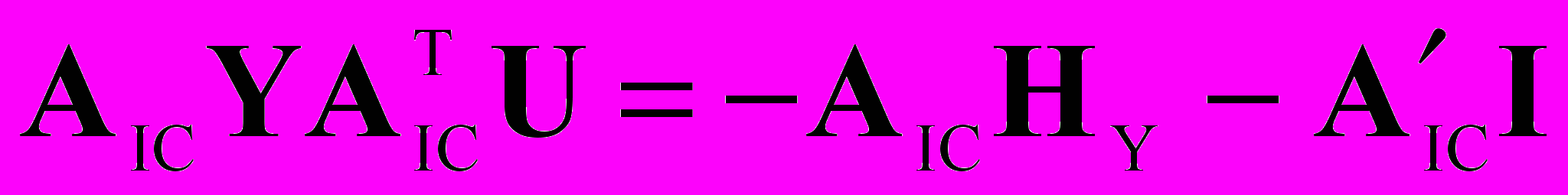(4)

где - клеточная матрица инцидентности, клетками матрицы являются единичные, нулевые матрицы или матрицы преобразований (5); - транспонированная матрица инцидентности; Y - блочная матрица проводимостей ветвей (элементов), образующих систему; H_Y - вектор, полученный из правых частей уравнений элементов в форме (1); . - матрица клетками, которой являются нулевые клетки или клетки производных матриц преобразования (5); U - вектор искомых напряжений узлов.

У каждого генератора система d,q координат (Парка-Горева) связана с его ротором и поэтому при их согласовании необходимо использовать следующие матрицы преобразований. Матрица преобразования:

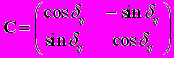, (5)

где δ _ij – угол между осями Парка-Горева двух различных генераторов.

Из структуры матрицы инцидентности и структуры матрицы видно, что их элементы определяются конфигурацией системы и выбором систем координат, к которым выполняется приведение. Вектор Н_Y и матрица Y определяются составом элементов системы.

Таким образом, разработанный алгоритм позволяет явно учесть состав и конфигурацию структурных элементов, составляющих систему и, следовательно, может быть использован при автоматизированной подготовке модели миниЭЭС, а также при управлении имитационной моделью (оперативные переключения, изменения состава и конфигурации и т.д.).

В разработанном алгоритме решения уравнений связи (4) матрица инцидентности выделяется явно. При этом становится возможно, непосредственно изменяя блоки матрицы, вносить изменения в схему расчета. При изменении состава элементов необходимо также изменять матрицу проводимостей элементов Y и вектор H_Y.

Использование матричных операций позволяет создать алгоритмы цифрового моделирования сложных переходов в любой их последовательности для самых различных эквивалентных схем миниЭЭС.

Таким образом, использование матрично-топологического подхода для моделирования взаимодействия структурных элементов дает возможность организовать эффективное управление моделью миниЭЭС и ее последовательную коррекцию при расчетах сложных переходов в системе.

Созданная алгоритмическая база «МЭЭС» обеспечивает формирование различных вариантов компьютерных программ для моделирования мини-энергосистем произвольной конфигурации и состава структурных элементов. Реализуется моделирование всех основных режимов работы, в том числе, статических, динамических, несимметричных.

Проекты, реализованные на базе алгоритмического аппарата «МЭЭС», внедрены на крупных предприятиях, получили высокие награды и дипломы, в том числе международного уровня.


Литература

1. Коротков Б.А., Попков Е.Н. Алгоритмы имитационного моделирования переходных процессов в электрических системах.. Л.: Изд-во Ленинградского университета, 1987. - 280 с.
   
2. Веников В.А. Кибернетические модели электрических систем. М.: Энергоатомиздат, 1982. - 328 c .
   
3. Бут Д.А. Синтез автономных электроэнергетических систем//Электричество - 1994. - №1. - с. 1-17.
   
4. Бусленко Н.П. Моделирование сложных систем. М.: Наука, 1978. - 440 с
   
5. Оре О. Теория графов. М.: Наука, 1980. - 336 с.
   
6. Веретенников Л.П. Исследование процессов в судовых электроэнергетических системах. Теория и методы. Л.: Судостроение, 1975. - 376 с.