Учебно-методическое пособие "Широкополосные сигналы" составлено в соответствии с программой дисциплины Методы обработки сигналов для студентов, обучающихся в бакалавриате по направлению Информационные технологии и системы связи.

Вид материала

Учебно-методическое пособие

Содержание Помехоустойчивость ШПСС Основные виды ШПС Частотно-модулированные (ЧМ) Многочастотные (МЧ) В необходимо иметь большое число частотных каналов N. Дискретные частотные (ДЧ) Дискретные составные частотные (ДСЧ) Принципы оптимальной фильтрации. Оптимальный фильтр ШПС А совпадает с амплитудным спектром сигнала и 2) φk= Фазоманипулированные сигналы Спектр ФМ сигналов Автокорреляционная функция (АКФ) Сигналы Баркера Формирование и обработка сигналов Баркера Особенности автокорреляционной функции М-последовательности 1.10 Усеченные М-последовательности 3. Порядок выполнения работы 4. Контрольные вопросы

Подобный материал:

• Современной Гуманитарной Академии (С) современная гуманитарная академия, 2011 методическое, 218.52kb.
• Учебно-методическое пособие для студентов Iкурса очной формы обучения, 250.7kb.
• Программа курса лекций, 51.42kb.
• Учебно-методическое пособие написано в соответствии с действующей программой дисциплины, 1482.87kb.
• Учебно-методическое пособие для студентов 1 курса, обучающихся по направлению «Психология»,, 425.52kb.
• Учебно-методическое пособие по курсу «Информационные технологии» для студентов Института, 1419.29kb.
• Рабочая программа дисциплины «администрирование в информационных системах» дс., 184.68kb.
• Учебно-методическое пособие составлено, 1450.47kb.
• Учебно-методический комплекс Для студентов, обучающихся по направлению «Юриспруденция», 330.85kb.
• Рабочая программа дисциплины «архитектура ЭВМ и сетей» опд., 203.61kb.

Учебно-методическое пособие “Широкополосные сигналы” составлено в соответствии с программой дисциплины Методы обработки сигналов для студентов, обучающихся в бакалавриате по направлению Информационные технологии и системы связи. Пособие состоит из двух частей. Часть первая – основные сведения о широкополосных сигналах, включает краткое изложение теории широкополосных сигналов. Вторая - методические указания по выполнению лабораторной работы.

1. Основные сведения о широкополосных сигналах
   
   1. Определение ШПС. Применение ШПС в системах связи
      

Широкополосными (сложными, шумоподобными) сигналами (ШПС) называют такие сигналы, у которых произведения активной ширины спектра F на длительность T много больше единицы. Это произведение называется базой сигнала B. Для ШПС

B = FT>>1 (1)

Широкополосными сигналы иногда называют сложными в отличие от простых сигналов (например, прямоугольные, треугольные и т.д.) с В=1. Поскольку у сигналов с ограниченной длительностью спектр имеет неограниченную протяженность, то для определения ширины спектра используют различные методы и приемы.

Повышение базы в ШПС достигается путем дополнительной модуляции (или манипуляции) по частоте или фазе на времени длительности сигнала. В результате, спектр сигнала F (при сохранении его длительности T) существенно расширяется. Дополнительная внутрисигнальная модуляция по амплитуде используется редко.

В системах связи с ШПС ширина спектра излучаемого сигнала F всегда много больше ширины спектра информационного сообщения.

ШПС получили применение в широкополосных системах связи (ШПСС), так как:

• позволяют в полной мере реализовать преимущества оптимальных методов обработки сигналов;
  
• обеспечивают высокую помехоустойчивость связи;
  
• позволяют успешно бороться с многолучевым распространением радиоволн путем разделения лучей;
  
• допускают одновременную работу многих абонентов в общей полосе частот;
  
• позволяют создавать системы связи с повышенной скрытностью;
  
• обеспечивают электромагнитную совместимость (ЭМС) ШПСС с узкополосными системами радиосвязи и радиовещания, системами телевизионного вещания;
  
• обеспечивают лучшее использование спектра частот на ограниченной территории по сравнению с узкополосными системами связи.
  

2. Помехоустойчивость ШПСС
   

Она определяется широко известным соотношением, связывающим отношение сигнал-помеха на выходе приемника q² с отношением сигнал-помеха на входе приемника ρ²:

q²= 2Вρ² (2)

где ρ² = Р_с/Р_п ( Р_с , Р_п - мощности ШПС и помехи);

q²=2E/ N_п, Е - энергия ШПС, N_п - спектральная плотность мощности помехи в полосе ШПС. Соответственно Е = Р_сТ, a N_п = Р_п /F;

В - база ШПС.

Отношение сигнал-помеха на выходе q² определяет рабочие характеристики приема ШПС, а отношение сигнал-помеха на входе ρ² — энергетику сигнала и помехи. Величина q² может быть получена согласно требованиям к системе (10...30 дБ) даже если ρ²<<1. Для этого достаточно выбрать ШПС с необходимой базой В, удовлетворяющей (2). Как видно из соотношения (2), прием ШПС согласованным фильтром или коррелятором сопровождается усилением сигнала (или подавлением помехи) в 2В раз. Именно поэтому величину

К_ШПС = q²/ρ² (3)

называют коэффициентом усиления ШПС при обработке или просто усилением обработки. Из (2), (3) следует, что усиление обработки К_ШПС = 2В. В ШПСС прием информации характеризуется отношением сигнал помеха h²= q²/2, т.е.

h²= Вρ² (4)

Соотношения (2), (4) являются фундаментальными в теории систем связи с ШПС. Они получены для помехи в виде белого шума с равномерной спектральной плотностью мощности в пределах полосы частот, ширина которой равна ширине спектра ШПС. Вместе с тем эти соотношения справедливы для широкого круга помех (узкополосных, импульсных, структурных), что и определяет их фундаментальное значение.

Таким образом, одним из основных назначений систем, связи с ШПС является обеспечение надежного приема информации при воздействии мощных помех, когда отношение сигнал-помеха на входе приемника ρ² может быть много меньше единицы. Необходимо еще раз отметить, что приведенные соотношения строго справедливы для помехи в виде гауссовского случайного процесса с равномерной спектральной плотностью мощности («белый» шум).

3. Основные виды ШПС
   

Известно большое число различных ШПС, свойства которых нашли отражение во многих книгах и журнальных статьях. ШПС подразделяются на следующие виды:

• частотно-модулированные (ЧМ) сигналы;
  
• многочастотные (МЧ) сигналы;
  
• фазоманипулированные (ФМ) сигналы (сигналы с кодовой фазовой модуляцией - КФМ сигналы);
  

• дискретные частотные (ДЧ) сигналы (сигналы с кодовой частотной модуляцией - КЧМ сигналы, частотно-манипулированные (ЧМ) сигналы);
  
• дискретные составные частотные (ДСЧ) (составные сигналы с кодовой частотной модуляцией - СKЧM сигналы).
  

Частотно-модулированные (ЧМ) сигналы являются непрерывными сигналами, частота которых меняется по заданному закону. На рисунке 1а, изображен ЧМ сигнал, частота которого меняется по V -образному закону от f₀-F/2 до f₀+F/2, где f₀ - центральная несущая частота сигнала, F - ширина спектра, в свою очередь, равная девиации частоты F= ∆f_д. Длительность сигнала равна Т.

На рисунке 1б представлена частотно-временная (f, t) - плоскость, на которой штриховкой приближенно изображено распределение энергии ЧМ сигнала по частоте и по времени.

База ЧМ сигнала по определению (1) равна:

B = FT=∆f_дT (5)

Частотно-модулированные сигналы нашли широкое применение в радиолокационных системах, поскольку для конкретного ЧМ сигнала можно создать согласованный фильтр на приборах с поверхностными акустическими волнами (ПАВ). В системах связи необходимо иметь множество сигналов. При этом необходимость быстрой смены сигналов и переключения аппаратуры формирования и обработки приводят к тому, что закон изменения частоты становится дискретным. При этом от ЧМ сигналов переходят к ДЧ сигналам.

Многочастотные (МЧ) сигналы (рисунок 2а) являются суммой N гармоник u(t) ... u_N(t), амплитуды и фазы которых определяются в соответствии с законами формирования сигналов. На частотно-временной плоскости (рисунок 2б) штриховкой выделено распределение энергии одного элемента (гармоники) МЧ сигнала на частоте f_k. Все элементы (все гармоники) полностью перекрывают выделенный квадрат со сторонами F и T. База сигнала B равна площади квадрата. Ширина спектра элемента F₀≈1/Т. Поэтому база МЧ сигнала

B = F/F₀=N (6)




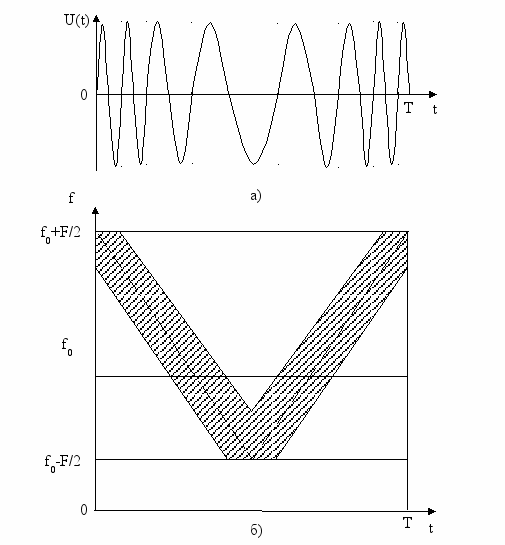
Рисунок 1 - Частотно-модулированный сигнал и частотно-временная плоскость

т. е. совпадает с числом гармоник. МЧ сигналы являются непрерывными и для их формирования и обработки трудно приспособить методы цифровой техники. Кроме этого недостатка, они обладают также и следующими:

а) у них плохой пик-фактор (см. рисунок 2а);

б) для получения большой базы В необходимо иметь большое число частотных каналов N. Поэтому МЧ сигналы в дальнейшем не рассматриваются.

Фазоманипулированные (ФМ) сигналы представляют последовательность радиоимпульсов, фазы которых изменяются по заданному закону. Обычно фаза принимает два значения (0 или π). При этом радиочастотному ФМ сигналу соответствует видео- ФМ сигнал (рисунок 3а), состоящий из положительных и отрицательных импульсов. Если число импульсов N, то длительность одного импульса равна τ₀ = T/N, а ширина его спектра равна приближенно ширине спектра сигнала F₀ =1/τ₀=N/Т. На частотно-временной плоскости (рисунок 3б) штриховкой выделено распределение энергии одного элемента (импульса) ФМ сигнала. Все элементы перекрывают выделенный квадрат со сторонами F и Т. База ФМ сигнала

B = FT =F/τ₀=N, (7)

т.е. B равна числу импульсов в сигнале.

Возможность применения ФМ сигналов в качестве ШПС с базами В = 10⁴ ...10⁶ ограничена в основном аппаратурой обработки. При использовании согласованных фильтров в виде приборов на ПАВ возможен оптимальный прием ФМ сигналов с максимальными базами Вмах=1000 ... 2000. ФМ сигналы, обрабатываемые такими фильтрами, имеют широкие спектры (порядка 10 ... 20 МГц) и относительно короткие длительности (60 ... 100 мкс). Обработка ФМ сигналов с помощью видеочастотных линий задержки при переносе спектра сигналов в область видеочастот позволяет получать базы В = 100 при F≈1 МГц, Т≈ 100 мкс.

Весьма перспективными являются согласованные фильтры на приборах с зарядовой связью (ПЗС). Согласно опубликованным данным с помощью согласованных фильтров ПЗС можно обрабатывать ФМ сигналы с базами 10² ... 10³ при длительностях сигналов 10^-4 ... 10^-1 с. Цифровой коррелятор на ПЗС способен обрабатывать сигналы до базы 4∙10⁴.




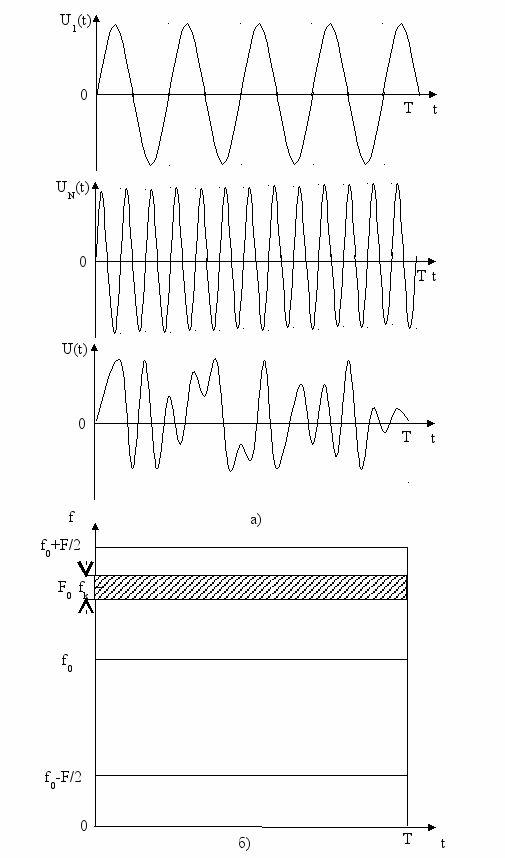
Рисунок 2 - Многочастотный сигнал и частотно-временная плоскость



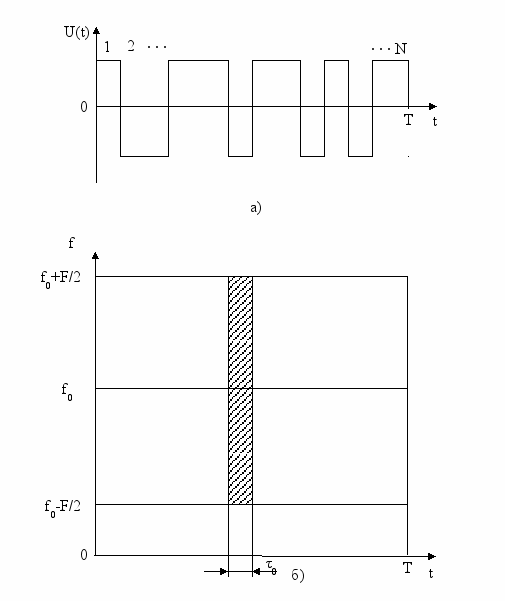
Рисунок 3 - Фазоманипулированный сигнал и частотно-временная плоскость

Следует отметить, что ФМ сигналы с большими базами целесообразно обрабатывать с помощью корреляторов (на БИС или на ПЗС). При этом, В = 4∙10⁴ представляется предельной. Но при использовании корреляторов необходимо в первую очередь решить вопрос об ускоренном вхождении в синхронизм. Так как ФМ сигналы позволяют широко использовать цифровые методы и технику формирования и обработки, и можно реализовать такие сигналы с относительно большими базами, то поэтомy ФМ сигналы являются одним из перспективных видов ШПС.

Дискретные частотные (ДЧ) сигналы представляют последовательность радиоимпульсов (рисунок 4а), несущие частоты которых изменяются по заданному закону. Пусть число импульсов в ДЧ сигнале равно М, длительность импульса равна Т₀=Т/М, его ширина спектра F₀=1/Т₀=М/Т. Над каждым импульсом (рисунок 4а) указана его несущая частота. На частотно-временной плоскости (рисунок 4б) штриховкой выделены квадраты, в которых распределена энергия импульсов ДЧ сигнала.

Как видно из рисунка 4б, энергия ДЧ сигнала распределена неравномерно на частотно-временной плоскости. База ДЧ сигналов

B = FT =МF₀МТ₀=М²F₀Т₀ = М² (8)

поскольку база импульса F₀T₀ = l. Из (8) следует основное достоинство ДЧ сигналов: для получения необходимой базы В число каналов M =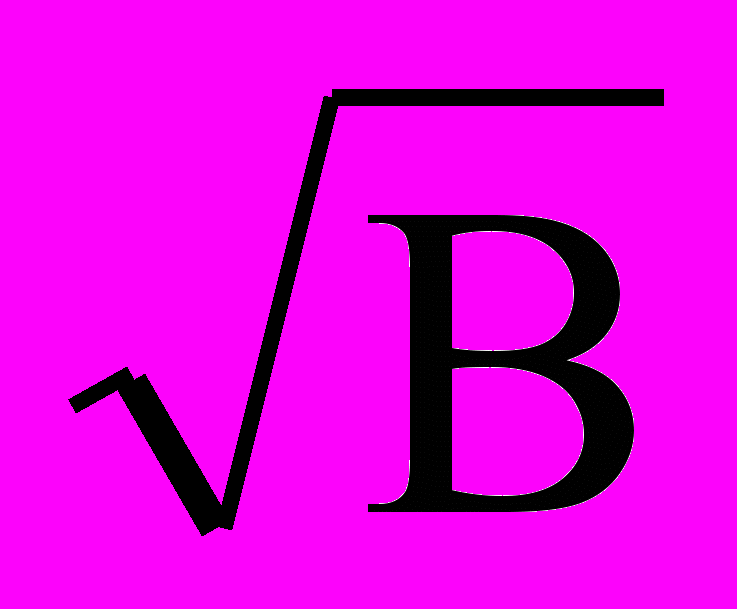, т. е. значительно меньше, чем для МЧ сигналов. Именно это обстоятельство и обусловило внимание к таким сигналам и их применение в системах связи. Вместе с тем для больших баз В = 10⁴ ... 10⁶ использовать только ДЧ сигналы нецелесообразно, так как число частотных каналов М = 10² ... 10³, что представляется чрезмерно большим.

Дискретные составные частотные (ДСЧ) сигналы являются ДЧ сигналами, у которых каждый импульс заменен шумоподобным сигналом. На рисунке 5а изображен видеочастотный ФМ сигнал, отдельные части которого передаются на различных несущих частотах. Номера частот указаны над ФМ сигналом. На рисунке 5б изображена частотно-временная плоскость, на которой штриховкой выделено распределение энергии ДСЧ сигнала. Рисунок 5б по структуре не отличается от рисунка 4б, но для рисунка 5б площадь F₀T₀ = N₀ -равна числу импульсов ФМ сигнала в одном частотном элементе ДСЧ сигнала. База ДСЧ сигнала

B = FT =М²F₀Т₀ = N₀М² (9)

Число импульсов полного ФМ сигнала N=N₀М



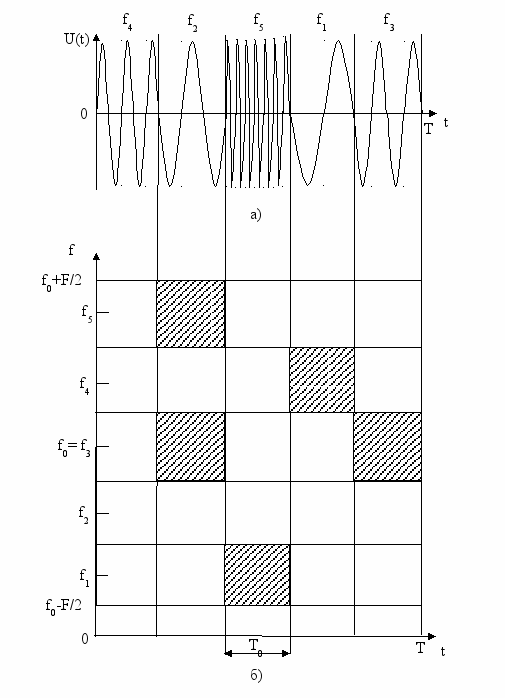
Рисунок 4 - Дискретный частотный сигнал и частотно-временная плоскость

Изображенный на рисунке 5 ДСЧ сигнал содержит в качестве элементов ФМ сигналы. Поэтому такой сигнал сокращенно будем называть ДСЧ-ФМ сигнал. В качестве элементов ДСЧ сигнала можно взять ДЧ сигналы. Если база элемента ДЧ сигнала B = F₀T₀ = М₀² то база всего сигнала B = М₀²М²




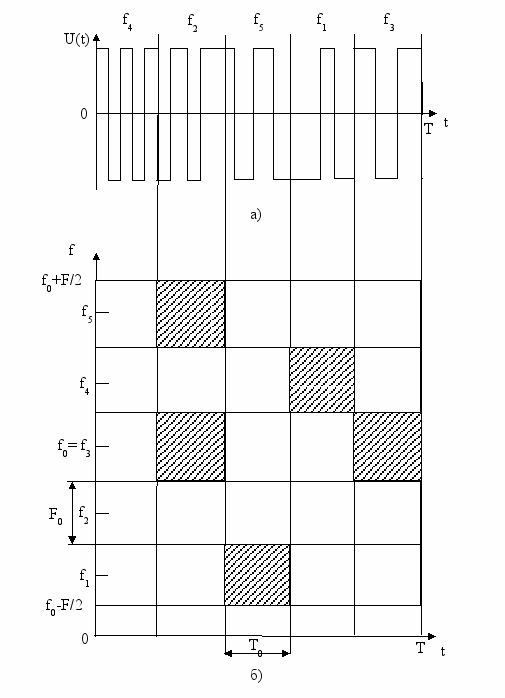
Рисунок 5 - Дискретный составной частотный сигнал с фазовой манипуляцией ДСЧ-ФМ и частотно-временная плоскость.

Такой сигнал можно сокращенно обозначать ДСЧ-ЧМ. Число частотных каналов в ДСЧ-ЧМ сигнале равно М₀М. Если ДЧ сигнал (см. рисунок 4), и ДСЧ-ЧМ сигнал имеют равные базы, то они имеют и одинаковое число частотных каналов. Поэтому особых преимуществ ДСЧ-ЧМ сигнал перед ДЧ сигналом не имеет. Но принципы построения ДСЧ-ЧМ сигнала могут оказаться полез­ными при построении больших систем ДЧ сигналов. Таким образом, наиболее перспективными ШПС для систем связи являются ФМ, ДЧ, ДСЧ-ФМ сигналы.

4. Принципы оптимальной фильтрации. Оптимальный фильтр ШПС
   

Прием и обработка сигналов различными радиотехническими устройствами, как правило, производится на фоне более или менее интенсивных помех. Выбор системы устройства зависит от того, какую из нижеперечисленных задач приходится при этом решать:

1 . Обнаружение сигнала, когда требуется только дать ответ, имеется ли в принятом колебании полезный сигнал или оно образовано только шумом.

2. Оценка параметров, когда требуется с наибольшей точностью определить значение одного или нескольких параметров полезного сигнала (амплитуду, частоту, временное положение и т.д.). Для теории радиотехнических цепей и сигналов наибольший интерес представляет изучение возможностей ослабления вредного действия помехи при заданном сигнале и заданной помехе путем правильного выбора передаточной функции приемника. Поэтому в дальнейшем будут определяться характеристики приемников, оптимально согласованных с сигналом и помехой. В зависимости от того, какая из перечисленных выше задач решается, критерии оптимальности фильтра данному сигналу при наличии помех с заданными статистическими характеристиками могут быть разными. Для задачи обнаружения сигнала в шумах наибольшее распространение получил критерий максимума отношения сигнал/шум на выходе фильтра.

Требования к фильтру, максимизирующему отношение сигнал-шум формулируются следующим образом. На вход линейного четырехполюсника с постоянными параметрами и передаточной функцией подается аддитивная смесь сигнала S(t) и шума n(t) ( рисунок 6 ) .



Рисунок 6

Сигнал полностью известен, это значит что заданы его форма и положение на оси времени. Шум представляет собой вероятностный процесс с заданными статистическими характеристиками. Требуется синтезировать фильтр, обеспечивающий получение на выходе наибольшего возможного отношения пикового значения сигнала к среднеквадратичному значению шума, иными словами определить передаточную функцию . При этом не ставится условие сохранения формы сигнала на выходе фильтра, так как для обнаружения его в шумах форма значения не имеет.

Приведем результаты решения задачи для "стандартной" помехи типа белый шум. Напомним, что белый шум представляет собой случайный процесс с равномерным распределением энергии по спектру частот, т.е. W(ω) = W₀ = const , причем 0<ω<∞, где W(ω) =мощность сигнала/полоса частот есть средняя мощность, приходящаяся на 1 Гц при заданной частоте ω, и называется спектральной плотностью мощности процесса. Найдено, что в случае белого шума

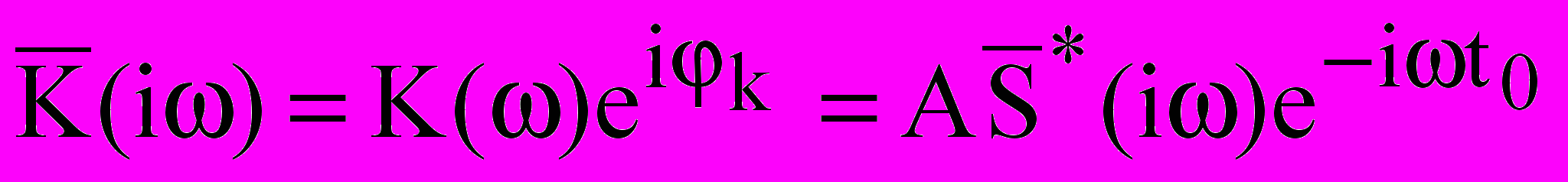(10)

Здесь А - произвольный постоянный коэффициент, 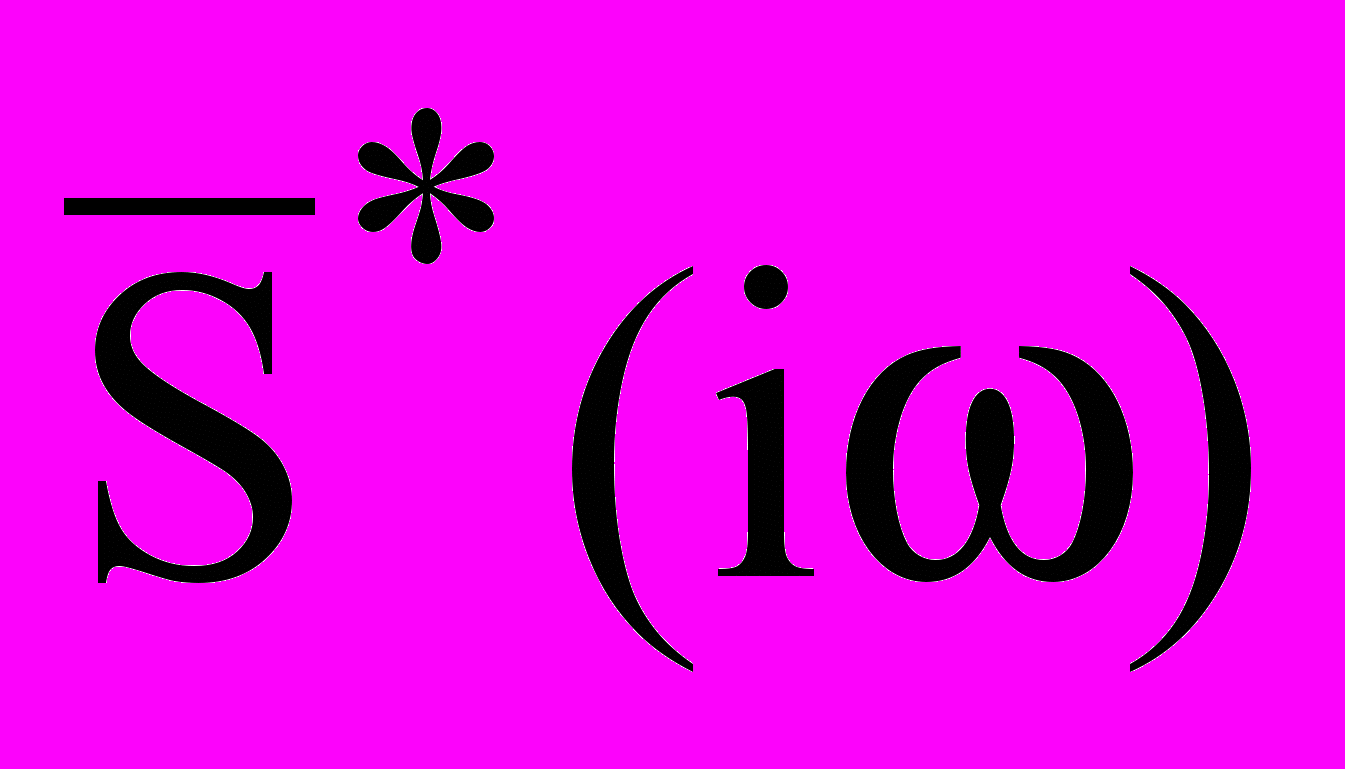- функция комплексно - сопряженная со спектральной функцией сигнала .

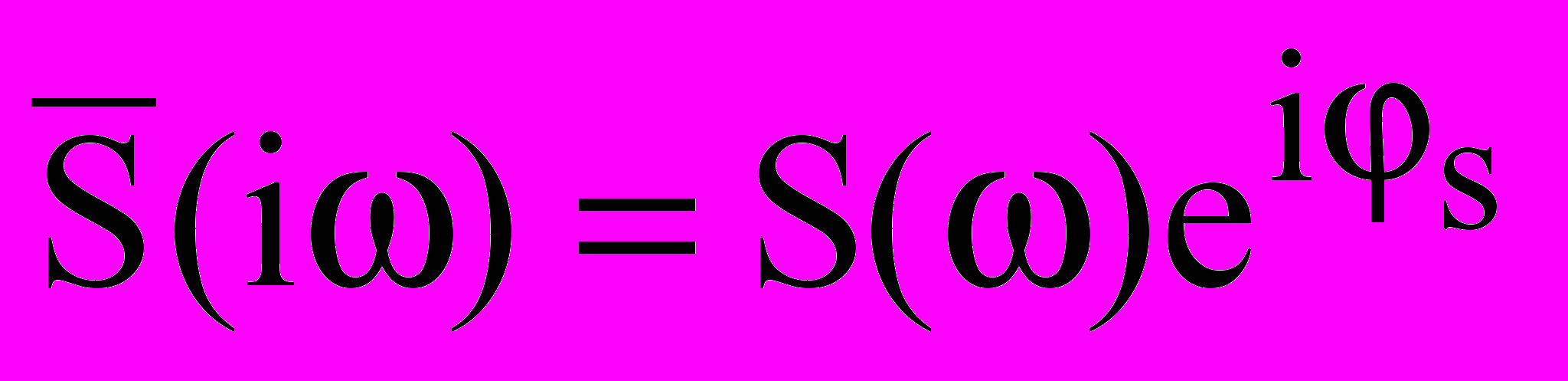Из соотношения (10) вытекают два условия для фазочастотной (ФЧХ) и амплитудно - частотной (АЧХ) характеристик согласованного фильтра:

1) K(ω)=AS(ω) (11)

т.е. модуль передаточной функции с точностью до постоянного коэффициента А совпадает с амплитудным спектром сигнала и

2) φ_k=-[φ_s(ω)+ωt₀] (12)

φ_s(ω) - фазовый спектр сигнала.

Физический смысл полученных выражений для АЧХ (11) И ФЧХ (12) оптимального фильтра ясен из следующих соображений. При выполнении соотношения (11) энергия шума, занимающего бесконечную полосу частот на входе фильтра, ослабляется на выходе значительно сильнее энергии сигнала, имеющего такую же ширину спектра, как и полоса пропускания приемника .

Первое слагаемое в выражении для ФЧХ -φ_s(ω) компенсирует фазовую характеристику входного сигнала φ_s(ω), в результате прохождения через фильтр в момент t₀ все гармоники сигнала складываются в фазе, образуя пик выходного сигнала. В то же время это приводит к изменению формы сигнала на выходе фильтра. Второе слагаемое ωt₀ означает задержку всех компонент сигнала на одно и то же время t₀>T_c, где Т_с - длительность сигнала. Физически это означает, что для полного использования энергии входного сигнала задержка отклика фильтра должна быть не менее длительности сигнала.

Использование выражения (10) сводит задачу синтеза согласованного фильтра к задаче построения электрической цепи по известному коэффициенту передачи .

Другой путь - определение импульсной характеристики цепи, а затем конструирование четырехполюсника с такой характеристикой.

По определению, импульсная характеристика цепи g(t) - это сигнал на ее выходе в ответ на воздействие в виде δ - функции, т.е. имеющее равномерную спектральную плотность для всех частот. В этом случае спектральная плотность сигнала на выходе 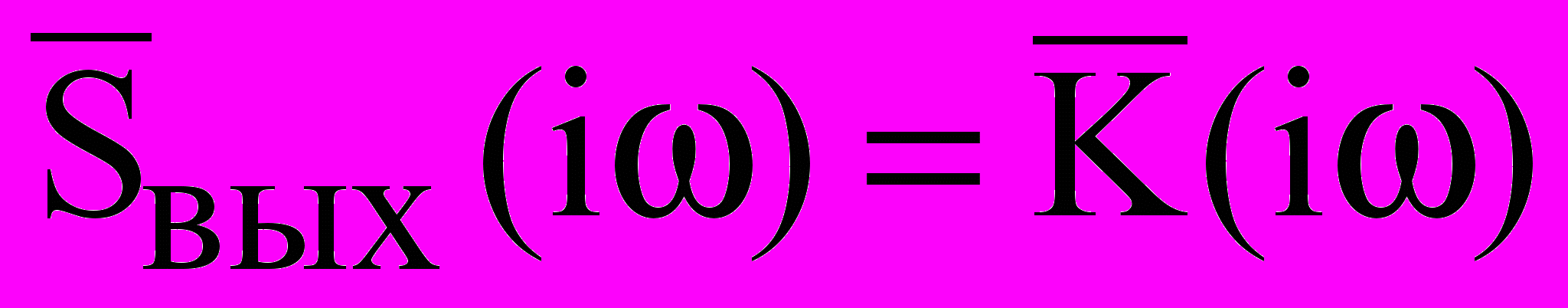и вид сигнала на выходе, согласно преобразованию Фурье и учитывая соотношение (10),

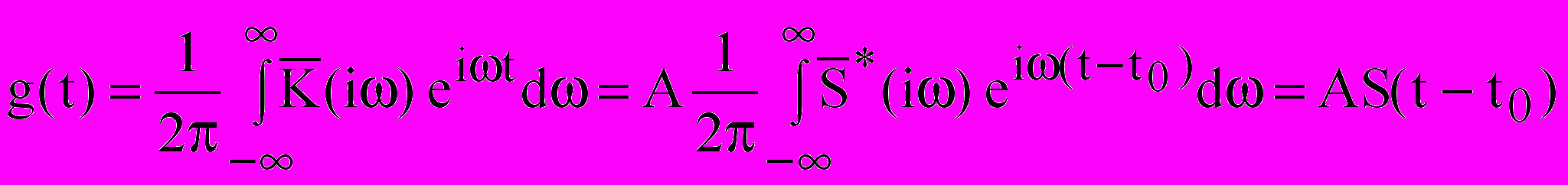(13)

Импульсная характеристика оптимального фильтра, т.е. реакция на δ импульс, является, таким образом, зеркальным отображением того сигнала, с которым этот фильтр согласован. Ось симметрии проходит через точку t₀/2 на оси абсцисс (рисунок 7).



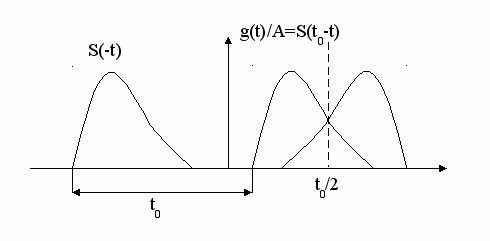
Рисунок 7

Форму выходного сигнала оптимального фильтра можно определить, используя общее соотношение

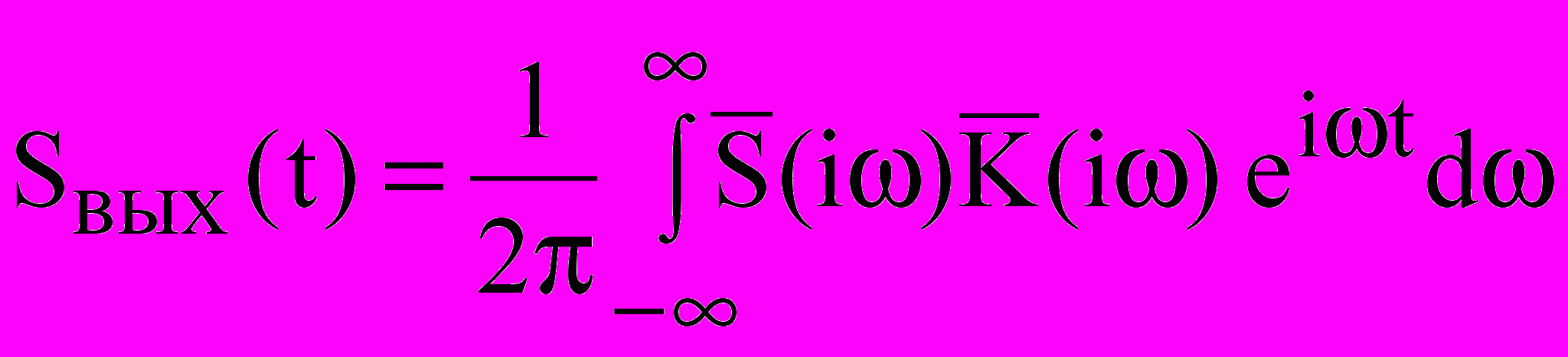(14)

По определению сигнал на выходе оптимального фильтра,

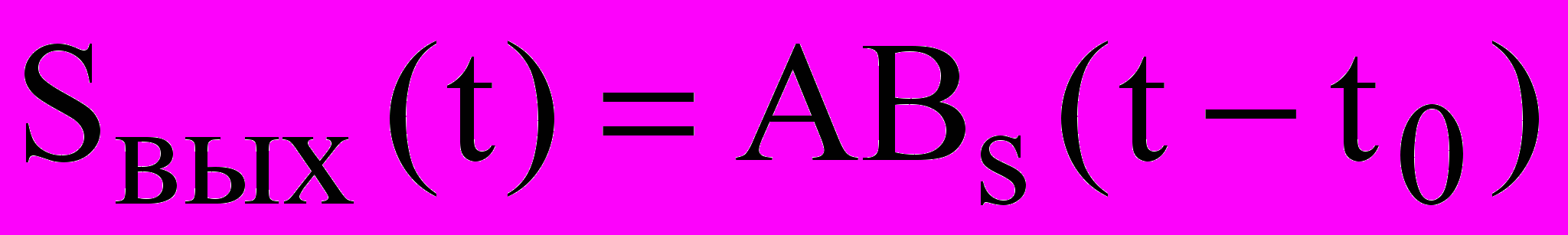(15)

где B_s(t-t₀) - автокорреляционная функция сигнала (АКФ).

Итак, сигнал на выходе согласованного фильтра с точностью до постоянного коэффициента А совпадает с автокорреляционной функцией входного сигнала. Отношение сигнал-шум на выходе является главной мерой эффективности оптимального фильтра (ОФ). Приведем лишь результат вычислений, согласно которым

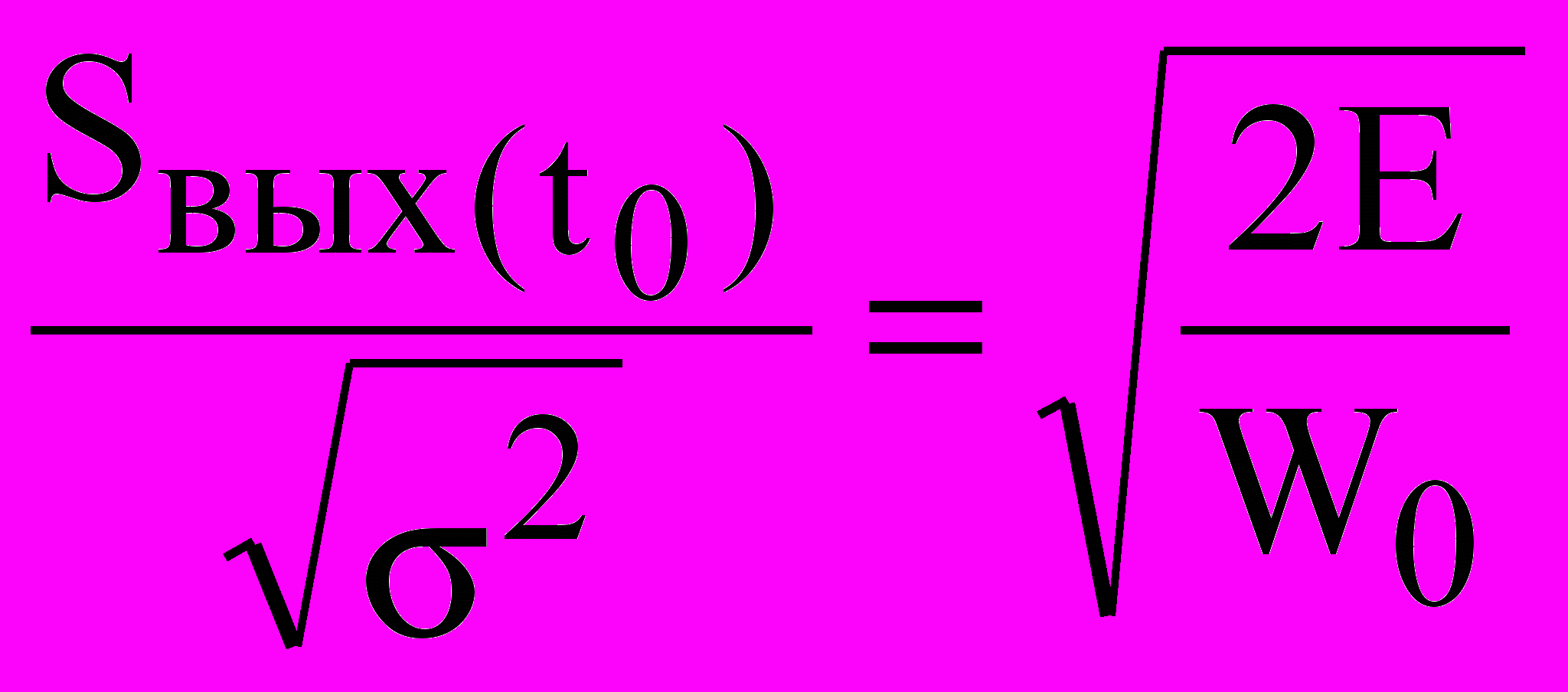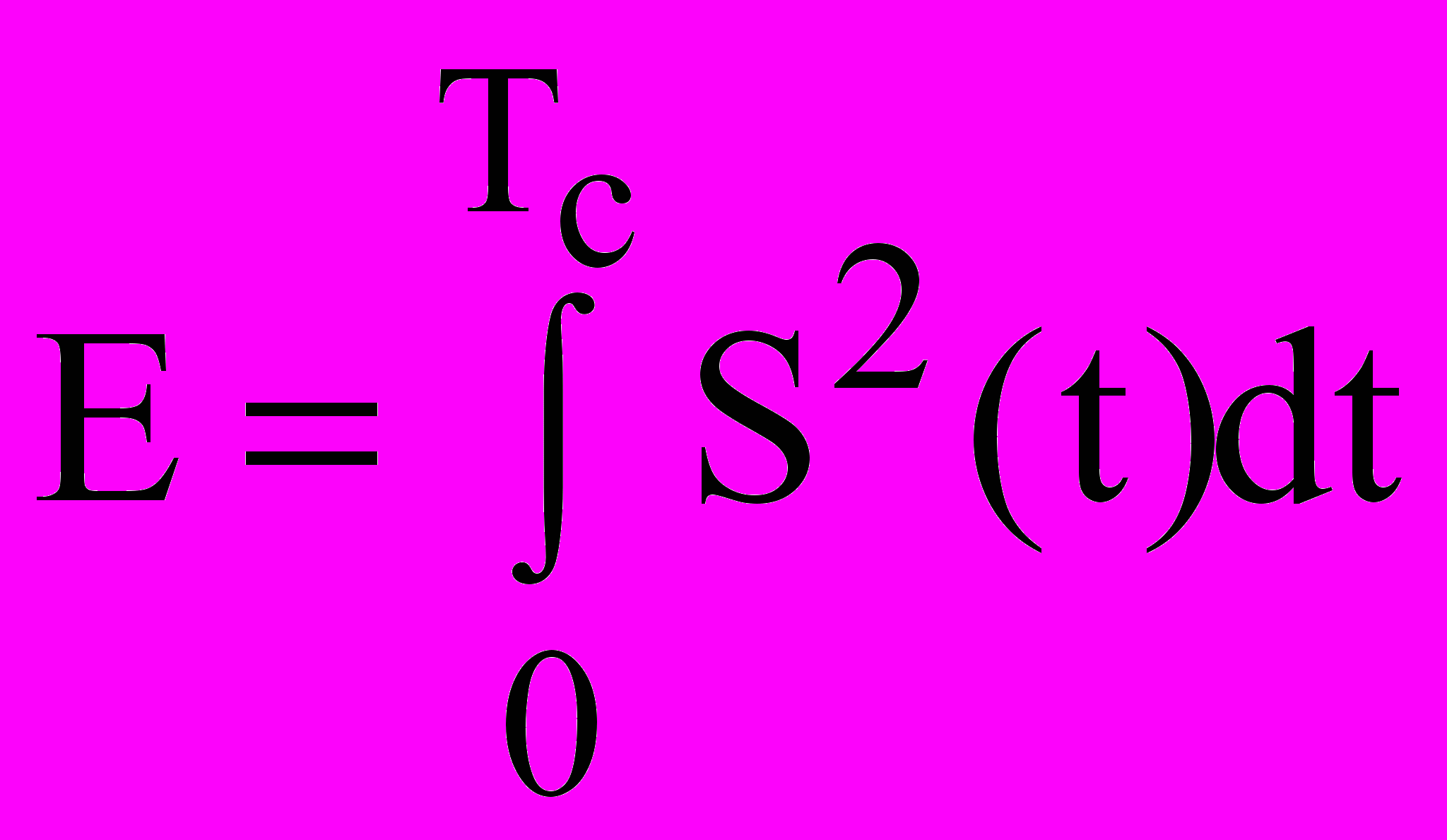, (16)

где 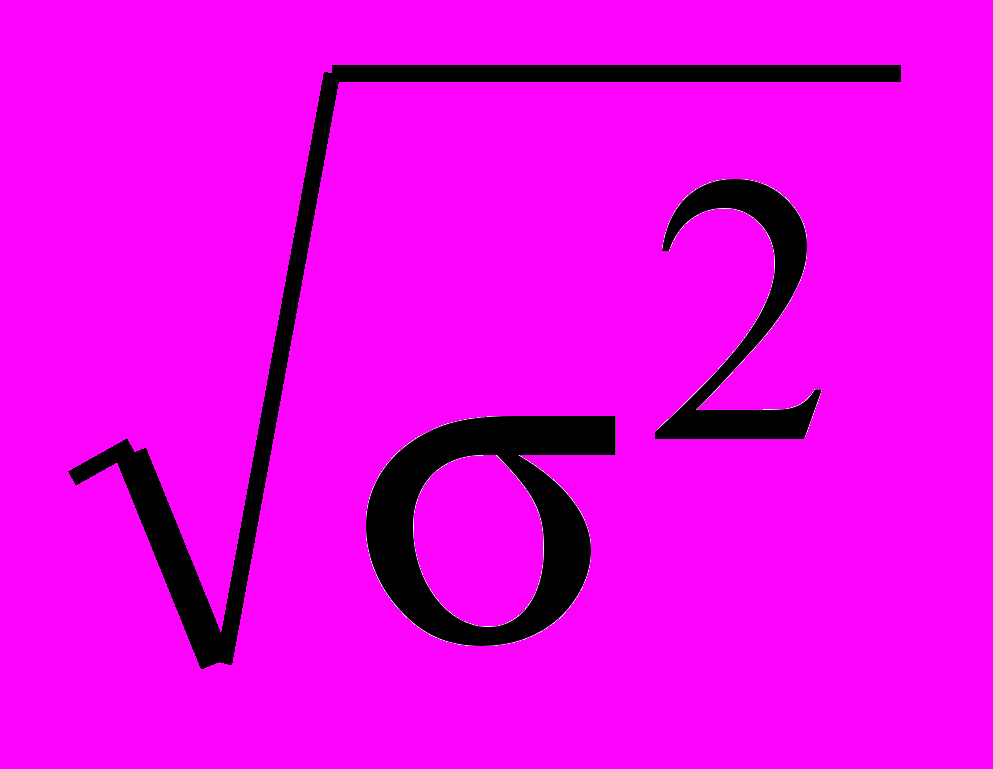- среднеквадратичное значение шума на выходе фильтра, пиковое значение сигнала на выходе;

Е - энергия сигнала на входе фильтра;

W₀ -спектральная плотность мощности белого шума.

Выражение (16), позволяющее определить эффективность согласованного фильтра, показывает, что при белом шуме отношение сигнал/шум на его выходе зависит только от энергии сигнала и энергетического спектра шума W_0. В случае ШПС: 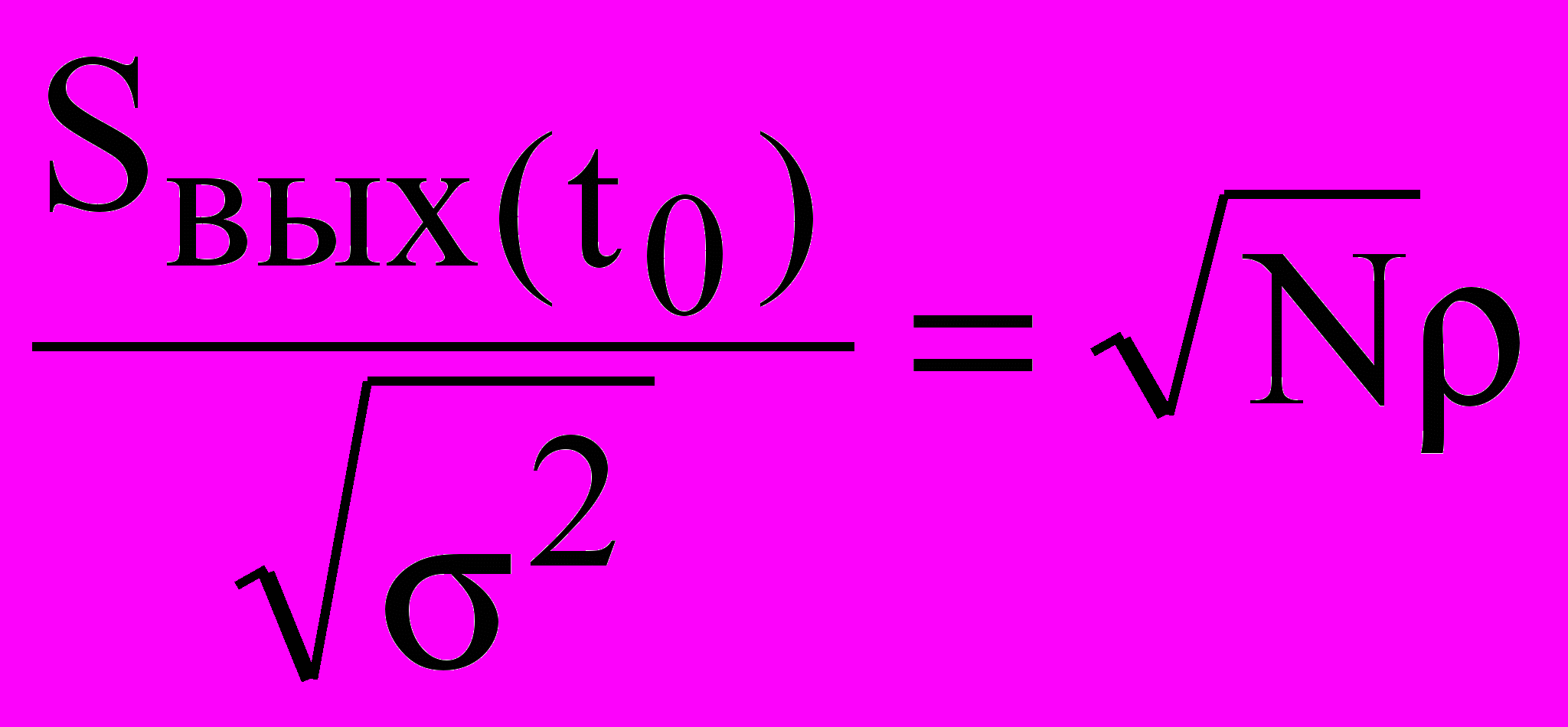(17)

E = NE₀ энергия сигнала, Е₀ – энергия элементарной посылки, N – число посылок в сигнале, ρ - отношение сигнал / шум на входе ОФ.

Из выражений (15,17) следует: во-первых, ОФ увеличивает отношение сигнал - шум по мощности на выходе в N раз, во-вторых, одна из возможных реализаций оптимального фильтра - коррелятор или программа, вычисляющая АКФ сигнала.

5. Фазоманипулированные сигналы
   

В качестве внутрисигнальной модуляции часто используют фазовую манипуляцию. Фазоманипулированные (ФМ) сигналы представляют собой последовательность радиоимпульсов равной амплитуды, начальные фазы которых изменяются по заданному закону. В большинстве случаев ФМ сигнал состоит из радиоимпульсов с двумя значениями начальных фаз: 0 и .

На рисунке 8а приведен пример ФМ сигнала, состоящего из 7 радиоимпульсов. На рисунке 8б представлена огибающая (в общем случае комплексная) этого же сигнала. В рассматриваемом примере огибающая представляет собой последовательность положительных и отрицательных единичных видеоимпульсов прямоугольной формы. Такое предположение о прямоугольности импульсов, образующих ФМ сигнал, справедливо для теоретических исследований. Однако при формировании ФМ сигналов и их передаче по каналам связи с ограниченной полосой пропускания импульсы искажаются, и ФМ сигнал перестает быть таким идеальным как на рисунке 8а. Огибающая полностью характеризует ФМ сигнал. Поэтому в работе исследуется свойства именно огибающей ФМ сигнала.

Прямоугольный импульс u(t) c единичной амплитудой и длительностью ₀, составляющей основу ФМ, записывается как u (t) = 1 при 0 t  ₀.

Огибающую, состоящую из N единичных видеоимпульсов можно представить в виде:

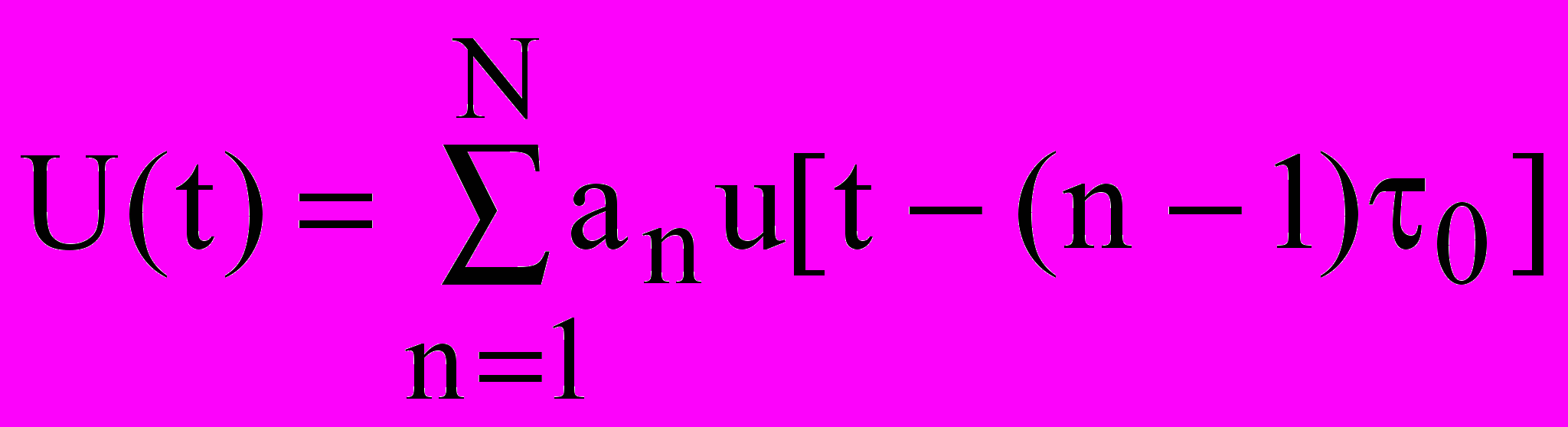
где амплитуда a_n принимает значения +1 или –1. Общая длительность ФМ сигнала T = N₀. Последовательность символов (амплитуд импульсов) A = (a₁, a₂ … a_n …a_N) называется кодовой последовательностью. Возможны следующие равнозначные обозначения кодовых последовательностей:

A =(111-1-11-1) = (1110010) =(+ + + - - + -), здесь N = 7.



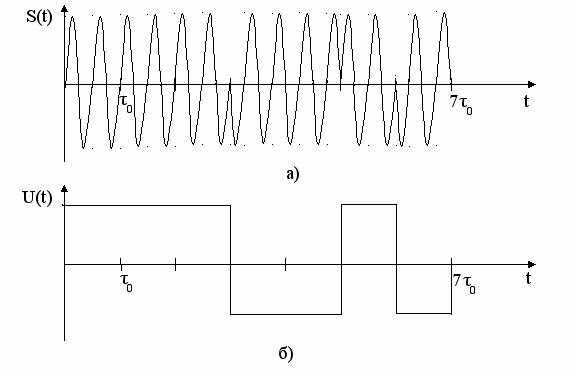
Рисунок 8 - ФМ сигнал, его комплексная огибающая

6. Спектр ФМ сигналов
   

Спектральные свойства ФМ сигналов определяются спектрами импульса u(t) и кодовой последовательности A. Спектр прямоугольного видеоимпульса S():

S() = ₀ [sin(₀/2)/(₀/2)] exp (- i₀/2)

Спектр прямоугольного сигнала состоит из трех сомножителей. Первый - равный τ₀ есть площадь импульса 1τ₀ . Второй множитель sin(₀/2)/(₀/2) в виде функции отсчета sin(x)/x характеризует распределение спектра по частоте. Третий множитель является следствием смещения центра импульса относительно начала координат на половину длительности импульса ₀/2.

Спектр ФМ сигнала G(), точнее спектр огибающей, с учетом теоремы о сдвиге, имеет следующий вид:

_N

G() = S()  a_n exp [-i(n-1)₀]

ⁿ⁼¹

Сумма в правой части является спектром кодовой последовательности A и обозначается в дальнейшем H(). Итак,

u(t)  S(), A  H(), U(t)  G(),

причем

G() = S()H().

Представление спектра ФМ сигнала в виде произведения удобно тем, что можно сначала отдельно найти спектры S() и H(), а затем, перемножив их, получить спектр ФМ сигнала. Свойства спектра прямоугольного импульса хорошо известны: он имеет лепестковую структуру с нулями в точках /, 2/ и т.д. Амплитудный спектр кодовой последовательности, в среднем, приближается к спектру белого шума и отличается значительными флуктуациями вокруг среднего, равного

<H ()> =

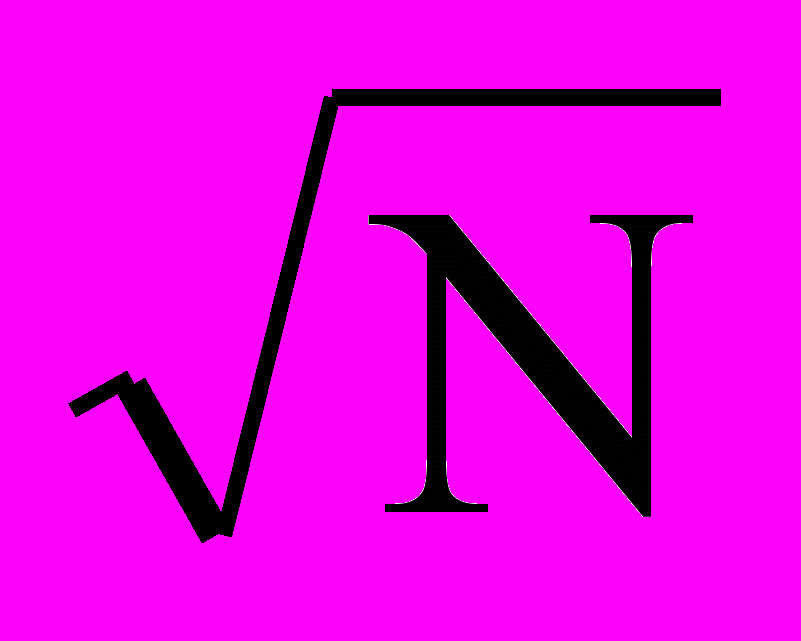
Для фазового спектра кодовой последовательности также характерна значительная изрезанность.

7. Автокорреляционная функция (АКФ)
   

АКФ ФМ сигналов имеет вид типичный для всех типов ШПС. Нормированная АКФ состоит из центрального (основного) типа с амплитудой 1, размещенного на интервале (-, ) и боковых (фоновых) максимумов, распределенных на интервале (-, ) и (, ).

Амплитуды боковых типов принимают различные значения, но у сигналов с “хорошей” корреляцией они малы, т.е. существенно меньше амплитуды центрального пика. Отношение амплитуды центрального пика (в данном случае 1) к максимальной амплитуде боковых максимумов называют коэффициентом подавления К. Для произвольных ШПС с базой В

К  1/

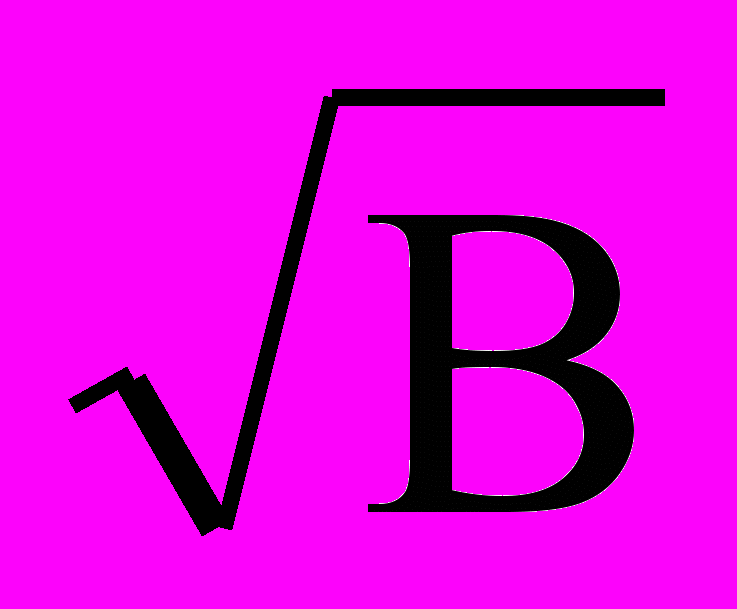
Для ФМ ШПС К1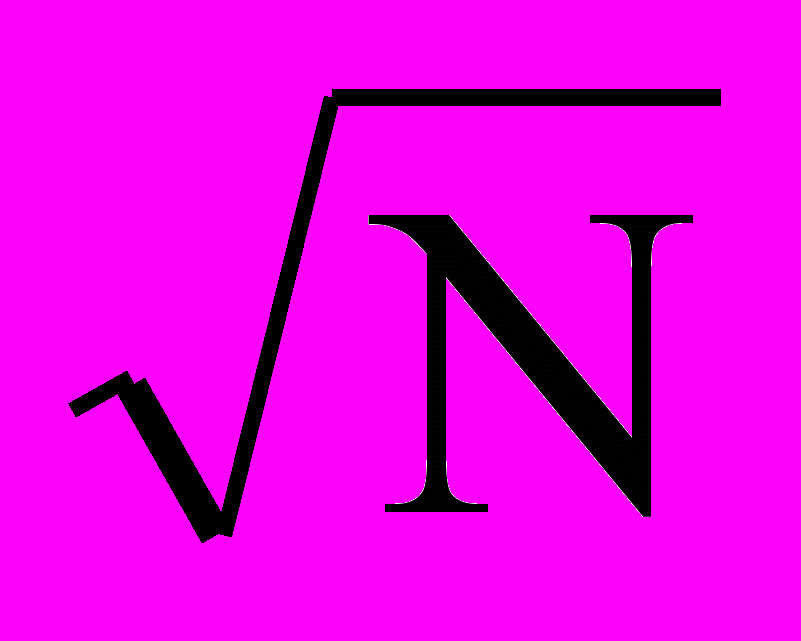. Пример АКФ ШПС дан на рисунке 9. Величина К существенно зависит от вида кодовой последовательности А. При правильном выборе закона формирования А можно добиться максимального подавления, а в ряде случаев – равенства амплитуд всех боковых максимумов.

8. Сигналы Баркера
   

Кодовая последовательность сигнала Баркера состоит из символов 1 и характеризуется нормированной АКФ вида:

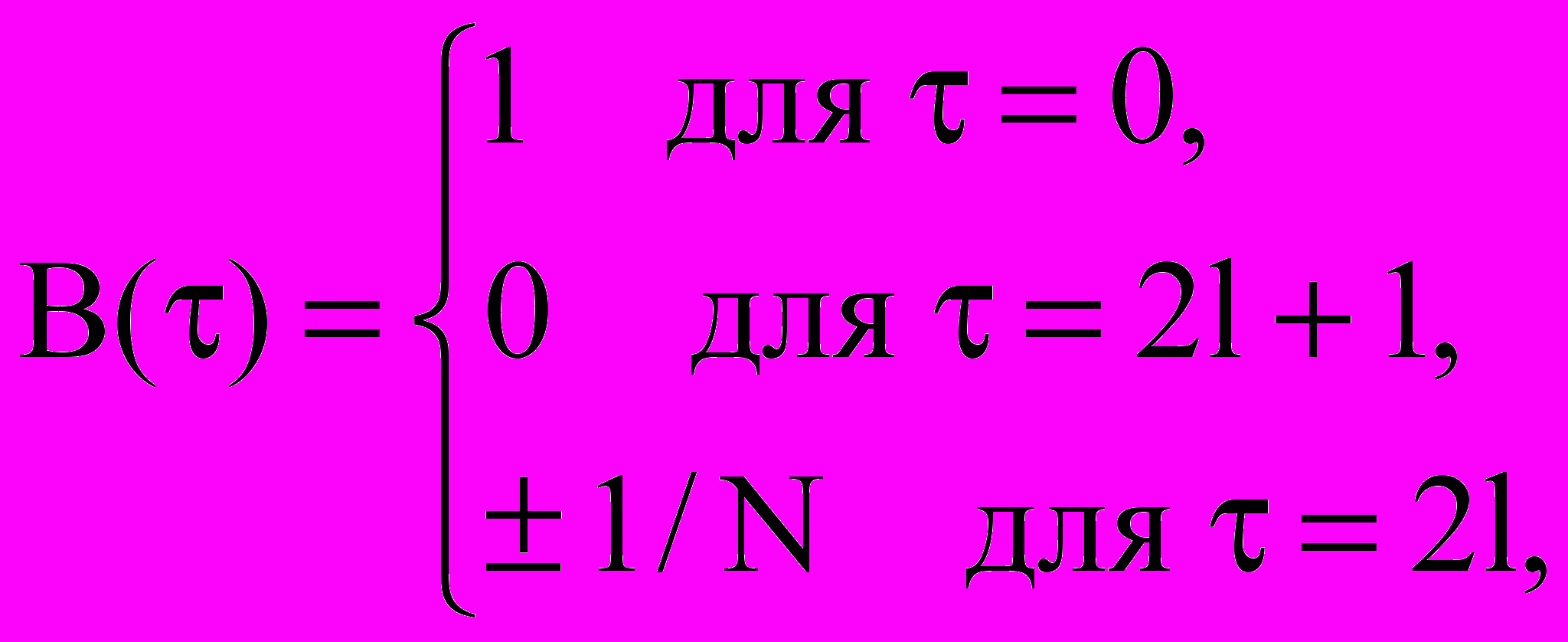(18)

где l = 0, 1, ... (N-1)/2.

Знак в последней строчке зависит от величины N. На рисунках 8-9 показаны ФМ сигнал, его комплексная огибающая и АКФ семизначного кода Баркера.

Из (18) следует, что одна из особенностей сигнала Баркера - равенство амплитуд всех (N-1) боковых максимумов АКФ, и все они имеют минимально возможный уровень, не превышающий 1/N. В таблице 1 приведены известные кодовые последовательности Баркера и их уровни боковых типов АКФ. Кодовые последовательности, обладающие свойствами (18), для N  13 не найдены.





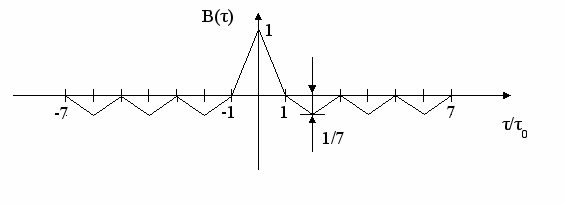
Рисунок 9 - АКФ семизначного кода Баркера


Таблица 1 Кодовые последовательности Баркера

Код	Кодовая последовательность	Уровень боковых лепестков
3	1 1 -1	-1/3
4	1 1 -1 1	1/4
5	1 1 1 -1 1	1/5
7	1 1 1 -1 -1 1 –1	-1/7
11	1 1 1 -1 -1 -1 1 -1 -1 1	-1/11
13	1 1 1 1 1 -1 -1 1 1 -1 1 -1 1	1/13

Формирование и обработка сигналов Баркера Формирование сигналов Баркера может осуществляться несколькими способами, так же, как и произвольного ФМ сигнала. Поскольку сигналы Баркера были первыми ПШС, причем с наилучшими АКФ, рассмотрим кратко один из возможных способов формирования и обработки сигналов Баркера.

На рисунке 10 изображен генератор сигнала Баркера с N=7. Генератор синхроимпульсов (ГСИ) формирует узкие прямоугольные синхроимпульсы, период следования которых равен длительности сигнала Баркера Т=7τ₀, а τ₀ - длительность одиночного (единичного) прямоугольного импульса. Генератор синхроимпульсов запускает генератор одиночных импульсов (ГОИ), который в свою очередь формирует одиночные прямоугольные импульсы длительностью τ₀ и периодом Т. Одиночные прямоугольные импульсы поступают на вход многоотводной линии задержки (МЛЗ), которая имеет N-1=6 секций с отводами через интервалы времени, равные τ₀. Число отводов, включая начало линии, равно 7. Так как кодовая последовательность Баркера с N =7 имеет вид 111-1 -11 -1, то импульсы с первого, второго, третьего и шестого отводов (счет ведется от начала линии) поступают на вход сумматора ( + ) непосредственно, а импульсы с четвертого, пятого и седьмого отводов поступают на вход сумматора через инверторы (ИН), которые превращают положительные одиночные импульсы в отрицательные, т. е. осуществляют изменение фазы на π. Поэтому инверторы называются также фазовращателями. На выходе сумматора имеет место видеосигнал Баркера (рисунок 8б), который затем поступает на один вход балансного модулятора (БМ), на другой вход которого подается радиочастотное колебание на несущей частоте, формируемое генератором несущей частоты (ГНЧ). Балансный модулятор осуществляет фазовую манипуляцию радиочастотного колебания ГНЧ в соответствии с кодовой последовательностью Баркера: видеоимпульсу с амплитудой 1 соответствует радиоимпульс с фазой 0, а видеоимпульсу с амплитудой -1 - радиоимпульс с фазой π. Таким образом, на выходе балансного модулятора имеет место радиочастотный сигнал Баркера (рисунок 8а).



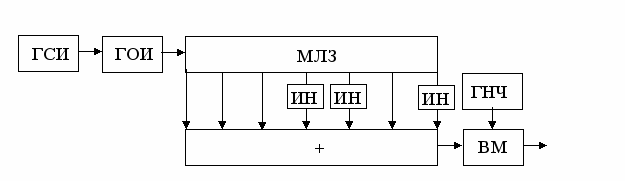
Рисунок 10 – Генератор сигнала Баркера с N = 7

Оптимальная обработка сигналов Баркера так же, как и других ШПС, производится либо с помощью согласованных фильтров, либо с помощью корреляторов. Возможно несколько способов построения согласованных фильтров и корреляторов, отличающихся друг от друга в техническом выполнении, но обеспечивающих одно и то же максимальное отношение сигнал-помеха на выходе. На рисунке 11 приведена схема согласованного фильтра для сигнала Баркера с N = 7. С выхода усилителя промежуточной частоты приемника сигнал поступает на согласованный фильтр одиночного импульса (СФОИ), который производит оптимальную обработку (фильтрацию) одиночного прямоугольного радиоимпульса с центральной частотой, равной промежуточной частоте приемника. На выходе СФОИ радиоимпульс имеет треугольную огибающую. Треугольные радиоимпульсы с длительностью по основанию 2 τ₀ поступают на МЛЗ, которая имеет 6 секций и 7 отводов (включая начало линии). Отводы следуют через τ₀. Так как импульсная характеристика согласованного фильтра совпадает с зеркально отраженным сигналом, то кодовую импульсную характеристику фильтра для сигнала Баркера с N=7 следует устанавливать в соответствии с последовательностью -11-1-1111. Поэтому радиоимпульсы со второго, пятого, шестого и седьмого отводов МЛЗ поступают в сумматор ( + ) непосредственно, а радиоимпульсы с первого, третьего и четвертого отводов — через инверторы (ИН), которые меняют фазу на π. На выходе сумматора имеет место АКФ сигнала Баркера, огибающая которой приведена рисунке 9.



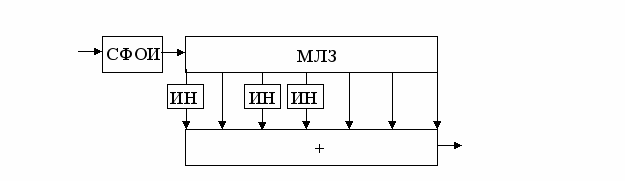
Рисунок 11 – Согласованный фильтр сигнала Баркера с N = 7

9. М – последовательности
   

Среди фазоманипулированных сигналов особое значение занимают сигналы, кодовые последовательности которых являются последовательностями максимальной длины или М -последовательностями.

М – последовательности принадлежат к разряду двоичных линейных рекуррентных последовательностей и представляют собой набор N периодически повторяющихся двоичных символов. Причем каждый текущий символ d_j образуется в результате сложения по модулю 2 некоторого числа m предыдущих символов, одни из которых умножаются на 1, а другие – на 0.

Для j-го символа имеем:

_m

d _j =  a _i d _{j - i} = a ₁ d _{j -1}  . . .  a _m d _{j –m} (4)

^{i = 1}

Где а₁…а_m – числа 0 или 1.

Технически генератор М-последовательности строится в виде регистра (последовательно включенных триггеров) с отводами, с цепью обратной связи и с сумматором по модулю 2. Пример такого генератора приведен на рисунке 12. Умножение на а₁…а_m в (4) означает просто наличие или отсутствие отвода, т.е. связи соответствующего триггера (разряда регистра) с сумматором. В m-разрядном регистре максимальный период равен: N^m – 1. Величина m называется памятью последовательности. Если отводы выбраны произвольно, то не всегда на выходе генератора будет наблюдаться последовательность максимальной длины. Правило выбора отводов, позволяющее получить последовательность с периодом N^m-1, предполагает найти неприводимые примитивные полиномы степени m с коэффициентами, равными 0 и 1. Не равные нулю коэффициенты в полиномах определяют номера отводов в регистре.

Так, при m=6 существует 3 примитивных многочлена:

а₆ а₅ а₄ а₃ а₂ а₁ а₀

p₁ ( x ) = x ⁶ + x + 1 1 0 0 0 0 1 1

p₂ ( x ) = x ⁶ + x ⁵ + x ² + x + 1 1 1 0 0 1 1 1

p₃ ( x ) = x ⁶ + x ⁵ + x ³ + x ² + 1 1 1 0 1 1 0 1


На рисунке 12 реализован первый вариант.




Рисунок 12 ­­­- Генератор М-последовательности с периодом N = 2⁶ – 1 = 63


Особенности автокорреляционной функции М-последовательности Наибольший интерес представляет нормированная автокорреляционная функция (АКФ). Различают два случая получения такой функции: в периодическом (ПАКФ) и апериодическом режимах. Периодическая АКФ имеет основной, равный единице, пик и ряд боковых выбросов, амплитуды которых 1/N. С ростом N ПАКФ приближается к идеальной, когда боковые пики становятся по сравнения с основным пренебрежимо малы.

Боковые пики АКФ в апериодическом режиме существенно больше боковых пиков ПАКФ. Среднеквадратичное значение боковых пиков (вычисленное через дисперсию) равно

^1/2  0,4/

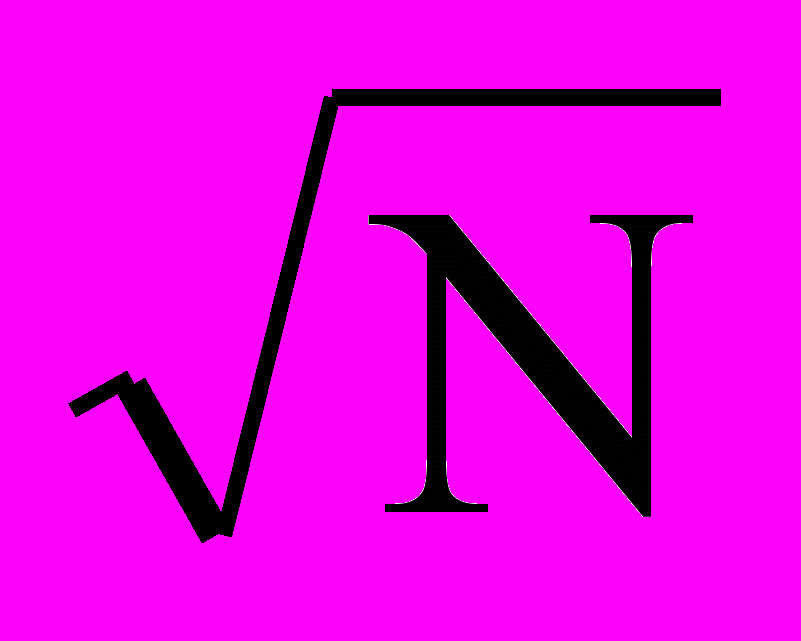
1.10 Усеченные М-последовательности

Разбивая М-последовательность (полный период N) на сегменты длительности N_с, можно получить большое число ШПС, рассматривая каждый из сегментов как самостоятельный сигнал. Если сегменты не перекрываются, то их число равно n = N/(N_c-1). Таким образом, можно получить большое число псевдослучайных последовательностей. Автокорреляционные свойства таких последовательностей значительно хуже, чем у М-последовательности той же длительности и зависят от N_c. Установленно, что у 90% сегментов u_б  3 /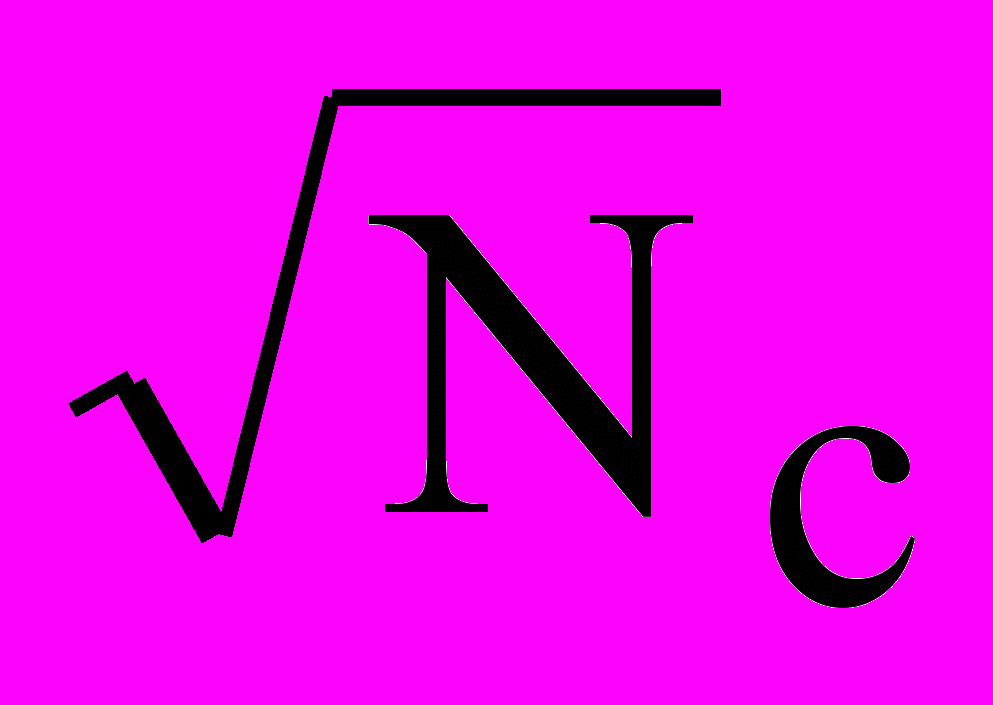, а у 50% - 2 /_.


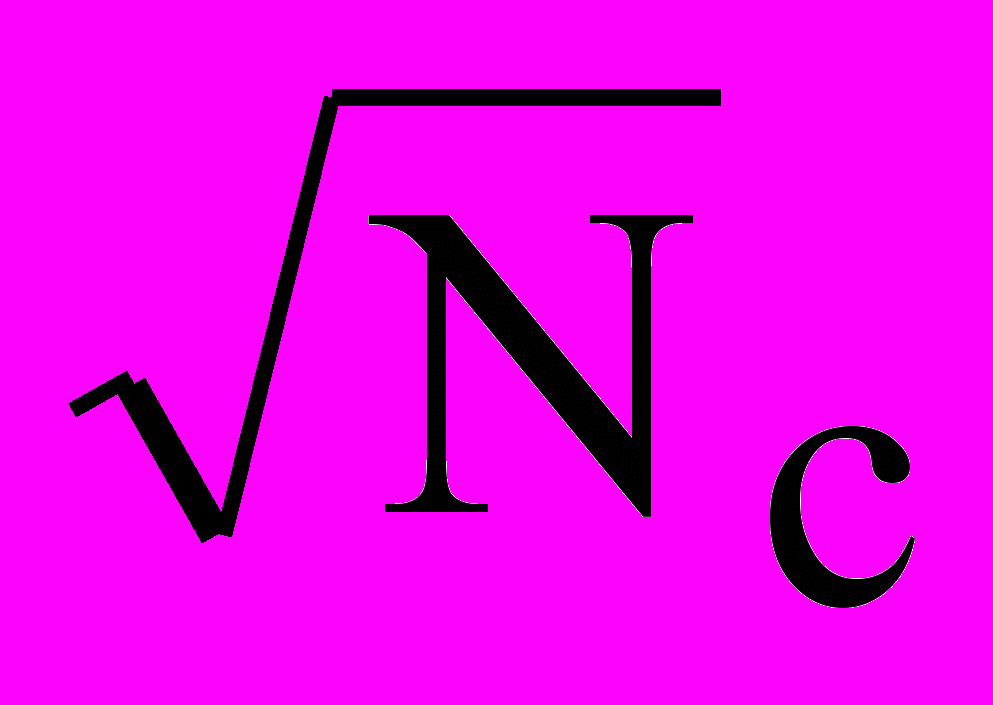2. Описание лабораторной работы

1. О программах.
   

Основным инструментом исследования в лабораторной работе является пакет программ, состоящий из программ shps.exe и spectr.exe.

Программа shps.exe представляет собой генератор исследуемых сигналов Он позволяет генерировать:

• произвольный сигнал (например, прямоугольный видеоимпульс или произвольную последовательность импульсов);
  
• сигналы Баркера с N = 3  13;
  
• М-последовательности порядка m = 3  7 (периода N_э = 7  127);
  
• усеченные М-последовательности m = 3  7 (периода N_э  7  127);
  
• белый шум.
  

Сигналы создаются в виде текстового файла posl.dat, содержащего численные значения отсчетов сигнала. Элементарная посылка (прямоугольный импульс, из которого состоят последовательности) представляется в виде 20 отсчетов сигнала. Отсчеты берутся с интервалом в 0.0025 сек, и длительность элементарной посылки составляет 0.05 сек.



0.05 сек.


1


-1




0.0025 сек

Программа позволяет подмешивать в генерируемые сигналы аддитивную помеху (белый шум) с эффективным значением в диапазоне – 460 Дб (среднеквадратичное отклонение помехи от 0.005 до 1 при уровне полезного сигнала = 1). Шум имеет нормальное распределение с нулевым средним и бесконечно узкой корреляционной функцией. Отсчеты различных реализаций шума сохранены в файлах: shum1.dat shum2dat, shum3.dat. Возможен учет явления многолучевости, т.е. прихода в точку приема не только исходного сигнала, но и его копии, сдвинутой во времени.

Вторая часть программы содержит оптимальный фильтр, перестраиваемый под вводимый сигнал. На выходе фильтра формируется файл optim.dat, который (в соответствии принципами оптимальной фильтрации) содержит свертку входного сигнала и его «чистой» копии, т.е. их взаимно корреляционную функцию. Параллельно подсчитываются отношения сигнал / шум на входе и выходе фильтра, как отношение максимального значения сигнала к среднеквадратичному значению шума. Вспомогательный файл optim_n.dat содержит отдельно «шумовую» составляющую сигнала, полученного на выходе фильтра.

Уже знакомая по предыдущим лабораторным работам программа spectr.ехе (автор доцент Вертоградов Г.Г.) позволяет получать амплитудный и фазовый спектр, автокорреляционную функцию сигналов, вводимых в виде текстовых файлов. (Инструкция к программе содержится в файле spectr.txt).


3. Порядок выполнения работы

1. Используя программы shps.exe и spectr, исследуйте амплитудный, фазовый спектры и автокорреляционную функцию прямоугольного импульса в отсутствии шумов. Для этого необходимо:
   

• запустить shps.exe
  
• выбрать произвольный сигнал
  
• количество посылок - 1
  
• посылка - 1
  
• шум приравнять нулю
  
• отменить многолучевость
  
• не включать оптимальный фильтр
  
• запустить spectr.exe
  
• в меню «файл» необходимо открыть файлы для сигнала – posl.dat (на вопрос: Переписать? надо ответить: Нет), для спектра – spectr1 и корреляционной функции – korel1. Для расчета спектра и корреляционной функции нажать F9, для просмотра результатов используйте меню «просмотр результатов». Если график виден не достаточно детально, то, изменив конечное время или частоту, можно растянуть его по оси. Иногда удобно на одном графике смотреть и сигнал, и корреляционную функцию. Важно также обратить внимание на то, что графики возможно пронормированы. (нормировку можно отключить, тогда по оси Y будут реальные значения функций).
  
• обратите внимание - на каких частотах спектр прямоугольного импульса обращается в ноль и какую частоту можно считать граничной частотой. Как эти частоты связаны с длительностью импульса (0.05 сек)?
  

2. Исследуйте несколько кодов Баркера (например, с номерами 7, 11, и 13), сравните их амплитудные спектры, фазовые спектры и корреляционные функции между собой, а также со своими аналогами для прямоугольного импульса. (Вид спектров некоторых кодов имеется в [1] стр. 94). Для этого необходимо:
   

• в программе shps.exe выбрать код Баркера
  
• ввести номер кода
  
• шум приравнять нулю
  
• отменить многолучевость
  
• не включать оптимальный фильтр
  
• запустить spectr.exe
  
• в меню «файл» необходимо открыть файлы для сигнала – posl.dat , спектра – spectr2 и корреляционной функции – korel2. Для расчета спектра и корреляционной функции – F9, для просмотра результатов используйте меню «просмотр результатов». Чтобы сравнить спектр данного сигнала со спектром прямоугольного импульса, можно в меню "График Спектра" последовательно для просмотра выбрать файлы spectr2 и spectr1.
  
• Измерьте уровень боковых лепестков корреляционной функции кодов Баркера. Во сколько раз они меньше центрального максимума?
  
• Измерьте толщину основного лепестка. Как она зависит от номера кода и длительности элементарной посылки?
  
• Повторите ту же процедуру для другого номера кода (N=7,11,13).
  

3. Пронаблюдайте автокорреляционную функцию этих же сигналов при наличии шумов. Для этого следуйте той же схеме, что и раньше, но задайте несколько значений шума (0.05; 0.2).
   
4. С помощью программы shps.exe создайте сигналы с произвольными кодовыми последовательностями с длинами равными кодам Баркера, но с кодировками отличными от них. Сравните амплитудные спектры и корреляционные функции этих сигналов и кодов Баркера. Например, в случае с N=7 для этого надо:
   

• запустить shps.exe
  
• выбрать произвольный сигнал
  
• количество посылок - 7
  
• посылка - 1,0,1,1,1,0 (или любые другие посылки)
  
• шум приравнять нулю
  
• отменить многолучевость
  
• не включать оптимальный фильтр
  
• запустить spectr.exe
  
• измерьте уровень боковых липестков корреляционной функции.
  
• (наверняка они уже не будут одинаковыми и равными 1/N, а это приведет к ухудшению условий приема ).
  

5. С помощью программы shps.exe создайте М-последовательность с m = 3...7. Для этого запустите программу, введите порядок характеристического многочлена и, используя таблицу 2, сам многочлен (любой из возможных). Коэффициент усечения выберите равным единице. Уровень шума - нулю. Исследуйте характеристики получившегося сигнала программой spectr: измерьте уровень боковых лепестков корреляционной функции, толщину основного максимума и ширину спектра сигнала. Для корреляционной функции m-последовательности с m=4 откройте файл korel3, т.к. она будет использоваться в дальнейшем.
   

6. Создайте произвольные последовательности с N=15 или m-последовательности с m=4 и характеристическим многочленом, которого нет в таблице 2 . С помощью программы spectr.exe сравните корреляционную функцию полученной последовательности с корреляционной функцией "правильной" m-последовательности, которая сохранена в файле korel3.
   
7. Создайте периодическую m-последовательность с m=4, и посмотрите как изменится ее корреляционная функция по сравнению с одиночным m-сигналом. Характерные особенности можно пронаблюдать на сигнале представляющем собой две m-последовательности, следующие одна за другой. Для этого надо рассчитать длительность m-последовательности в секундах, и подставить полученное значение в качестве задержки между лучами. Корреляционная функция полученного сигнала будет иметь два основных пика и минимальный уровень боковых лепестков между ними.
   
8. Используя оптимальный фильтр, встроенный в программе, исследуйте при каком максимальном уровне помех возможно использование кодов Баркера для надежной передачи информации. Условием надежного приема будем считать требование превышения сигнала над уровнем помех в 2 раза. Для этого необходимо:
   

• в программе shps.exe выбрать код Баркера
  
• ввести номер кода (7, 11, 13)
  
• ввести уровень шума (0.5, 1, 1.5, 2, 3, …)
  
• отменить многолучевость
  
• включить оптимальный фильтр
  
• запустить spectr.exe
  
• в меню просмотр результатов выбрать график сигнала – optim.dat и там же optim_n.dat. Отключите нормировку. На экране будет сигнал на выходе фильтра и отдельно шум на выходе.
  
• Измерьте максимальный уровень сигнала и шума.
  
• Проделайте аналогичную операцию и для более длинных последовательностей (m-последовательностей пятого и большего порядка.) Вы увидите, что даже если помеха в несколько раз превышает полезный сигнал, информация может быть выделена с большой надежностью. Так m-последовательность длиной 127 элементарных посылок может быть скрыта в шуме в 12 раз превышающем амплитуду полезного сигнала. А оптимальным фильтром такую последовательность мы легко можем выделить из шума. Причем только фильтр настроенный именно на этот сигнал может его заметить. Это обстоятельство объясняет высокую скрытность широкополосных систем связи.
  

9. В реальной ситуации в точку приема приходят сигналы, отразившиеся от различных препятствий на пути распространения (слои ионосферы, здания, холмы и т.п.). Эти сигналы приходят с различным запаздыванием и, перекрываясь во времени, вызывают замирания результирующего сигнала. Исследуйте: какое время задержки должно быть между прямоугольными импульсами длительности 0.35 сек (7 посылок), чтобы при приеме они не накладывались бы друг на друга (их можно было различить). И какое время задержки должно быть между сигналами Баркера той же длительности (семизначный код), чтобы их можно было различить. Для этого необходимо:

• запустить shps.exe
  
• выбрать произвольный сигнал
  
• количество посылок - 7
  
• посылка - 1,1,1,1,1,1,1
  
• шум приравнять нулю
  
• задержка между лучами (0.05, 0.2, 0.04, 0.7, 0.8)
  
• включить оптимальный фильтр
  
• запустить spectr.exe
  
• посмотреть график сигнала на выходе фильтра – файл optim.dat
  
• подобрать такое время задержки, чтобы оба пика были четко разделены.
  
• проделайте то же самое для семизначного кода Баркера и определите минимальную задержку при которой эти сигналы можно разделить.
  
• сделайте вывод - какой из сигналов (прямоугольный или код Баркера) эффективнее применять для борьбы с многолучевостью.
  

Таблица 2. Некоторые характеристические многочлены, порождающие М-последовательности.

m=3	m=6	m=8		10000010110
110	100001	10001110	m=10	10000100011
101	101101	10010101	1000000100	10001110101
	110011	11100001	1000001101
m=4	101011	10010110	1000010011	m=12
1001			1000110111	100000101001
1100	m=7	m=9	1010110101	110010100000
	1000001	100001000	1010101011	100100000110
m=5	1000100	100001101		101100000100
10010	1111000	101011011	m=11	101000011000
10100	1101010	110001010	10000000010
11011	1111011	110010001	10000001011
11110		100110100	10000010101

Коэффициенты следуют в порядке а_m a_m-1 … a₁ . Очевидно a₀ , равное 1, в формировании М-последовательности не участвует

4. Контрольные вопросы

1. Что такое "сложные" сигналы? Чем объясняется их повышенная помехоустойчивость в сравнении с "простым" сигналом?
   
2. Фаза радиоимпульсного сигнала, манипулированного по закону семизначного кода Баркера. Суммарная длительность сигнала 35 мкс. Частота несущей - 100МГц. Определите:
   

а) ширину спектра сигнала;

б) базу сигнала;

в) при какой многолучевости целесообразно применять сигнал для выполнения условия разделения лучей;

г) как изменяется отношение сигнал/шум на выходе по сравнению со входом, если шум белый:

3. В прямоугольный радиоимпульсный сигнал 220мкс, обрабатываемый на приеме оптимально, ввели фазовую манипуляцию по закону Баркера с N = 11. Вопросы:
   

а) как изменится отношение сигнал/шум на выходе оптимального фильтра ;

б) как изменится разрешающая способность.

4. Образуйте М-последовательность по правилу d_j = d_j-u +d_j-3.
   
5. Какие задачи могут решаться при приеме сигнала в присутствии помех?
   
6. Назовите критерий согласованности фильтра с заданным сигналом.
   
7. Как учитываются параметры помехи при построении согласованного фильтра?
   
8. Дайте определение помехи типа белый шум.
   
9. Поясните физический смысл АЧХ и ФЧХ согласованного фильтра.
   
10. От чего зависит отношение сигнал/шум на выходе оптимального фильтра?
    
11. Какой вид имеет сигнал на выходе согласованного фильтра?
    

5. Литература

1. Шумоподобные сигналы в системах передачи информации. Под ред. В.Б. Пестрякова. – М., “Сов. радио”, 1973, -424c.

2. Ю.С. Лёзин. Введение в теорию радиотехнических систем. – М.: Радио и связь, 1985, -384c.

3. Л.Е. Варакин. Системы связи с шумоподобными сигналами. - М.: Радио и связь, 1985, -384c.