Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной техники Кафедра вычислительной техники (специальность 220100). учебное пособие
| Вид материала | Учебное пособие |
| 0.4.2 Сортировка методом распределяющего подсчета 0.5 заливка области с затравкой |
- Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной, 1650.9kb.
- Рабочая программа для специальности: 220400 Программное обеспечение вычислительной, 133.96kb.
- Государственный Технический Университет. Факультет: Автоматики и Вычислительной Техники., 32.46kb.
- Образования Республики Молдова Колледж Микроэлектроники и Вычислительной Техники Кафедра, 113.64kb.
- Постоянное развитие и углубление профессиональных навыков в области информационных, 54.56kb.
- «Программное обеспечение вычислительной техники и автоматизированных систем», 1790.14kb.
- Задачи дисциплины: -изучение основ вычислительной техники; -изучение принципов построения, 37.44kb.
- Лекция №2 «История развития вычислительной техники», 78.1kb.
- Система контроля и анализа технических свойств интегральных элементов и устройств вычислительной, 582.84kb.
- Московский государственный инженерно-физический институт (технический университет), 947.05kb.
0.4.2 Сортировка методом распределяющего подсчета
Понятно, что одна из важнейших работ в алгоритме построчного сканирования - сортировка. В связи с заведомо ограниченной разрешающей способностью растровых дисплеев (не более 2048) иногда целесообразно использовать чрезвычайно эффективный алгоритм сортировки методом распределяющего подсчета.
Для рассмотрения алгоритма предположим, что надо отсортировать числа, заданные в массиве с именем "Исходный_массив"; количество сортируемых чисел задается скаляром "Кол-во_чисел"; сортируемые числа J удовлетворяют условию:
|
Для сортировки потребуются описания:
int Max_число; /* Верхняя граница значений */
int *Повтор; /* Длина этого массива = Max_число */
int Кол_чисел; /* Кол-во сортируемых чисел */
int *Исходный_массив; /* Длина этого массива >= Кол_чисел */
int *Результат; /* Длина этого массива >= Кол_чисел */
int ii,jj, kk; /* Рабочие переменные */
- Обнуляется служебный массив для подсчета числа повторений исходных кодов.
- for (ii=0; ii
- Сортируемый массив просматривается и вычисляется количество раз повторений каждого числа:
- for (ii= 0; ii < Кол_чисел; ++ii) {
- jj= Исходный_массив[ii];
- Повтор[jj]= Повтор[jj] + 1;
- }
- Суммируется количество повторений каждого числа, так что значение Повтор[J] даст начальное расположение группы чисел, равных J, в отсортированном массиве:
- jj= 0;
- for (ii=0; ii
- jj= jj + Повтор[ii];
- Повтор[ii]= jj;
- }
- Просматривается исходный массив и числа из него заносятся в массив результатов той же длины. Индекс занесения числа J в массив результатов равен значению J-го элемента массива Повтор. После занесения числа J значение Повтор[J] уменьшается на 1:
- for (ii= 0; ii < Кол_чисел; ++ii) {
- jj= Исходный_массив[ii];
- kk= Повтор[jj];
- Результат[kk]= jj;
- Повтор[jj]= Повтор[jj] - 1;
- }
0.5 ЗАЛИВКА ОБЛАСТИ С ЗАТРАВКОЙ
Как уже отмечалось, для приложений, связанных в основном с интерактивной работой, используются алгоритмы заполнения области с затравкой.
При этом тем или иным образом задается заливаемая (перекрашиваемая) область, код пиксела, которым будет выполняться заливка и начальная точка в области, начиная с которой начнется заливка.
По способу задания области делятся на два типа:
гранично-определенные, задаваемые своей (замкнутой) границей такой, что коды пикселов границы отличны от кодов внутренней, перекрашиваемой части области. На коды пикселы внутренней части области налагаются два условия - они должны быть отличны от кода пикселов границы и кода пиксела перекраски. Если внутри гранично-определенной области имеется еще одна граница, нарисованная пикселами с тем же кодом, что и внешняя граница, то соответствующая часть области не должна перекрашиваться;
внутренне-определенные, нарисованные одним определенным кодом пиксела. При заливке этот код заменяется на новый код закраски.
В этом состоит основное отличие заливки области с затравкой от заполнения многоугольника. В последнем случае мы сразу имеем всю информацию о предельных размерах части экрана, занятой многоугольником. Поэтому определение принадлежности пиксела многоугольнику базируется на быстро работающих алгоритмах, использующих когерентность строк и ребер (см. предыдущий раздел). В алгоритмах же заливки области с затравкой нам вначале надо прочитать пиксел, затем определить принадлежит ли он области и если принадлежит, то перекрасить.
Заливаемая область или ее граница - некоторое связное множество пикселов. По способам доступа к соседним пикселам области делятся на 4-х и 8-ми связные. В 4-х связных областях доступ к соседним пикселам осуществляется по четырем направлениям - горизонтально влево и вправо и в вертикально вверх и вниз. В 8-ми связных областях к этим направлениям добавляются еще 4 диагональных. Используя связность мы может, двигаясь от точки затравки, достичь и закрасить все пикселы области.
Важно отметить, что для 4-х связной прямоугольной области граница 8-ми связна (рис. а) и наоборот у 8-ми связной области граница 4-х связна (см. рис. б). Поэтому заполнение 4-х связной области 8-ми связным алгоритмом может привести к "просачиванию" через границу и заливке пикселов в примыкающей области.
В общем, 4-х связную область мы можем заполнить как 4-х, так и 8-ми связным алгоритмом. Обратное же неверно. Так область на рис. а мы можем заполнить любым алгоритмом, а область на рис. б, состоящую из двух примыкающих 4-х связных областей можно заполнить только 8-ми связным алгоритмом.
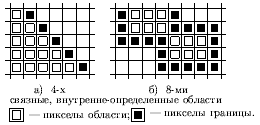
Рис. 0.5.1: Связность областей и их границ
С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренне, так и гранично-определенной области. В [] рассматриваются совсем короткие рекурсивные подпрограммы заливки. В [] - несколько более длинные итеративные подпрограммы.
