Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной техники Кафедра вычислительной техники (специальность 220100). учебное пособие

Вид материала

Подобный материал:

1 ... 6 7 8 9 10 11 12 13 ... 44

0.2.3 Улучшение качества аппроксимации векторов

Выше было отмечено, что растровая генерация отрезков имеет следующие недостатки:
 неточное расположение начала и конца,
 ступенчатый вид отрезка,
 яркость зависит от наклона и длины.

Ясно, что первый недостаток не может быть устранен программным путем. Неравномерность яркости обычно не слишком заметна и может быть скомпенсирована очевидным образом, требующим, в общем случае, вещественной арифметики, но в связи с реально небольшим количеством различимых уровней яркости достаточно обойтись целочисленным приближением, причем очень грубым.

Наиболее заметно ухудшает качество изображения ступенчатость. Имеется следующие способы борьбы со ступенчатостью :

 увеличение пространственного разрешения за счет усовершенствования аппаратуры,

 трактовка пиксела не как точки, а как площадки конечного размера, яркость которой зависит от размера площади пиксела, занятой изображением отрезка,

 "размывание" резкой границы, за счет частичной подсветки пикселов, примыкающих к формируемому отрезку. Понятно, что при этом ухудшается пространственное разрешение изображения.

В данном пункте мы рассмотрим модифицированный алгоритм Брезенхема, трактующий пиксел как конечную площадку. В следующем пункте будет рассмотрен общий подход, использующий низкочастотную фильтрацию для "размывания" границ изображения.

Модифицированный алгоритм Брезенхема

Основная идея алгоритма состоит в том, чтобы для ребер многоугольника устанавливать яркость пиксела пропорционально площади пиксела, попавшей внутрь многоугольника.

На рис. приведена иллюстрация построения ребра многоугольника с тангенсом угла наклона 11/21.

На рис. а) показан результат генерации многоугольника с использованием ранее рассмотренного алгоритма Брезенхема при двухуровневом изображении (пиксел или закрашен или не закрашен).

На рис. б) показан результат генерации многоугольника с вычислением интесивности пикселов, через которые проходит ребро многоугольника. Интенсивность вычисляется пропорциональной площади части пиксела, попавшей внутрь многоугольника.

На рис. в) показан результат генерации многоугольника с вычислением интесивности пиксела, через который проходит ребро многоугольника в соответствии с модифицированным алгоритмом Брезенхема.

Как видно из рис. при построении ребра многоугольника с тангенсом угла наклона t (0  t  1) могут захватываться либо один пиксел (пикселы (0,0), (2,1), (4,2), (6,8)) либо два пиксела (пикселы (1,0) и (1,1), (3,1) и (3,2), (5,2) и (5,3)). Если захватывается один пиксел, то часть его площади, попавшая внутрь многоугольника, равна dy + t/2 (рис. a).

Если же захватывается два пиксела, то часть площади нижнего пиксела, попавшая внутрь многоугольника равна 1 - [((1 - dy)²)/ 2t], а верхнего - [((dy - 1 + 2)²)/ 2t] (см. рис. б). Суммарная площадь частей для двух пикселов, попавшая внутрь многоугольника, равна dy + t/2.

Если теперь в исходном алгоритме Брезенхема (см. 0.2.2) заменить отклонение E на E' = E + (1-t), то 0  E'  1) и значение E' будет давать значение той части площади пиксела, которая находится внутри многоугольника.

Выполняя преобразование над значением отклонения для первого шага (см. 0.2.2) получим, что начальное значение станет равным 1/2. Максимальное значение отклонения E'_max, при превышении которого производится увеличение Y-координаты занесения пикселов, станет равным (1 - t).

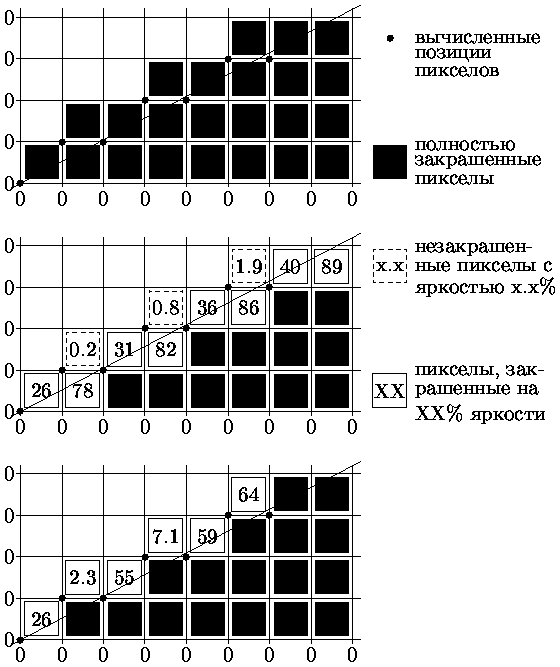
Рис. 0.2.5: Устранение ступенчатости ребер многоугольника: а) генерация ребер без устранения ступенчатости; б) точное вычисление интенсивности пикселов границы; в) формирование пикселов границы по модифицированному методу Брезенхема.

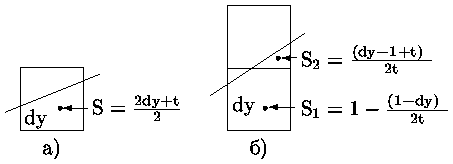
Рис. 0.2.6: Устранение ступенчатости за счет учета площади пикселов, пересекаемых ребром многоугольника.

Для того, чтобы оперировать не дробной частью максимальной интенсивности, а непосредственно ее значениями достаточно домножить на полное число уровней интенсивности I тангенс угла наклона (t), начальное (E') и максимальное (E'_max) значения отклонения.

В результате получается следующий алгоритм, пригодный для случая 0  dY  dX:
X= x1;
Y= y1;
Px= x2 - x1;
Py= y2 - y1;
t= IPy / Px;
E'= I/2;
E'_max= I - IPy / Px;
i= Px;
PutPixel(X, Y, t/2); /* Первая точка вектора */
while (i = i - 1  0) {
if (E'  E'_max) {
X= X + 1;
Y= Y + 1;
E' = E'- E'_max;
} else
X= X + 1;
E' = E'+ t;
PutPixel(X, Y, E'); /* Очередная точка вектора */
}

Для избавления от вещественной арифметики при манипулировании с E' можно домножить уже упомянутые величины на 2Px. Но в этом случае при занесении пикселов потребуется деление E' на 2Px.

В Приложении 2 приведена процедура V_BreM, реализующая модифицированный алгоритм Брезенхема для генерации ребра заполненного многоугольника и пригодная для любого октанта.

0.2.4 Улучшение качества изображения фильтрацией

Мы здесь рассмотрим методы, основанные на "размывании" границы.

Один из них заключается в том, что изображение строится с большим пространственным разрешением, чем позволяет дисплей. При выводе на экран атрибуты пиксела экрана вычисляются усреднением по группе пикселов изображения, построенного с большим разрешением. Т.е. пикселы изображения рассматриваются как подпикселы соответствующих пикселов экрана. Усредняющая маска перемещается по изображению с шагами, равными ее размеру.

Другой метод заключается в усреднении изображения без изменения его разрешения. В этом случае усредняющая маска перемещается по изображению с единичными шагами.

Очевидно, что первый метод должен давать более качественное изображение, но при больших затратах ресурсов. Для усреднения предложены различные маски ([,]).

Простейшее усреднение - равномерное (рис. ). Улучшить усреднение можно за счет использования весов, задающих влияние отдельных подпикселов на атрибут пиксела экрана (см. рис. ).

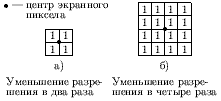
Рис. 0.2.7: Маски для равномерного усреднения изображения

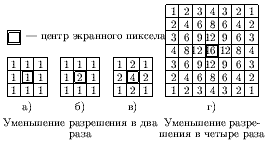
Рис. 0.2.8: Маски для взвешенного усреднения изображения

Эти массивы должны быть пронормированы для получения единичного коэффициента передачи, чтобы не вызывать неправильного смещения средней яркости изображения. Нормирующий коэффициент равен 1 / (сумму членов массива).

Ясно, что эти преобразования, примененные изображению зашумленному случайными импульсными помехами, будут подавлять шум. Это так называемые низкочастотные фильтры.

В Приложении 3 приведено несколько процедур фильтрации, реализующих оба рассмотренных метода - с понижением и без понижения разрешения.

Blog

0.2.3 Улучшение качества аппроксимации векторов

Модифицированный алгоритм Брезенхема

0.2.4 Улучшение качества изображения фильтрацией