Задача механизма вывода

Вид материала

Задача

Содержание Общая схема управляющего компонента экспертной системы (интерпретатора, механизма вывода) Синтаксическая выборка Рис.1 Схема работы интерпретатора представлена Стратегии как механизм управления Таблица 1 Классификация стратегий механизма поиска в экспертных системах Стратегии, учитывающие специфику ПрО Стратегия задана явно Неявное задание стратегии Б) неявное по выполнению Б) глобальные стратегии Б) знания об истории работы механизма вывода Б) сравнительная полезность Рис.2 Классификация методов поиска решений в экспертных системах Основные механизмы логического вывода в продукционных системах.

Подобный материал:

• 2. Порты ввода/вывода, 253.14kb.
• 1scsi (Small Computer System Interface), 197.4kb.
• Лекция Мультиплексирование ввода/вывода и асинхронный ввод/вывод, 220.73kb.
• Контрольная работа (приложение работает правильно) 20 баллов. Опрос на лекциях 1 балл,, 34.71kb.
• Реферат, 408.47kb.
• Задача потребителя, 91.38kb.
• Исследование многошагового нечеткого вывода на примере построения экспертной системы, 87.87kb.
• Устройства вывода информации Основными устройствами вывода являются, 40.73kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Экспертная система разработана для имитации процесса принятия решения экспертом- человеком, 162.54kb.

Управляющий компонент экспертных систем


А.Ньюэлл и М.Саймон обосновали 2 гипотезы, на которых базируются исследования по искусственному интеллекту:

А- гипотеза символических систем;

Б – гипотеза поиска.


Согласно 1-ой гипотезе символические системы имеют необходимые и достаточные условия для осуществления интеллектуальных действий.


Символические системы – набор символов, образующих символические структуры и набор процессов. Символические структуры – типы данных в некотором языке, причем они могут:

• обозначать объекты, процессы и другие символьные структуры;
  
• обозначать процесс, т.е. могут быть интерпретированы.
  

Согласно 2-ой гипотезе – символические системы решают задачи при помощи поиска, т.е. они генерируют потенциальные решения и постепенно модифицируют их, пока последние не будут удовлетворять заданным условиям поиска.


Общая схема управляющего компонента экспертной системы (интерпретатора, механизма вывода)

Интерпретатор

Память состояний



Данные

Рабочая память

Образцы

Модули (правила)

Задача механизма вывода – определить на основании текущего состояния рабочей памяти (РП) какой модель и с какими данными будет работать.


По окончании работы текущего модуля интерпретатор проверяет условия окончания задачи, и если они не удовлетворены, то переходит к следующему циклу работы. Каждый модуль снабжен неким образом-описанием, указывающим, когда и при каких условиях он выполняется.


Этапы работы интерпретатора в каждом цикле

1. Выборка.
   
2. Сопоставление.
   
3. Разрешение конфликтов.
   
4. Выполнение.
   

С точки зрения теории работа механизма вывода зависит от состояния рабочей памяти и базы знаний (БЗн); на практике же учитывается работа системы, т.е. поведение механизма вывода в предыдущих циклах (это состояние запоминается в памяти состояния или протоколе работ).

Источниками знаний для выполнения этих этапов являются в общем случае база знаний, рабочая помять и память состояний.


Для повышения эффективности работы механизма вывода функционирование системы управляется стратегиями управления, т.е. некоторыми эвристиками. Встраивание определенных функций в механизм вывода повышает эффективность работы, но ограничивает степень воздействия на процесс функционирования.


В механизм вывода встраивают также общую схему поиска решений (метод), а через стратегии управляют деталями поиска. Эти компоненты механизма вывода будут рассмотрены дальше.


Рассмотрим содержание этапов работы интерпретатора.

Выборка – определение подмножества РП и БЗн, которые будут участвовать в текущем цикле работы системы. Для этого применяют один из двух подходов:

Синтаксическая выборка	Семантическая выборка
Грубый отсев знаний, данных, выполняемый на основании формальных знаний, встроенных в системы разработчиком	Выборка осуществляется на основании таких сведений, как модель предметной области (ПрО), целей, задач и подзадач. Семантические знаний вводятся экспертом и представляют собой метаправила. В результате работы происходи выделение активного набора данных и правил, т.е. осуществляется фокусирование выполнения системы на определенном массиве данных и модулей.

Сопоставление - определяются активные данные и модели, которые готовы к работе. Модуль готов к работе, если среди активных данных есть такие, которые удовлетворяют условиям этого модуля, указанным в образце; такие модули называют означенными. Результат этого этапа – набор означенных модулей или конфликтный набор (КН); однако не определено, какие из элементов конфликтного набора следует предпочесть при выполнении процедур поиска.


Разрешение конфликтов – выбор из конфликтного набора тех означенных модулей, которые будут выполняться в текущем цикле. На данном этапе работы механизм вывода оценивает модули на предмет полезности при достижении цели.


Выполнение – выполнение выбранных означенных модулей и модификация состояния РП.





Рис.1 Схема работы интерпретатора представлена


Для реализации этой схемы применимы две архитектуры:

1. Поход, использующий управляемые образцами правила. Применим для небольших автономных фрагментов БЗн; понятен не программисту.
   
2. Подход, использующие управляемые образцами модули. Применим для сложных фрагментов БЗн, не понятен непрограммисту.
   

Стратегии как механизм управления


Необходимость использования в экспертных системах нетрадиционных методов управления знаниями вызвана неформализованностью решаемых ими задач. Эти особенности приводят к тому, что процесс решения нельзя представить в виде детерминированной последовательности правил. В таких случаях к исполнению пригодно одновременно несколько модулей-правил. При этом не существует надежной информации, позволяющей выбрать то или иное предпочтительное правило. Задача механизма выбора состоит в том, чтобы выбрать эффективное функционирование системы в этих условиях.


Основным механизмом, обеспечивающим разнообразие управлений в рамках общей схемы работы интерпретатора, являются стратегии.

Стратегии можно рассматривать как:

1. средство разрешения конфликтов;
   
2. способ представления метода поиска;
   
3. средство повышения эффективности метода (схемы поиска), встроенного в механизм вывода.
   

Использование стратегий важно в тех случаях, когда конфликтное множество велико; во избежании «слепого» перебора необходимо использовать знания, направляющие процесс выбора текущего модуля. Эти знания не являются явными и не выражены в общей форме. Возможность направлять поиск влияет на интеллектуальность экспертных систем.


Стратегии:

• знания о том, какой модуль следует выбрать при наличии нескольких модулей, готовых к работе;
  
• метазнания о том, как и когда использовать различные источник знаний объектного уровня (знания о ПрО). Здесь важно подчеркнуть необходимость явного задания подобных знаний, т.е. в форме, которую можно проанализировать; явное задание знаний обеспечивает гибкое поведение системы;
  

не только средство оптимизации данного метода поиска (т.е. выбор лучшего метода), но и как средство для выбора самого метода.

Таблица 1

Классификация стратегий механизма поиска в экспертных системах

Признаки классификации(параметры)
1.Общность	2.Явное/неявное задание	3.Содержание стратегии (совокупность независимых параметров)
Стратегии, не зависящие от способа представления знаний (стратегии, поиска от целей или от данных) Стратегии, не зависящие от ПрО (стратегии множества поддержки в логике предикатов) Стратегии, учитывающие специфику ПрО (имеют ограниченное применение, но более эффективны, т.к. имеют знания о ПрО) Стратегии, учитывающие специфику целей (управляют процессом в зависимости от текущих целей)	Стратегия задана явно, если она может быть идентифицирована как отдельная сущность системы. Смена стратегии в этой ситуации безболезненна для экспертной системы. Неявное задание стратегии: А) концептуально неявное – механизм стратегии может быть рассредоточен по системе, т.е. результат проявляется как побочный эффект выполнения другой части системы. Б) неявное по выполнению – идея выражена явно, однако из-за специфики выполнения имеется некоторая вложенность стратегий в другие конструкции системы.	1.масштаб А) локальные стратегии – те, которые определяют результат работы механизма вывода в текущем цикле работы системы; Б) глобальные стратегии – определяют некоторую работу линию рассуждения механизма вывода, т.е. общую последовательность выполнения циклов. 2.состав знаний, используемых стратегий А) знания о текущем цикле работы механизма вывода ; Б) знания об истории работы механизма вывода 3.полезность А) индивидуальная полезность – в ходе работы механизма вывода характеризует некоторое знание само по себе вне сравнения с другими; Б) сравнительная полезность – определяет ценность знаний при сравнении с другими в процессе работы механизма вывода.

Методы поиска решений в экспертных системах


Методы решения задач, основанные на сведении их к поиску, зависят от:

1. требований, предъявляемых к решению особенностей ПрО;
   
2. от пользователями.
   

Особенности ПрО ( с точки зрения методов решения задачи) можно охарактеризовать следующими параметрами:

• размер, объем пространства, где следует искать решение;
  
• изменяемость области (динамика-статика);
  
• полнота модели, описывающей ПрО;
  
• определенность данных о решаемой задаче, характеризующаяся степенью точности (ошибочности), полноты (неполноты) задачи.
  

Требования пользователя к решению, к результату задачи можно охарактеризовать:

• количество решений (одно, два, несколько);
  
• свойство результата;
  
• способ получения.
  

Многогранность решаемых экспертными системами задач не позволяет применить один метод поиска решения; одни методы из ниже перечисленных превосходят другие по некоторым специфическим особенностям:

1. Методы поиска в одном пространстве (условия – небольшая размерность, полнота информации, точность информации, (полнота модели);
   
2. Методы поиска в иерархическом пространстве (условия – область большой размерности);
   
3. Модели поиска при неточных и неполных данных;
   
4. Модели поиска, использующие несколько моделей (условия – могут быть объединены с целью повышения эффективности функционирования системы).
   

Классификация представлена на рис. 2





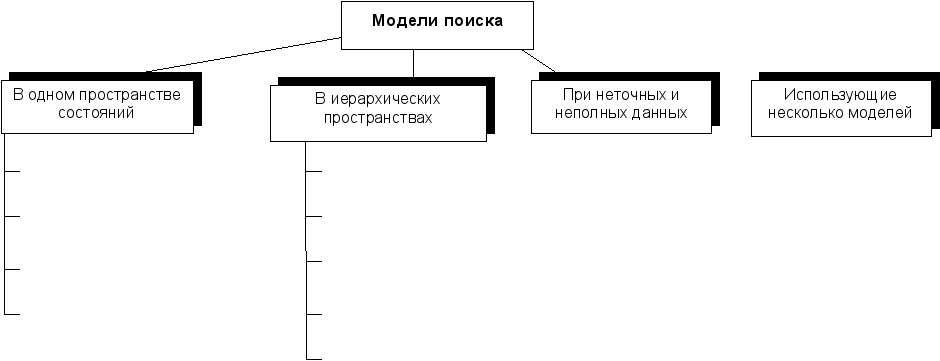
Поиск в пространстве состояний Поиск а факторизованном пространстве

Поиск методом редукции Поиск в фиксированном пространстве


Эвристический поиск Поиск в изменяющемся множестве иерархических пространств


Поиск «генерация-проверка» Метапространтсва в иерархии пространств


Принцип наименьших свершений


Рис.2 Классификация методов поиска решений в экспертных системах


Поиск в пространстве состояний


Формулировка задачи:

Пусть дано (S₀, F, S_t),

где S₀ - начальное состояние,

F - множество операторов перехода из состояния i в j;

S_t - множество конечных состояний.


Решение задачи:

Найти такую последовательность операторов F, которая преобразует начальное состояние S₀ в конечное S_t.


Процесс решения задачи:

Можно представить в виде графа G=(X,Y), где

X –множество вершин;

Y – (x_i, x_j)  X.

Если пара (x_i, x_j) неупорядочена, то эту пару называют ребром, а сам граф – неупорядоченным.


Если для каждой пары (x_i, x_j) задано направление, то (x_i, x_j) называют дугой, а граф – направленным (упорядоченным); (x_i, x_j) - концевые точки (вершины) ребра (дуги).


Поиск в пространстве состояний – направленный граф. Пара (x_i, x_j) свидетельствует о наличии оператора f, причем f  F,переводящем состояние x_i в x_j.

С точки зрения поиска в пространстве состояний для x_i выделяют множество направленных пар (x_i, x_j)  Y, т.е. дуг, исходящих из родительской вершины x_i и вершин (дочерних), куда эти дуги направлены:


(x_i, x_j)

x_i x_i+1


(x_i, x_j^’)

x_i+2


Множество дуг, исходящих из x_i – множество операторов f, которые могут быть применены к состоянию, соответствующему x_i.


В множестве X - выделяют вершины X₀,, соответствующие начальному состоянию S₀, X_t, соответствующих целевым состояниям S_t, причем S_t может быть задано не явно, а через свойства целевых состояний.

Граф G может быть задан явно или неявно; неявное задание графа определяет множество X₀  X и множество всех операторов, которые, будучи примененными к некоторой вершине графа, дают его дочерние вершины.


Процесс построения графа G:

1. поиск вершины x₀;
   
2. применение к x₀ всех операторов f, порождающих дочерние вершины – процесс раскрытия вершин; причем целевая вершина не может быть раскрыта;
   
3. процесс окончен, если все нераскрытые вершины – целевые.
   

X₁ x₁₁

X₂ x₁₂

x₀ x₃


В практических целях требуется обеспечить полноту поиска, т.е. найти все целевые вершины (обеспечить перебор всех вершин). Для этого требуется установить порядок перебора вершин; обычно выделяют поиск в глубину и поиск в ширину.


При поиске в глубину раскрывается та вершина, которая была построена самой последней. Признаком окончания поиска являются: достижение целевой вершины; достижение терминальной вершины; глубина поиска больше максимальной заданной глубины (рис.3).




















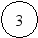
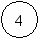
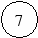
Рис.3 Иллюстрация поиска «в глубину»


При поиске в ширину вершины раскрываются в том же порядке, в каком они порождаются (рис.4).




















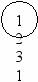
Рис.4 Иллюстрация поиска «в ширину»


При использовании каждого из методов будут найдены все решения; однако метод поиска в ширину требует большей памяти, т.к. при его реализации запоминаются все пути поиска, а не один, как в случае поиска в глубину.


Если в граф G ввести f, переводящие состояние S_i в предшествующее S_i-1, то поиск можно организовать не только от S₀ к S_i, но и от S_i к S_0.


Поиск 1-го типа называют поиском от данных или прямым поиском; поиск 2-го типа – поиском от цели ли обратным поиском. Можно также организовать поиск в 2-х направлениях, это будет бинаправленный поиск.


Эвристический поиск


Методы поиска в глубину / ширину называют «слепым» поиском, т.к. в них не определен порядок раскрытия вершины, и этот порядок не зависит от расположения цели. Стремление к уменьшению времени поиска привело к формулированию эвристик, т.е. использованию некой информации о предметной области, сужающей пространство поиска в графе G c целью выбора только тех путей, которые с максимальной вероятностью приводят к цели.


Одним из способов сокращения перебора является выбор «информированного» оператора; другой – использование эвристик для оценки дальнейшего продвижения к целевой вершине. Для этого вводят понятие «Оценочной»функции, такой, что она сокращает объем перебора, не уменьшая полноты. Обычно использование эвристик уменьшает полноту поиска.


Основные механизмы логического вывода в продукционных системах.


Логический вывод - центральное понятие в экспертных системах. Оно имеет два аспекта: использование рассуждения для нахождения различных предположений, которые обусловлены имеющимися фактами и правилами, или для изучения заключений, которые представляют интерес и могут быть (а могут и не быть) истинными. Первый метод носит название прямой цепочки рассуждений, а второй - обратной цепочки рассуждений. Почти все экспертные системы построены либо на первом, либо на втором методе.


Прямая цепочка рассуждений


Прямая цепочка рассуждений предполагает использование правил для дедукции (логического вывода) новых фактов, а также фактов, которые имплицитно существовали и ранее, но могут быть сделаны явным посредством применения правил.


Механизм вывода просматривает циклически все правила, исследуя каждое из них по очереди, выясняя, является ли истинной информация, находящаяся в части условий правил. В случае истинности факта он добавляется к хранимым истинным фактам в рабочую память (базы данных) экспертной системы.


Проведение опроса при выборе этой стратегии предполагает исследование нерелевантных возможных решений, из-за чего общее число задаваемых вопросов иногда может оказаться меньшим. Однако вопросы могут показаться пользователю необычными, т.к. их планировали, имея в виду определенные ключевые проверки. Пользователь может сразу не понять, почему компьютер задает именно эти вопросы.


Суть стратегии прямого вывода состоит в том, что задается последовательность вопросов, построенных таким образом, что каждый из них позволяет отбросить большую группу потенциальных ответов, благодаря чему значительно сужается пространство поиска.


Подобная прямая цепочка рассуждений на практике практически неприменима в следующих ситуациях: в системах с реальным числом правил имеется столь много подразумеваемых (скрытых) фактов, что, будучи обнаруженными, они затмят те несколько фактов, которые действительно представляют интерес и являются полезными.

Однако, системы, основанные на прямой цепочке рассуждений, существует. Любая система подобного рода имеет дополнительный механизм для того, чтобы определить, с каким следующим правилом ей предстоит работать. Механизм выбора четко устанавливает приоритет выбора тех или иных фактов и правил.

Прямой вывод применим в тех ситуациях, когда число потенциальных решений неуправляемо, а количества блоков данных, определяющих начальное состояние системы, невелико.


Экспертные системы, построенные на базе прямой цепочки рассуждений, чаще всего применяются в планировании и проектировании.


Обратная цепочка рассуждений


Выбор этой стратегии исходит из посылки, что интерес представляет заключение, не являющее истинным фактом. Мы хотим выяснить, не обусловлен ли данный факт известными фактами и правилами.


Механизм вывода может провести такое исследование посредством определения всех правил, которые приводят к данному факту как заключению. Однако может случиться так, что ни одно из правил не может быть использовано непосредственно для определения рассматриваемого заключения из-за того, что необходимо установить истинность его посылок. В таком случае мы должны идти в обратном порядке и попытаться определить достоверность тех посылок в тех правилах, которые могут применяться для установления истинности конечного вывода. Перемещение на много уровней назад в древовидной структуре даст нам факты, которые являются истинными.


При использовании обратной цепочки рассуждений общее число задаваемых вопросов может быть больше, но т.к. они все ориентированы на концепцию высокого уровня, которую проверяет система, то лежащая в их основе модель кажется более понятной.


Экспертные системы, основанные на обратной цепочке рассуждений, как правило, применяются при диагностике или классификации.


Сравнение основных стратегий рассуждений


Обычно проблема выбора цепочки рассуждений не возникает, т.к сама задача указывает способ рассуждений, и только один подход оказывается реализуемым. Если предполагается небольшое число возможных альтернатив, то эффективнее использовать обратную цепочку рассуждений. Задача, включающая неизменную последовательность шагов, на каждом из которых возникает много возможностей, всегда решается с помощью прямой цепочки рассуждений.