М. В. Николаенко, Ю. А. Малышев применение компьютерных моделей при техническом конструировании студентами физиками
| Вид материала | Документы |
- Авдеева Зинаида Константиновна применение моделей на основе когнитивных карт при разработке, 27.57kb.
- Применение компьютерных технологий при изготовлении выплавлямых моделей рабочих колес, 30.82kb.
- Никуленко Татьяна Николаевна моу «чсош №1 с углубленным изучением отдельных предметов», 239.69kb.
- Концепция Применение компьютерных технологий при проведении химического эксперимента, 559.32kb.
- «Применение компьютерных технологий в современном сравнительном переводоведении», 193.71kb.
- Урок биологии с использованием компьютерных моделей на тему «Биосинтез. Хемосинтез», 38.16kb.
- Уроках математики с использованием компьютерных технологий при обобщении материала, 120.59kb.
- Прогнозирование нефтегазовых залежей на основе физико-геологических моделей в сейсмогеологических, 562.17kb.
- Методические указания и контрольные задания для студентов заочного отделения по специальности, 483.97kb.
- Методика подготовки к егэ и применение информационно-компьютерных технологий. Учитель, 513.25kb.
М.В. НИКОЛАЕНКО, Ю.А. МАЛЫШЕВ
ПРИМЕНЕНИЕ КОМПЬЮТЕРНЫХ МОДЕЛЕЙ
ПРИ ТЕХНИЧЕСКОМ КОНСТРУИРОВАНИИ
СТУДЕНТАМИ ФИЗИКАМИ
Умение пользоваться экспериментом для объяснения физических явлений не только оптимизирует процесс усвоения знаний студентов, но и способствует развитию их творческой инициативы. Однако творческая активность стимулируется не столько привлечением экспериментов к объяснению физических явлений, сколько умением самостоятельно разрабатывать и изготавливать новые лекционные демонстрации, лабораторные работы и пр. физико-технические конструкции.
В связи с этим, возникает проблема оптимизации учебного процесса по курсу «Техническое конструирование и моделирование», призванного для обучения студентов – будущих преподавателей физики методам технически грамотной разработки и изготовления конструкций и моделей для школьного физического эксперимента и для кружков детского технического творчества.
В работе [1] показано, что важнейшим звеном процесса конструирования является этап создания эскизного проекта, грамотная разработка которого опирается на рабочие формулы, описывающие физические явления в конструкции и особенности взаимодействия её элементов.
Очевидно, что любого рода конструкции являются сложными устройствами, поэтому вывод их рабочих формул даже для прикидочных расчетов оказывается очень трудоёмким делом, заниматься которым в полном объеме с привлечением методов математической физики при ограниченном числе часов, отпущенных на курс «Техническое конструирование и моделирование», не представляется возможным. Однако важность данной задачи заставляет искать методы расчетов сложных конструкций адекватные знаниям и возможностям студентов.
На наш взгляд, наиболее перспективным методом анализа при конструировании сложных устройств силами студентов является метод компьютерного моделирования [2]. Попытаемся объяснить наше утверждение на примере разработки устройства для демонстрации колебаний в сложных системах.
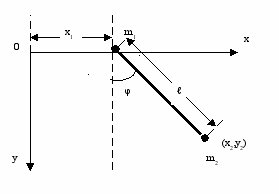
Рассмотрим, к примеру, задачу о колебаниях математического маятника, точка подвеса которого прикреплена к другому телу, имеющему возможность свободно (без трения) перемещаться горизонтально по оси ОХ (рис.1). Как сконструировать данное устройство?
Для решения поставленной задачи конструирования мы должны вначале увидеть движение всей системы, если, к примеру, отклонить тело массы m2 на угол φ0 и отпустить. Чтобы рассчитать элементы предложенной конструкции, мы должны получить уравнения, описывающие процесс движения тела – опоры массы m1 и тела маятника массы m2.
К
 ак известно [3], разработка компьютерной модели начинается с записи основных законов, которыми можно наиболее полно описать процессы в разрабатываемом устройстве. В данном случае эти законы выражены уравнениями Лагранжа:
ак известно [3], разработка компьютерной модели начинается с записи основных законов, которыми можно наиболее полно описать процессы в разрабатываемом устройстве. В данном случае эти законы выражены уравнениями Лагранжа: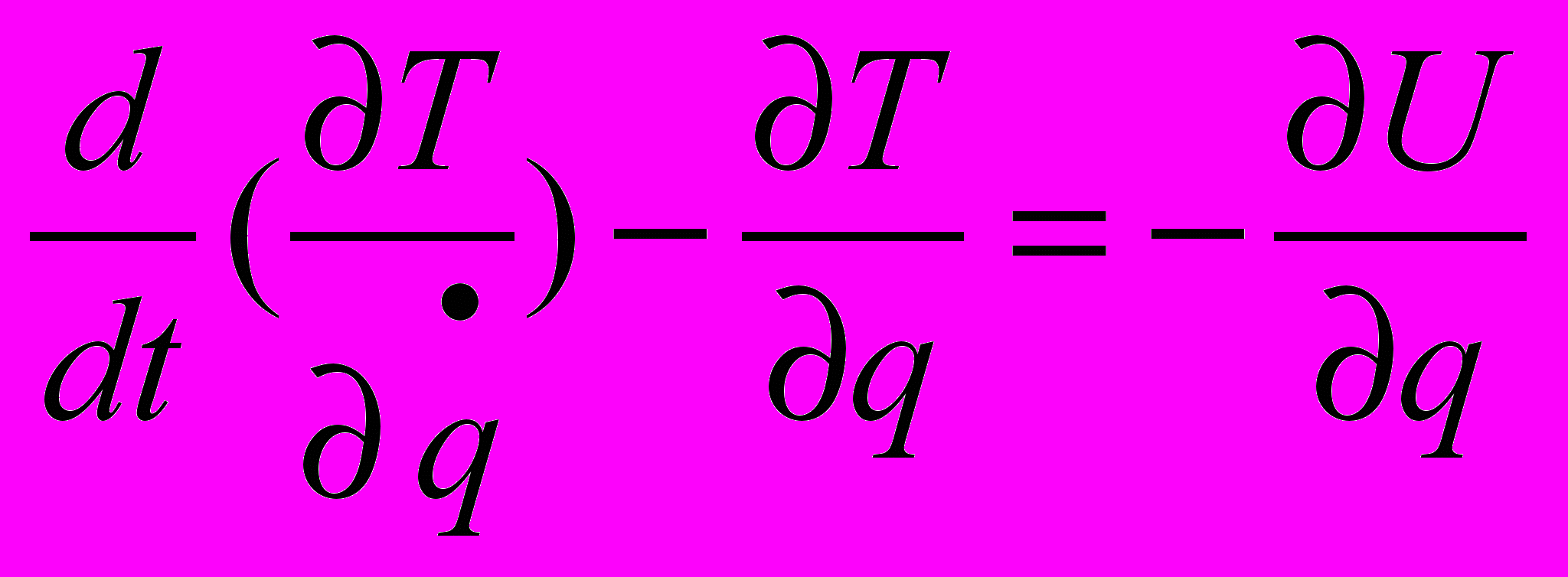
Рис.1. Система двух тел
Для их решения выберем в качестве независимых обобщенных координат, полностью описывающих процесс в исследуемой системе переменные х1 и φ.
В таком случае получаем систему уравнений Лагранжа
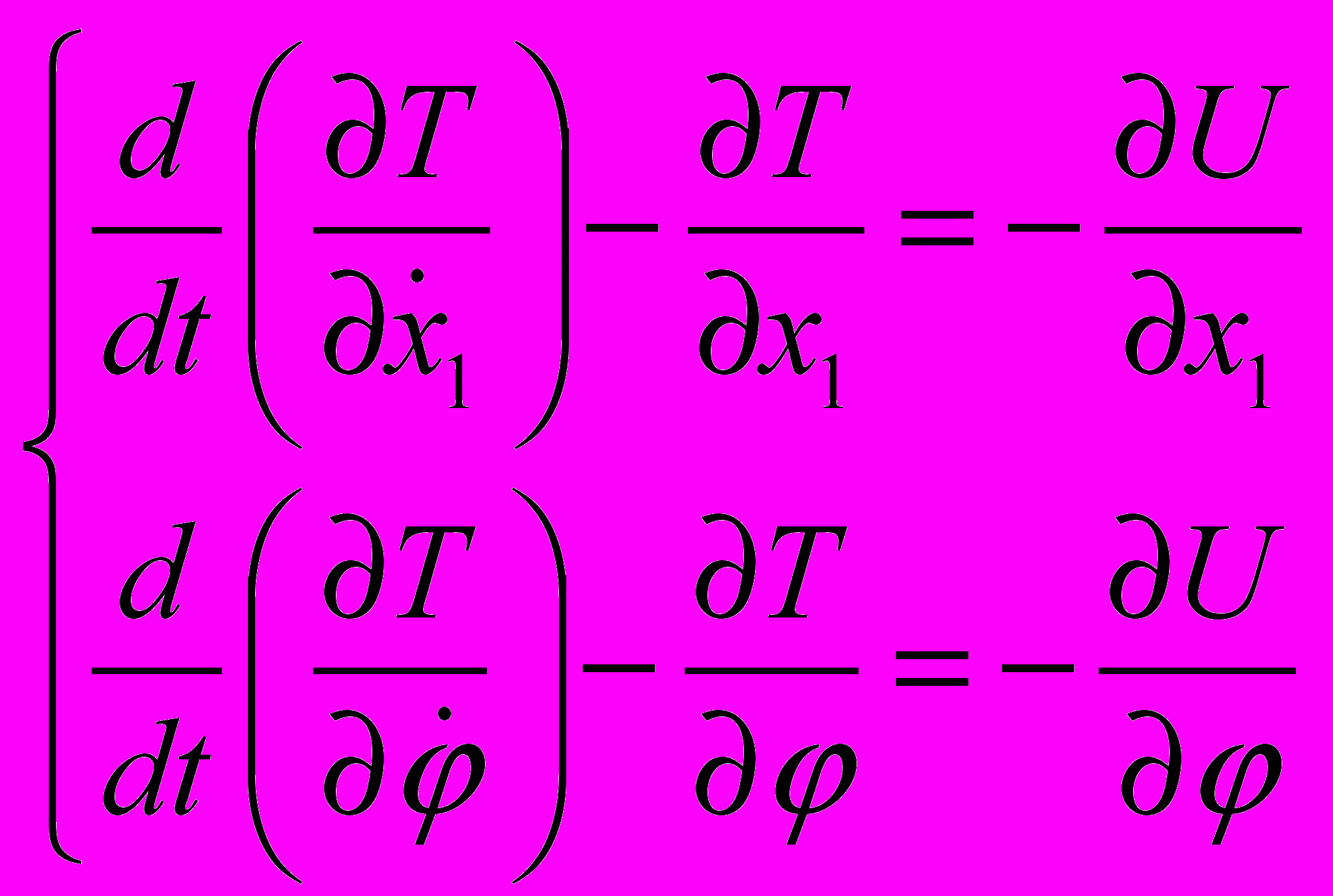 (1)
(1)Из рис.1. следует, что
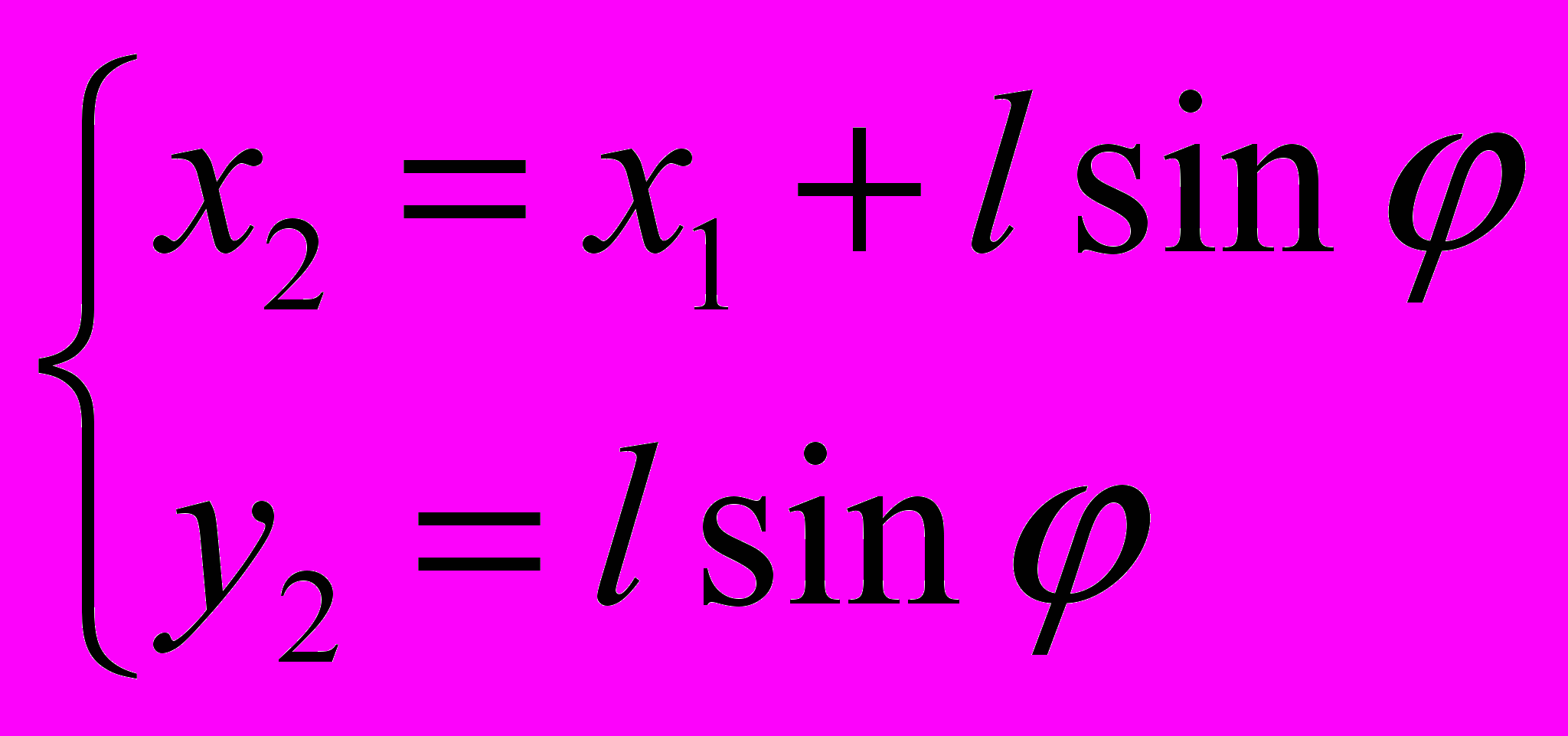
При данных определениях координат кинетическая энергия системы имеет вид:
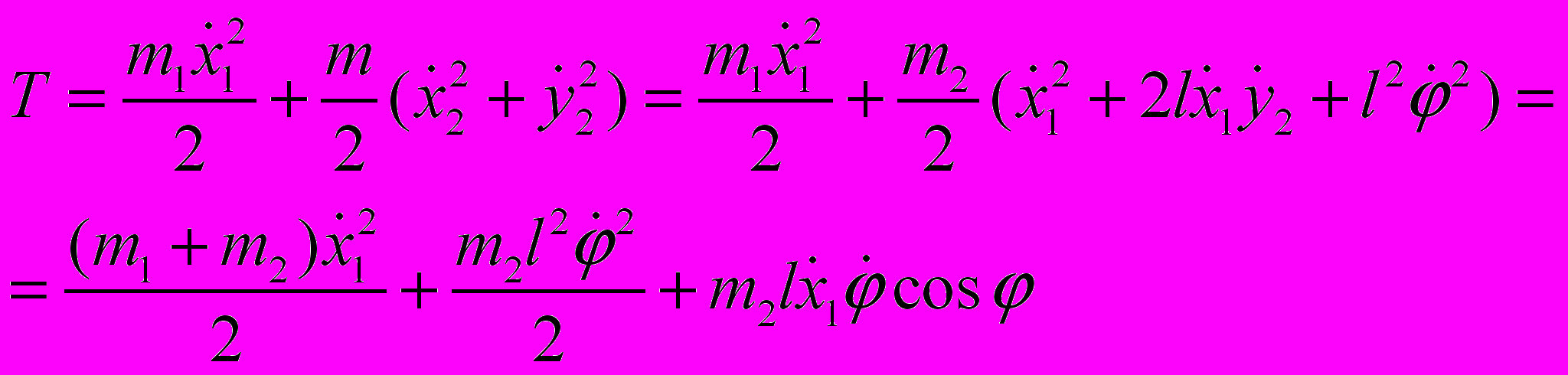 (2)
(2)Потенциальная энергия равна:
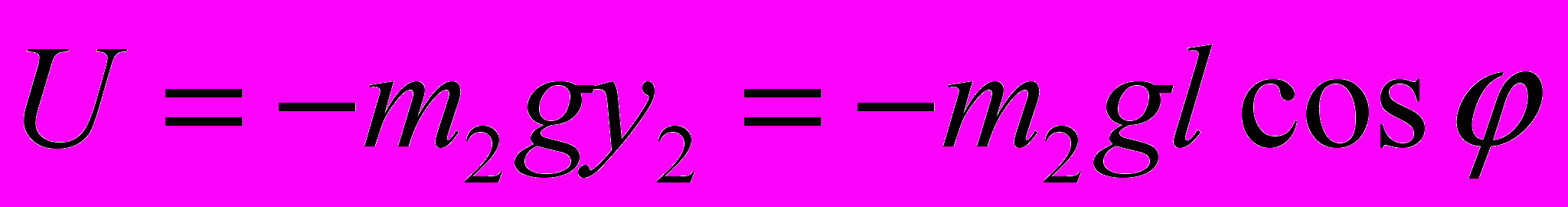 (3)
(3)Вычислим все производные от
 и
и  и подставим полученные выражения в (1), Получим систему из двух уравнений:
и подставим полученные выражения в (1), Получим систему из двух уравнений: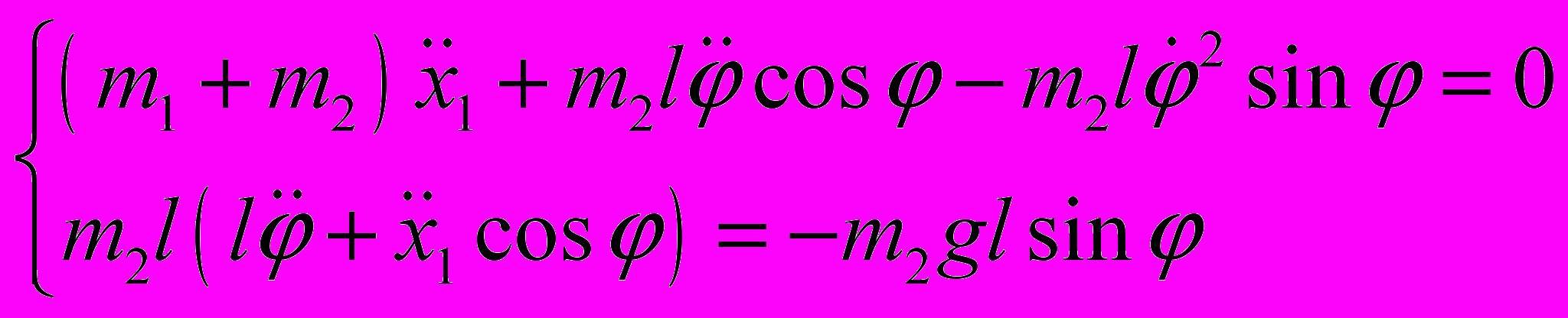 (4)
(4)Выражая
 из второго уравнения системы и подставляя его в первое уравнение, мы получим систему двух нелинейных уравнений:
из второго уравнения системы и подставляя его в первое уравнение, мы получим систему двух нелинейных уравнений: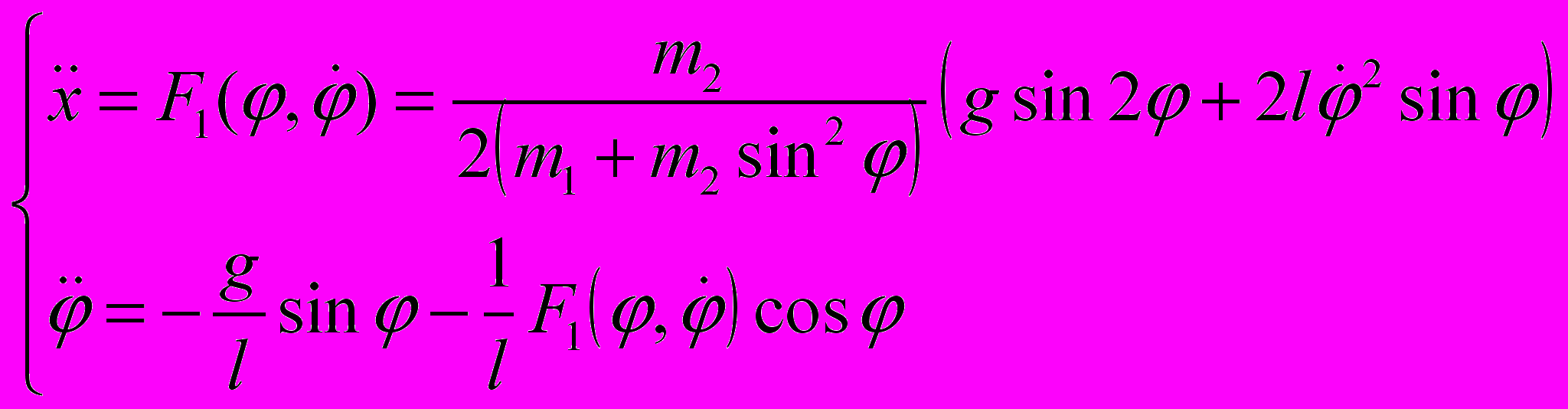 (5)
(5)Решение этой системы уравнений в аналитических функциях трудно и потому чрезвычайно осложняет анализ физического процесса движения предложенной, казалось бы, простой конструкции.
Таким образом, как уже говорили, мы сталкиваемся с педагогической проблемой целесообразности дальнейшего математического анализа уравнений (5). Решить эту проблему мы можем с помощью методов компьютерного моделирования, основанных на численном решении подобных уравнений.
При использовании компьютера нам остается лишь подготовить уравнения системы (5) к виду, понятному компьютеру и запрограммировать его на расчет координат интересующих нас объектов и на построение графиков движения тела-опоры и тела маятника.
Подготовим уравнения системы (5) к виду понятному компьютеру. Для этого, введя обозначения
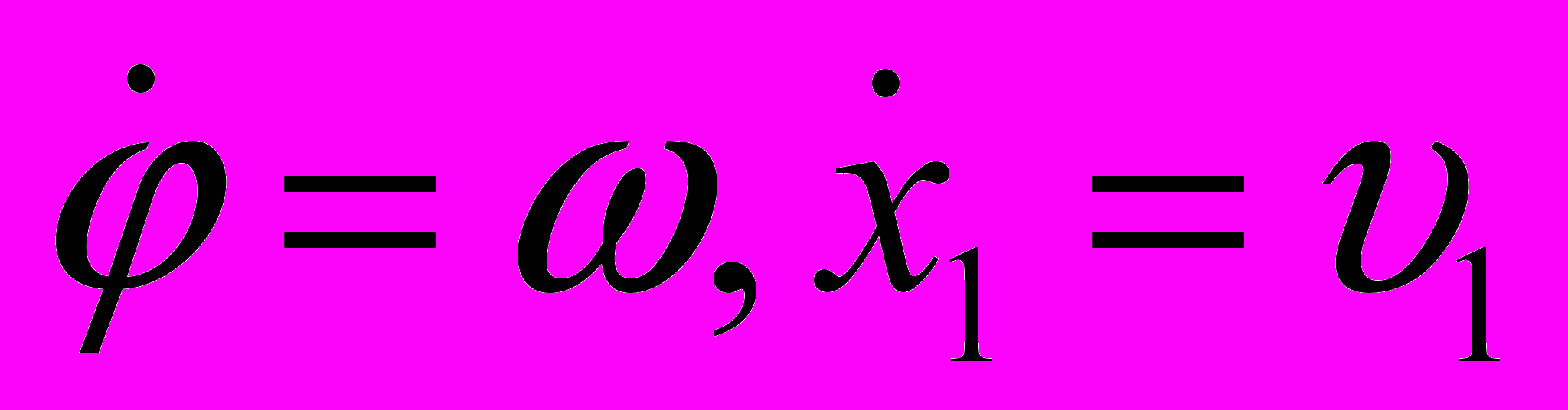 , преобразуем их к системе дифференциальных уравнений первого порядка:
, преобразуем их к системе дифференциальных уравнений первого порядка: 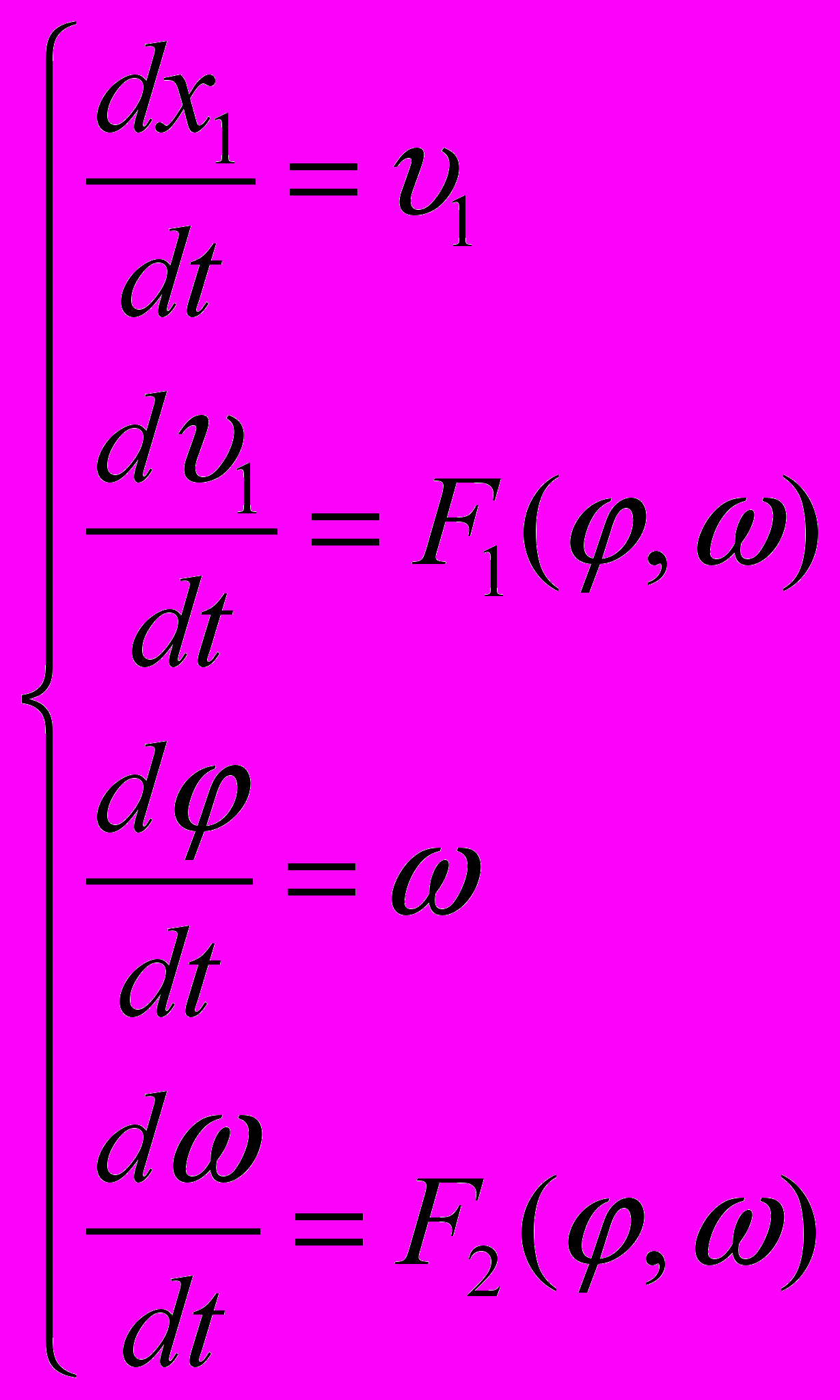 , (6)
, (6)где
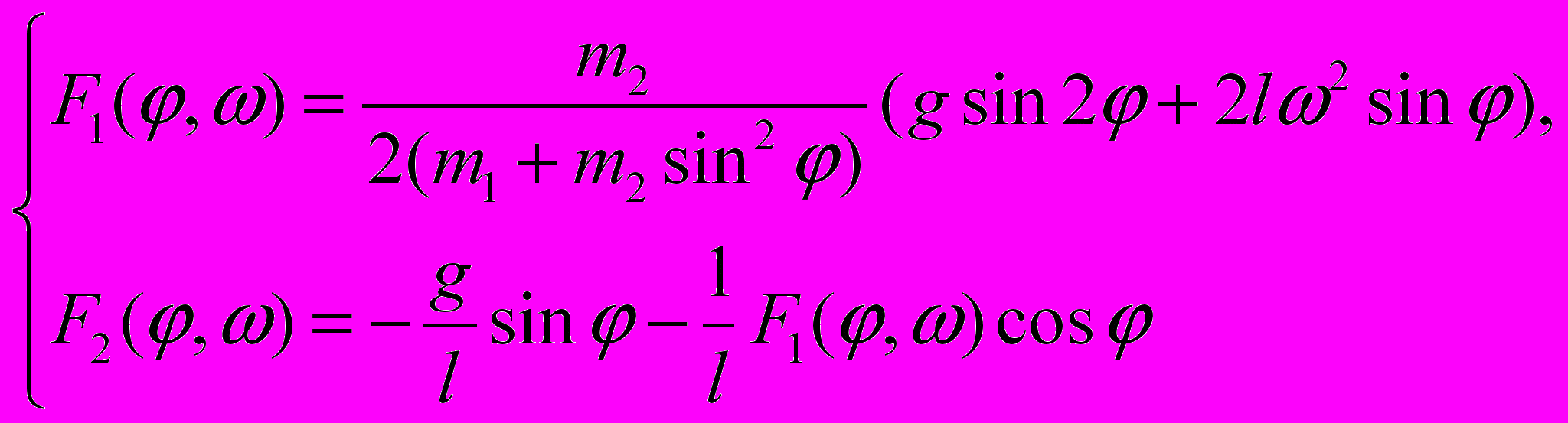 (7)
(7)Используем наиболее простой для обучения метод Эйлера решения уравнений системы (6). В соответствии с этим методом решение уравнений (6) следует проводить по схеме:
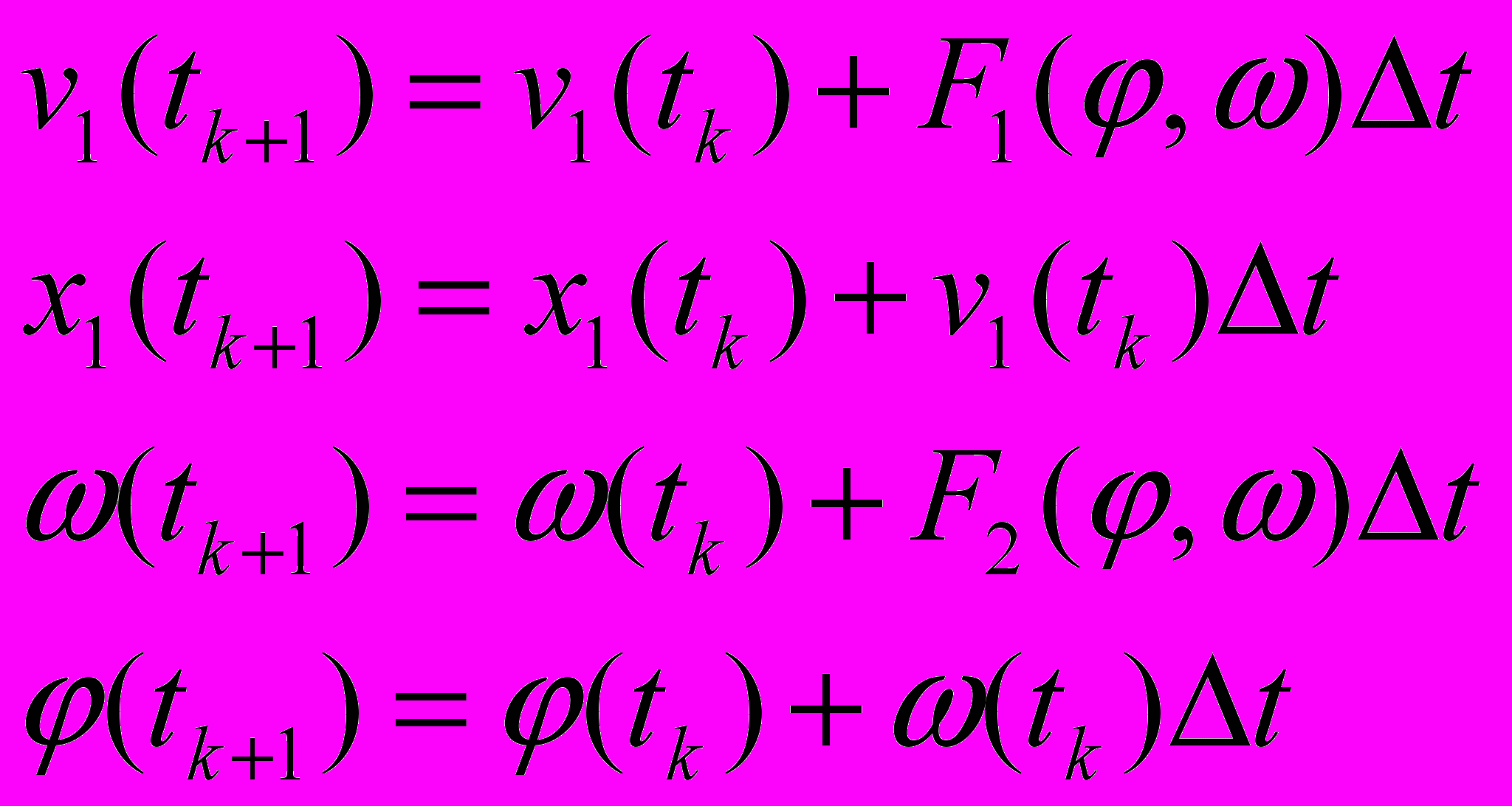 (8)
(8)Процедура Эйлера на языке программирования выглядит так:
procedure Eiler;
begin
x:=x+v*dt;
v:=v+F1*dt;
fi:=fi+omega*dt;
omega:=omega+F2*dt;
t:=t+dt;
end;
При организации цикла расчета обобщенных координат следует иметь в виду, что
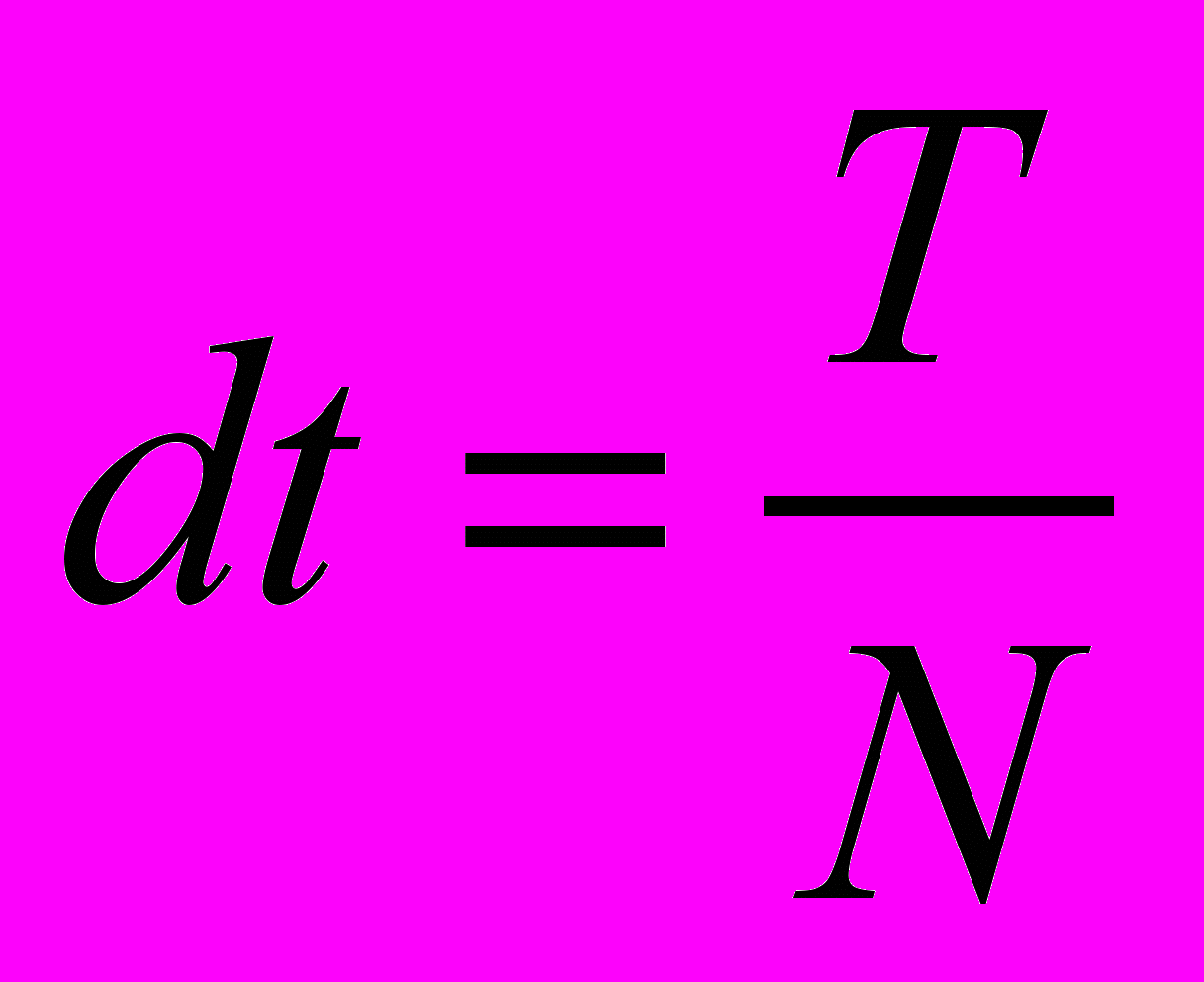 , T- время наблюдения процесса. При k=1, x1(t1)=0, φ(t1)=φ0. Для организации цикла расчета по схеме (8) индекс к должен пробегать значения от 1 до N.
, T- время наблюдения процесса. При k=1, x1(t1)=0, φ(t1)=φ0. Для организации цикла расчета по схеме (8) индекс к должен пробегать значения от 1 до N.Программа (компьютерная модель) расчета координат тел m1 и m2 и построения графиков их движения
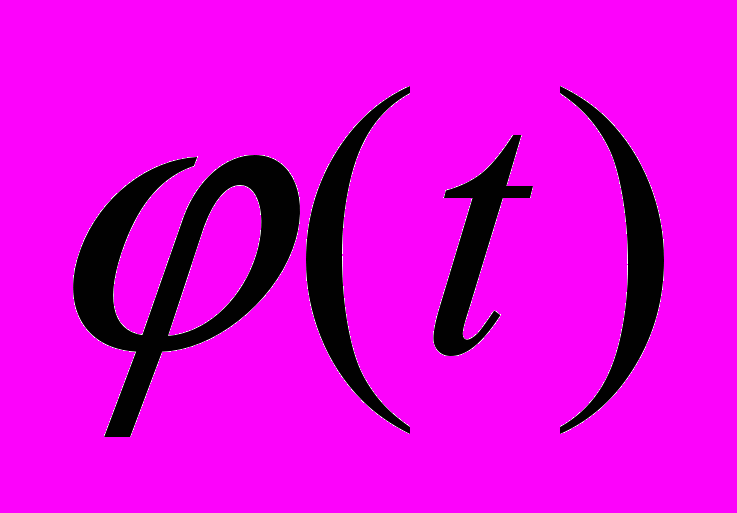 и
и 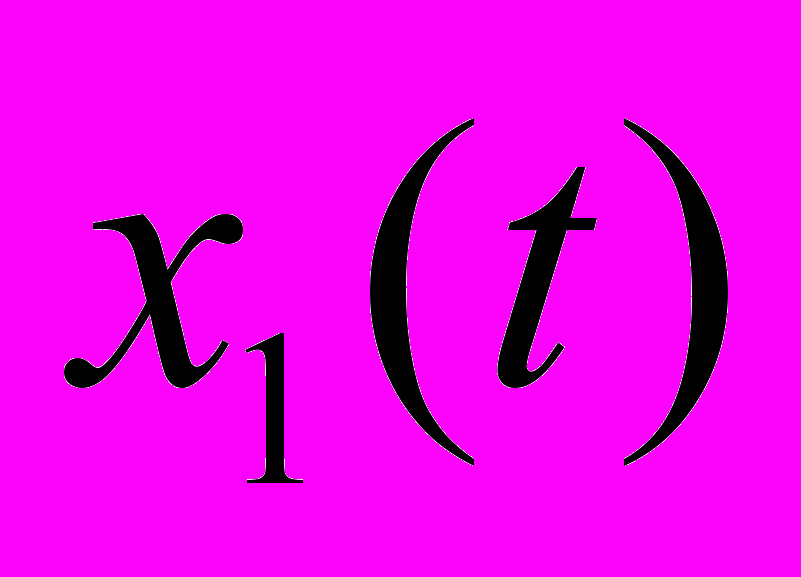 была организована на языке Дельфи. Полученные графики явились, фактически, результатом компьютерного эксперимента
была организована на языке Дельфи. Полученные графики явились, фактически, результатом компьютерного экспериментаНаблюдение графиков зависимости х1(t) показало, что движение по х тела m1 может быть представлена в виде суммы двух движений, одного, в виде линейного полинома:
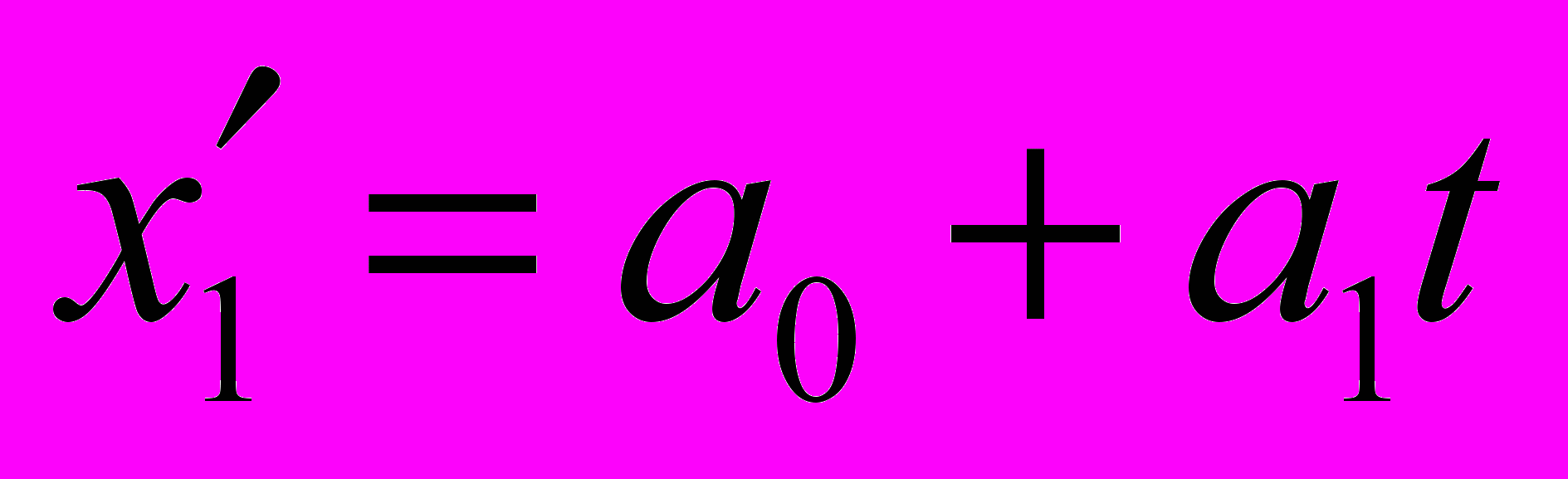 (9)
(9)и другого, имеющего вид гармонических колебаний
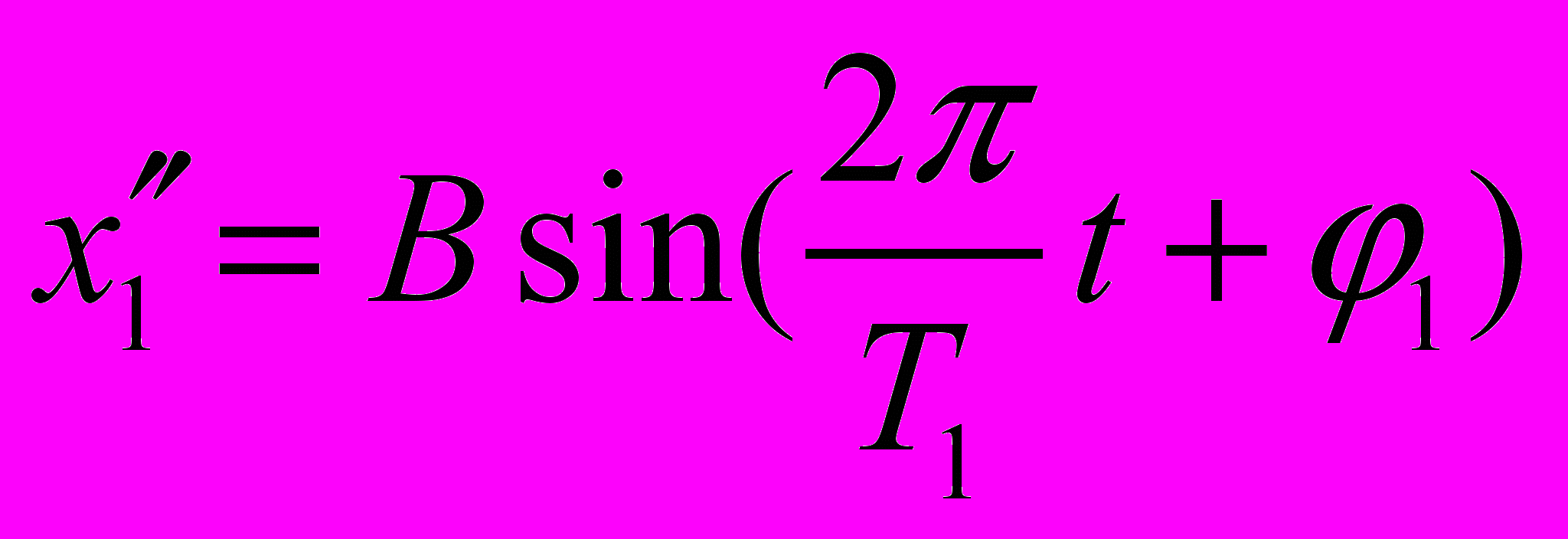 , (10)
, (10)так что полное уравнение движения тела-опоры массой m1 должно быть записано в виде:
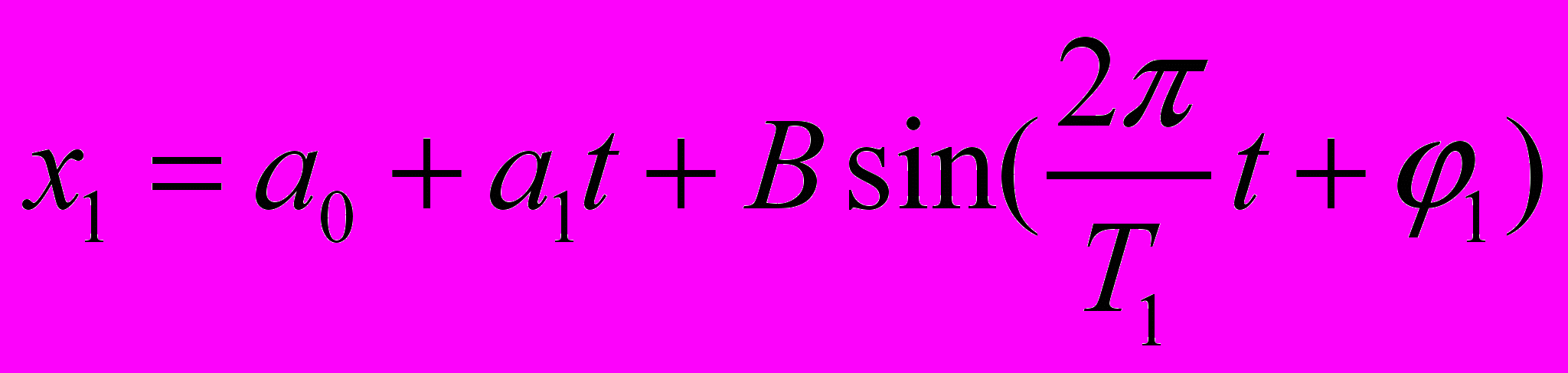 . (11)
. (11)Рассчитать коэффициенты полинома (линейной регрессии) (9)
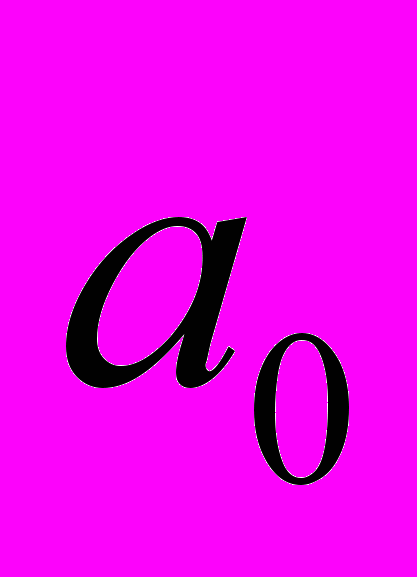 и
и  мы можем, решая систему линейных уравнений:
мы можем, решая систему линейных уравнений: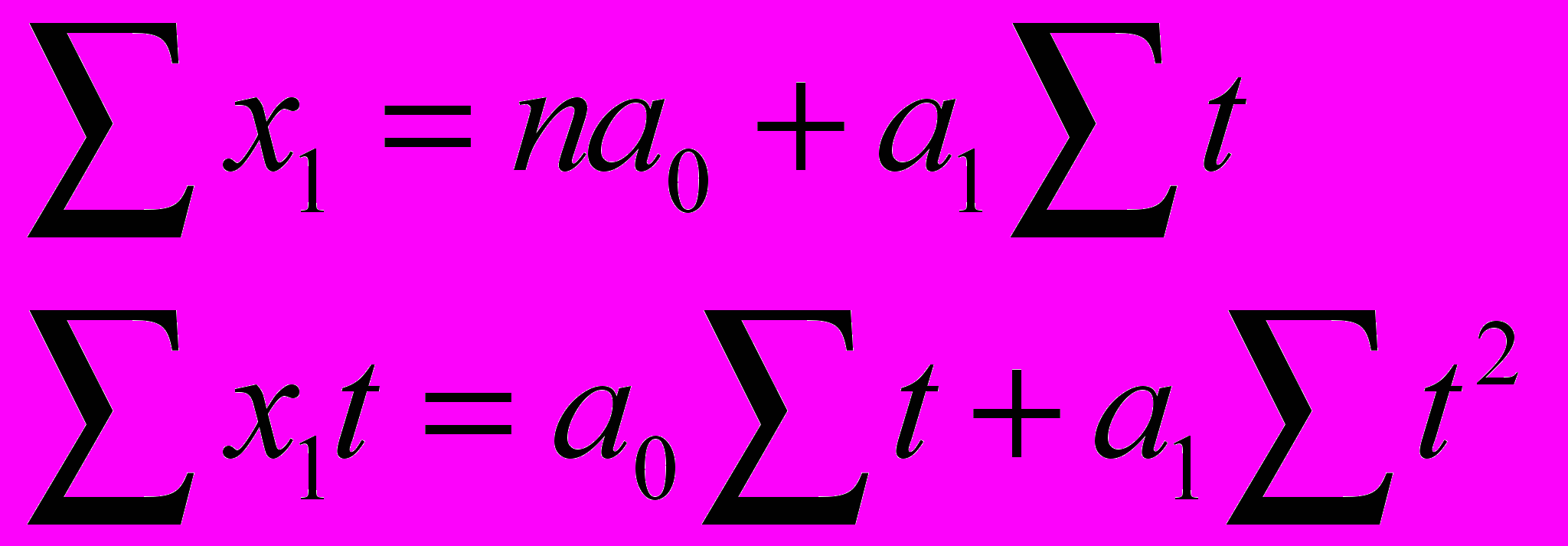 ,
,что проделано в программе исследований. Однако при этом мы не получим выражений для
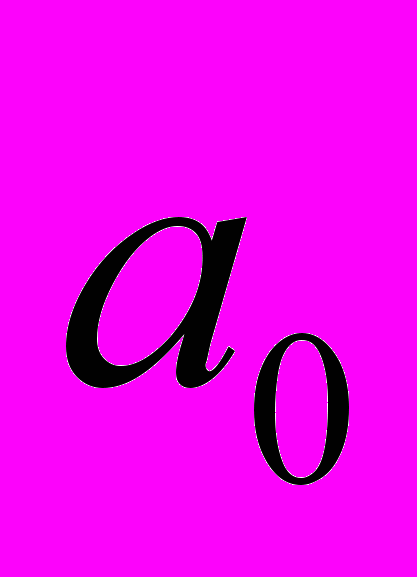 и
и  , содержащих в явном виде параметры m1, m2,
, содержащих в явном виде параметры m1, m2,  ,
, 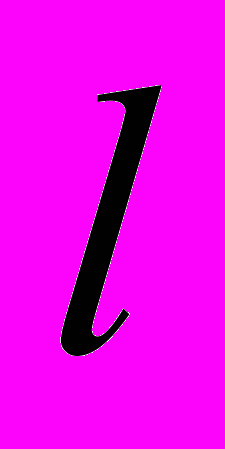 , и следовательно не сможем оценить их влияния на конструкцию демонстрационного устройства. Для этого надо провести многофакторный анализ, используя статистические методы планирования эксперимента. Однако в данном случае необходимые нам знания о связи
, и следовательно не сможем оценить их влияния на конструкцию демонстрационного устройства. Для этого надо провести многофакторный анализ, используя статистические методы планирования эксперимента. Однако в данном случае необходимые нам знания о связи 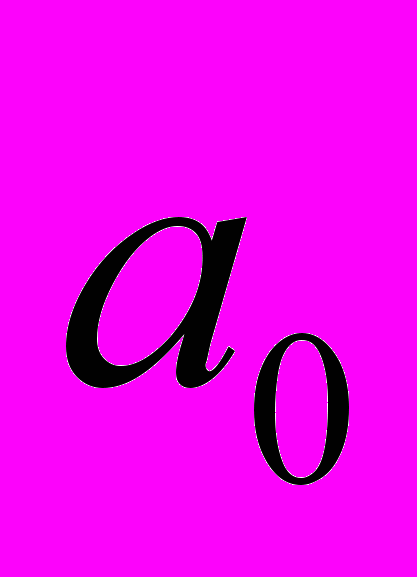 и
и  с m1, m2,
с m1, m2,  и
и 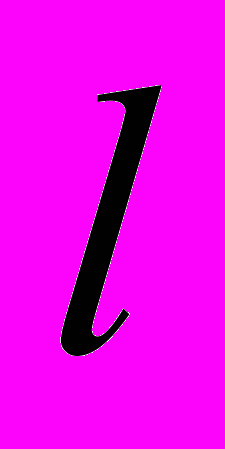 ,мы можем получить из физических соображений.
,мы можем получить из физических соображений. Если в начальный момент времени тело m1 находилось в начале координат, то (11) будет иметь вид:
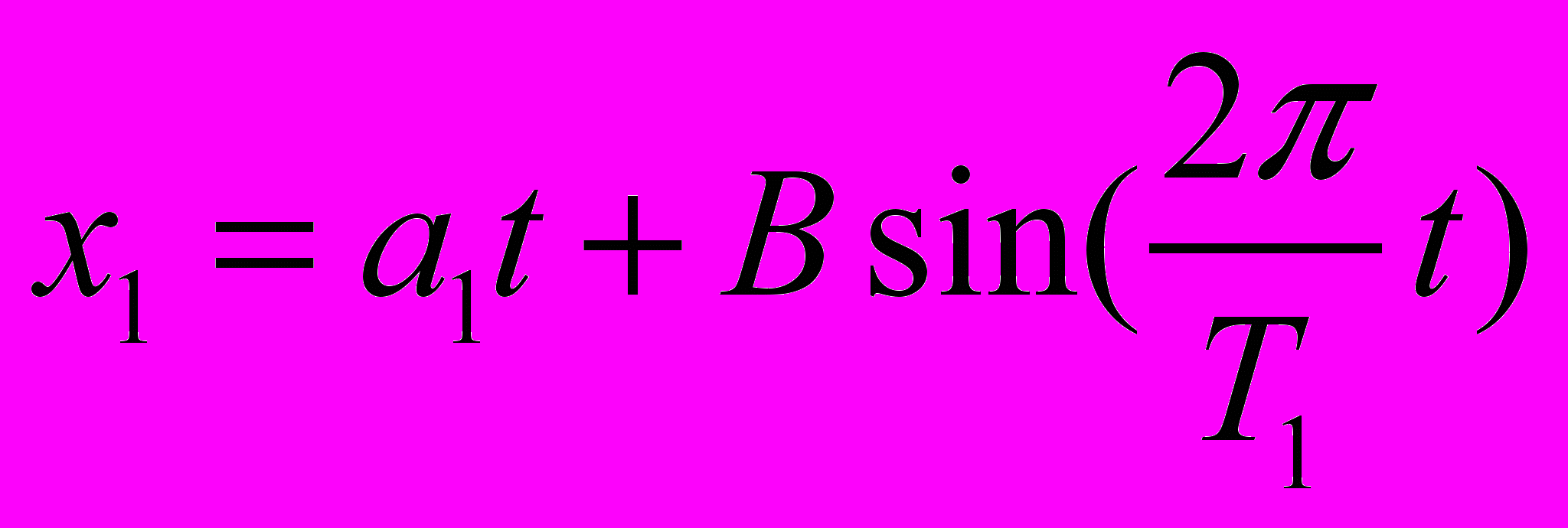 . (12)
. (12)Так как поступательное движение (9) определяется импульсом, полученным от тела-маятника m2, длиной
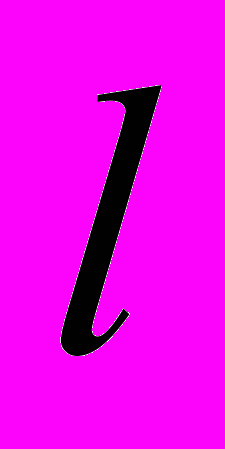 , то нетрудно определить значения коэффициентов
, то нетрудно определить значения коэффициентов  и
и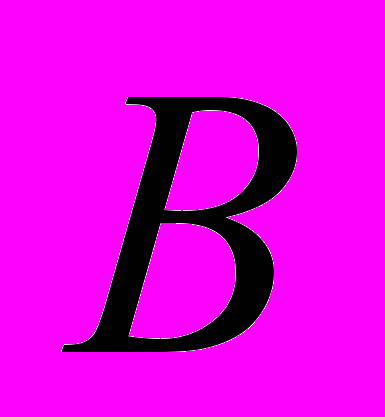 :
: 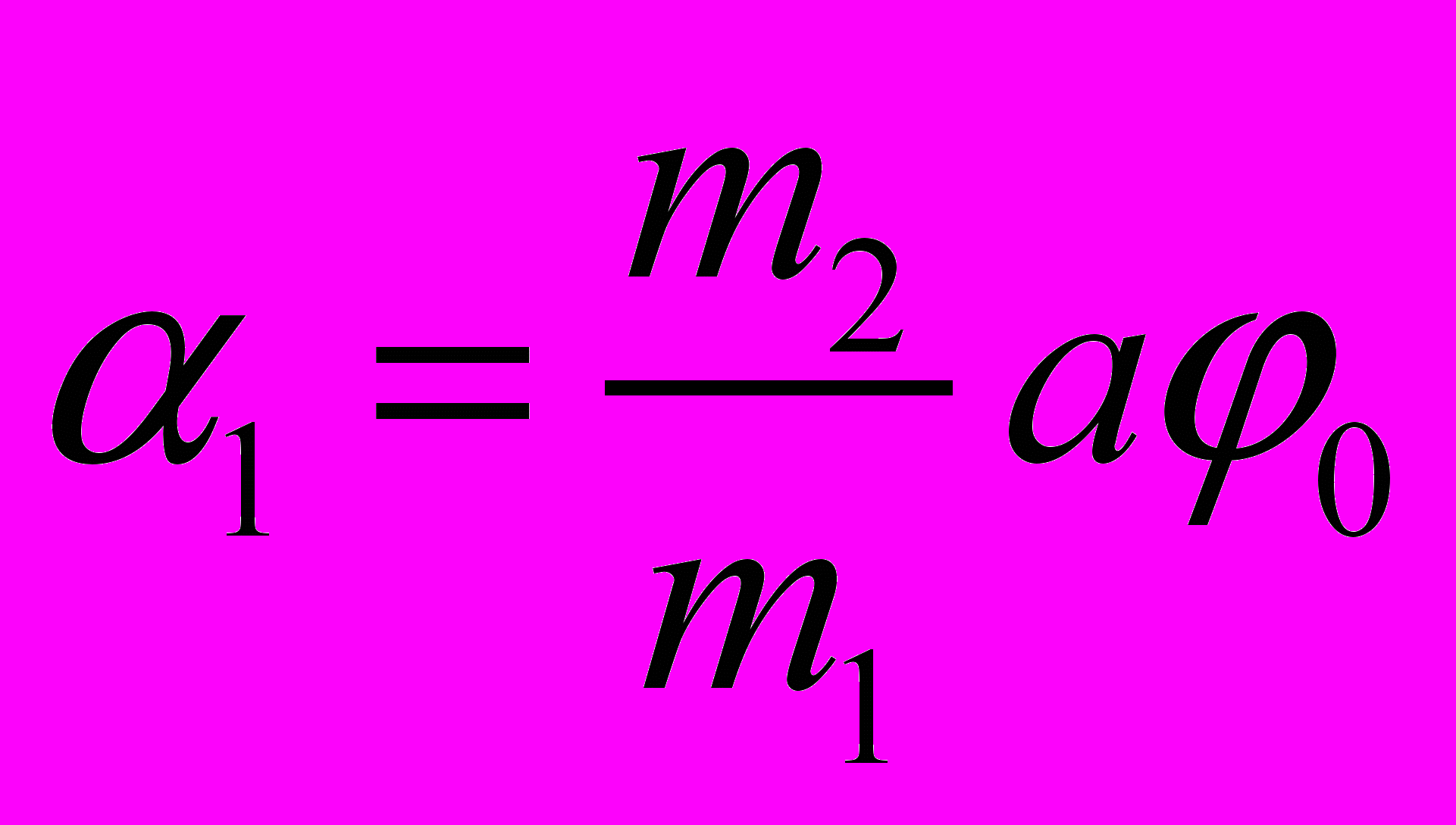 и
и 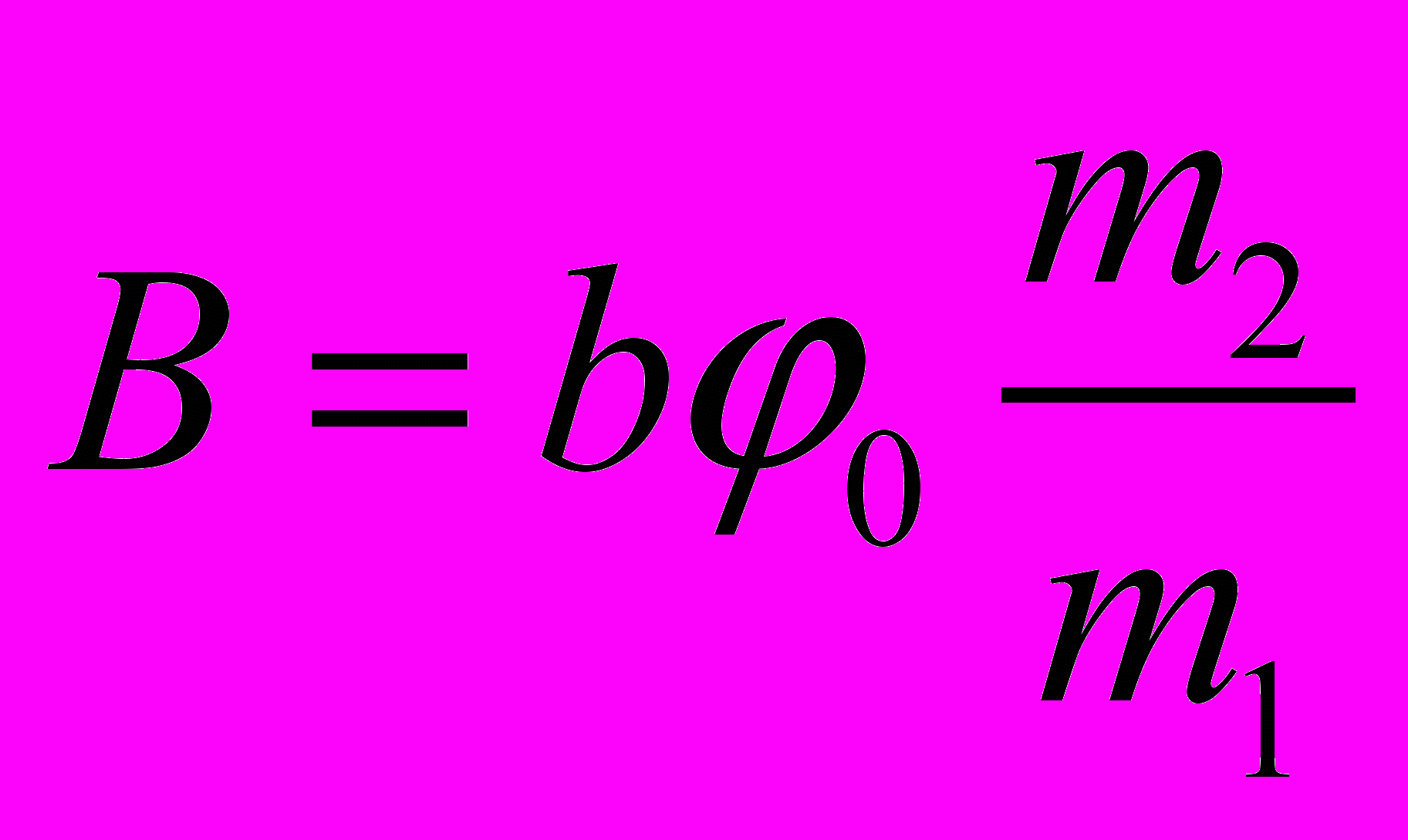 , где
, где  и
и 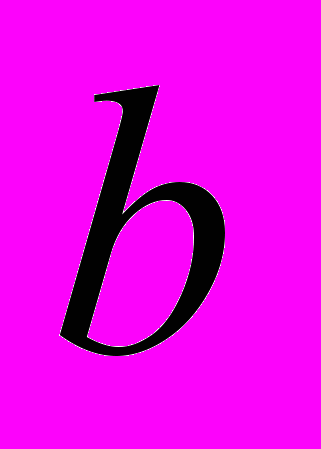 константы. Для определения значения
константы. Для определения значения  необходим многофакторный анализ поведения графиков
необходим многофакторный анализ поведения графиков 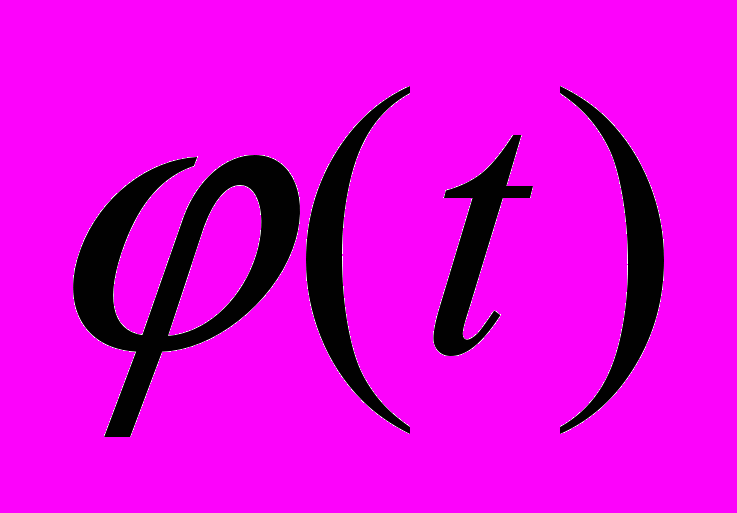 и
и 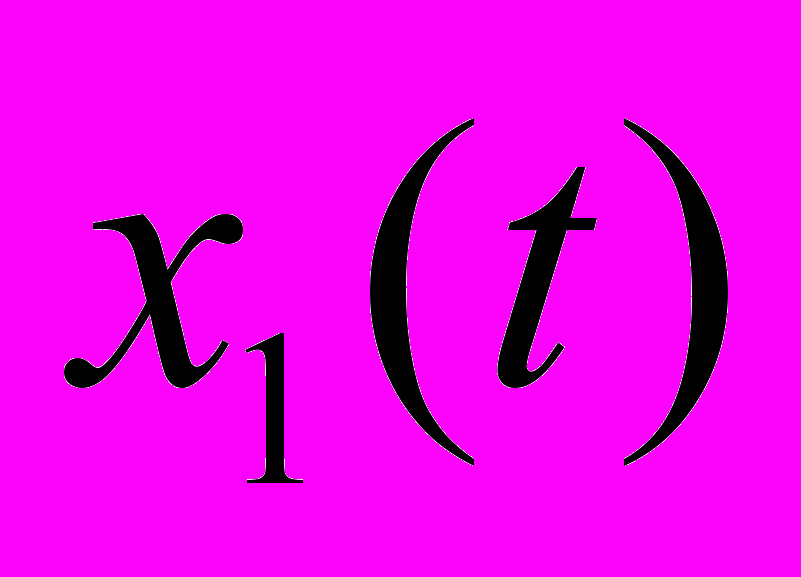 в зависимости от изменений исследуемых параметров.
в зависимости от изменений исследуемых параметров.Итак, полученные в результате компьютерного эксперимента графики, позволили нам получить приближенное аналитическое выражение для оценки характера движения. Конечно, выражение (12) можно было бы получить и без компьютерного эксперимента, но это лишь пример, иллюстрирующий метод, который может оказаться единственно доступным в других случаях, как, например, при наблюдении колебаний двойного маятника (опора одного маятника является телом другого).
Формула (12) является рабочей формулой, позволяющей сделать определенные выводы о соотношении масс
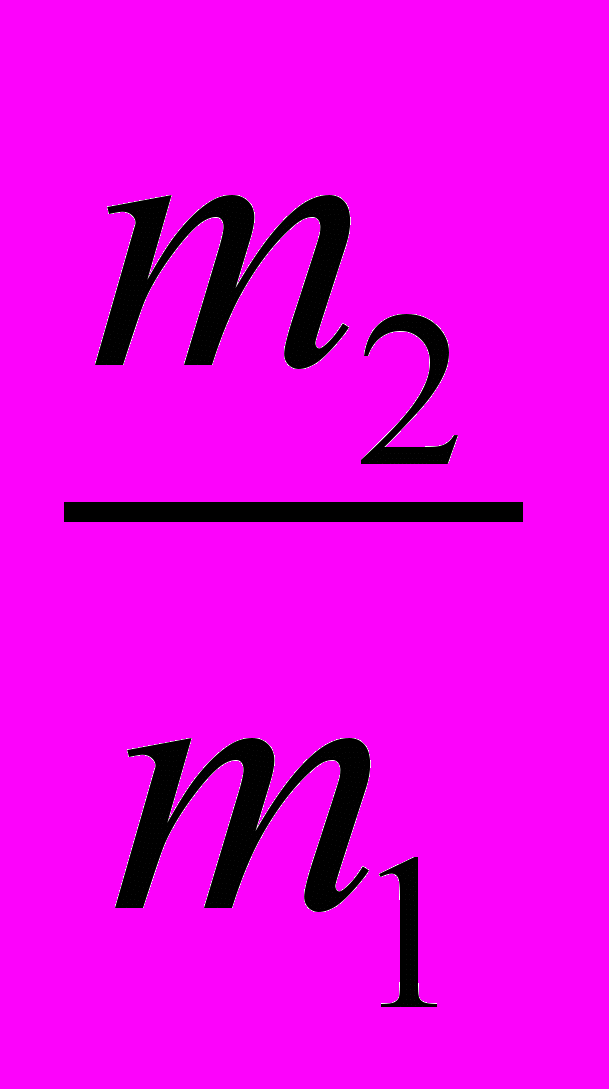 , о длине маятника
, о длине маятника 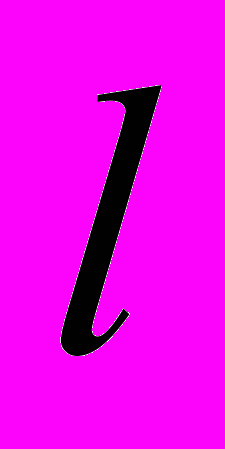 и соответственно о конструкции и геометрических размерах устройства, предназначенного для показа данного явления в большой аудитории.
и соответственно о конструкции и геометрических размерах устройства, предназначенного для показа данного явления в большой аудитории.Для получения более строгих зависимостей характера движения элементов системы рис.1 от масс, длин и др. необходимо использовать статистические методы обработки результатов компьютерного эксперимента, проводимого по определенным методикам (методикам планирования эксперимента).
___________________
1. Гуржий В.С., Николаенко В.Н., Чабан В.И. Проектирование и изготовление конструкций физико-технических устройств и моделей студентами физиками // Инновационные тенденции в системе высшего и среднего образования: Материалы второй международной заочной научно-практической конференции. – Саратов: Изд-во «Научная книга», 2005.
2. Х. Голд, Я. Тобочник. Компьютерное моделирование в физике. – М.: Изд-во «Мир», 1990.
3. Железовский Б.Е., Каменский Ю.В., Николаенко В.Н. Технология компьютерного моделирования в экспериментальной физике: Ч.1: Компьютерное моделирование в механике. Учебно-методическое пособие для студентов вуза. – Саратов: «Научная книга», 2008.
