Татистической проверке гипотез о сходстве параметров различных объектов и выявлении закономерностей в изменении параметров объекта(ов) во времени и пространстве
| Вид материала | Закон |
СодержаниеРаспределение измеренных величин Унимодальное распределение Мультимодальное распределение. |
- Надежность объектов при постепенных отказах. Основные расчетные модели, 131.76kb.
- Будем понимать набор параметров, характеризующих рынок некоторого финансового актива, 218.16kb.
- А. А. Кузьмина Московский государственный университет экономики, статистики и информатики,, 70.02kb.
- Аннотация научно-образовательного материала, 27.05kb.
- Лекция 13, 99.82kb.
- 230100 – Информатика и вычислительная техника, 2067.45kb.
- Дмитрий Волков, dsvolk@jet msk su Инфосистемы Джет, 2004, 503.28kb.
- Практическое задание: Настройка конфигурации Настройка параметров учёта Настройка параметров, 117.94kb.
- 2 билет №1, 119.4kb.
- Целью Типовой инструкции является упорядочение в крае деятельности по обеспечению безопасности, 939.27kb.
Статистические методы в геоэкологических исследованиях (часть1)
Статистические методы используются для оценки средних параметров объекта и статистической проверке гипотез о сходстве параметров различных объектов и выявлении закономерностей в изменении параметров объекта(ов) во времени и пространстве.
Основные определения и понятия
Параметры любого природного объекта не являются постоянной величиной, а изменяются в пределах какого то определенного интервала (например Ph воды в родниках г.Саратова имеет значения 6,54-8). Все значения измеряемого параметра называются генеральной совокупностью. Поскольку все значения измерить невозможно в статистических исследованиях анализируется выборка – измеренные значения параметра. Для сбора достоверной выборки (отражающей реальное изменение параметра) необходимы следующие условия.
1. Условие массовости. Достоверность результатов увеличивается при массовом отборе проб. При количестве проб менее 20 достоверность выводов мала и возможность применения статистических методов сильно ограничено.
2. Условия однородности. Одинаковая методика измерения и проведение измерений в границах одного объекта, например одного водоносного горизонта.
3. Условие случайности. Отсутствие временной и/или пространственной упорядоченности при отборе проб. Например если при исследовании загрязнения тяжелыми металлами какого либо района пробы на содержания свинца будут отбираться преимущественно вдоль дорог то средние значения загрязнений на единицу площади исследованной территории по результатам такого отбора будут завышены и реальная картина площадного загрязнения будет неверной.
4. Условие независимости. Результаты каждого наблюдения не должны зависеть от результатов предыдущих наблюдений.
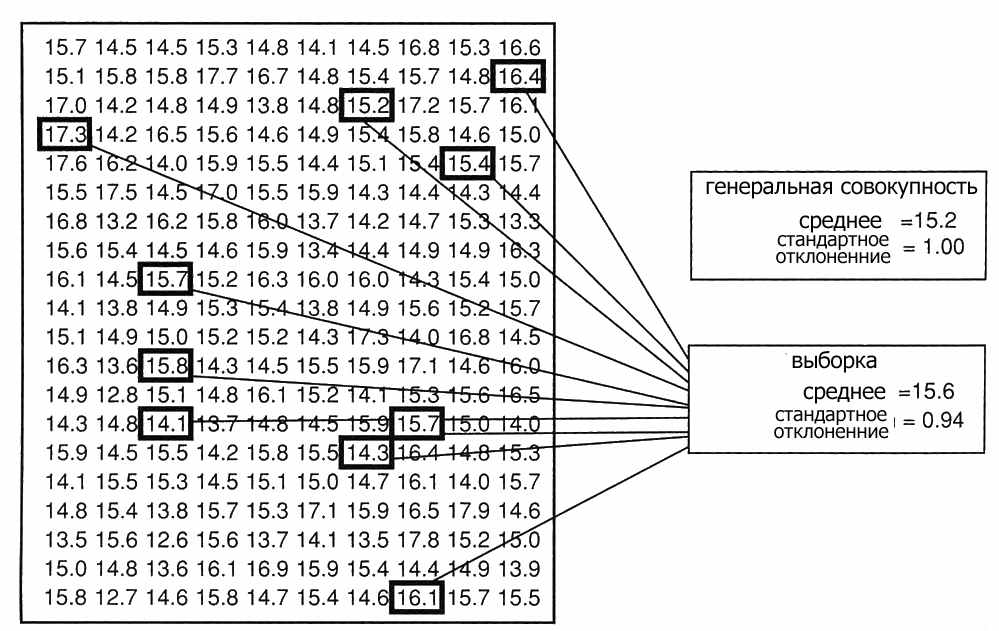
Рис. 1 Распределение поверхностной температуры почвы на квадратном участке поля. Всего 200 участков с разной температурой. Во время исследований взято 10 измерений.
Шкалы измерений. Переменные различаются также тем "насколько хорошо" они могут быть измерены или, другими словами, как много измеряемой информации обеспечивает шкала их измерений. Очевидно, в каждом измерении присутствует некоторая ошибка, определяющая границы "количества информации", которое можно получить в данном измерении. Другим фактором, определяющим количество информации, содержащейся в переменной, является тип шкалы, в которой проведено измерение. Различают следующие типы шкал:(a) номинальная, (b) порядковая (ординальная), (c) интервальная (d) относительная (шкала отношения). Соответственно, имеем четыре типа переменных: (a) номинальная, (b) порядковая (ординальная), (c) интервальная и (d) относительная.
- Номинальные переменные используются только для качественной классификации. Это означает, что данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам; при этом вы не сможете определить количество или упорядочить эти классы. Например, вы сможете сказать, что 2 индивидуума различимы в терминах переменной А (например, индивидуумы принадлежат к разным национальностям). Типичные примеры номинальных переменных - пол, национальность, цвет, город и т.д. Часто номинальные переменные называют категориальными.
- Порядковые переменные позволяют ранжировать (упорядочить) объекты, указав какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной. Однако они не позволяют сказать "на сколько больше" или "на сколько меньше". Порядковые переменные иногда также называют ординальными. Типичный пример порядковой переменной - социоэкономический статус семьи. Мы понимаем, что верхний средний уровень выше среднего уровня, однако сказать, что разница между ними равна, скажем, 18% мы не сможем. Само расположение шкал в следующем порядке: номинальная, порядковая, интервальная является хорошим примером порядковой шкалы.
- Интервальные переменные позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Вы можете не только сказать, что температура 40 градусов выше, чем температура 30 градусов, но и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры от 30 до 40 градусов.
- Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля, таким образом, для этих переменных являются обоснованными предложения типа: x в два раза больше, чем y. Типичными примерами шкал отношений являются измерения времени или пространства. Например, температура по Кельвину образует шкалу отношения, и вы можете не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения.
Распределение измеренных величин какого-либо параметра объекта можно охарактеризовать гистограммой – графиком частоты распределения. Гистограмма может быть симметричной – нормальное распределение или ассиметричной например логнормальное распределение.
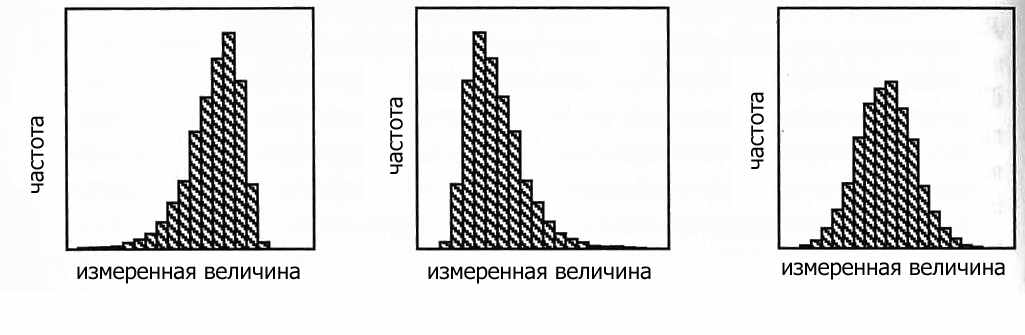
Построение гистограммы является наиболее оптимальным способом для определения или оценки условия однородности выборки.
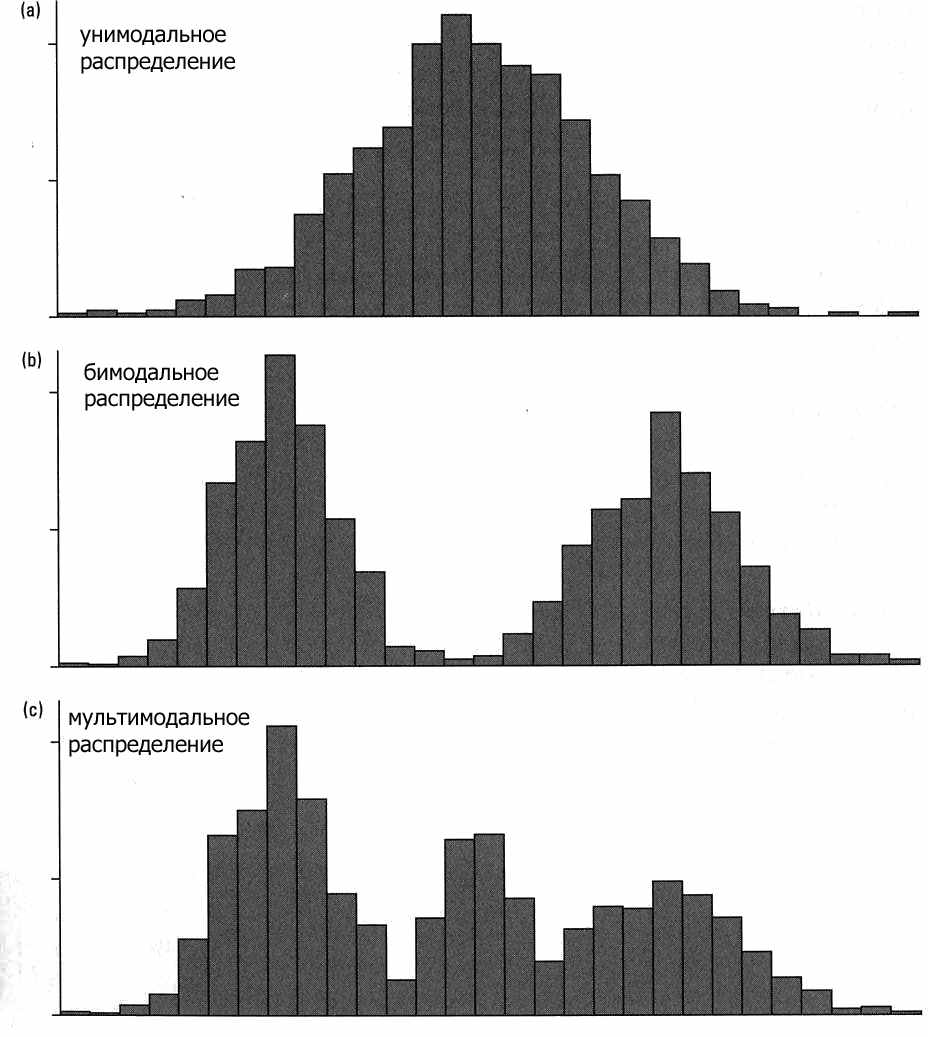
Унимодальное распределение - это распределение, имеющее только одну моду (пик). Типичный пример - это нормальное распределение, которое также и симметрично, в то время как многие унимодальные распределения несимметричны.
Мультимодальное распределение. Распределение, имеющее несколько мод (т.е. два или более "пика").Мультимодальность распределения выборки часто является показателем того, что распределение не является нормальным. Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Мультимодальность часто может показывать, что выборка не является однородной и наблюдения порождены двумя или более "наложенными" распределениями. Иногда мультимодальность распределения означает, что выбранные инструменты не подходят для измерения (например "проблемы разметки" в естественных науках,"смещенные ответы" в социальных).
Среднее. Среднее показывает "центральное положение" (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют статистики (например, среднее), дающие информацию о популяции в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна. Среднее = (
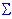 xi)/n где n - число наблюдений (объем выборки). В исследованиях используется среднее арифметическое для нормального распределения и среднее геометрическое для логнормального распределения данных.
xi)/n где n - число наблюдений (объем выборки). В исследованиях используется среднее арифметическое для нормального распределения и среднее геометрическое для логнормального распределения данных. Мода. Мода выборки (термин был впервые введен Пирсоном, 1894) - это значение, которое наиболее часто встречающееся в выборке.
Медиана. Медиана выборки (термин был впервые введен Гальтоном, 1882) - это значение, которое разбивает выборку на две равные части. Половина наблюдений лежит ниже медианы, и половина наблюдений лежит выше медианы. Медиана вычисляется следующим образом. Изучаемая выборка упорядочивается в порядке возрастания. Получаемая последовательность называется вариационным рядом или порядковыми статистиками. Если число наблюдений нечетно, то медианой является число в середине ряда. Если число наблюдений четно, то медиана оценивается как среднее арифметическое чисел расположенных в середине ряда:
| m= | am+am+1 |
| 2 |
Дисперсия. Дисперсия популяции - квадрат отклонений от среднего (термин впервые введен Фишером, 1918) вычисляется по формуле:
 2 =
2 = 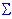 (xi-µ)2/N где µ - среднее N - размер популяции.
(xi-µ)2/N где µ - среднее N - размер популяции.Несмещенная оценка дисперсии вычисляется по формуле: s2 =
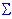 (xi-xbar)2/n-1 где
(xi-xbar)2/n-1 гдеxbar - выборочное среднее n - число наблюдений в выборке.
Стандартное отклонение. Стандартное отклонение (термин был впервые введен Пирсоном, 1894) - это широко используемая мера разброса или вариабельности (изменчивости) данных. Стандартное отклонение популяции определяется формулой:
 = [
= [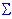 (xi-µ)2/N]1/2 где µ - среднее популяции N - размер популяции.
(xi-µ)2/N]1/2 где µ - среднее популяции N - размер популяции.Выборочное стандартное отклонение или оценка стандартного отклонения вычисляется по формуле: s = [
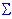 (xi-x-bar)2/n-1]1/2 где
(xi-x-bar)2/n-1]1/2 гдеxbar - выборочное среднее
n - число наблюдений в выборке.
Стандартная ошибка. Термин стандартная ошибка среднего был впервые введен Юлом (Yule, 1897). Эта величина характеризует стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности, и зависит от дисперсии генеральной совокупности (сигма) и объема выборки (n):
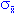 = (
= ( 2/n)1/2 где
2/n)1/2 где 2 - дисперсия генеральной совокупности и n - число наблюдений в выборке. Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле:
2 - дисперсия генеральной совокупности и n - число наблюдений в выборке. Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле: 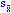 = (s2/n)1/2 где
= (s2/n)1/2 гдеs2 - выборочная дисперсия (наилучшая оценка дисперсии популяции) и
n - объем выборки.
Доверительный интервал для среднего. Доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится "истинное" среднее популяции. В некоторых статистических или математических программных пакетах (например, в системе STATISTICA) вы можете построить доверительные интервалы для любого p-уровня; например, если среднее в вашей выборке равно 23, а нижняя и верхняя границы для p=.05 равны 19 и 27 соответственно, то вы можете заключить, что с 95% вероятностью среднее выборки больше 19 и меньше 27. Если вы установите меньшее значение p-уровня, то интервал будет шире, и увеличится "уверенность" в оценке, и наоборот; как мы знаем из прогнозов погоды, чем "неопределеннее" прогноз (т.е. шире доверительный интервал), тем скорее он сбудется. Заметим, что ширина доверительного интервала зависит от размера выборки и дисперсии наблюдений. Вычисление доверительных интервалов основывается на предположении, что переменная в совокупности нормально распределена. Эта оценка может быть неверной, если это предположение не выполнено, и пока размер выборки мал, например, n меньше 100.
Пример
| Данные | 8 | 12 | 10 | 7 | 7 | 11 | 8 | Среднее = 9 |
| Отклонение от среднего | 1 | 3 | 1 | 2 | 2 | 2 | 1 | Среднее отклонений = 12/7=1,7 |
| Квадрат отклонений от среднего | 1 | 9 | 1 | 4 | 4 | 4 | 1 | Дисперсия 24/7=3,4 |
| Квадрат отклонений от среднего | 1 | 9 | 1 | 4 | 4 | 4 | 1 | Несмещенная оценка дисперсии 24/(7-1)=4 |
| Квадратный корень от дисперсии (несмещенной оценки дисперсии) называется стандартным отклонением. Имеет те же единицы измерения, что и исходные данные охватывает ~68% интервал от среднего значения популяции. т.е. 68% данных выборки находится в интервале = среднее ± стандартное отклонение. Коэффициент вариации – безразмерная величина вариации данных CV=стандартное отклонение/среднее*100% отражает разброс данных выборки в процентах Стандартная ошибка – интервал в котором находится среднее значение генеральной совокупности. Стандартная ошибка = стандартное отклонение/ 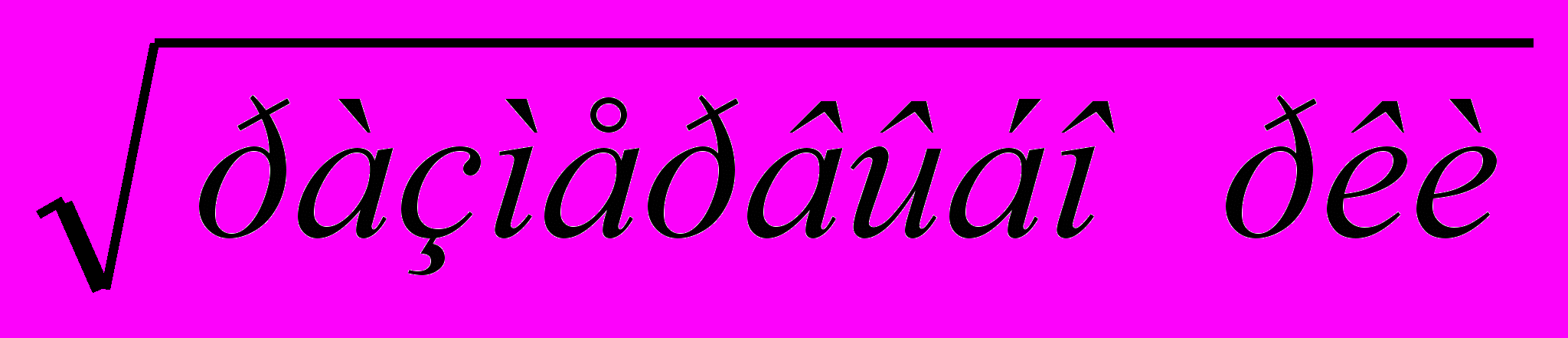 =2/ =2/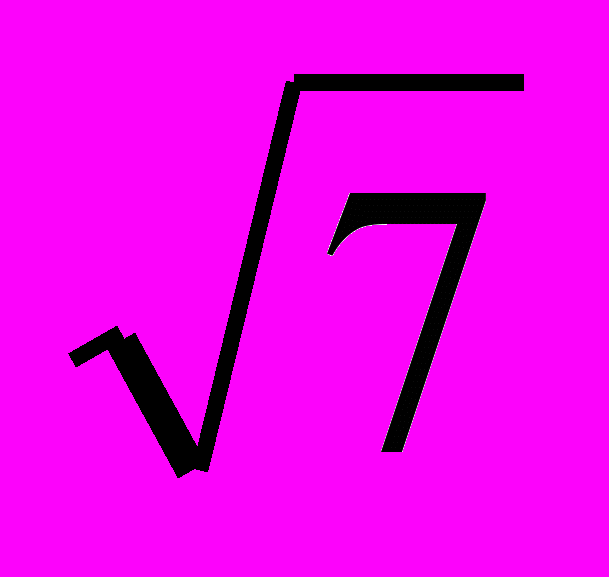 =0,76. =0,76.Таким образом с вероятностью 68% мы можем утверждать, что среднее значение генеральной совокупности лежит в интервале 9 ± 0,76 Доверительный интервал – оценочный интервал в котором с заданной нами вероятностью находится среднее генеральной совокупности, обычно доверительный интервал выбирается равным 95 %. (надо помнить что на практике мы всегда анализируем выборку – часть генеральной совокупности). Данный параметр используется в большинстве статистических исследований и определяет допустимую вероятность ошибки при статистических исследованиях. 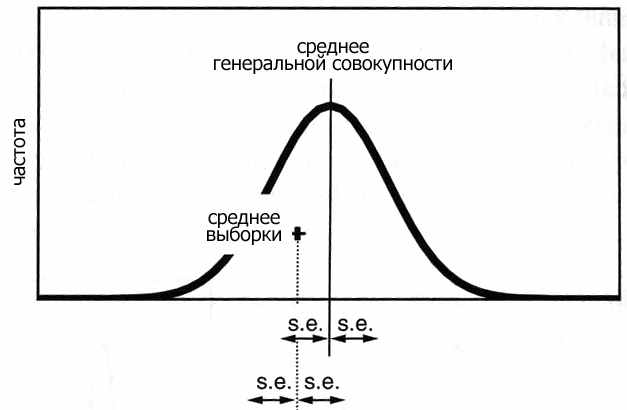 s.e. – границы стандартной ошибки s.e. – границы стандартной ошибки | ||||||||
Эксцесс. Эксцесс (термин был впервые введен Пирсоном, 1905) или точнее, коэффициент эксцесса измеряет "пикообразность" распределения. Если эксцесс значимо отличен от 0, то функция плотности либо имеет более закругленный, либо более острый пик, чем пик плотности нормального распределения. Функция плотности нормального распределения имеет эксцесс равный 0. Оценка эксцесса (выборочный эксцесс) вычисляется по формуле: Эксцесс = [n*(n+1)*M4 - 3*M2*M2*(n-1)]/[(n-1)*(n-2)*(n-3)*
 4] где Mj равен
4] где Mj равен 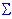 (xi-Meanx)j n - число наблюдений
(xi-Meanx)j n - число наблюдений  4 - стандартное отклонение (сигма), возведенное в четвертую степень.
4 - стандартное отклонение (сигма), возведенное в четвертую степень.Асимметрия. Асимметрия или коэффициент асимметрии (термин был впервые введен Пирсоном, 1895) является мерой несимметричности распределения. Если этот коэффициент отчетливо отличается от 0, распределение является асимметричным. Плотность нормального распределения симметрична относительно среднего. Асимметрия = n*M3/[(n-1)*(n-2)*
 3] где M3 равно
3] где M3 равно 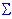 (xi-Среднееx)3
(xi-Среднееx)3  3 стандартное отклонение (сигма), возведенное в третью степень n число наблюдений. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна.
3 стандартное отклонение (сигма), возведенное в третью степень n число наблюдений. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна.Статистический уровень значимости (p-уровень). Статистическая значимость результата представляет собой меру уверенности в его "истинности" (в смысле "репрезентативности выборки"). Более точно, p-уровень - это показатель, обратно пропорциональный надежности результата. Более высокий p-уровень соответствует более низкому уровню доверия найденным в выборке результатам, например, зависимостям между переменными. А именно, p-уровень представляет собой вероятность ошибки, связанной с обобщением наблюдаемого результата на всю популяцию. Например, p-уровень = .05 (т.е. 1/20) показывает, что имеется 5% вероятность того, что найденная в выборке зависимость между переменными является лишь случайной особенностью данной выборки. Иными словами, если данная зависимость в популяции отсутствует, а вы многократно проводили бы подобные эксперименты, то примерно в одном из двадцати повторений эксперимента можно было бы ожидать такой же или более сильной зависимости между изучаемыми переменными. Во многих исследованиях p-уровень .05 рассматривается как "приемлемая граница" уровня ошибки
