Лекция 2, часть 2

Пусть A - код точки - начала отрезка,

B - код точки - конца отрезка.


Возможные варианты:

• A = B= 0000
  

Этот случай означает, что обе точки лежат внутри прямоугольника (т. е. отсечение не требуется)

• C= A & B  0
  

В этом случае точки лежат по одну сторону от какой-либо отсекающей линии (с внешней ее стороны), следовательно, рисовать вообще ничего не нужно.

• В противном случае необходимо находить точки пересечения с некоторыми из отсекающих прямых (для прямых, которые пересекает AB, соответствующий бит в AB установлен в 1), разбить наш отрезок найденными точками пересечения и затем применить тот же анализ кодов концов уже для этих подотрезков. Один из возможных вариантов реализации окончательного алгоритма приведен ниже:
  

Алгоритм:


Пусть A=(x1,y1) , B=(x2,y2);

(x_лево, y_верх, x_право, y_низ) - отсекающий прямоугольник


Функция код(<точка>) возвращает код, значение которого описано выше


Отсечь (x1, y1, x2, y2, x_лево, y_верх, x_право, y_низ)

{

пока( ( код(A) | код(B) ) && ( !( код(A) & код(B) ) ) )

{

если( код(A) == 0) // т.е. A внутри

поменять(A,B); //меняем координаты местами, чтобы A всегда лежала снаружи

если( код(A) & 0x01 ) // т.е. A лежит слева от отсекающего прямоугольника

{

y1+=(y2-y1)*(x_лево-x1)/(x2-x1);

x1=x_лево;

}

иначе если( код(A) & 0x02 ) // т.е. A лежит сверху от отсекающего прямоугольника

{

x1+=(x2-x1)*(y_верх-y1)/(y2-y1);

y1=y_верх;

}

иначе если( код(A) & 0x04 ) // т.е. A лежит справа от отсекающего прямоугольника

{

y1+=(y2-y1)*(x_право-x1)/(x2-x1);

x1=x_право;

}

иначе если( код(A) & 0x08 ) // т.е. A лежит снизу от отсекающего прямоугольника

{

x1+=(x2-x1)*(y_низ-y1)/(y2-y1);

y1=y_низ;

}

}

}


На выходе AB - отсеченный отрезок.


3) Алгоритм средней точки (midpoint) (авторы те же)


Случаи, в которых отрезок лежит целиком снаружи или внутри отсекаемой области выявим изложенным в п.2 методом.

В общем случае возьмем среднюю точку нашего отрезка AB (обозначим ее C₁) и применим к отрезкам AC₁ и C₁B этот алгоритм рекурсивно. Следующие средние точки отрезков AC₁ и C₁B обозначим C₂ и C₃ соответственно (см. Рис. 2).

И так далее, пока размер оставшихся отрезков не станет меньше размера пиксела.

Алгоритм:


Отсечение (точка A, точка B)

{

Если (длина AB меньше размера пиксела ) выход;

Если ( AB лежит вне отсекающего прямоугольника ) выход;

Если ( AB лежит внутри отсекающего прямоугольника ) { Рисовать AB; выход; }

Отсечение (A, (A+B)/2)

Отсечение ((A+B)/2),B)

}


Простой алгоритм, но не очень эффективный на практике, так как требует большой глубины рекурсии.


2.2. Отсечение выпуклым многоугольником.

Алгоритм Cyrus-Beck [Cyrus-Beck, 1978]


Для каждого ребра возможны 3 случая:

а) обе его вершины лежат выше или ниже Ax (например на Рис. 4 1-2)

б) его вершины лежат по разные стороны от Ax (например на Рис. 4 3-4)

найдем точку пересечения и запомним ее;

в) вырожденные случаи: ребро лежит на Ax или одна из его вершин лежит на Ax



Для всего многоугольника возможны 2 случая:

1. Точки пересечения отрезка и многоугольника отсутствуют либо лежат на границе:
   

а) все вершины лежат выше или ниже Ax ;
б) одно из ребер лежит на Ax ;
в) только одна вершина лежит на Ax ;

ничего рисовать не надо


2) Существует непустое пересечение внутренней части многоугольника с отрезком,

при этом точек пересечения с границами ровно 2 (в силу выпуклости)

а) существует 2 точки пересечения Ax с ребрами ;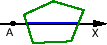
б) существует 1 точка пересечения Ax с ребром и 1 точка пересечения Ax с вершиной;
в) существует 2 точки пересечения Ax с вершинами (не одного ребра).

если x1 < x2 - координаты точек пересечения, то отрезок, который нужно рисовать - это [x1,x2][0,l]


2.2. Отсечение невыпуклым многоугольником без самопересечений.

Создадим список точек пересечения Ax c многоугольником:


Для каждого ребра возможны 4 случая:

а) обе его вершины лежат выше или ниже Ax (например, на Рис. 5 3-4): ничего не заносим в наш список
б) его вершины лежат по разные стороны от Ax (например, на Рис. 5 1-2): заносим в список точку пересечения
в) ребро лежит на Ax ничего не заносим в наш список
г) вершина лежит на Ax г 1) если другие вершины смежных ребер лежат по одну сторону от Ax: ничего не заносим в список
г 2) если другие вершины смежных ребер лежат по разные стороны от Ax: заносим эту вершину в список,

Далее, список точек пересечения должен быть отсортирован по возрастанию (их количество обязано быть четным , т.к. для каждого "входа" в многоугольник должен существовать и "выход"):

x1 < x2 < x3 < x4 и т.д., тогда искомый отрезок - это :

[0,l]  ([x1,x2]  [x3,x4]  [x5,x6] …) (т.к. нечетная точка - всегда точка "входа", а четная - точка "выхода")


2.3. Комбинированный алгоритм Кузьмина. [Kuzmin, 1995]


Алгоритм Кузьмина является модификацией алгоритма Брезенхема, позволяющей сразу решать задачу и отсечения по прямоугольнику, и рисования отрезка. Ниже приводятся основные идеи алгоритма. Точное описание можно найти в [Kuzmin, 1995]

Найдем для двух случаев начальные значения x, y и e₀ , далее будем действовать по алгоритму Брезенхема. Ради целочисленности алгоритма все переменные, связанные с e, по-прежнему домножены на 2a.


1) Горизонтальный случай (Рис. 7).

Рис. 7. Горизонтальный случай.

В этом случае y=y1; а вот x надо найти. Для этого будем следовать алгоритму Брезенхема, как если бы мы рисовали без отсечения, тогда первая точка с координатой y1 будет нарисована тогда, когда для некоего x=xв будет выполнено следующее: xR  (xв , xв+1] , где R - точка пересечения нашего отрезка с прямой y= y1- 0.5 xв=*(y1 -)+1= (a*(2*y1-1))/(2*b) +1 (Деление целочисленное (т.е. возвращает целую часть частного) !!) e=(yP0- yP1)*2a= (y1 -*xв)*2a= =2*(a*y1- b*xв) e0=2b - a - e=2b - a- 2*a*y1+ 2*b*xв= = 2b*(xв+1) - a*(2*y1+1)

2) Вертикальный случай (Рис. 8).

Рис. 8. Вертикальный случай.

В этом случае x=x1; а вот y надо найти исходя из значения e0 Пусть yв=x1*(b/a)=(x1*b)/a (Деление целочисленное (т.е. возвращает целую часть частного) !!) e0=(*x1-yв-)*2a = 2b*x1-a*(2*yв+1) Тогда возможны 2 варианта: e0 < 0 тогда первая точка - P1 (x=x1 , y= yв) и e0= e0 + 2*b e0  0 тогда первая точка - P2 (x=x1 , y= yв+1) и e0= e0 + 2*b-2*a

Условием выхода из алгоритма является:

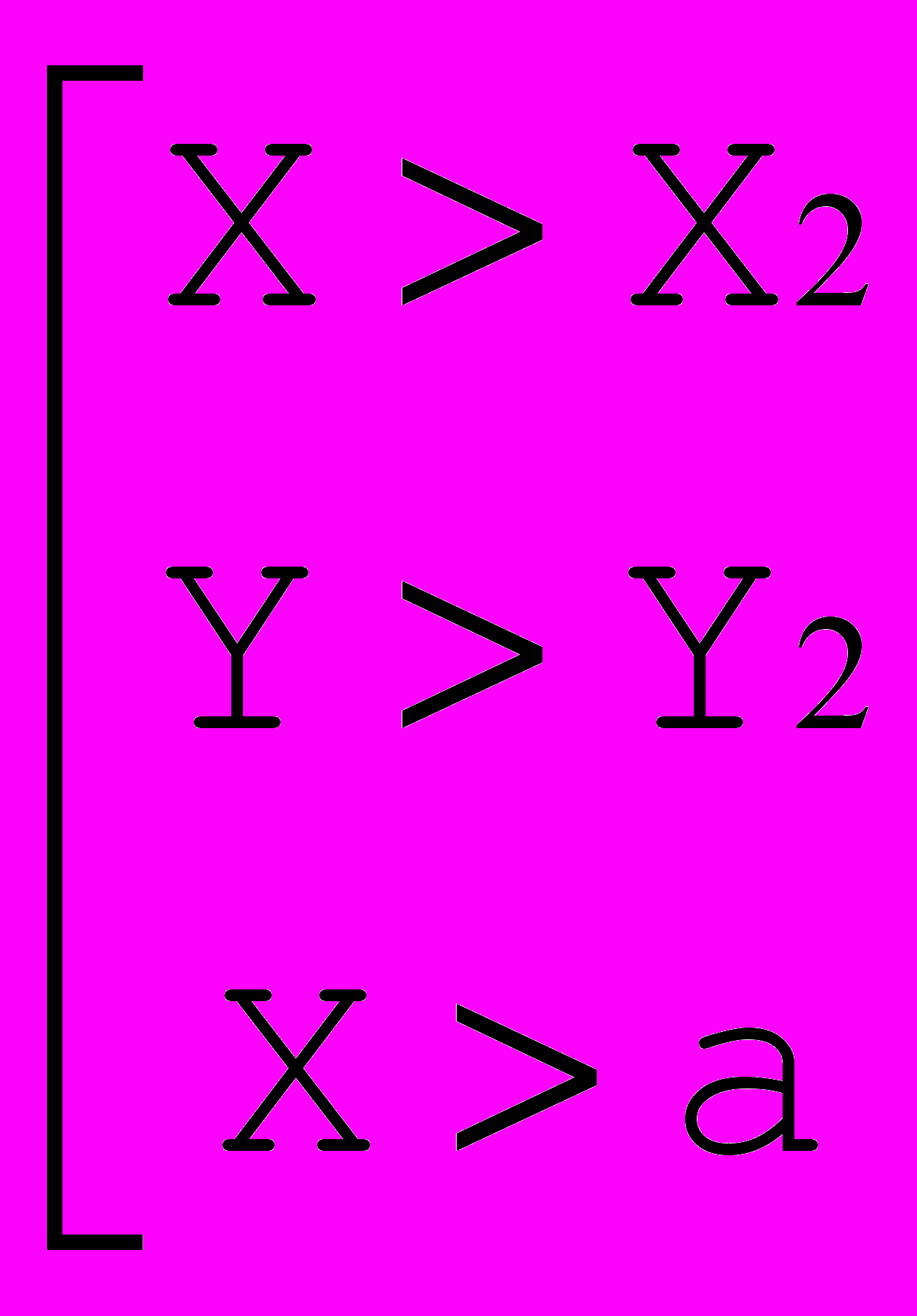(т.е. достижение края прямоугольника или конца отрезка)


СПИСОК ЛИТЕРАТУРЫ


[Cyrus-Beck, 1978] Cyrus M., Beck J. Generalized Two- and Three-Dimensional Clipping //Computers & Graphics.- 1978.- Vol. 3.- pp. 23-28.

[Kuzmin, 1995] Kuzmin Y.P. Bresenham's Line Generation Algorithm with Built-in Clipping //Computer Graphics Forum.- 1995.- Vol. 14, No. 5 (Dec.).