Многопараметрическая оптимизация
| Вид материала | Задача |
- Optimization Toolbox – Оптимизация, 780.37kb.
- Місця збереження документів, 153.78kb.
- Учебная программа по дисциплине: «Оптимизация налогообложения» Специальность: 080105, 151.71kb.
- Оптимизация производственной программы предприятия Выбор портфеля финансовых активов, 75.23kb.
- Моделирование и оптимизация систем с распределенными параметрами, 14.61kb.
- Рассматривается оптимизация эксплуатационных режимов судовых электроэнергетических, 65.28kb.
- Многопараметрическая оценка эффективности информатизации региональной экономики 08., 245.28kb.
- Рабочая программа по дисциплине опд. Ф. 08 Моделирование и оптимизация, 200.55kb.
- Ф-рабочая программа по дисциплине утверждено ученым советом факультета трансферных, 219.93kb.
- Международная конференция «алгебра и линейная оптимизация», посвященная 100-летию проф., 36.6kb.
Многопараметрическая оптимизация
1. Определение коэффициентов веса параметров
1.1. Постановка задачи
В задачах, которые мы рассматривали до сих пор, в критерий входил только один параметр, например, прибыль. Однако зачастую свести наши желания к какому-нибудь одному критерию достаточно трудно, и вообще говоря, желаемых целей может быть много. Как же в таком случае принимать оптимальное решение, которое согласно определению является наилучшим только в одном единственном смысле.
Задачи, в которых оптимизацию производят по нескольким параметрам, называют задачами многопараметрической или векторной оптимизации. Многопараметрическая оптимизация представляет собой попытку найти некоторый компромисс между теми параметрами, по которым требуется оптимизировать решение.
Важным элементом при такой оптимизации является назначение коэффициентов веса каждого оптимизируемого параметра. Распространенный метод — определение коэффициентов веса с помощью экспертов, который представляет собой, по существу, обычное обсуждение, с той лишь разницей, что свое мнение эксперты выражают не словами, а цифрами. Методы экспертных оценок широко распространены в спорте, например, в фигурном катании, гимнастике. Нет основания считать неприемлемым коллективное мнение специалистов и при принятии оптимальных решений.
Предложено достаточно много методов определения экспертных оценок. Рассмотрим три из них.
1.2. Непосредственное назначение коэффициентов веса
При непосредственном назначении коэффициентов веса каждый эксперт оценивает сравнительную важность рассматриваемых параметров, которые будут входить в целевую функцию. В этом методе каждый 1-ый эксперт для каждого k-го параметра должен назначить коэффициент веса аik таким образом, чтобы сумма всех коэффициентов веса, назначенных одним экспертом для различных параметров, равнялась единице. Это требование можно записать так:
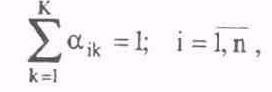
где n — число экспертов.
Алгоритм 1.1. Непосредственное назначение коэффициентов веса
1. Определить число параметров К, которые будут включены в целевую функцию.
2. Сделать таблицу по форме, представленной на рис. 7.1.1, которую мы будем называть базовой.
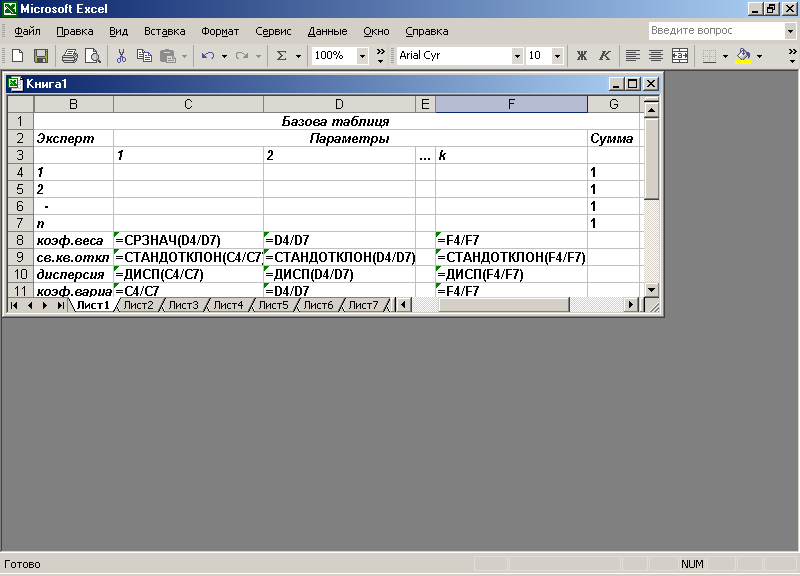
Рис.1.1
> Ввести функции Excel, определяющие среднее значение, среднее квадратическое отклонение, дисперсию, как это показано в ячейках C8:F10.
> В ячейки C11F11 ввести формулы для определения коэффициента вариабильности. После этих работ таблица подготовлена к вводу результатов экспертизы.
3. Значения коэффициентов веса, назначаемые каждым экспертом, ввести в ячейки C4:F7.
На экране: результат экспертизы. В ячейках C8:F8 находятся усредненные значения коэффициентов веса.
Значение коэффициента вариабильности показывает величину разброса экспертных оценок. При v0,2 оценки экспертов можно считать согласованными. В случае v>0,2 целесообразно провести с экспертами содержательное обсуждение важности оцениваемых параметров, после чего повторить экспертизу. При сохранении величины разброса целесообразно учитывать вероятностный характер экспертных оценок по методам, приведенным ниже.
Пример заполнения таблицы приведен на рис. 1.2, в которой принято число параметров три: А, Б, В и число экспертов n = 8.
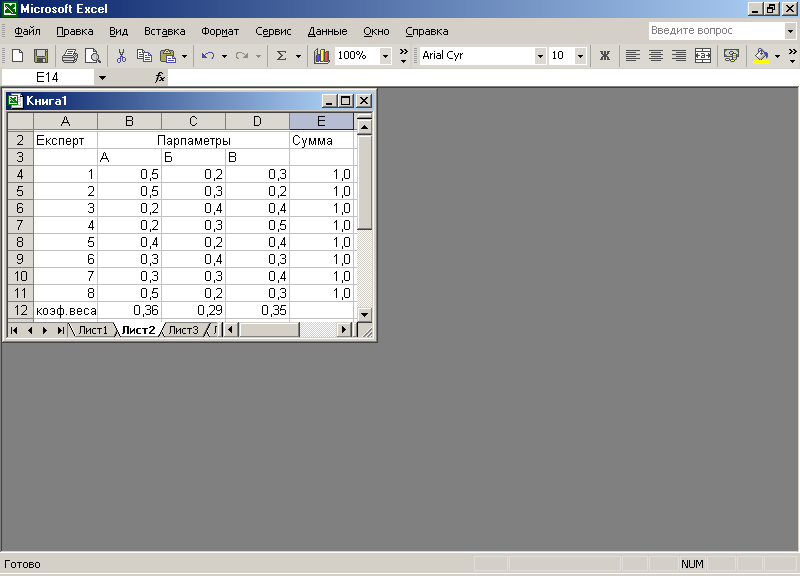
Рис. 1.2
Как показывает опыт, удовлетворение экспертами требования
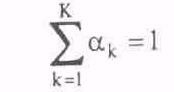
при К>3, вызывает затруднение.
Для того чтобы избежать выполнения этого требования, можно коэффициенты веса определять и другими методами, рассморенными ниже.
1.3. Оценка важности параметров в баллах
При оценке важности параметров в баллах каждый эксперт оценивает параметры по десятибалльной системе. При этом оценка, назначаемая каждым экспертом каждому параметру, не связана с оценками, которые он же назначает другим параметрам. Например, всем параметрам можно назначать одинаковую оценку. Определение экспертных оценок в баллах производится по следующему алгоритму.
Алгоритм 1.2. Определение коэффициентов веса оценки важности параметров в баллах
- Сформировать таблицу по форме, представленной на рис. 1.3, в которую вносятся оценки всех параметров в баллах, сделанные каждым экспертом.
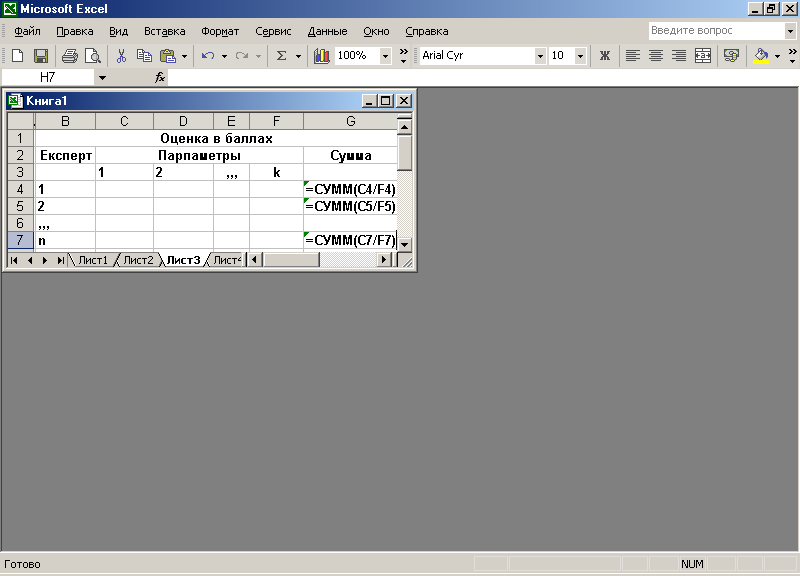
Рис. 1.3.
В ячейках G4:G7 введены функции суммирования.
- Составить базовую таблицу (рис.1.4), аналогичную таблице, показанной на рис. 1.1, в ячейки J4:M7 которой ввести указанные функции.
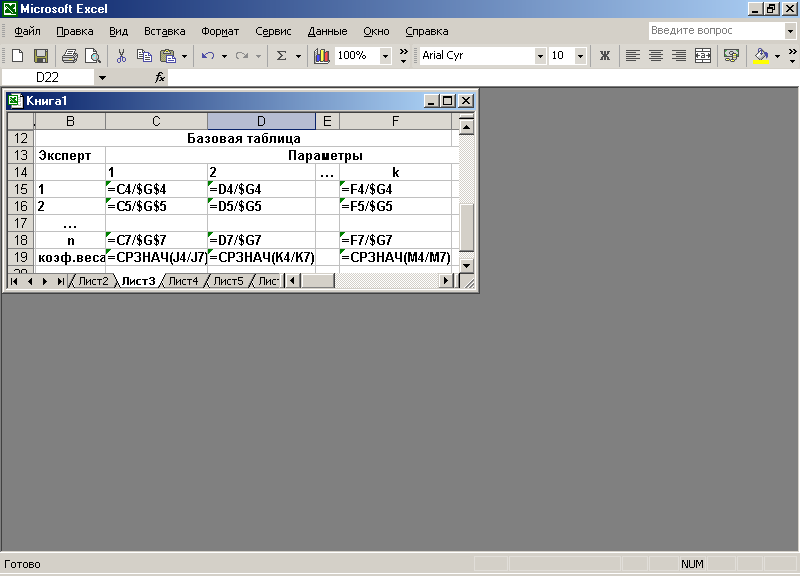
Рис.1.4.
Эти формулы обеспечивают переход от оценок параметров в баллах к значениям коэффициентов веса, сумма которых для всех параметров равна единице у каждого эксперта. В таблице (рис. 1.4) в ячейках J8:M8 находятся результаты проведенной экспертизы.
Пример исходных оценок в баллах по форме рис. 1.3 представлен на рис. 1.5, а результат определения экспертных оценок по форме рис.1.4 — на рис.1.6.
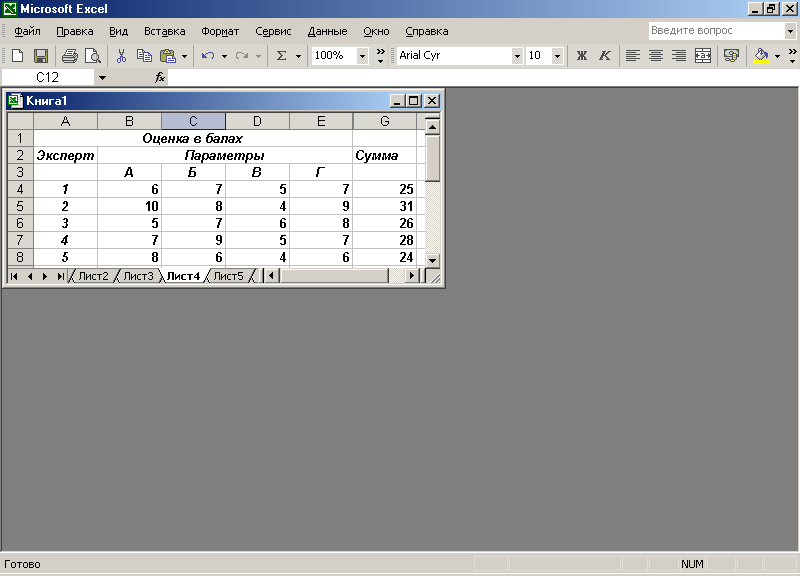
Рис.1.5
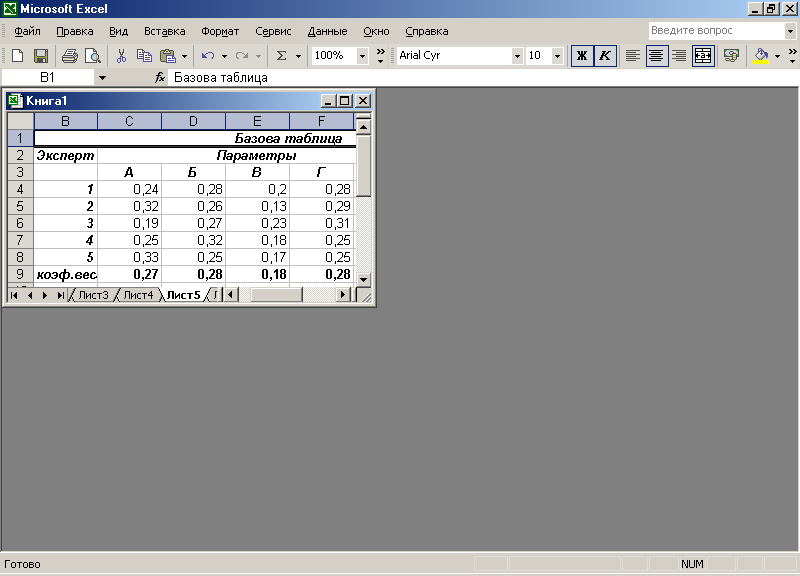
Рис.1.6
1.4. Метод парных сравнений
Если при k>3 одновременная оценка всех параметров вызывает затруднения, их можно оценивать еще одним методом, который называется методом парных сравнений. Этот метод реализуется с помощью следующего алгоритма.
Алгоритм 1.3. Определение коэффициентов веса методом парных сравнений
1. Определить число оцениваемых параметров k и число экспертов n. В дальнейшем принимаем k = 5; n = 4.
2. Для каждого эксперта составить отдельную таблицу по форме, представленной на рис. 1.7.
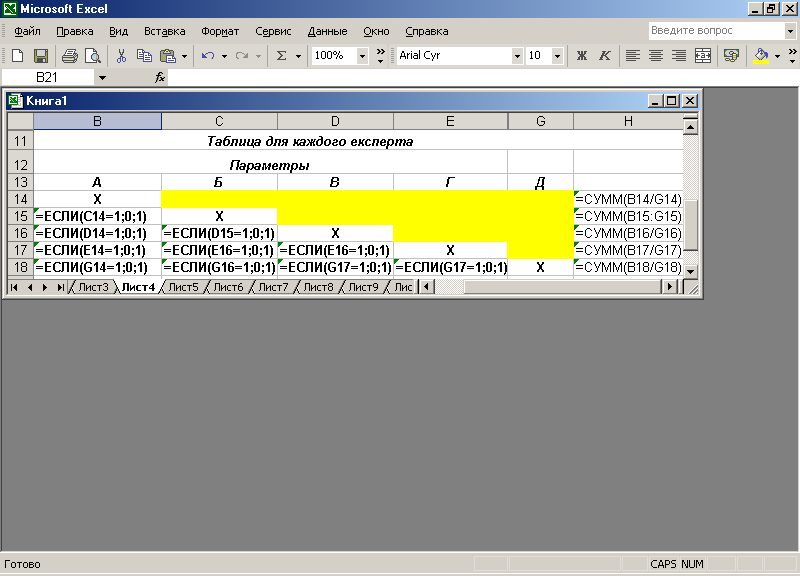
Рис.1.7
3. В этой таблице эксперт должен ввести оценку парных сравнений, которая заключается в следующем. Если k-ый параметр важнее j-ro, то в ячейке, принадлежащей k-ой строке и j-му столбцу, указывается 1, в противном случае — 0.
Пример заполнения такой таблицы первым экспертом приведен на рис. 1.8, из которой видно, что по оценке этого эксперта параметр А менее важен, чем параметр Б (D16 = 0) и Д (G16 = 0), но более важен, чем В (Е16 = 1) и Г (F16 = 1).
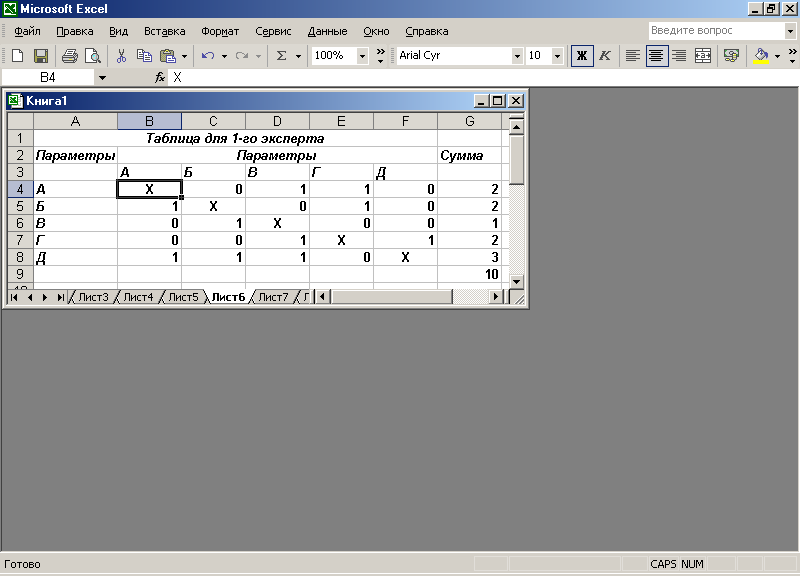
Рис.1.8
4.Составить базовую таблицу (рис. 1.9), в ячейки которой введены формулы для 1-го эксперта.
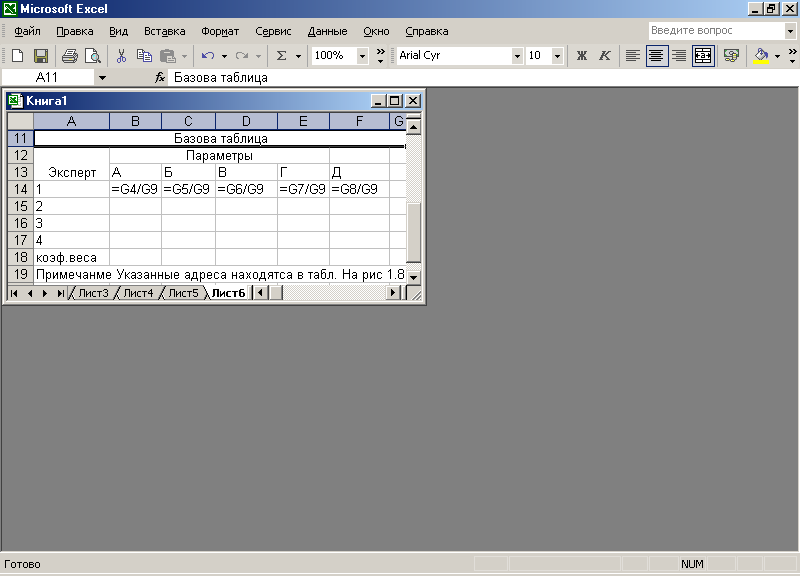
Рис.1.9
Базовая таблица, представленная на рис. 1.9, является формой для ввода результатов экспертизы.
Пример заполнения таблицы для 1-го эксперта по данным рис. 1.8 приведен на рис. 1.10 в ячейках B5:G5. Данные в ячейках B5:G7 из таблиц для остальных экспертов вводятся аналогично.
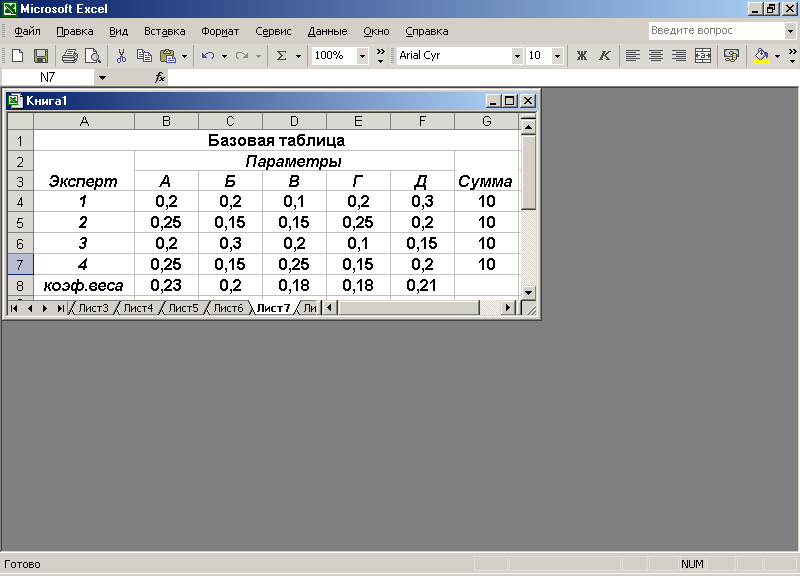
Рис.1.10
В этой таблице в ячейках B8:F8 приведены окончательные результаты проведенной экспертизы.
ІІ. Оптимизация по нескольким параметрам
2.1. Обобщенная целевая функция
Возможной реализацией многопараметрической оптимизации является обобщенная целевая функция Роб, которая записывается следующим образом:
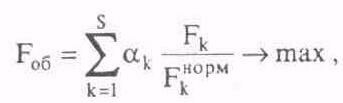 (2.1)
(2.1)где Fk — k-ая целевая функция,
Fkнорм — нормирующее значение k-ой целевой функции,
s — число составляющих целевых функций,
k— коэффициент веса k-ой целевой функции.
При этом перед составляющими целевой функции, которые максимизируются, ставится знак плюс, перед минимизируемыми — минус. Из (2.1) следует, что для формирования обобщенной целевой функции необходимо знать k и Fkнорм.. Значения Fkнорм принимаются при максимизации k-ой составляющей целевой функции:
Fkнорм =Fkmax,
при ее минимизации
Fkнорм =Fkmin .
Решение по обобщенной целевой функции рассмотрим для нашей задачи, приведенной на рис. 2.1.
Алгоритм 2.1. Оптимизация по обобщенной целевой функции
1. Вызвать таблицу с условиями задачи (рис. 2.1).
2. Определить, какие составляющие целевые функции будут входить в обобщенные. Принимаем:
ЦФ1 — максимизация прибыли,
ЦФ2 — минимизация используемых финансов.
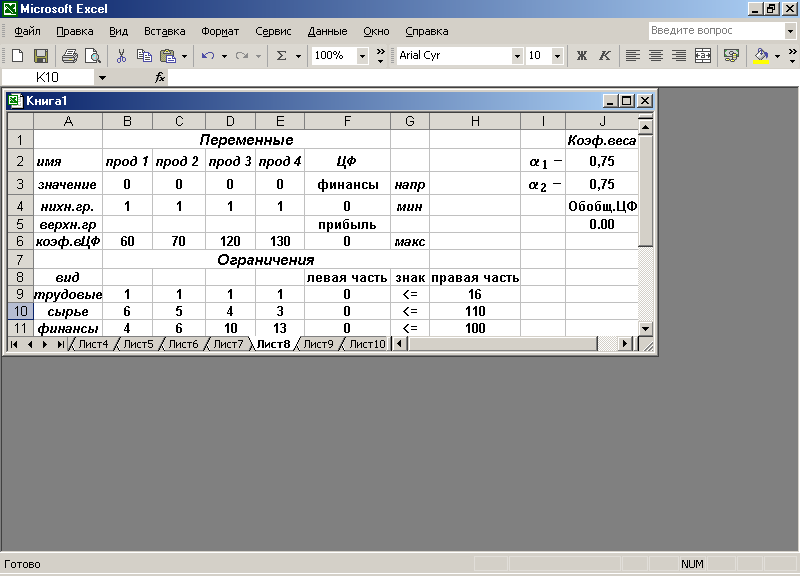
Рис.2.1.
3. При минимизации хотя бы для одной составляющей необходимо ввести нижние границы значений переменных. Вводим 1 в ячейки В4, С4, D4, Е4.
4. Ввести условия задачи.
5. Решить задачу при максимизации прибыли. На экране: результат решения задачи F6=mахЦФ1 = 1290.
6. Ввести в ячейку F4 значения ЦФ2, которые равны левой части в ограничении по финансам (F11).
7. Решить задачу при минимизации используемых финансов. На экране: результат решения задачи F4 =minЦФ2 = 33.
8. Провести экспертизу и определить коэффициенты веса. Принимаем 1=0,75; 2=0,25.
9. Ввести эти данные, как показано на рис. 2.1, в ячейки J2:J3.
10. Сформулировать обобщенную целевую функцию J6 = ЦФоб= J2*F6/1290 - J3*F4/33.
11. Решить задачу по обобщенной целевой функции.
Результаты решения по трем целевым функциям приведены в таблице (рис.2.2). Из этой таблицы видно следующее: при решении по обобщенной целевой функции величины прибыли и используемых финансов имеют промежуточные значения по сравнению с решением по составляющим целевым функциям.
Такое положение не распространяется на значения переменных.
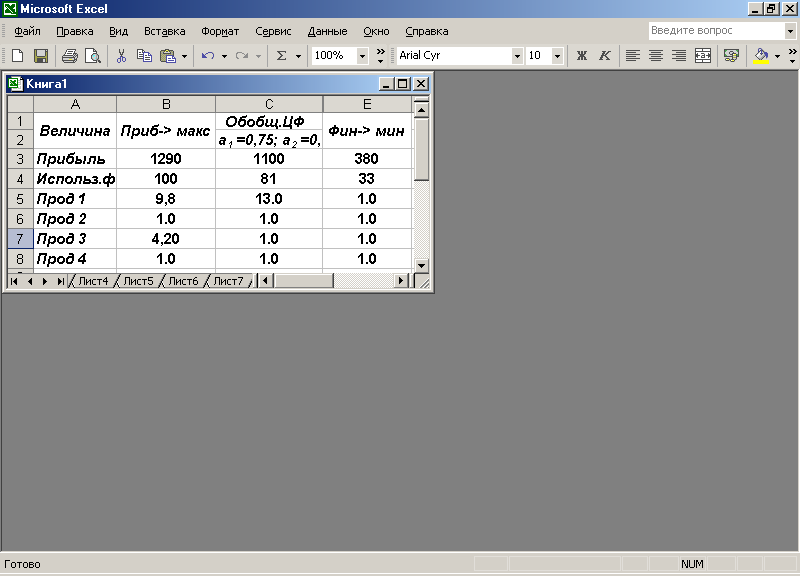
Рис.2.2
2.2. Оптимизация по ресурсам
При оптимизации по ресурсам целевая функция записывается следующим образом:
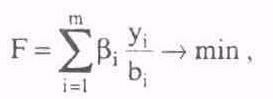 (2.2)
(2.2)где yi — количество неиспользованного i-го ресурса,
bi — количество располагаемого i-го ресурса,
i — коэффициент веса i-го ресурса,
m — количество ресурсов.
Нетрудно видеть, что смысл оптимизации по данной целевой функции заключается в максимизации использования ресурсов. При этом очередность их использования определяется назначенным коэффициентом веса. Решение по такой целевой функции рассмотрим на примере нашей базовой задачи (рис. 3.3.4).
Алгоритм 2.2. Оптимизация по ресурсам
1. Вызвать таблицу с условиями задачи (рис. 2.3).
2. Ввести значения y1, у2, у3 в F2:H11.
3. Изменить знаки неравенства в ограничениях на равенства в J9:J11.
4. Ввести значения коэффициентов веса в J2:J4.
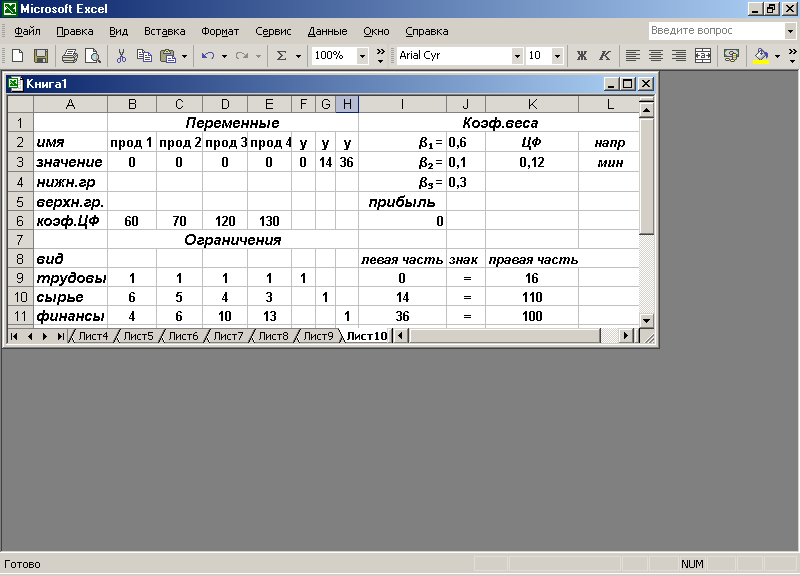
Рис. 2.3
5. Сформулировать целевую функцию
K2=(J2*F3/K9 +J3*G3/K10 + J4*H3/K11).
6. Ввести условия задачи по алгоритмам главы 3.
7. Решить задачу по алгоритмам главы 3. На экране: результат решения задачи.
Для определения влияния коэффициентов веса на результат решения задачи можно решать ее при различных значениях этих коэффициентов. Результаты решения задачи при различных коэффициентах веса приведены на рис. 2.4, из которого видно, что увеличение коэффициента веса ресурса обеспечивает его равномерное использование. Например, для финансов:
при 3=0,5 неиспользуемые финансы у3=0, т. е. финансы используются полностью, а при 3=0,2 неиспользуемые финансы у3=36.
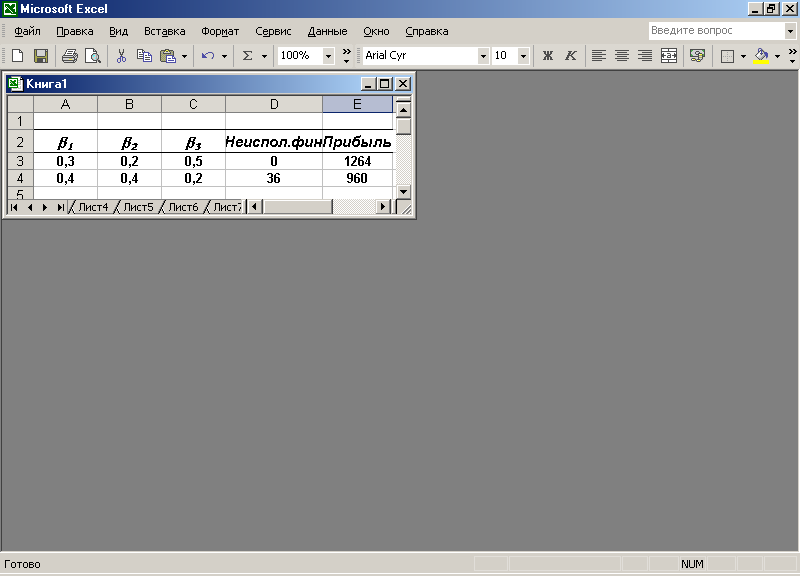
Рис. .2.4
Таким образом, назначая различные коэффициенты веса, можно получать такие оптимальные решения, которые удовлетворяют поставленным требованиям.
2.3. Метод последовательных уступок
Этот метод заключается в следующем: выбирают несколько противоречивых параметров, один из них назначают в качестве целевой функции, а для других последовательно принимаются конкретные значения. Задача оптимизации решается несколько раз при различных принятых значениях параметров. Этот метод рассмотрим на примере задачи, которая решалась в 2.2.
Алгоритм 2.3. Оптимизация методом последовательных уступок
- Вызвать таблицу с условиями задачи (рис. .2.5).
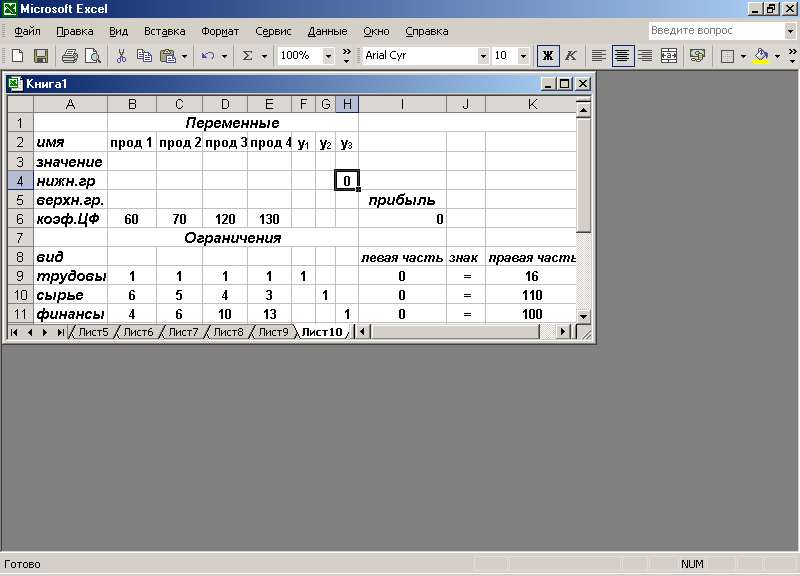
Рис. 2.5
2. Принять параметры, по которым будем решать задачу.
Принимаем в качестве целевой функции прибыль, значения которой находятся в ячейке 16, ,а в качестве задаваемого параметра — величину неиспользуемых финансов уз, значение которой вводится в ячейку ввода исходных данных Н4.
В качестве первого значения вводим у3=50.
3. Вызвать диалоговое окно Поиск решения.
4. Изменить граничные условия Y3>=Н4 на НЗ = Н4.
5. Провести параметрический анализ, вводя на каждом шаге значения неиспользуемых финансов в ячейку Н4.
Результат параметрирования показан на рис. 2.6.
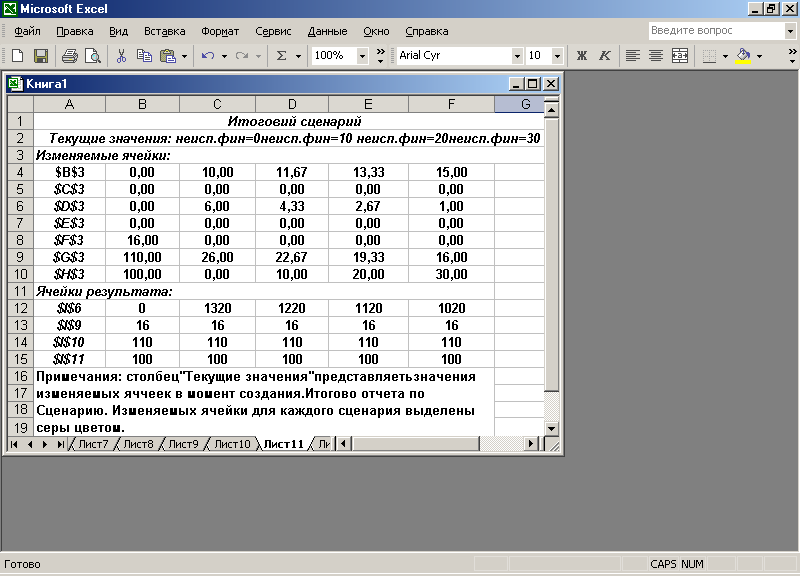
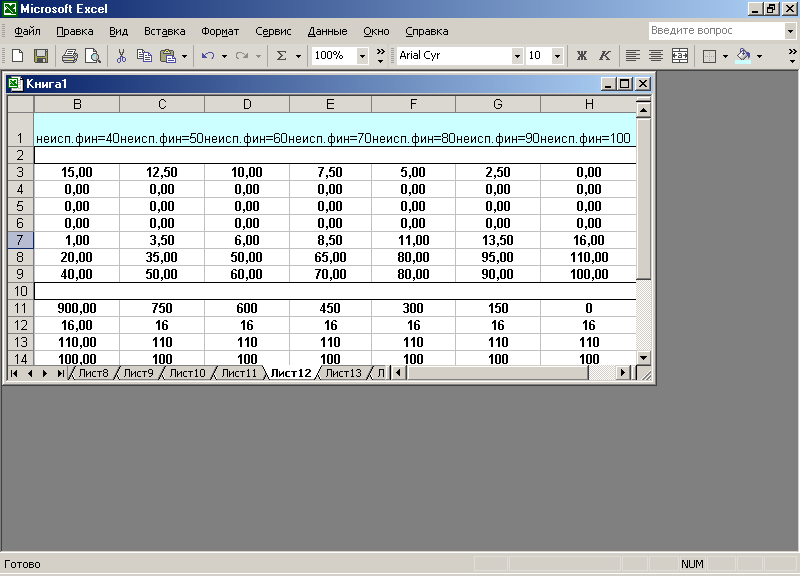
Рис. 2.6
6. Отредактировать отчет.
На экране: результат редактирования (рис. 2.7).
Для наглядного представления влияния неиспользуемых финансов на прибыль построим график.
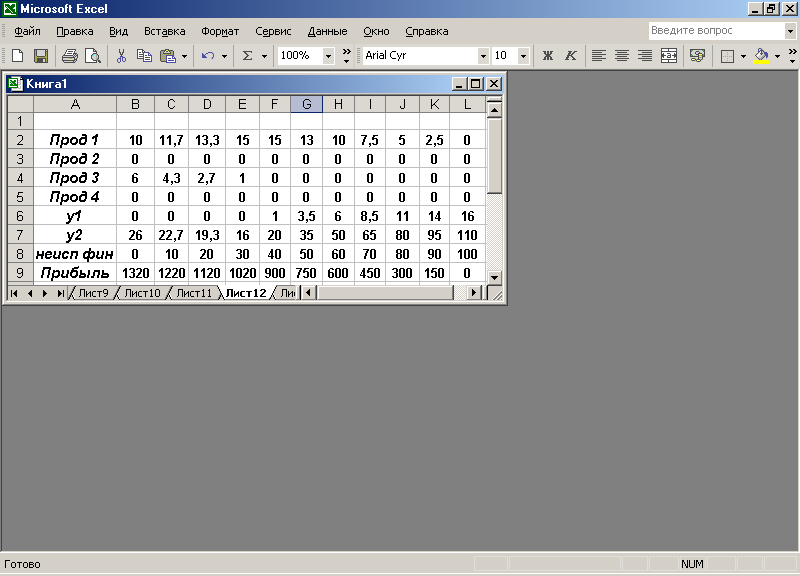
Рис. 2.7
Алгоритм 2.4. Графическое представление последовательных уступок
1. Выделить A8:L9 (рис. 7.2.7).
2. Мастер диаграмм:
> шаг 2 — График
> шаг 3 — Вид2
> шаг 4 — 1 стр. метки; 1 столб.
> шаг 5 — Убрать легенду, ввести названия графика и осей.
На экране: график последовательных уступок.
- Выполнить форматирование диаграммы. На экране: рис. 2.8.
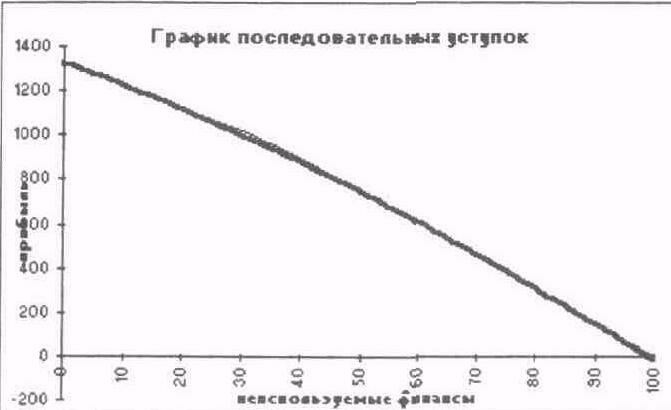
Рис. 2.8
Из таблицы (рис. 2.7) видно, что если мы хотим иметь прибыль, скажем, 1020, то при этом величина неиспользуемых финансов будет равна 30. Если же мы хотим иметь неиспользованных финансов 60, то прибыль при этом будет равна 600.
Таким образом, пользуясь этим алгоритмом и графиком, можно находить соответствующие значения искомых величин, которые могут быть полезны при анализе, выполняемом на этапе принятия оптимального решения.
