Содержание введение
| Вид материала | Реферат |
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- Содержание введение, 1420.36kb.
- Содержание Содержание 1 Введение, 82.41kb.
- Содержание разделов дисциплины, объем в лекционных часах-60 часов, 48.53kb.
- Содержание учебной дисциплины. Введение. Раздел, 159.08kb.
- Краткое содержание информационного сайта муниципального образования, 693.73kb.
- Черноиванова Наталья Николаевна г. Волгоград. 2010 г. Содержание введение 2 стр пояснительная, 184.65kb.
- Содержание Аннотация, 625.36kb.
- Содержание: стр, 753.82kb.
- Содержание введение, 283.8kb.
Двойственная задача – вспомогательная задача ЛП, формулируемая с помощью определённых правил непосредственно из исходной, или прямой задачи.
Прямая задача ЛП в стандартной форме:
максимизировать (минимизировать)
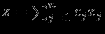
при ограничениях
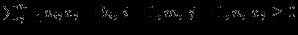
В состав включаются избыточные и остаточные переменные.
 |  | 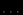 | 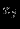 | 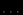 | 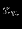 | | |
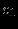 | 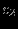 | 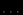 | 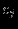 | 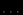 | 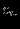 | | |
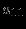 | 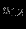 | 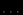 | 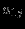 | 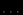 | 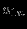 | 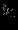 |  |
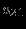 | 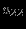 | 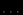 | 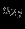 | 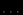 | 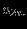 | 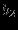 | 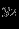 |
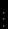 | 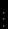 | 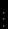 | 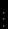 | 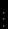 | 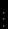 | 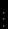 | 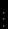 |
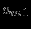 | 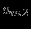 | 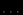 | 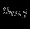 | 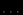 | 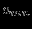 | 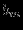 |  |
Для формулировки двойственной задачи расположим коэффициенты прямой задачи согласно схеме:
- каждому ограничению прямой задачи соответствует переменная двойственной задачи;
- каждому переменной прямой задачи соответствует ограничение двойственной задачи;
- коэффициенты при некоторой переменной, фигурирующие в ограничения прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи.
Информация о других условиях двойственной задачи (направление оптимизации, ограничения и знаки двойственных переменных) представлена в таблице:
| Прямая задача в стандартной форме. | Двойственная задача | ||
| Целевая функция | Целевая функция | Ограничения | Переменные |
| Максимизация | Минимизация | 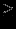 | Не ограничены в знаке |
| Минимизация | Максимизация | 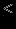 | Не ограничены в знаке |
Рассмотрим пример:
Прямая задача:
максимизировать
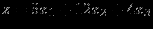
при ограничениях

Прямая задача в стандартной форме:
максимизировать
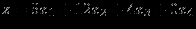
при ограничениях
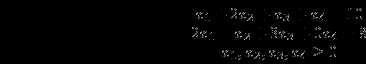
Двойственная задача:
минимизировать
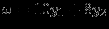
при ограничениях:
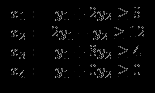
(означает, что y1>0). y1, y2 не ограничены в знаке.
Заключение
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.
Библиографический список
1.Онегов, В.А. Исследование операций. Задачи, методы, алгоритмы. – Киров: ВГПУ, 2001.
2. Сборник задач и упражнений по высшей математике: мат. программирование: Учеб. Пособие/ А.В. Кузнецов, В.А. Сакович, Н.И. Холод; Под. общ. ред. А.В. Кузнецова – Мн.: Выш. шк., 2002
3. ссылка скрыта, ссылка скрыта Линейное программирование - Издательство: Факториал Пресс, 2003.
4. Н. И. Глебов, Ю. А. Кочетов, А. В. Плясунов, Методы оптимизации учебное пособие , Новосибирск: Новосибирский государственный университет, 2000
5. etod.narod.ru/
