Метод нахождения потенциалов переноса в неподвижных плоских и цилиндрических капиллярно-пористых телах
| Вид материала | Реферат |
СодержаниеПостановка задачи. Fо и конечного косинус-преобразования Фурье по переменной Х Г=1 для решения системы (1)-(6) применено последовательно одностороннее преобразование Лапласа по Fo |
- Гидрофобная защита капиллярно-пористых строительных материалов с использованием электрохимических, 328.74kb.
- М. И. Прудников Метод триботехнических испытаний цилиндрических поверхностей трения, 168.82kb.
- Строительная механика раздел, 343.1kb.
- Стендовые доклады 15 июня секция механизмы быстрого ионного переноса в твердых телах, 425.37kb.
- Бесконтактный метод измерения электропроводности металлов, 55.62kb.
- Предлагается рассмотрение нескольких задач переноса субстанций (теплоты, массы и количества, 120.53kb.
- Предложен метод неразрушающего акустического контроля многофазных макрооднородных композитных, 14.58kb.
- Расчёт коэффициента передачи по току низкочастотного фильтра, 265.15kb.
- Лекция 1, 259.64kb.
- Изучение свойств анаэробноотверждаемых клеев в цилиндрических соединениях, 194.69kb.
УДК 517.956(075.8)
МЕТОД НАХОЖДЕНИЯ ПОТЕНЦИАЛОВ ПЕРЕНОСА В НЕПОДВИЖНЫХ ПЛОСКИХ И ЦИЛИНДРИЧЕСКИХ КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛАХ
К.А. Чуев
Губкинский институт (филиал) ГОУ ВПО «Московский государственный открытый университет», 309188 Белгородская область, г. Губкин, ул. Комсомольская д.16
kot111208@mail.ru.
С использованием одностороннего преобразования Лапласа и конечных преобразований Фурье и Ханкеля предложен метод получения аналитического решения системы уравнений линейной термодинамики, с граничными условиями третьего рода для неограниченной пластины и бесконечного цилиндра, позволяющий рассчитывать кинетику потенциалов переноса при проведении тепломассообменных процессов для них
Введение.
Математическое моделирование явлений переноса в капиллярно-пористых средах, к которым относятся значительное число материалов пищевой, химической и строительной промышленности, имеют важное значение, при модификации существующих и разработке новых технологий, и в частности в процессах сушки, увлажнения, пропитки и т.д.
Сушка влажных капиллярно-пористых тел является типичным нестационарным процессом, протекающим при наличии градиентов потенциалов переноса [1]. Известные математические модели базируются в основном, на диффузионно-фильтрационных представлениях о влагопереносе, которые формализируются в виде сопряженной системы линейных дифференциальных уравнений в частных производных А.В.Лыкова с соответствующими сопряженными краевыми условиями, выражающими суперпозицию механизмов переноса потенциалов [2].
Постановка задачи.
Как правило, при математической формулировке явлений переноса в неподвижных капиллярно-пористых средах используют три искомых потенциала: локальные влагосодержание, температура и давление. Считаем, что геометрия тел обладает симметрией. Начальные условия задаются в виде постоянных значений потенциалов, и на оси симметрии отсутствует перенос субстанции. На границе тел рассматривается дифференциальный баланс теплоты как суперпозиция механизмов переноса теплопроводностью, конвективного теплообмена с окружающей средой с учетом фазовых превращений, а также дифференциальный баланс массы как суперпозиция механизмов переноса диффузией, термодиффузией, бародиффузией и конвективным массообменном. [1]. В этом случае система принимает вид:
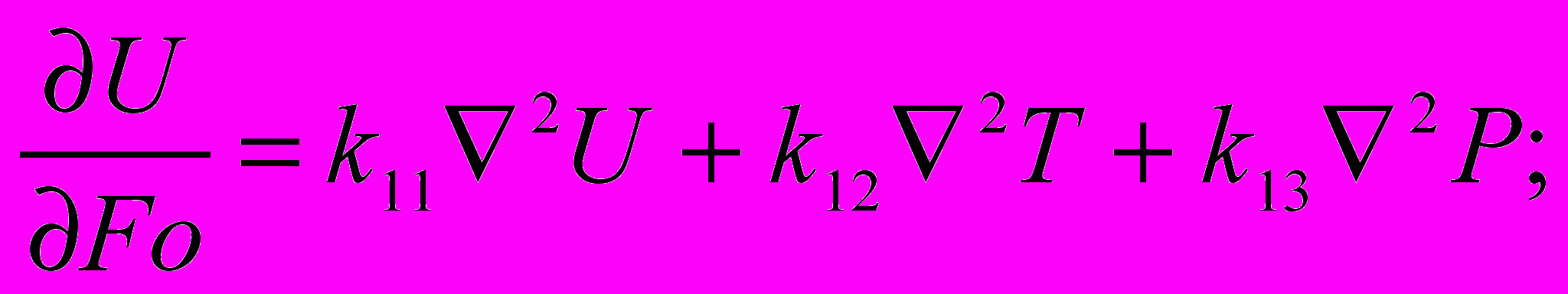 (1)
(1)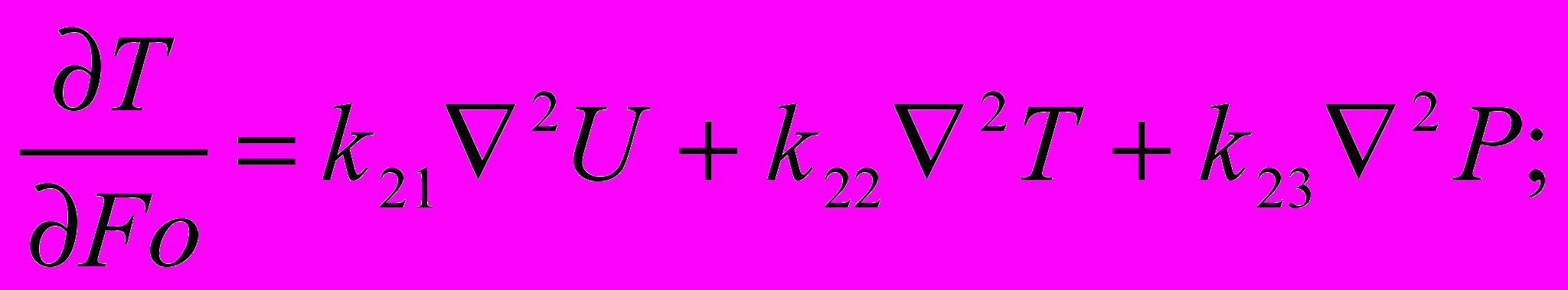 (2)
(2) (3)
(3)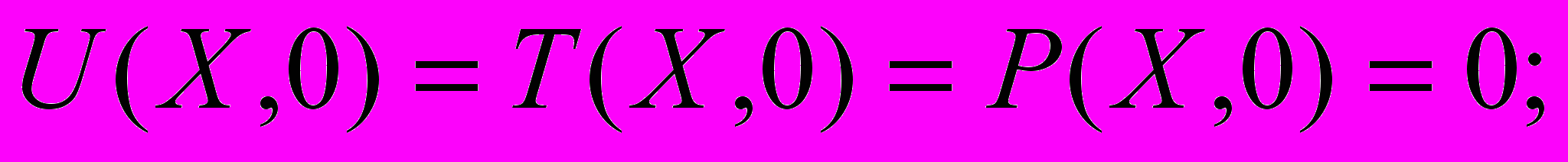 (4)
(4)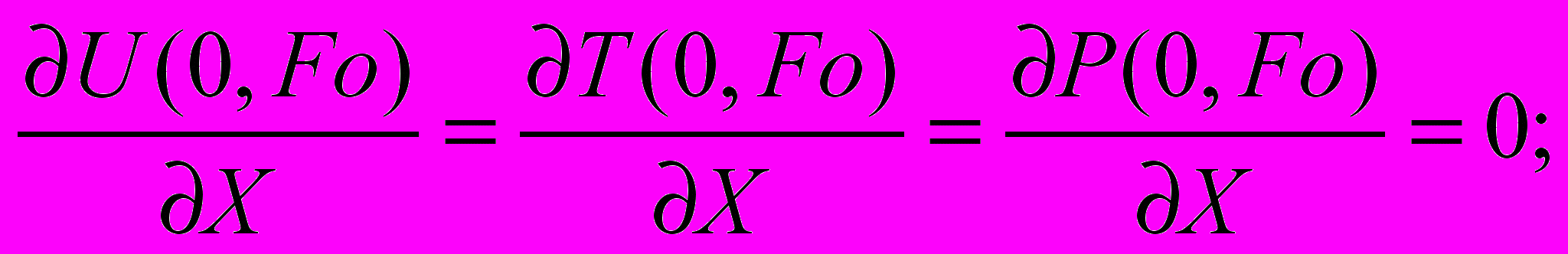 (5)
(5)
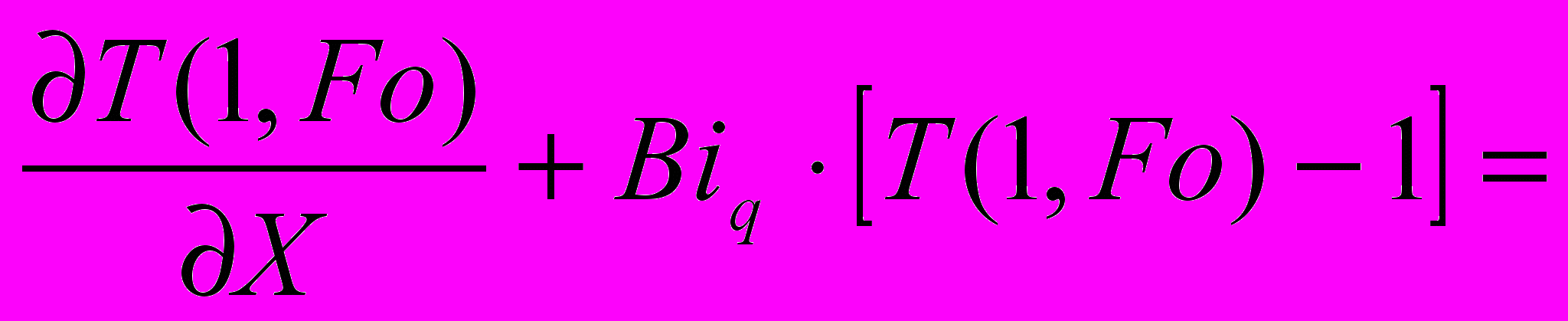
 (6)
(6) 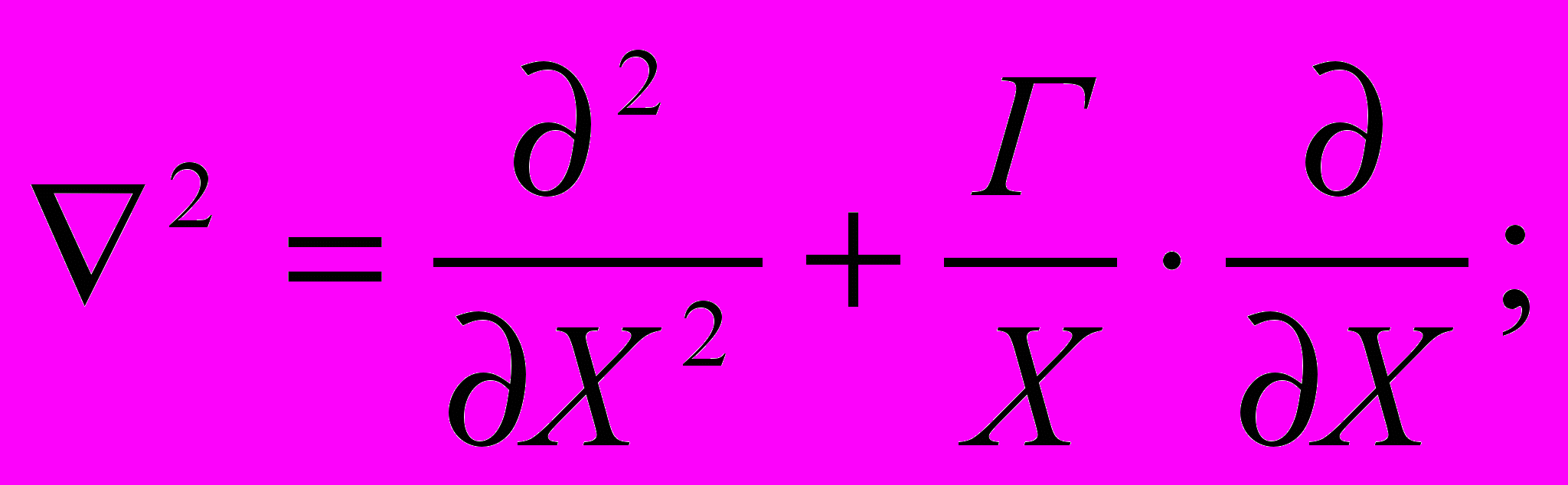
где Fo– безразмерный критерий Фурье,
 постоянные коэффициенты переноса, Bim, Biq, BiP – массообменное, теплообменное и фильтрационные числа Био; Г- постоянная формы, равная для неограниченной пластины нулю, для бесконечного цилиндра – единице; U,T,P-относительные влагосодержание, температура и давление.
постоянные коэффициенты переноса, Bim, Biq, BiP – массообменное, теплообменное и фильтрационные числа Био; Г- постоянная формы, равная для неограниченной пластины нулю, для бесконечного цилиндра – единице; U,T,P-относительные влагосодержание, температура и давление.Алгоритм решения.
1) При Г=0 последовательным применением одностороннего преобразования Лапласа [3] по переменной Fо и конечного косинус-преобразования Фурье по переменной Х с характеристическим уравнением
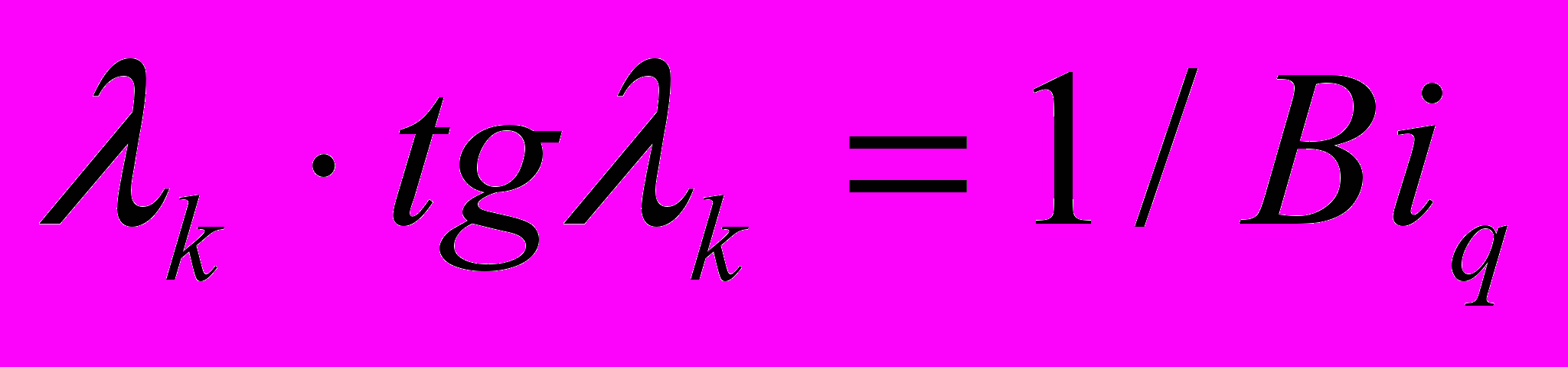 система (1)-(6) становится алгебраической относительно изображений потенциалов, после решения которой получен результат в векторной форме в пространстве оригиналов с неизвестными U(1,Fo), P(1,Fo):
система (1)-(6) становится алгебраической относительно изображений потенциалов, после решения которой получен результат в векторной форме в пространстве оригиналов с неизвестными U(1,Fo), P(1,Fo):
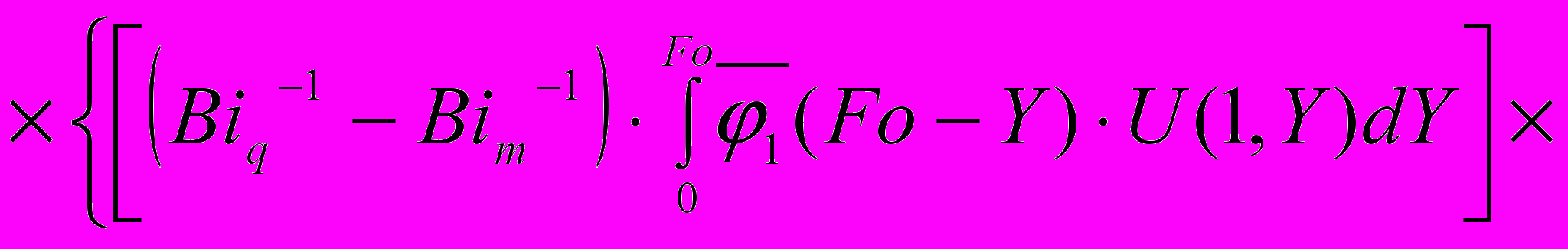
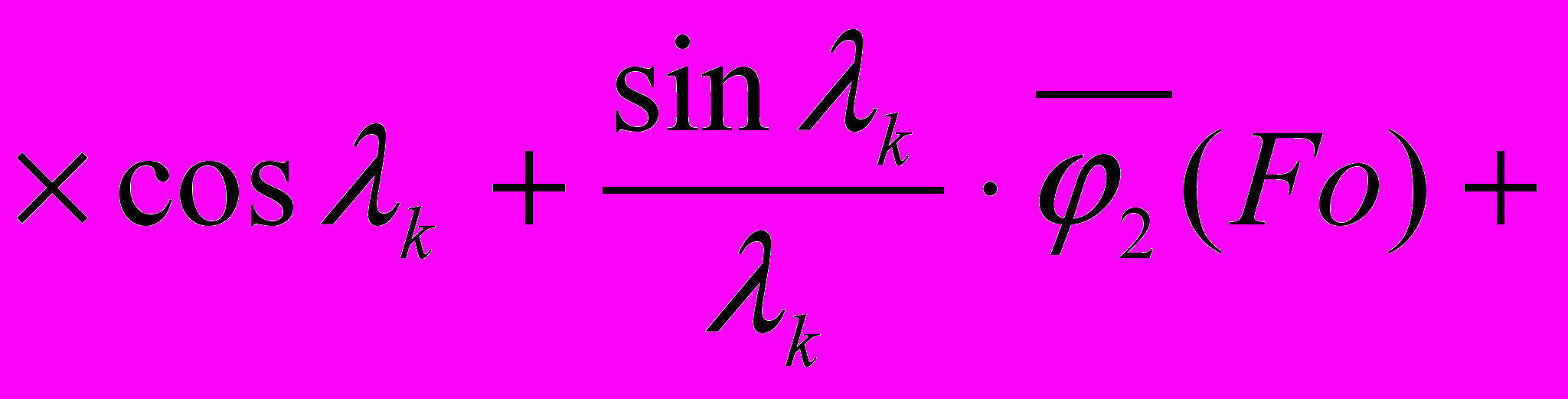
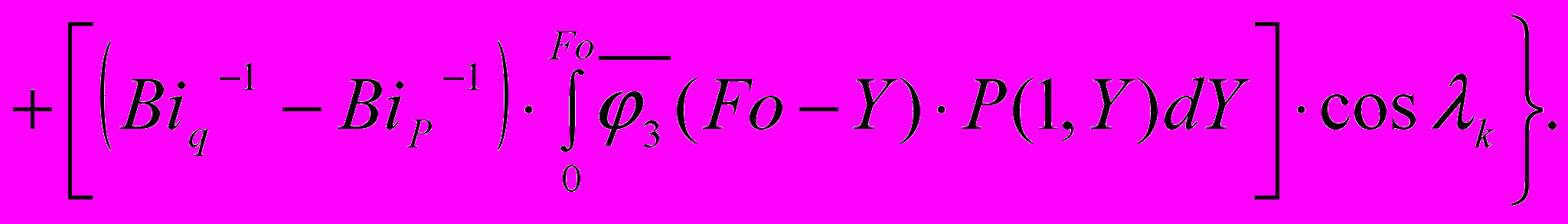 (7)
(7)где
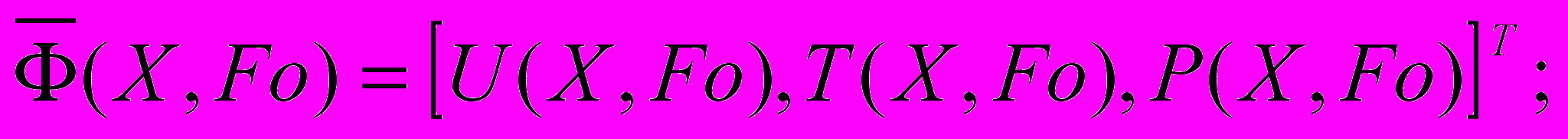
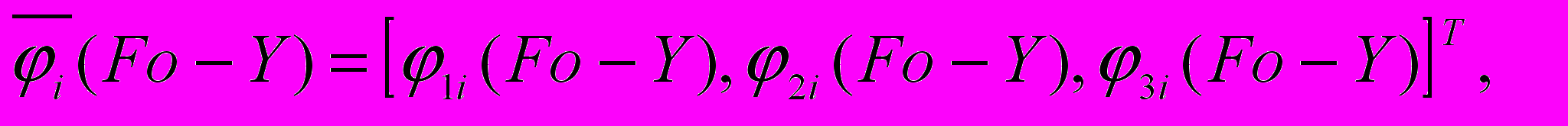
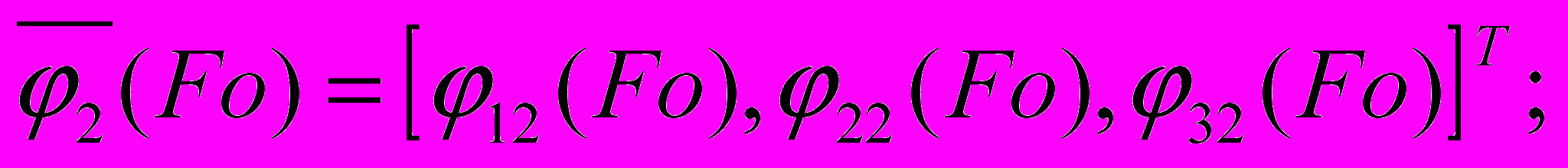
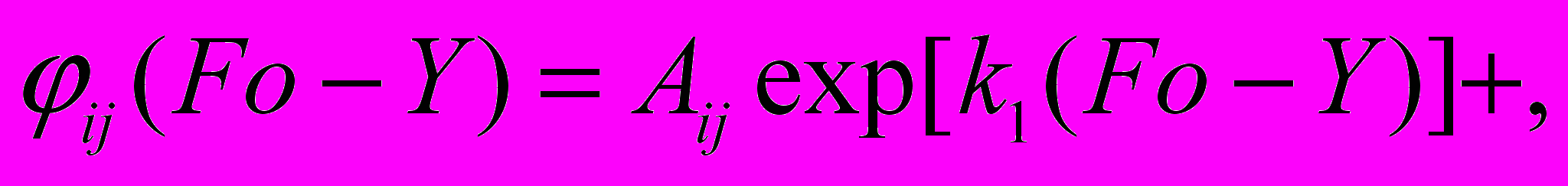

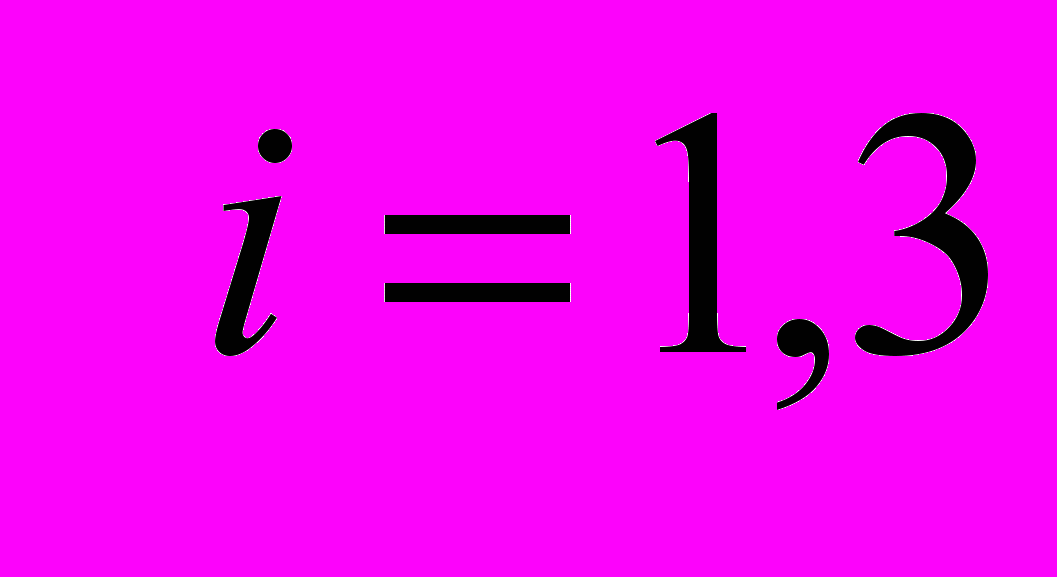
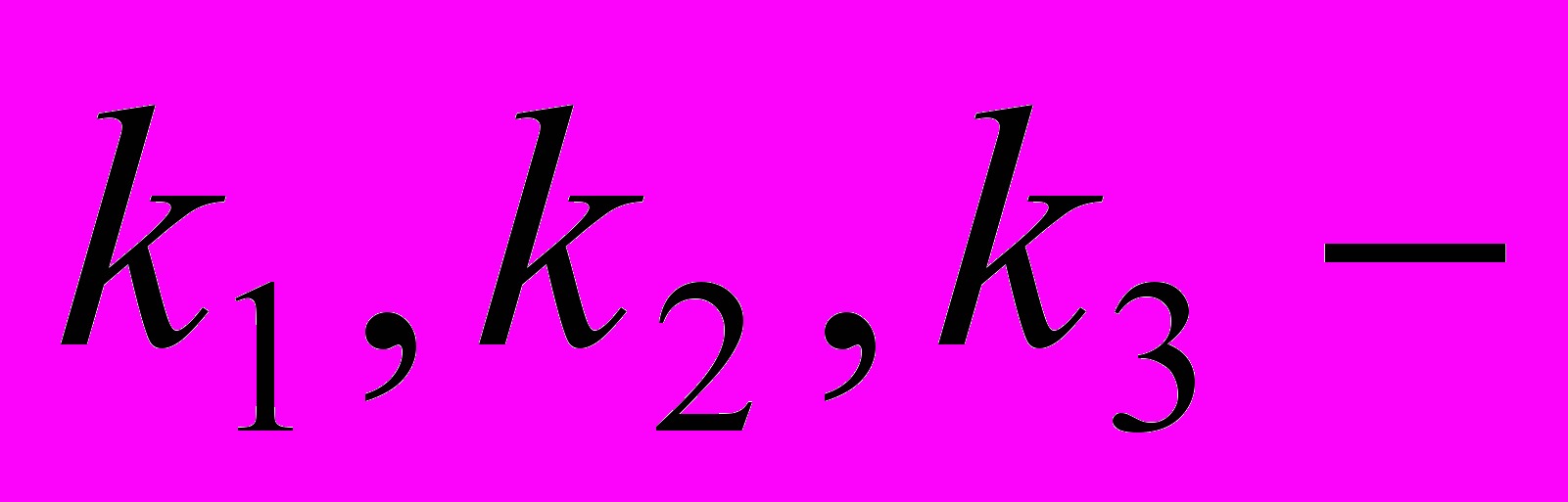 корни уравнения:
корни уравнения: 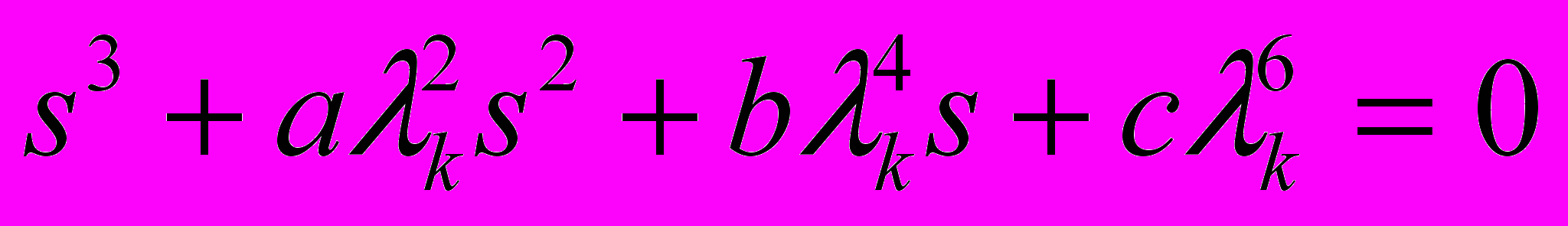 ; (8)
; (8) постоянные коэффициенты, зависящие от определяющих критериев задачи.
постоянные коэффициенты, зависящие от определяющих критериев задачи.Если в (7) положить Х=1, то получим систему интегральных уравнений [4] типа Вольтера], относительно
 . Вновь переходя к изображениям по Лапласу, решение при переходе к оригиналам, с учетом свертки [3], имеет вид:
. Вновь переходя к изображениям по Лапласу, решение при переходе к оригиналам, с учетом свертки [3], имеет вид: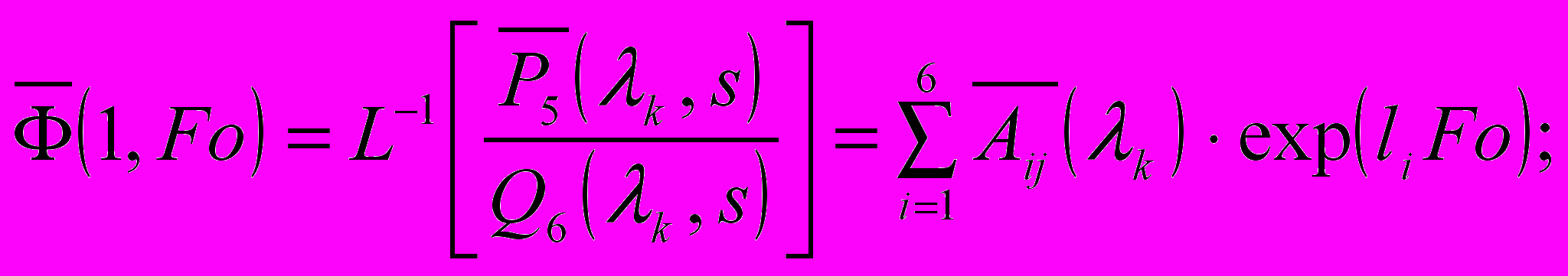
 (9)
(9)где
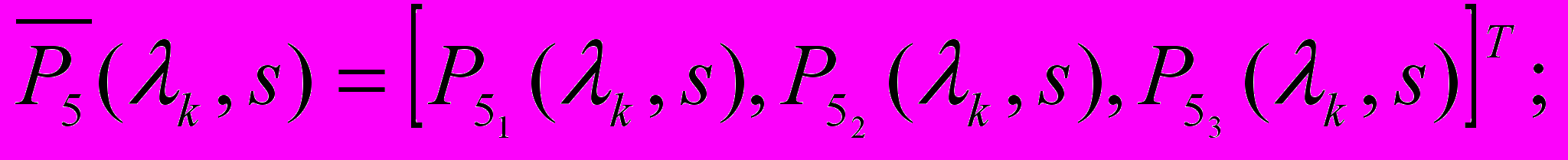
 соответственно полиномы пятой и шестой степени s с коэффициентами, зависящими от
соответственно полиномы пятой и шестой степени s с коэффициентами, зависящими от 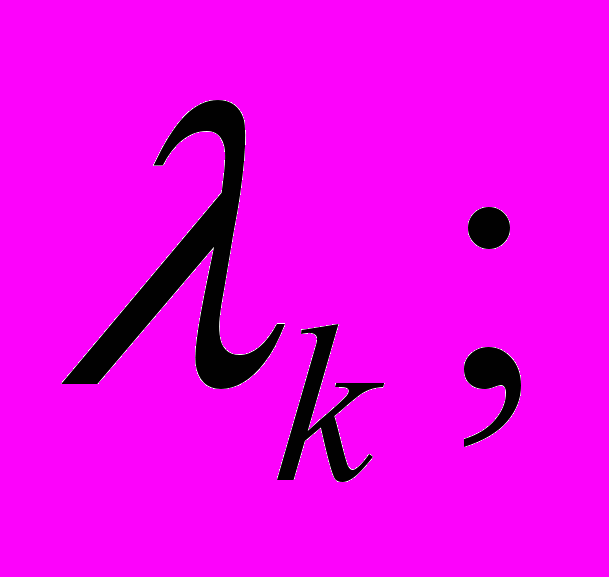
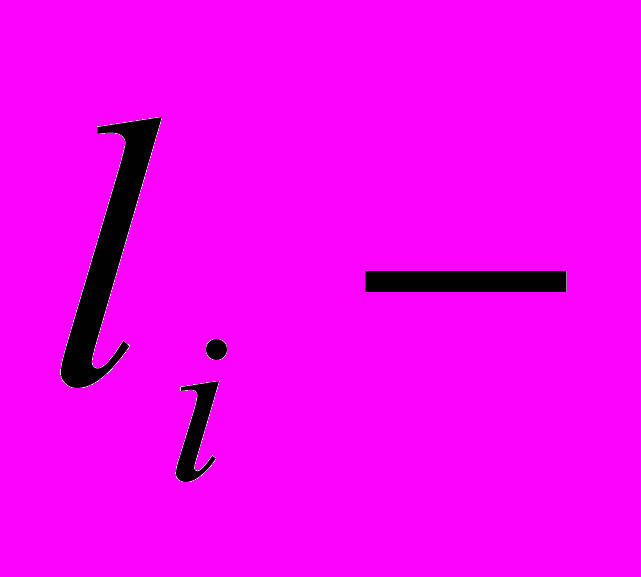 корни уравнения
корни уравнения 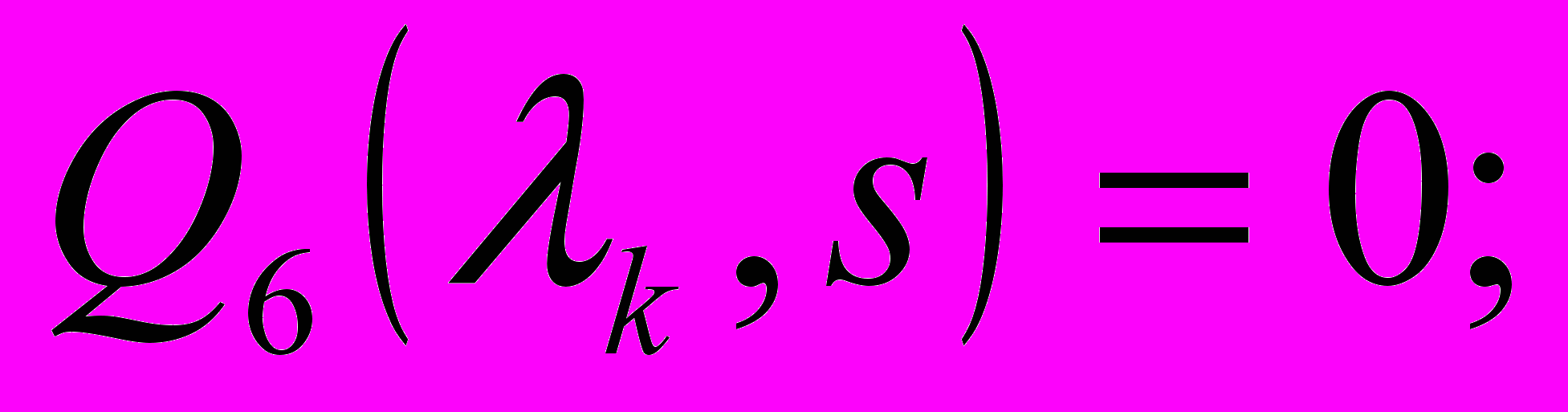
 вектор постоянных. С учетом (9) выражение (7) является решением системы (1)-(6), причем верхний предел суммы, заменяется на конечное число N для обеспечения заданной точности.
вектор постоянных. С учетом (9) выражение (7) является решением системы (1)-(6), причем верхний предел суммы, заменяется на конечное число N для обеспечения заданной точности.Исходя из физического смысла задачи, корни уравнения (8) должны быть либо тремя действительными отрицательными, либо одним отрицательным и двумя комплексно-сопряженными с отрицательной действительной частью. Аналогичные рассуждения применимы и для корней
 уравнения
уравнения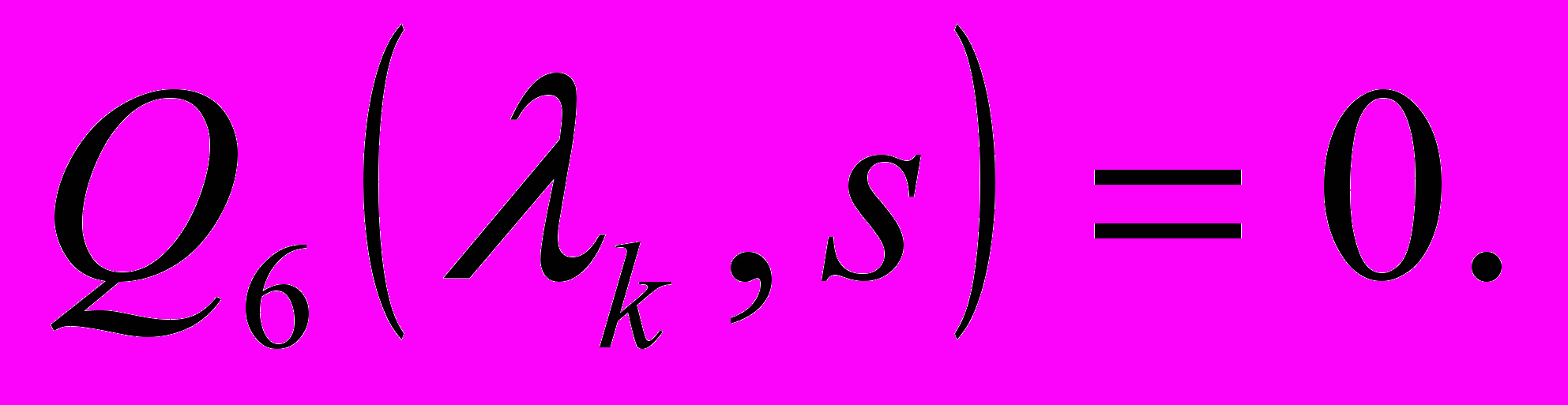
2) При Г=1 для решения системы (1)-(6) применено последовательно одностороннее преобразование Лапласа по Fo и конечное интегральное преобразование Ханкеля по Х с характеристическим уравнением
 , где
, где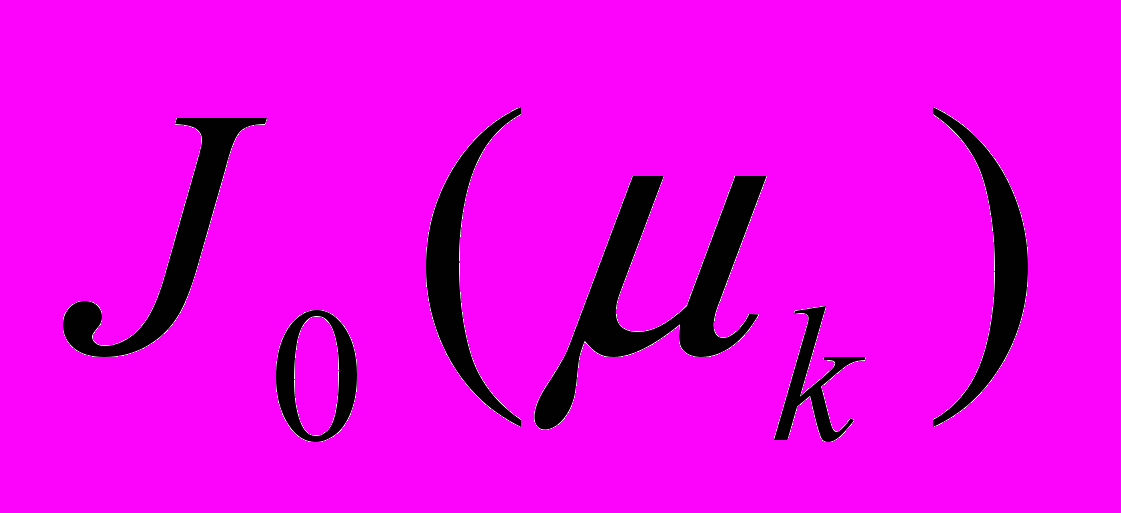 ,
,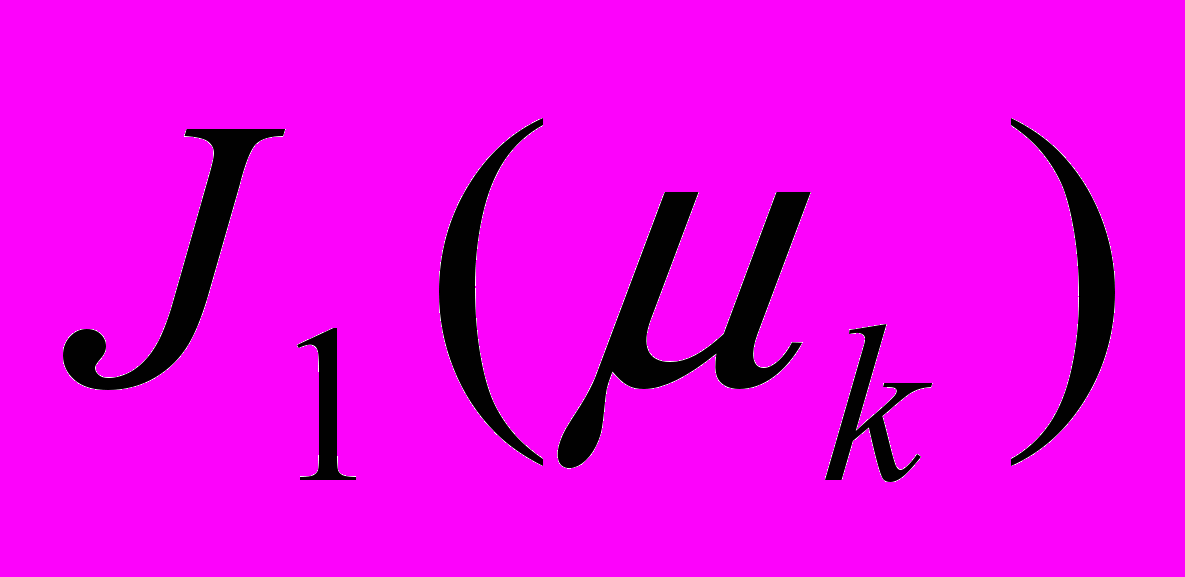 – функции Бесселя первого рода нулевого и первого порядков. Действуя аналогичным образом по предыдущему алгоритму, получено решение системы (1)-(6):
– функции Бесселя первого рода нулевого и первого порядков. Действуя аналогичным образом по предыдущему алгоритму, получено решение системы (1)-(6):


 (10)
(10)Используя для безразмерных критериев, диапазоны изменения, полученные на основе анализа физико-химических свойств ряда капиллярно-пористых материалов показано, что корни характеристических уравнений в подавляющем своем большинстве удовлетворяют наложенным условиям физичности. Это означает, что система (1)-(3) может быть классифицирована как система уравнений в частных производных параболического типа по Хеллвигу.
Выводы.
Полученные результаты, в виде формул (7), (10) представлены сходящимися рядами, удобны для практических расчетов. В суммах можно ограничится 8-10 членами ряда, из-за их быстрой сходимости. Предложенный подход может быть адаптирован для шара (случай Г=2). Предложенный метод позволяет избежать использование не вполне обоснованных численных технологий в смысле аппроксимации, устойчивости и сходимости.
Литература
1. Лыков А. В. Тепломассообмен: (Справочник) – М.: Энергия, 1978. – 480 с.
2. Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. – М.: Высшая школа, 2001. – 550 с.
3. Деч Г. Руководство к практическому применению преобразования Лапласа и z-преобразования. – М.: Фмзматгиз. 1971. 288 с.
4. Петровский Н.Г. Лекции по интегральным уравнениям. – М.: Наука. 1965. - 246 с.
A METHOD FOR FINDING POTENTIAL TRANSFER TO THE FIXED PLANE AND CYLINDRICAL CAPILLARY-POROUS BODICS
K.A. Chuev
Gibkin Institure (branch) GOU VPO «Moscow State Open University»
With one-sided Laplace transform and finite Fourier transform and Hankel proposed a method for obtaining analytical solutions of linear systems of equations of thermodycal, with the boundary conditions of the third kind for an infinite plate and infinite cylinder, allowing to calculate the kinetics of the potential transfer of heat and mass transfer during the process for them
