В. И. Молчанов Проектирование червячных передач с колёсами из неметаллических материалов Учебное пособие

Вид материала

Таблица 1.1 - Основные характеристики неметаллических материалов, применяемых для изготовления червячных колёс
2.1 Свойства капролона и определение допускаемых напряжений
2.2 Исходные червяки для метало полимерных червячных передач
2.3 Расчёт зубчатого колеса на прочность при изгибе

Подобный материал:

1 2 3

Таблица 1.1 - Основные характеристики неметаллических материалов, применяемых для изготовления червячных колёс

Материал	Плотность, кг/м³	σ_B_{, МПа}	Е ∙ 10^-3 ^МПа	НВ, МПа	Тепло- стой- кость, ˚С	Коэффи- циент теплопро- водности λ (при 20˚С), Вт/(м ˚С)
Текстолит Капрон Капролон В Древеснослоистый пластик ДСП-Г Полиамидная смола	1300…1400 1130 1160 1300 …	100 60…70 90…95 100…110 40…50	10 1,5 2…3 1…2,5 1,2	250…350 100…120 200…250 250 140…150	120…125 180…260 215…220 150…170 205…210	0,25…0,35 0,30 1,2 … …

Примечание. Колёса из капрона и капролона менее чувствительны к погрешностям изготовления и монтажа, лучше прирабатываются, наматывания материала на червяк не наблюдаются.

Наибольшее распространение в отечественной промышленности нашёл капрон. Но так как основным потребителем этого полимера является промышленность синтетических волокон, то на долю машиностроения приходится только незначительная часть общего объёма производства капрона.В связи с этим большой интерес представляет в настоящее время новый полимер - капролон.

Капролон получается путём химического формования, представляющего собой способ изготовления изделий, при котором исходным веществом является мономер, а полимер в виде готовых изделий, монолитных блоков или заготовок получается непосредственно в форме. При химическом формовании устраняются технологические операции, связанные с получением полимера в виде гранул с дальнейшей переработкой его в изделия литьём под давлением.

В России капролон выпускается по техническим условиям ТУ 6-05-983-73 в виде блоков и заготовок, из которых методом механической обработки изготавливаются изделия конструкционного и антифрикционного назначения большого веса и габаритов. Основным недостатком такой технологии является наличие значительного количества отходов в виде стружки и обрезков. При получении из блоков деталей антифрикционного назначения (втулки, вкладыши и пр.) количество отходов достигает 70% от веса блока, а при фрезеровании венцов червячных колёс – 50%. В зарубежной практике подобные изделия типа труб получаются методом центробежного формования, который в отечественной промышленности пока не нашёл достаточного развития как метод переработки пластмасс в изделия.

1.3 Расчёт и конструирование червячных колёс из неметаллических материалов

1.3.1 Критерии работоспособности

Основными видами разрушений, ограничивающими нагрузочную способность червячных передач с пластмассовыми колесами, являются усталостный излом зуба у основания, обусловленный концентрацией напряжений, и повреждение рабочей поверхности зубьев, происходящее вследствие износа или прогрессирующего усталостного выкрашивания. Реже встречаются разрушения зубьев, вызванные износом, пластической деформацией и заеданием.

Характер разрушения зависит от многочисленных геометрических, технологических и эксплуатационных факторов, включающих форму и размеры зуба, точность изготовления и монтажа, шероховатость и твердость рабочих поверхностей, наличие концентраторов, остаточных напряжений и т. п., а также величину нагрузки, характер нагружения и скорость деформирования, свойства окружающей среды, требуемый срок службы и другие факторы.

Передачи с червячными колёсами из ДСП-Г часто рассчитывают на износ рабочих поверхностей зубьев и прочность при изгибе, передачи из текстолита - на износ, прочность при изгибе и контактную прочность зубьев, передачи из капрона и других полиамидов – на прочность при изгибе. Однако в каждом отдельном случае конструктор определяет порядок расчёта в зависимости от ответственности и режима работы передачи.

Контактные напряжения можно, с известными допущениями, определить из задачи Герца для случая сжатия двух цилиндров, соприкасающейся по общей образующей. Приближённость решения этой задачи объясняется тем, что пластмассы под нагрузкой не следуют точно закону Гука, и поэтому значения модуля упругости непостоянны. Различны также значения коэффициента Пуассона. Коэффициент Пуассона для текстолита и ДСП примерно равен 0,2, а для полиамидов 0,44.

1.3.2 Особенности расчёта червячных передач с колёсами из неметаллических материалов

Длительная прочность полимерных конструкций является дока недостаточно изученной. Как указывается в работах [10, 11], учет фактора времени в расчете на длительную прочность возможен либо заменой предельных характеристик прочности в уравнениях кратковременной прочности функциями времени разрушения при одномерном нагружении, либо представлением выбранного критерия кратковременной прочности выражением для эквивалентного напряжения, вводимого затем вместо напряжения при линейном растяжении (сжатии) в формулу для расчета времени до разрушения. Предел долговременной прочности можно определить по диаграммам долговременной прочности для ожидаемой длительности нагружения.

В связи с резко выраженной температурно-временной зависимостью деформационных свойств пластмасс и существенном изменением формы и размеров пластмассовых деталей при нагружении во многих случаях более приемлемым критерием оценки их несущей способности является результат расчета по допустимым перемещениям, которые рассчитываются из условий функциональной взаимозаменяемости. Считают (см., например, [12]), что выбор размеров нагруженных пластмассовых деталей на основе гипотезы предельных деформаций является предпочтительным. Конструктивная определенность деталей, выполненных по 5…7-му классу точности, сохраняется при изменении размеров до 3…4% (соответственно 3…4-й класс — 0,5…1%) [13]. Удовлетворительная работа деталей из пластмасс обеспечивается при остаточных деформациях 1…2% для термопластов и 0,1% для реактопластов. Допускаемые напряжения, определенные исходя из приведенных значений допустимых деформаций, обеспечивают устойчивое сохранение конструктивной определенности пластмассовой детали.

Для умеренно нагруженных червячных колёс срок службы практически не ограничивается прочностью. В деталях, для которых характерно протекание релаксационных процессов, напряжения снижаются с течением времени. В нагруженных зубьях деформация постоянно возрастает и в определенный момент времени достигается ее предельное значение. При циклических нагрузках в случае, если наибольшая деформация не превышает значения предельной деформации текучести ε_max≤ε_T, материал не повреждается. Если интервалы между циклами действия нагрузки достаточно велики, происходит восстановление первоначальной формы зуба. Длительность нагружения в этом случае принимается равной времени, в течение которого достигается максимальная величина деформации t_Σ = mах(Δt_1, Δt_{2, …,}Δt_n). В случае, когда наибольшая деформация превышает деформацию текучести (ε_max>ε_т), происходит постоянное накопление повреждений материала вследствие образования микротрещин или вытяжки. Длительность нагружения определяется суммированием всех циклов нагружения:

N

t_Σ= ΣΔt_i.

i =1

Одним из основных видов расчета червячных колес на прочность является расчет зубьев на изгиб, при котором наиболее характерно проявляется специфика поведения пластмасс под нагрузкой. Эта специфика определяется в первую очередь раз-носопротивляемостью материала растяжению и сжатию и зависимостью напряжения изгиба от скорости (частоты) деформирования.

1.3.3 Конструирование червячных колёс из неметаллических материалов

В ряде случаев (в редукторах небольшой мощности) при скорости скольжения υ < 4м/с пластмассы можно применять в червячных передачах для замены бронзы и других сплавов цветных металлов (рис. 1.1). КПД двухзаходных червячныхредукторов с венцами из ДСП-Г незначительно отличается от КПД аналогичных редукторов с венцами из бронзы Бр А9Ж4.

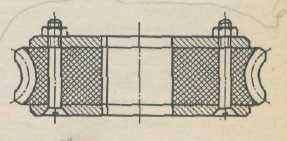
Рисунок 1.1 – Червячное колесо из ДСП-Г

Нагрузочная способность и допускаемые контактные напряжения для червячных передач с венцами из ДСП-Г и других пластиков нужно определить из условия ограничения температуры нагрева в зависимости от скорости скольжения.

Максимальная мощность при непрерывном режиме длительной работы для венцов из ДСП-Г может быть достигнута при температуре масла не свыше 70…75°С и скорости скольжения υ < 1,5…1,7 м/с.

Конструкция червячного колеса должна соответствовать его назначению, обеспечивать работоспособность колеса в заданных условиях эксплуатации. Важным требованием является технологичность конструкции, что позволяет экономить материал, упростить формующий инструмент и оснастку, снизить стоимость изготовления. Прочность, надежность и долговечность передачи зависят от применяемого материала, размеров червячных колес, наличия и расположения арматуры, точности изготовления и других факторов. Получить конструкцию, удовлетворяющую предъявленным к ней требованиям, можно лишь при условии полного учета специфических особенностей физико-механических и технологических свойств полимерных материалов.

Одним из перспективных путей повышения несущей способности полимерных червячных колес и их эксплуатационных характеристик является использование металлических армирующих элементов. Армированием пластмассовых червячных колес металлом достигаются увеличение изломной прочности зубьев, усиление прочности и надежности соединения червячного, колеса с валом, повышение стабильности размеров пластмассового венца, снижение расхода полимерного материала, повышение технологичности изготовления передач и снижение _х себестоимости зубчатой передачи.

Решение этой задачи состоит в использовании арматуры, усиливающей каждый зуб колеса в отдельности.

Наиболее верными представляются конструктивные решения, основанные на введении армирующего элемента непосредственно в тело полимерного зуба. Примером такого решения может служить конструкция капролонового колеса, представленная на рисунке 1.2 [14].

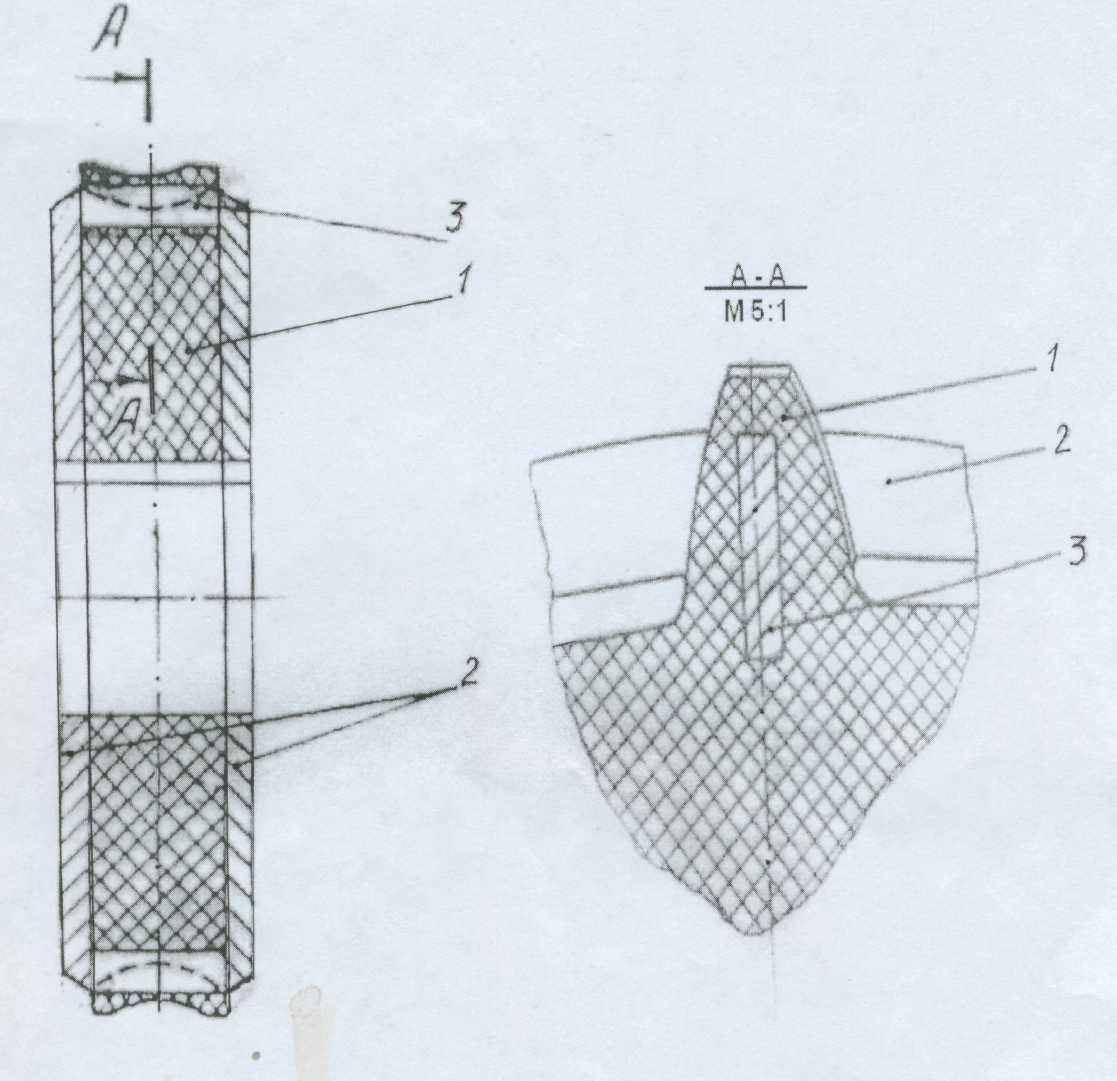
Рисунок 1.2 – Армированное червячное колесо

В процессе передачи от витков червяка вращающего момента все зубья полимерного корпуса 1 поочерёдно нагружаются, при этом, благодаря наличию рёбер 3 и металлических дисков 2, усиливается каждый зуб колеса в отдельности.

В результате повышается изломная прочность зубьев и долговечность передачи в целом.

Кроме этого, предлагаемая конструкция колеса повысит жёсткость и стабильность размеров пластмассового венца при сохранении прочности и надёжности соединения червячного колеса с валом. Колесо из полимерного материала (капролона В) с упрочняющими рёбрами испытано в различных конструкциях и показало, что долговечность его повышается в 2,5 раза.

2 Методичка расчёта на прочность червячных цилиндрических передач с колёсами из капролона

2.1 Свойства капролона и определение допускаемых напряжений

Основные свойства капролона В как конструкционного материала приведены в таблице 2.1.

Таблица 2.1 – Физико-механические и термические свойства капролона В конструкционного назначения.

Показатель

Капролон В (ТУ 6-05-983-73)

Плотность ρ, кг/м³

Температура плавления Т_пл, °С

Теплостойкость по Мартенсу Т_м, °С

Теплостойкость по ВИКА Т_в, °С

Предел прочности, МПа:

при растяжении σ_р

при сжатии σ_сж

при изгибе σ_и

Относительное удлинение при разрыве ε_отн, %

Модуль упругости при растяжении Е_р, ГПа

Ударная вязкость, кДж/м²:

без надреза

с надрезом

Твёрдость по Бринеллю НВ, МПа

Водопоглащение за 24 ч Вп₂₄, %

Водопоглащение максимальное Вп_max_, %

1150…1160

220…225

75…76(60…75*)

190..220

90..95

100…110

120…150

6…20

2,060…2,310

100…150

4…6

200…250

1,5…2,0

6…7

* Температура размягчения при изгибе.

Колёса из капролона менее чувствительны к погрешностям изготовления и монтажа, лучше прирабатываются, наматывания материала на червяк не наблюдается. Однако область применения червячных передач с колёсами из капролона ограничивается относительно невысокой их несущей способностью (Т₂= 160…210Нм), лимитируемой изгибной выносливостью зубьев [2].

Допускаемое напряжение при расчёте на выносливость при изгибе рассчитывается по формуле:

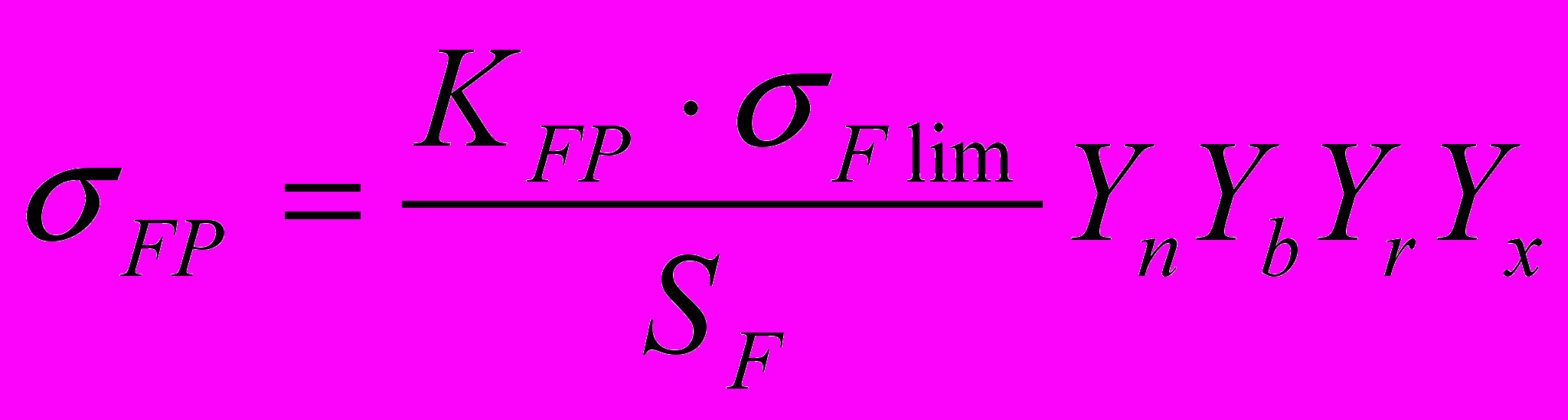, (2.1)

где σ_Flim– условный предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемен напряжений для исходной передачи, Нм. Его значения, определённые эквивалентно, следует принимать: 44,7 и 45,4 МПа – соответственно для передач с исходным червяком по ГОСТ 19036-81 (зуб колеса нормальной толщины) и утоненным витком червяка (зуб колеса утолщённый).

Коэффициент К_FP характеризует отношение условных пределов изгибной выносливости для проектируемой и исходной передач, т.е. К_FP = σ*_Flim/σ_Flim. При этом, если σ*_Flim > σ_Flim, то значение коэффициента К_FP принимается равным 1.

Коэффициент безопасности S_F для полиамидных червячных колёс следует принимать при постоянной нагрузке равным 2…2,7, знакопеременной – 3…4.

Коэффициент долговечности Y_N определяется по формуле:

,

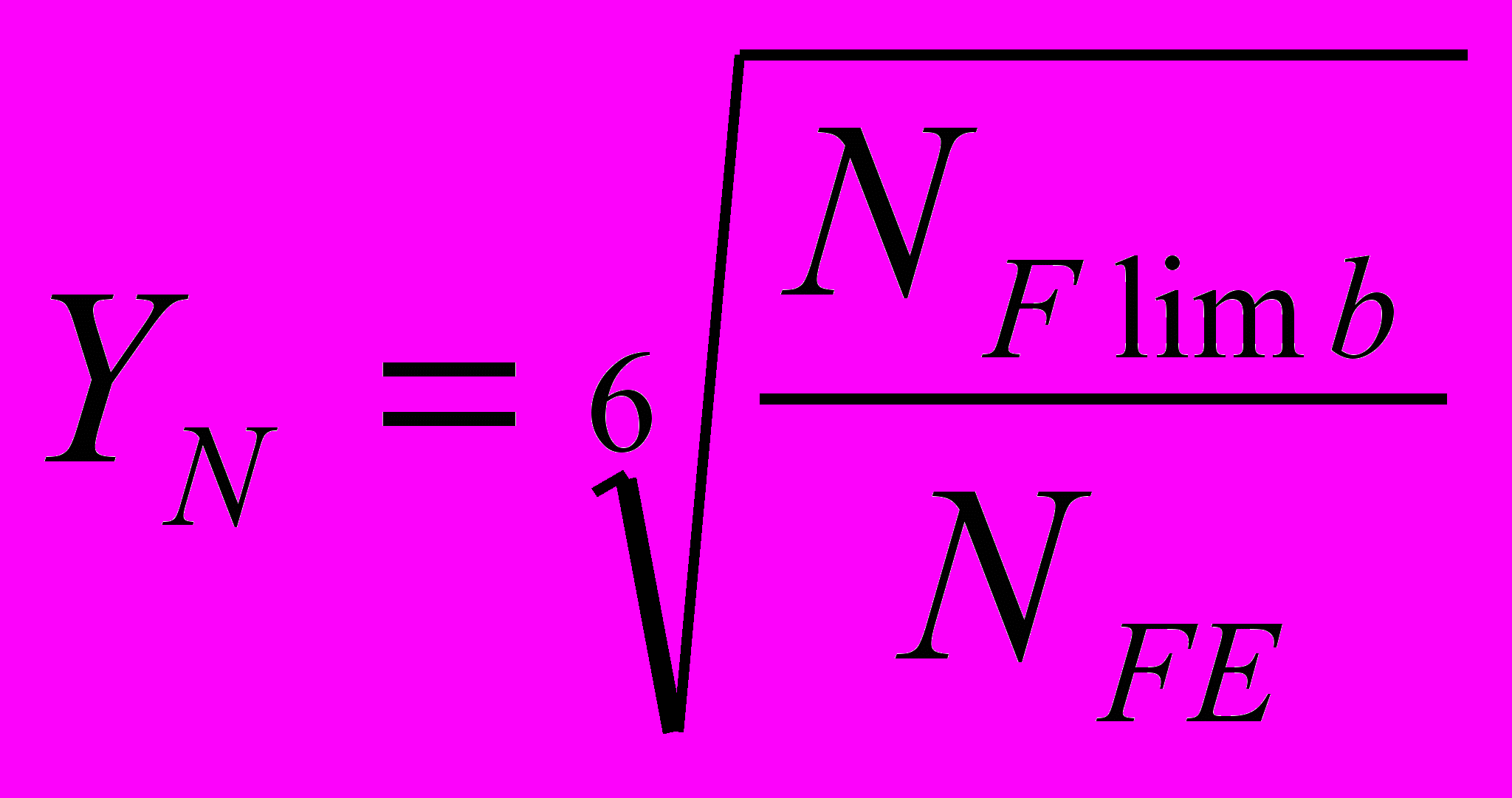где N_Flimb – условное базовое число циклов перемен напряжений, для капролона N_Flimb= 10⁶; N_FE – эквивалентное число циклов перемен напряжений. Так как большинство червячных передач работает при длительных нагрузках, близких к постоянным, то N_FE = 60n₂t, где n₂ – частота вращения червячного колеса, мин^-1; t – время работы на данном режиме за период эксплуатации, ч.

Коэффициент Y_b, учитывающий градиент напряжений и чувствительность материала к концентрации напряжений (опорный коэффициент), можно принимать для капролоновых колёс равным 1,3.

Учёт шероховатости переходной поверхности (коэффициент Y_R) и размеров червячного колеса (коэффициент Y_X) производится следующим образом: при шероховатости поверхности R_Z≤ 40 мкм Y_R = 1, а Y_X= 1,05 – 0,000125d₂, где d₂– делительный диаметр червячного колеса.

2.2 Исходные червяки для метало полимерных червячных передач

При выборе рационального исходного червяка для металлополимерной червячной передачи, обеспечивающего её максимальную несущую способность, необходимо руководствоваться следующими условиями:

полимерный зуб колеса и металлический виток червяка должны быть равно прочными по излому;

переходная кривая у излома зуба долджна иметь такой радиус, при котором концентрация напряжений минимальна.

Исходя из указанных особенностей и условий, на основе параметров исходного червяка по ГОСТ 19036-81, были разработаны два исходных червяка ZA для металлополимерных червячных передач. Один из них имеет утолщённый на величину 0,348 модуля зуб колеса и стандартный угол профиля α_x = 20°, а другой – утолщённый на 0,545 модуля зуб при угле профиля α_x= 15° (рисунок 2.1). Переходные кривые у оснований зубьев полностью скруглены с целью уменьшения концентрации напряжений.

Новые исходные червяки обеспечивают возможность повышения изломной прочности пластмассового зуба колеса за счёт избыточной прочности металлического витка соответственно на 35 и 12,5%. Они предназначены для сочетания материалов сталь-капролон в в диапазоне рабочих температур при длительной эксплуатации (-60)…(+60)°С.

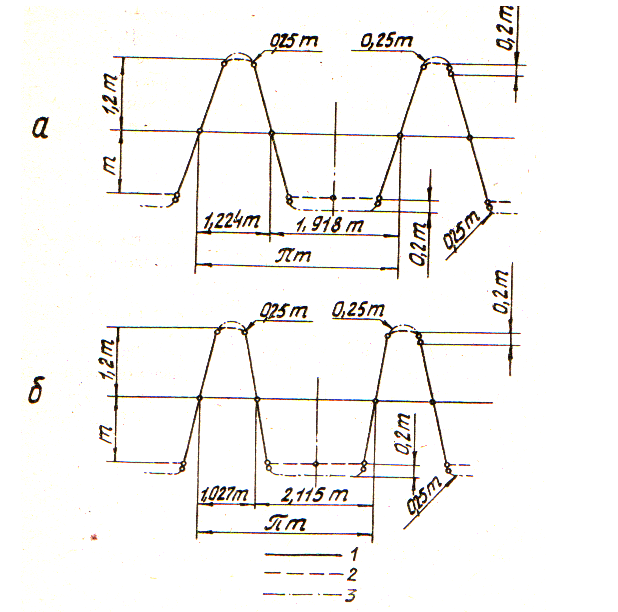
Рисунок 2.1 – Исходные червяки для металлополимерных червячных передач:

а – с утолщённым зубом при α_х = 20˚;

б – с утолщённым зубо при α_х= 15˚;

1 – совпадающие контуры витков исходного червяка и исходного производящего червяка, 2 – контур витков исходного червяка, 3 – контур витков исходного производящего червяка

2.3 Расчёт зубчатого колеса на прочность при изгибе

В качестве основы расчёта передачи принимается расчё на изгибную выносливость червячных передач согласно методическим рекомендациям ВНИИ редуктор, построенным аналогично рекомендациям СЭВ РС 2204 и ГОСТ 21354, но имеющий при подобной структуре формул для расчётных и допускаемых напряжений ряд особенностей. Выявленные факторы, существенно влияющие на изгибную выносливость передач с капролоновыми колёсами (концентрация напряжений и др.), учитываются в расчёте соответствующими дополнительными коэффициентами.

2.3.1 Проектный расчёт передачи

Модуль металлической червячной передачи определяется по известной зависимости [1], преобразованной применительно к металлополимерной в следующий вид:

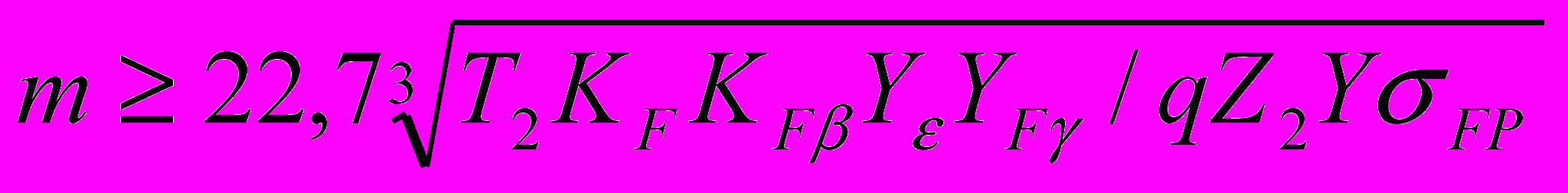, (2.2)

где Т₂ – вращающий момент на колесе, Нм, Т₂ = Т₁ uη. Здесь Т₁– вращающий момент на червяке, который при заданных передаваемой мощности Р, кВт, и частоте вращения червяка n₁, мин^-1, определяется по формуле Т₁= 9550 Р/n₁ и выражается в Нм, u – передаточное число, η – К.П.Д. червячной передачи.

Далее в формуле (2.2)

К_F – коэффициент нагрузки, К_F= К_АК_FvК_FτК_FαК₁, где К_А – коэффициент, учитывающий внешнюю динамическую нагрузку (не учтённую в циклограмме нагружения), принимается равным 1 по ГОСТ 21354; К_Fv – коэффициент, учитывающий динамическую нагрузку, для инженерных расчётов рекомендуется принимать К_Fv = 1,1…1,3.

Формула для коэффициента К_Fτ, учитывающего влияние скорости деформирования на величину расчётного напряжения, имеет вид:

К_Fτ = 1 + К_n₂ (1 - К_Е) [1-ехр(-К_Е/ К_n₂)],

где К_n₂ = τn₂Z₂/60 – коэффициент, зависящий от частоты вращения колеса n₂, мин^-1, диаметра колеса (числа зубьев Z₀) и времени релаксации капролона τ, с; К_Е = Е^*/Е⁰(Е⁰и Е^* - соответственно мгновенный и длительный модули упругости капролона при растяжении (Е⁰ = 2,20 ГПа и Е^* = 0,70 ГПа)).

При К_n₂ ≥ 10^-1 К_Fτ = 1; при 10^-1 ≤ К_n₂ ≤ 10³ К_Fτ изменяется от 1,16 (при К_Е = 0,2) до 1,24 (при К_Е =0,5); при К_n₂ > 10³ К_Fτ зависит от К_Е следующим образом:

К_Е	0,2	0,4	0,6	0,8	1,0
К_Fτ	1,16	1,23	1,23	1,15	1,0

Коэффициент К_Fα учитывает распределение передаваемой нагрузки между зубьями с приложенной по их высоте контактной нагрузкой в виде треугольника, и его следует принимать в диапазоне 0,5…0,72, ориентируясь на нижние значения.

Поправочный коэффициент К₁, учитывающий высокую податливость капролоновых зубьев, принимается по аналогии с коэффициентом К_Fα: 0,5 ≤ К₁ ≤ 0,72.

Коэффициент К_Fβ= σ_Fma/σ_F, учитывающий неравномерность распределения напряжения по длине зуба, зависит, в основном, от жосткости отдельных участков зуба, а также от исходного червяка, характера контакта и других факторов. Значения коэффициента К_Fβрекомендуется принимать по кривым “а“, изображённым на рисунке 2.2. Эти значения (К_Fβ = 1,15…1,35) следует рассматривать как средние в диапозоне чисел зубьев червячного колеса Z₂= 28…40, часто вращающихся на практике.

Коэффициент Y_FS, учитывающий влияние формы зуба и концентрацию напряжений, рекомендуется находить по зависимости:

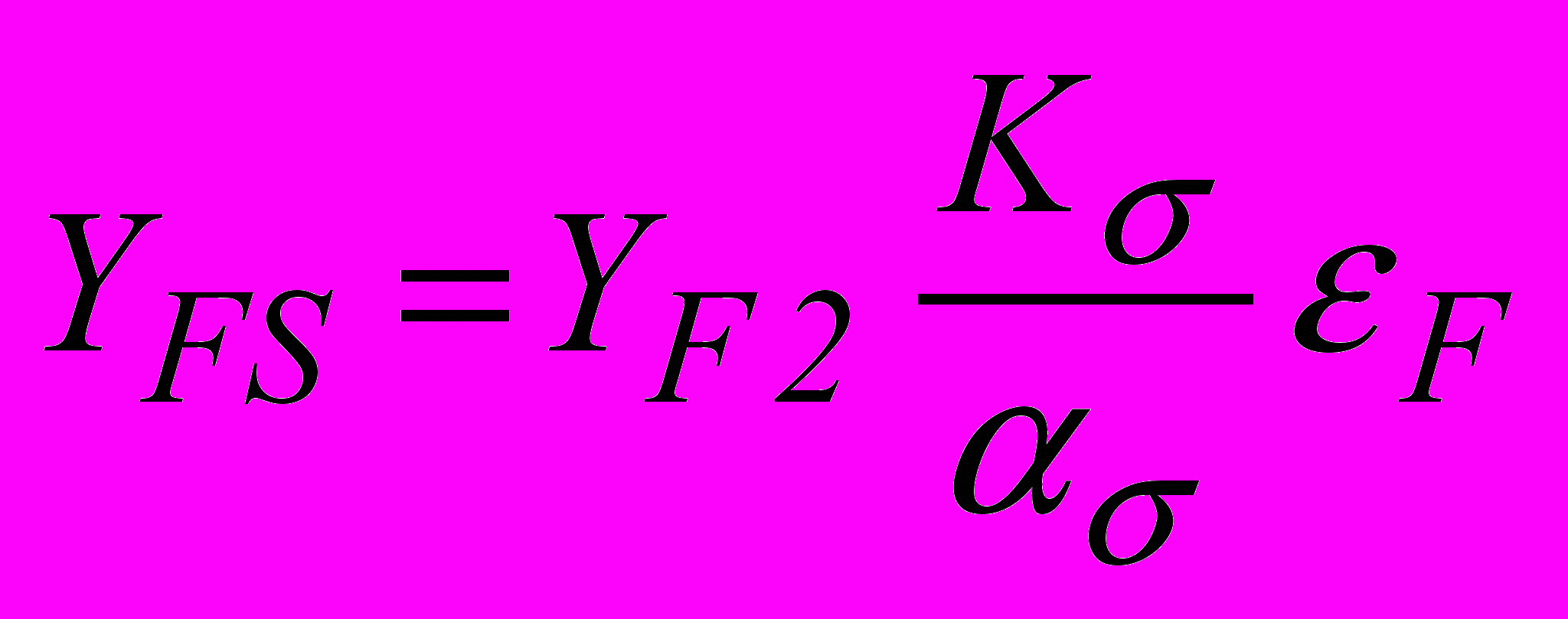, (2.3)

где Y_F₂ – коэффициент формы зуба для металлических червячных колёс, который можно выбирать сначала в виде Y (расчёт по номинальным напряжениям) по таблице 2.2 в зависимости от эквивалентного числа зубьев Z_V₂= Z₂/cos³γ, а затем пересчитывать, используя соотношение 1/Y = α_σY_F₂, где α_σ– теоетический коэффициент концентрации напряжений, α_σ = 1,72[8].

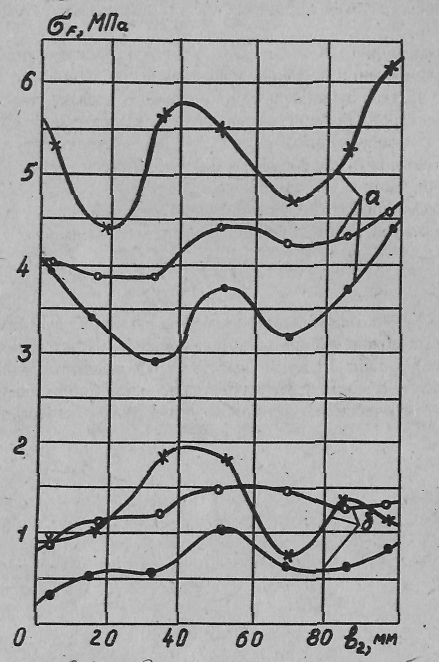
Рисунок 2.2 – Эпюры напряжений изгиба от удельной нагрузки

F_Ft₂/l΄_min = 12,6 кН/м по длине зуба червячного колеса:

а – радиальные; б – тангенциальные; х – нормальный зуб, α_х = 20˚;

_º - утолщённый зуб, α_х = 20˚; • - утолщённый зуб, α_х = 15˚

Таблица 2.2 – Коэффициент формы зуба Y [8,1]

Коэффициент смещения червяка, x	Значение Y при числе зубьев колеса Z₂, равном
Коэффициент смещения червяка, x	31	40	50	63	80	100
-1	-	-	0,237	0,276	0,306	0,324
0	0,370	0,378	0,380	0,380	0,379	0,378
+1	0,484	0,463	0,451	0,444	0,426	0,416

Значение коэффициентного коэффициента концентрации напряжений К_σдля капролона принимают в диапозоне 1,5…1,75.

Коэффициент деформационной анизотропии капролона ζ_Fпри изгибе поперечной силой можно принимать равным 0,82, как и для полиамида П-6.

При расчёте по максимальным местным напряжениям удобнее сразу использовать следующие значения коэффициента формы зуба Y_F₂ в зависимости от эквивалентного числа зубьев колеса Z_V₂:

Z_V2	20	24	26	28	30	32	35	37
Y_F2	1,98	1,88	1,85	1,80	1,76	1,71	1,64	1,61
Z_V2	40	45	50	60	80	100	150	300
Y_F2	1,55	1,48	1,45	1,40	1,34	1,30	1,27	1,24

Примечание: пересчитанный по формуле коэффициент Y_FS подставляется в знаменатель подкоренного выражения формулы (2.2) вместо коэффициента Y.

При расчёте на изгибную выносливость зубьев колеса из капролона, когда нагрузка распределена между двумя одновременно зацепляющимися зубьями, считают, что в вершине зуба приложена только некотарая часть полной нагрузки (по раннее приведённой рекомендации К_Fα= 0,5); для этого случая принимают коэффициент Y_ζ, учитывающий перекрытие зубьев, равным 1.

Значение коэффициента Y_Fγ, учитывающего влияние угла наклона зуба на несущую способность косозубого капролонового колеса, принимаются по таблице 2.3.

Таблица2.3 – Значение коэффициента Y_Fγ

Длительный угол подъёма γ, град.	Значения коэффициента Y_Fγ при базовом числециклов для капролона N_Flimb = 10⁶
5	0,84
10	0,9
15	0,92
20	0,96
25	1,13
30	1,2

В формулу (2.2) входят также:

q – коэффициент диаметра червяка;

Z₂– число зубьев червячного колеса;

σ_FP – допускаемое напряжение при расчёте на выносливость при изгибе, МПа.

Геометрические параметры, входящие в указанную формулу, выбираются из предварительного проектировочного расчёта.

2.3.2 Уточнённый расчёт минимальной суммарной длины контактных линий для передач с червяками ZA

Для расчёта червячной передачи на прочность необходимо знать величину минимальной суммарной длины контактных линий. Структура алгоритма расчёта представлена на рисунке 2.3.

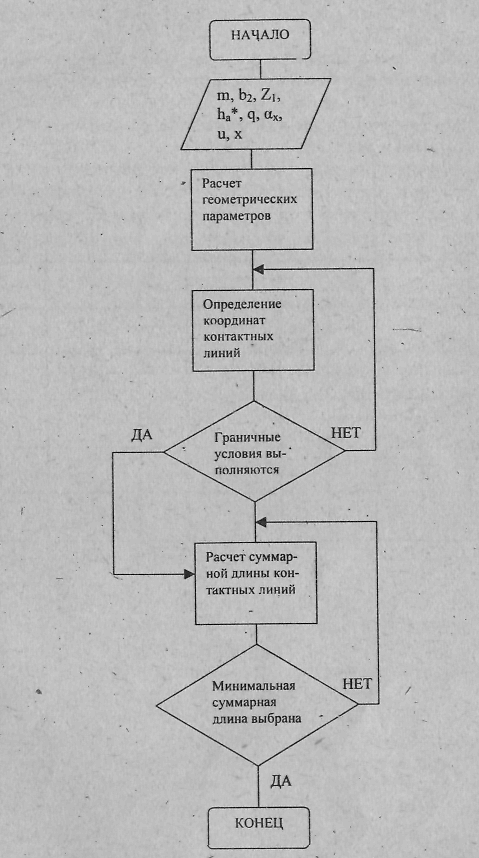
Рисунок 2.3 – Структура алгоритма расчёта минимальной суммарной длины контактных линий передач с червяками ZA

Форма и расположение контактных линий являются важным критерием работоспособности червячной передачи. Увеличение коэффициента смещения у передач с червяками ZA ведёт к значительному уменьшению суммарной длины контактных линий. При уменьшении угла профиля увеличиваются длина поля зацепления, коэффициент перекрытия и, следовательно, суммарная длина контактных линий.

На рисунке 2.4 приведена зависимость величины l΄_min от коэффициента смещения при углах профиля α_x = 20 и 15˚.

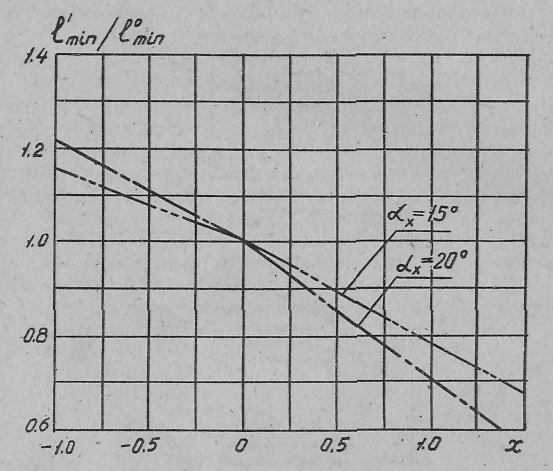
Рисунок2.4 – Зависимость величины l΄_min, значение которой при x = 0, принято равным 1, от коэффициента смещения x и угла профиля α_х

2.3.3 Определение температуры червячного колеса

ввиду низкой теплопроводности каполона выделяющееся тело аккумулируется в объёме колеса и вызывает повышение температуры, приводящее к снижению прочности венца и ускоренному выходу передачи из строя.

Температура, возникающая в результате накапливания тела в теле червячного колеса, используется в расчётах на изгиб и при определении перемещений зуба. Источником тепла в объёме зуба являются разогрев от циклического изгиба и контактного сжатия и трение рабочих поверхностей зубьев.

Зависимость для определения максимальной температуры зуба удобно применять в виде:

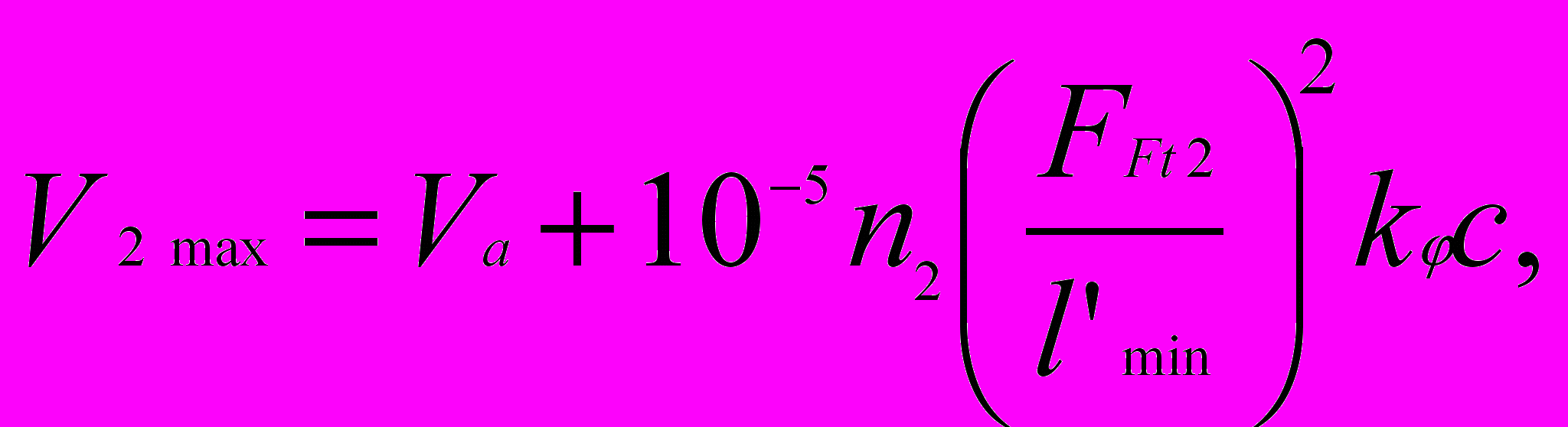(2.4)

где V_a – температура окружающей среды вне корпуса редуктора, ˚С;

n₂ – частота вращения колеса, мин^-1;

k_φ – коэффициент, характеризующий сдвиг фаз между напряжениями и деформациями, МПа^-1, равным sin φ/Е_дин (φ – угол сдвига фаз между амплитудами напряжений и деформаций, Е_дин – динамический модуль упругости капролона, Е_дин = 3200 МПа); для конструкционных пластмасс величина коэффициента К_φ колеблется в пределах (0,5…2,5) 10^-5МПа^-1;

с – коэффициент:

Blog

В. И. Молчанов Проектирование червячных передач с колёсами из неметаллических материалов Учебное пособие