Научные основы методов прогноза напряженно-деформированного состояния горных пород при разработке месторождений нефти и газа

Вид материала

5. Деформирование пород на контактах блоковых структур
6. Практическое применение результатов исследований
Численное моделирование процессов сдвижения на Уренгойском газоконденсатном месторождении.

Подобный материал:

1 2 3 4

Было установлено, что уплотнение коллекторов в целом выше при более слабых вмещающих породах, особенно на границах области снижения давления. В то же время в центральной части уплотнение близко к максимальному и слабо зависит от жесткости вмещающих пород. Уплотнение также увеличивается с ростом радиуса коллектора, однако уже при R/H  2 влияние этого фактора становится несущественным. Наконец, относительное уплотнение коллектора зависит от его начальной толщины. При прочих равных условиях относительное уплотнение выше для более тонкого коллектора, что проявляется на флангах залежи; в центральной части влияние этого фактора практически отсутствует. В целом результаты данных расчетов показали, что даже при небольшом отношении R/H деформации коллекторов в центральной части нефтегазовых месторождений близки к условиям одномерного уплотнения. Однако в краевых частях области снижения исходного пластового давления условия одномерного уплотнения не выполняются и напряженное состояние имеет более сложный вид. Оседания земной поверхности, кроме вышеназванных параметров, зависят также от соотношения жесткости покрывающих и подстилающих пород. Наибольшие оседания земной поверхности имеют место при более жестких подстилающих породах. В целом степень влияния упругих свойств вмещающих пород на уплотнение коллекторов и оседания земной поверхности уменьшается с ростом размеров коллектора, т.е. деформации горного массива определяются прежде всего величиной уплотнения продуктивного слоя.

Далее была рассмотрена зависимость параметров напряженно-деформирован-ного состояния от ряда специфических факторов: неравномерности распределения пластового давления в продуктивных слоях, куполообразного строения коллекторов нефти и газа, распространения воронки депрессии за пределы залежи. Указанные факторы в той или иной мере характерны для всех месторождений нефти и газа, однако подробный анализ их влияния на НДС горных пород в литературных источниках отсутствует.

Помимо естественной геологической неоднородности продуктивных пластов, неравномерность распределения пластового давления вызывается самим характером работы добывающих скважин. Распределение давления в зоне влияния отдельной скважины имеет осесимметричный характер и может быть найдено из выражения

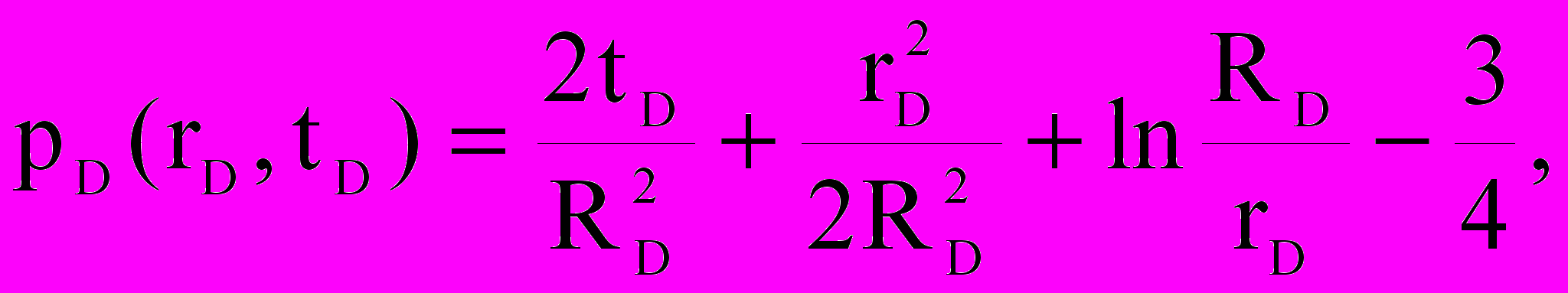
(26)

где R_D, r_D, р_Dи t_D –безразмерные величины: R_D= R_k/R_c; r_D= r/R_c; t_D= kt / (n_общR²_c); p_D= 2kh [p₀-p] / (Q).

В этих формулах: r, t – текущий радиус точки и текущее время работы скважины; R_k- радиус контура питания; R_c– радиус скважины; k – проницаемость пласта; h – толщина пласта;  - вязкость флюида; n – пористость; _общ – коэффициент сжимаемости системы флюид-порода; p₀, р – начальное и текущее пластовое давление.

На рис.8 показана эпюра пластового давления для одного из расчетных примеров и соответствующие ей деформации уплотнения коллектора. Расчетная эпюра уплотнения соответствует картине падения пластового давления, однако величины уплотнения в центре модели и на контуре питания составляют 61.0 и 60.8мм, т.е. различаются совершенно незначительно. При этом, если использовать средневзвешенное значение давления, то уплотнение составит 61.6мм. Данный пример показывает, что в большинстве случаев для расчета деформаций горного массива можно не учитывать неравномерность пластового давления, обусловленного работой отдельных скважин. Этот вывод имеет важное практическое значение, т.к. при использовании показателей средневзвешенного давления нет необходимости существенного сгущения конечно-элементных сеток в районе добывающих скважин, что упрощает построение расчетных моделей.

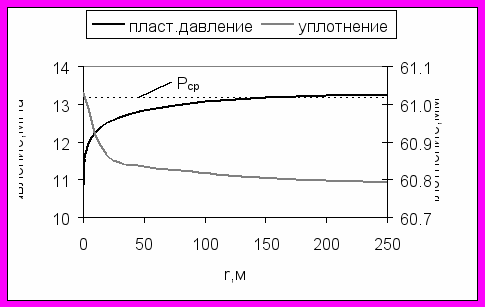
Рис. 8. Пластовое давление и уплотнение коллектора в зоне влияния скважины

Следующий рассматриваемый фактор связан с тем, что коллектора нефти и газа имеют куполообразное строение, т.к. приурочены к сводовым частям геологических структур-ловушек углеводородов. Поскольку углы наклона крыльев складок составляют первые градусы или даже минуты, расчетные модели обычно строят в виде прямолинейных пластов с постоянной глубиной залегания. Влияние подобной идеализации геометрии залежи было рассмотрено на численном примере коллектора толщиной 50 м, радиусом R=1500 м, залегающего на глубине Н=1500 м (рис.9). Предполагалось, что водонефтяной контакт расположен на 100м ниже купольной части, что при данных размерах залежи является довольно большой величиной. Рассчитывались оседания земной поверхности, которые сравнивались с аналогичными величинами для коллектора плоской формы с постоянной глубиной залегания Н=1500 м.

Рис. 9. Фрагмент конечно-элементной модели коллектора куполообразной формы

В базовом варианте (Е=5000 МПа; =0,2; падение давления 5 МПа) максимальное оседание поверхности для плоского коллектора составило 28.9 мм, для куполообразного – 27.8мм, т.е. меньше на 4%. Данное явление можно объяснить тем, что сводчатая структура вмещающих пород является более жесткой. С увеличением размеров коллектора разница в оседаниях уменьшается. Расчеты показали, что оседания поверхности для двух вариантов геометрии коллектора практически не различаются уже при радиусе R=3000 м, т.е. при R/Н=2. Т.о., идеализация геометрии коллекторов в виде плоских пластов с постоянной глубиной залегания наиболее заметна для месторождений с малым отношением R/Н. При этом допущение о плоской форме коллектора дает незначительное увеличение сдвижений массива, т.е. обеспечивает расчетам некоторый запас прочности.

Явление распространения воронки депрессии за пределы водонефтяного (или газоводяного) контакта связано с тем, что после пуска скважин в эксплуатацию за счет перепада давлений начинается приток законтурных вод в залежь. Общие особенности развития деформационных процессов при падении давления за пределами залежи были рассмотрены на численном примере коллектора радиусом R=3000м, глубиной Н=1500 м и толщиной 100м. При Е=5000 МПа, =0,2 и падении давления 5 МПа максимальное уплотнение коллектора составляет 90 мм. Рассчитывались деформации земной поверхности при распространении депрессионной воронки за пределы залежи на некоторое расстояние R, которое варьировалось от 0 до 1.0R. Если в базовом варианте (депрессионная воронка не выходит за пределы залежи) граничный угол сдвижения, определяемый на точку с оседанием 10мм, составил 50, то при R=3000 м граничный угол достиг 27. Данный пример служит объяснением того факта, что на ряде месторождений инструментальные наблюдения фиксируют аномально низкие углы сдвижения. Так, на Уренгойском газоконденсатном местрождении установлено, что мульда оседания земной поверхности распространяется за границы ГВК до 8-10км, т.е. граничный угол сдвижения доходит до 10-15. Это можно объяснить только падением давления в областях, удаленных от газоводяного контакта. Указанные особенности необходимо учитывать при проектировании инструментальных наблюдений за сдвижением земной поверхности. При определении длин профильных линий целесообразнее всего руководствоваться накопленными сведениями о граничных углах сдвижения на уже исследованных месторождениях со сходными горно-геологическими условиями. При отсутствии таких данных минимальное значение граничного угла сдвижения необходимо определять расчетными методами с максимальным учетом особенностей конкретного месторождения.

В целом выполненный анализ влияющих факторов дает возможность оценить последствия определенной схематизации геометрических и деформационных параметров, которая неизбежна при построении расчетных моделей реальных объектов. Должный учет выявленных закономерностей позволяет повысить обоснованность прогнозных оценок напряженно-деформированного состояния горных массивов при добыче нефти и газа.

Далее были рассмотрены особенности применения МССМ-модели для прогноза напряженно-деформированного состояния горных массивов при добыче нефти и газа. МССМ-модель пренебрегает сжимаемостью минеральных зерен скелета породы, что, согласно выполненных исследований, вполне допустимо для большинства практических случаев. При разгрузке и повторной нагрузке породы поведение материала считается упругим и коэффициент сжимаемости находится по значению индекса декомпрессии k:

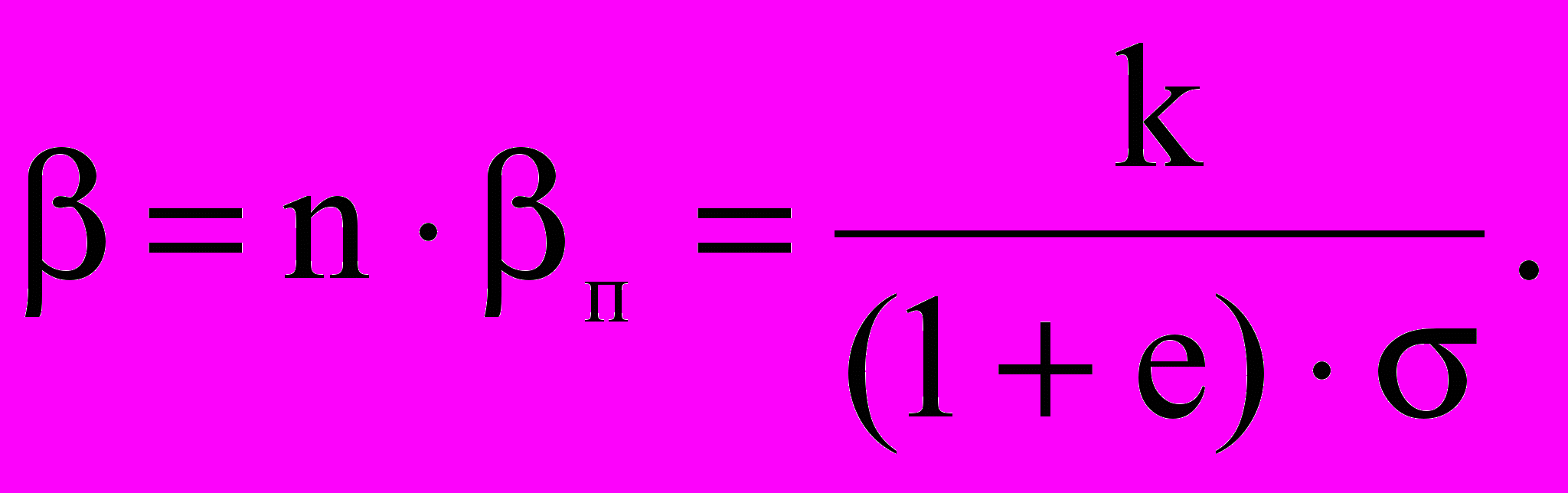
(27)

Используя соотношения теории упругости, можно установить зависимость между индексом декомпрессии k и упругими параметрами Е и :

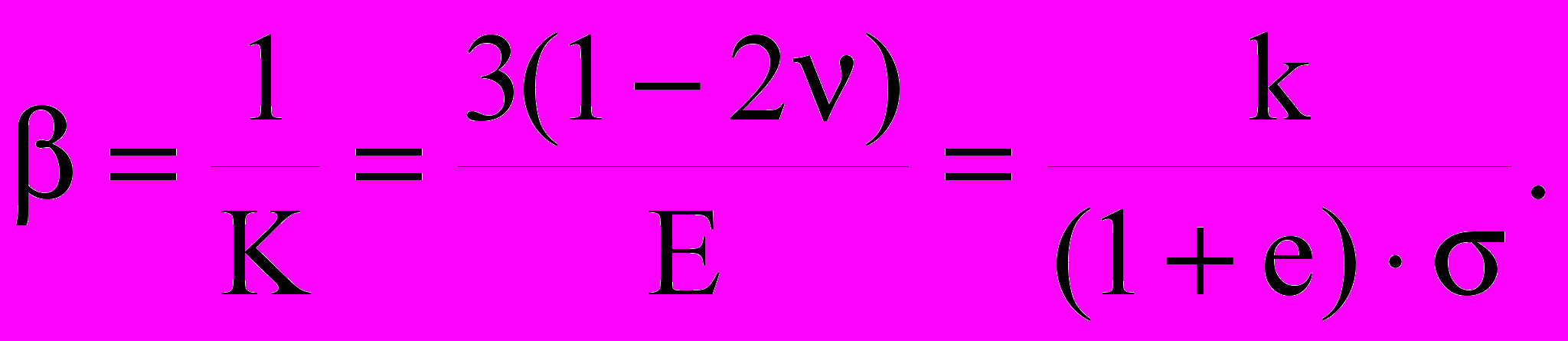
(28)

При первичной нагрузке подобное простое соотношение между упругими и компрессионными параметрами существует только для условий одномерного уплотнения, когда вертикальные и горизонтальные эффективные напряжения связаны уравнением _x= _y= k₀_z, где k₀- коэффициент бокового давления при первичном уплотнении:

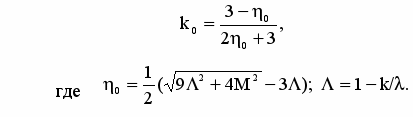
(29)

В этм случае можно формально ввести некоторый ‘пластический’ коэффициент Пуассона по соотношению _pl = k₀/(1+k₀) и установить зависимость между компрессионными параметрами , k₀и характеристиками линейно-деформируемой среды. Если напряженное состояние коллектора близко к условиям одномерного уплотнения, такой подход дает хорошее соответствие с численными расчетами на основе МССМ-модели. В определенных условиях это может быть полезно с точки зрения экономии компьютерных ресурсов.

Особенности напряженно-деформированного состояния горного массива при уплотнении коллекторов согласно МССМ-модели были рассмотрены на ряде примеров, условия которых обеспечивали максимальную величину уплотнения от 90 мм до 2.7 м. В одном из примеров рассматривался коллектор толщиной 50 м, радиусом 6000м, залегающий на глубине 2000 м. Пористость коллектора 20%, = 0,010, k = 0,005, =0,20, М=0,984, объемный вес покрывающих пород 0,022 МН/м³. Рассчитывались деформации коллектора и горного массива при снижении пластового давления от 20 до 14 МПа. Данные условия обеспечивают максимальное уплотнение 90мм. Расчетный характер напряженного состояния коллектора и горного массива показан на рис. 10.

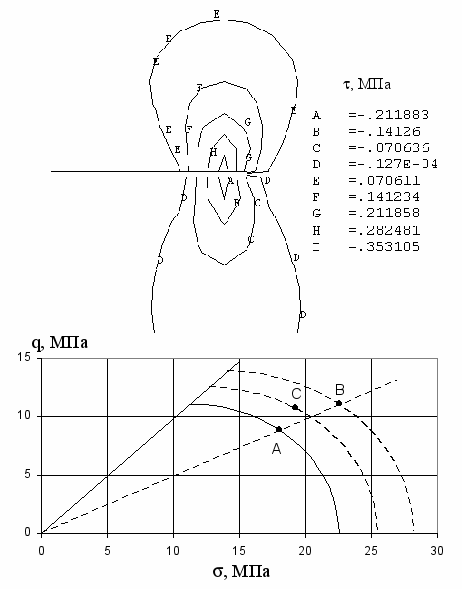
Рис. 10. Характер напряженного состояния коллектора

при падении пластового давления

Касательные напряжения в горном массиве приурочены к краевой части продуктивной зоны и весьма малы по величине, что легко объясняется незначительным уплотнением коллектора. Если взять две точки в центре модели и на краю продуктивной зоны, то в них исходное напряженное состояние коллектора одинаковое и в диаграмме q -  характеризуется точкой А (рис.10). Параметр р_с, задающий начальную границу эллиптической области упругих деформаций, равен 22,6 МПа. После падения пластового давления на 6 МПа напряженное состояние коллектора в центре модели достигает точки В и формирует новую, более обширную область упругих деформаций с параметром р_с= 28,2 МПа. Точки А и В лежат на прямой c уравнением q=₀∙, т.е. прирост эффективных горизонтальных напряжений соответствует теоретическому значению коэффициента бокового давления. Напряженное состояние в краевой части коллектора характеризуется точкой С, которая лежит выше линии одномерного уплотнения, т.е. девиаторная часть тензора напряжений прирастает интенсивне. Тем не менее, точка С не достигает предельной линии q=М∙, т.е. разупрочнения не возникает и коллектор в краевой зоне также деформируется в режиме уплотнения.

Расчеты, выполненные для условий существенного уплотнения коллектора (2.7 м), показали сходные результаты. Несмотря на значительные абсолютные величины сдвижений, касательные напряжения в горном массиве оказались довольно небольшими. Данный факт можно объяснить тем, что сдвижения распределяются на значительные области горного массива. Напряженное состояние в краевой части коллектора не достигает предельной линии q=М∙, т.е. породы также деформируются в режиме уплотнения. При этом рост эффективной нагрузки происходит по траектории, приблизительно нормальной к эллиптической поверхности текучести. Данные расчеты показывают, что применение МССМ-модели для расчета деформаций коллекторов обеспечивает представительные результаты при большом разнообразии горно-геологических условий и физико-механических свойств продуктивных пород.

5. Деформирование пород на контактах блоковых структур

и оценка интенсивности техногеннх сейсмических явлений

Геодинамические процессы довольно широко распространены при разработке полезных ископаемых, в том числе при добыче нефти и газа. В основу современных представлений о геодинамике недр и земной поверхности при добыче полезных ископаемых положена концепция блочной структуры горного массива, развитая в работах И.М.Петухова, И.М.Батугиной и многих других ученых. Известно, что сама по себе блочная структура массива вследствие различия физико-механических свойств отдельных блоков и контактных зон порождает весьма неравномерное распределение тензора напряжений. Разработка твердых полезных ископаемых или добыча нефти в условиях неравнокомпонентного исходного поля напряжений может многократно усилить опасность техногенного воздействия на недра. Современные геомеханические модели и методы позволяют с любой степенью детальности исследовать поведение блочных сред, однако неопределенность входящих в расчетную модель параметров позволяет получать только сильно приближенные решения. При рассмотрении задач о механическом поведении блочных массивов необходимо анализировать расчетные области размерами в сотни метров или даже десятков километров, включающие в себя слагающие блоки и разграничивающие их разломные зоны. Очевидно, что параметрическое обеспечение таких моделей весьма проблематично, т.к. знание физико-механических свойств огромных массивов и разломных зон в принципе невозможно. Тем не менее, используя результаты маркшейдерско-геодезических измерений деформаций больших территорий, методом обратных расчетов можно получить значения входящих параметров, которые дают удовлетворительное соответствие наблюдаемым на практике деформациям. Несмотря на всю относительность, такой подход позволяет на качественном уровне исследовать поведение блочного массива.

Подобные расчеты были выполнены для анализа напряженного состояния блочной структуры горного массива в регионе Верхнекамского месторождения калийно-магниевых солей (ВКМКС). Моделируемый участок массива имеет размеры по глубине 5,0 км, в плане 4545 км и захватывает гг.Березники и Соликамск. За основу расчетной модели были взяты тектонические блоки II,III,IY,Y рангов, выделенные на территории ВКМКС проф. В.В.Филатовым (Уральский государственный горный университет, г.Екатеринбург). На данной модели были рассмотрен ряд ситуаций, способных вызвать аномальные движения земной поверхности, зафиксированные геодезическими наблюдениями в разломных зонах. Анализировалась реакция блочного массива на природные сейсмические воздействия, вызванные незначительным природным землетрясением интенсивностью 3-4 балла. Расчеты показали, что при действии волны сжатия на земной поверхности в районе нарушений возникает всплеск поднятий, масштабы которого зависят от упругих свойств блоков и разломных зон. При действии волны растяжения соответственно возникают оседания поверхности. В качественном плане полученные смещения соответствует - и - аномалиям современных движений земной поверхности, которые были типизированы В.А. Сидоровым и Ю.О. Кузминым. Данные результаты позволяют сделать вывод о том, что аномальные величины вертикальных движений земной поверхности, являющиеся частью геодинамической обстановки, могут быть обусловлены природной сейсмичностью региона.

На другой модельной ситуации рассматривалась возможность возникновения - аномалии в результате изменения физико-механических свойств среды, слагающей разлом. Изменения свойств могут быть вызваны, например, выпадением атмосферных осадков, изменением гидрогеологического режима и другими природными факторами. Рассматривалось изменение упругих свойств относительно начального значения в разломной зоне шириной 100 м на глубину от поверхности на 100 м. Расчеты показали, что в зависимости от изменения модуля упругости можно наблюдать изменение глубины прогиба возникающей мульды и упругое поднятие краев борта. Таким образом, аномальные просадки поверхности в районе нарушения (-аномалии) могут объясняться, помимо фоновой сейсмичности региона, сезонными изменениями свойств нарушения в результате действия различных природных факторов.

Данные расчеты, с одной стороны, показывают высокую степень относительности задач расчета напряженно-деформированного состояния больших объемов горного массива. Меняя такие весьма неопределенные параметры, как геометрия разлома, физико-механические свойства блоков и разломных зон, можно получать самые различные величины смещений. С другой стороны, полученные деформации в качественном плане вполне соответствуют экспериментальным данным. Это дает возможность выполнить оценку сдвижений и деформаций, возникающих на контактах блоковых структур вследствие добычи углеводородов.

Задача была рассмотрена для условий, характерных для нефтяных месторождений севера Пермского края. Рассчитывалось напряженно-деформированное состояние горного массива при падении пластового давления на 5 МПа в продуктивном пласте мощностью 30 м, находящегося на глубине 2000 м. Характеристики продуктивных пород (Е = 2000 МПа,  = 0.25) в данных условиях обеспечивают максимальное уплотнение коллектора величиной h = 62.5 мм. Предполагалось, что в краевой части коллектора по всей мощности разреза проходит субвертикальная зона междублокового контакта (рис.11).

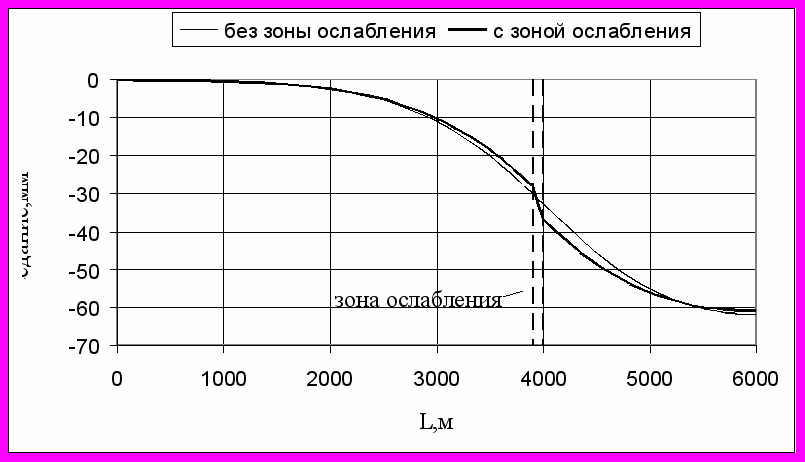
Рис. 11. Мульды оседания при наличии и отсутствии зоны ослабления

мощностью 100 м (k = 0.2).

Поскольку ширина контактных зон является крайне неопределенным параметром, ее мощность в расчетах варьировалась от 100 до 500 м. Модуль упругости пород в контактных зонах определялся в зависимости от модуля упругости пород соответствующего слоя по соотношению Е' = E₀  k, где Е', E₀ - модуль упругости соответственно нарушенных и ненарушенных пород, k – коэффициент ослабления. Коэффициент ослабления k варьировался от 0,8 до 0,2. Расчеты показали, что зоне нарушения наблюдается некоторая концентрация деформаций, где на контакте нарушенных и ненарушенных пород происходит прирост оседаний относительно мульды сдвижения в монолитном массиве (рис.11). Величина прироста оседаний определяется мощностью и физико-механическими свойствами ослабленных пород. Оседания возрастают при снижении упругих свойств пород и уменьшении ширины ослабленной зоны. Выполненные расчеты, несмотря на их условность, дают общее качественное представление о характере деформаций на контактах блоков при добыче углеводородов.

Основной вывод заключается в том, что заметные деформации могут возникать на узких (мощностью до 50-100 м), линейно вытянутых зонах ослабления, заполненных сильно дислоцированными, разрушенными породами. Данные результаты относятся к деформациям, которые обусловлены техногенным фактором, т.е. добычей нефти или газа. Собственно геодинамические, т.е. вызываемые природными причинами, аномальные движения земной поверхности практически не поддаются расчетам и прогнозам и подлежат контролю с помощью систем геодинамического мониторинга.

При анализе геодинамической обстановки на месторождениях нефти и газа одной из наиболее важных задач является прогноз интенсивности техногенных сейсмических явлений. Известные математические модели очага техногенного (а в отдельных случаях и природного) землетрясения говорят о нем как о модели неустойчивого роста трещины в разломе, т.е. активизации существующих тектонических разломных структур в форме сдвига их бортов. Впереди развивающейся в разломе магистральной трещины возникает область объемного разрушения за счет создания множества микротрещин. Трущиеся при сдвиге борта разлома порождают дробленый материал, в результате чего большая часть энергии, высвобождаемой при сдвиге, расходуется на образование в бортах разлома зоны дробленой породы. Указанным представлениям соответствует известная модель скольжения с разупрочнением Дж.Райса (рис. 12).

_s

_res

^*

_p

_res

_p

^*

_p

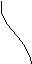
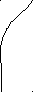
Рис. 12. Модель активизации тектонического разлома

Началу скольжения по разлому соответствует достижение касательным напряжением _res своего максимального значения _р. До этого наблюдается как рост касательного напряжения, так и рост касательного к поверхности разлома смещения _s. При достижении величиной _s значения _p (и соответственно касательного напряжения _р) начинается неустойчивый рост трещины в разломе и падение касательных напряжений до величины остаточной прочности ^*. При достижении остаточной прочности перемещение _sможет расти неограниченно при неизменной величине ^*, что соответствует свободному перемещению данного участка одного борта разлома относительно другого, расположенного за пределом зоны разупрочнения.

Разность параметров (_р- ^*) рассматривается как сброс напряжений. Скорость высвобождения энергии  при подвигании сдвиговой трещины (энергия разрушения) дается выражением:

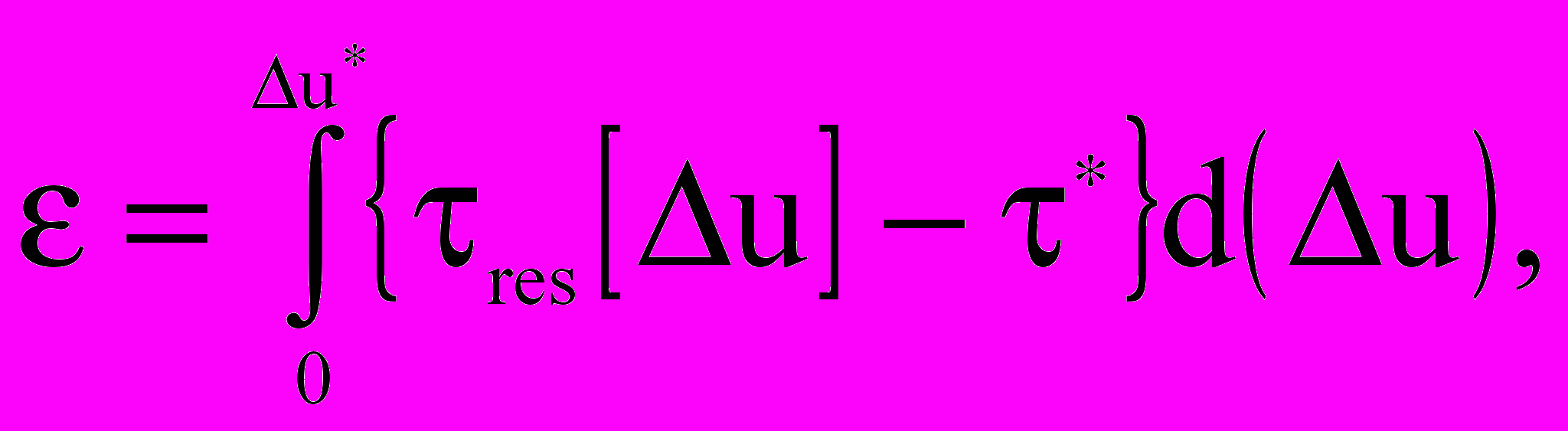
(30)

где u^* - величина перемещения при скольжении.

Рассматриваемая задача сводится к расчету НДС горного массива, содержащего поверхности ослабления. Для реализации модели Дж.Райса хорошо подходит модель деформирования пород по системам трещин, т.к. она использует полную диаграмму деформирования пород по контактам (рис. 5), которая практически аналогична модели скольжения с разупрочнением (рис. 12). Реализация модели для оценки магнитуд техногенных сейсмических событий заключаются в следующем.

Разлом представляется средой, разбитой системой трещин вдоль поверхности раздела. В результате численного решения методом конечных элементов задачи скольжения с разупрочнением в каждом элементе разлома, где касательные смещения _s превысили величину _p, определяется сброс напряжений (_р- ^*). Также определяется разница между касательным смещением _s^* на участке стабилизации итерационного процесса и величиной _р. Значение высвобождающейся в i-м элементе энергии находится как


(31)
_i=(_р- ^*)(_р- _s^*),

где _s^* - максимальное достигнутое касательное смещение в i-м элементе.

Единичное значение энергии для решаемой задачи находится как среднее значение по элементам, вышедшим в запредельное состояние. Нормированное значение высвобождающейся энергии получается путем перемножения найденной величины на вертикальный размер L зоны запредельного состояния:

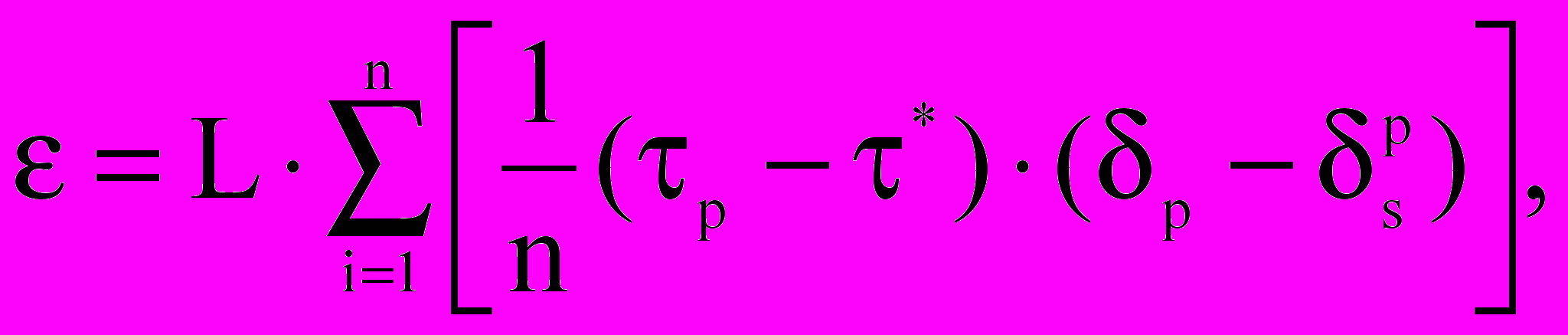
(32)

где n – число элементов, вышедших в запредельное состояние.

Полная энергия сейсмического события получается перемножением нормированного значения (32) на линейный размер зоны сдвига по простиранию разлома. При этом допускается определенный произвол в выборе размеров сдвигающихся зон, однако расчеты говорят о том, что это не имеет существенного значения.

Оценочные расчеты магнитуд сейсмических явлений были выполнены применительно к отработке Уньвинского нефтяного месторождения на территории Пермского края. На первом этапе были рассчитаны оседания горного массива при падении давления на 6, 10 и 20 МПа. Применяемые при этом параметры модели были определены из условия наилучшей сходимости расчетов с результатами инструментальных наблюдений. На втором этапе более детально рассматривался расчетный фрагмент в районе коллекторов, вырезанный из общей расчетной схемы (рис. 13).

Пласт Бш

600 м

-1950

карбонаты

зоны влияния

нагнетательных

скважин

тектонический разлом

-2250

терригенные породы

Пласт Тф

1500 м

Рис.13. Общая расчетная схема задачи активизации разлома

В качестве граничных условий на границах фрагмента задаются перемещения, полученные из решения общей задачи. Оценивалась возможность возникновения динамических подвижек по нарушению в виде ослабленной вертикальной зоны мощностью 5 м, рассекающей продуктивную толщу и слой карбонатов. Для прочностных свойств разломной зоны задавалось С = 0,05 МПа,  = 20, ^*= 10, _о= 10, _р, = 1,0 мм.

Р
(33)
асчеты показали, что без противодавления жидкости в разломе сдвига его бортов не возникает даже при падении давления в коллекторах на 20 МПа. Возможность динамических сдвижений возникает при операциях нагнетания флюида для поддержания пластового давления. Была выполнена серия расчетов с вариацией давлений нагнетания жидкости в разлом и падения давления в коллекторах. Магнитуды возникающих сейсмических событий оценивались по формуле:

М=(logЕ-4.9)/1.5,

где Е -нормированное значение энергии, уменьшенное в 100 раз согласно значения сейсмического к.п.д. =0,01. При этом условно рассматривались ситуации с размерами разлома по простиранию L=250 м, 500 м и 1000 м. Было установлено, что с увеличением размера L свыше 1000 м его дальнейший рост уже незначительно сказывается на величине магнитуды (рис. 14).

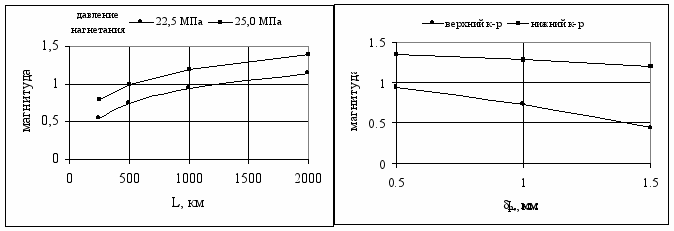
Рис. 14. Зависимость магнитуд сейсмических событий от размера разлома

по простиранию и параметра _р.

Также на рис. 14 представлен график зависимости магнитуд от основной характеристики полной диаграммы сдвига - параметра _р. На рис. 14 видно, что при уменьшении _р от 0,5мм до нуля магнитуда может вырасти не более чем на 0,2 единицы, т.е. довольно незначительно. Т.е. в рассматриваемом примере для анализа техногенной сейсмичности вполне можно воспользоваться табличными значениями показателя _р. В целом количество выделяемой энергии довольно слабо зависит от падения пластового давления (в рассматриваемых условиях) и определяется прежде всего давлением нагнетания флюида, размерами нарушения, а также характеристиками полной диаграммы сдвига по поверхности раздела.

Полученные значения магнитуд не превышают 1,5, что следует считать предельно возможным для данных условий. Рост магнитуды, например, до 2,5 не представляется реальным, т.к. для этого требуется увеличение в 10 раз единичного значения энергии, определяемой по формуле (32). Это возможно только в случае активизации весьма крупного разлома с размерами зоны заводнения по высоте более 300м. Сейсмические события подобной интенсивности фиксируются только с помощью чувствительных приборов и не оказывают заметного влияния на поверхностные, подземные объекты и геологическую среду региона месторождения.

Аналогичные расчеты по оценке возможности сейсмических событий на Астраханском газоконденсатном месторождении показали значения магнитуд до 2,5 единиц при прогнозном падении давления на 2010 г. Вследствие довольно значительных энергетических показателей сейсмических событий был сделан вывод о необходимости организации сейсмологического мониторинга отработки месторождения.

Анализ данной методики оценки техногенной сейсмичности приводит к выводу о возможности активизации разломных структур просто при их заводнении, что подтверждается многочисленными фактами наведенной сейсмичности при нагнетании флюида в недра. Так, например, три сейсмические события с магнитудой 7 на газовом месторождении Газли произошли при падении давления всего на 5 МПа, однако перед каждым землетрясением месторождение интенсивно заводнялось. В целом можно сделать вывод о том, что разработанная численная модель вполне адекватно воспроизводит механизм активизации разломных структур и ее можно применять для оценки техногенного сейсмического риска при отработке месторождений углеводородов.

6. Практическое применение результатов исследований

Прогноз оседаний земной поверхности на нефтяных месторождениях Западной Сибири. Расчеты напряженно-деформированного состояния горного массива и земной поверхности были выполнены на целом ряде нефтяных месторождений Западной Сибири (Усть-Балыкское, Мамонтовское, Чумпасское, Западно-Сургутское и ряд других), где в зоне влияния добычи нефти находятся ответственные объекты - жилая застройка и сложное промышленное оборудование.

Основное внимание уделялось обоснованию упругих и компрессионных свойств пород-коллекторов. Для решения этой задачи применялись различные методы: непосредственные испытания образцов продуктивных пород, все доступные справочные данные, эмпирические и теоретические зависимости. С целью уменьшения степени неопределенности входящих параметров на всех объектах производились исследования по влиянию физико-механических свойств горного массива и коллектора на величины оседаний земной поверхности. Расчетные максимальные оседания земной поверхности для ряда нефтяных месторождений показаны в табл.3.

Таблица 3 – Результаты прогноза оседаний для ряда нефтяных месторождений

Западной Сибири

Месторождение	Продуктивные объекты	Суммарная мощность, м	Макс. оседание, мм
Усть-Балыкское	БС1-5, БС10	35	122
Мамонтовское	АС4-6, БС8, БС10-11	33	124
Правдинское	БС5-6, БС8-9	20	40
Приобское	АС10-АС12	45	360
Западно-Сургутское	БС1-4, БС10	25	89
Восточно-Сургутское	БС10, ЮС1-1, ЮС2-2	23	45
Родниковое	БС12	10	36
Чумпасское	АВ1, БВ6, БВ18-22	31	124
Ватинское	АВ1-2, БВ8, ЮВ1	24	82

Оседания получены для падения исходного пластового давления на 3-5 МПа, что в среднем характерно для месторождений Западной Сибири. Расчеты говорят, что при отработке месторождений системами с поддержанием пластового давления максимальные оседания поверхности не превышают 100-150 мм, иногда при большой мощности продуктивных объектов – 300-350 мм. Этот вывод подтверждается имеющимся опытом инструментальных наблюдений на Усть-Балыкском геодинамическом полигоне. Оседания подобной величины, равномерно распределенные на огромной площади месторождений, не могут нарушить нормальный режим эксплуатации объектов на земной поверхности. Однако потенциальную опасность могут представлять концентрации деформаций на земной поверхности, вызванные различного рода структурными неоднородностями горного массива.

Несмотря на сравнительно небольшие величины сдвижений, на основе данных расчетов были спроектированы и реализованы наблюдательные станции в районах ответственных объектов - высотной жилой застройки и сложного промышленного оборудования, требующего высокой степени промышленной безопасности.

Численное моделирование процессов сдвижения на Уренгойском газоконденсатном месторождении. На территории крупнейшего в мире Уренгойского газоконденсатного месторождения находится крупный населенный пункт - город Новый Уренгой. Инструментальные наблюдения на станции, созданной на месторождении в 1974-76 гг., к 1995 году зафиксировали оседания величиной до 340 мм. При продолжении добычи газа возможно негативное влияние деформационных процессов на подрабатываемые объекты, в связи с чем был выполнен прогноз напряженно-деформированного состояния горного массива.

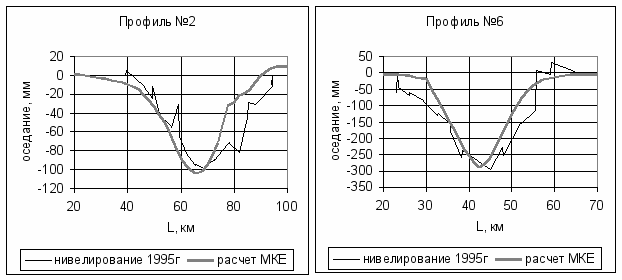
Деформационные параметры массива определялись методом «обратных расчетов». Были созданы расчетные схемы по ряду профилей, где продуктивные объекты строились по картам эффективных газонасыщенных толщин, а величины действующих нагрузок определялись по картам изобар. В результате серии расчетов было установлено, что удовлетворительное соответствие расчетных и экспериментальных данных достигается при параметрах шатровой модели для пород сеномана  = 0,007; k = 0,003; М = 1,2. (рис. 15).

Blog

Научные основы методов прогноза напряженно-деформированного состояния горных пород при разработке месторождений нефти и газа