Научные основы методов прогноза напряженно-деформированного состояния горных пород при разработке месторождений нефти и газа

Вид материала

Автореферат

Содержание Рис.6. Примеры компрессионных кривых ряда месторождений. 4. Прогноз напряженно-деформированного состояния горных пород

Подобный материал:

• Программа научной конференции «геомеханика в горном деле», 112.96kb.
• Программа научно-практической конференции «Современные вызовы при разработке и обустройстве, 279.73kb.
• Программа научно-практической конференции «Современные вызовы при разработке и обустройстве, 279.73kb.
• Геохимические методы поисков месторождений нефти и газа содержание учебной дисциплины, 74.47kb.
• Определение свойств горных пород и оценка сопротивляемости горных пород разрушению, 79.2kb.
• Водонапорная гидрогеологическая система и её трансформация при разработке месторождений, 338.72kb.
• Программа курса «Методы поисков и разведки месторождений нефти и газа», 115.98kb.
• А. А. Трофимука Приоритетное направление со ран геофизика, геодинамика Физические поля, 208.47kb.
• Разработка спектрально-акустического метода контроля изменения напряженного состояния, 293.41kb.
• Удк 622. 831: 622. 502 551. 14 550343. 4 Совершенствование методов оценки геодинамического, 633.09kb.

Рис.6. Примеры компрессионных кривых ряда месторождений.

При этом для песчано-глинистых и карбонатных коллекторов коэффициент сжимаемости твердой фазы на один-два порядка ниже, чем коэффициент сжимаемости пор, т.е. объемная деформация пористых пород возникает главным образом за счет деформаций порового пространства. Для изучения сжимаемости порового пространства коллекторов производились компрессионные испытания, т.е. получали зависимость пористости (или коэффициента пористости) образцов от всестороннего эффективного давления при нагрузке и разгрузке (рис.6).

Компрессионная зависимость дает полное представление о деформируемости порового пространства, т.к. с ее помощью можно найти коэффициент сжимаемости пор в заданном интервале всестороннего давления:


(11)


_п = n/(n) = e/(e),

где n - пористость, e - коэффициент пористости.

Поскольку сжимаемость твердой фазы значительно меньше сжимаемости пор, то общую сжимаемость породы можно без большой погрешности определить по формуле (10) с помощью табличных значений _тв. Испытания показали, что в широком интервале напряжений пористость можно представить в виде линейной функции от логарифма всестороннего давления. Это дает основание применять для расчета деформаций коллекторов хорошо разработанные «шатровые» модели.

Результаты выполненных испытаний в сочетании со справочными данными, известными эмпирическими и теоретическими зависимостями предоставляют достаточно материала для обоснования параметров механических моделей, которые применялись для расчета показателей напряженно-деформированного состояния горных массивов на месторождениях нефти и газа. Для перехода от физико-механических свойств образцов к соответствующим показателям горного массива использовались известные эмпирические и теоретические зависимости, а также, при наличии необходимой информации, метод «обратных расчетов». В общем виде применение метода «обратных расчетов» состояло в следующем. На первом этапе выполнялась предварительная оценка физико-механических показателей на основе всей имеющейся информации – лабораторных экспериментов, справочных данных, эмпирических и теоретических зависимостей. На втором этапе производилась серия расчетов НДС массива с вариацией входящих параметров. На данном этапе выявлялись наиболее значимые факторы, устанавливались характер и степень их влияния на расчетные показатели НДС горных пород. Наконец, на третьем этапе с учетом выявленных закономерностей производилась окончательная калибровка моделй для наилучшего соответствия расчетных и экспериментальных данных. Анализ мирового опыта показывает, что именно такой подход обеспечивает наилучшую надежность прогнозных оценок напряженно-деформированного состояния горного массива.


4. Прогноз напряженно-деформированного состояния горных пород

при разработке месторождений углеводородов


Породы, залегающие на больших глубинах, практически всегда насыщены одним или несколькими флюидами (обычно водой, нефтью или газом). Изменение пластового давления при добыче флюида оказывает сильное влияние на механическое состояние породы. В некоторых случаях (например, при термических способах добычи или при закачке воды для поддержания пластового давления) на напряженно-деформированное состояние могут влиять температурные эффекты. Однако большинство процессов, происходящих при добыче нефти и газа, можно считать изотермическими. В этом случае уравнения закона Гука имеют вид:



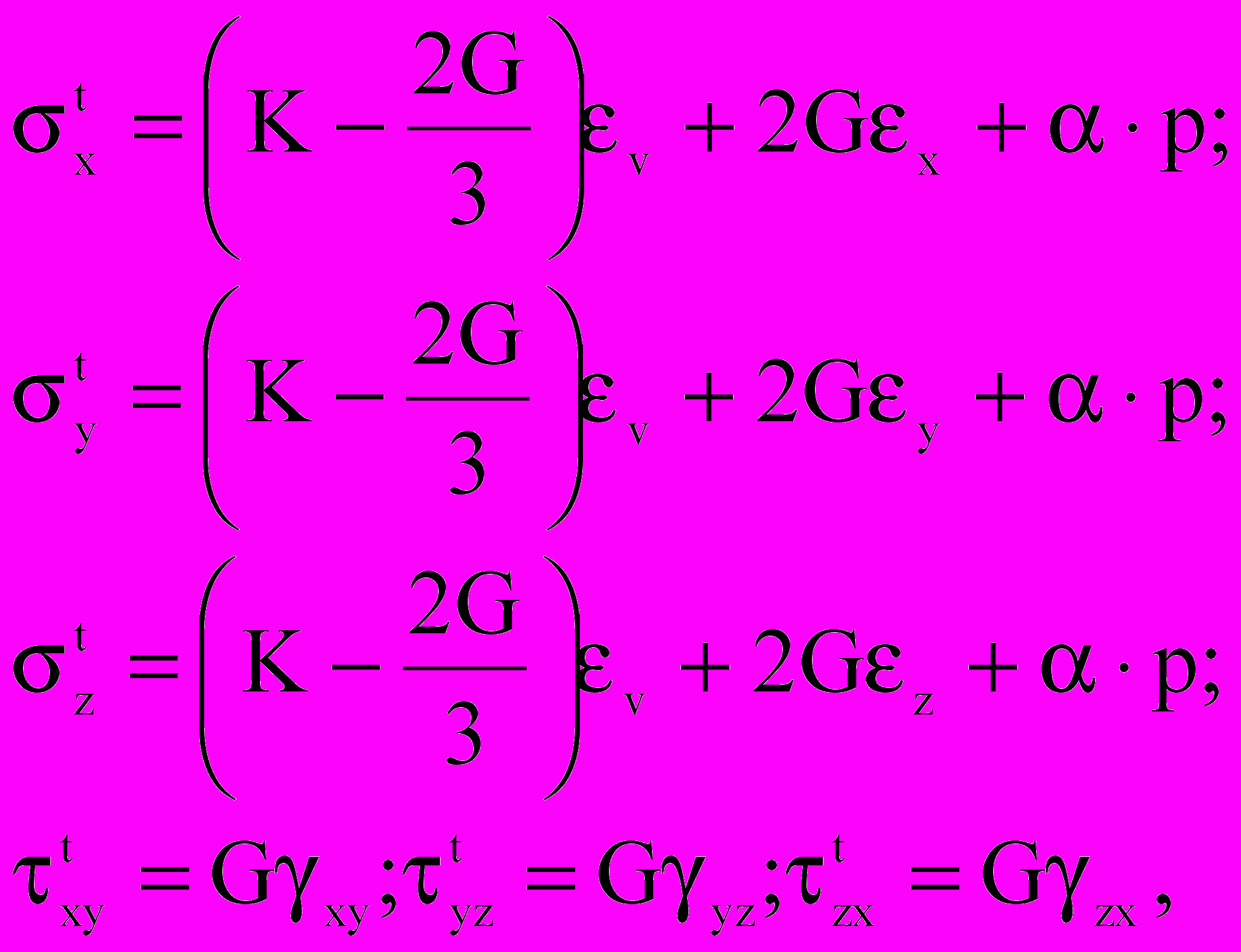
(12)

где ^t_ij - полные напряжения; K, G – модуль объемного сжатия и модуль сдвига; р – поровое давление;  - коэффициент разгрузки.

Для полной характеристики упругой пористой среды уравнения состояния (12) должны быть дополнены уравнением фильтрации находящегося в порах флюида:


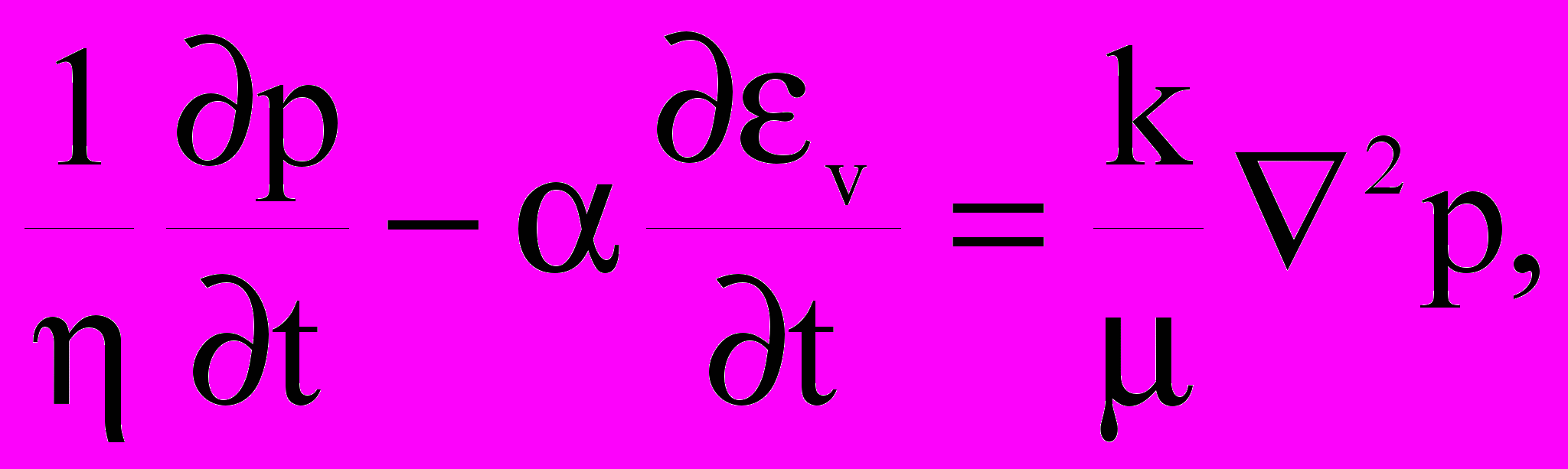
(13)

где  – модуль Био; k,  - проницаемость породы и вязкость флюида; _v – объемная деформация породы.

В наиболее общем варианте для расчета напряженно-деформированного состояния пористой среды необходимо совместное решение уравнений теории упругости (12) и уравнения фильтрации (13). Однако в ряде случаев, при определенных видах напряженного состояния, можно упростить вид уравнения фильтрации и решать его независимо от уравнений теории упругости. Например, если деформирование пород происходит с сохранением постоянного объема (_v=0), то уравнение фильтрации преобразуется к виду




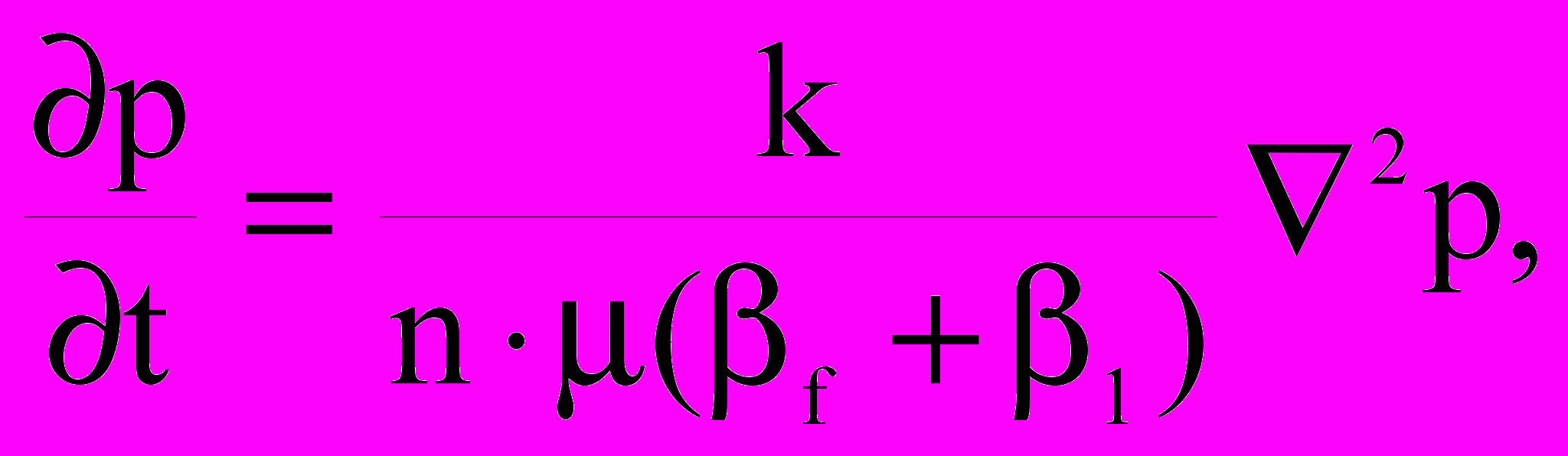
где _f – сжимаемость флюида; ₁ - сжимаемость породы при _v=0.

Другие характерные виды напряженного состояния возникают при одномерном уплотнении (_x=_y=0, ^t_z = const), при плоской деформации (_z= 0, ^t_x = ^t_y = const) и при постоянстве среднего давления: (^t_x + ^t_y + ^t_z)/3 = const. В этих случаях в уравнении фильтрации будут фигурировать коэффициенты сжимаемости породы ₂, ₃ и ₄. Т.е., уравнение фильтрации в общем виде записывается


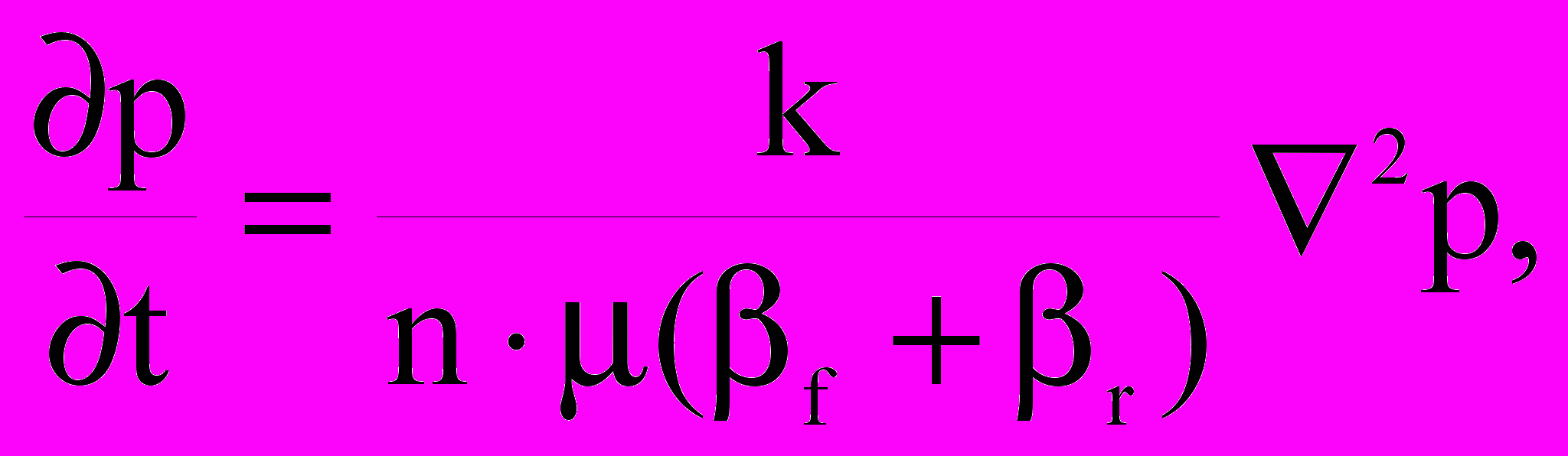
(14)

где _r – некоторый постоянный коэффициент сжимаемости породы. При этом можно показать, что при произвольном напряженном состоянии выполняется соотношение ₁  _r  ₄. Уравнение (14) решается независимо от уравнений теории упругости, т.к. не содержит в явном виде _v. Коэффициент сжимаемости флюида обычно значительно больше сжимаемости породы, поэтому общая сжимаемость системы флюид-порода _общ=(_f+_r) определяется в основном коэффициентом _f. В качестве примера в табл.2 представлены коэффициенты сжимаемости, рассчитанные для условий, характерных для нефтяных месторождений севера Пермского края.


Таблица 2 - Коэффициенты сжимаемости системы флюид-порода

Сжимаемость породы r, МПа-1	1	2	3	4
	3,25∙10-5	1,214∙10-4	1,658∙10-4	1,925∙10-4
Общая сжимаемость общ, МПа-1	1,032∙10-3	1,121∙10-3	1,166∙10-3	1,192∙10-3

Можно видеть, при изменении коэффициента сжимаемости породы от минимального значения ₁ до максимального ₄ общая сжимаемость системы _общ изменяется довольно незначительно – на 15%, а для наиболее вероятных значений  (от ₂ до ₃) изменяется еще меньше – на 5%. Подобное соотношение между коэффициентами сжимаемости характерно для большинства практических случаев, поэтому гидродинамическое моделирование разработки нефтяных и газовых месторождений производится на основе уравнений вида (14), т.е. деформационные свойства горных пород учитываются применением соответствующих коэффициентов сжимаемости _r.

Приведенные сведения показывают, что для расчета напряженно-деформиро-ванного состояния горных массивов на месторождениях нефти и газа в общем случае нет необходимости в разработке строгих методов совместного решения уравнений теории упругости (пластичности) и фильтрации флюида. Для решения поставленных в работе задач с достаточной для практических целей точностью целесообразно использовать геомеханические модели и методы расчета НДС насыщенных пористых сред при использовании показателей пластового давления в качестве исходных данных.

Наиболее простой вид напряженного состояния при добыче нефти и газа возникает при одномерном уплотнении, т.е. при отсутствии горизонтальных деформаций (_x=_y =0) и постоянстве полных вертикальных напряжений (^t_z = const). Для данных условий из уравнений закона Гука (12) можно найти вертикальную деформацию уплотнения:


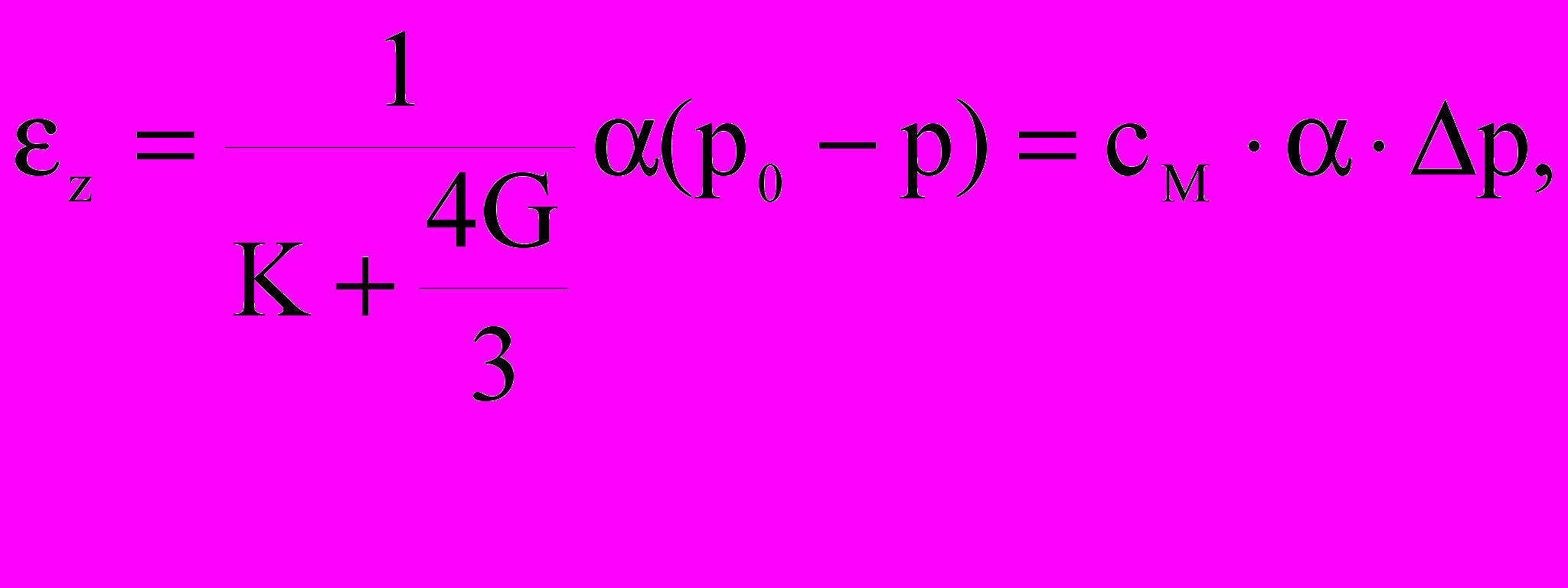
(15)

где с_м - коэффициент одномерного уплотнения; р – падение давления.

Уравнение (15) можно применять для глубоко залегающих плотных низкопористых пород, деформации которых при больших давлениях с достаточной степенью точности соответствуют теории упругости. В более общем случае необходимо учитывать специфические законы деформации пористых сред. Работы К. Терцаги, М. Био, Ф. Гасмана, В.М.Добрынина показывают, что объемные деформации пористой среды складываются из деформаций твердой фазы и порового пространства при изменении внешнего всестороннего давления ^t и давления жидкости в порах:


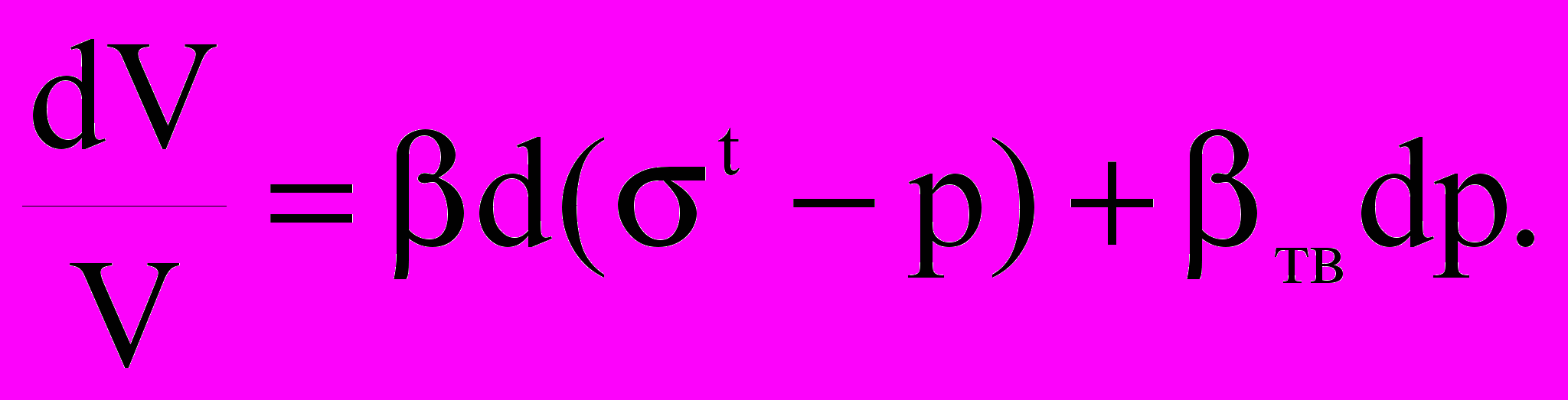
(16)


Данное уравнение преобразовывается к наиболее простому виду при использовании принципа эффективных напряжений:


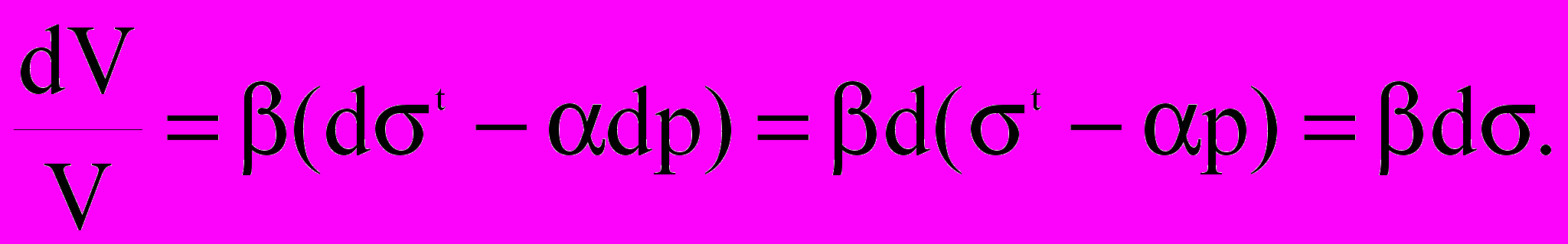
(17)


Слабой стороной методики использования эффективных напряжений является неопределенность, связанная с учетом изменения коэффициента разгрузки  при росте всестороннего давления. Однако в большинстве практических случаев зависимость коэффициента разгрузки от давления можно не учитывать, поэтому в расчетах использовались эффективные напряжения. Сжимаемость твердой фазы коллекторов принималась по табличным данным (для песчано-глинистых коллекторов _тв = 0,030 ГПа^-1, для карбонатных – _тв = 0,025 ГПа^-1), сжимаемость пор определялась по результатам компрессионных испытаний на основе зависимостей (1):


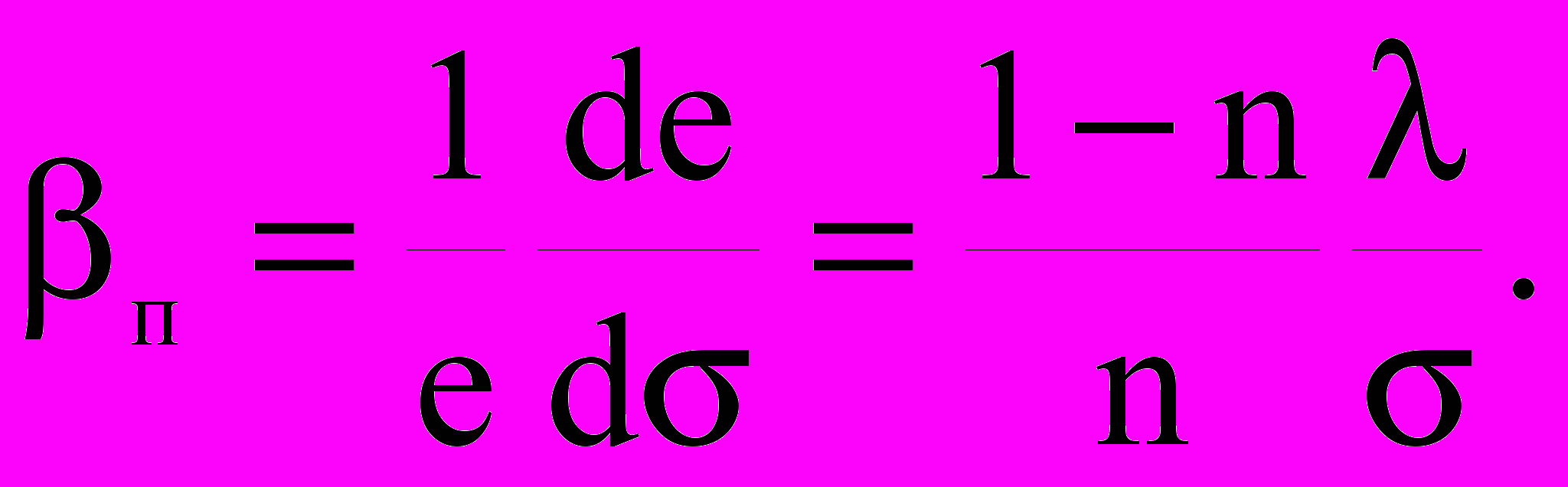
(18)


С учетом этих соотношений можно найти объемную деформацию коллектора при изменении эффективного давления от ₁ до ₂:



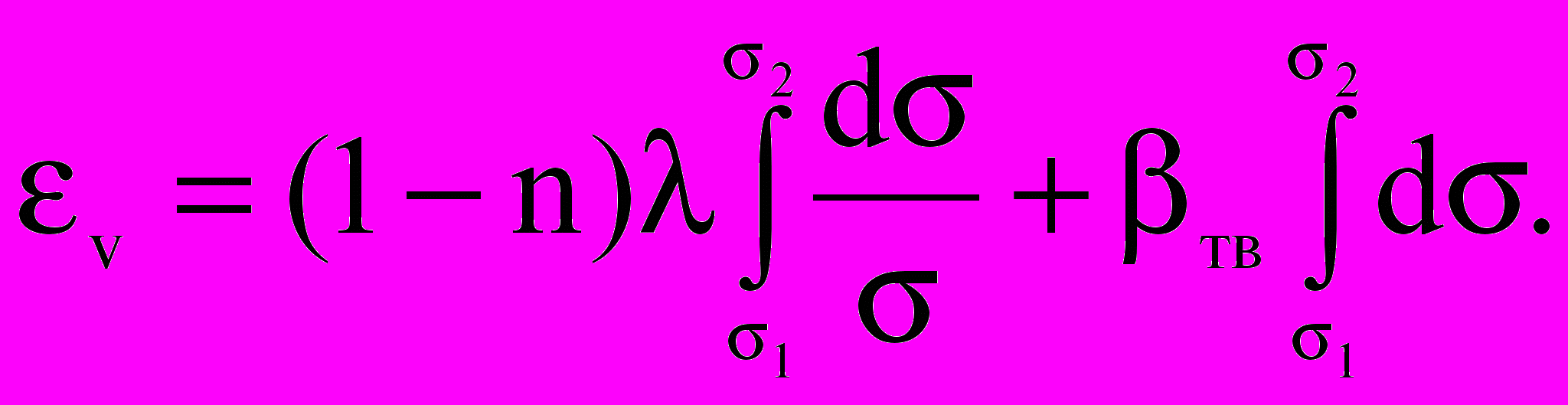
(19)


На основе выражения (19) были получены аналитические зависимости для расчета вертикальных деформаций уплотнения в различных условиях– при снижении давления в подстилающих водоносных слоях, с учетом и без учета сжимаемости твердой фазы, для коллектора большой толщины. Наиболее простой вид имеет формула для расчета уплотнения без учета сжимаемости твердой фазы:


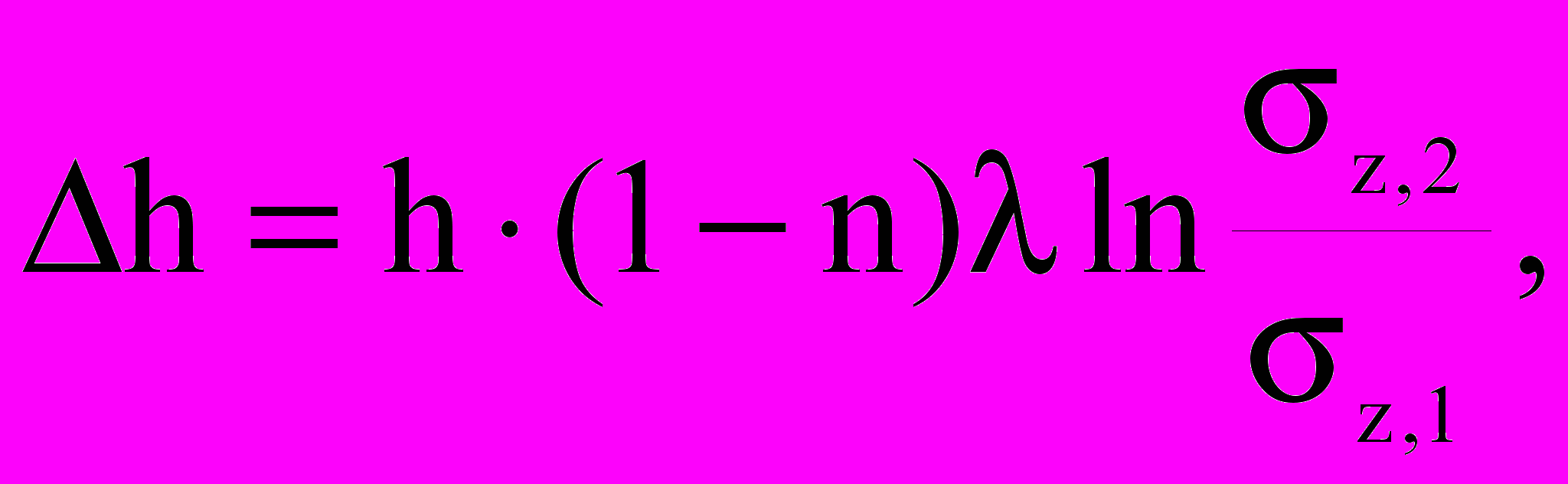
(20)


где h – уплотнение; h – начальная толщина коллектора; _z,1, _z,2 – начальное и конечное значение эффективных вертикальных напряжений.

Специальные сопоставительные расчеты показали, что использование табличных значений для сжимаемости твердой фазы коллекторов обеспечивает достаточную для практических целей точность. Даже при неучете сжимаемости твердой фазы погрешность расчета вертикальной деформации обычно не превышает 10%. Это подтверждает правомерность использования механических моделей «шатрового» типа. Поскольку величина одномерного уплотнения представляет собой верхний предел возможных оседаний поверхности, то полученные аналитические зависимости позволяют сделать предварительные выводы об общем уровне напряженного состояния массива. Это дает возможность в дальнейшем более обоснованно подходить к построению общих расчетных моделей изучаемых объектов.

Подробные расчеты напряженно-деформированного состояния выполнялись методом конечных элементов. Реализация модельных представлений основана на теории вязкопластичности, т.е. считается, что общие деформации состоят из упругой и необратимой вязкопластической составляющих:


(21)

{}={^el}+{^vp}.

Упругие деформации рассчитываются на основе закона Гука, для определения вязкопластических деформаций используется известное соотношение:


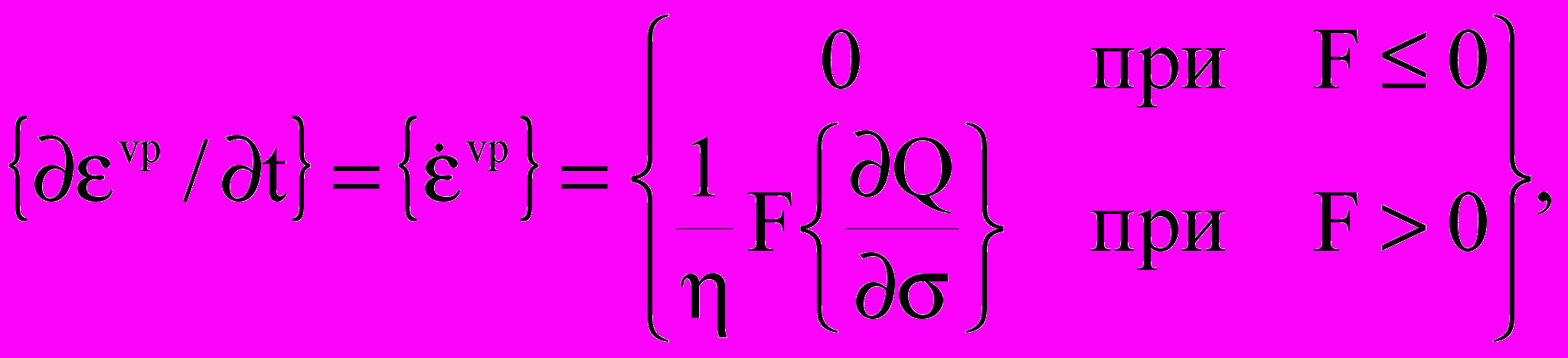
(22)


где  - параметр вязкости, играющий роль регулятора сходимости итерационного процесса. Непосредственно деформации находятся путем численного интегрирования (22) по времени:


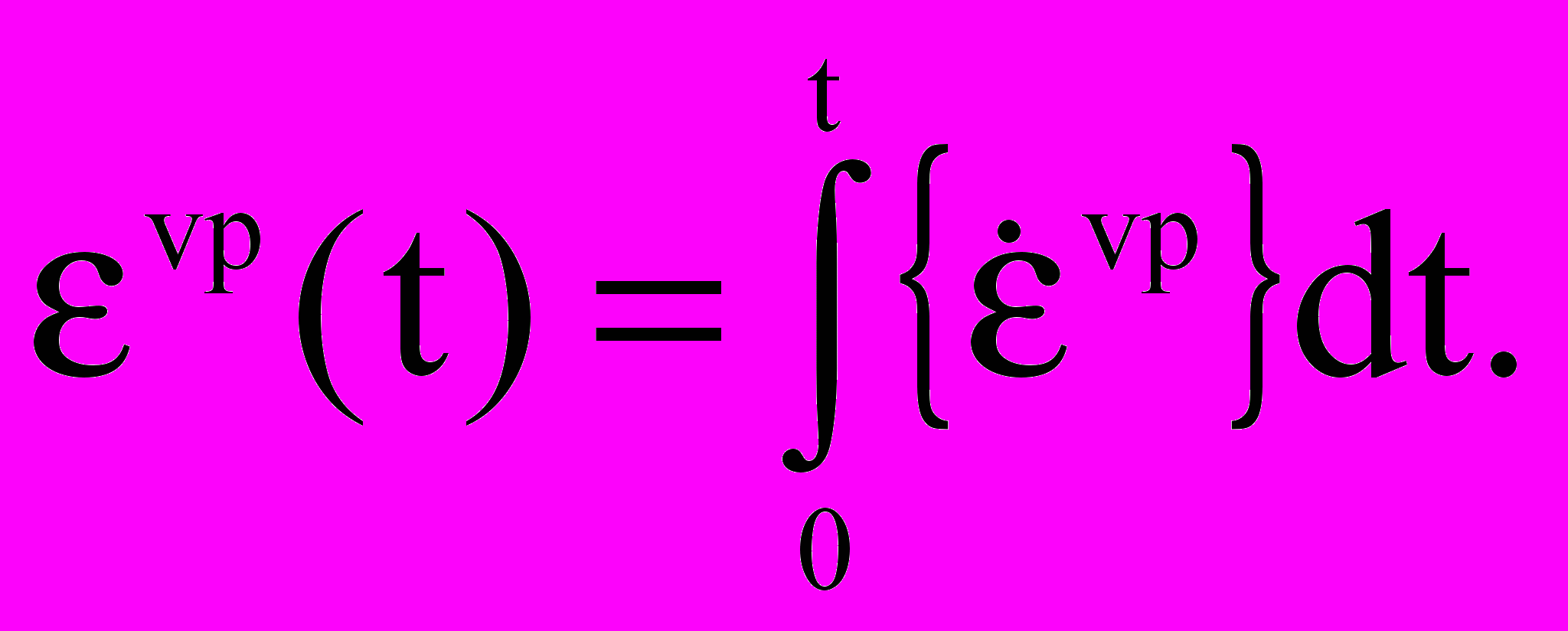
(23)


Реализация моделей была выполнена в конечно-элементных программах “GEOTECH” (разработка ПермГТУ) и “ANSYS”.

Характерной особенностью расчетов деформаций насыщенных сред является учет пластового давления на основе соотношения между полными и эффективными напряжениями:

{^t} = {} + {m}p, (24)

где { ^t } = { ^t _x,  ^t _y,  ^t _z,  ^t _xy,  ^t _yz,  ^t _zx}^т – полные напряжения;

{} = {_x, _y, _z, _xy, _yz, _zx} ^т – эффективные напряжения;

{m} = {1, 1, 1, 0, 0, 0} ^т.


С учетом (24) можно получить общее соотношение МКЕ в виде:


[K^e ] {^e} = {F^e} - {F^e_p}, (25)

где {F^e_p} – вектор дополнительных узловых сил, обусловленных давлением насыщающей жидкости.

С помощью выражения (25) был решен ряд модельных задач для исследования характера и степени влияния различных факторов на параметры уплотнения коллекторов и деформации горного массива. Рассматривались как общие моменты моделирования напряженного состояния горных массивов (выбор типа и размеров модели, задание граничных условий), так и специфические особенности, характерные для месторождений углеводородов. Было установлено, что ориентировочные размеры расчетной области по вертикали и горизонтали должны быть в 46 раз больше соответственно глубины и радиуса коллектора. При данных размерах влияние типа задаваемых граничных условий становится несущественным. Рассмотрение объемной задачи с коллектором эллиптической формы показало, при соотношении большой и малой полуосей a/b ≥ 2 профиль мульды сдвижения вдоль малой полуоси эллипса можно определять расчетом на плоской модели (плоская деформация).

Для анализа полного характера уплотнения коллекторов была выполнена серия расчетов осесимметричной модели, в которых варьировалось отношение G/G_k (G_k - модуль сдвига пород коллектора, G - модуль сдвига вмещающих пород) и отношение R/H (R – радиус коллектора, H – глубина залегания). По результатам расчетов строились графики относительного уплотнения (h/h^max) в зависимости от текущего радиуса r (рис.7) для анализа характера уплотнения на всем протяжении продуктивных пластов (максимальное значение h^max соответствует условиям одномерного уплотнения).



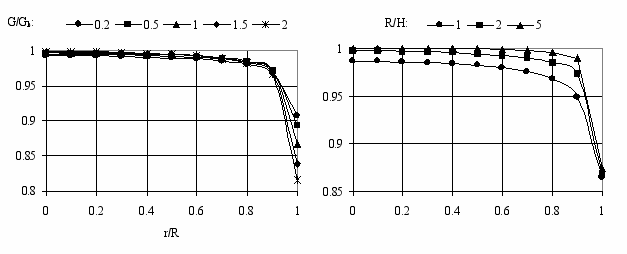
Рис. 7. Влияние упругих свойств вмещающих пород и геометрических размеров

коллекторов на характер их уплотнения.