Методы риск-менеджмента

О том, что ведение бизнеса связано с различного рода рисками, люди знают давно. С давних пор предприниматели считаются людьми рисковыми. В самом деле, в те времена нужно было обладать недюжинной отвагой, чтобы решиться на деревянном судне переплыть океан в поисках уникального товара, положившись на волю ветров и морской пучины. Дальняя дорога автоматически означала высокорискованность всей затеи, однако и цена за риск была высокой: чем дальше товар закупался, тем дороже его можно было продать в силу отсутствия конкурентов. Уже тогда предприниматели стали интуитивно понимать основное правило современного риск-менеджмента: «Чем выше ожидаемая прибыль, тем выше сопутствующий риск».

В современном обществе одной из главных задач является оценка рискованности стратегии финансового управления. В более частном случае требуется оценить рискованность стратегии размещения средств на фондовом рынке. Поскольку задача эта сложная, то и характеризоваться она одним показателем, например, полученной прибылью за определённый срок, не может. В результате анализа возможных стратегий управления удалось сформулировать тринадцать показателей, которые в совокупности дают полную картину эффективности управления.

Показатели эффективности стратегии игры.
1. Количество сделок – полное количество операций (считается только число закрытых на конец анализируемого периода сделок).
2. Полная прибыль – накопленная прибыль в процентах от первоначальных вложений.
3. Максимальная прибыль за одну сделку – максимальная прибыль (в процентах), полученная в одной сделке.
4. Средняя прибыль на одну сделку – отношение полной прибыли (в процентах) к количеству сделок.
5. Максимальная положительная серия – длина максимальной серии положительных сделок.
6. Доля прибыльных сделок – процентное отношение количества прибыльных сделок к полному количеству сделок.
7. Максимальное падение капитала – наибольшие совокупные потери за анализируемый период (см. поясняющий рис. 1 ниже).
8. Максимальный убыток за одну сделку – максимальный убыток, понесенный в одной сделке.
9. Максимальная отрицательная серия – длина максимальной серии отрицательных сделок.
10. Доля убыточных сделок – процентное отношение количества убыточных сделок к полному количеству сделок.
11. Максимальная нулевая серия – длина максимальной серии неучастия в торгах.
12. Вознаграждение/Риск – отношение полной прибыли к максимальному падению капитала.
13. Вознаграждение/Риск в одной сделке – отношение максимальной прибыли в одной сделке, к максимальному убытку в одной сделке.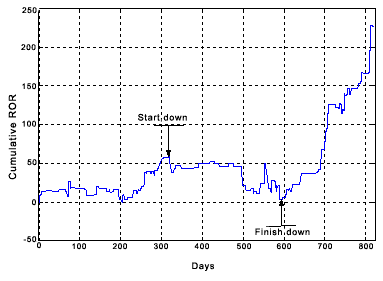

Рисунок 1. Максимальное падение капитала.

В данном случае мерой риска выступает максимальный убыток – либо в одной сделке, либо за весь анализируемый интервал времени.
В 60-х гг. математик Г. Марковиц предложил другую величину, характеризующую риск. Это позволило ему формализовать задачу минимизации риска портфеля активов и найти эффективное её решение. Так родилась теория оптимального портфеля. С помощью этой теории можно составлять максимально диверсифицированные портфели – такие, риск которых минимален по сравнению со всеми другими возможными портфелями из акций тех же компаний. В качестве меры риска Марковиц рассматривает стандартное отклонение, характеризующее вероятность отклонения доходности портфеля от ожидаемого значения. Чем больше стандартное отклонение, тем более рискованный портфель, потому что вероятность отклонения от ожидаемой доходности портфеля выше. Таким образом, любой портфель можно охарактеризовать двумя параметрами – ожидаемой доходностью и риском. Если построить плоскость в координатах доходность/риск, то любой портфель может быть изображён точкой на этой плоскости, а все возможные портфели из заданного набора акций образуют облако, как на рис.2.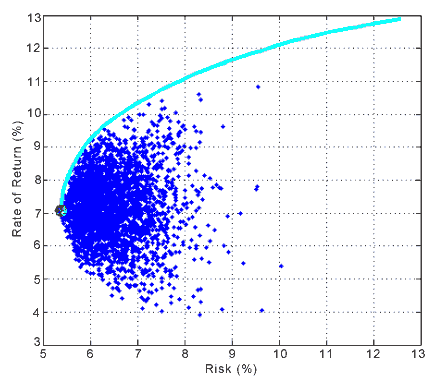

Рисунок 2. Эффективная граница и случайные портфели.

Как видно из рисунка, множество всех возможных портфелей имеет чёткую границу слева. Это значит, например, что при риске 6% из данных акций нельзя составить портфель с ожидаемой доходностью меньше 5% и больше 9%. С практической точки зрения интерес представляет верхняя часть границы, которая называется эффективной границей. При заданном уровне риска портфеля с большей ожидаемой доходностью, чем тот, что находится на эффективной границе, не существует. И наоборот, при заданном уровне ожидаемой доходности невозможно сформировать портфель с меньшем уровнем риска.
Кроме того, существует портфель с минимально возможным риском – так называемый минимальный портфель. На рис.2 он показан красной точкой. Портфель с меньшим риском (при любой ожидаемой доходности), чем у минимального портфеля, сформировать невозможно.
С момента создания классической теории появился ряд полезных усовершенствований. В частности, подобным образом можно формировать портфели с возможностью коротких продаж. Согласно этой модели определяется, сколько и каких активов нужно продать и как оптимальным образом распределить средства между оставшимися. Такое обобщение носит название модели Блэка, и основное её отличие состоит в возможности формирования портфелей с любой заданной доходностью. При этом не надо забывать, что и риск меняется соответственно. Есть и другие, более тонкие, новшества. Они связаны со способом расчёта необходимых для вычислений параметров – ожидаемой доходности портфеля акций и матрицей ковариаций, отражающей степень их взаимосвязи.
При выполнении некоторых предположений о характере фондового рынка можно развить теорию оптимального портфеля и построить модель, которая связывает ожидаемую доходность выбранного актива (или портфеля) с ожидаемой доходностью рыночного портфеля, в качестве которого часто берут один из основных рыночных индексов, например, S&P500. Такая модель была разработана рядом крупных исследователей финансового рынка, прежде всего, лауреатом Нобелевской премии Уильямом Шарпом, а также Джоном Линтнеру, Джеком Трейнору и Яном Моссиным, и носит название САРМ – модель ценообразования основных активов.
При выводе САРМ были сделаны следующие допущения:
• инвестор руководствуется только двумя факторами – доходностью и риском;
• инвесторы действуют рационально – при одной и той же ожидаемой доходности они предпочитают актив с минимальным риском;
• все инвесторы имеют один и тот же инвестиционный горизонт;
• оценки основных параметров активов инвесторы производят одинаковым образом;
• поведение индивидуального инвестора не влияет на равновесные цены актива;
• нет операционных издержек или помех, препятствующих свободному спросу и предложению активов.
Фактически, модель представляет собой регрессию относительных приращений цены выбранного актива (или портфеля) и рыночного портфеля. Чтобы построить графическую интерпретацию модели, нужно нанести на плоскость точки, горизонтальные координаты которых представляют доходности рыночного портфеля, а вертикальные – соответствующие доходности актива. Если внимательно посмотреть на образовавшееся облако точек, можно заметить, что оно вытянуто вдоль некоторой прямой – характеристической прямой ценной бумаги (см. рис.3).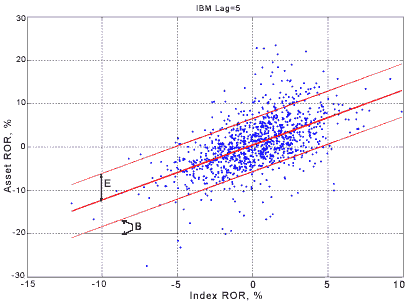

Рисунок 3. Графическая интерпретация модели САРМ.

Основное утверждение модели – курсовая доходность выбранного актива (или портфеля) прямо пропорциональна курсовой доходности рыночного портфеля.
Двумя важными параметрами, характеризующими конкретный актив, являются:
• показатель «бета», характеризующий угол наклона прямой;
• показатель Е, харатеризующий степень концентрации облака вдоль прямой.
«Бета» является показателем чувствительности актива к изменению цены рыночного портфеля. Если, например, «бета» равно 1.5, это значит, что при изменении рыночного портфеля на +1% цена актива изменится на +1.5 %. Более чувствительным к рынку активам соответствуют большие значения «бета». Этот показатель отвечает за систематический (или рыночный) риск актива, который нельзя диверсифицировать.
Показатель Е отражает «остаточную» доходность, зависящую от специфики конкретного актива. Ему соответствует несистематический риск, который можно уменьшить путём составления портфеля активов.
Обобщением модели САРМ можно считать модель арбитражной теории ценообразования (АРТ модель), хотя последняя выводилась из других предположений. В основу арбитражной теории ценообразования заложено одно утверждение: в условиях равновесного рынка арбитраж (любого вида) невозможен. Если такая возможность есть, рынок быстро её «ликвидирует». Под арбитражем понимается получение гарантированной прибыли на фондовом рынке. Дальнейшие рассуждения по поводу невозможности создания арбитражного портфеля приводят к основному уравнению ценообразования активов, которое и может рассматриваться как практический результат теории. Интересно отметить тот факт, что уравнение АРТ является обобщением уравнения САРМ, хотя арбитражная теория строилась как её альтернатива. Согласно этому уравнению, на изменение стоимости актива влияет не только рыночный фактор (стоимость рыночного портфеля), но и другие, в том числе нерыночные, факторы риска – курс национальной валюты, стоимость энергоносителей, уровень инфляции и безработицы и так далее. Если в качестве факторов риска рассматривать только один – стоимость рыночного портфеля, - то уравнение совпадает с уравнением САРМ. Учёт нескольких факторов позволяет строить более строгую модель. Это приводит к более точному прогнозу изменения цены актива и уменьшению несистематического риска даже без составления больших портфелей.
В классической модели САРМ учитывался только один фактор, и актив характеризовался двумя параметрами – коэффициентом чувствительности «бета», характеризующим риск, связанный с этим фактором, и средней остаточной доходностью Е, отвечающей за специфический риск, то есть риск, не объясняющийся влиянием выбранного фактора. В модели АРТ появилась возможность учитывать несколько факторов. Теперь актив характеризуется набором показателей «бета», каждый из которых представляет собой чувствительность актива к определённому фактору и характеризует систематический риск, связанный с влиянием именно этого фактора, и, по-прежнему, остаточной доходностью Е. Только теперь величина специфического (необъяснённого факторами) риска стала гораздо меньше.
С развитием математического аппарата стали появляться новые, более сложные, технологии оценки рисков. Одной из них является технология Value-at-Risk (VaR), получившая довольно широкую известность. В основе этой технологии лежит оценка возможных будущих потерь с достаточной степенью надёжности. Если, например, приобретён портфель акций (длинная позиция), и стоимость портфеля на текущий момент составляет 100 единиц, то выражение «недельный VaR этого портфеля составляет 20 % по уровню доверия 0.95» следует понимать так:
вероятность того, что стоимость портфеля в течение недели уменьшится более чем на 20 единиц, составляет 5 %; или, что эквивалентно, так:
вероятность того, что стоимость портфеля в течение недели не упадёт более чем на 20 единиц, составляет 95 %.
С точки зрения статистики показатель VaR является квантилем (по определённому доверительному уровню) распределения изменений цен. Например, если относительные изменения цен распределены по стандартному нормальному закону (с нулевым средним и единичной дисперсией), то пятипроцентный квантиль будет равен –1.65 (см. рис. 4).
Одним из известных показателей, основанных на технологии VaR, является показатель Expected Short Fall (ESF). Если VaR определяет пограничный уровень, который возможные потери не превысят с заданной вероятностью, то ESF показывает величину этих потерь в случае, если неблагоприятное стечение обстоятельств всё же произошло. Другими словами, он оценивает, насколько потери превысят пограничный уровень, определяемый VaR. Так, чтобы определить этот показатель на рис.4, нужно найти среднее значение закрашенной области.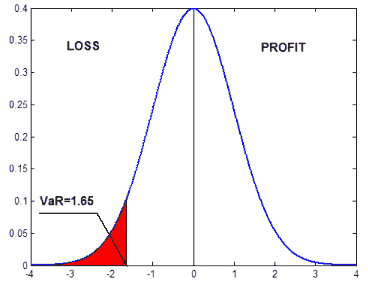

Рисунок 4. Иллюстрация к понятию VaR.

На сегодняшний день технологии, основанные на VaR, безусловно, являются мощнейшим инструментом риск-менеджмента. Однако следует признать, что существует ряд проблем при их практическом применении. Некоторые из проблем связаны с отсутствием исторических данных, другие - с тонкостями методов вероятностных оценок, но наиболее важными, видимо, следует считать проблемы, связанные с составлением отображения флуктуаций факторов риска в возможные потери. В приведённом выше примере такой проблемы не возникает, поскольку оценивается изменение цены, напрямую приводящее к потерям. В более сложных стратегиях эта связь может быть не столь очевидна, её идентификация и отслеживание зачастую требует гораздо больших интеллектуальных усилий. Но это уже отдельная тема для размышлений.
e-MasterTrade

Ведущий специалист группы
математического моделирования
Вечерин С. Н.

Blog

Методы риск-менеджмента

Содержание

МЕТОДЫ РИСК-МЕНЕДЖМЕНТА