Литература: [1,8-11,16,18]

Вид материала

Подобный материал:

1 2

§4. Решение задачи ЛП двухфазным симплекс-методом

Двухфазный симплекс-метод (или. метод искусственного базиса) применяется в тех случаях, когда и задаче ЛП в канонической форме затруднительно определить н.д.б.р. с помощью эквивалентных преобразований (привести систему ограничений к диагональному виду).

Пример 7. Следующую задачу ЛП решить двухфазным симплекс-методом:

min f(x)=x1-x2+1 (13)

при ограничениях

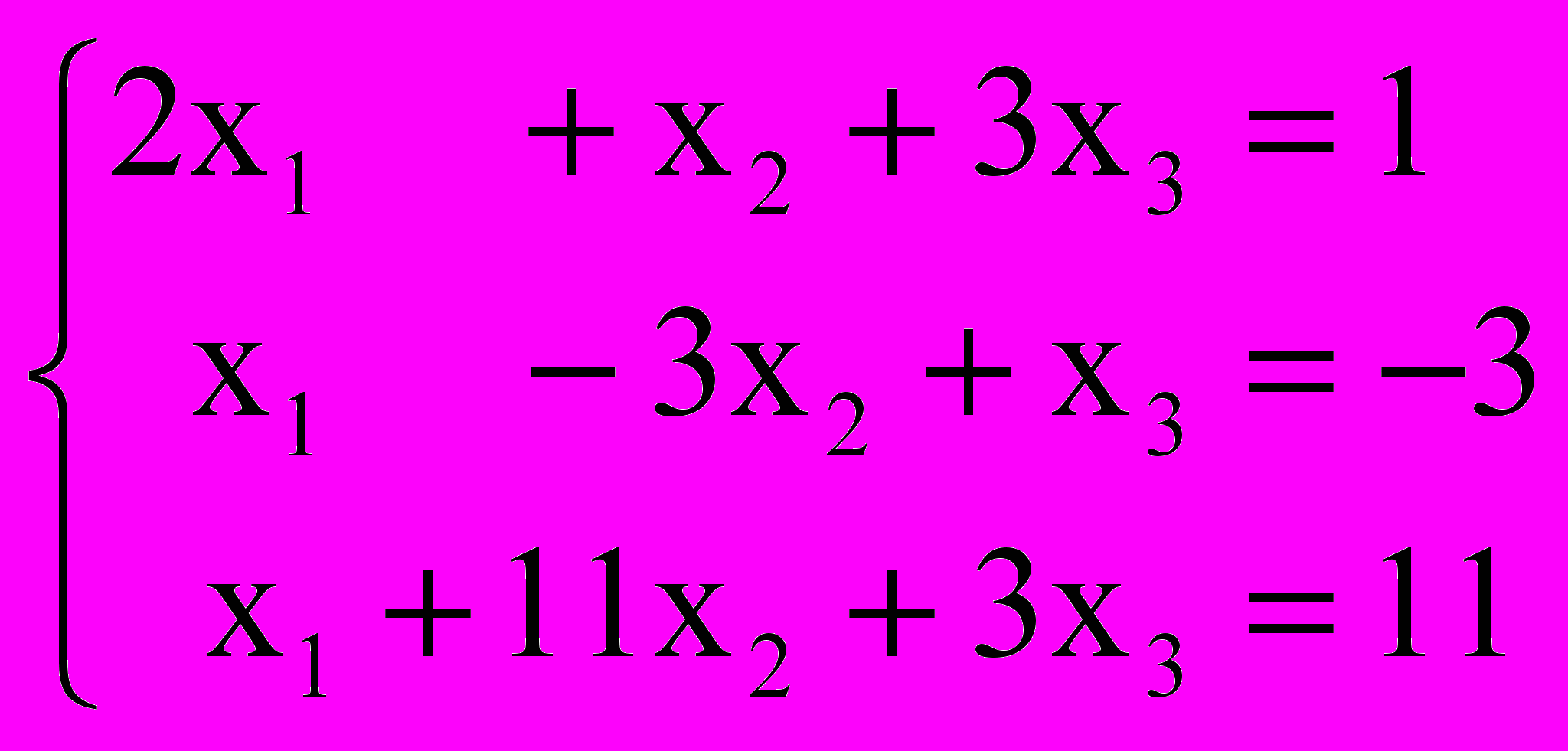(14)

x₁, x₂, x₃≥0 (15)

Первая фаза (цель: при- помощи искусственного базиса и симплекс-метода определить базисные переменные из числа исходных переменных).

В систему (14) вводим искусственные переменные x₃≥0, x₅≥0, x₆≥0 (предварительно умножив обе части второго неравенства на -1), новую целевую функцию как сумму всех искусственных переменных, а старую присоединяем к ограничениям:

min z(x) = x₄ + x₅ + x₆ (16)

при ограничениях

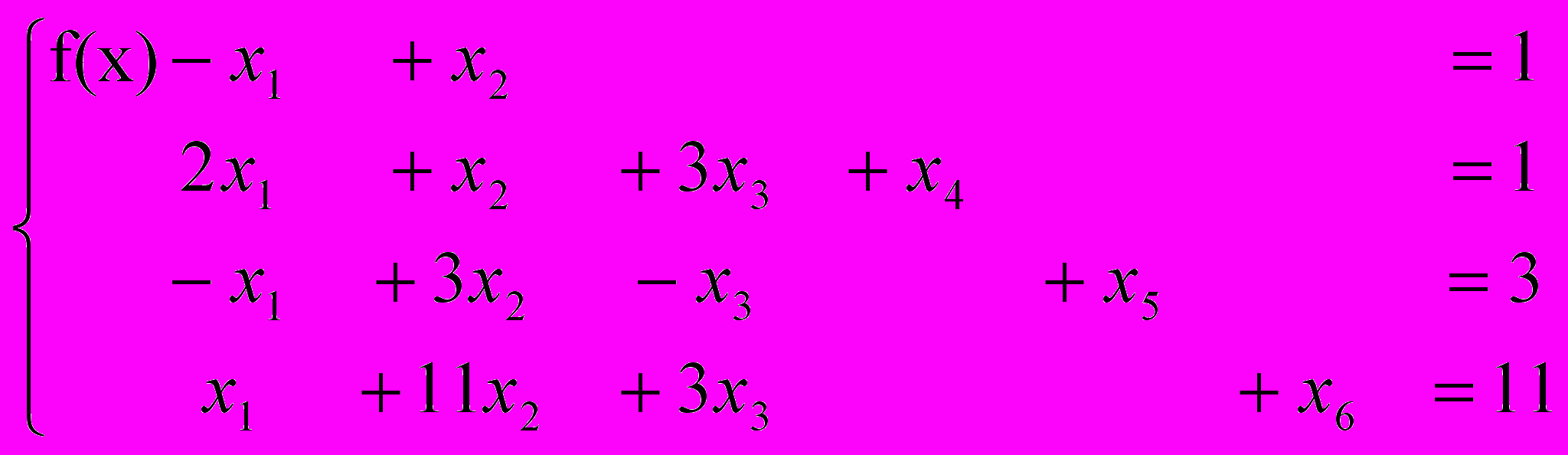(17)

Искусственные переменные x₄, x₅, x₆ выбираем в качестве базисных, а все остальные x₁, x₂, x₃ - небазисных. По правилу симплекс-метода исключаем базисные переменные из целевой функции (16) (при помощи уравнений системы (17), содержащих эти переменные):

z(x)= -2 x₁ - 15 x₂ - 5 x₃ + 15

или, что все равно

z(x)+2x₁+15 x₂+5 x₃=15 (19)

Начальное д.б.р.

x⁰=(x₁⁰, x₂⁰, x₃⁰, x₄⁰, x₅⁰, x₆⁰)=(0, 0, 0, 1, 3,11)

называется искусственным базисом. При помощи этого базиса, и выражений (19), (17) строим начальную симплекс-таблицу I-ой фазы.

		x₁	x₂	x₃	x₄	x₅	x₆
z	15	2	15	5	0	0	0
f	1	-1	1	0	0	0	0
x₄	1	2	(1)	3	1	0	0
x₅	3	-1	3	-1	0	1	0
x₃	11	1	11	3	0	0	1

До конца I фазы роль нулевой строки играет строка для z, все остальное как в симплекс-методе (см. примеры 5,6). Следует только заметить, что строка для f не участвует в выборе ведущей строки.

Из (16) видно, что min z(x) = 0 и достигается при x₄= x₅ = x₆=0, те, задача (16)-(18) будет решена, если все искусственные переменные будут вытеснены из базиса, а z=0. Это и будет означать конец первой фазы и переход ко второй фазе.

Обратите внимание, что в первой таблице ведущей может быть любая из последних трех строк (предвестник зацикливания). В таких случаях можно выбрать любой из них - выберем первую строку.

Так как искусственная переменная x₄ выходит из базиса, то соответствующий столбик в дальнейшем можно исключить.

В результате соответствующих преобразований получим вторую симплекс-таблицу.

		x₁	x₂	x₃	x₄	x₅
z	0	-28	0	-40	0	0
f	0	-3	0	-3	0	0
x₂	1	2	1	3	1	0
x₅	0	-7	0	-10	0	1
x₆	0	-21	0	-30	0	0

Из таблицы следует, что min z достигнут, однако искусственные переменные x₅ и x₆ еще не выведены из базиса. В такой ситуации правила симплекс-метода "не работают" (т.к. ввиду отсутствия в нулевой строке положительных оценок нельзя выбрать ведущий столбик). Задача здесь одна - вывести оставшиеся искусственные переменные из базиса. Выведем сначала x₅. Умножим все элементы этой строки на -1 (что допустимо, т.к. в нулевом столбике стоит 0). Введем в базис вместо x₅ переменную x₁. С этой целью строку для x₅ поделим на 7 и с "ведущим элементом" 1 выполним элементарные преобразования (как в симплекс-методе). В результате получим таблицу:

		x₁	x₂	x₃	x₆
z	0	0	0	0	0
f	0	0	0	9/7	0
x₂	1	0	1	1/7	0
x₁	0	1	0	10/7	0
x₆	0	0	0	0	1

Остается в базисе еще x₆. Ее из числа базисных вывести нельзя, так как все элементы таблицы равны нулю, кроме 1 в столбике для x₆. Это говорит о том, что в системе (14) третье уравнение было "лишним" и потому последнюю строку таблицы можно вычеркнуть. Действительно, третье уравнение в (14) является линейной комбинацией первых двух (оно получается вычитанием второго уравнения, умноженного на 3, из первого уравнения, умноженного на 2),

Вычеркивая столбик для x₆и строку для z приходим к таблице,

		x₁	x₂	x₃
f	0	0	0	9/7
x₂	1	0	1	1/7
x₁	0	1	0	10/7

содержащей только элементы исходной задачи (13)-(15) и с базисными переменными из числа исходных переменных.

Таким образом, задача I фазы выполнена.

Вторая фаза (цель: применяя обычный симплекс-метод к полученной в результате I фазы таблице, получить оптимальное решение исходной задачи).

Д.б.р. для последней таблицы есть

x⁰=(0, 1, 0)

Заметим, что это вырожденное д.б.р., так как в нем базисная переменная x₁ - 0. То есть здесь мы можем получить зацикливание.

В качестве упражнения II фазу предлагается сделать самостоятельно.

Теперь можно привести алгоритм двухфазного симплекс-метода:

1) привести задачу ЛП к канонической форме;

2) ввести в ограничения искусственные переменные и составить новую целевую функцию z;

3) исключить из новой целевой функции все искусственные переменные;

4) используя искусственные переменные в качестве базисных, построить начальную симплекс-таблицу;

5) использовать симплекс-метод, исключая из таблиц столбики для искусственных переменных по мере их выхода из базиса до тех пор, пока min z=0 и все искусственные переменные не будут выведены из базиса;

6) вычеркнуть строчку для z и перейти ко второй фазе;

7) во второй фазе, к таблице, полученной в результате первой фазы, применить симплекс-метод до тех пор, пока не найдется оптимальное решение исходной задачи или не выявится его отсутствие.

П р и м е ч а н и я к двухфазному симплекс-методу

1. Если в результате первой фазы окажется, что min z > 0, то система ограничений исходной задачи (в канонической форме) несовместна. Во всех остальных случаях первая фаза разрешима.

2. Если min z= 0 и в таблице остались искусственные переменные, то, используя элементарные преобразования, эти переменные следует вывести из числа базисных, а вместо них ввести исходные переменные (см. пример 7).

3. Пусть каноническая форма задачи ЛП получена с помощью слабых переменных. Применение двухфазного симплекс-метода упростится, если искусственные переменные ввести только в те ограничения, ж которых слабая переменная либо отсутствует (исходное ограничение-равенство), либо не может войти в базис (введена в ограничение со знаком минус).

§5. Решение транспортной задачи методом потенциалов.

В экономике существует большое число задач, сводимых к моделям транспортных задач (см., например, задачи в разделе I). Условие классической транспортной задачи (ТЗ) дано в §4 раздела I, а ее математическая модель - в том же разделе формулами (5)-(8).

Обозначим через P₁,...,P_n пункты производства (или хранения) продукции, а через M₁,...,M_m -пункты ее потребления. В модели (5)-(8);.

c_ij- стоимость перевозки единицы продукции по маршруту (P_i, M_j);

xij - объем перевозок по маршруту (Pi, Mj);

ai - предложение в пункте Pi;

bj - спрос в пункте Mj

Известными являются следующие данные: (a₁,...,a_m) - вектор предложений, b=(b₁,...,b_n) - вектор спроса,

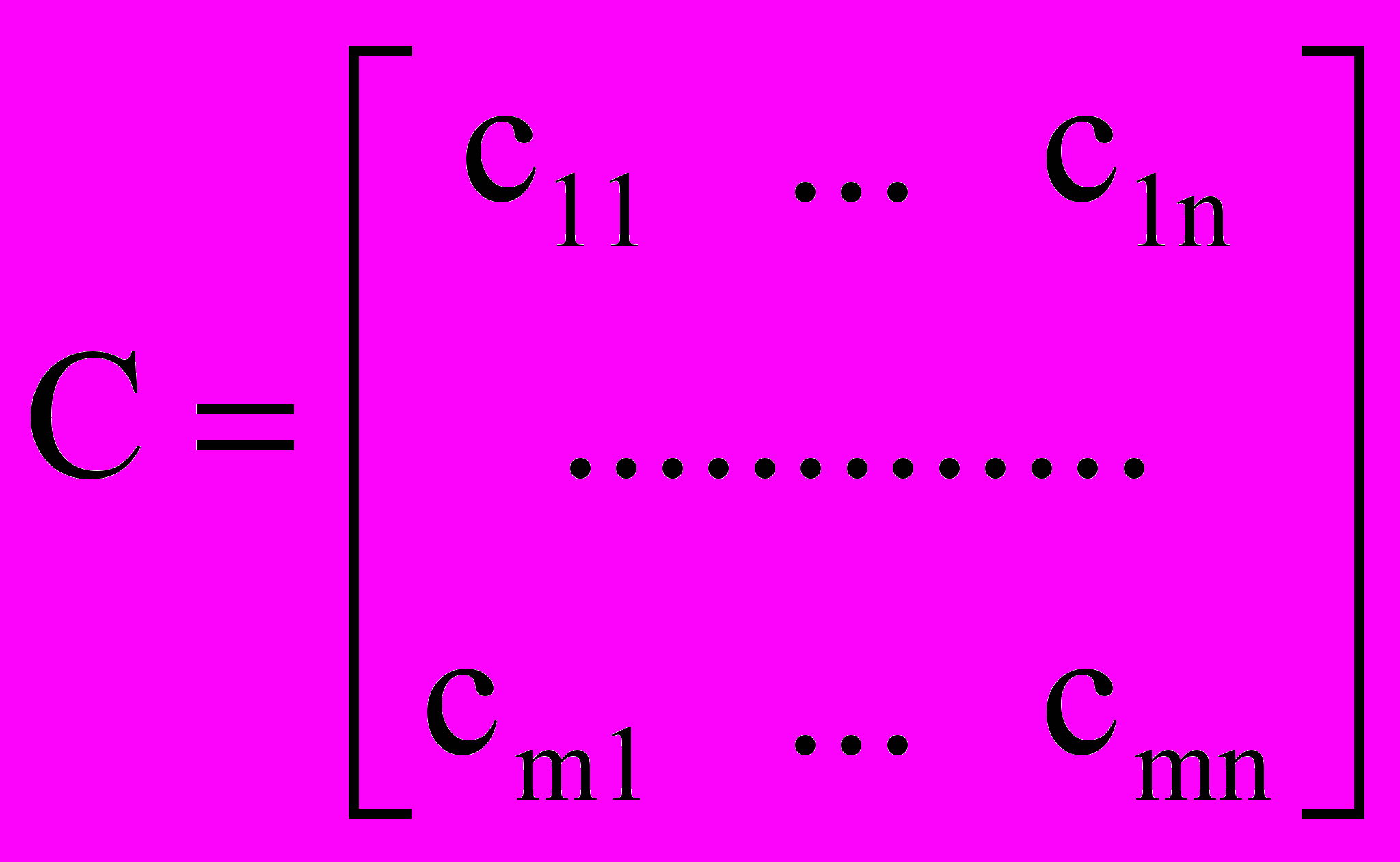- матрица транспортных издержек.

Неизвестными являются перевозки x_ij, т.е. матрица (или план) перевозок

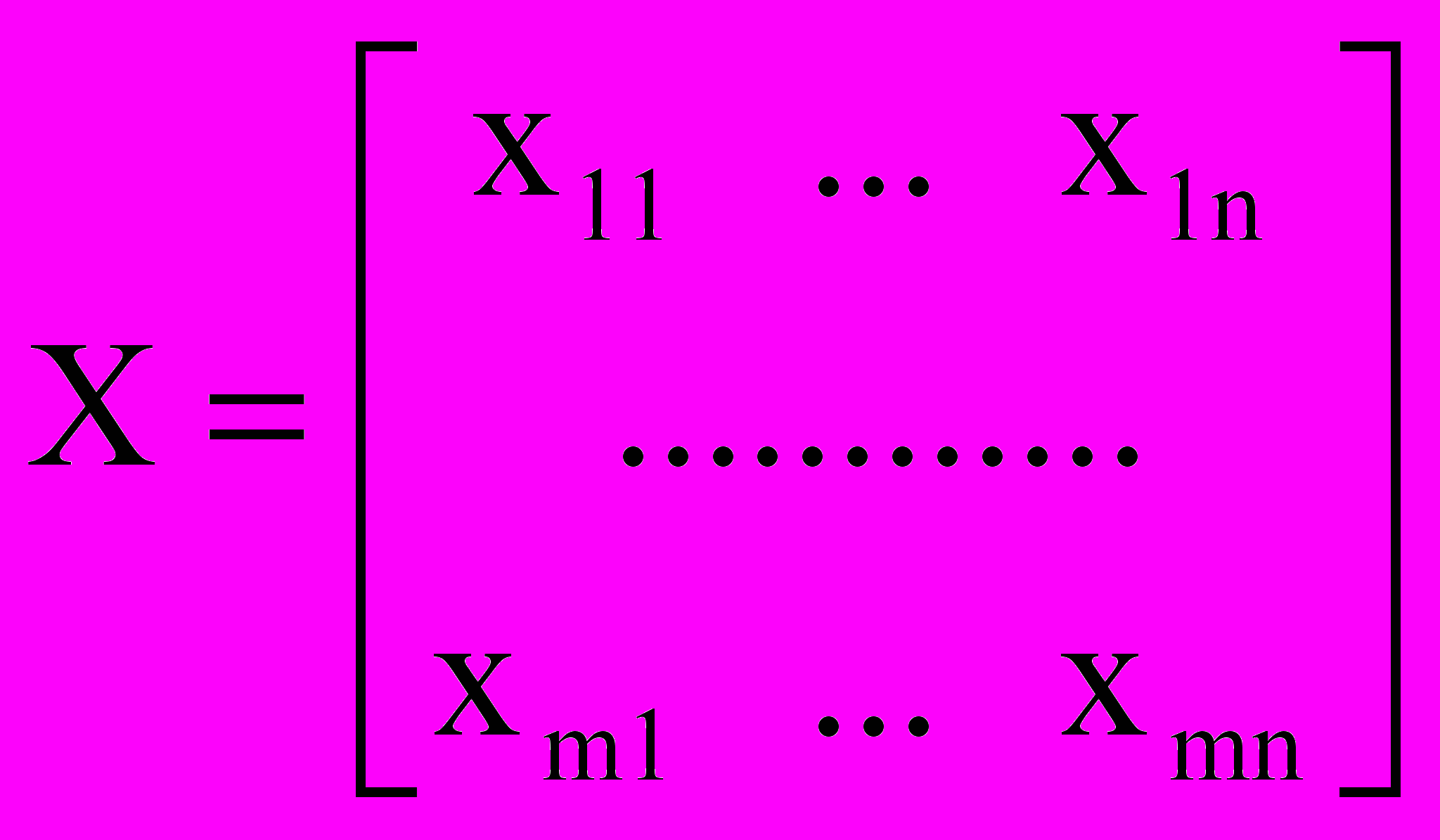
В задаче (5) - (8) требуется найти такой план перевозок X*, чтобы:

1) Элементы этой матрицы удовлетворяли всем ограничениям (6) - (8) (условие допустимости).

2) Элементы этой матрицы соответствовали минимальному значению целевой функции (5) (условие оптимальности).

Такой план называется оптимальным планом перевозок. Метод решения ТЗ называется методом потенциалов.

Если пункты производства P₁,...,P_m трактовать как филиалы одной фирмы, то в ТЗ лицом принимающим решение (планирующим органом), является эта фирма.

Свойства транспортной задачи.

1.ТЗ имеет оптимальное решение тогда и только тогда, когда

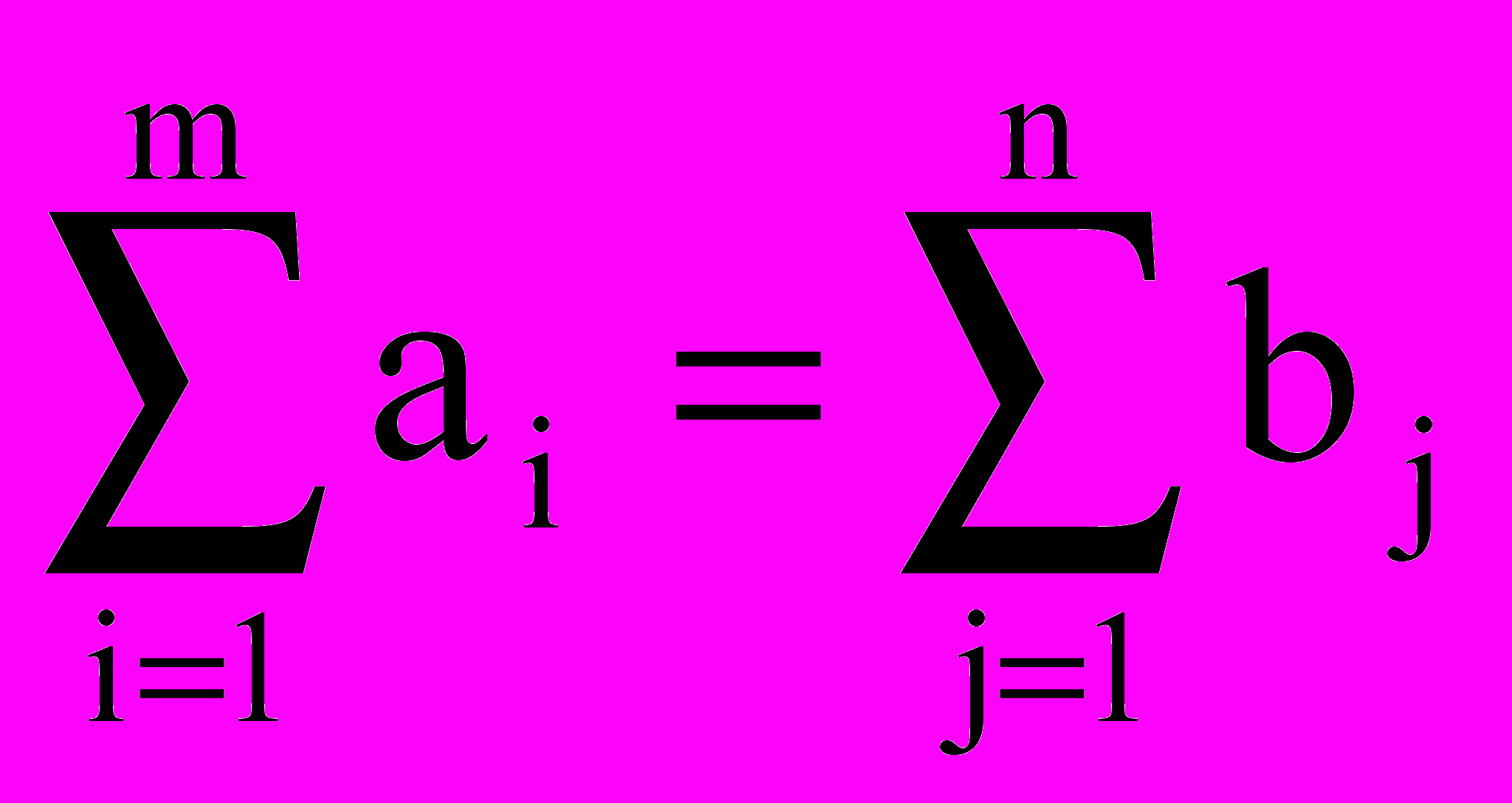(20)

2. Если план X* является оптимальным, то ему соответствует система из m+n чисел u₁,…,u_m и v₁,…,v_n (называемых потенциалами), удовлетворяющих условию:

ui+vj=cij для всех xij>0, (21)

ui+vj≤cij для всех xij*=0, (22)

3. Если все числа a1,...,am и b1,...,bm - целые и выполнено условие (20), то элементы оптимального плана являются целыми числами.

4. Ранг системы векторов условий ТЗ (т.е. число линейно независимых столбцов матрицы ограничений) равен m+n-1. План перевозок X, содержащий ровно m+n-1 ненулевых перевозок, называется опорным планом (ОП) и играет роль д.б.р. в задаче ЛП. План, содержащий меньше чем m+n-1 ненулевых элементов называется вырожденным.

Пример 8. Решить следующую ТЗ методом потенциалов.

а=(40,30,20),

b=(30,25,15,20),

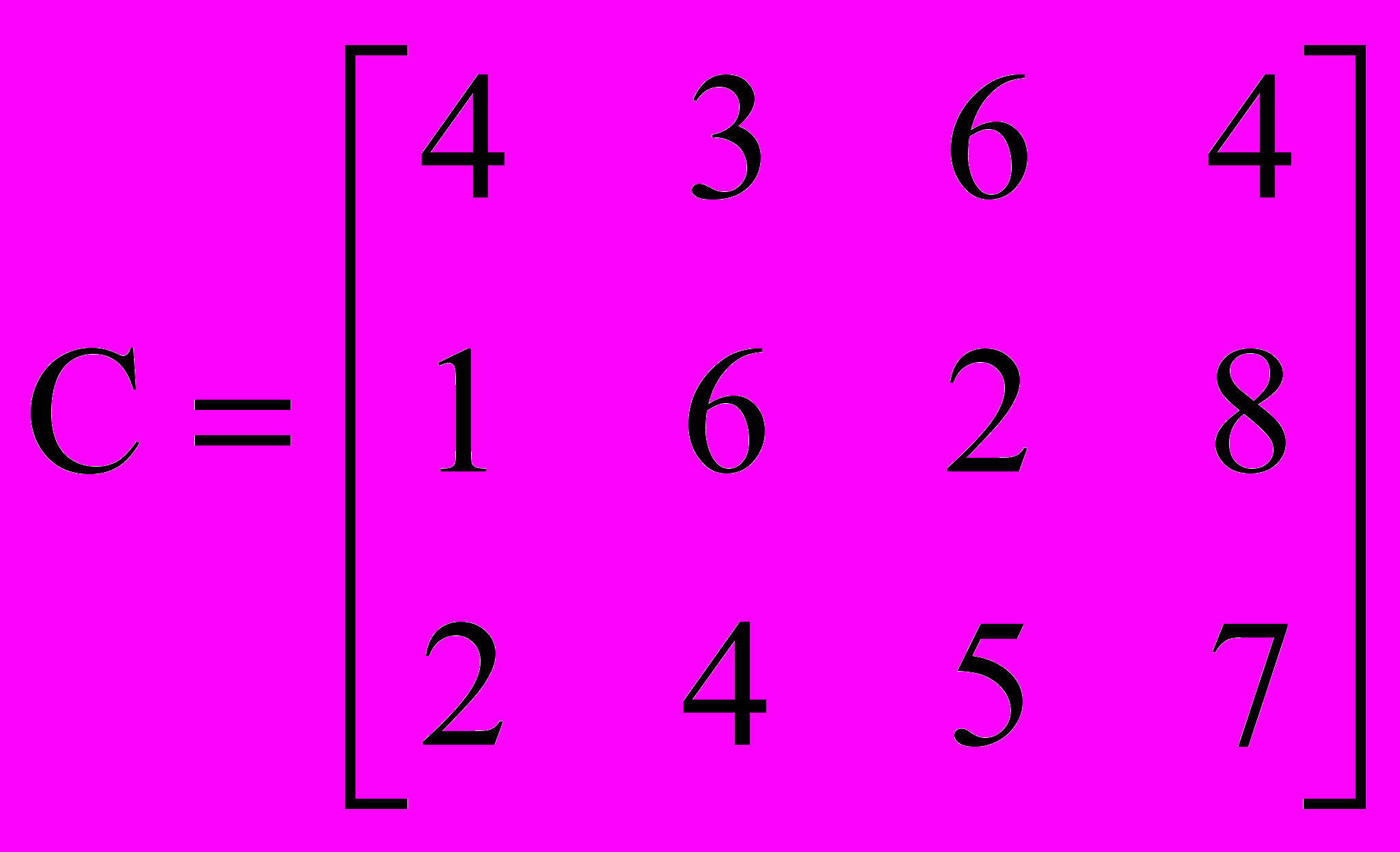
Решение. Проверим условие (20):

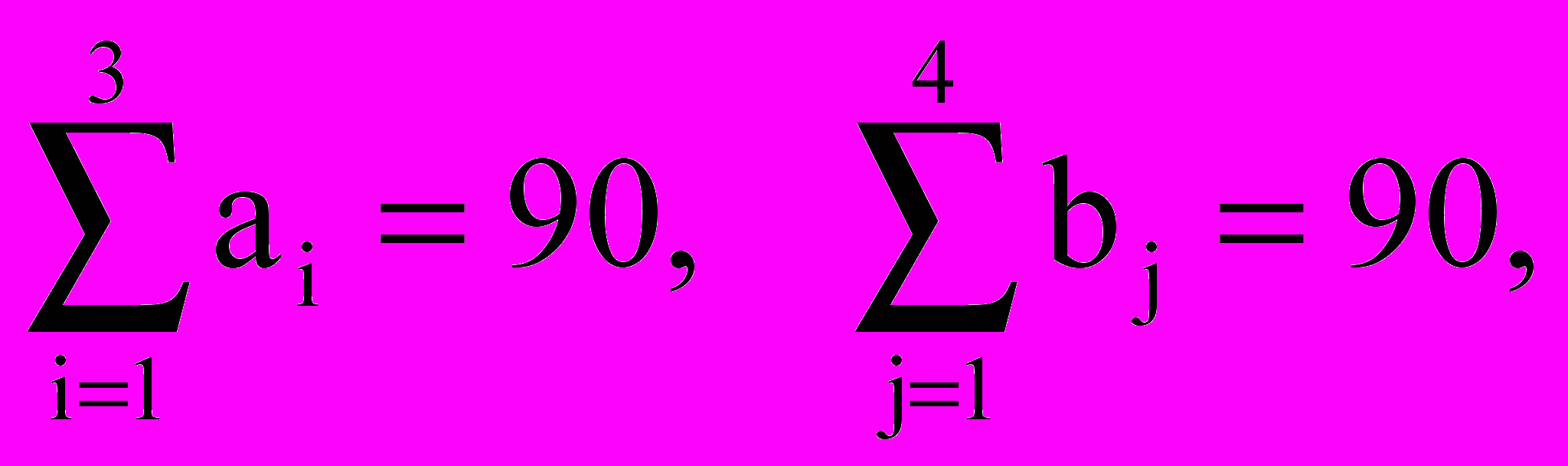
т.е. ТЗ имеет оптимальное решение. Строим рабочую таблицу, которая первоначально содержит только транспортные издержки, спросы и предложения.

Таблица 1.

	M₁	M₂	M₃	M₄
P₁	4	3 25	6	4 15	40
P₂	1 - 30	6	2 + 0	8	30
P₃	2 + z	4	5 - 15	7 5	20
	30	25	15	20	ai bj

Затем в этой же таблице строим начальный ОП методом "минимальной стоимости" (об этом и других методах построения начального ОП можно прочитать, например, в [8,9]):

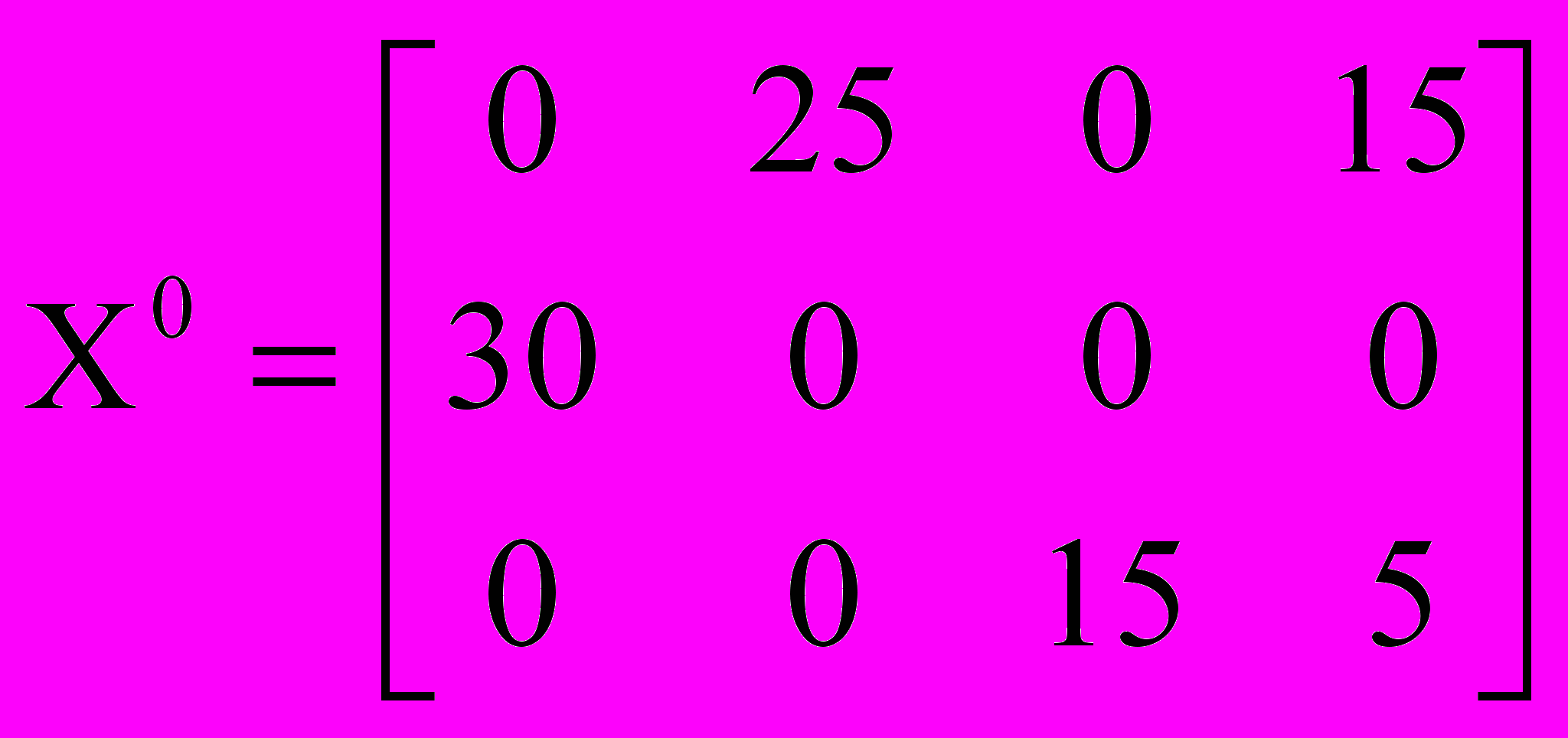
План является вырожденным, так как m+n-1=6, (см. свойство 4), а для X⁰ число ненулевых перевозок равно 5.

Проверим данный план на оптимальность при помощи критерия (21)-(22) Сначала для x_ij>0 в плане X⁰ вычислим потенциалы по формуле (21):

u₁+v₂=c₁₂=3

u₁+v₄=c₁₄=4

u₂+v₁=c₂₁=1 (23)

u₃+v₃=c₃₃=5

u₃+v₄=c₃₄=7

В этой системе 7 неизвестных и 5 уравнений, т.е. ее нельзя решить. Поэтому выбираем сами u₁=0 (см. примечание ниже). Тогда из первых двух уравнений найдем: v₂=3, v₄=4; Из последних двух: u₃=3, v₃=2. Далее вычисления прерываются (следствие вырожденности плана Х⁰). В таких случаях вводят фиктивные перевозки, записывая в соответствующие клетки 0, но считая эти перевозки ненулевыми. Существует много способов определения фиктивного маршрута (клетки) так, чтобы система потенциалов определялась однозначно. (см., например, [8], стр. 116).

Для фиктивных перевозок мы выберем клетку (2,3) по следующим соображениям:

а) этот маршрут наиболее дешевый (c₂₃ =2)

б) при добавлении уравнения

u₂+v₃=c₂₃=2

система (23) разрешается однозначно:

u₁=0, u₂=0, u₃=3;

v₁=1, v₂=3, v₃=2, v₄=4;

Теперь проверим выполнение неравенств (22) для нашего плана (для х_ij=0 в X⁰):

u₁+v₁-c₁₁=-3<0

u₁+v₃-c₁₃=-4<0

u₂+v₂-c₂₂=-3<0

u₂+v₄-c₂₄=-4<0

u₃+v₁-c₃₁=+2>0 ←

u₃+v₂-c₃₂=+2>0 ←

Видим, что критерий оптимальности не выполнен (последние два неравенства), так что план X⁰ неоптимален.

Надо построить новый план перевозок. Идея состоит в изменении объема перевозок по некоторым из маршрутов. Для определения этих маршрутов строим цикл - последовательность ненулевых клеток таблицы (маршрутов), в которой соседними являются две и только две ненулевые клетки одного столбика или одной строки, а последняя клетка последовательности находится либо в том же столбике, либо в той же строке, что и начальная клетка последовательности. "Вершины" цикла (т.е. клетки, вошедшие в цикл) и показывают те маршруты, по которым нужно изменить объемы перевозок. Остается определить начальную клетку цикла - клетку с наихудшей (положительной) оценкой в системе (24).

В данном случае можно взять как клетку (3,1) так и (3,2). Возьмем клетку (3,1) и напишем в эту клетку пока неизвестное число z (в таблицу 1). Начиная с этой клетки, строим цикл (см. таблицу 1): (3,1) → (3,3) → (2,3) → (2,1). Впишем в начальную клетку знак "+" и далее последовательно ''-'', "+" по вершинам цикла, как это показано в таблице 1. Значение z (объем новых перевозок по маршруту (3,1)) определяется из условия: z=min{

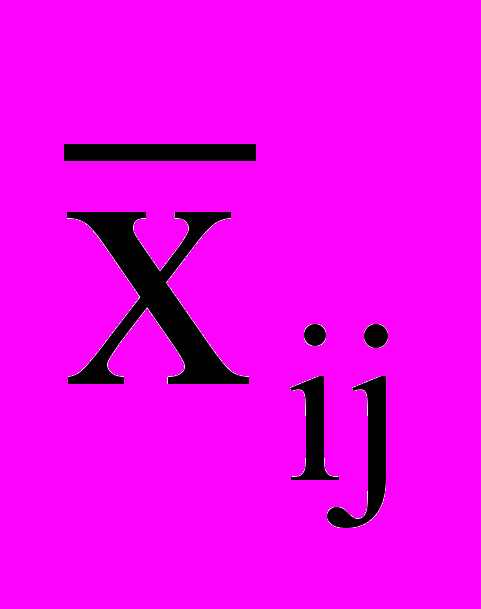}, где

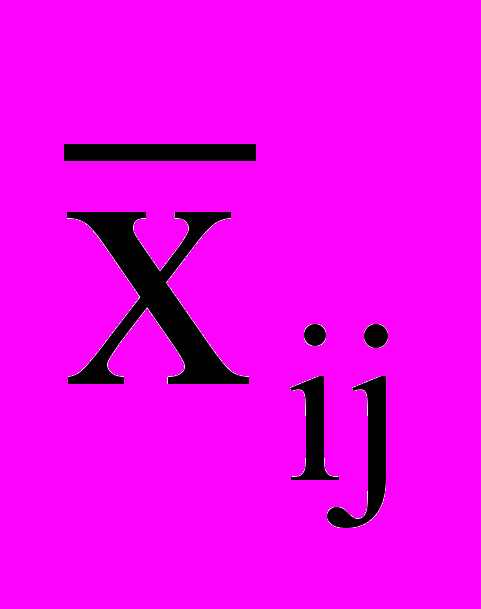- объем перевозок по маршрутам, отмеченным знаком "-". Итак z=min{15,30}=15. Эту величину 15 отнимаем из объема перевозок, отмеченных знаком “-“, и прибавляем к объемам перевозок, отмеченных знаком "+" (балансируем). Результаты записываем в новую таблицу, перенося туда остальные перевозки без изменения:

Таблица 2.

	M₁	M₂	M₃	M₄
P₁	4	3 25	6	4 + 15	40
P₂	1 15	6	2 15	8	30
P₃	2 15	4 + z	5	7 - 5	- 20
	30	25	15	20	a_i b_j

Получим новый ОП:

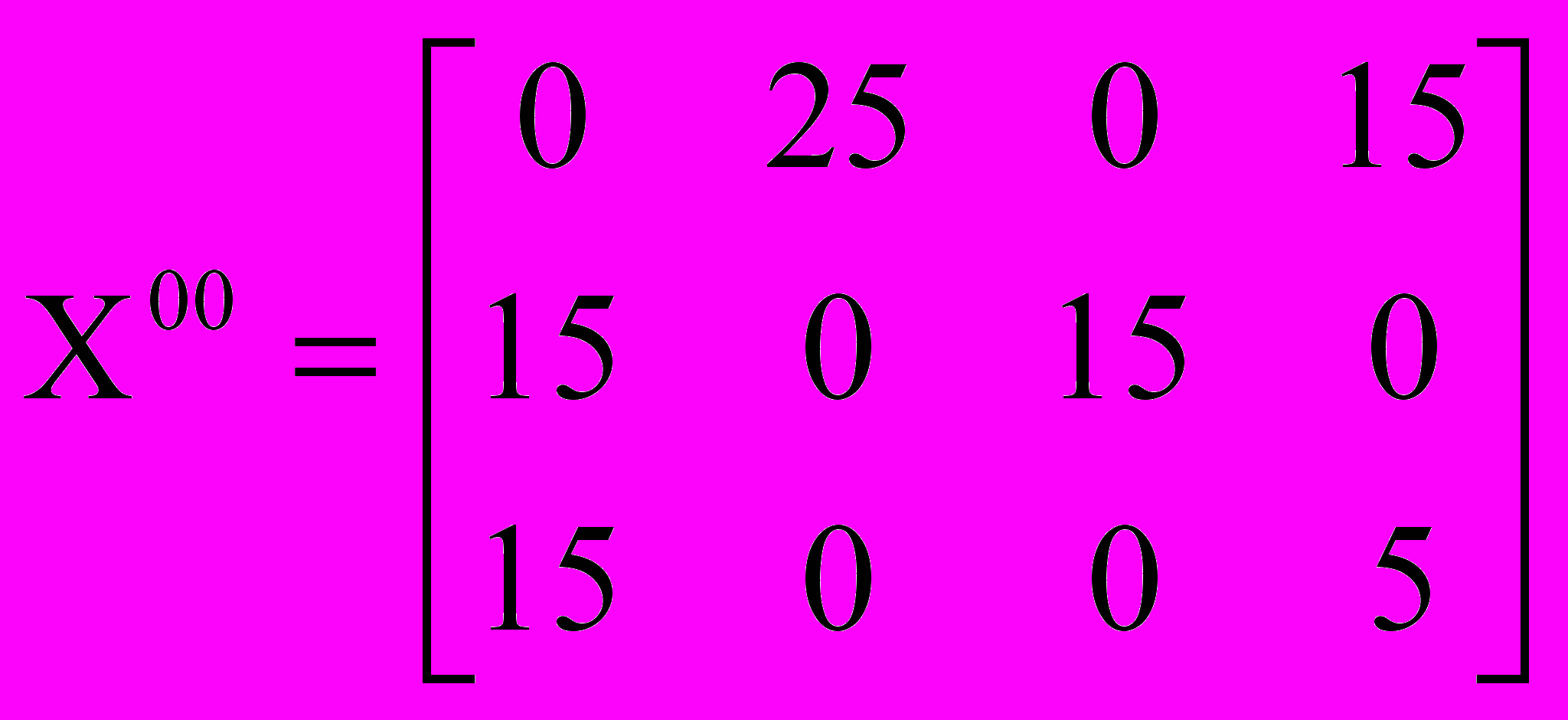
Видно, что он невырожденный, следовательно при проверке на оптимальность плана X⁰⁰ система (21) разрешится однозначно (не нужно будет вводить фиктивные перевозки).

Самостоятельно проверьте, что ОП X⁰⁰ неоптимален, и что на третьей итерации получается оптимальный опорный план (выполнены все неравенства (22)):

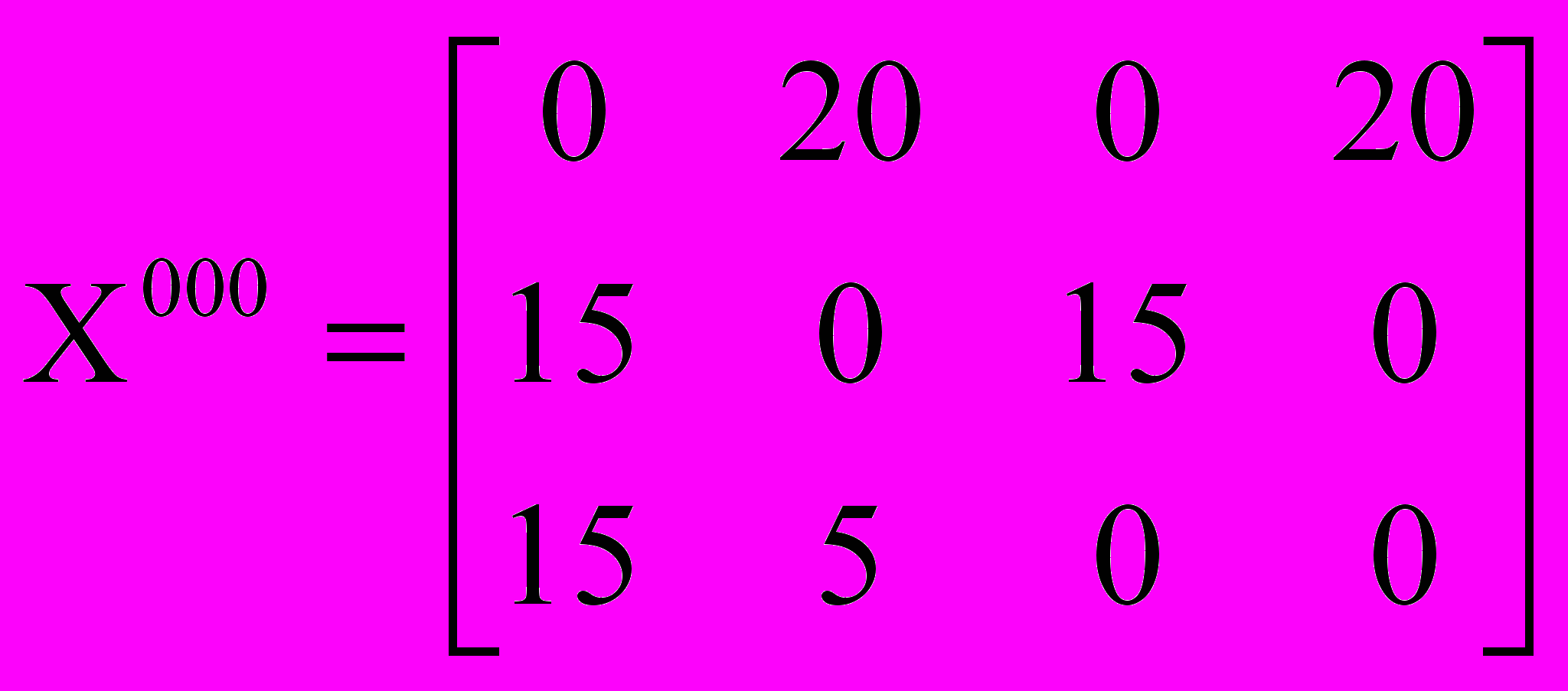
Вычислите суммарные стоимости перевозок по X⁰, X⁰⁰, X⁰⁰⁰ по формуле (5) и убедитесь в оптимальности плана перевозок X⁰⁰⁰.

Как видно из решенного примера, алгоритм метода потенциалов следующий:

1) Занести данные задачи (транспортные издержки, спросы и предложения) в специальную рабочую таблицу;

2) Вычислить начальный ОП;

3) Проверить ОП на оптимальность;

3.1) Найти значения потенциалов для данного ОП по формуле (21); если ОП вырожденный, то ввести фиктивные перевозки;

3.2) Проверить выполнение неравенств (22): если они все выполнены, то данный ОП оптимален - вычисления прекратить; если нет, то перейти к пункту 4;

4) Построить новый ОП;

4.1) Построить цикл;

4.2) Изменить по вершинам цикла объемы перевозок;

4.3) Заполнить новую рабочую таблицу и перейти к пункту 3.

Примечания к методу потенциалов.

1. Систему потенциалов однозначно можно вычислить только для невырожденного ОП, при этом одному из потенциалов нужно придать произвольное значение (обычно u₁=0, т.к. в системе ограничений закрытой ТЗ имеется одно линейно зависимое ограничение).

2. В случае вырожденного ОП нужно ввести фиктивные перевозки с таким расчетом, чтобы из системы (21) однозначно вычислить все потенциалы.

3. Цикл всегда существует и единственен для каждой свободной клетки таблицы (для невырожденного ОП).

4. Если для какой-то свободной клетки (x_ij= 0) оптимального ОП в соотношении (22) достигается строгое равенство, то это говорит о неединственности оптимального ОП.

В зависимости от содержательной трактовки чисел с_ij транспортная задача может быть поставлена на минимизацию суммарного расстояния или времени Пробега транспорта или на минимизацию расхода горючего, более общей является открытая модель ТЗ (когда не требуется выполнения равенства (20)) и сетевая постановка ТЗ (когда один и тот же пункт выступает в роди производителя и потребителя),. Открытые ТЗ решаются путем сведения к замкнутой ТЗ (вводятся фиктивные потребители или производители), а для решения сетевых ТЗ существуют специальные методы (например, метод динамического программирования).

Blog

Литература: [1,8-11,16,18]