Курсовой проект по дисциплине «Автоматизированные информационно-управляющие системы» по теме «Управление спи с коммутацией сигналов»
| Вид материала | Курсовой проект |
СодержаниеСПИ с коммутацией каналов (КК ) СПИ с коммутацией сообщений (КС) |
- Курсовой проект по дисциплине: «Микропроцессорные информационно-управляющие системы, 542.35kb.
- Методические указания по курсовому проектированию для студентов специальности 210100, 395.17kb.
- Рабочей программы дисциплины Автоматизированные информационно-управляющие системы, 23.35kb.
- 05. 11. 16 Информационно-измерительные и управляющие системы (промышленность)*, 39.92kb.
- Алгоритмы и средства регистрации и обработки сигналов акустической эмиссии для автоматизированной, 240.87kb.
- Автоматизированные информационно-измерительные системы, 199.1kb.
- «Автоматизированные информационно-управляющие системы», 49.13kb.
- Комплекс образовательной профессиональной программы (опп) по специальности 180305 «Корабельные, 458.44kb.
- Программы вступительного экзамена в аспирантуру по специальности 05. 11. 16 Информационно-измерительные, 71.85kb.
- Артеменко Юрий Николаевич исследование и разработка информационно-измерительной системы, 450.64kb.
1 2
Министерство путей сообщения
Российской Федерации
Московский государственный университет
путей сообщения (МИИТ)
Кафедра «Управление и информатика в технических системах»
Курсовой проект
по дисциплине
«Автоматизированные информационно-управляющие системы»
по теме
«Управление СПИ с коммутацией сигналов»
Вариант№4
Выполнил: ст.гр. АУИ - 511
Демкин Е.С.
Проверил: Давыдюк В.Б.
Москва - 2008
Исходные данные
- Схема СПИ
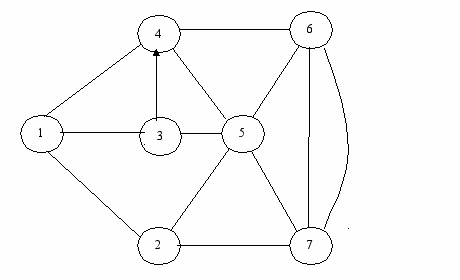
- Матрица потоков сообщений [φ]:
| φ15 | φ 23 |
| 60 | 70 |
- Количество источников сообщений на УК4: N4=400;
- Интенсивность передачи сообщений элементарным источником λ42[чис-1]: 0,6;
- Матрица емкостей ветвей B=[bij]
b12
b13
b14
b25
b27
b34
b46
b35
b56
b57
b45
b67
60
70
50
60
35
40
0
30
0
20
60
0
- Диапазон длительности сообщений: ∆ti [c]
∆ti
0÷160
160÷440
440÷740
740÷1050
1050÷1400
- Средние длительности в диапазонах:
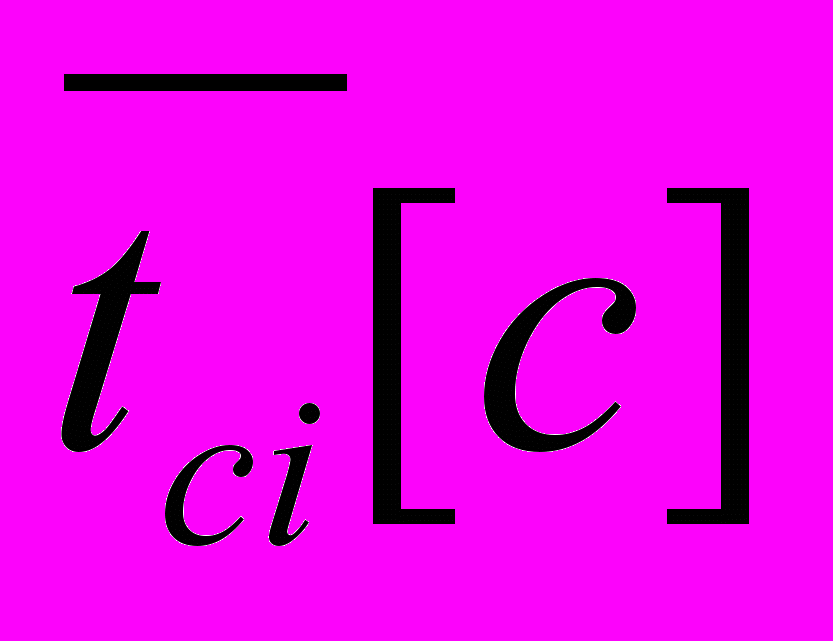 .
.
∆ti
0÷160
160÷440
440÷740
740÷1050
1050÷1400
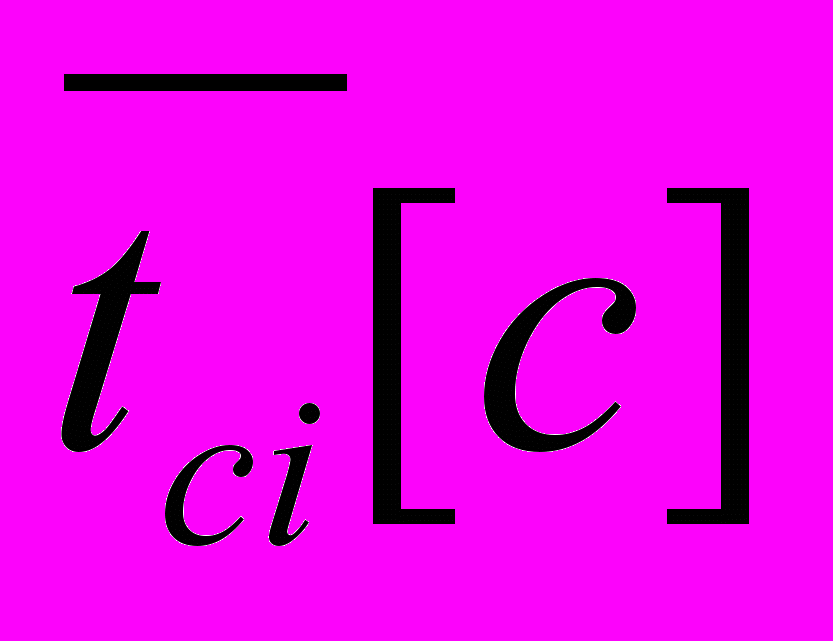
70
280
560
890
1250
- Количество наблюдений в диапазонах: mi
| ∆ti | 0÷160 | 160÷440 | 440÷740 | 740÷1050 | 1050÷1400 |
| mi | 600 | 200 | 36 | 9 | 3 |
- Матрица надежности ветвей связи W=[Wij]
Ветви связи
1-2
1-3
2-5
2-7
3-5
3-4
1-4
4-5
4-6
5-6
5-7
6-7
α
6
6
5
9
9
3
5
6
8
9
7
8
- Формула для вычисления показателей надежности:

Рабочее задание
1. Дать общую характеристику СПИ как большой системы. Описать задачи и структуру управления коммутируемой СПИ. Обосновать выбор целевой функции.
2. По статистическим данным построить гистограмму распределения длительности сообщений. Ввести и рассчитать оценку максимального правдоподобия для параметра экспоненциального закона распределения. Проверить гипотезу о экспоненциальности закона распределения с помощью критерия Пирсона и критерия Колмогорова.
3. Методом динамики средних рассчитать нагрузку, создаваемую потоком сообщений на УК4 в УК2, и дисперсию количества одновременно передаваемых сообщений. Построить график плотности распределения вероятностей количества одновременно передаваемых сообщений.
4. Разработать алгоритм для построения вторичной сети с помощью линейного программирования. Дать математическую формулировку задачи. Составить симплекс-таблицу и кратко описать симплекс-метод решения. Составить блок – схему алгоритма симплекс-метода. Решить на ПЭВМ задачу по заданным данным и построить вторичную сеть СПИ.
5. Построить матрицы надежных маршрутов (дистанционную таблицу) и маршрутную таблицу.
1. Общая характеристика систем передачи информации как большой системы.
Современные системы передачи информации (ПИ) включают в себя телефонные, телеграфные, радиорелейные сети, а также специальные – спутниковые системы передачи данных (ПД).
Телефонная сеть крупного города (Москва, Санкт-Петербург) содержит десятки телефонных станций на 10 и более тысяч номеров, разветвленную и протяженную систему линий связи.
Телеграфная сеть страны содержит десятки тысяч аппаратов. Поэтому по признаку масштабности СПИ можно отнести к большим системам.
СПИ подразделяются на 3 вида:
Не коммутированные СПИ (Нк)
Каждая СПИ состоит из узлов коммутации (УК) и линий связи (ЛС), которые подразделяются на:
- Воздушные;
- Кабельные;
- Линии радиосвязи.
В Нк СПИ УК соединяются ЛС жестко:
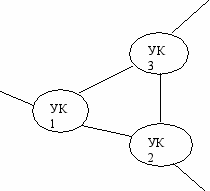

Рисунок 1.1- Не коммутированные СПИ
“ + ”- нет потери времени на соединение
“ - “- ЛС недоиспользуется в том случае, если нагрузка на сеть отличается от расчетной. В данной системе потоки сообщений плохо распределяются в пространстве.
СПИ с коммутацией каналов (КК )

Рисунок 1.2 - СПИ с коммутацией каналов
С помощью коммутирующей аппаратуры формируются пучки каналов, поэтому информация более равномерно распределяется в пространстве и во времени.
“-“-сложная аппаратура;
- потеря времени на соединение.
СПИ с коммутацией сообщений (КС)

Рисунок 1.3- СПИ с коммутацией сообщений (КС)
В данной системе на УК имеется не только коммутационная аппаратура, но и запоминающее устройство (ЗУ).
В такой системе в начале анализируется адрес сообщения, затем устанавливается наиболее приемлемый маршрут, проверяется свободность маршрута, действует правило приоритетов, после этого осуществляется передача сообщений.
Еще более эффективно используются каналы связи (загрузка каналов, распределение информации в пространстве и во времени).
“-“- время образования маршрута увеличивается;
- усложняется аппаратура и ее обслуживание.
Общая структура управления сетями передачи информации

Рисунок 1.4 - Общая структура управления сетями передачи информации
УУ на УК вырабатывает сигналы управления на коммутирующей аппаратуре и других устройствах на УК.
Центральное управляющее устройство (ЦУУ) анализирует информацию о состоянии сети (нагрузка на сеть, наличие повреждений, узкие места), решает задачу распределения потоков сообщений между УК и вырабатывает командные сигналы на УК.
Перед любой СПИ ставится главная задача: передать информацию своевременно, полностью, без искажений.
Отсюда показателями, которые должны учитываться при составлении целевой функции могут быть:
- Вероятность искажений информации.
- Среднее время соединения.
- Средняя длина очереди.
- Среднее число отказов.
- Пропускная способность.
- Надежность передачи сообщений.
Для НК СПИ показателем является:
- Оптимальное распределение пучков каналов.
Для КК СПИ:
- Формирование оптимальных пучков каналов.
- Формирование маршрутов минимальной длины (стоимости).
Для КС СПИ:
- Формирование оптимальных пучков каналов.
- Формирование маршрутов минимальной длины (стоимости).
- Минимальное время передачи сообщения.
- Минимальная вероятность искажения информации.
Графовая модель сети передачи информации
СПИ удобно моделировать с помощью графов.
УК ставят в соответствие вершину графа.
ЛС – дуги либо ребра графа.
ЛС могут быть однонаправленными или двунаправленными. Или, соответственно, ориентированные или неориентированные графы.
ЛС характеризуется длиной, емкостью (количеством одновременно передаваемых сообщений), надежностью, стоимостью.
УК характеризуется коммутационной способностью (количеством коммутаций), надежностью, стоимостью.
При анализе СПИ, обычно считают коммутационную способность безграничной, а надежность равной 1.
Между любой парой УК устанавливается маршрут (ветвь связи или путь ПИ), который характеризуется длиной, емкостью, надежностью, стоимостью.
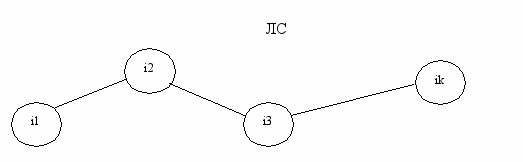
Рисунок 1.5 - Графовая модель сети передачи информации
L: (длина)- сумма длин всех ЛС.
C: (емкость) – минимальная емкость ЛС, входящая в данный маршрут.
W: (надежность) – произведение вероятностей исправной работы каждой ЛС, входящей в данный маршрут, при условии, что функционирование и работа ЛС не зависят друг от друга.
При разработке модели СПИ формируются:
- геометрическая структура графа;
- матрица смежности: C=[Cij];
- весовая матрица длин: CL= [C Lij];
- весовая матрица емкостей: B=[bij];
- матрица надежности: W=[wij];
- для учета нагрузки формируется матрица потока сообщений Ф=[ φij], где φij характеризует количество сообщений из i узла в j.
2 Обработка статистических данных
2.1 Построение гистограммы и статистической функции распределения вероятностей
Таблица 2.1.1- Таблица расчетных данных
-
Интервал сообщений
0÷160
160÷440
440÷740
740÷1050
1050÷1400
Кол-во. наблюдений mi
600
200
36
9
3
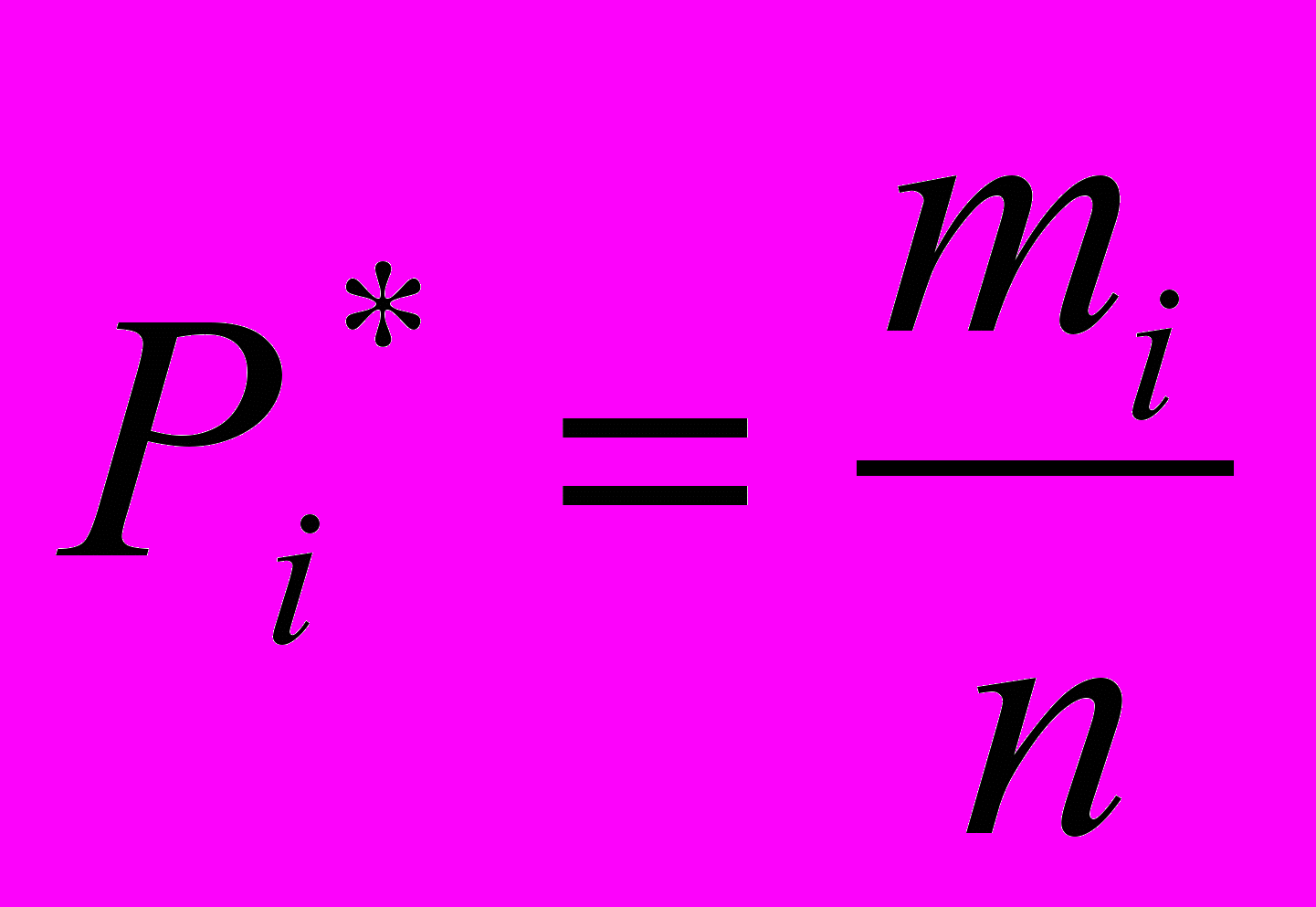
0.7075
0,2358
0,0425
0,0106
0,0036

0,0044
0,00084
0,0001416
0,0000342
0,0000102
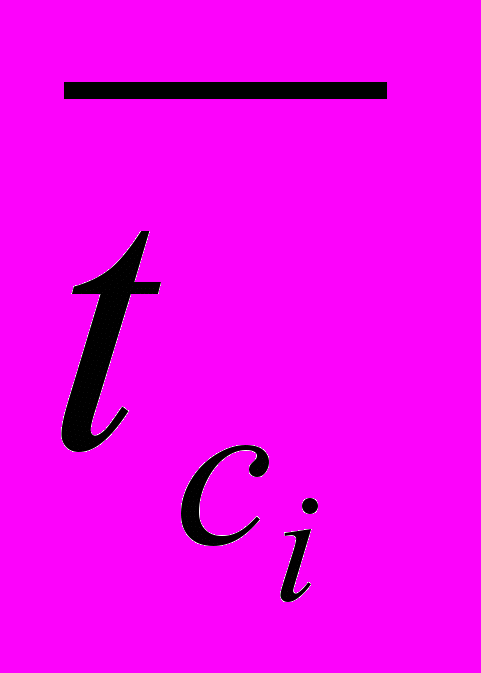
70
280
560
890
1250

0,7075
0,9533
0,9858
0,9964
1
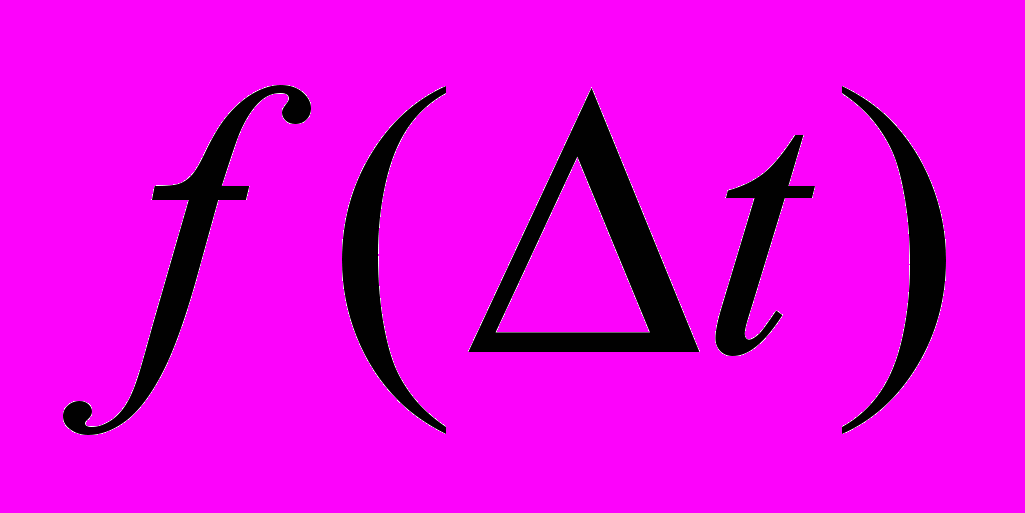
0,006527
0,002297
0,002297
0,000369
0,000369
0,0000521
0,0000521
0,00000689
0,00000689
0,00000071
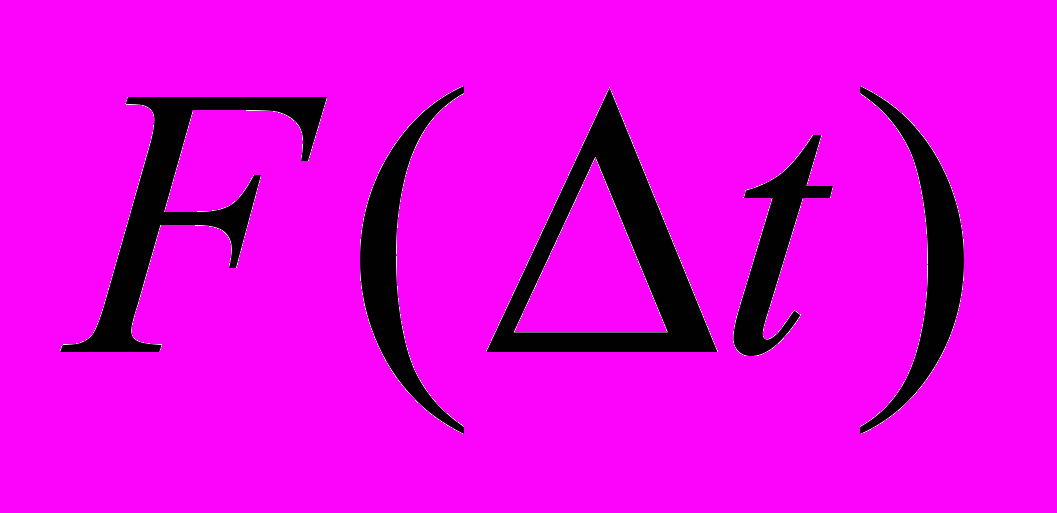
0
0,6481
0,6481
0,9434
0,9434
0,992
0,992
0,9989
0,9989
0,9998
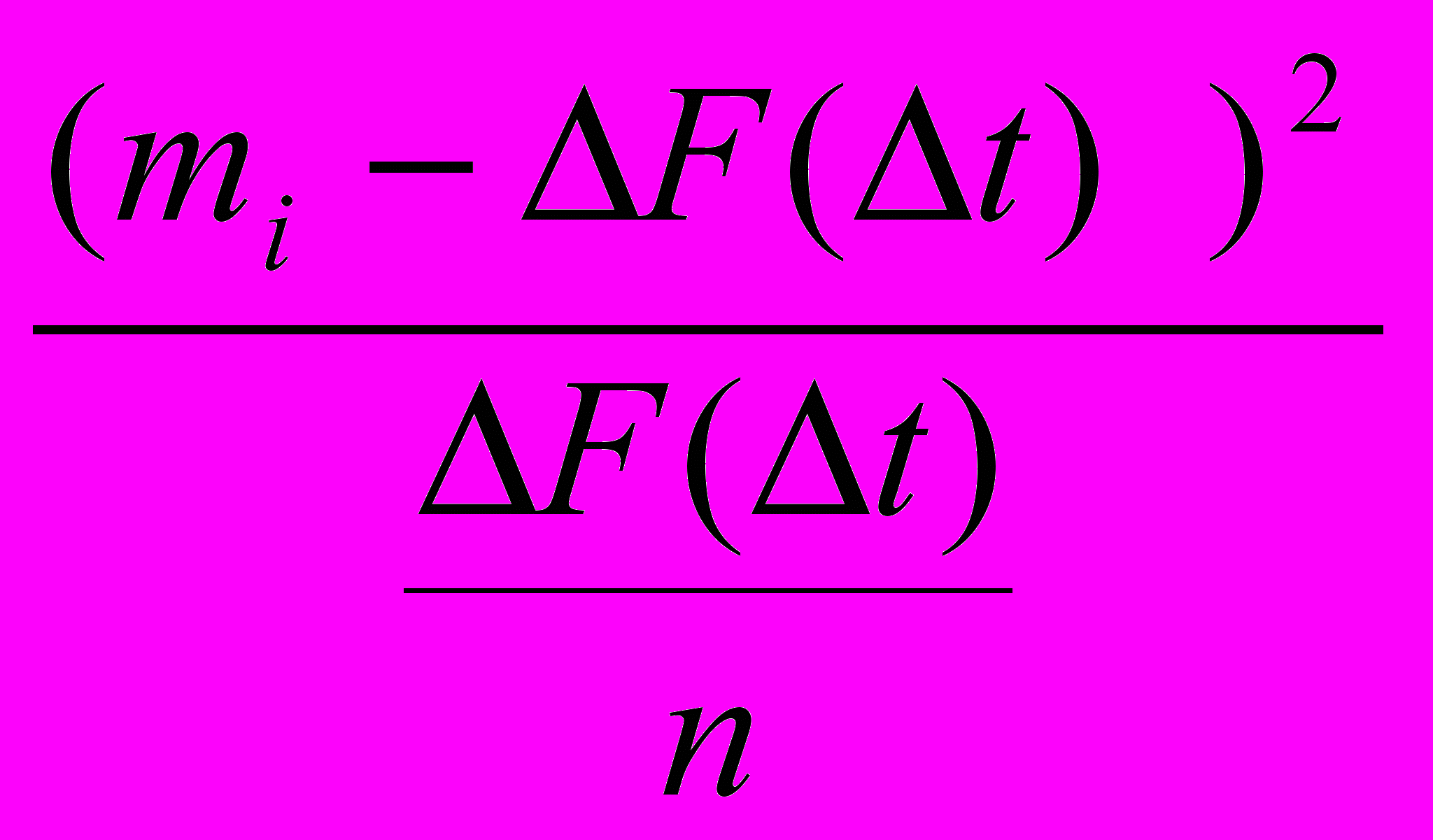
4,624
10,1496
0,6593
1,6945
5,4612
| -
-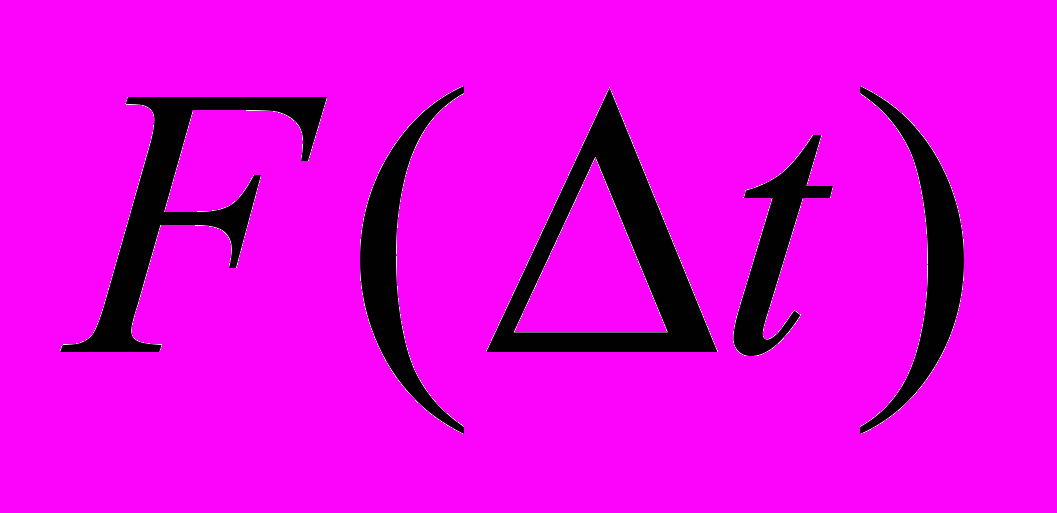 |
|
0,0594
0,0099
0,0062
0,0025
0,0002
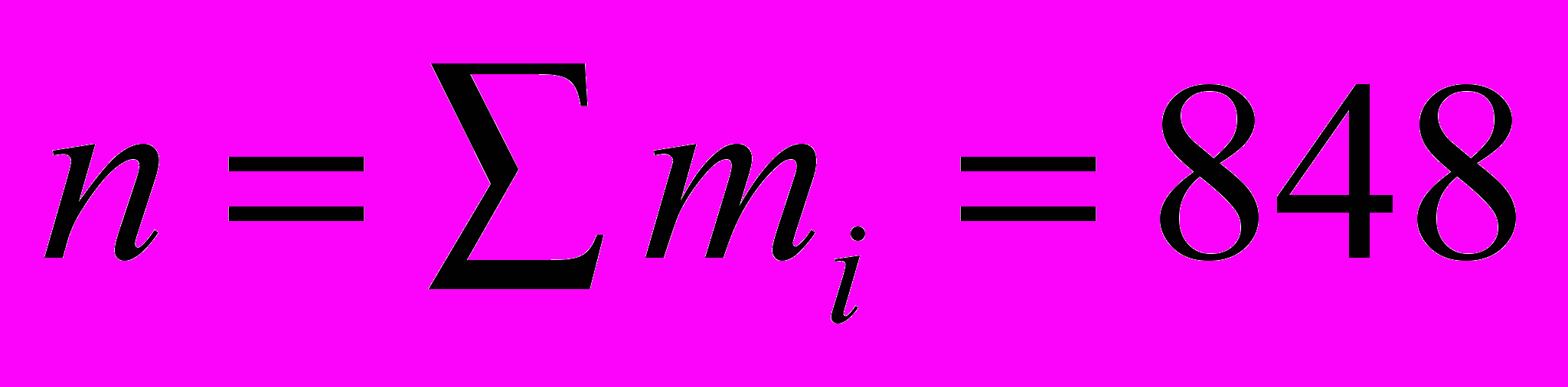
По данным расчетной таблицы строим гистограмму распределения длительности сообщения (рисунок 2.1.1) и статистическую функцию распределения (рисунок 2.1.2).
2.2 Определение оценок параметров экспоненциального закона распределения
По гистограмме можно сделать предположение, что случайная величина распределена по экспоненциальному закону.
Тогда функция плотности вероятности распределения будет иметь вид:

И функция распределения имеет вид:
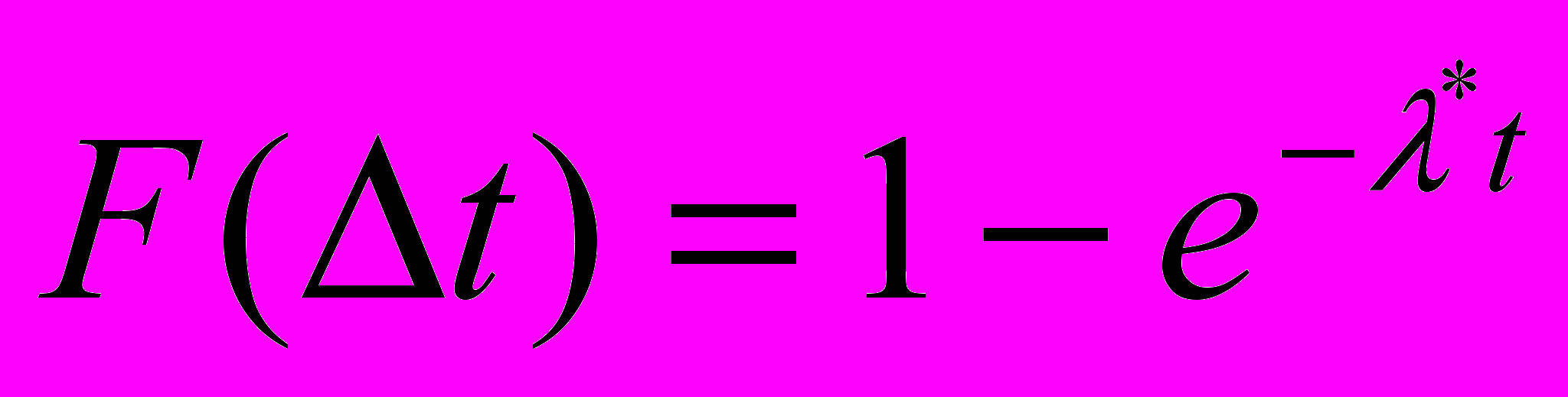
где λ*- оценка математического ожидания.
Для определения λ* воспользуемся методом максимального правдоподобия.
Составляем функцию максимального правдоподобия
 :
: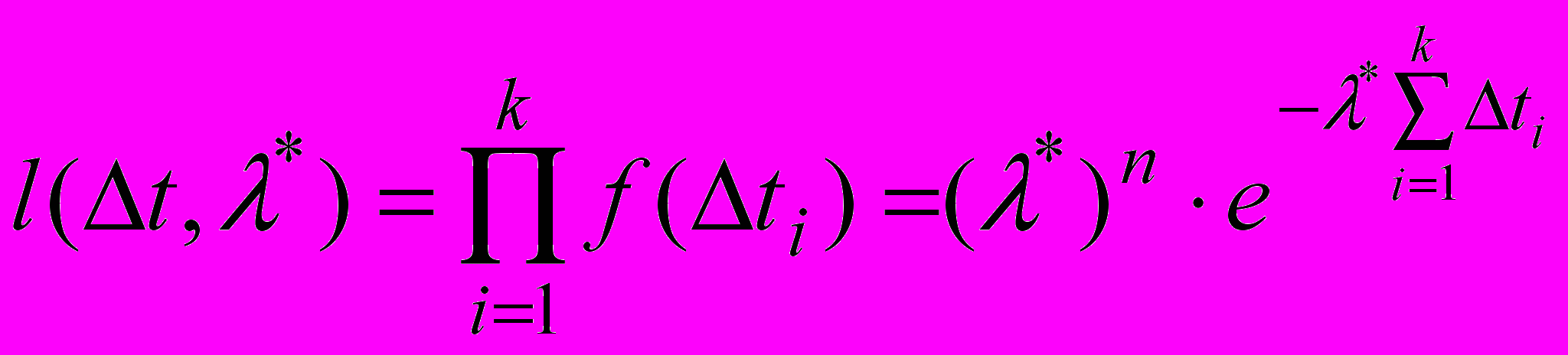
где k = 5 – количество диапазонов длительностей сообщений.
Исследуем на экстремум
 :
:
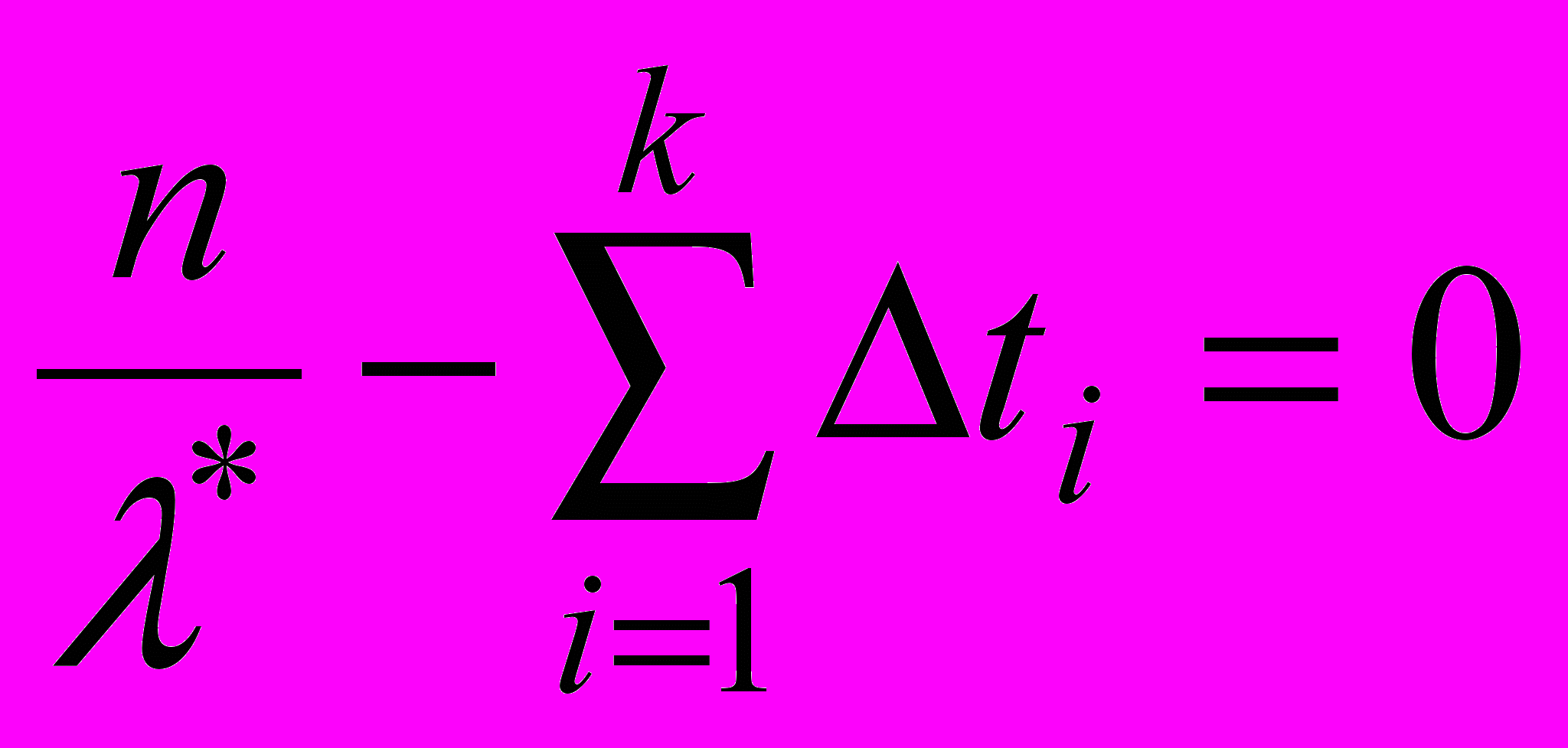

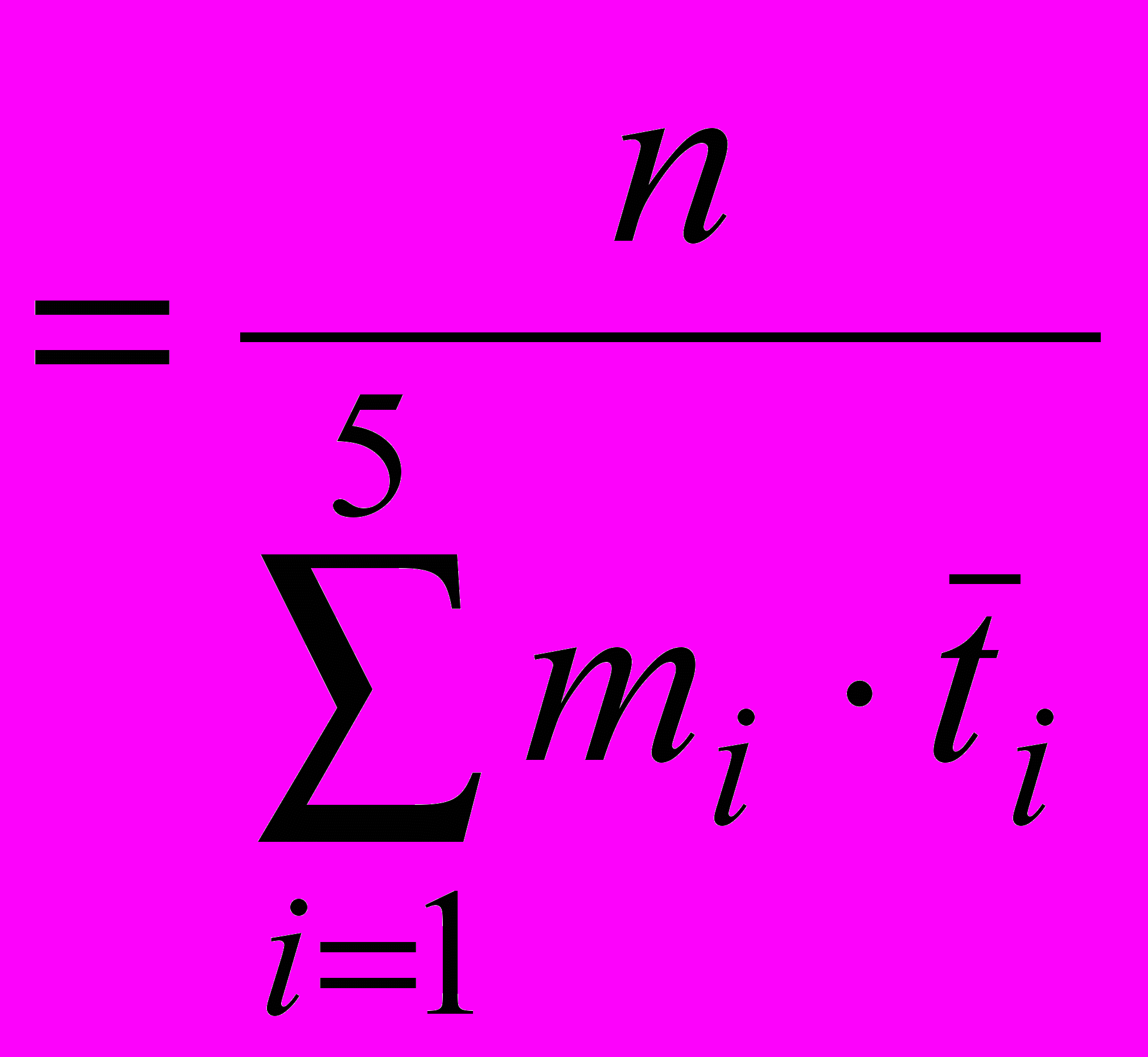

Исследуем на несмещённость, состоятельность и эффективность.
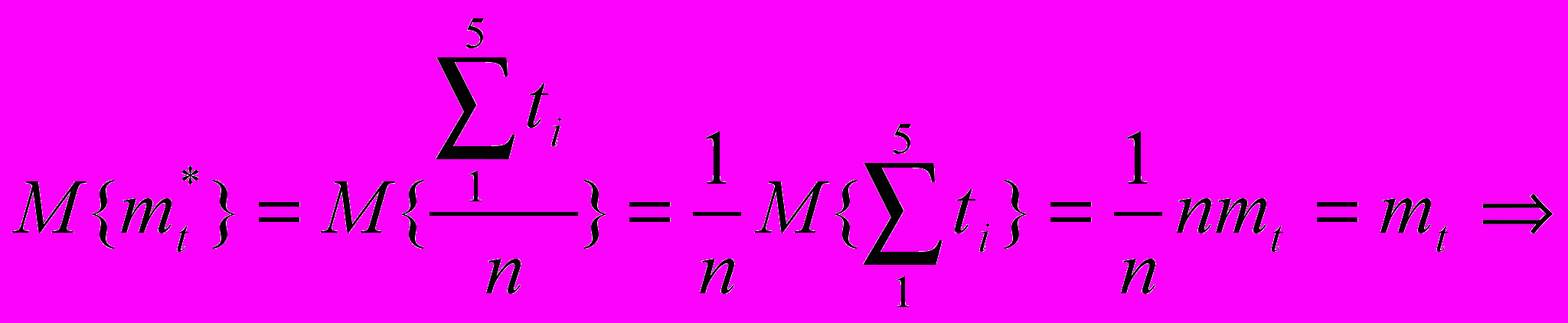 данная оценка является несмещенной
данная оценка является несмещеннойПроверим, является ли оценка состоятельной и эффективной:
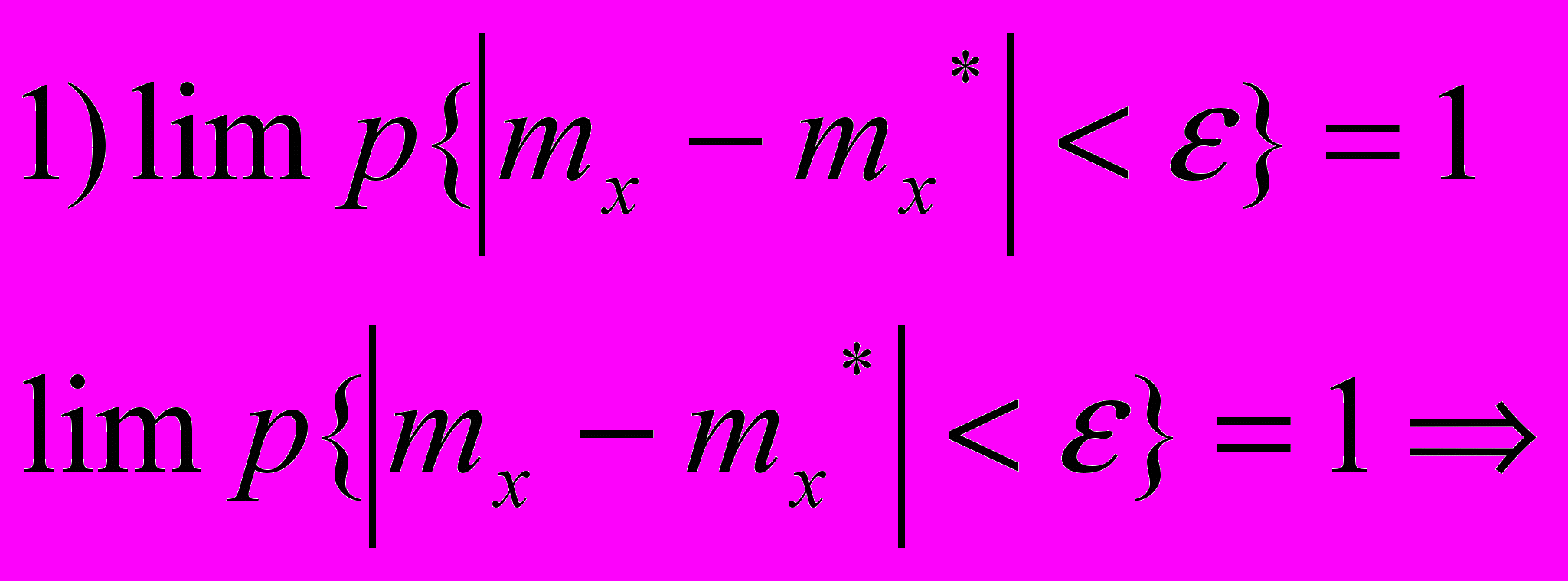 оценка состоятельна
оценка состоятельна оценка эффективная
оценка эффективная
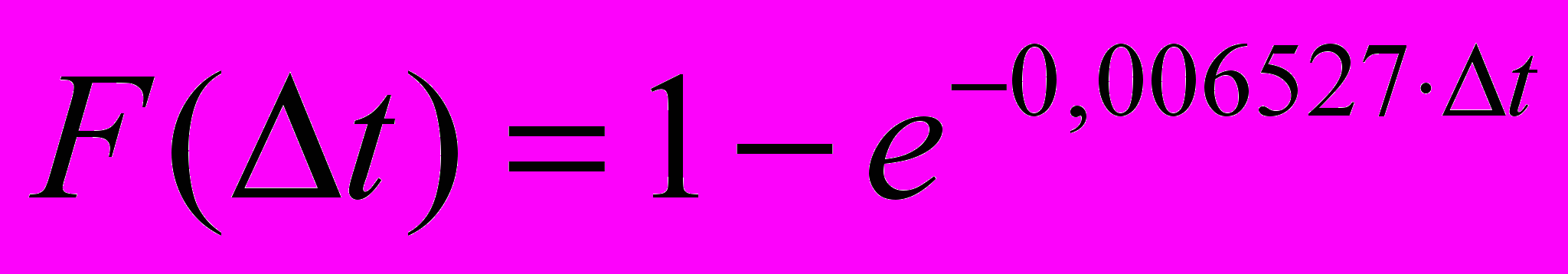
Значения
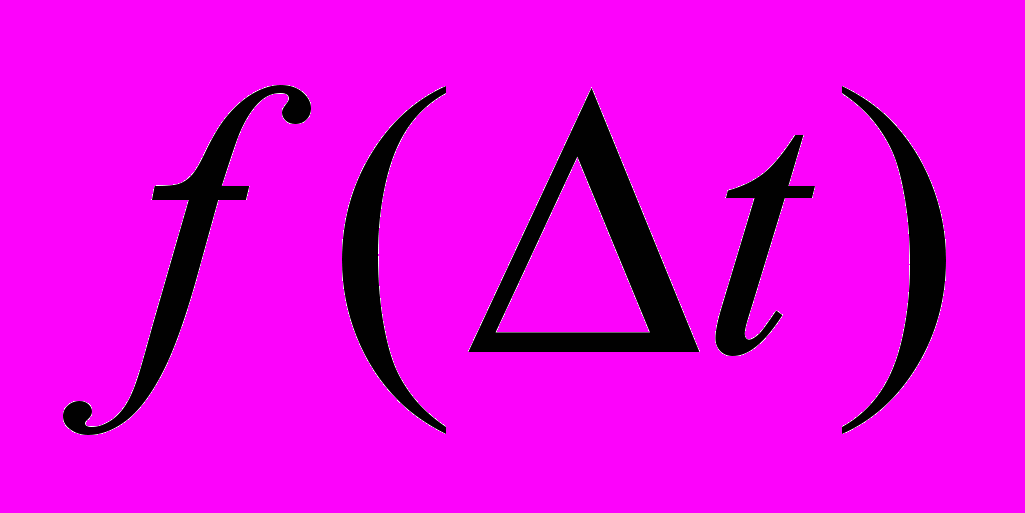 и
и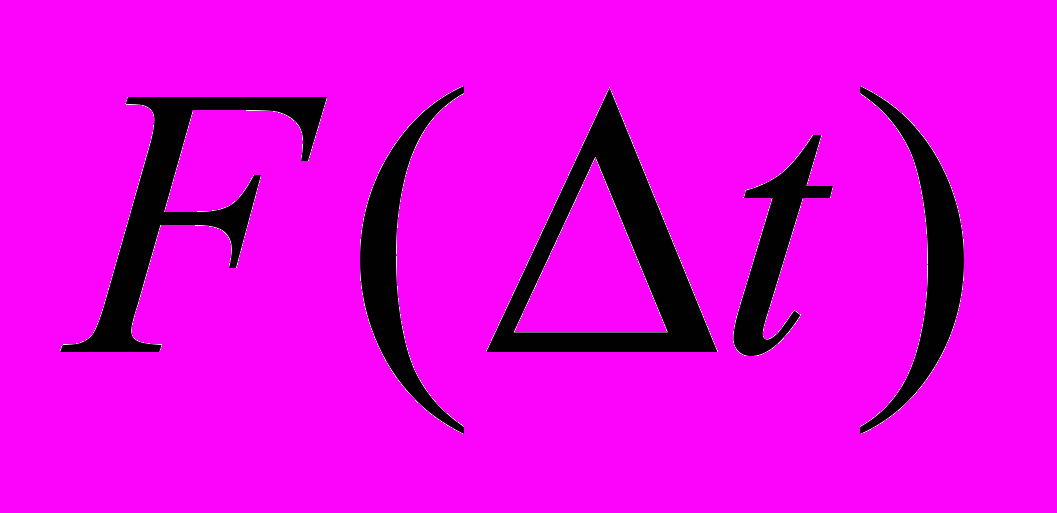 приведены в таблице 2.1.1
приведены в таблице 2.1.1Построим функцию плотности вероятности (рисунок 2.1.1) и функцию распределения (рисунок 2.1.2).
f(t)
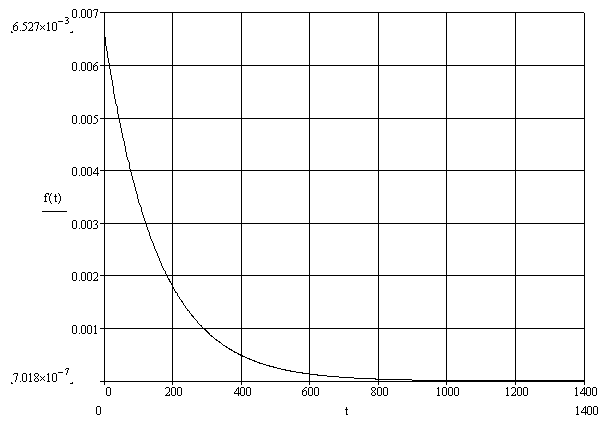
F(t)

2.3 Проверка гипотезы о предполагаемом законе распределения
1) по критерию согласия Колмогорова:
Из рисунка 2.1.2 определяем:
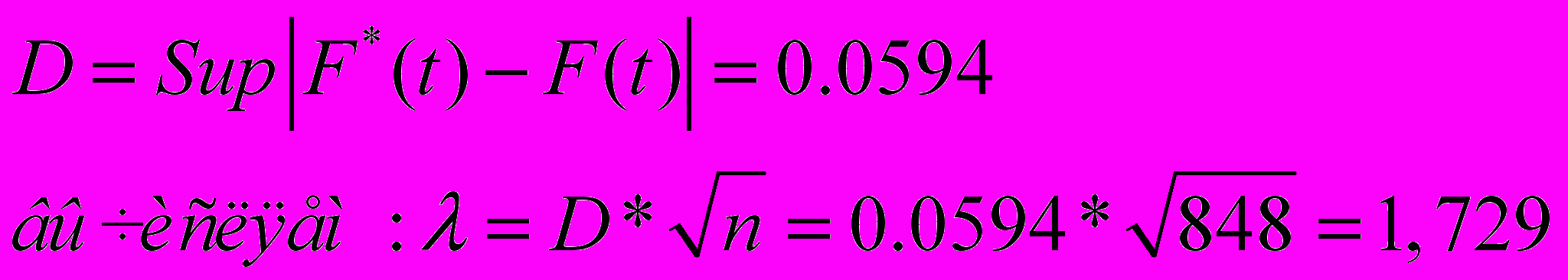
по таблице распределения Колмогорова для λ определяем вероятность p(λ).
p=1-Q(λ)=1-0.9121=0.0879
P<0.1 - гипотеза не принимается.
2) по критерию Пирсона
по функции плотности вероятности рассчитана величина pi –вероятность того, что при n испытаниях в i-ый интервал попадет mi- случайных величин:
pi =F(i+1)-F(i);
далее рассчитана вспомогательная величина:

расчетные данные приведены в таблице 2.1.1
Величина:
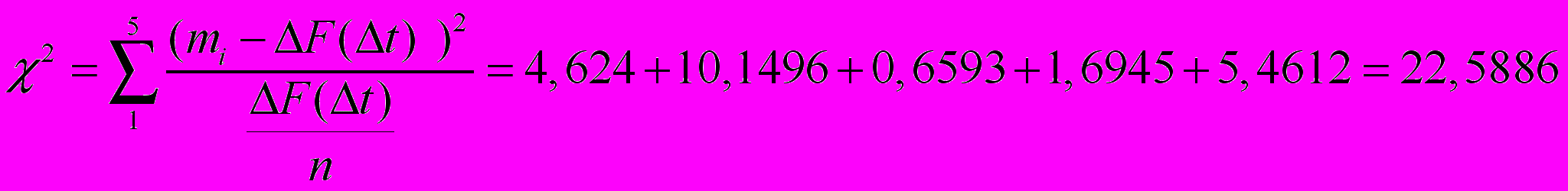
Определяем число степеней свободы:
S=k-1-J к=5, J=1, где к- число интервалов на гистограмме, J -количество числовых характеристик;
S= 5 – 1 – 1 = 3
По таблице распределения Пирсона (χ2) определяем вероятность p, p=0.05.
p<0.1, следовательно, гипотеза о экспоненциальном распределении не принимается.
2.4 Построение доверительного интервала для оценок параметров закона распределения с вероятностью β=0,9.
В некоторых случаях интересуются не точными значениями оценки параметра, а некоторым интервалом внутри которого может находиться истинный параметр.
Доверительный интервал можно рассматривать как меру погрешности точечной оценки.
Необходимо построить доверительный интервал для оценки параметра математического ожидания.
λ*=
