Курсовой проект по дисциплине «Автоматизированные информационно-управляющие системы» по теме «Управление спи с коммутацией сигналов»

Вид материала

Курсовой проект

Подобный материал:

• Курсовой проект по дисциплине: «Микропроцессорные информационно-управляющие системы, 542.35kb.
• Методические указания по курсовому проектированию для студентов специальности 210100, 395.17kb.
• Рабочей программы дисциплины Автоматизированные информационно-управляющие системы, 23.35kb.
• 05. 11. 16 Информационно-измерительные и управляющие системы (промышленность)*, 39.92kb.
• Алгоритмы и средства регистрации и обработки сигналов акустической эмиссии для автоматизированной, 240.87kb.
• Автоматизированные информационно-измерительные системы, 199.1kb.
• «Автоматизированные информационно-управляющие системы», 49.13kb.
• Комплекс образовательной профессиональной программы (опп) по специальности 180305 «Корабельные, 458.44kb.
• Программы вступительного экзамена в аспирантуру по специальности 05. 11. 16 Информационно-измерительные, 71.85kb.
• Артеменко Юрий Николаевич исследование и разработка информационно-измерительной системы, 450.64kb.

;

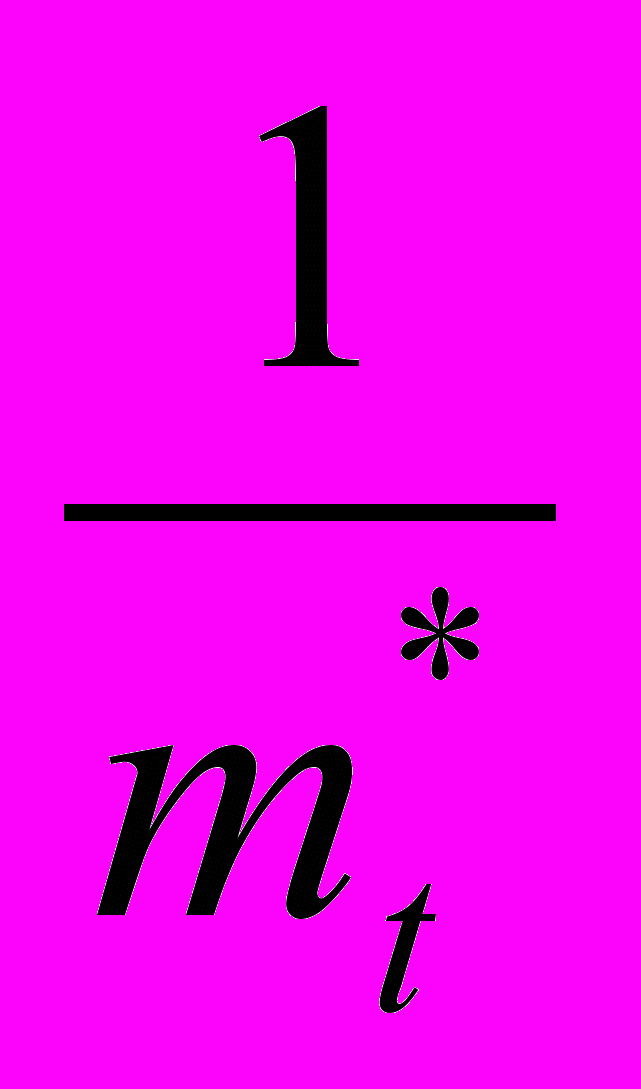λ^*=0,006527.

а) для оценки дисперсии



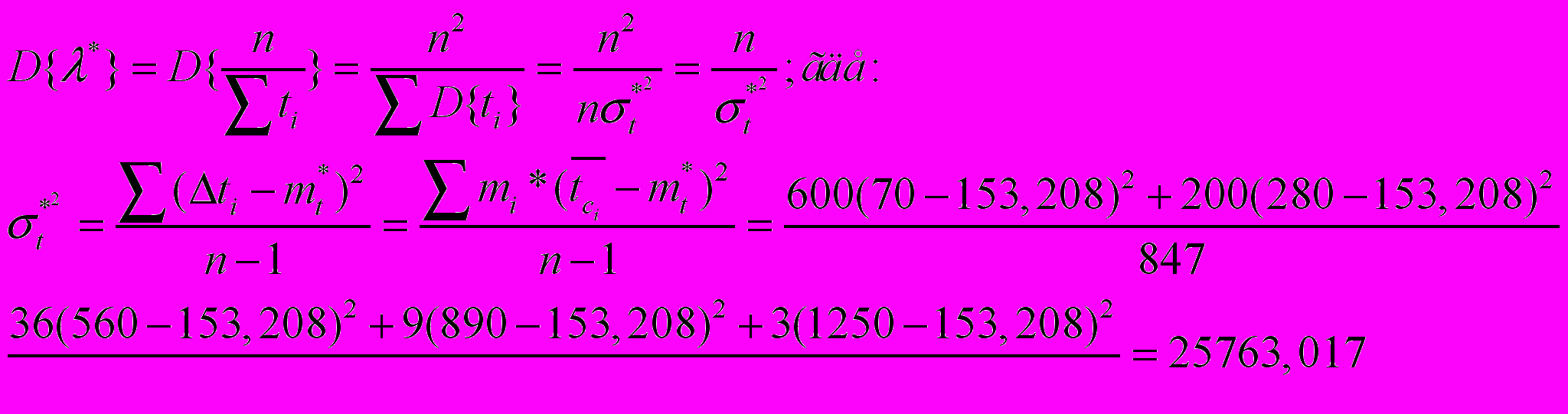
Таким образом:

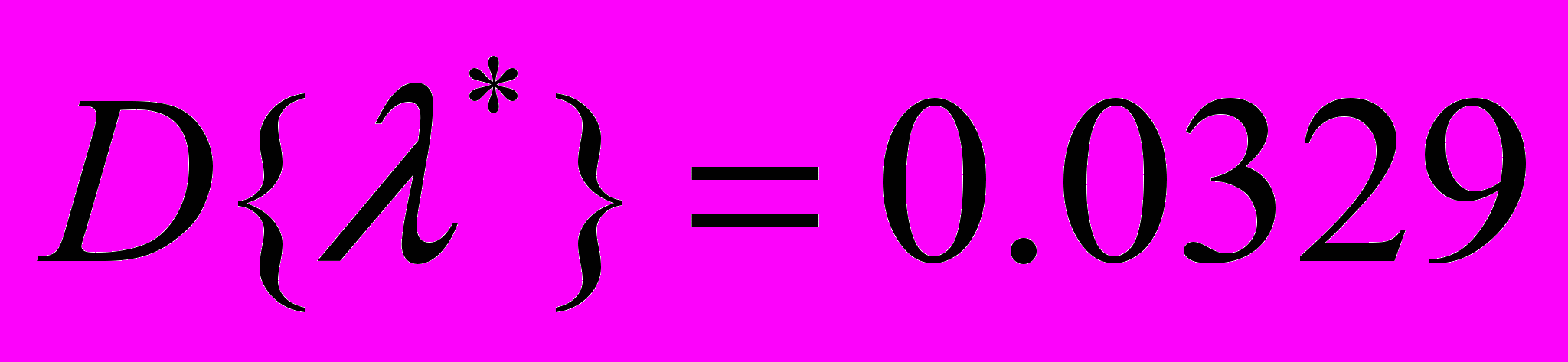
По таблице нормального распределения β=0.9

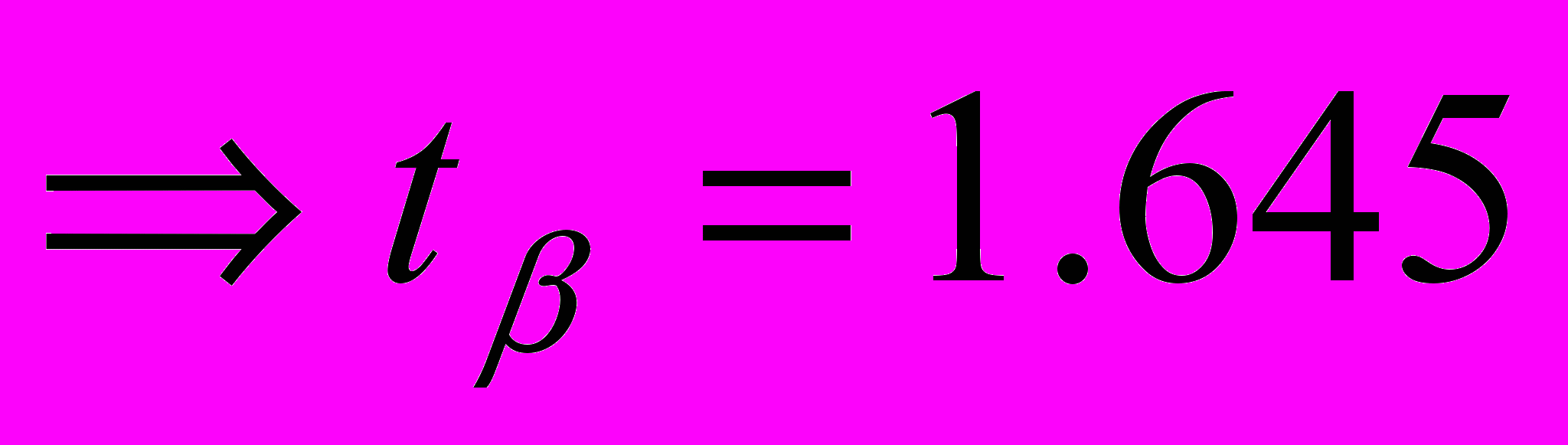
доверительный интервал:

Далее определяем

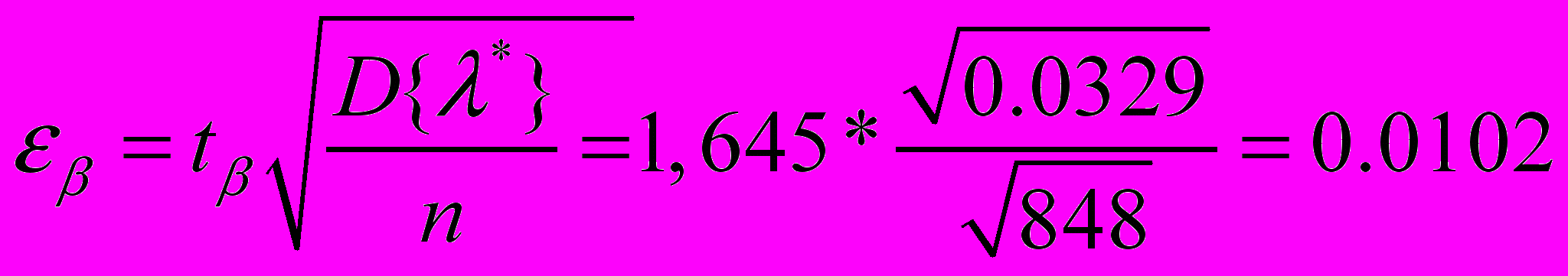
Таким образом, получим доверительный интервал:



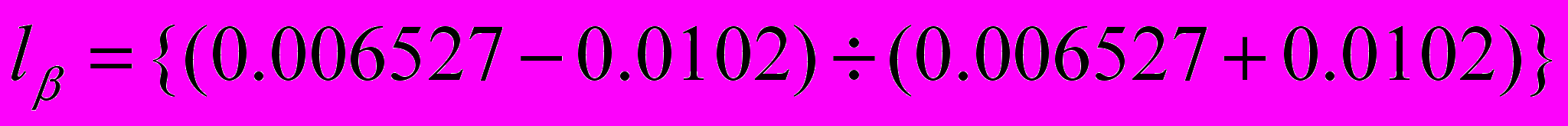
3 Определение потока сообщения на УК4 методом динамики средних

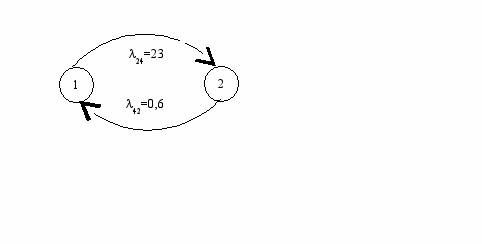
3.1 Граф соединений и уравнения динамики средних


По исходным данным интенсивность передачи сообщений из узла 4 в узел 2: λ₄₂=0,6[час^-1].

Количество источников сообщения на УК4: N4=400

Определим λ₄₂ как обратную величину от оценки математического ожидания случайного события:



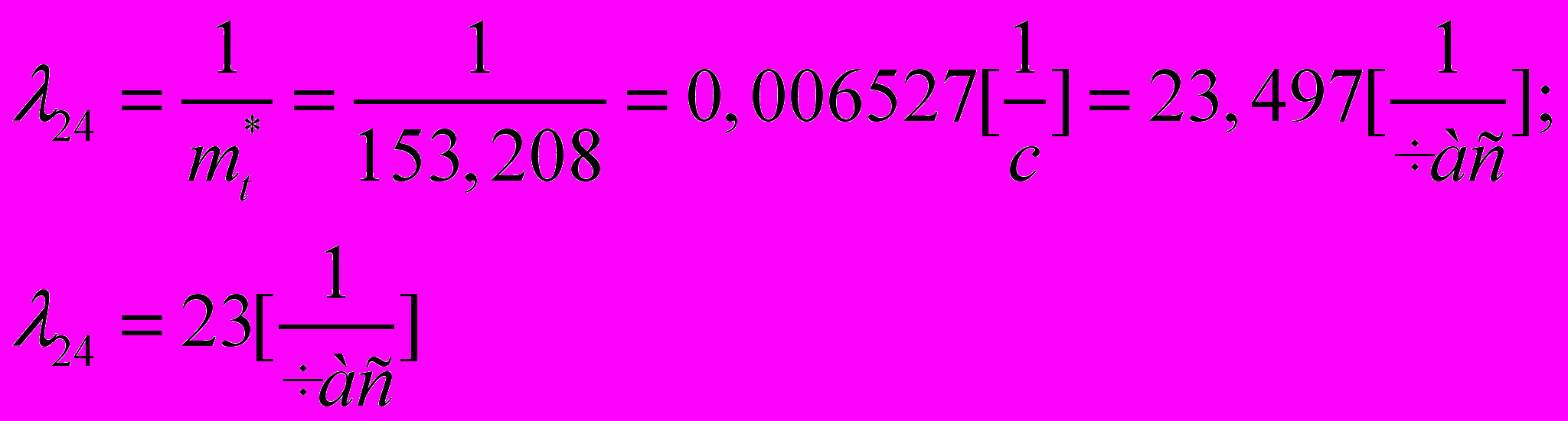
Составим граф состояний одного элемента:

1. элемент работает
   
2. элемент не работает
   

Пусть μ₁-среднее число рабочих элементов

μ₂-среднее число нерабочих элементов.

Тогда можно составить число систему уравнений по методу динамики средних:



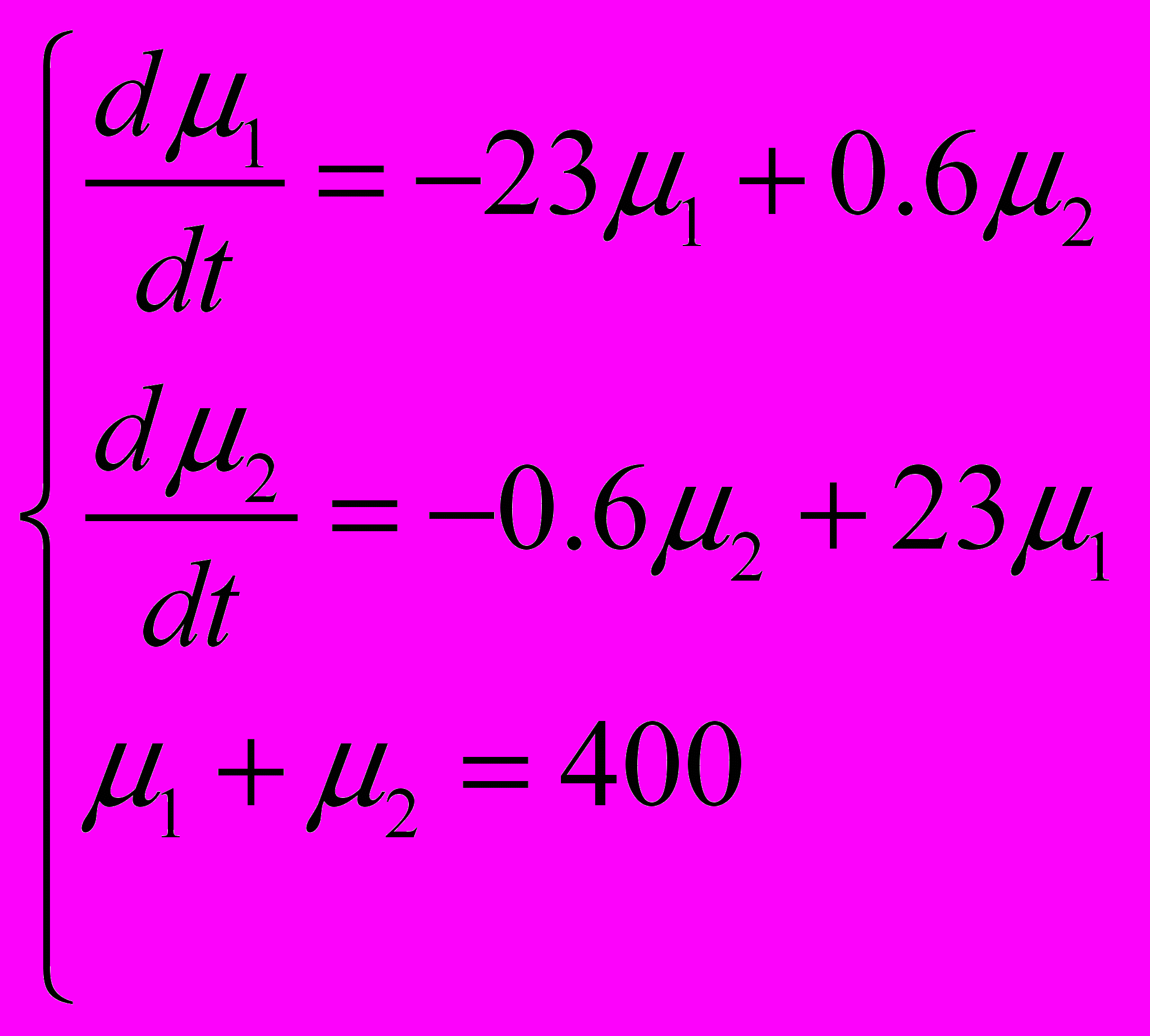
Решим эту систему уравнений:



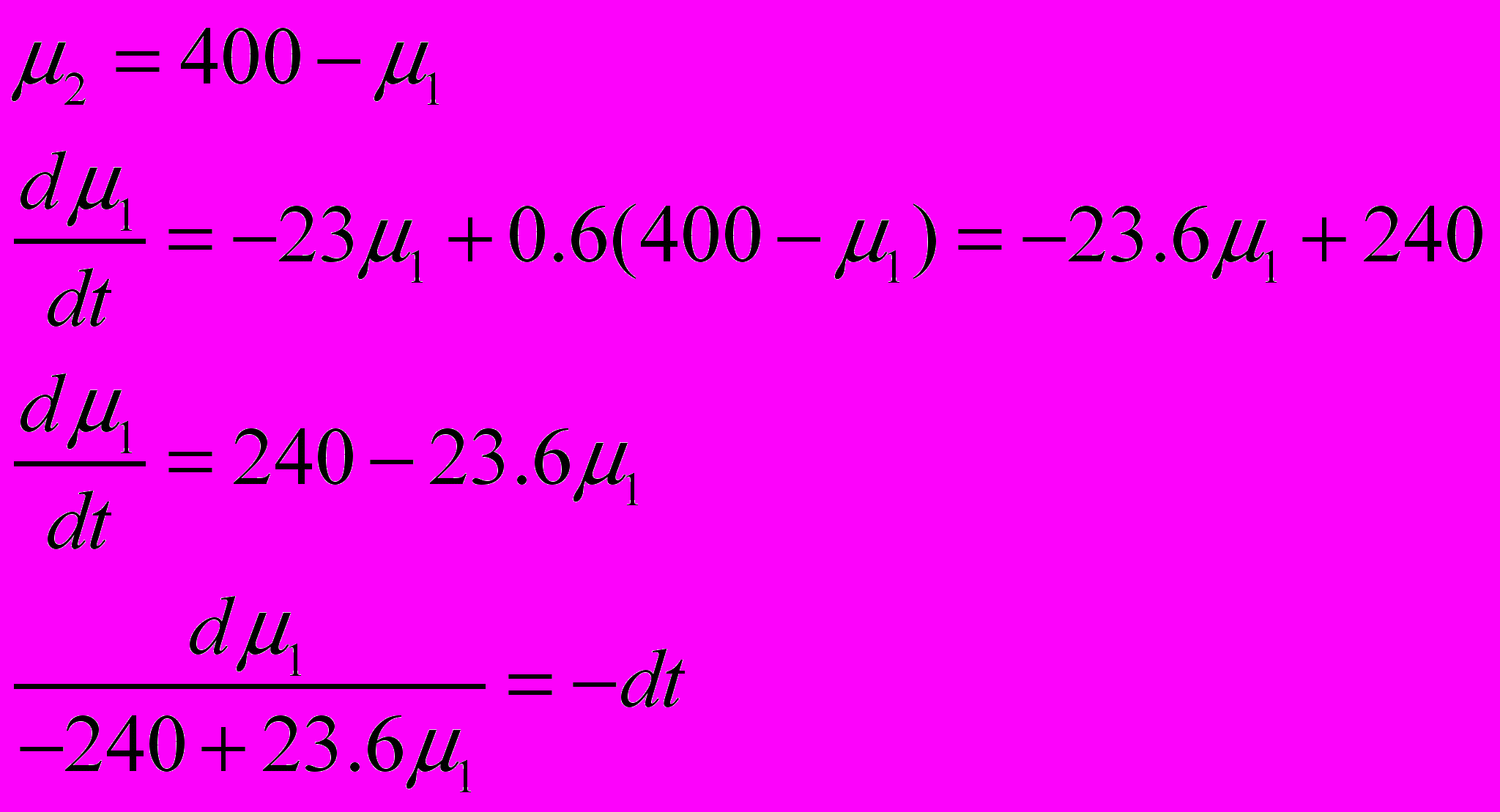
Проинтегрируем:



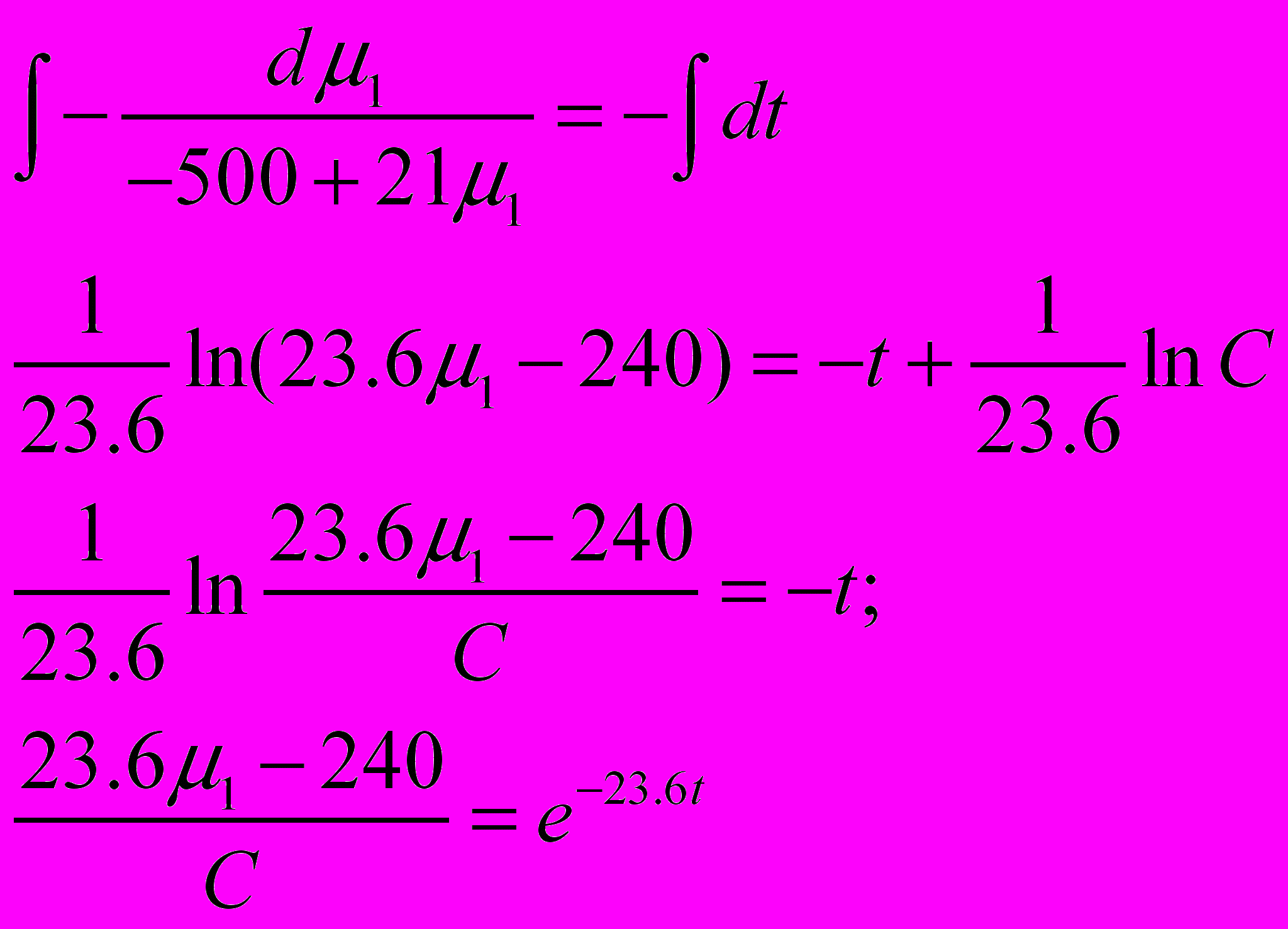
Тогда

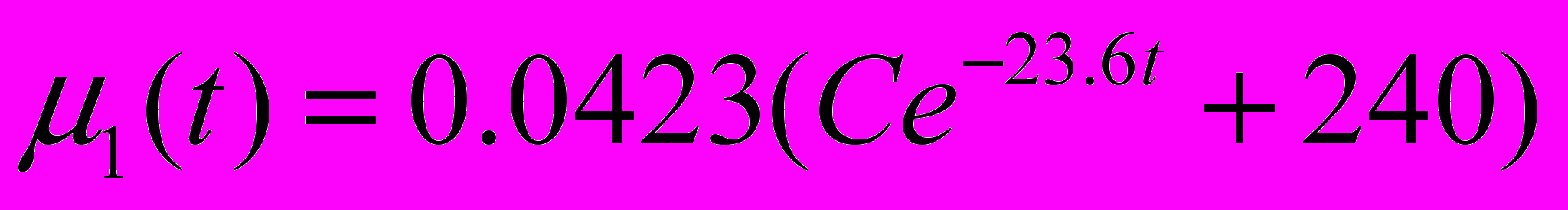
Определим постоянную интегрирования С:

При t=0,

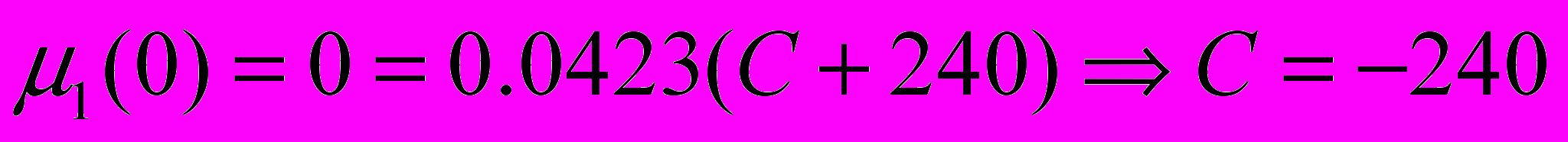
Таким образом

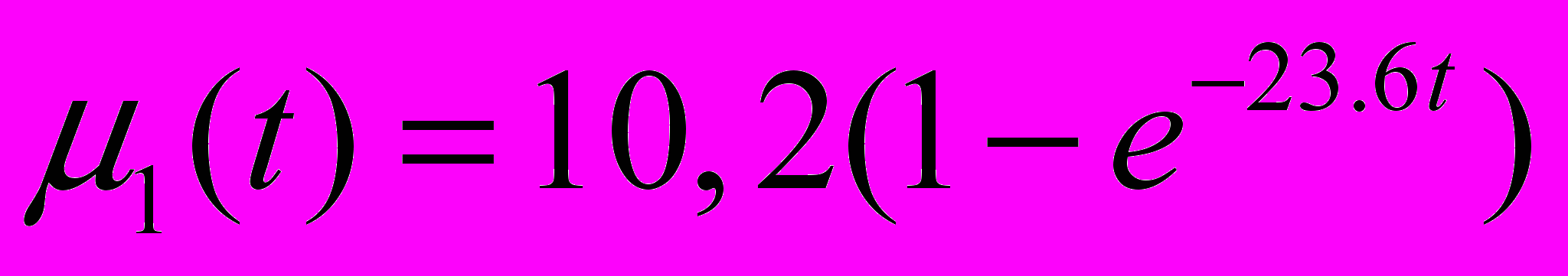
При 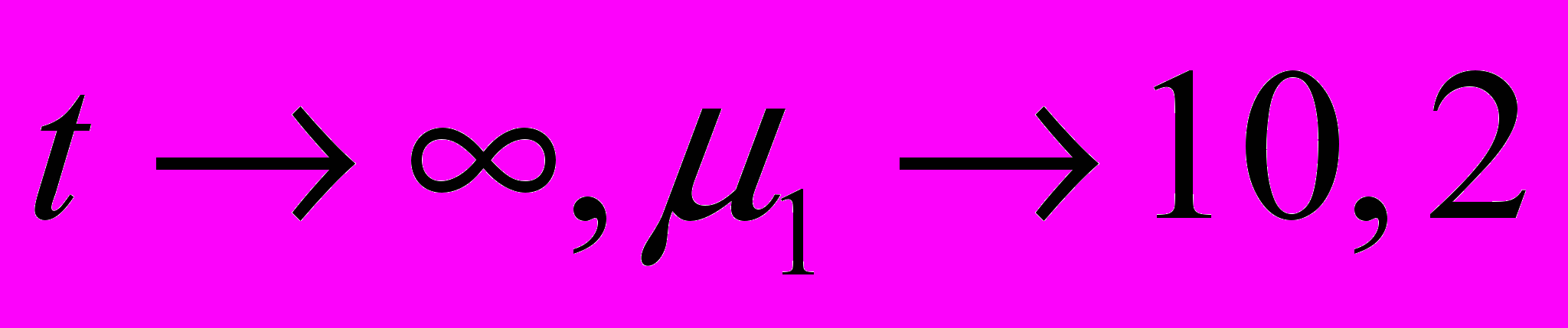, тогда на УК4 действует поток сообщений φ₄₂=24.

При этом μ₂(t)=400-μ₁(t)=389,8+10,2e^-23.6t

Отсюда время переходного процесса:




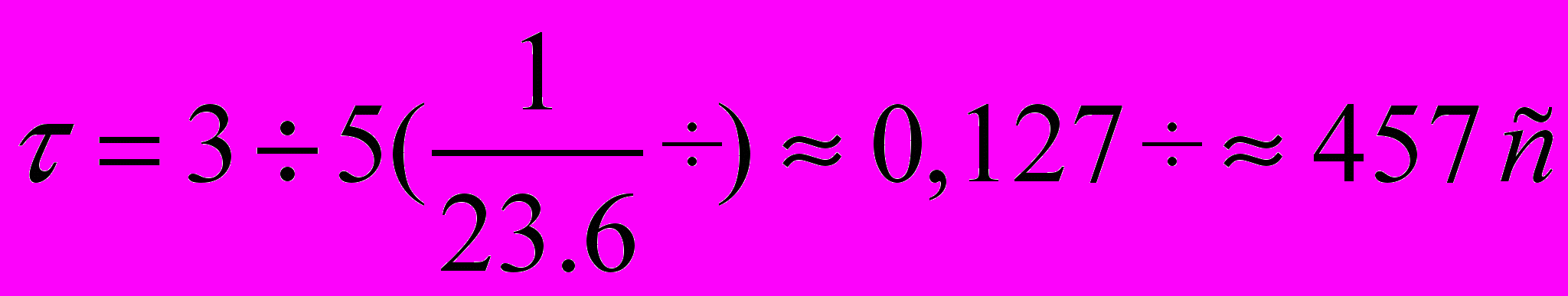
3.2 График средних численностей состояния и дисперсии количества одновременно передаваемых сообщений.

3.2.1 Построение графика средних численностей состояния




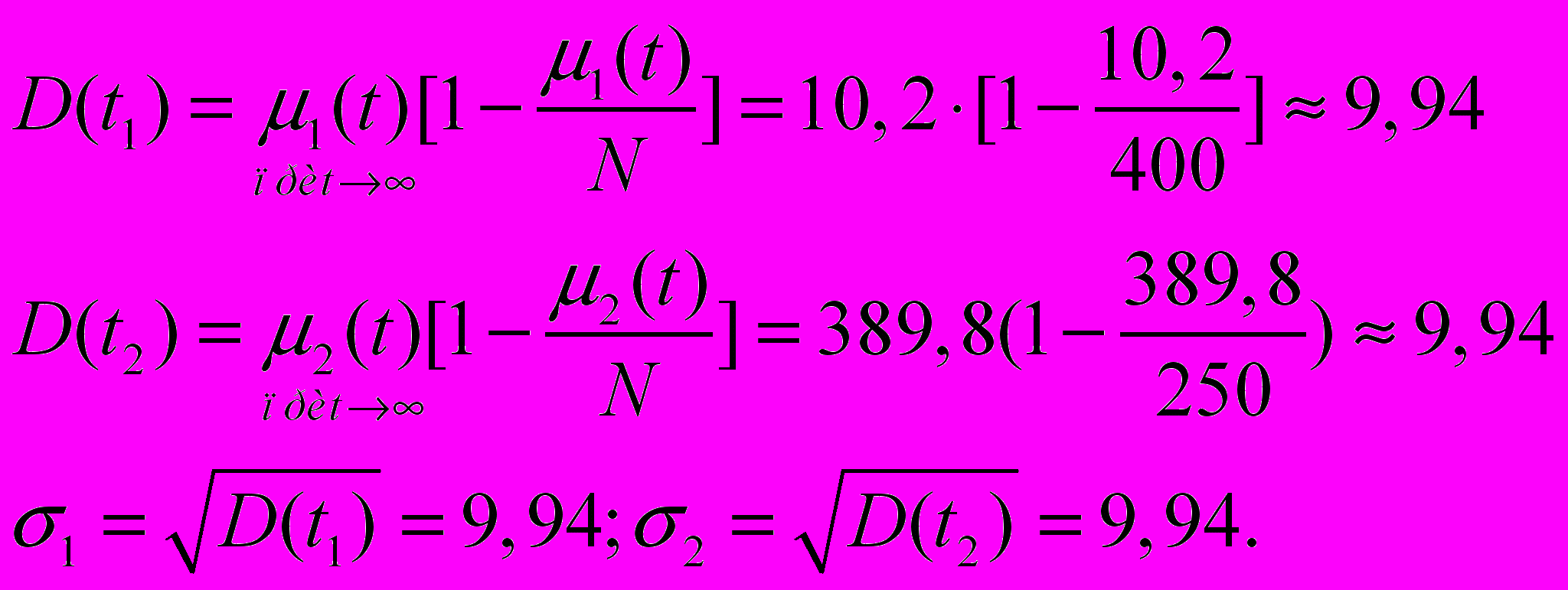
Точки для построения 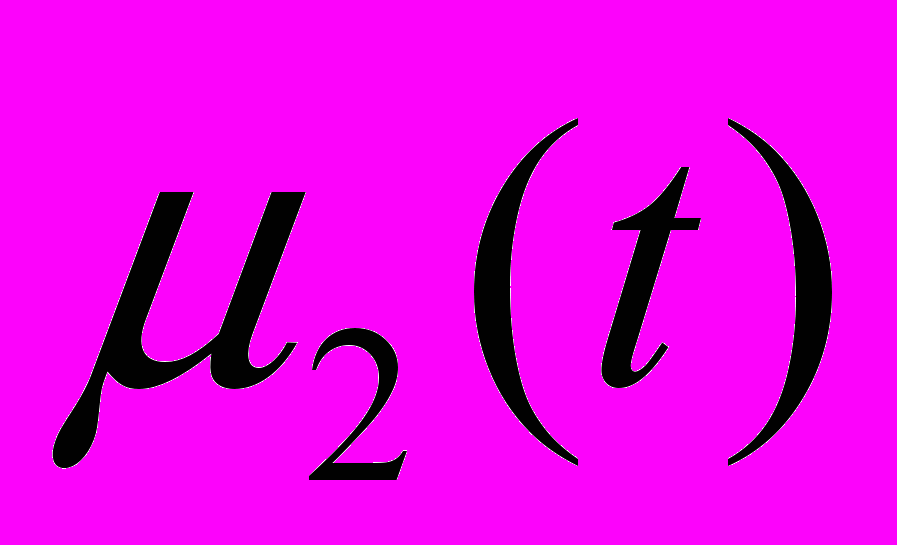, 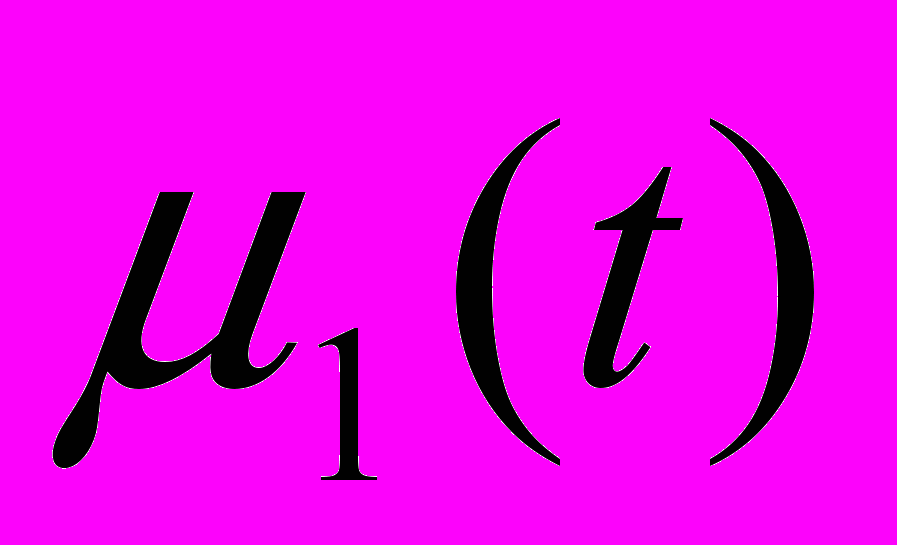сведем в таблицу 3.2.1.1

Таблица 3.2.1.1- Построение,

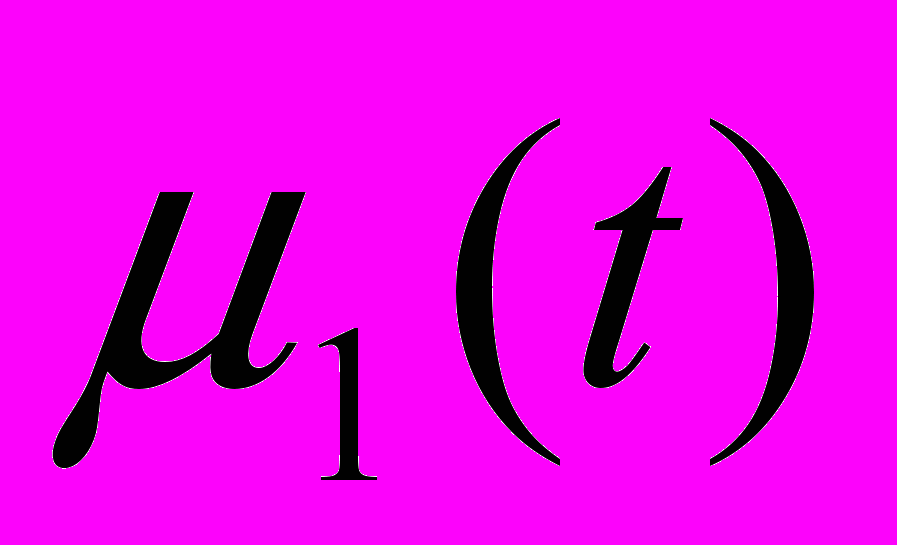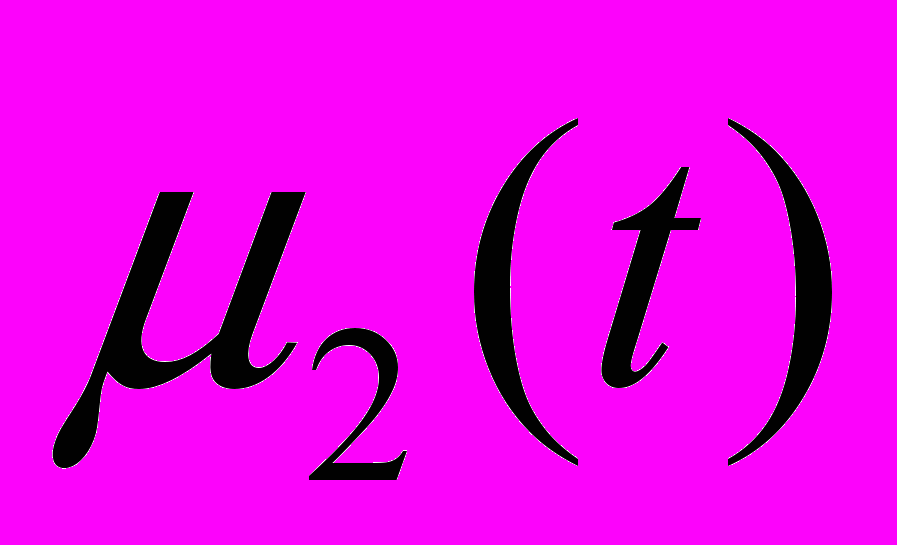
t
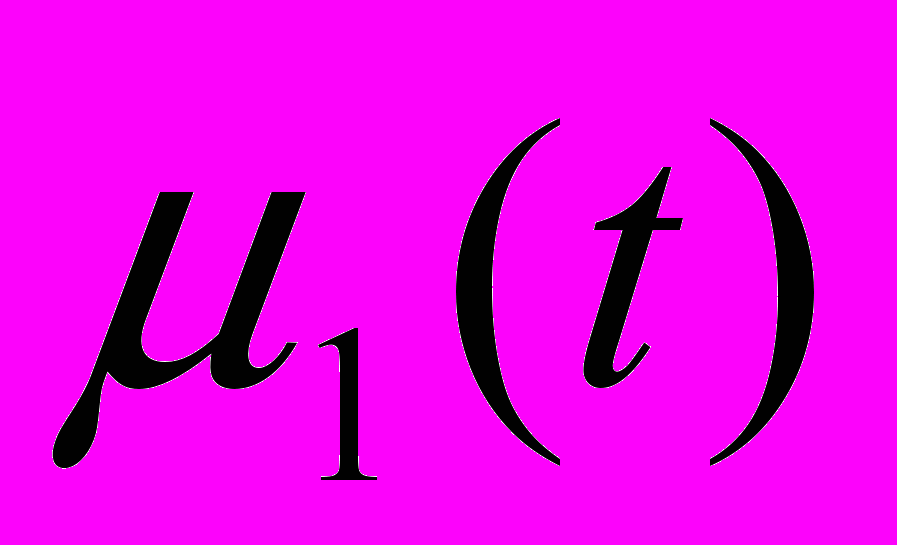
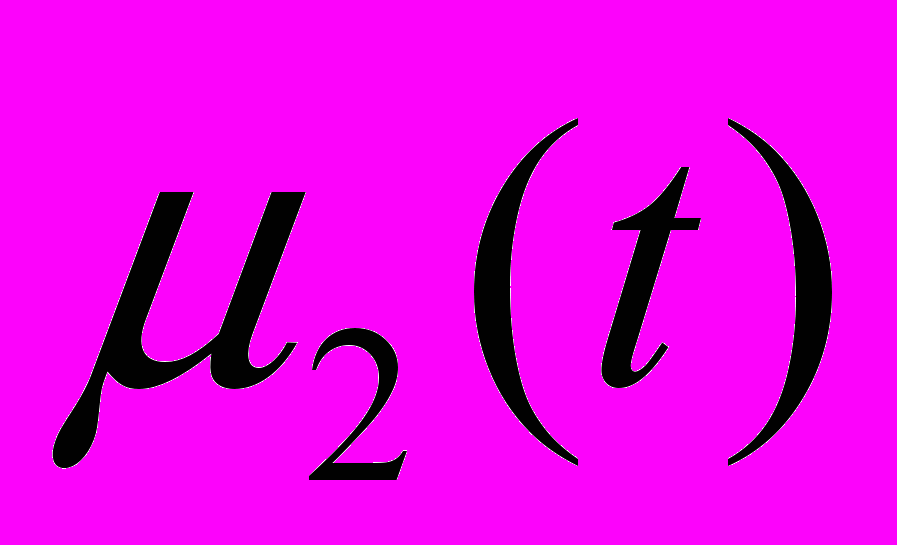
0	0	400
0,1	9,2369	390,763
0,2	10,1090	389,8909
0,3	10,1914	389,8086
0,4	10,1991	389,8008
0,5	10,1999	389,8001
0,6	10,1999	389,80001
0,7	10,2	389,8
0,8	10,2	389,8
0,9	10,2	389,8

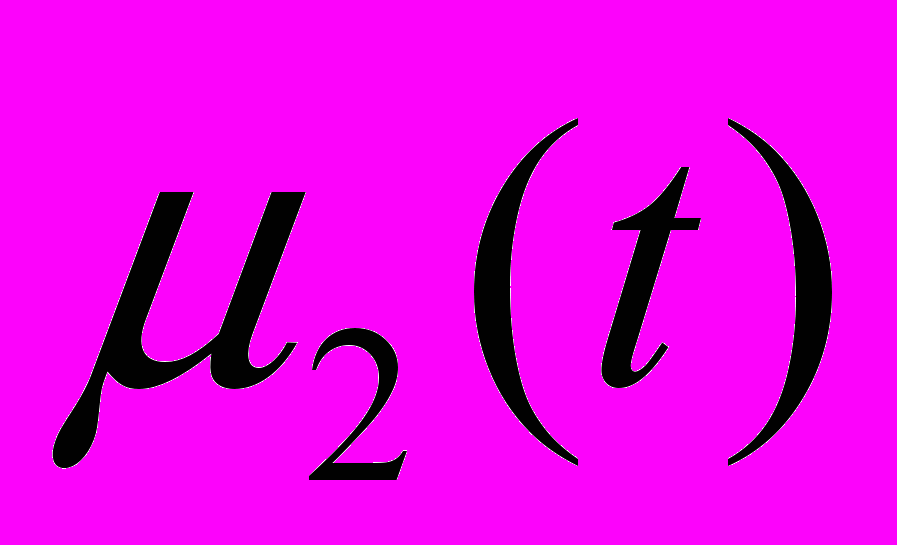
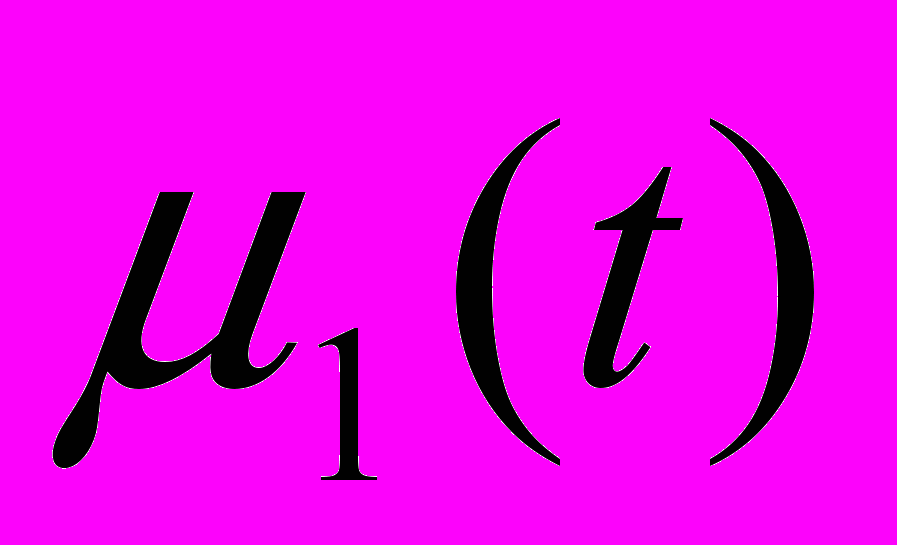
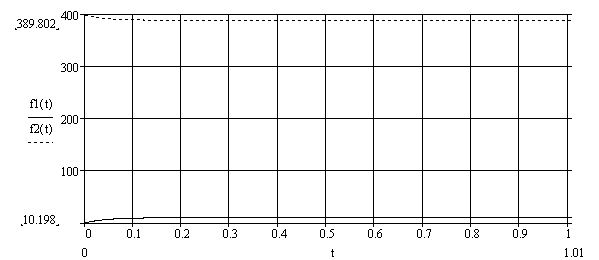
Рисунок 3.2.1.1 - Построение ,


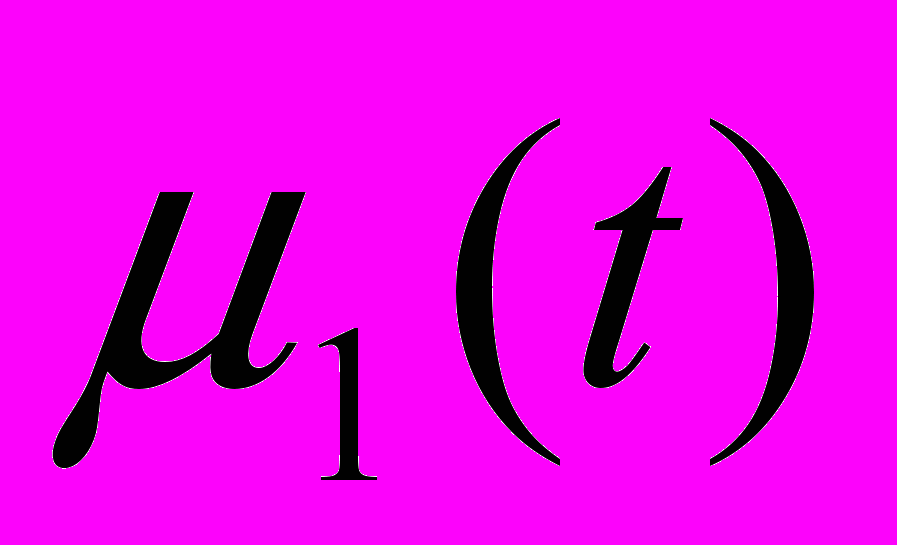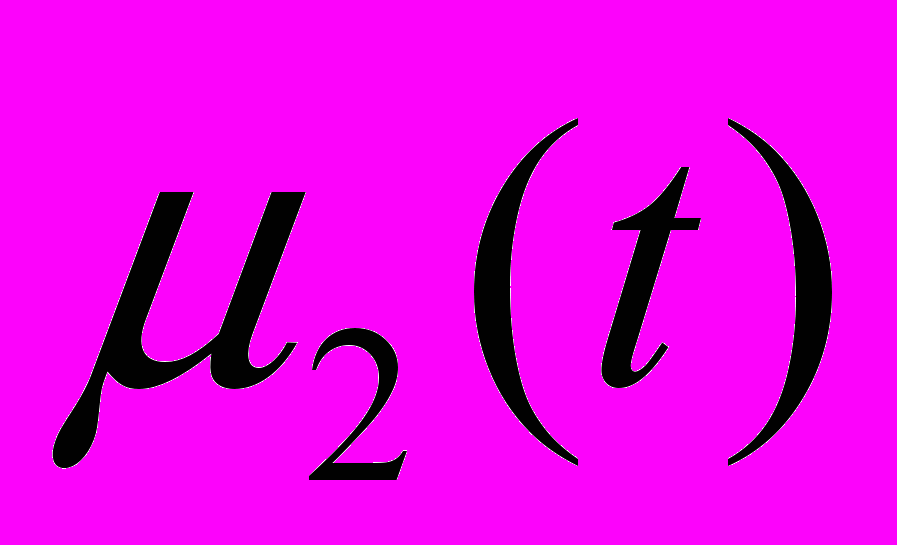
3.2.2. Расчет дисперсии количества одновременно передаваемых сообщений.

Источник передает сообщения, когда он находится в состоянии «1», т.е. в рабочем состоянии. Тогда дисперсия вычисляется по формуле:



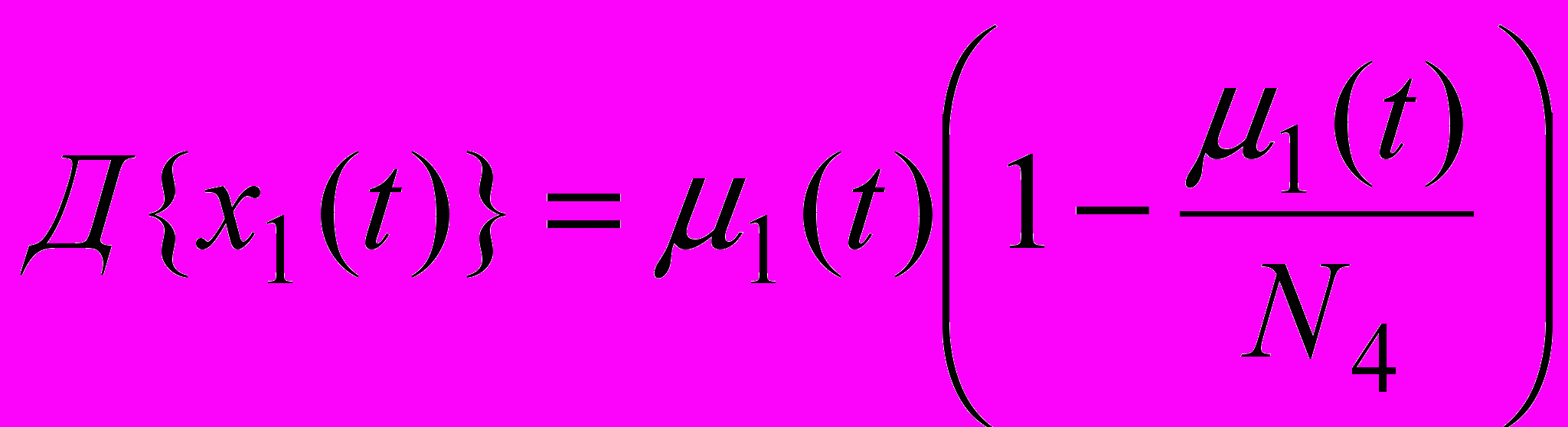
Дисперсия является функцией времени. Рассчитаем дисперсию в установившемся режиме, т.е. при t=. В установившемся режиме значение 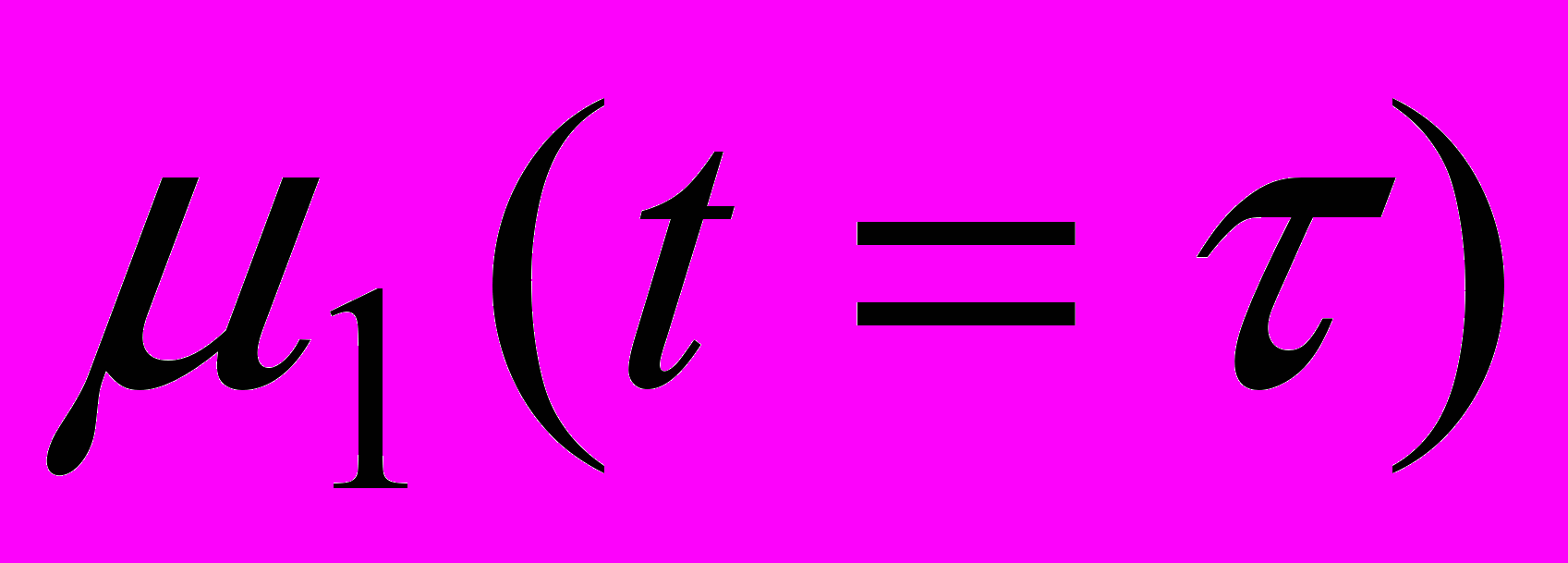равно 23. Подставим это значение и получим :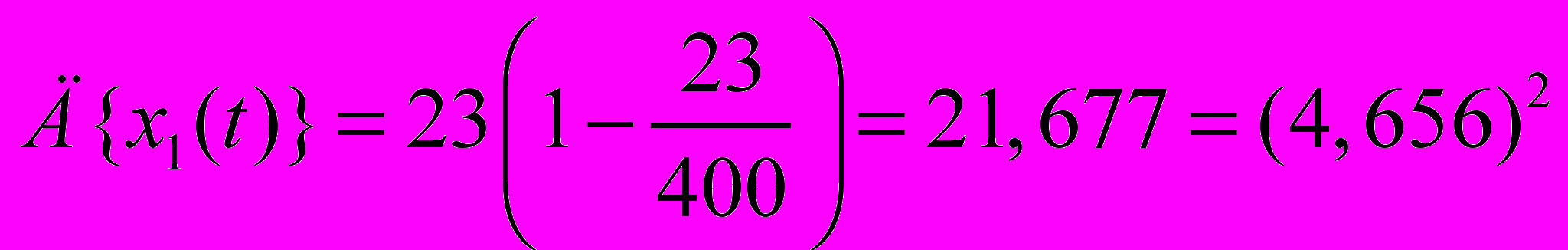




3.2.3. Графики плотности распределения вероятностей количества одновременно передаваемых сообщений.


Воспользовавшись данными, полученными в п. 3.2.2 и 3.1, построим график плотности распределения вероятности количества одновременно передаваемых сообщений.

Так как количество источников сообщений N₄ = 500, т.е. достаточно большое число, то можно сказать, что количество одновременно передаваемых сообщений распределяется по нормальному закону. Тогда плотность распределения вероятности определяется по формуле:



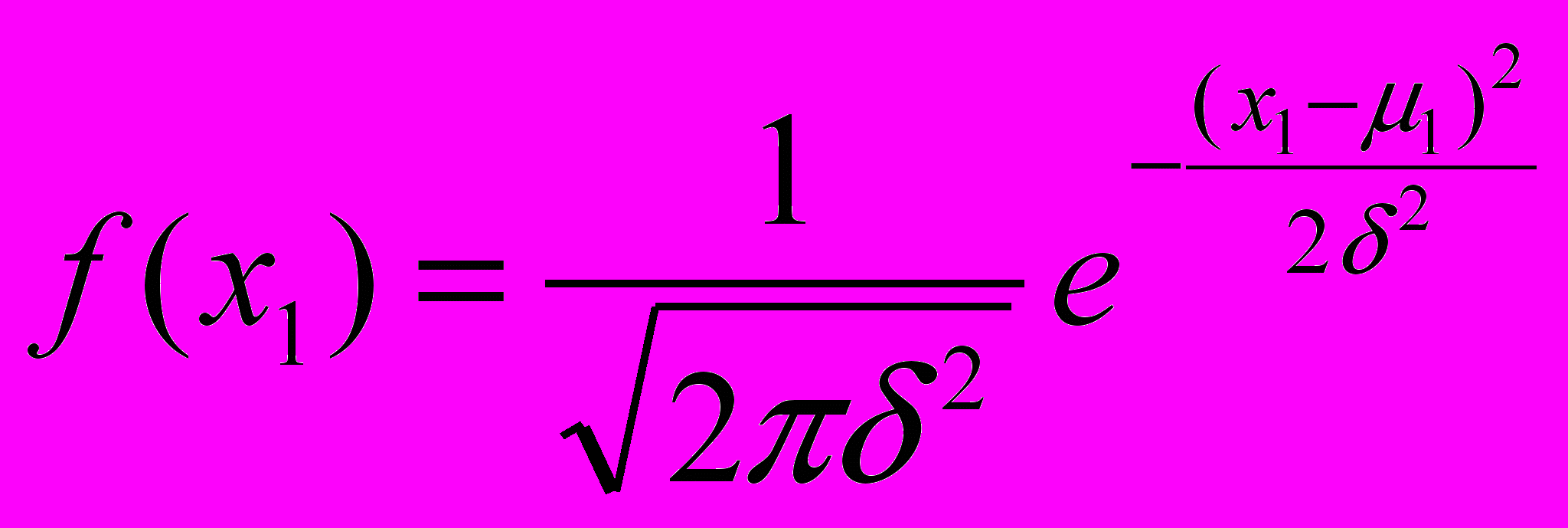
Где ² = Д{х₁(t)} = 21,677 х₁ = ₁ = 23



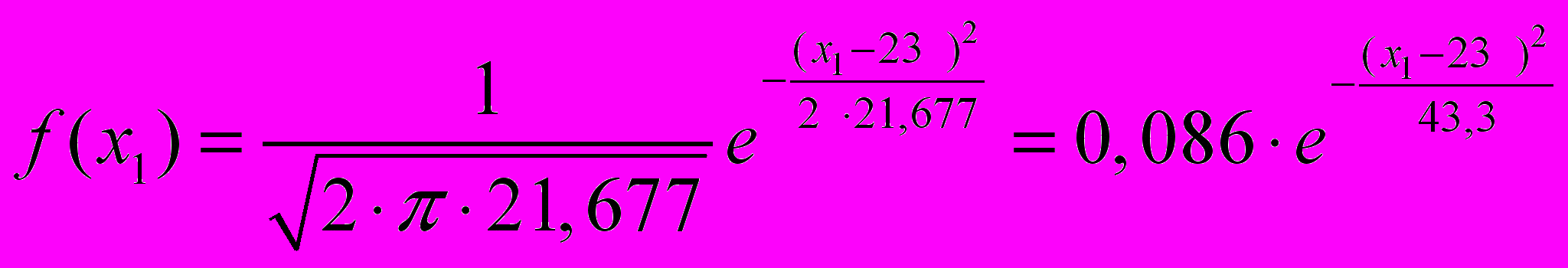
Определим величину «3»:

3 =




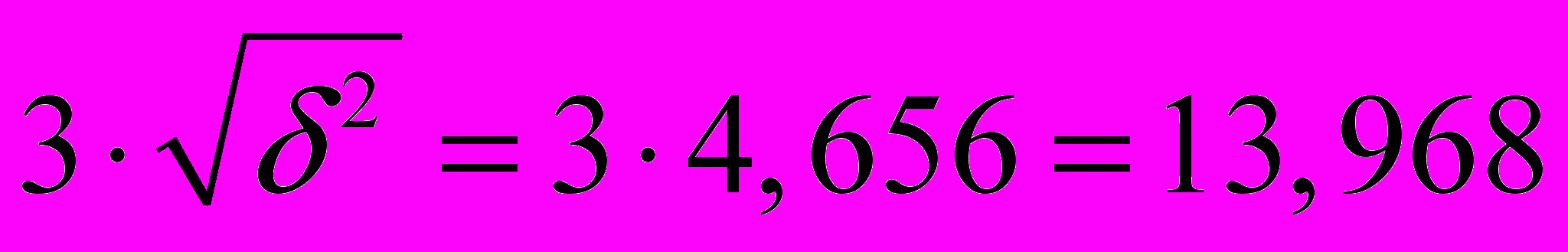
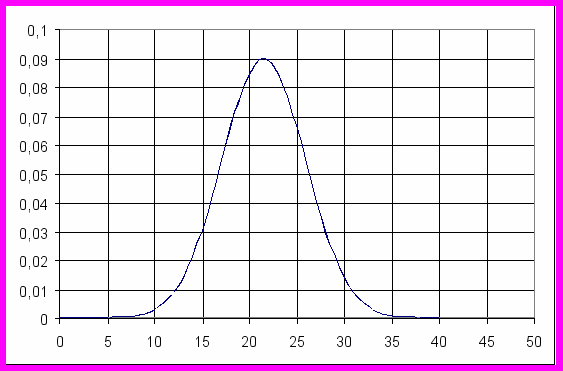
Рисунок 3.2.3.1- График плотности распределения вероятностей количества одновременно передаваемых сообщений


4 Разработка алгоритма управления СПИ по критерию максимальной производительности

4.1 Маршрутизация

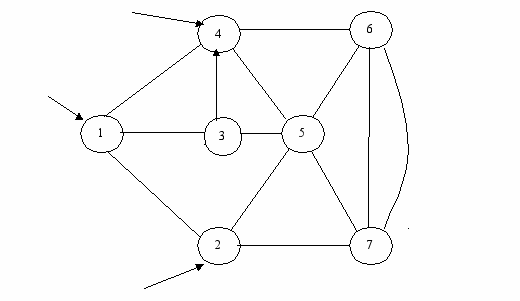µ₄₂


µ₁₅


µ₂₃


рисунок 4.1.1 - Граф СПИ


По исходным данным построим матрицы емкостей и смежности.

	0	1	1	1	0	0	0
	1	0	0	0	1	0	1
	1	0	0	1	1	0	0
С=	1	0	0	0	1	1	0
	0	1	1	1	0	1	1
	0	0	0	1	1	0	1
	0	1	0	0	1	1	0

Матрица емкостей

	0	60	70	50	0	0	0
	60	0	0	0	60	0	35
	70	0	0	40	30	0	0
В=	50	0	0	0	20	0	0
	0	60	30	20	0	0	20
	0	0	0	0	0	0	0
	0	35	0	0	20	0	0

Так как b₄₆= b₅₆= b₆₇=0, то граф имеет вид:



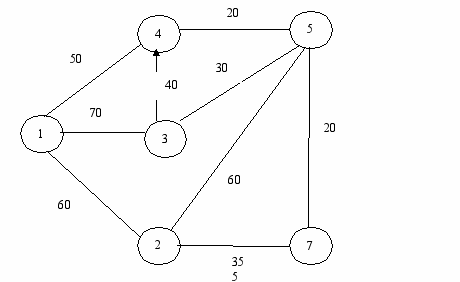
Рисунок 4.1.2 - Перестроенный граф СПИ


Тогда матрица смежности имеет вид:

	0	1	1	1	0	0
	1	0	0	0	1	1
	1	0	0	1	1	0
С=	1	0	0	0	1	0
	0	1	1	1	0	1
	0	1	0	0	1	0

Составим матрицу потоков сообщения:

φ₂₃=60; φ₁₅=70; φ₄₂=23

	0	0	0	0	70	0
	0	0	60	0	0	0
	0	0	0	0	0	0
Ф=	0	23	0	0	0	0
	0	0	0	0	0	0
	0	0	0	0	0	0

По матрице смежности составим деревья путей.




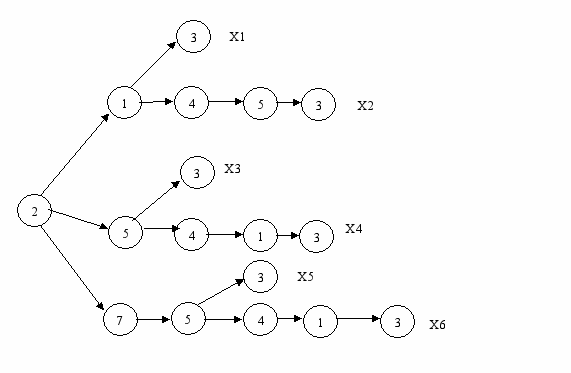
Рисунок 4.1.3 - Дерево путей из узла 2 в узел 3

М₂₃{213,21453,253,25413,2753,275413}




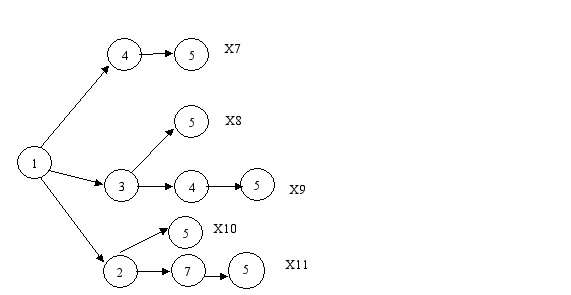
Рисунок 4.1.4 - Дерево путей из узла 1 в узел 5

М₁₅{145,135,1345,125,1275}




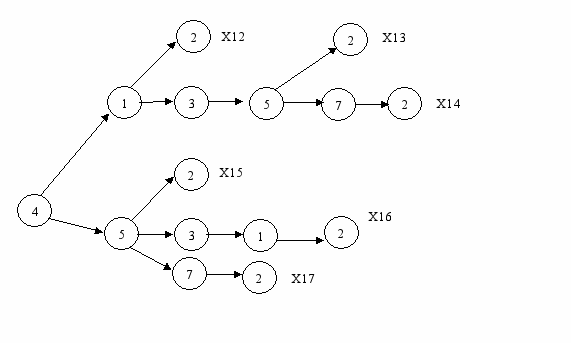
Рисунок 4.1.5 - Дерево путей из узла 4 в узел 2


М₄₂{412,41352,413572,452,45312,4572}


4.2 Построение симплекс-таблицы


Составим целевую функцию:

F=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+

x17;

Ограничения на поток сообщения:



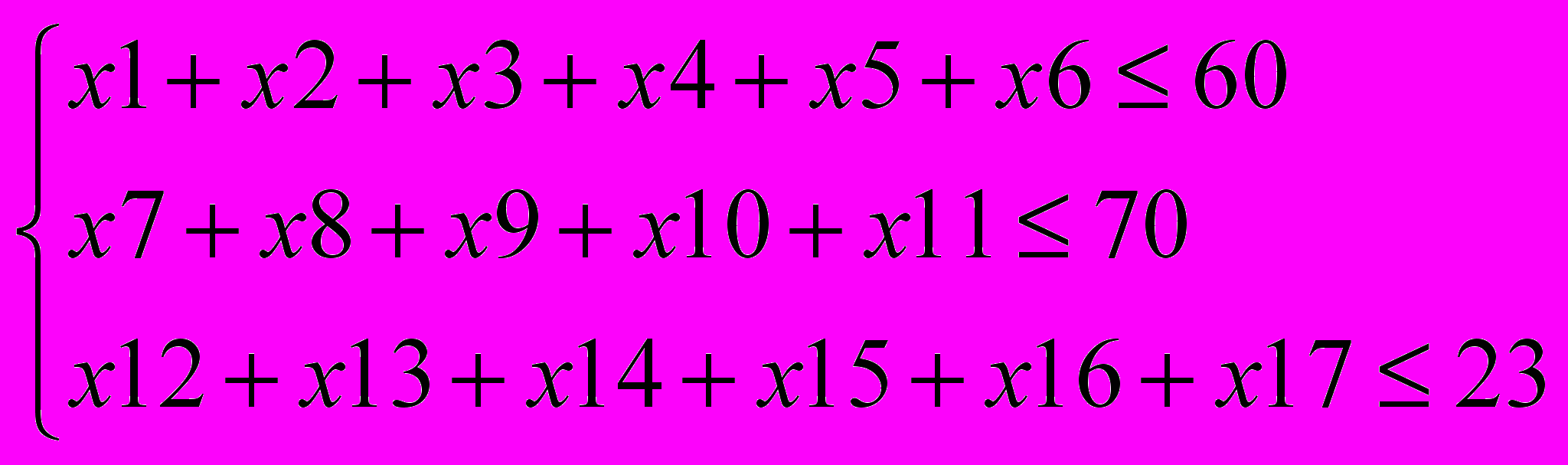
Ограничения по пропускным способностям линий связи:


x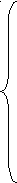1+x2+x10+x11+x12+x16≤60

x1+x4+x6+x8+x9+x13+x14+x16≤70

x2+x4+x6+x7+x12+x13++x14≤50

x3+x4+x10+x13+x15≤60

x5+x6+x11+x14+x17≤35

x9≤40

x2+x3+x5+x8+x13+x14+x16≤30

x5+x6+x11+x14+x17≤20

x2+x4+x6+x7+x9+x15+x16+x17≤60


Для того, чтобы построить симплекс-таблицу, необходимо перейти к основной задаче линейного программирования.

Целевая функция будет иметь вид:



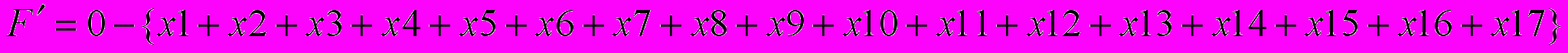
Ограничения вида неравенств, заменяем на ограничения вида равенств:



где х1,…х17-свободные переменные;

y1,..,y12- базисные переменные.

Таблица 4.2 -Симплекс-таблица

	CК	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14	X15	X16	X17
F	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Y1	60	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
Y2	70	0	0	0	0	0	0	1	1	1	1	1	0	0	0	0	0	0
Y3	23	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1
Y4	60	1	1	0	0	0	0	0	0	0	1	1	1	0	0	0	1	0
Y5	70	1	0	0	1	0	1	0	1	1	0	0	0	1	1	0	1	0
Y6	50	0	1	0	1	0	1	1	0	0	0	0	1	1	1	0	0	0
Y7	60	0	0	1	1	0	0	0	0	0	1	0	0	1	0	1	0	0
Y8	35	0	0	0	0	1	1	0	0	0	0	1	0	0	1	0	0	1
Y9	40	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0
Y10	30	0	1	1	0	1	0	0	1	0	0	0	0	1	1	0	1	0
Y11	20	0	0	0	0	1	1	0	0	0	0	1	0	0	1	0	0	1
Y12	60	0	1	0	1	0	1	1	0	1	0	0	0	0	0	1	1	1

4.3 Расчет на ЭВМ потоков сообщения


Решим данную задачу с помощью симплекс метода на ЭВМ.

тогда, по таблице симплекс-метода:

х1=9,25 х3=10,00 x4=21,5 x5=19,25 х9=38,5 х10=28,5 x12=22,25 x14=0,75

- Х_j = 0 означает, что по данному пути не передаются сообщения, т.е. данный путь не является рациональным.

- Х_{i j}  0 означает, что по данному пути передается определенное количество сообщений.



4.4 Построение вторичного графа СПИ

Построим вторичный граф СПИ при оптимальном распределении

каналов. Сначала составим массив всех путей, по которым

передается количество сообщений, больше нуля:

Таблица 4.4.1 – Таблица для построения вторичного графи СПИ

Путь	Номер пути	Количество сообщений, Х
2-1-3	1	9.25
2-5-3	3	10.00
2-5-4-1-3	4	21.50
2-7-5-3	5	19.25
1-3-4-5	9	38.50
1-2-5	10	28.50
4-1-2	12	22.25
4-1-3-5-7-2	14	0.75

Построим вторичный граф СПИ.



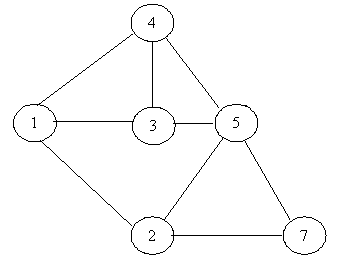
Рисунок 4.4.1 - Вторичный граф СПИ

5 Разработка алгоритма управления СПИ по критерию максимальной надежности

5.1 Построение матрицы надежных маршрутов

(дистанционной таблицы)

По исходным данным построим матрицу надежности:

	1	0,996	0,996	0,995	0	0	0
	0,996	1	0	0	0,995	0	0,999
	0,996	0	1	0,993	0,999	0	0
W=	0,995	0	0	1	0,998	0,998	0
	0	0,995	0,999	0,998	1	0,999	0,997
	0	0	0	0,998	0,999	1	0,998
	0	0,999	0	0	0,997	0,998	1

Перейдем к матрице ненадежности по формуле:

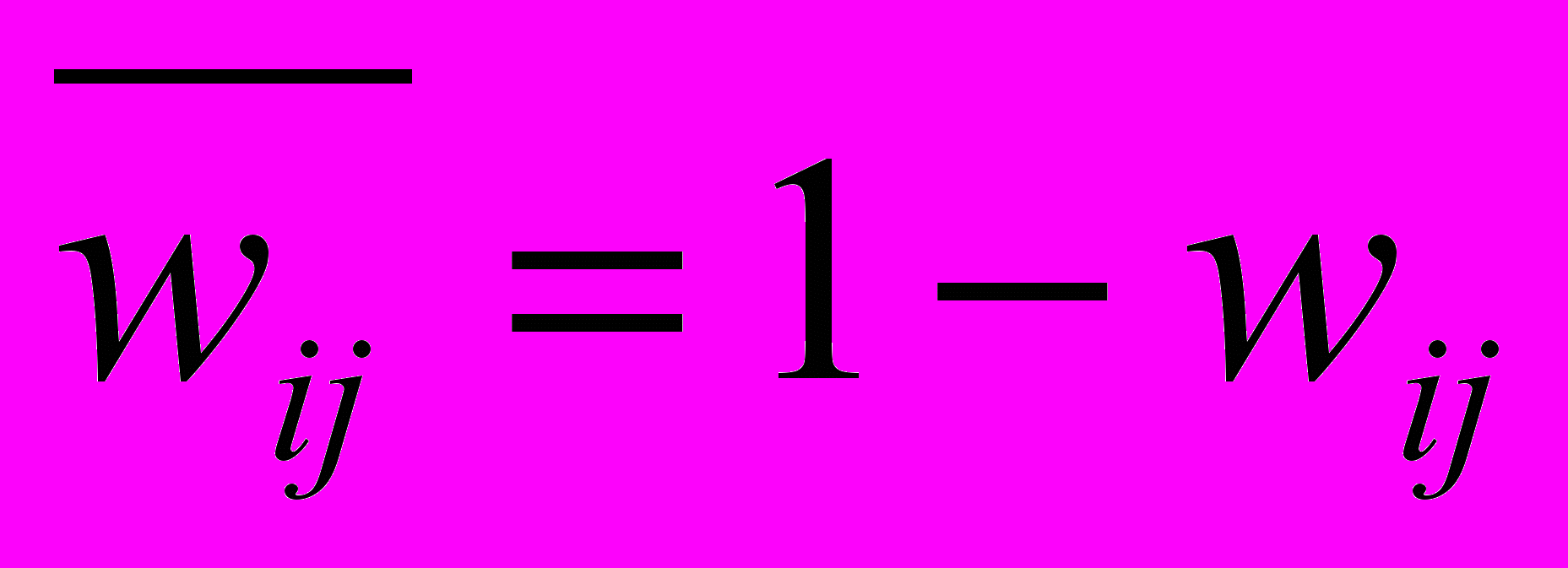
	0	4	4	5
	4	0			5		1
	4		0	7	1
	5			0	2	2
		5	1	2	0	1	3
				2	1	0	2
		1			3	2	0

Определим матрицу минимальной ненадежности с помощью операций Шимбела – Оттермана:

	0	4	4	5	5	7	5
	4	0	6	7	4	3	1
	4	6	0	3	1	2	4
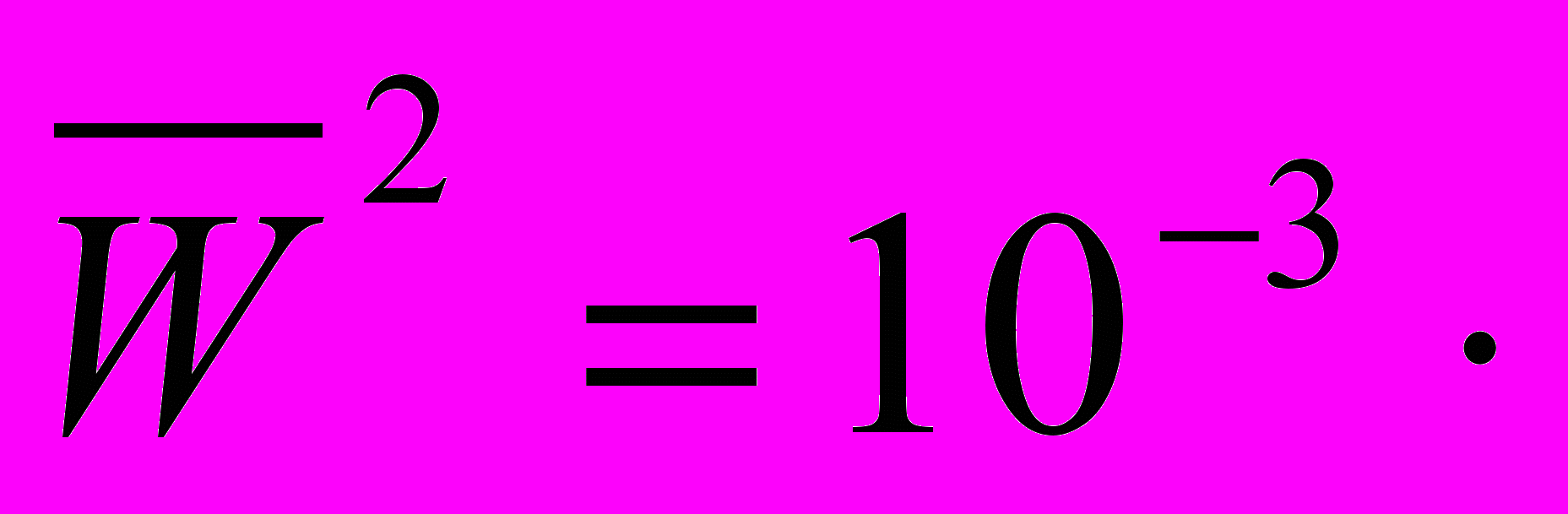	5	7	3	0	2	2	4
	5	4	1	2	0	1	3
	7	3	2	2	1	0	2
	5	1	4	4	3	2	0

	0	4	4	5	5	6	5
	4	0	5	4	4	3	2
	4	5	0	3	1	2	4
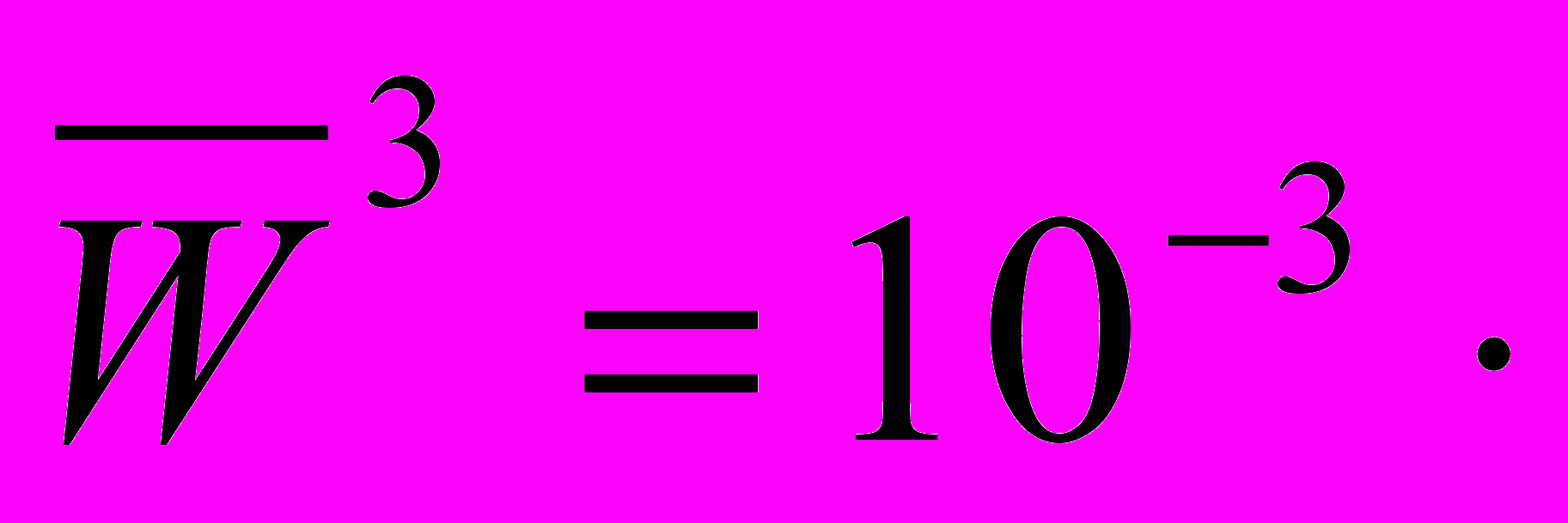	5	4	3	0	2	2	4
	5	4	1	2	0	1	3
	6	3	2	2	1	0	2
	5	2	4	4	3	2	0

	0	4	4	5	5	6	5
	4	0	5	4	4	3	2
	4	5	0	3	1	2	4
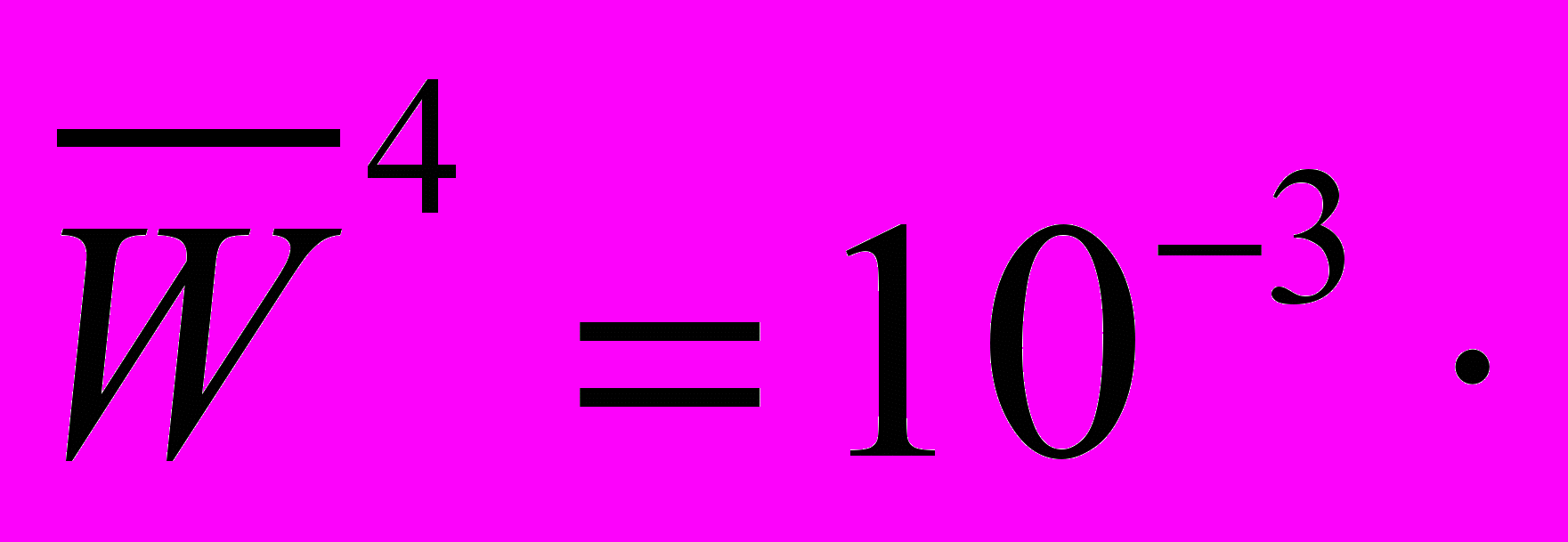	5	4	3	0	2	2	4	=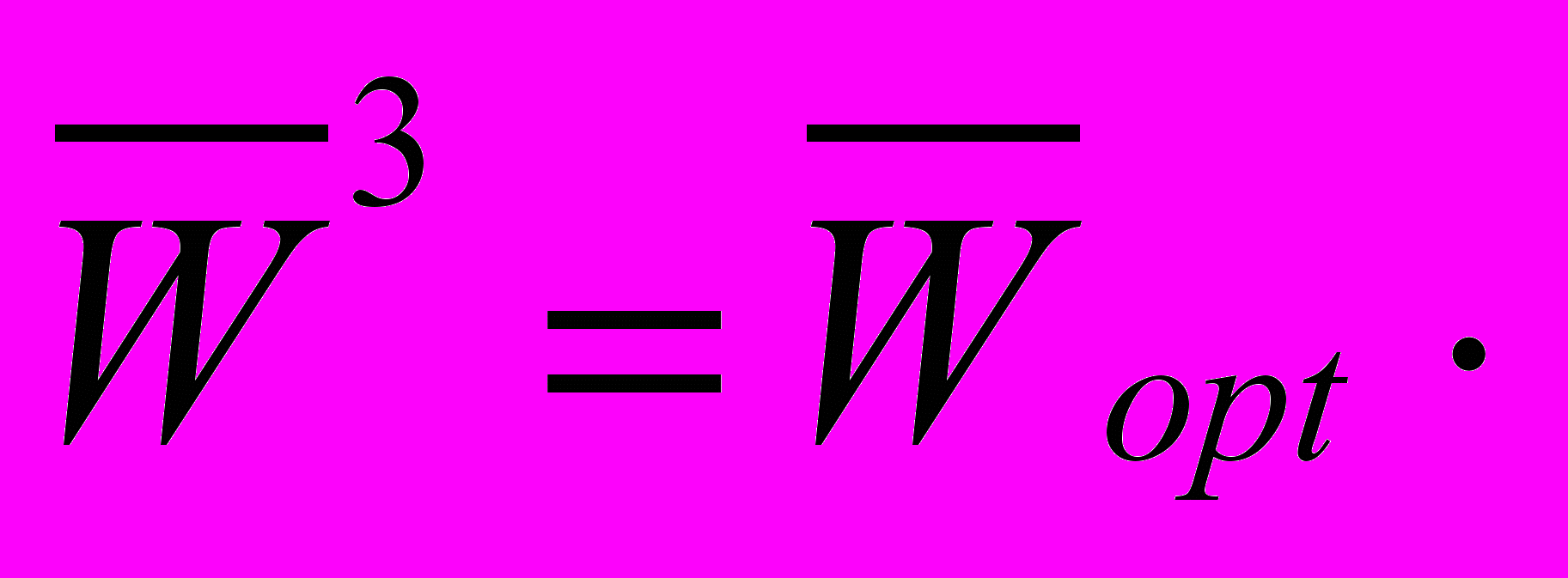
	5	4	1	2	0	1	3
	6	3	2	2	1	0	2
	5	2	4	4	3	2	0

Дистанционная таблица имеет вид:

0	4	4	5	5	6	5
4	0	5	4	4	3	2
4	5	0	3	1	2	4
5	4	3	0	2	2	4
5	4	1	2	0	1	3
6	3	2	2	1	0	2
5	2	4	4	3	2	0

5.2 Построение маршрутной таблицы


Для построения маршрутной таблицы 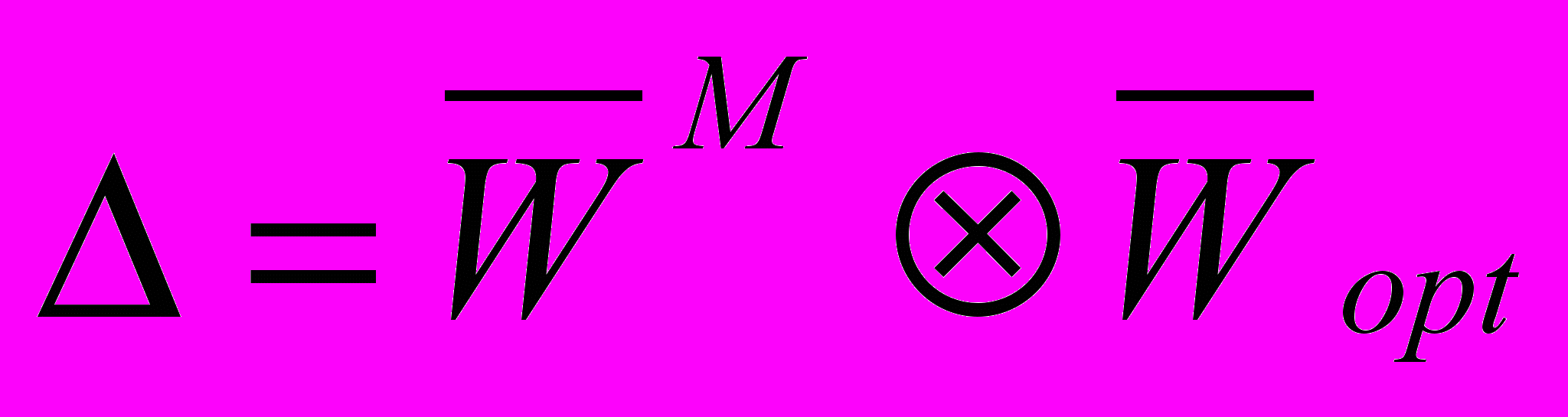, необходимо вычислить матрицу 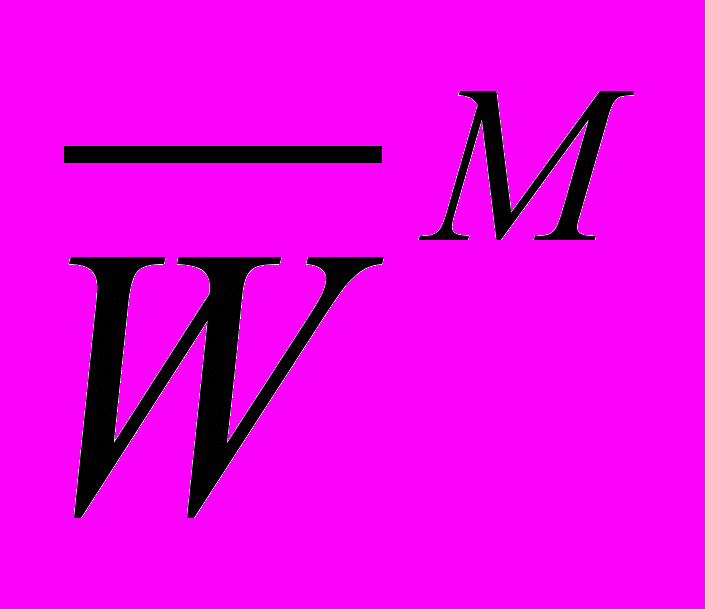, получаемую в результате замены диагональных элементов на ∞ в исходной матрице.

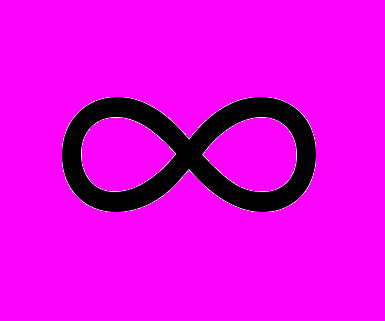		4	4	5
	4		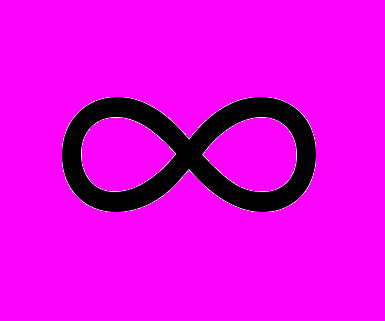		5		1
	4			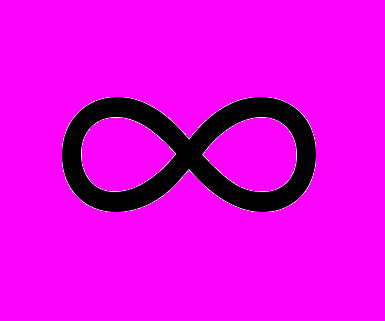7	1
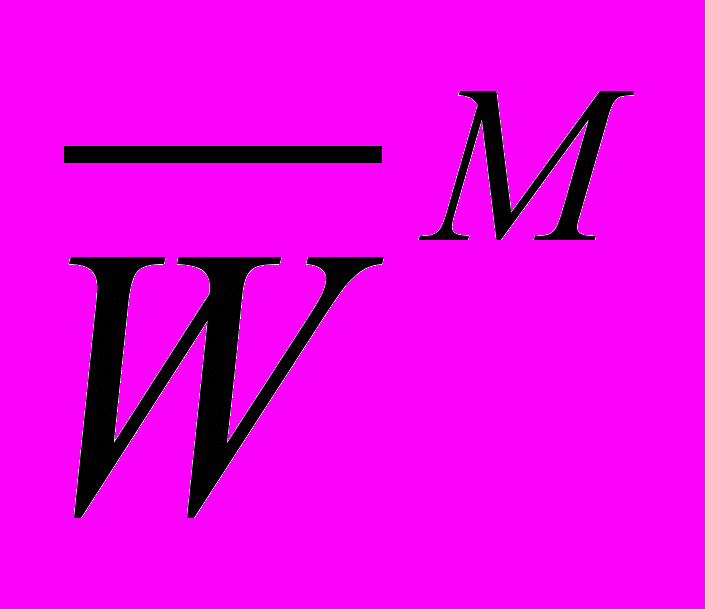=	5				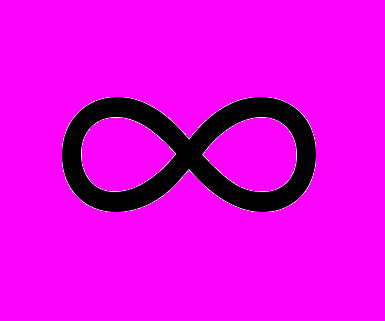2	2
		5	1	2		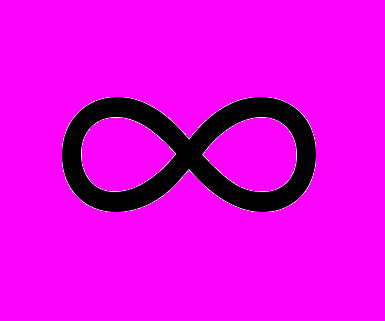1	3
				2	1		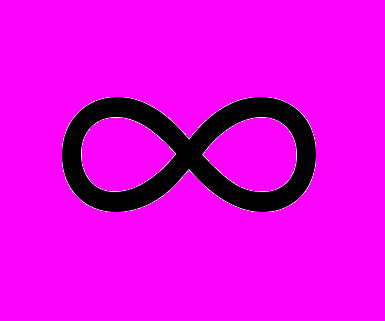2
		1			3	2

	0	4	4	5	5	6	5
	4	0	5	4	4	3	1
	4	5	0	3	1	2	4
	5	4	3	0	2	2	4
	5	4	1	2	0	1	3
	6	3	2	2	1	0	2
	5	1	4	4	3	2	0

Рассчитаем маршрутную таблицу:

δ ₁₂=min[∞+4, 4+0, 4+5, 5+4, 10³+4, 10³+3, 10³+1]=2;

δ ₁₃=min[∞+4, 4+5, 4+0, 5+3, 10³+1, 10³+2, 10³+4]=3;

δ ₁₄=min[∞+5, 4+4, 4+3, 5+0, 10³+2, 10³+2, 10³+4]=4;

δ ₁₅=min[∞+5, 4+4, 4+1, 5+2, 10³+0, 10³+1, 10³+3]=3;

δ ₁₆=min[∞+6, 4+3, 4+2, 5+2, 10³+1, 10³+0, 10³+2]=3;

δ ₁₇=min[∞+5, 4+1, 4+4, 5+4, 10³+3, 10³+2, 10³+0]=2;


δ ₂₁=min[4+0, ∞+4, 10³+4, 10³+5, 5+5, 10³+6, 1+5]=1;

δ ₂₃=min[4+5, ∞+5, 10³+0, 10³+3, 5+1, 10³+2, 1+4]=7;

δ ₂₄=min[4+5, ∞+4, 10³+3, 10³+0, 5+2, 10³+2, 1+4]=7;

δ ₂₅=min[4+5, ∞+4, 10³+1, 10³+2, 5+0, 10³+1, 1+3]=7;

δ ₂₆=min[4+6, ∞+3, 10³+2, 10³+2, 5+1, 10³+0, 1+2]=7;

δ ₂₇=min[4+5, ∞+1, 10³+4, 10³+4, 5+3, 10³+2, 1+0]=7;


δ ₃₁=min[4+0, 10³+4, ∞+4, 7+5, 1+5, 10³+6, 10³+5]=1;

δ ₃₂=min[4+4, 10³+0, ∞+5, 7+4, 1+4, 10³+3, 10³+1]=5;

δ ₃₄=min[4+5, 10³+4, ∞+3, 7+0, 1+2, 10³+2, 10³+4]=5;

δ ₃₅=min[4+5, 10³+4, ∞+1, 7+2, 1+0, 10³+1, 10³+3]=5;

δ ₃₆=min[4+6, 10³+3, ∞+2, 7+2, 1+1, 10³+0, 10³+2]=5;

δ ₃₇=min[4+5, 10³+1, ∞+4, 7+4, 1+3, 10³+2, 10³+0]=5;


δ ₄₁=min[5+0, 10³+4, 10³+4, ∞+5, 2+5, 2+6, 10³+5]=1;

δ ₄₂=min[5+4, 10³+0, 10³+5, ∞+4, 2+4, 2+3, 10³+1]=6;

δ ₄₃=min[5+5, 10³+5, 10³+0, ∞+3, 2+1, 2+2, 10³+4]=5;

δ ₄₅=min[5+5, 10³+4, 10³+1, ∞+2, 2+0, 2+1, 10³+3]=5;

δ ₄₆=min[5+6, 10³+3, 10³+2, ∞+2, 2+1, 2+0, 10³+2]=6;

δ ₄₇=min[5+5, 10³+1, 10³+4, ∞+4, 2+3, 2+2, 10³+0]=6;


δ ₅₁=min[10³+0, 5+4, 1+4, 2+5, ∞+5, 1+6, 3+5]=3;

δ ₅₂=min[10³+4, 5+0, 1+5, 2+4, ∞+4, 1+3, 3+1]=6;

δ ₅₃=min[10³+5, 5+5, 1+0, 2+3, ∞+1, 1+2, 3+4]=3;

δ ₅₄=min[10³+5, 5+4, 1+3, 2+0, ∞+2, 1+2, 3+4]=4;

δ ₅₆=min[10³+6, 5+3, 1+2, 2+2, ∞+1, 1+0, 3+2]=6;

δ ₅₇=min[10³+5, 5+1, 1+4, 2+4, ∞+3, 1+2, 3+0]=6;


δ ₆₁=min[10³+0, 10³+4, 10³+4, 2+5, 1+5, ∞+6, 2+5]=5;

δ ₆₂=min[10³+4, 10³+0, 10³+5, 2+4, 1+4, ∞+3, 2+1]=7;

δ ₆₃=min[10³+5, 10³+5, 10³+0, 2+3, 1+1, ∞+2, 2+4]=5;

δ ₆₄=min[10³+5, 10³+4, 10³+3, 2+0, 1+2, ∞+2, 2+4]=4;

δ ₆₅=min[10³+4, 10³+4, 10³+1, 2+2, 1+0, ∞+1, 2+3]=5;

δ ₆₇=min[10³+5, 10³+1, 10³+4, 2+4, 1+3, ∞+2, 2+0]=7;


δ ₇₁=min[10³+0, 1+4, 10³+4, 10³+5, 3+5, 2+6, ∞+5]=2;

δ ₇₂=min[10³+4, 1+0, 10³+5, 10³+4, 3+4, 2+3, ∞+1]=2;

δ ₇₃=min[10³+5, 1+5, 10³+0, 10³+3, 3+1, 2+2, ∞+4]=5;

δ ₇₄=min[10³+5, 1+4, 10³+3, 10³+0, 3+2, 2+2, ∞+4]=6;

δ ₇₅=min[10³+4, 1+4, 10³+1, 10³+2, 3+0, 2+1, ∞+3]=5;

δ ₇₆=min[10³+6, 1+3, 10³+2, 10³+2, 3+1, 2+0, ∞+2]=6;


УО - узел отправления

УН – узел назначения


Таблица 5.2.1 - Маршрутная таблица

УО УН	1	2	3	4	5	6	7
1		2	3	4	3	3	2
2	1		7	7	7	7	7
3	1	5		5	5	5	5
4	1	6	5		5	6	6
5	3	6	3	4		6	6
6	5	7	5	4	5		7
7	2	2	5	6	5	6

6 Выводы

1. По исходным данным были построены графики функции плотности вероятности и функции распределения вероятности. По этим графикам было сделано предположение об экспоненциальности закона распределения. Далее по критериям согласия Пирсона и Колмогорова была принята гипотеза об экспоненциальности закона распределения.
   
2. Мы осуществили переход от ЗЛП к ОЗЛП. С помощью симплекс-метода определили максимальный поток передаваемых сообщений. Окончательное решение задачи было получено после построения вторичной сети СПИ.
   
3. По исходным данным была сформирована матрица надежности, с помощью которой путем некоторых преобразований была получена матрица минимальных длин. Конечным результатом явилось построение маршрутной таблицы.
   

Список литературы:

1. Лекции по предмету «Автоматизированное управление в технических системах», доц. Давыдюк В.Б.

2. Теория вероятности. Вентцель Е.С. Наука. М 1969 г.