Методические указания и задания к контрольной роботе Архангельск 2009

Вид материала

Методические указания

Подобный материал:

• Методические указания и задания к выполнению контрольной работы по дисциплине, 246.08kb.
• Рабочая программа, методические указания по выполнению курсовой работы, темы курсовых, 1694.43kb.
• Методические указания и задания контрольной работы по дисциплине «Маркетинг» составлены, 814.73kb.
• Методические указания и задания по контрольной работе по дисциплине «Деньги, кредит,, 260.6kb.
• Методические указания и задания для контрольной работы студентам идо, 594.75kb.
• Методические указания вводятся в учебный процесс с 2007, 390.16kb.
• Тамбовский Государственный Технический Университет внешнеэкономическая деятельность, 218.63kb.
• Методические указания к курсу, методические указания и задания к контрольной работе, 525.08kb.
• Методические указания и контрольные задания по английскому языку орёл 2009, 222.99kb.
• Методические указания по выполнению контрольной работы по учебной дисциплине «валютные, 450.92kb.

П о р я д о к р е ш е н и я з а д а ч и


Решение задачи следует начать с выяснения структуры ме­ханизма и определения входных и выходных звеньев. Требуется выделить внешнюю пару зубчатых колес и эпициклический меха­низм, в состав которого входят центральные колеса, водило и колеса-сателлиты. Определить вид эпициклического механизма (планетарный, дифференциальный) в зависимости от числа вход­ных звеньев. У планетарного механизма одно из центральных ко­лес закреплено (неподвижно), а у дифференциального оба центральных колеса подвижны.

Число зубьев одного из колес эпициклического механизма определяется из условия соосности центральных колес.

При решении задачи аналитическим методом необходимо опре­делить передаточное число механизма:

u_{з. м} = u_1,2 · u_{э. м}


или

u_{з. м} = u _э.м · u_{5, 6}

где: u_{з. м} – передаточное число всего механизма;

u_{1, 2} – передаточное число от первого колеса ко второму;

u_{5, 6} – передаточное число от пятого колеса к шестому;

u _э.м – передаточное число эпициклического механизма.

Передаточное число внешней пары зубчатых колес

u_{1, 2} = –

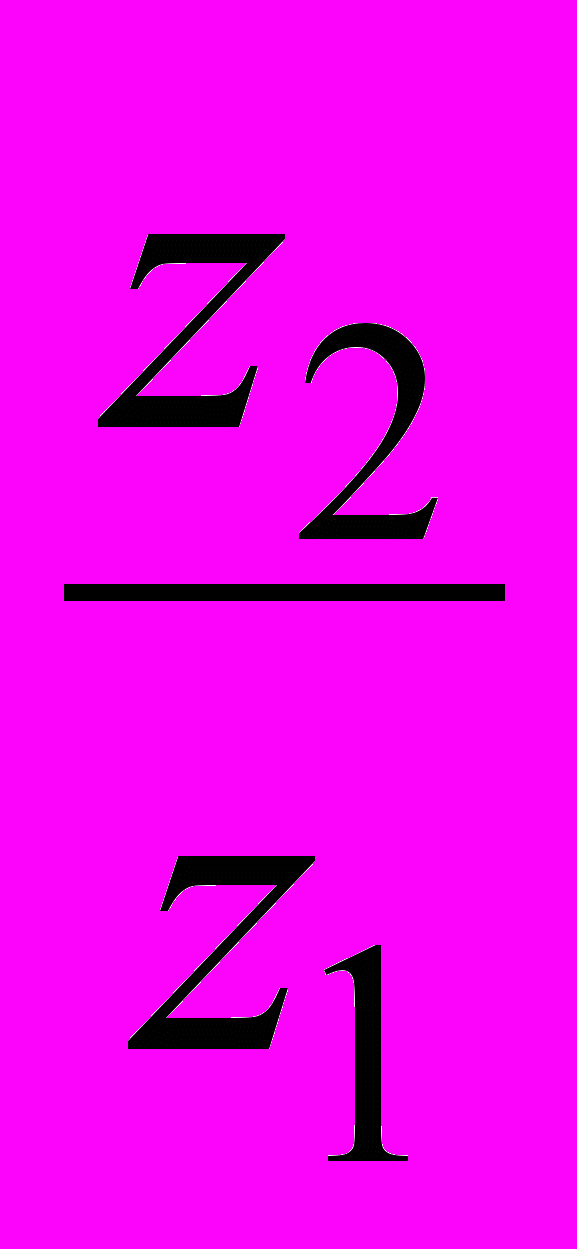
где z₁ и z₂ – число зубьев первого и второго колес. Знак "-" при внешнем зацеплении указывает, что второе колесо вращается в сторону, обратную вращению первого колеса.

Так как

u_{1, 2} =

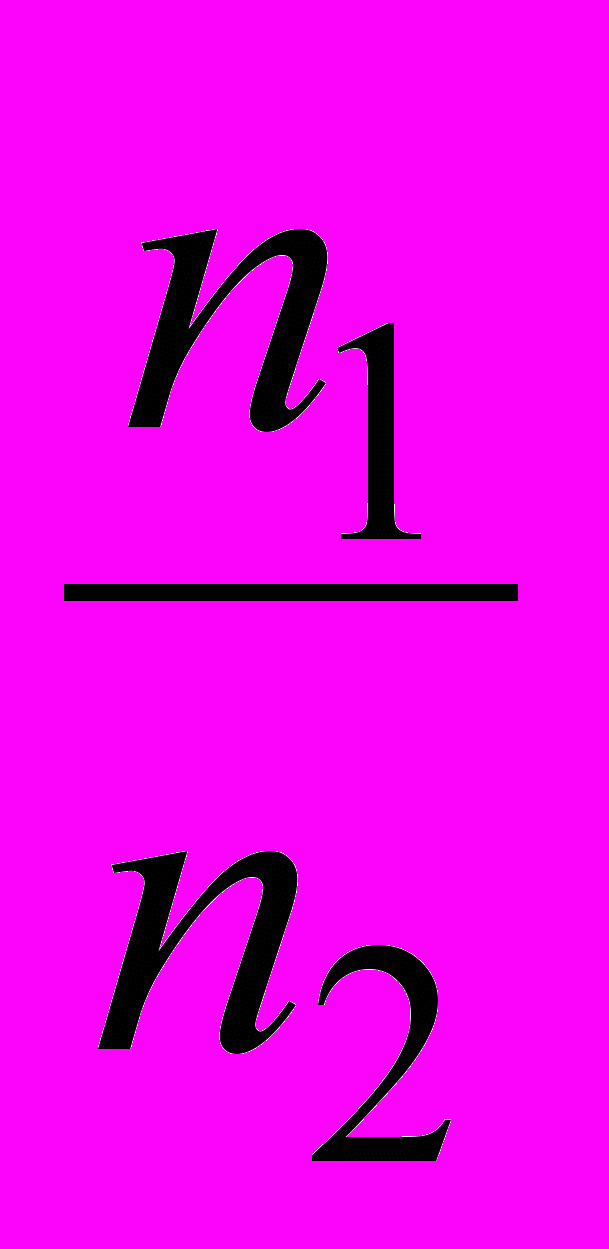
то

n₂ = –

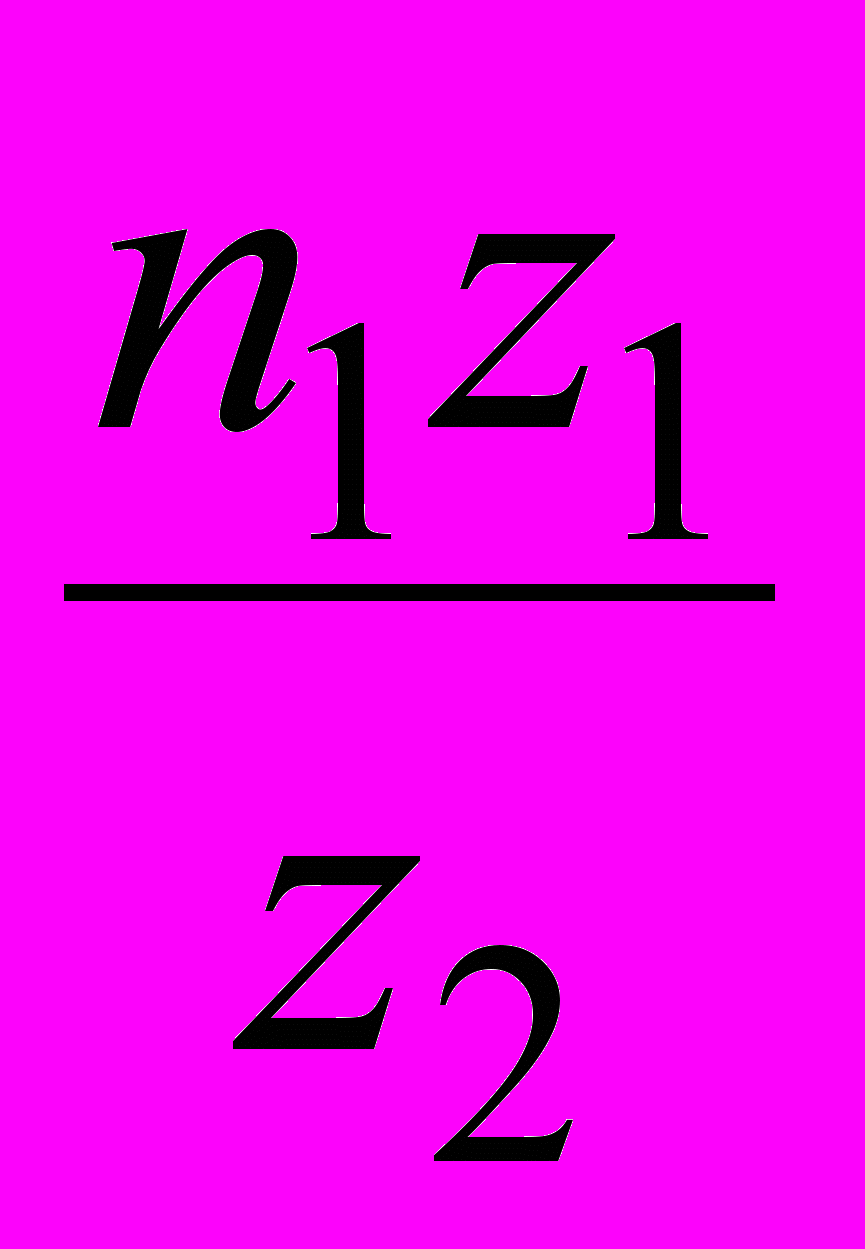
Для определения передаточного числа эпициклического механизма и частоты вращения его входного звена (центрального колеса или водила) следует составить уравнение Виллиса. Общий вид уравнения:

=


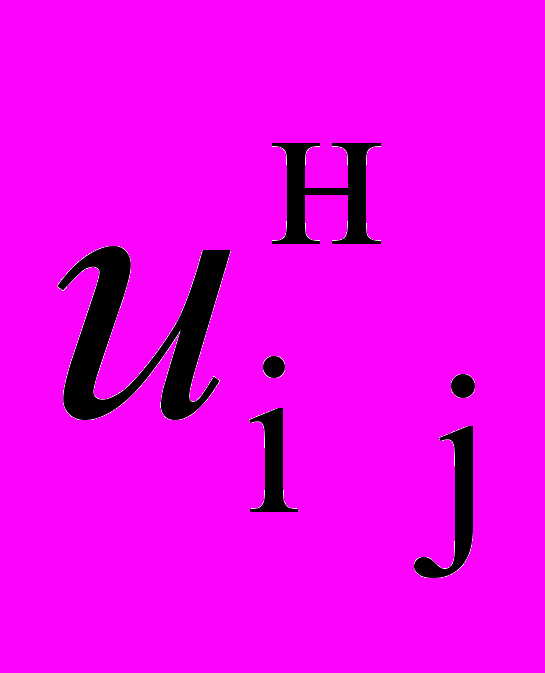где 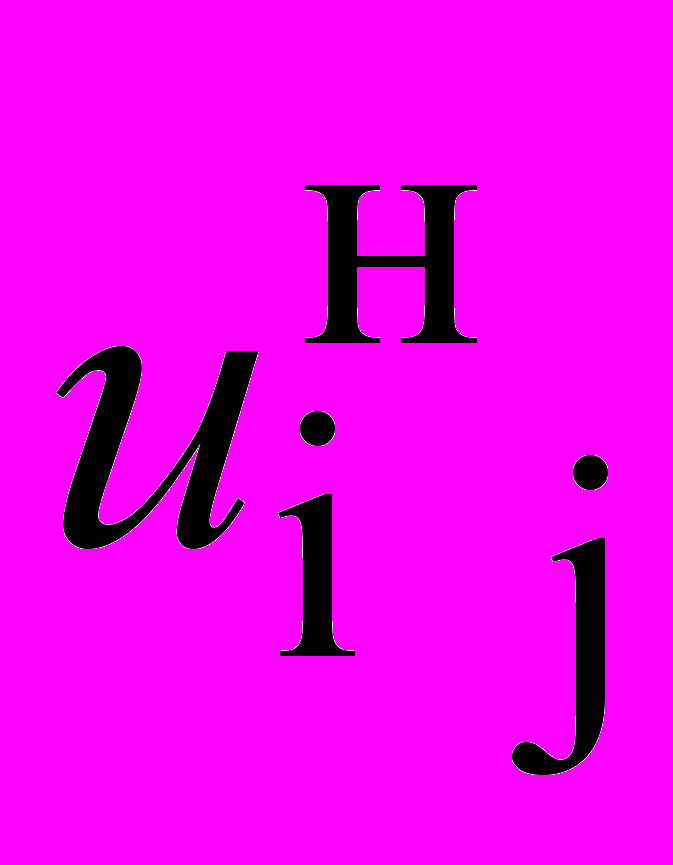– передаточное число от входного центрального колеса к другому центральному при остановленном водиле;

n_i; – частоты вращения соответствующих колес, мин^-1;

n_н – частота вращения водила, мин^-1.

Значение 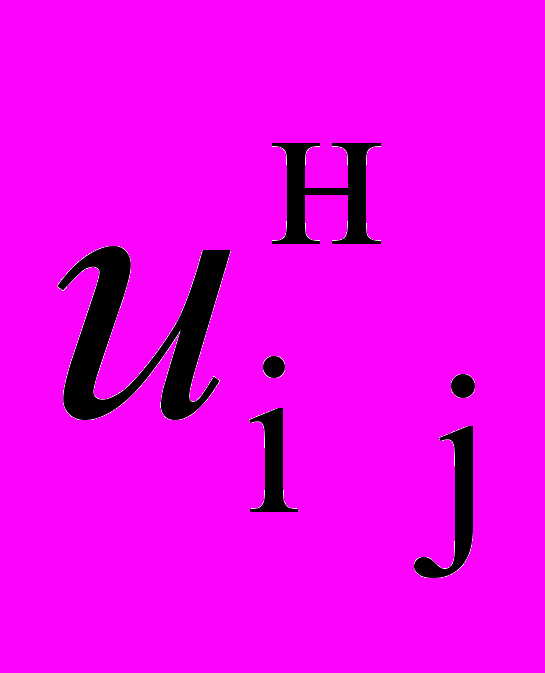определяется как произведение отношений чи­сел зубьев колес, входящих в зацепление. При расчете этой ве­личины следует внимательно отнестись к определению знаков от­ношений.


=

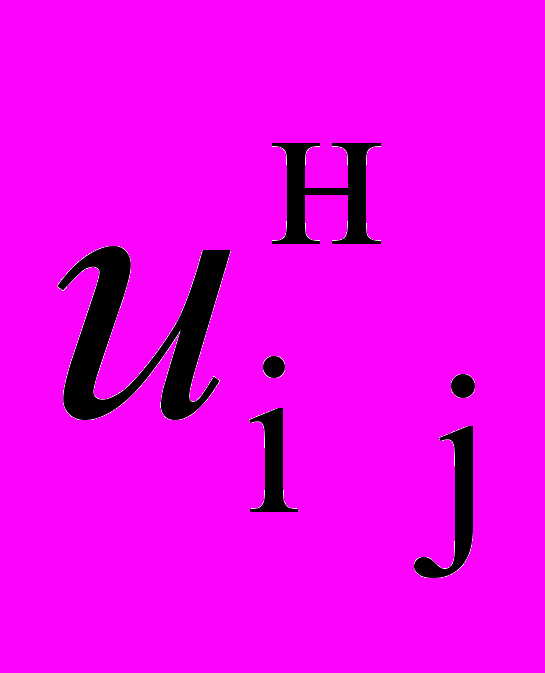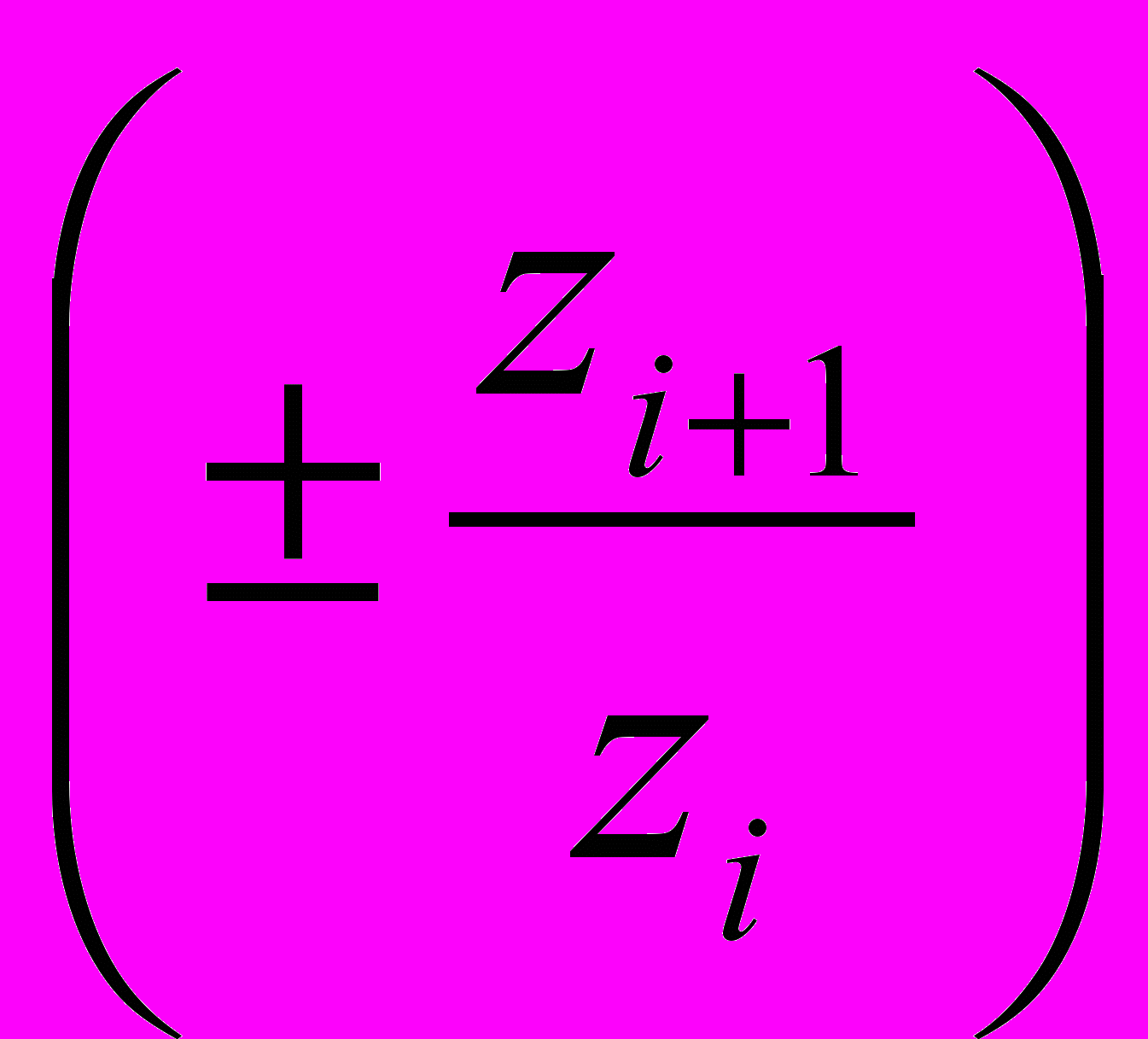
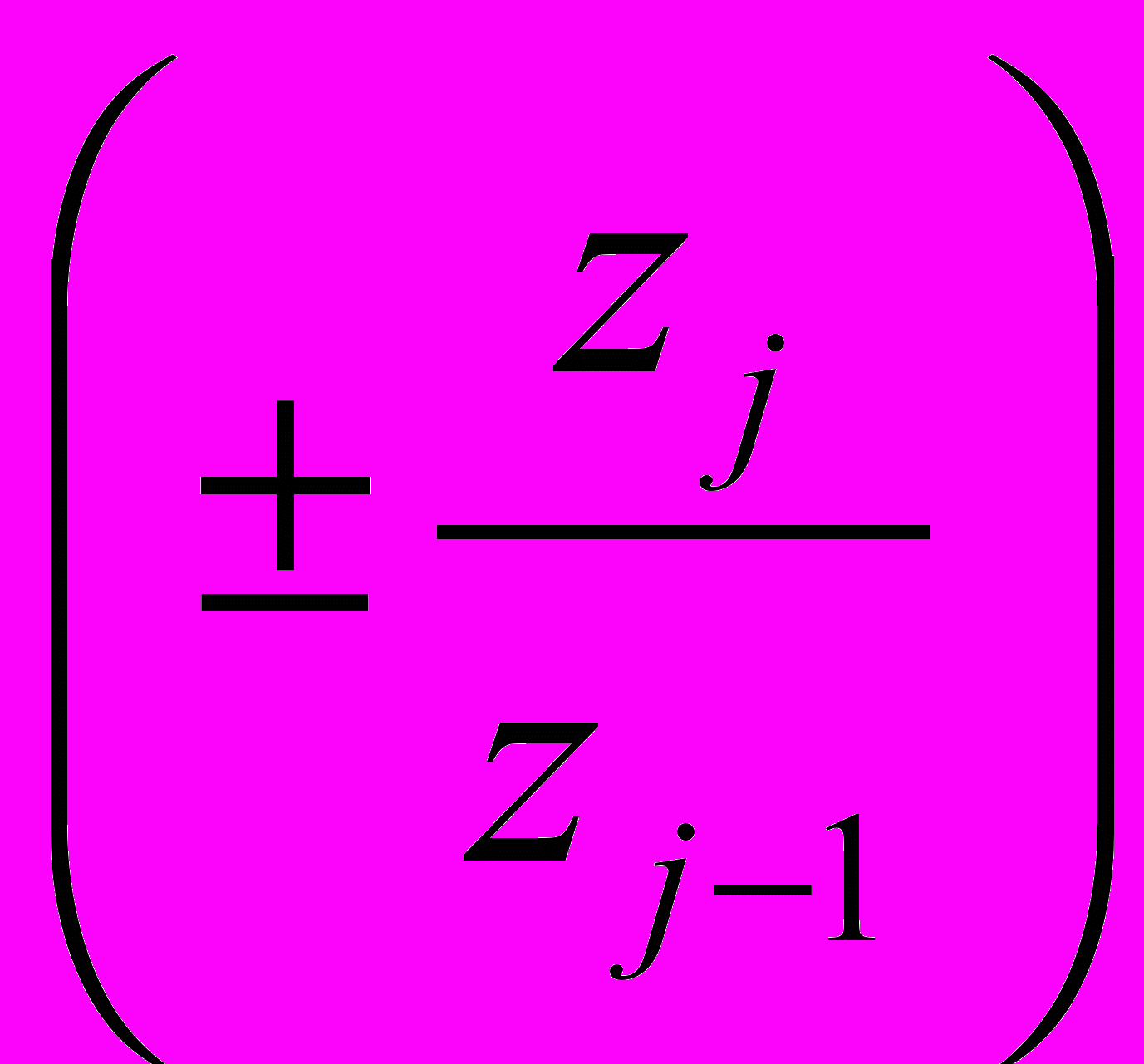
При внутреннем зацеплении пары зубчатых колес ставят знак "+", а при внешнем зацеплении - знак "–".

Уравнение Виллиса преобразуется относительно искомой ве­личины. У планетарного механизма = 0. Определению подлежат u_iн и u_н. У дифференциального механизма известны n_i и n_н , находят .

Для определения частоты вращения колес-сателлитов требуется составить уравнение Виллиса для одной из ступеней переда­чи механизма и решить его относительно искомой величины.