Рич Р. К. Политология. Методы исследования: Пер с англ. / Предисл. А. К. Соколова

Вид материала

Анализ

Содержание Размер выборки для определения уровней точности(в процентах с доверительным интервалом в 95%, р=0,5) РАСПРЕЛЕЛЕНИЕ χ Таблица А.5 Значения коэффициента корреляции для различных уровней значимости Этические проблемы в эмпирических исследованиях

Подобный материал:

• Рич Р. К. Политология. Методы исследования: Пер с англ. / Предисл. А. К. Соколова, 6313.29kb.
• Н. Ю. Алексеенко под редакцией д-ра биол наук, 1890.25kb.
• Сорокин П. А. С 65 Человек. Цивилизация. Общество / Общ ред., сост и предисл., 11452.51kb.
• Дэвид Дайчес, 1633.42kb.
• Mathematics and the search for knowledge morris kline, 498.28kb.
• Указатель литературы по методам и методикам исследования общие вопросы психологического, 348.83kb.
• edo ru/site/index php?act=lib&id=186 Густав Эдмунд фон Грюнебаум Классический, 2844.73kb.
• «хм «Триада», 9393.37kb.
• Анастази А. А 64 Дифференциальная психология. Индивидуальные и групповые разли- чия, 11288.93kb.
• Шелтон Г. М. – Ортотрофия. Основы правильного питания, 3135.34kb.

Таблица А.2

Размер выборки для определения уровней точности
(в процентах с доверительным интервалом в 95%, р=0,5)

Размер совокупности	Размер выборки для следующих уровней точности
	± 1%	± 2%	± 3%	± 4%	± 5%	± 10%
500	+	+	+	222	83
1 000	+	+	+	385	286	91
1 500	+	+	638	441	316	94
2 000	+	+	714	476	333	95
2 500	+	1 250	769	500	345	96
3 000	+	1 364	811	517	353	97
3 500	+	1 458	843	530	359	97
4 000	+	1 538	870	541	364	98
4 500	+	1 607	891	549	367	98
5 000	+	1 667	909	556	370	98
6 000	+	1 765	938	566	375	98
7 000	+	1 842	959	574	378	99
8 000	+	1 905	976	580	381	99
9 000	+	1 957	989	584	383	99
10 000	5 000	2 000	1 000	588	385	99
15 000	6 000	2 143	1 034	600	390	99
20 000	6 667	2 222	1 053	606	392	100
25 000	7 143	2 273	1 064	610	394	100
50 000	8 333	2 381	1 087	617	397	100
100 000	9 091	2 439	1 099	621	398	100
→ ∞	10 000	2 500	1 111	625	400	100

^* Доля в выборке единиц, обладающих измеренными характеристиками; для других значений р необходимый размер выборки будет меньше.

⁺ В этих случаях более 50% объема выборки дадут большую точность, чем требуемая. Поскольку нормальное распределение – это лишь грубое приближение к гипергеометрическому распределению, где п составляет более 50% oт N, формула, используемая при этих подсчетах, не применяется.

Источник: Таrо Y. Elementary Sampling Theory. – Englewood Cliffs, NJ.: Prentice-Hall, 1967. Р.398.


Таблица А.3

Размер выборки для определения уровней точности
(в процентах с доверительным интервалом в 99,7 %, р=0,5)^*

Размер совокупности	Размер выборки для следующих уровней точности
	± 1%	± 2%	± 3%	± 4%	± 5%
500	+	+	+	+	+
1 000	+	+	+	+	474
1 500	+	+	+	726	563
2 000	+	+	+	826	621
2 500	+	+	+	900	662
3 000	+	+	1364	958	692
3 500	+	+	1458	1003	716
4 000	+	+	1539	1041	735
4 500	+	+	1607	1071	750
5 000	+	+	1667	1098	763
6 000	+	2903	1765	1139	783
7 000	+	3119	1842	1171	798
8 000	+	3303	1905	1196	809
9 000	+	3462	1957	1216	818
10 000	+	3600	2000	1233	826
15 000	+	4091	2143	1286	849
20 000	+	4390	2222	1314	861
25 000	11842	4592	2273	1331	869
50 000	15517	5056	2381	1368	884
100 000	18367	5325	2439	1387	892
→ ∞	22500	5625	2500	1406	900

^* Доля в выборке единиц, обладающих измеренными характеристиками; для других значений р необходимый размер выборки будет меньше.

⁺ В этих случаях более 50% объема выборки дадут большую точность, чем требуемая. Поскольку нормальное распределение – это лишь грубое приближение к гипергеометрическому распределению, где п составляет более 50% oт N, формула, используемая при этих подсчетах, не применяется.

Источник: Таrо Y. Elementary Sampling Theory. – Englewood Cliffs, NJ.: Prentice-Hall, 1967. Р.399.

Таблица А.4

РАСПРЕЛЕЛЕНИЕ χ²

df	0,05	0,01	0,001	df	0,05	0,01	0,001
1 2 3 4 5	3,841 5,991 7,815 9,488 11,070	6,635 9,210 11,345 13,277 15,086	10,827 13,815 16,266 18,467 20,515	26 27 28 29 30	38,885 41,337 40,113 42,557 43,773	45,642 48,278 46,963 49,588 50,892	54,052 56,893 55,476 58,302 59,703
6 7 8 9 10	12,592 14,067 15,507 16,919 18,307	16,812 18,475 20,090 21,666 23,209	22,457 24,322 26,125 27,877 29,588	32 34 36 38 40	46,194 48,602 50,999 53,384 55,759	53,486 56,061 58,619 61,162 63,691	62,487 65,247 67,985 70,703 73,402
11 12 13 14 15	19,675 21,026 22,362 23,685 24,996	24,725 26,217 27,688 29,141 30,578	31,264 32,909 34,528 36,123 37,697	42 44 46 48 50	58,124 60,481 62,830 65,171 67,505	66,206 68,710 71,201 73,683 76,154	76,084 78,750 81,400 84,037 86,661
16 17 18 19 20	26,296 27,587 28,869 30,144 31,410	32,000 33,409 34,805 36,191 37,566	39,252 40,790 42,312 43,820 45,315	52 54 56 58 60	69,832 72,153 74,468 76,778 79,082	78,616 81,069 83,513 85,950 88,379	89,272 91,872 94,461 97,039 99,607
21 22 23 24 25	32,671 33,924 35,172 36,415 37,652	38,932 40,289 41,638 42,980 44,314	46,797 48,268 49,728 51,179 52,620	62 64 66 68 70	81,381 83,675 85,965 88,250 90,531	90,802 93,217 95,626 98,028 100,425	102,166 104,716 107,258 109,791 112,317

Примечание. Для нечетных значений п между 30 и 70 можно взять среднее геометрическое табличных значений для df – 1 и df + l. Для больших значений п можно использовать выражение 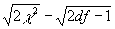как нормальное отклонение с единичным колебанием, принимая во внимание, что вероятность χ² соответствует вероятности одного из концов нормальной кривой.

Источник: Fisher R.A., Yates F. Statistical Tables for Biological, Agricultural and Medical Research, 6th ed., published by Longman Group, Ltd., London (previously published by Oliver and Boyd, Edinburgh), Table IV.

Таблица А.5

Значения коэффициента корреляции для различных уровней значимости

df	0,1	0,05	0,01	0,001	df	0,1	0,05	0,01	0,001
1 2 3 4 5	0,98769 0,90000 0,8054 0,7293 0,6694	0,99692 0,95000 0,8783 0,8114 0,7545	0,999877 0,990000 0,95873 0,91720 0,8745	0,9999988 0,99900 0,99116 0,97406 0,95074	16 17 18 19 20	0,4000 0,3887 0,3783 0,3687 0,3598	0,4683 0,4555 0,4438 0,4329 0,4227	0,5897 0,5751 0,5614 0,5487 0,5368	0,7084 0,6932 0,6787 0,6652 0,6524
6 7 8 9 10	0,6215 0,5822 0,5494 0,5214 0,4973	0,7067 0,6664 0,6319 0,6021 0,5760	0,8343 0,7977 0,7646 0,7348 0,7079	0,92493 0,8982 0,8721 0,8471 0,8233	25 30 35 40 45	0,3233 0,2960 0,2746 0,2573 0,2428	0,3809 0,3494 0,3246 0,3044 0,2875	0,4869 0,4487 0,4182 0,3932 0,3721	0,5974 0,5541 0,5189 0,4896 0,4648
11 12 13 14 15	0,4762 0,4575 0,4409 0,4259 0,4124	0,5529 0,5324 0,5139 0,4973 0,4821	0,6835 0,6614 0,6411 0,6226 0,6055	0,8010 0,7800 0,7603 0,7420 0,7246	50 60 70 80 90 100	0,2306 0,2108 0,1954 0,1829 0,1726 0,1638	0,2732 0,2500 0,2319 0,2172 0,2050 0,1946	0,3541 0,3248 0,3017 0,2830 0,2673 0,2540	0,4433 0,4078 0,3799 0,3568 0,3375 0,3211

Источник: Fisher R.A., Frank Y. Statistical Tables for Biological, Agricultural and Medical Research, 6th ed., published by Longman Group, Ltd., London (previously published by Oliver and Boyd, Edinburgh), Table VII.

Приложение Б

ЭТИЧЕСКИЕ ПРОБЛЕМЫ В ЭМПИРИЧЕСКИХ ИССЛЕДОВАНИЯХ

Американская политологическая ассоциация всесторонне изучила этические проблемы, встающие перед политологами в их преподавательской и исследовательской деятельности. В материалах, опубликованных в итоге этой большой работы, можно найти много полезных советов специалистам. Мы воспроизводим здесь часть правил поведения, разработанных ассоциацией, прямо касающихся эмпирических исследований¹.