Geum.ru

Министерство сельского хозяйства и продовольствия республики беларусь

Вид материалаДокументы
Расчет колебаний годового стока по данным наблюдений.
Расчет колебаний годового стока при отсутствии наблюдений.
10.5. Внутригодовое распределение стока
Типовое распределение месячного стока рек Карелии в
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

Расчет колебаний годового стока по данным наблюдений. При наличии данных наблюдений за период не менее 10 лет расчет колебаний годового стока ведется по теоретической кривой обеспеченности.

Порядок построения теоретической кривой обеспеченности поясним на примере, исходные данные для которого приведены в первых двух графах табл. 10.5.


Т а б л и ц а 10.5. Вычисление коэффициента вариации среднегодовых

расходов

Год
Средний годовой расход Qср, м3/с
Номер

по пор.
Год
Средний годовой расход Qср, в порядке убывания, м3/с
Модульный коэффициент К
К–1
(К–1)2
Процент обеспеченности, р

1
2
3
4
5
6
7
8
9

1983
647
1
1987
874
1,41
0,41
0,1681
5,6

1984
619
2
1992
790
1,27
0,27
0,0729
13,7

1985
517
3
1994
722
1,16
0,16
0,0256
21,8

1986
433
4
1989
682
1,10
0,10
0,0100
29,8

1987
874
5
1983
647
1,04
0,04
0,0016
37,8

1988
602
6
1984
619
1,00
0,00
0,0000
45,9

1989
682
7
1988
602
0,97
–0,03
0,0009
54,0

1990
472
8
1993
580
0,93
–0,07
0,0049
62,1

1991
517
9
1985
517
0,83
–0,17
0,0289
70,1

1992
790
10
1991
517
0,83
–0,17
0,0289
78,2

1993
580
11
1990
472
0,76
–0,24
0,0576
86,2

1994
722
12
1986
433
0,70
–0,30
0,0900
94,4

Сумма
7455






7455
12
0,00
0,4894




1. Располагаем в убывающем порядке все имеющиеся расходы (графы 3—5).

2. Определяем среднемноголетний расход по формуле (10.14)


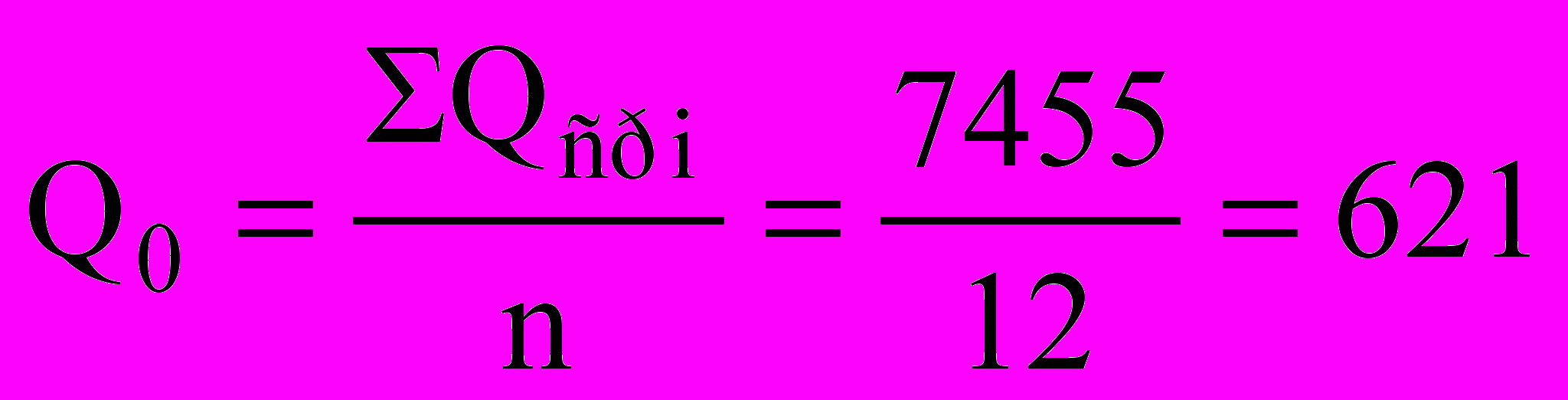м3/с


3. Вычисляем модульные коэффициенты для всех среднегодовых расходов по соотношению (10.18) и заносим их в графу 6.


К = Qср / Q0.


4. Находим отклонения модульных коэффициентов от единицы (графа 7) и возводим эти отклонения в квадрат (графа 8).

Проверкой правильности вычислений служат суммы граф 6 и 7. Первая из них должна равняться общему числу членов ряда, а вторая – нулю.

5. Определяем процент обеспеченности каждого расхода по формуле (10.22) и заносим его в графу 9:

6. Вычисляем коэффициент вариации по формуле (10.26)


.


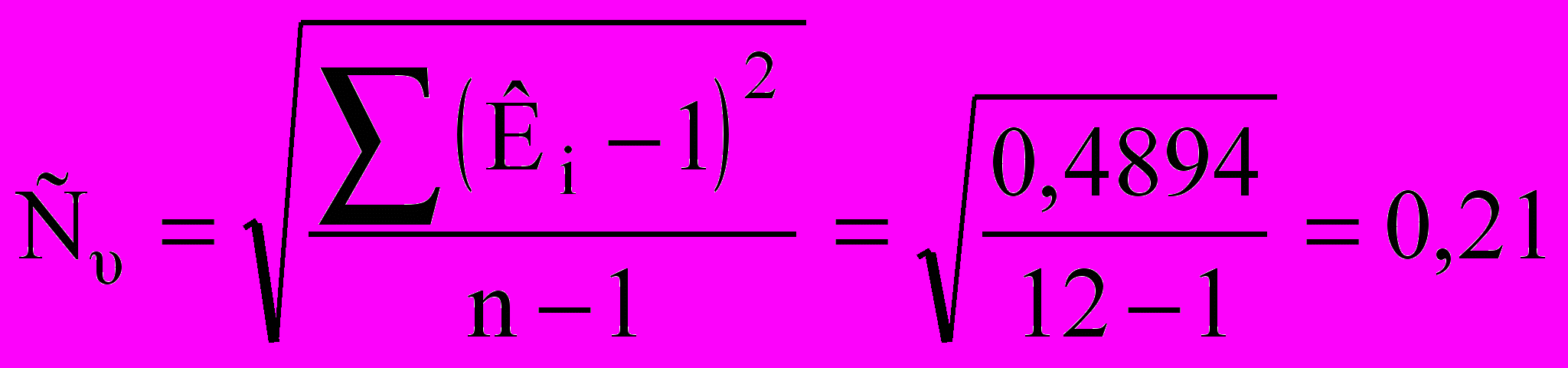7. Находим коэффициент асимметрии по зависимости (10.28)


Cs = 2 Cυ = 2 · 0,21 = 0,42.


8. По найденному значению Cs, пользуясь табл.10.4, устанавливаем отклонения ординат кривой обеспеченности Ф от середины при Cυ = 1 и заносим их в табл. 10.6.


Т а б л и ц а 10.6. Расчет ординат кривой обеспеченности среднегодовых

расходов

Расчетные показатели
Величина показателей при проценте обеспеченности р

1
5
10
25
50
75
90
95
99

Отклонение ординат Ф от середины при Cυ=1
2,63
1,74
1,32
0,65
–0,06
–0,71
–1,22
–1,51
–2,03

Cυ Ф
0,55
0,37
0,28
0,14
–0,01
–0,15
–0,25
–0,32
–0,42

Модульный коэффициент К
1,55
1,37
1,28
1,14
0,99
0,85
0,75
0,68
0,58

Средний годовой расход Q м3/с
962
850
795
708
615
527
466
422
360


9. Определяем модульные коэффициенты по формуле


К = 1 + Ф Cυ. (10.30)


10. Вычисляем среднегодовые расходы по зависимости


Qср = Q0 К. (10.31)


11. По данным табл.10.6 строим кривую обеспеченности среднегодовых расходов (рис. 10.5).





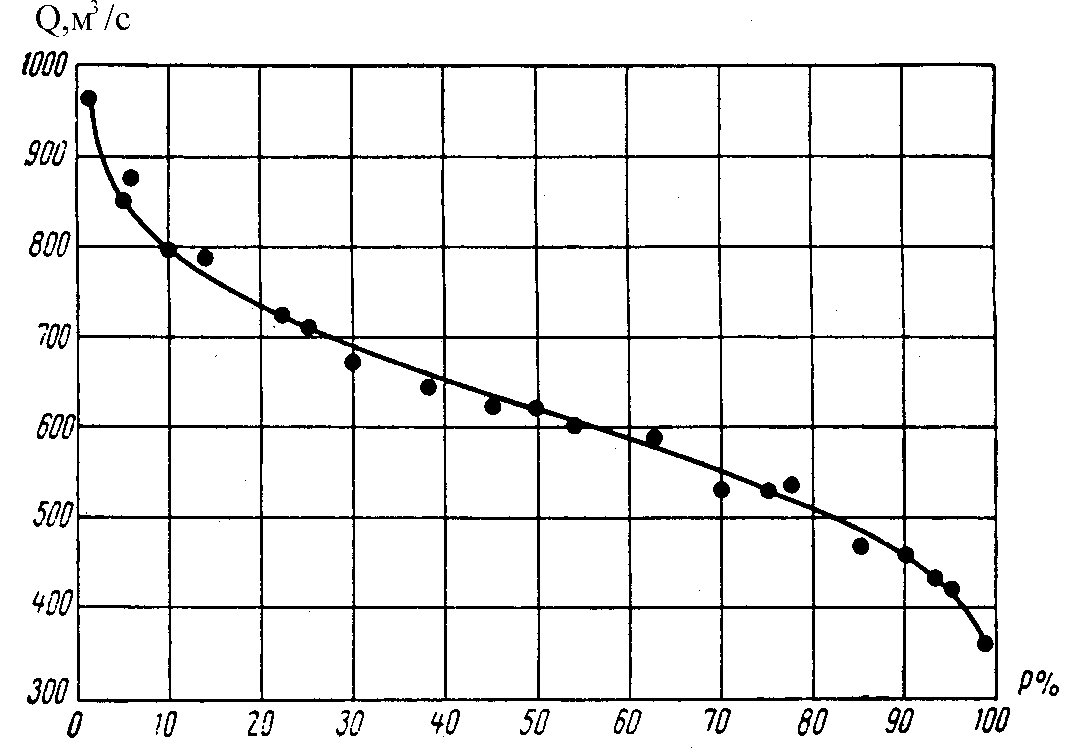
Рис. 10.5. Теоретическая кривая обеспеченности


12. Наносим на построенный график опытные точки, соответствующие расходам и их обеспеченностям (графы 5 и 9 таблицы 10.5).

Для расчета колебаний годового стока при 5–10-летнем периоде наблюдений прибегают к удлинению имеющегося ряда путем построения графика связи годового стока рассматриваемой реки и реки-аналога (см. параграф 10.3).

Расчет колебаний годового стока при отсутствии наблюдений. Для определения коэффициента вариации годового стока неизученных рек предложен ряд эмпирических зависимостей. Широкое применение в практических расчетах получила формула Д. Л. Соколовского


Cυ = а – 0,063 lg (F + 1), (10.32)


где а – географический параметр. Параметр а для европейской части СНГ можно определить по специальной карте [10]. Он изменяется от 0,45–0,50 на севере до 0,75–0,90 на юге. При этом на территории Беларуси он изменяется в сравнительно узких пределах: от 0,55 на севере до 0,62 на юге.

F – площадь водосбора реки, км2.

Коэффициент вариации среднемноголетнего годового стока в условиях Беларуси можно определить по карте изолиний, представленной на рис. 10.6 [6].




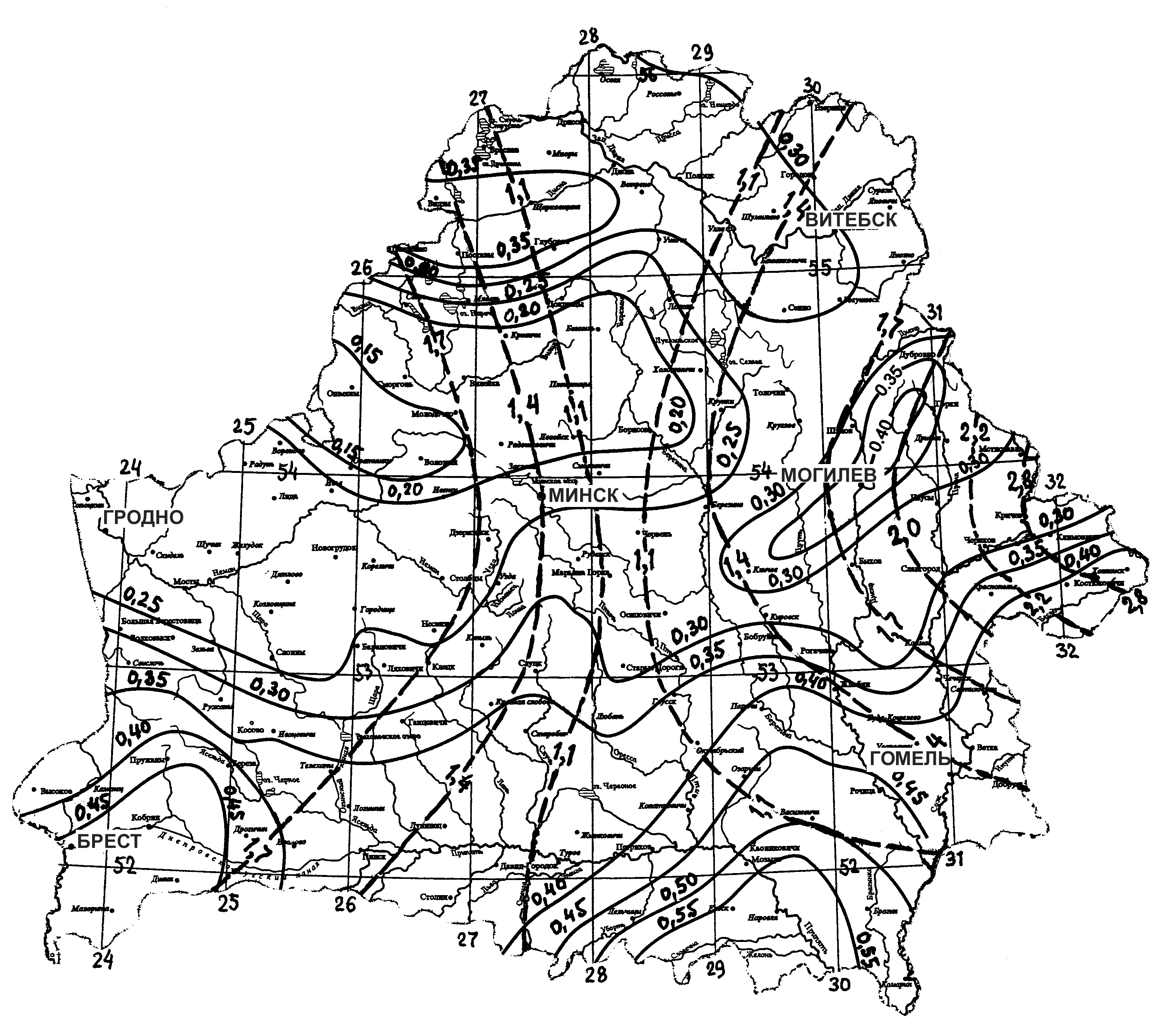
Рис.10.6. Коэффициента вариации среднемноголетнего годового стока

(сплошные линии) и географический параметр А0 5% обеспеченности

(штриховые линии) для территории Беларуси.


М. Э. Шевелевым предложены формулы для определения коэффициента вариации годового стока рек различной водности:

для бассейнов средней водности с площадями водосбора F>1000 км2 и нормой стока М0=1,5÷15 л/(с·км2)


Cυ = 0,78 – 0,29 lg М0 – 0,06 lg F; (10.33)


для малых рек с площадями водосбора F<1000 км2


Cυ = 0,73 – 0,29 lg М0 – 0,03 lg F; (10.34)


для бассейнов со значительной озерностью


Cυ = 0,78 – 0,29 lg М0 – 0,08 lg f0, (10.35)


где f0 – озерность бассейна

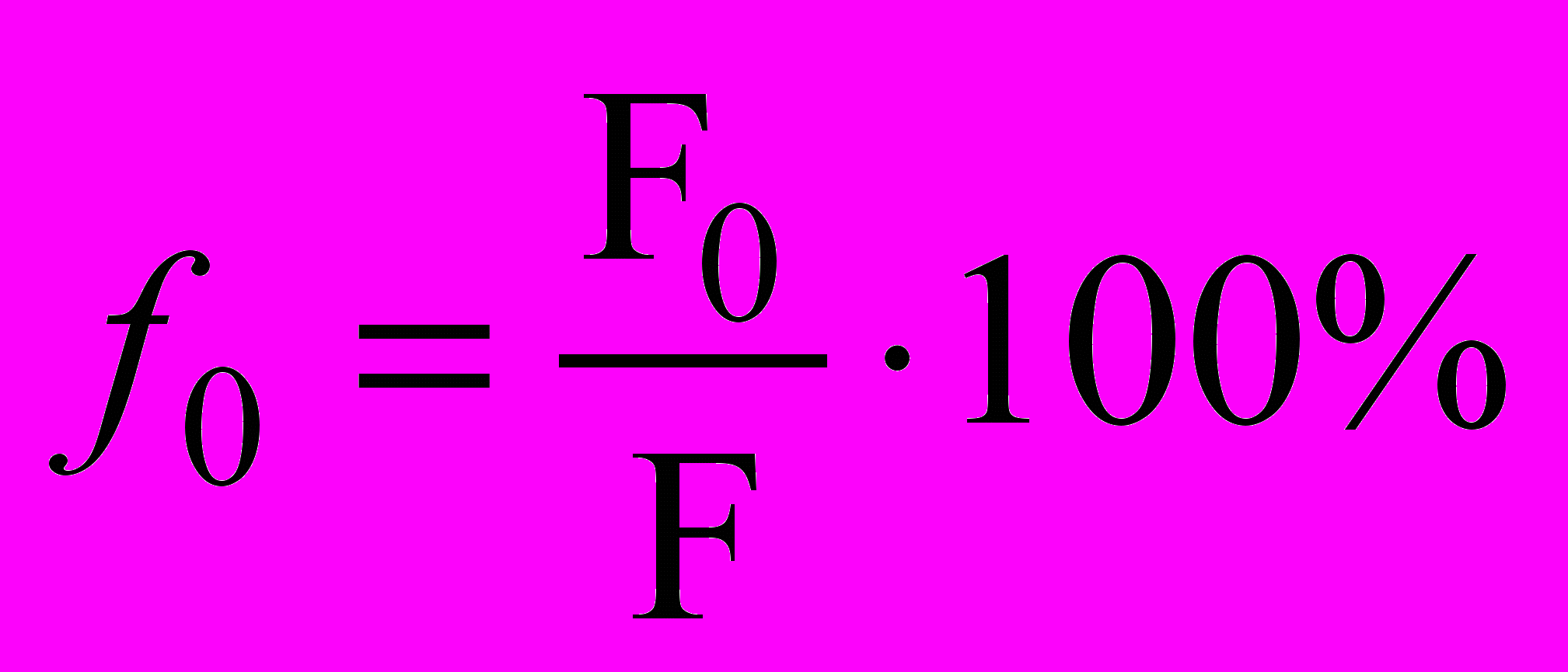, (10.36)


где F0 – площадь озер в бассейне, км2.

После определения коэффициента вариации дальнейший расчет колебаний годового стока неизученных рек ведется в последовательности, рассмотренной ранее.

По изложенному методу можно рассчитывать колебания не только среднегодовых расходов, но и других характеристик стока как годовых, так и за отдельные периоды года, например за навигацию, период весеннего половодья и др.

Пример. Для расчетного створа в устье р. Проня (притока р. Сож) с площадью водосбора F = 4910 км2 требуется определить среднегодовые расходы 10, 50 и 90%-ной обеспеченности.

Решение. 1. По карте изолиний (рис. 10.1) устанавливаем, что р. Проня имеет среднемноголетний модуль стока М0 = 5,75 л/(с·км2)

2. Определяем среднемноголетний расход по формуле


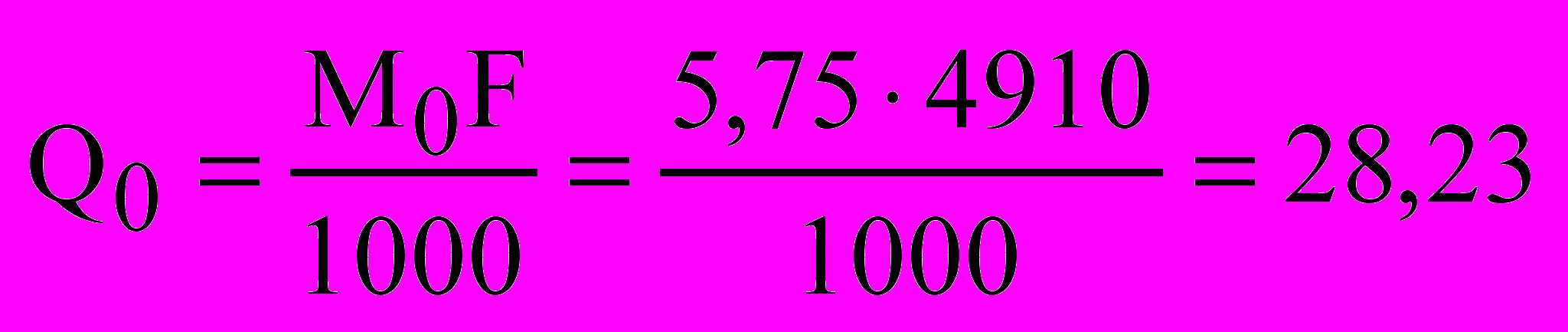м3/с.


3. Коэффициент вариации вычисленный по формуле (10.32) при а = 0,58 равен 0,347, по формуле (10.33) – 0,34,найденный по карте изолиний (рис. 10.6) – 0,32. Принимаем для дальнейшего расчета среднее значение Cυ = 0,336.


Cυ = а – 0,063 lg (F + 1) = 0,55 – 0063 lg (4910 + 1) = 0,32.


4. Находим коэффициент асимметрии по соотношению (10.28)


Cs = 2 Cυ = 2 · 0,336 = 0,672.


5. Определяем модульные коэффициенты для лет расчетной обеспеченности по формуле (10.30). Значения отклонений ординат кривой обеспеченности Ф от середины при Cυ = 1 устанавливаем по табл. 10.4 для найденного значения Cs = 0,672

К10% = 1 + 1,33·0,336 = 1,45;

К50% = 1 + (–0,11)·0,336 = 0,96;

К90% = 1 + (–1,18)·0,336 = 0,60.


6. Определяем среднегодовые расходы расчетной обеспеченности по формуле (10.31)

Q10% = К10% Q0 = 1,45·28,23 = 40,93 м3/с;

Q50% = К50% Q0 = 0,96·28,23 = 27,10 м3/с;

Q90% = К90% Q0 = 0,60·28,23 = 16,94 м3/с.


По статистическим данным в устье р. Проня Q0 = 29,5 м3/с; погрешность расчета составляет – 4,5%.

10.5. Внутригодовое распределение стока


Для решения многих водохозяйственных задач мало знать величину годового стока для лет различной водности, а нужно еще уметь установить распределение стока по сезонам и месяцам года.

Внутригодовое распределение стока выражают в процентах или долях от объема годового стока, а также в виде месячных модульных коэффициентов, представляющих отношения среднемесячных расходов к среднегодовому:


К = Qср.мес. / Qср.год . (10.37)


Последний способ применяется на практике чаще.

В практических расчетах приходится выявлять внутригодовое распределение стока для года средней водности, а также для маловодных и многоводных лет расчетной обеспеченности:

При наличии данных наблюдений за многолетний период внутригодовое распределение стока устанавливают по фактическим значениям среднемесячных расходов в реальные годы с обеспеченностями стока, близкими к расчетным.

Внутригодовое распределение стока неизученных рек определяют по методу гидрологических аналогий. Основные положения, которыми нужно руководствоваться при выборе реки-аналога изложены в п. 10.3. 3десь же дополнительно укажем, что для правильного выбора реки-аналога желательно иметь наблюдения за уровнями рассматриваемой реки хотя бы за 1–2 года. Сопоставление графиков колебания уровней обеих рек за эти годы позволит выявить степень согласованности внутригодового распределения стока рассматриваемой реки и реки-аналога.

Расчет внутригодового распределения стока неизученных рек по методу аналогий ведется в следующей последовательности:

по данным многолетних наблюдений на реке-аналоге определяют для нее среднегодовые расходы для лет расчетной водности;

выбирают по реке-аналогу реальные годы для установления внутригодового распределения стока;

подсчитывают для выбранных реальных лет месячные модульные коэффициенты;

пользуясь картой изолиний нормы стока или данными по реке-аналогу, устанавливают для рассматриваемой реки среднемноголетний расход;

определяют для нее значения среднегодовых расходов для лет расчетной водности;

подсчитывают среднемесячные расходы рассматриваемой реки для лет расчетной водности, принимая для нее такие же значения месячных модульных коэффициентов, как и для реки-аналога.

Внутригодовое распределение стока неизученных рек можно приближенно оценить по типовым схемам, составленным исследователями для различных районов страны (табл. 10.7, 10.8).


Т а б л и ц а 10.7. Типовое распределение месячного стока рек СНГ

(по С.Н. Никитину)

Район или бассейн
Модульные коэффициенты по месяцам

I
II
III
IV
V
VI
VII
VII
IX
X
XI
XII

Европейский Север
0,2
0,15
0,2
1,0
5,2
1,7
0,8
0,6
0,55
0,9
0,5
0,2

Кольский полуостров
0,3
0,25
0,2
0,3
4,0
3,4
1,0
0,95
0,9
0,9
0,6
0,4

Ленинградская область
0,3
0,25
1,0
4,2
1,8
0,6
0,5
0,5
0,6
0,8
1,1
0,4

Верхняя Волга
0,3
0,25
1,0
4,2
2,0
0,6
0,5
0,5
0,5
0,8
1,0
0,4

Средняя Волга
0,2
0,25
0,25
5,0
2,9
0,9
0,4
0,3
0,25
0,4
0,55
0,6

Северный Урал
0,1
0,1
0,1
0,5
4,6
2,5
0,9
0,7
0,7
1,0
0,6
0,2

Средний Урал
0,1
0,1
0,1
0,9
5,6
1,4
0,6
0,6
0,8
1,0
0,6
0,2

Южный Урал
0,1
0,1
0,2
4,0
3,4
1,7
0,8
0,4
0,2
0,4
0,4
0,3

Башкирия
0,1
0,1
0,15
1,8
4,7
1,6
1,1
0,7
0,6
0,55
0,5
0,2

Верхняя Обь и Енисей
0,25
0,25
0,3
4,8
2,5
0,8
0,6
0,45
0,4
0,65
0,7
0,3

Забайкалье
0
0
0
0,4
1,5
1,9
2,7
2,2
2,7
0,4
0,15
0,05

Западное

Приморье
0,05
0,05
0,05
0,1
4,6
2,0
1,4
1,6
1,3
0,55
0,2
0,1

Восточное

Приамурье
0,05
0,05
0,05
1,2
1,9
1,4
2,8
1,7
1,3
1,0
0,4
0,15


Т а б л и ц а 10.8. Типовое распределение месячного стока рек Карелии в

зависимости от процента озерности бассейна (по Д.Л. Соколовскому)

Озерность бассейна, %
Модульные коэффициенты по месяцам

I
II
III
IV
V
VI
VII
VII
IX
X
XI
XII

1
0,25
0,20
0,20
0,7
4,2
1,8
1,0
0,7
0,7
0,9
1,0
0,4

1–3
0,30
0,25
0,75
0,7
3,4
2,0
1,1
0,8
0,7
1,0
1,0
0,5

3–5
0,35
0,3
0,3
0,6
2,7
2,0
1,2
1,0
0,8
1,1
1,1
0,5

5–10
0,55
0,5
0,4
0,6
2,3
1,7
1,2
1,0
1,0
1,1
1,1
0,6

10–20
0,7
0,55
0,5
0,6
1,9
1,6
1,3
1,0
1,0
1,1
1,1
0,7

Более 20
0,7
0,7
0,65
0,6
1,2
1,4
1,3
1,1
1,1
1,2
1,2
0,8