Задачи лп, формулируемые как задачи цлп, как правило, по своей природе не допускают подхода, основанного на округлении. Один из эффектов округления это потеря допустимости решения ( см рис. 1). Пример. ( Задача коммивояжера ( зк ))

Вид материала

Задача

Содержание Пример. ( Задача коммивояжера ( ЗК )).

Подобный материал:

• И. Д. Салмин московский инженерно-физический институт (государственный университет), 27.33kb.
• Е. В. Чижонков 1 год, 4 курс, отделение механики  Погрешность метода и вычислительная, 54.05kb.
• А. Ю. Горицкий 1 год, 3 курс, поток механиков  Задача, 39.92kb.
• Как научить младших школьников решать текстовые задачи?, 124.64kb.
• Основным в процессе программирования является разработка алгоритма. Это один из наиболее, 1285.17kb.
• Белая Холуница Кировская область Описание проекта Название проекта Алгоритмы и основы, 179.54kb.
• Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 24.28kb.
• Задачи и их решение Стандартные и нестандартные задачи Задачи «на работу» Задачи «на, 157.13kb.
• Цели и задачи управления персоналом, 1630.21kb.
• Решение задачи одним из математических методов, 440.71kb.

2.5. Постановки задач целочисленного программирования ( ЦП ).

Пример. Задача целочисленного линейного программирования ( ЦЛП ).

Задачей ЦЛП называют следующую задачу оптимизации :



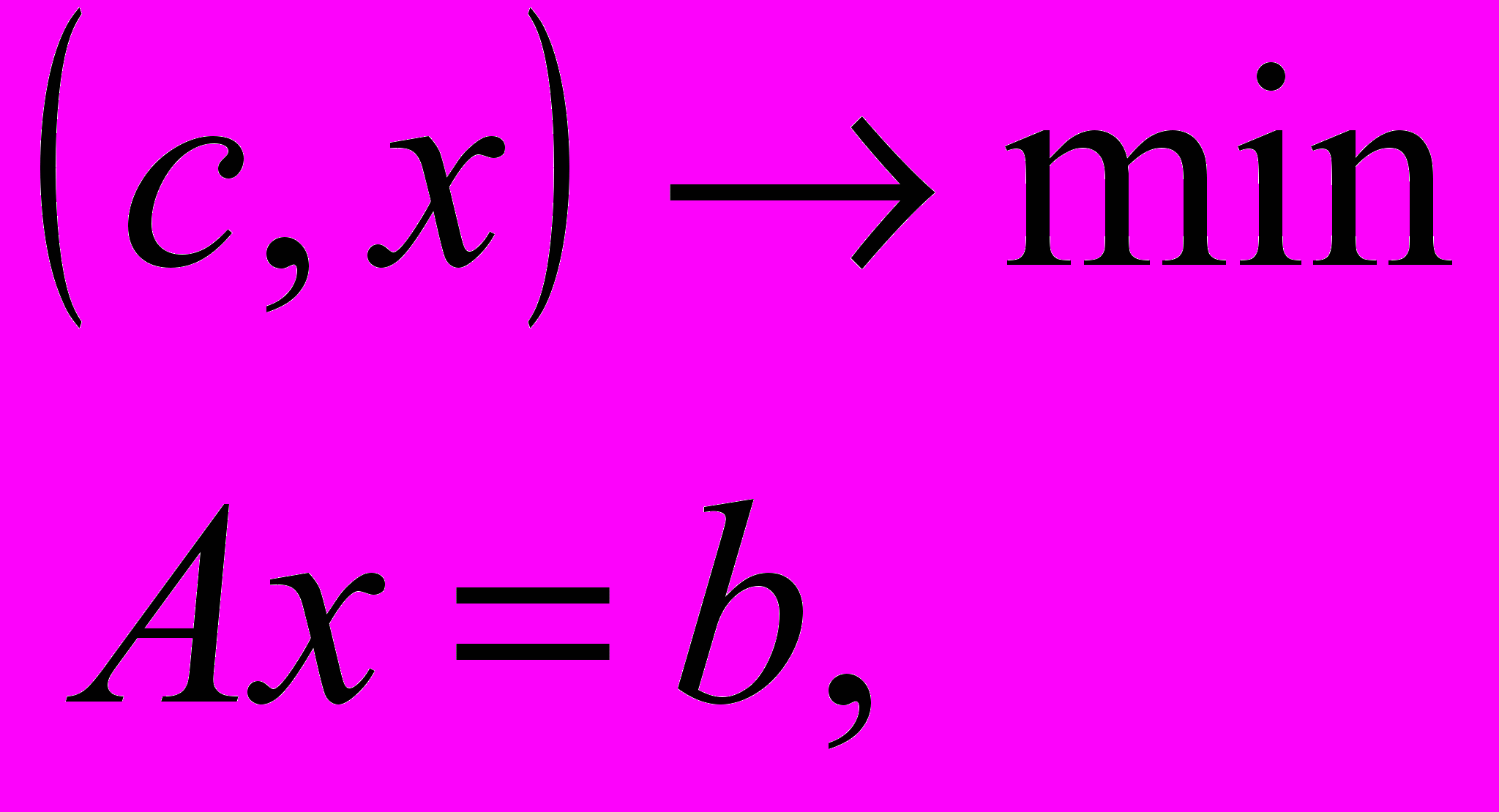
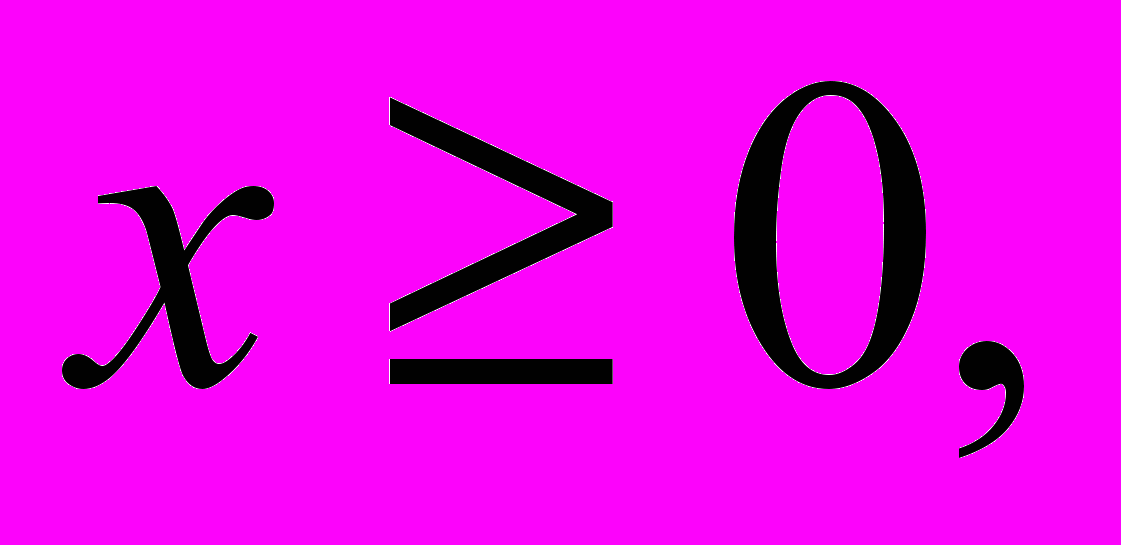x- целочисленно.

З
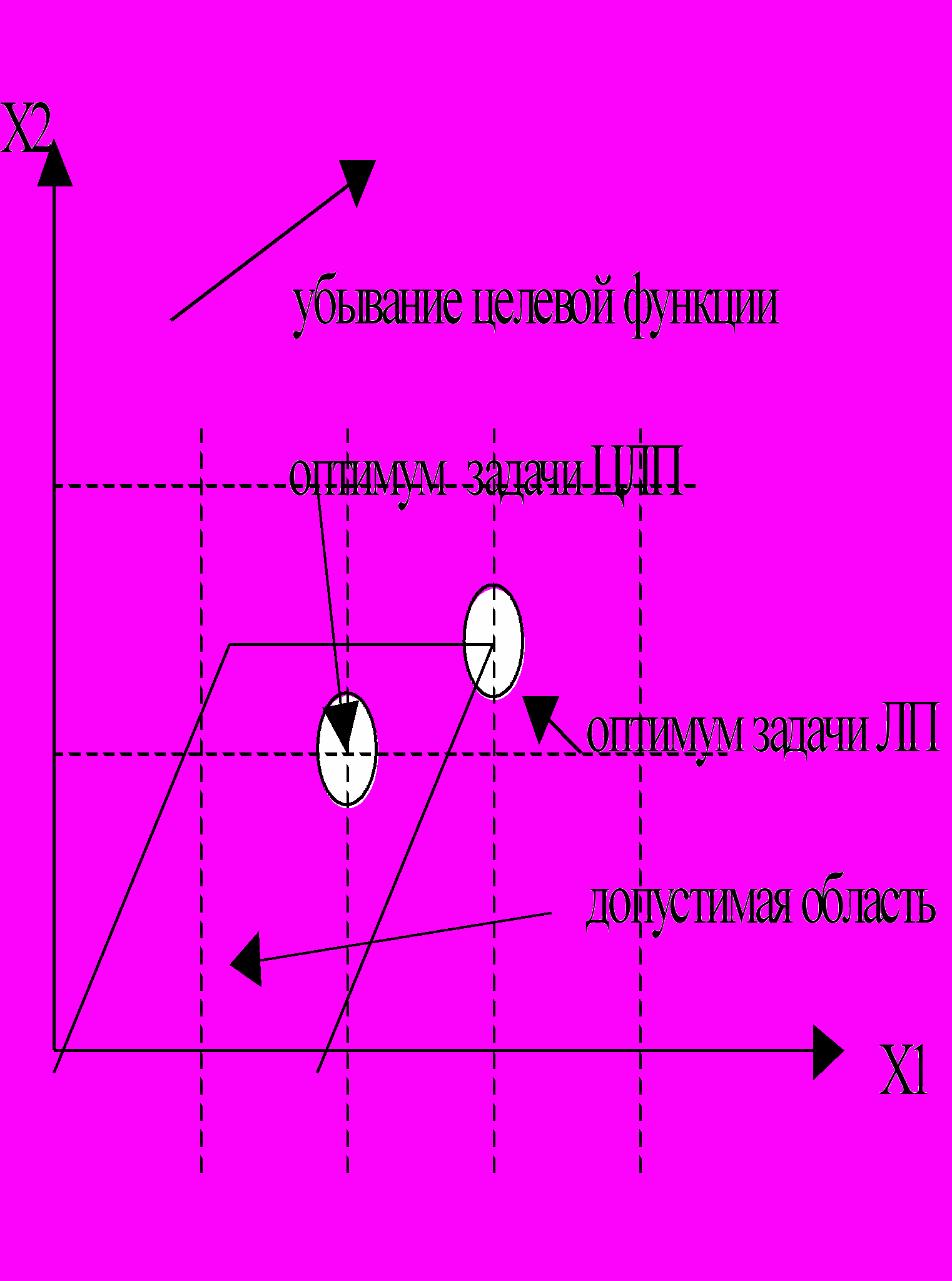
десь c,x  Rⁿ, A  R^{n x m}, b  R^m. Элементы матрицы A и векторов b и c предполагаются целыми. На рис.1 приведен пример двумерной задачи ЦЛП.

Рис.1. Четыре целочисленные точки, ближайшие к оптимуму задачи ЛП, недопустимы.

В некоторых приложениях дробные решения недопустимы, например в приложении, где x_j - число самолетов, назначаемых на маршрут j. Задачи ЛП, формулируемые как задачи ЦЛП, как правило, по своей природе не допускают подхода, основанного на округлении. Один из эффектов округления - это потеря допустимости решения ( см. рис.1).

Пример. ( Задача коммивояжера ( ЗК )). Коммивояжеру необходимо объехать n городов 1,2,...,n, начиная с города 1, и посещая каждый город ровно 1 раз, по самому короткому маршруту.

Обозначим [c_ij] матрицу расстояний между городами. Сопоставим дуге (i,j) переменную x_ij и, положив x_ij = 1 если дуга (i,j) содержится в обходе, и x_ij = 1 в противном случае, можно сформулировать ЗК следующим образом:



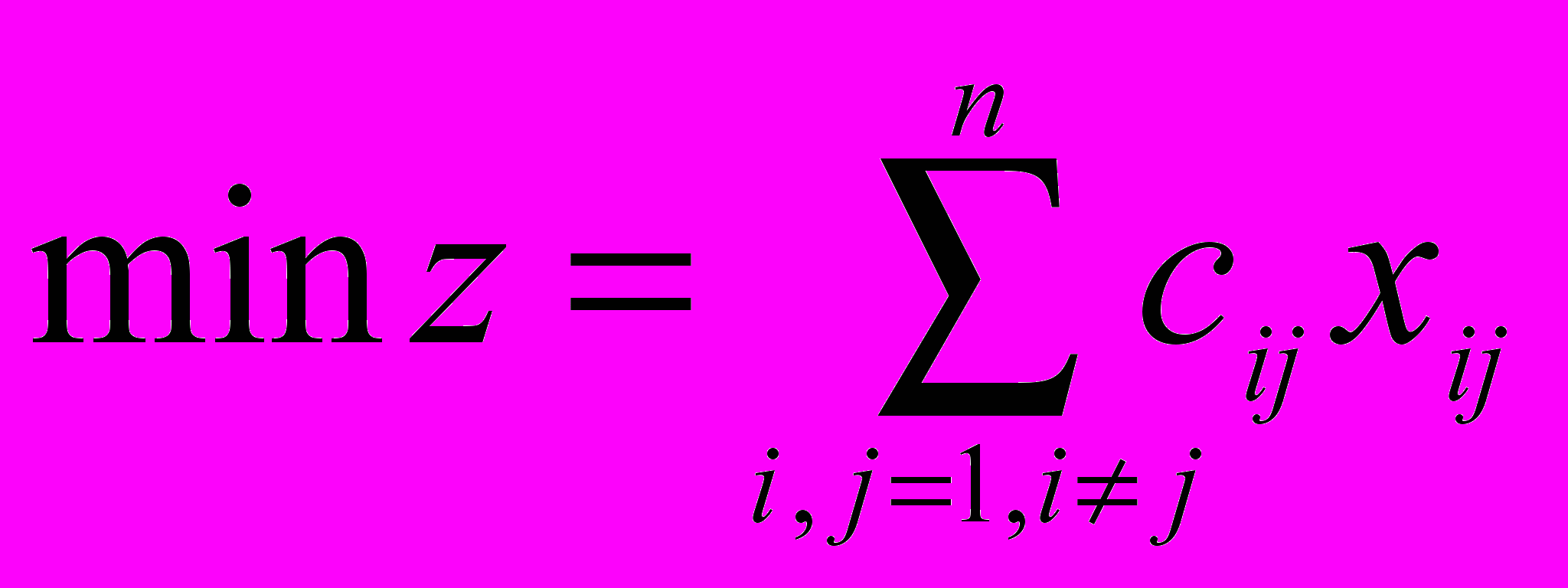
( a ) 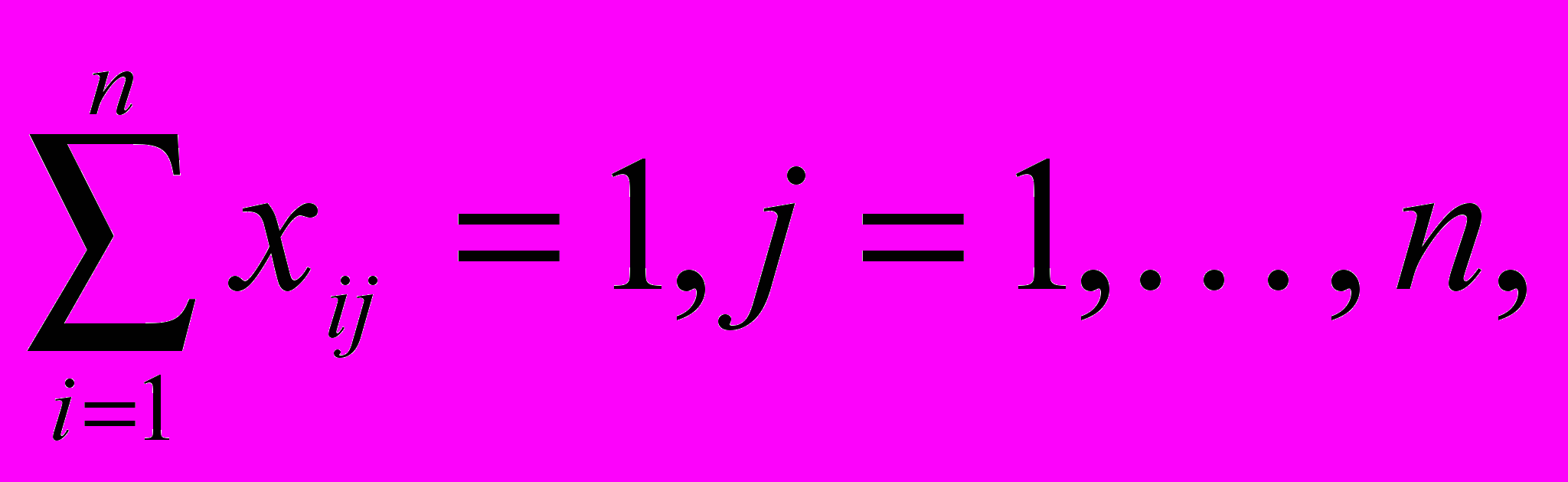(1)

(б )

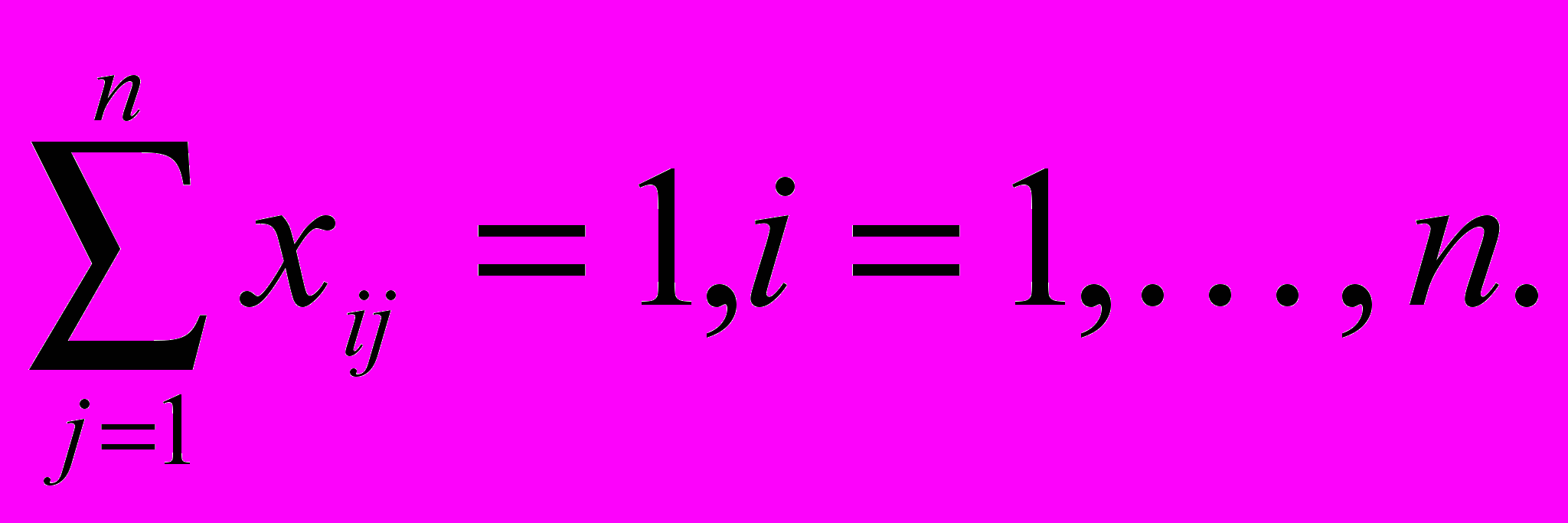
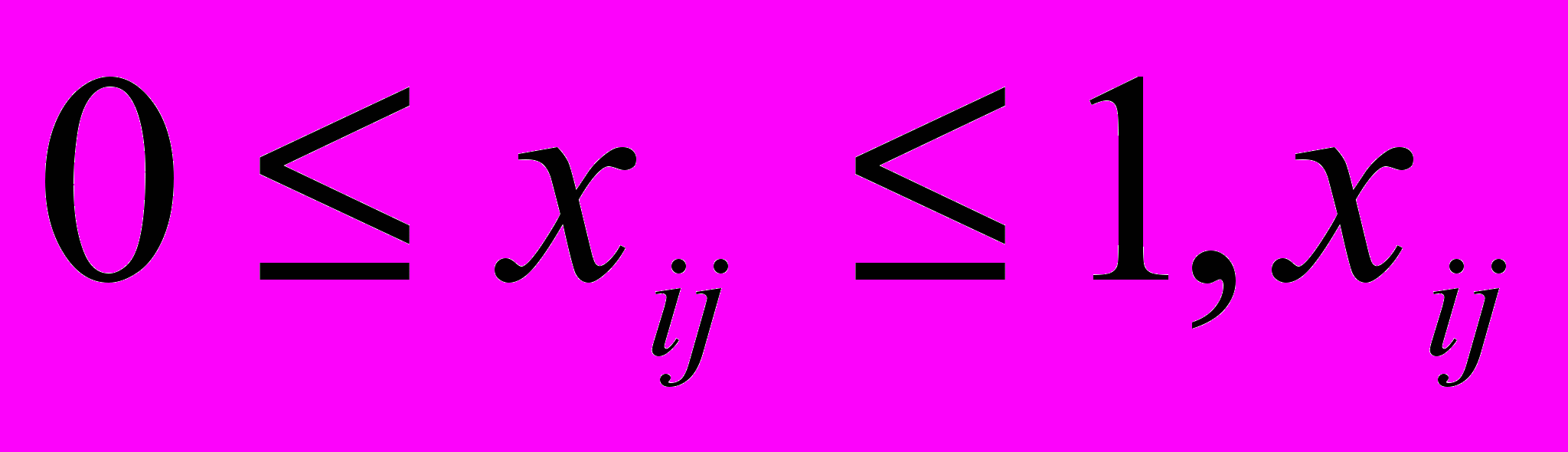- целые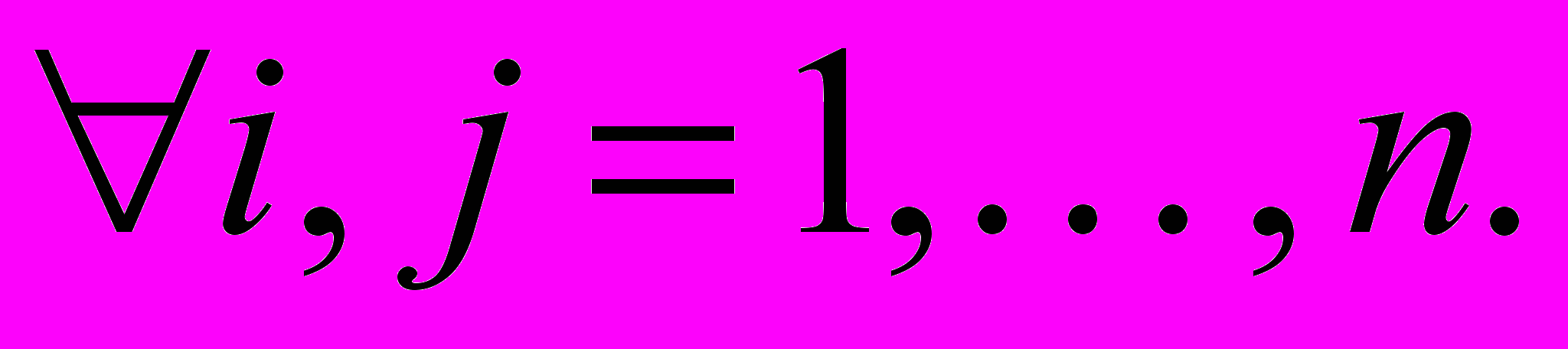

Равенства (а) выражают тот факт, что в каждую вершину входит ровно одна дуга, а равенства (б) - тот факт, что из каждой вершины выходит ровно одна дуга.

В действительности, задача (1) описывает задачу о назначении и содержит в своем допустимом множестве маршрутов маршруты, состоящие из нескольких замкнутых циклов. Нужны дополнительные ограничения для исключения подобных решений.

Пример.( задача о заполнении рюкзака ).

Даны целые числа w₁,…,w_n; c₁,…,c_n; k. Требуется максимизировать функцию



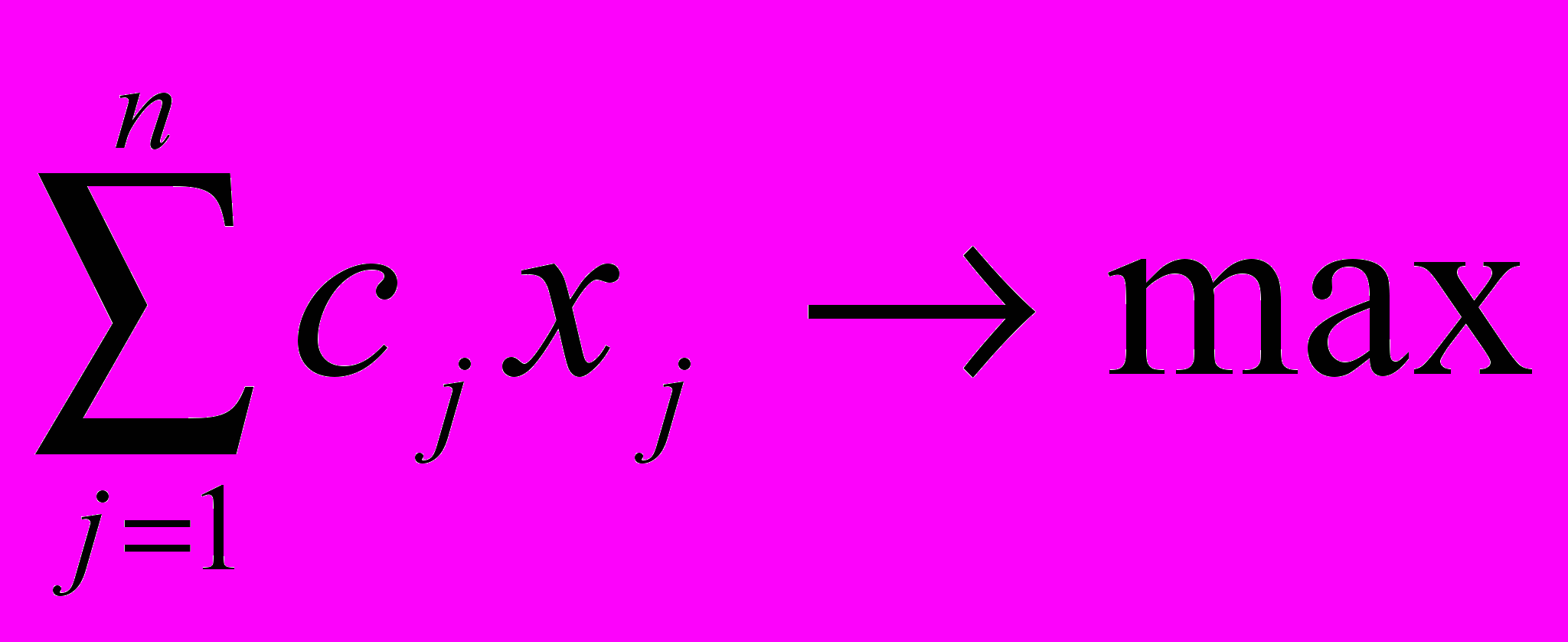
при условиях



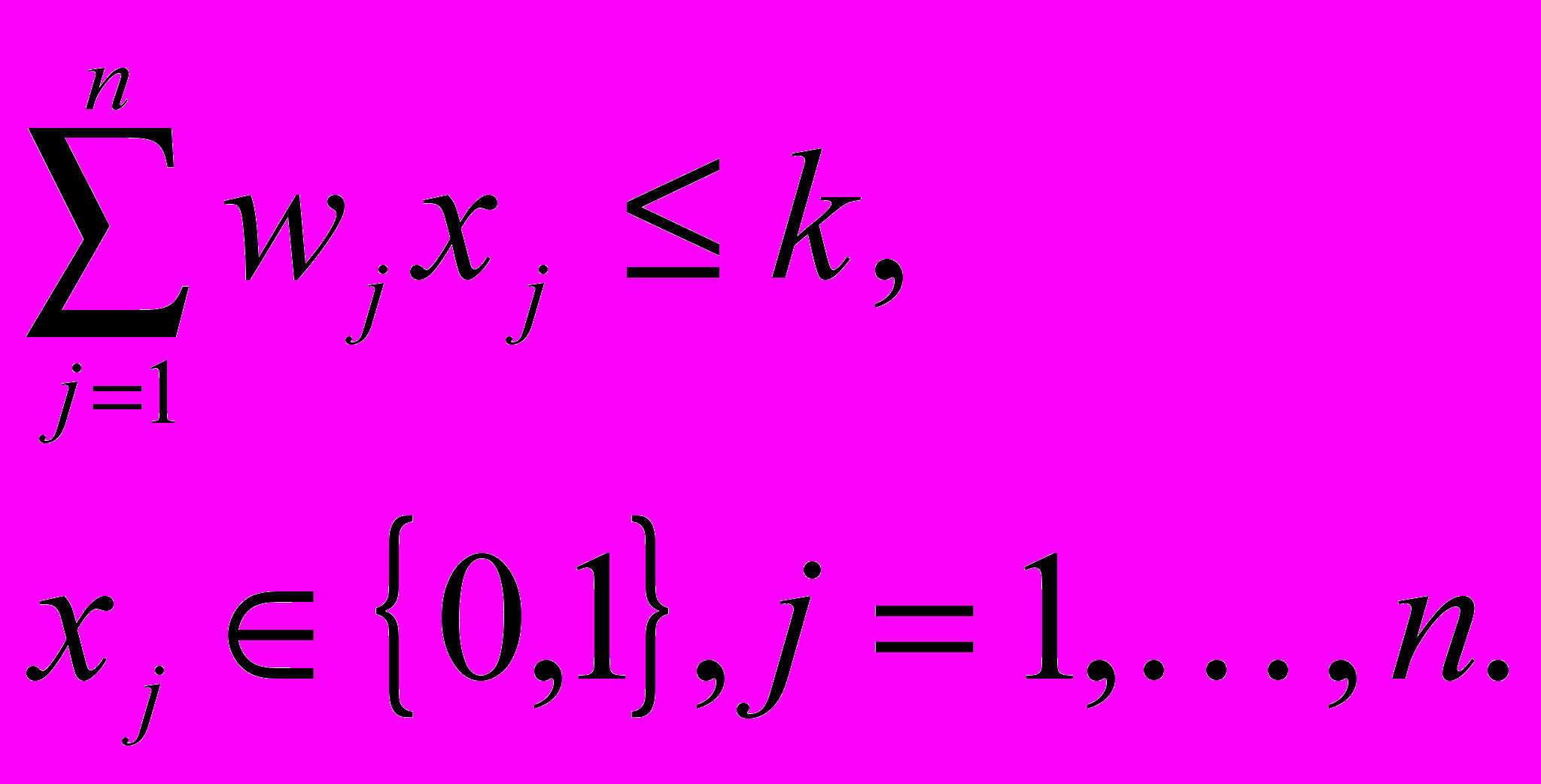
Для решения задач ЦП существует множество методов решения, которые будут рассмотрены в следующих разделах.