Моделирование динамики численности популяции с возрастной и половой структурой и оптимизация промысла
| Вид материала | Автореферат |
- Рабочая программа по дисциплине опд. Ф. 08 Моделирование и оптимизация, 200.55kb.
- Моделирование динамики конфигураций организационных систем на сетях петри, когнитивных, 33.91kb.
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Математическое моделирование мировой динамики глава 12 Иерархия моделей мировой динамики, 216.48kb.
- Влияние экологических факторов на структуру и динамику численности популяции колорадского, 319.06kb.
- Моделирование и оптимизация систем с распределенными параметрами, 14.61kb.
- Обыкновенно смысл половой любви полагается в размножении рода, которому она служит, 2193.89kb.
- Уральская академия государственной службы, 639.53kb.
- «Уголовное право», 85.42kb.
- Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.
На правах рукописи

РЕВУЦКАЯ ОКСАНА ЛЕОНИДОВНА
МОДЕЛИРОВАНИЕ ДИНАМИКИ ЧИСЛЕННОСТИ ПОПУЛЯЦИИ
С ВОЗРАСТНОЙ И ПОЛОВОЙ СТРУКТУРОЙ
И ОПТИМИЗАЦИЯ ПРОМЫСЛА
Специальность 03.01.02 – биофизика
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Владивосток – 2011
Работа выполнена в Учреждении Российской Академии наук
Институте комплексного анализа региональных проблем
Дальневосточного отделения РАН
Научный руководитель: доктор биологических наук, профессор
Фрисман Ефим Яковлевич
Официальные оппоненты: доктор физико-математических наук, профессор
Абакумов Александр Иванович
доктор биологических наук, профессор
Дулепов Владимир Иванович
Ведущая организация: Московский государственный университет имени М.В. Ломоносова, кафедра биофизики Биологического факультета (г. Москва)
Защита состоится «18» ноября 2011 г. в 14.00 часов на заседании диссертационного совета Д 005.007.02 в Институте автоматики и процессов управления ДВО РАН по адресу: 690041, г. Владивосток, ул. Радио, 5.
С диссертацией можно ознакомиться в библиотеке Института автоматики и процессов управления ДВО РАН.
Автореферат разослан «14» октября 2011 г.
Ученый секретарь
диссертационного совета
 Е.Л. Гамаюнов
Е.Л. ГамаюновОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Диссертационная работа направлена на решение фундаментальной проблемы математической экологической биофизики, связанной с моделированием временной динамики природных популяций и экосистем и анализом динамических процессов и механизмов, определяющих их развитие.
Актуальность темы. Обоснование и развитие классических матричных моделей динамики численности популяций (Leslie, 1945, 1948; Lefkovitch, 1965; Свирежев, Логофет, 1978; Логофет, 1991; Логофет, Белова, 2007) позволяют подробно описывать и исследовать роль и значение возрастной структуры и стадийности развития для поддержания и эволюции популяционной цикличности (Hastings, 1992; Lebreton, 1996; Kooi and Kooijman, 1999). В большинстве работ, посвященных проблемам эволюции жизненного цикла, достаточно подробно рассматриваются вопросы формирования возрастной структуры и ее роли в развитии экологически лимитированных популяций (Charlesworth, 1993; Greenman et al., 2005, Фрисман, Жданова, 2006, 2009). Формирование половой структуры рассматривается здесь, зачастую, как сопутствующий процесс, однозначно определяющийся значениями коэффициентов выживаемости разнополых ровесников. Вместе с тем, в случае полигамных видов, как формирование половой структуры, так и характер популяционной динамики в целом, оказываются существенно связаны с параметрами, определяющими тип «брачных отношений» и роль самцов в процессе воспроизводства. Это отмечалось многими авторами (Скалецкая и др., 1980; Frisman et al., 1982; Bessa-Gomes et al., 2010; Jenouvrier et al., 2010), однако детальных модельных исследований проведено не было.
Построение математических моделей, описывающих динамику численности популяций с возрастной и половой структурами, и исследование их динамических режимов является необходимым условием для решения важных прикладных задач оптимального управления популяциями. Действительно, разработка оптимальной стратегии эксплуатации промысловых видов (оптимизация процесса «сбора урожая») неразрывно должна быть связана с изучением их популяционной структуры, в частности, возрастной и половой структуры. Во-первых, пополнение популяции является сложным процессом, включающим выживание и рост неполовозрелых самок и самцов, переходы в старшие возрастные классы и т.д.; на каждую из этих характеристик изменение плотности популяции и промысел могут влиять по-разному. Во-вторых, промысловики в большинстве случаев интересуются только частью эксплуатируемой популяции (например, зрелыми деревьями, достаточно крупными рыбами, достигшими товарного размера, взрослыми тюленями или их детенышами).
Изучение закономерностей, определяющих популяционную структуру, ее динамику и устойчивость, как и разработка оптимальных стратегий эксплуатации популяций давно находятся в ряду основных задач многих исследователей (Скалецкая и др., 1979; Holbauer, Sigmund, 1980; Абакумов, 1993; Furta, 1997). Вместе с тем, несмотря на большое количество работ, посвященных данной тематике, остается много нерешенных вопросов, связанных с анализом особенности динамики возрастной и половой структуры популяций, исследованием механизмов их регуляции и поиском путей адекватного оптимального управления. Получению ответов на некоторые из этих вопросов и посвящено данное диссертационное исследование.
Цель диссертационной работы - изучение механизмов формирования и развития динамических режимов, возникающих в простейших моделях динамики численности лимитированной популяции с возрастной и половой структурой и связанных с плотностно-зависимой регуляций численностей возрастных групп и промыслом.
Для достижения поставленной цели необходимо было решить следующие задачи:
1. Построение и исследование модели динамики численности двухвозрастной популяции, представленной совокупностью двух возрастных классов: младшего, включающего неполовозрелых особей, и старшего, состоящего из половозрелых особей.
2. Построение и исследование модели динамики численности популяции, состоящей из трех групп: младшей, включающей неполовозрелых особей, и двух старших, представленных самками и самцами, участвующими в размножении.
3. Постановка и решение задачи оптимизации промыслового изъятия из двухвозрастной популяции для двухкомпонентной (без явного учета половой структуры) и трехкомпонентной (с учетом половой структуры) моделей.
4. Применение математических моделей для описания динамики численности охотничье-промысловых животных (на примере Еврейской автономной области (ЕАО)).
Методы исследования. Для построения моделей в работе используется аппарат рекуррентных уравнений. При исследовании математических моделей применяются элементы математического анализа и критерии устойчивости систем. Проведение численных экспериментов включает в себя построение фазовых и параметрических портретов, бифуркационных диаграмм, ляпуновских показателей, карт динамических режимов. При решении задачи оптимизации промысла используются аналитические методы решения задач безусловной оптимизации, базирующиеся на условиях оптимальности, и метод динамического программирования Беллмана. Для оценки параметров моделей использованы методы наименьших квадратов и безусловной оптимизации Левенберга-Маркварда.
Научная новизна работы. В рамках исследования модели динамики численности популяции с возрастной и половой структурой удалось одновременно проследить формирование возрастной и половой структур и явно учесть асимметричность влияния полов на демографические процессы. Данное исследование позволило описать картину качественного изменения динамического поведения популяции в зависимости от уровня различий характеристик полов, определяющих процессы выживания и воспроизводства.
Рассмотрены оптимальные стратегии эксплуатации двухвозрастной популяции, которые могут быть получены на основе динамических моделей как не учитывающих половую структуру, так и учитывающих ее. В результате исследования показано, что промысел двухвозрастной популяции с постоянной оптимальной равновесной долей изъятия при определенных значениях популяционных параметров может приводить к колебаниям численности. Стабилизация динамики системы происходит при стратегии промысла, основанной в регулярном изъятии излишка численности над значением, соответствующего величине максимального прироста популяции.
Методом математического моделирования проведен анализ основных тенденций изменения численности и влияния внешних факторов (кормовых запасов и высоты снежного покрова) на динамику промысловых животных, обитающих на территории ЕАО; получены оценки ряда характеристик как популяционных динамических процессов (интенсивность годового воспроизводства, миграционный баланс), так и факторов, наиболее существенно определяющих и влияющих на эти процессы (репродуктивный потенциал, емкость среды обитания, максимально возможная численность популяции и т.п.), найдены оценки оптимальных долей изъятия.
Основные положения, выносимые на защиту:
1. Тип динамики модели двухвозрастной популяции (переход к равновесным состояниям или регулярным циклам, квазипериодические или хаотические колебания) зависит от соотношения параметров, описывающих репродуктивный потенциал популяции, выживаемость особей разных возрастных групп, и типа плотностно-зависимого лимитирования численности. Увеличение средней индивидуальной приспособленности особей, (т.е. увеличение коэффициентов плодовитости и выживаемости) в экологически лимитированных популяциях может приводить к потере устойчивости и возникновению хаотических аттракторов, структура и размерность которых меняются при изменении параметров модели.
2. Увеличение репродуктивных потенций самцов и уменьшение доли самцов, необходимой для успешного воспроизводства популяции, приводит к увеличению степени хаотизации, а половая асимметричность коэффициентов выживаемости - к увеличению размерности хаотических аттракторов.
3. При промысле из двухвозрастной популяции с плотностным лимитированием выживаемости молоди оптимальным является изъятие особей из одного возрастного класса. Доли изъятия определяются значениями популяционных параметров и соотношениями цен.
4. Промысел из двухвозрастной популяции с постоянной оптимальной равновесной долей изъятия при определенных значениях популяционных параметров приводит к колебаниям численности. Стабилизация динамики системы происходит при стратегии промысла, основанной в регулярном изъятии излишка численности над значением, соответствующего величине максимального прироста популяции.
5. Применение динамических моделей (в том числе и модифицированных вариантов с учетом влияния внешних факторов) для описания поведения численности охотничье-промысловых видов млекопитающих и оценка параметров модели по данным учета животных позволяют описать тенденции изменения численности для каждого вида и рассчитать оптимальные в данных условиях квоты изъятия.
Научная и практическая значимость работы. Часть диссертационной работы, содержащая исследование математических моделей, имеет теоретическое значение и может служить дополнением в развитии математических теорий популяционной биологии. Результаты прикладной части работы представляют интерес для специалистов в области оптимального природопользования, оптимального ведения охотничьих хозяйств и особо охраняемых природных территорий и могут быть обоснованием для определения, планирования и ограничения квот изъятия охотничье-промысловых животных, обитающих на территории Еврейской автономной области.
Апробация работы. Основные результаты работы докладывались и обсуждались на 28 научных конференциях: International Union of Game Biologist XXVIII Congress, Упсала, Швеция, 2007; 6th European Nonlinear Dynamics Conference (ENOC-2008), Saint-Petersburg, Russia, 2008; International Symposium on Wild Boar and Other Suids. Sopron (Hungary), 2008, York, UK, 2010; 4th International Scientific Conference on Physics and Control (Physcon 2009), Catania, Italy, 2009; на Национальной научной конференции с международным участием «Математическое моделирование в экологии» (Экоматмод-2009), Пущино, 2009 г.; на Международной конференции «Математика. Компьютер. Образование», Дубна, 2008, Пущино, 2009 гг.; на III международной конференции "Математическая биология и биоинформатика", Пущино, 2010 г.; на Дальневосточных математических школах - семинарах имени академика Е.В. Золотова, Хабаровск, 2005, 2008, Владивосток, 2006, 2007, 2009 гг.; на Дальневосточной конференции студентов, аспирантов и молодых ученых по теоретической и прикладной математике, Владивосток, 2009 г.; на научной конференции «Природопользование на Дальнем Востоке России», Хабаровск, 2006 г.; на региональных школах - семинарах молодых ученых, аспирантов и студентов «Территориальные исследования Дальнего Востока», Биробиджан, 2005, 2007, 2009 гг.; на Международных конференциях «Современные проблемы регионального развития», Биробиджан, 2006, 2008, 2010 гг.; и других.
Личный вклад автора. Автору принадлежит выбор методов исследования, проведение аналитических и численных расчетов, анализ результатов. В совместных работах автором выполнено исследование модели динамики численности двухвозрастной популяции с линейным видом зависимости выживаемости от численности, изучение модели динамики популяции с учетом возрастной и половой структурой и решение задачи оптимизации промысла. В практической части работы автор самостоятельно сделал все вычислительные эксперименты, направленные на оценку коэффициентов моделей, и дал биологическую интерпретацию полученных результатов.
Публикации. По теме диссертации опубликовано 14 работ, в том числе 5 статей в журналах, входящих в Перечень изданий ВАК РФ.
Структура и объем диссертации. Работа состоит из введения, 4 глав, заключения, списка литературы (262 источников, в том числе 144 иностранных). Диссертация изложена на 162 страницах, иллюстрирована 42 рисунками и 4 таблицами.
Благодарности. Автор выражает глубокую благодарность научному руководителю доктору биологических наук, профессору Е.Я. Фрисману за постановку задачи, ценные советы, критические замечания и поддержку на всех этапах работы.
Автор благодарит всех сотрудников лаборатории математического моделирования динамики региональных систем ИКАРП ДВО РАН за неоценимую помощь, обсуждение и неизменную моральную поддержку на всех этапах работы.
Автор искренне признателен специалистам природоохранных структур А.Н. Феоктистову, В.М. Паневину, А.Ю. Калинину, Ю.А. Панину, Н.Н. Яковлеву, В.Н. Ростову, А.А. Аверину за предоставленные данные материалов учетных работ и интерес к работе.
СОДЕРЖАНИЕ ДИССЕРТАЦИОННОЙ РАБОТЫ
Во введении обоснованы актуальность темы, сформулированы цели работы, перечислены основные этапы и методы работы, показаны вклад автора в проведенное исследование, степень новизны и практическая значимость результатов исследований.
Глава 1. Моделирование динамики численности популяции
(обзор литературы)
Первая глава диссертации посвящена обзору моделей, предназначенных для описания и изучения режимов динамики численности: однородной популяции, развивающейся в стационарной среде обитания, однородной популяции, развивающейся в меняющейся среде, популяции с возрастной структурой, популяции с возрастной и половой структурами. Также обсуждаются работы, посвященные оптимизации промысла. На основе проведенного обзора ставятся задачи диссертационного исследования.
Глава 2. Построение и исследование модели динамики численности двухвозрастной популяции
Во второй главе проводится исследование динамических режимов модели, описывающей поведение численности двухвозрастной популяции с сезонным характером размножения (модель с дискретным временем).
В § 2.1. приводится описание и исследование модели динамики численности популяции, состоящей из двух возрастных классов: младшего, включающего неполовозрелых особей, и старшего, состоящего из особей, участвующих в размножении. Уравнения динамики численности такой популяции имеют вид:
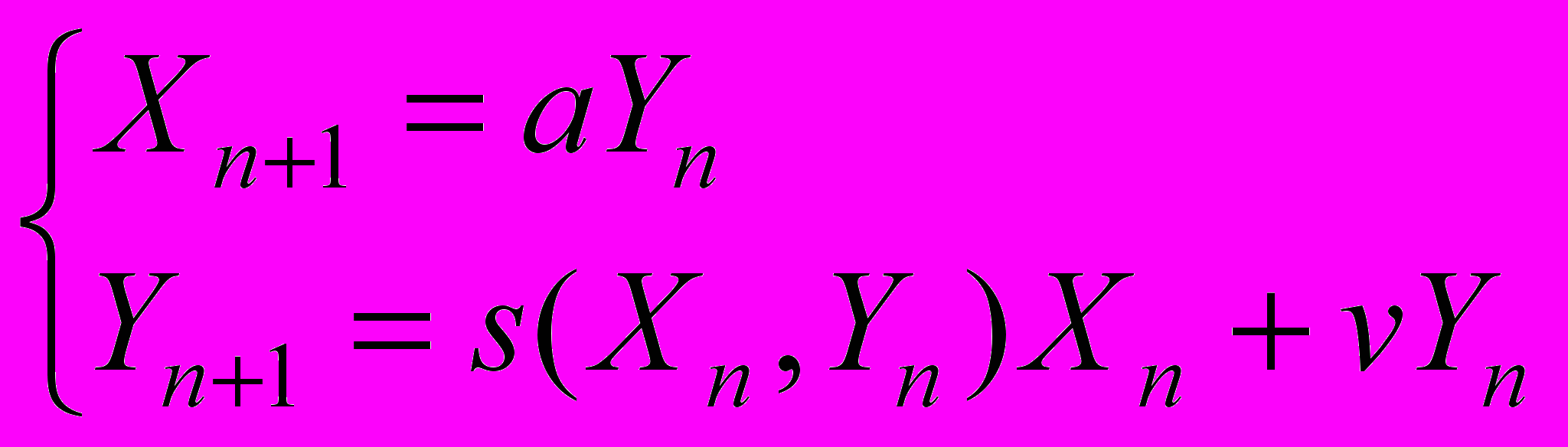 , (1)
, (1)где n – номер сезона размножения, X (X>0) и Y (Y>0) – численности младшего и старшего возрастного класса, соответственно, a (a>0) – репродуктивный потенциал популяции, v (0<v≤1) – коэффициент выживаемости взрослых особей, s(X,Y) – функция выживаемости неполовозрелых особей, зависящая от плотности молоди и взрослых особей. Эта функция считается линейной (дискретный аналог модели Ферхюльста для двухвозрастной популяции):
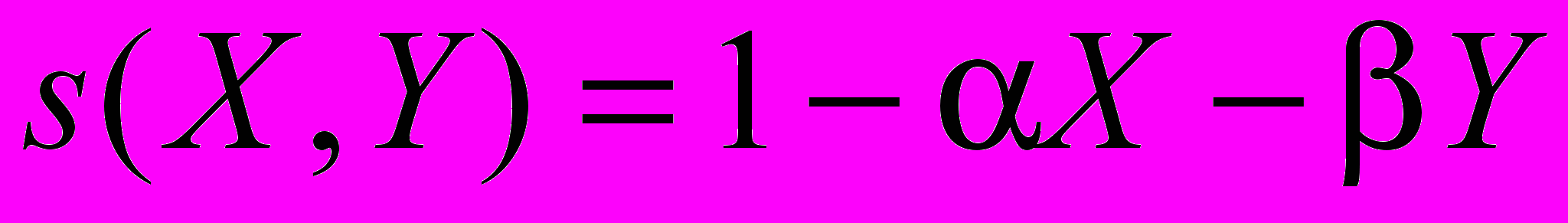 , где α (α≥0) и β (β≥0) – коэффициенты, характеризующие интенсивности конкурентного воздействия неполовозрелых и половозрелых особей.
, где α (α≥0) и β (β≥0) – коэффициенты, характеризующие интенсивности конкурентного воздействия неполовозрелых и половозрелых особей. Исследование системы упрощается, если ввести параметр ρ=β/α и перейти к новым переменным, «относительным» численностям популяции:
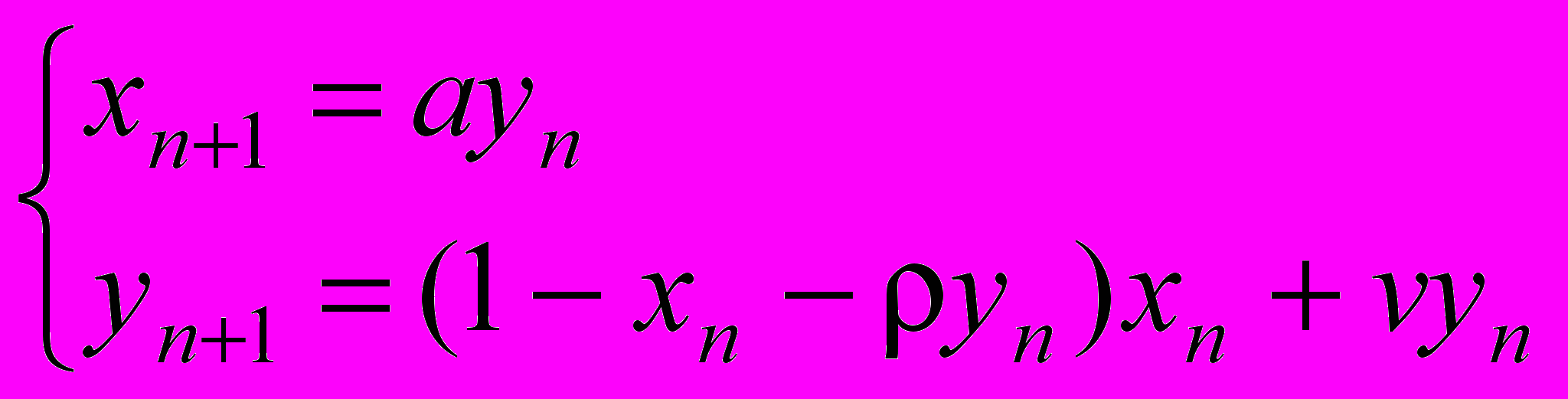 . (2)
. (2)Найдено единственное нетривиальное равновесное решение системы (2), определены условия его существования и устойчивости. Показано, что в зависимости от соотношения коэффициентов, характеризующих интенсивность конкурентного воздействия возрастных групп ρ и выживаемость старшего возрастного класса v, с ростом коэффициента рождаемости a возможны три сценария динамики численности двухкомпонентной популяции: во-первых, возникновение квазипериодических колебаний численности, которые при дальнейшем изменении параметров системы приобретают хаотический характер (рис. 1 а); во-вторых, появление периодических колебаний (рис. 1 б), и, в-третьих, переход к регулярным циклам и обратно к равновесию с последующим выходом на квазипериодический режим динамики (рис. 1 в).
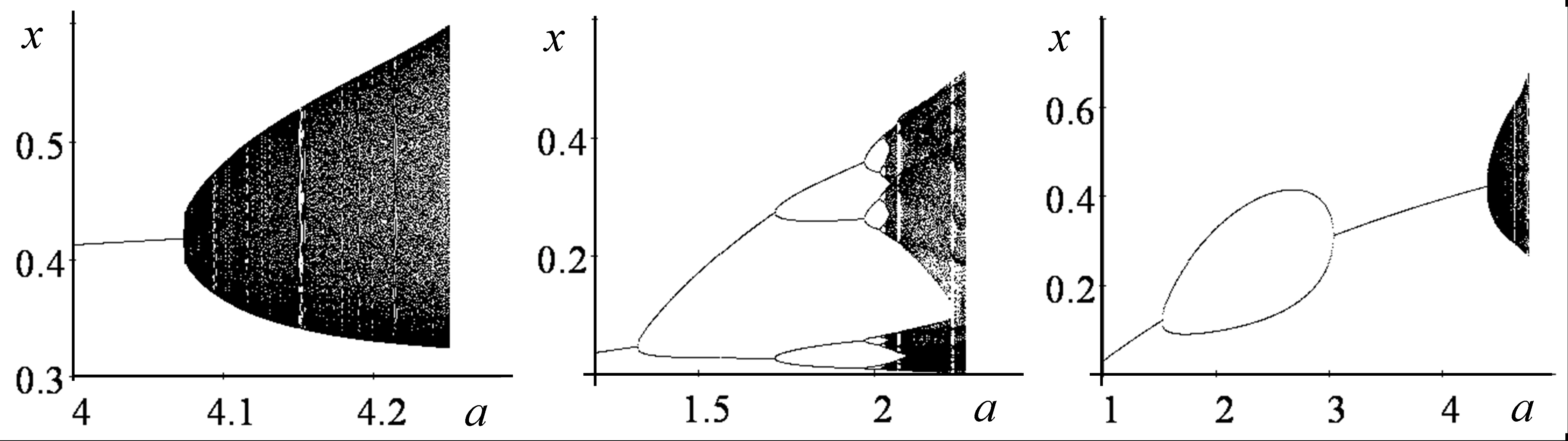 | ||
| а) v=0.3 ρ=4 | б) v=0.2, ρ=10 | в) v=0.15, ρ=4 |
Рис.1. Сценарии изменений предельных распределений численности неполовозрелых особей x в аттракторах системы (2) в зависимости от величины параметра a. Поведения предельных распределений численности половозрелых особей y аналогичны
В § 2.2. исследуется модель динамики численности популяции, которая может быть представлена совокупностью трех групп: младшей, включающей неполовозрелых особей, и двух старших, состоящих из самок и самцов, участвующих в размножении. Предлагаемая модель может быть записана системой трех рекуррентных уравнений
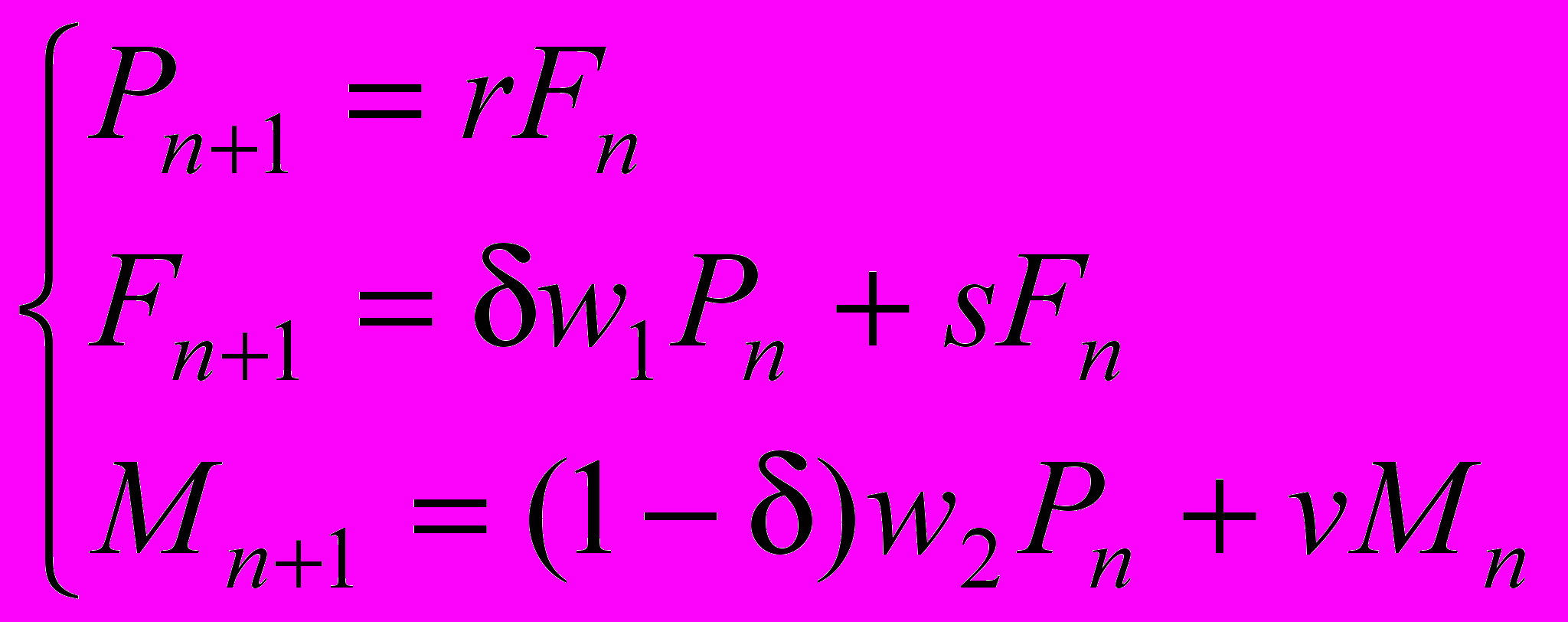 , (3)
, (3)где n – номер сезона размножения, P (P>0) – численность особей в младшем возрастном классе, F (F>0) и M (M>0) – численности самок и самцов, участвующих в размножении, r (r>0) – коэффициент рождаемости, δ (0<δ<1) – доля самок среди новорожденных, w1 (0<w1≤1) и w2 (0<w2≤1) – выживаемости неполовозрелых, s (0<s<1) и v (0<v<1) – выживаемости половозрелых самок и самцов, соответственно.
Предполагается, что рождаемость r зависит от соотношения численностей самцов и самок в популяции, и выбирается в виде зависимости
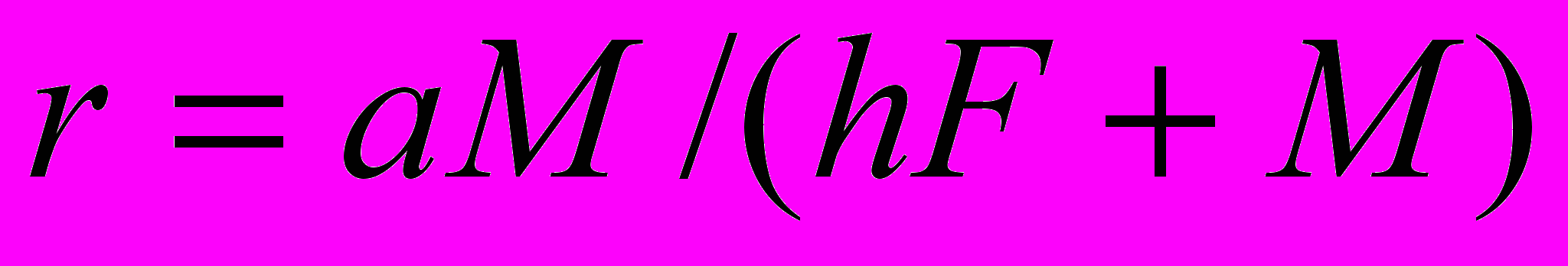 , где a (a>0) – максимально возможное число потомков, приходящихся на одну оплодотворенную самку, h (h>0) – соотношение самцов и самок в популяции, при котором оплодотворенными оказываются ровно половина самок.
, где a (a>0) – максимально возможное число потомков, приходящихся на одну оплодотворенную самку, h (h>0) – соотношение самцов и самок в популяции, при котором оплодотворенными оказываются ровно половина самок. Полагается, что выживаемости неполовозрелых самок и самцов линейно зависят от численности младшего возрастного класса:
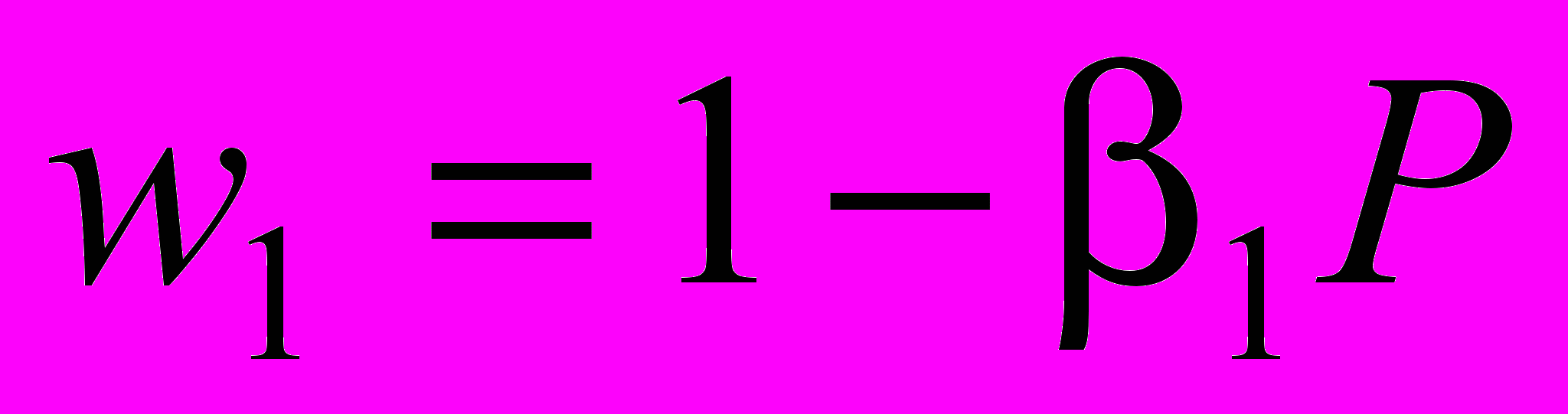 ,
, 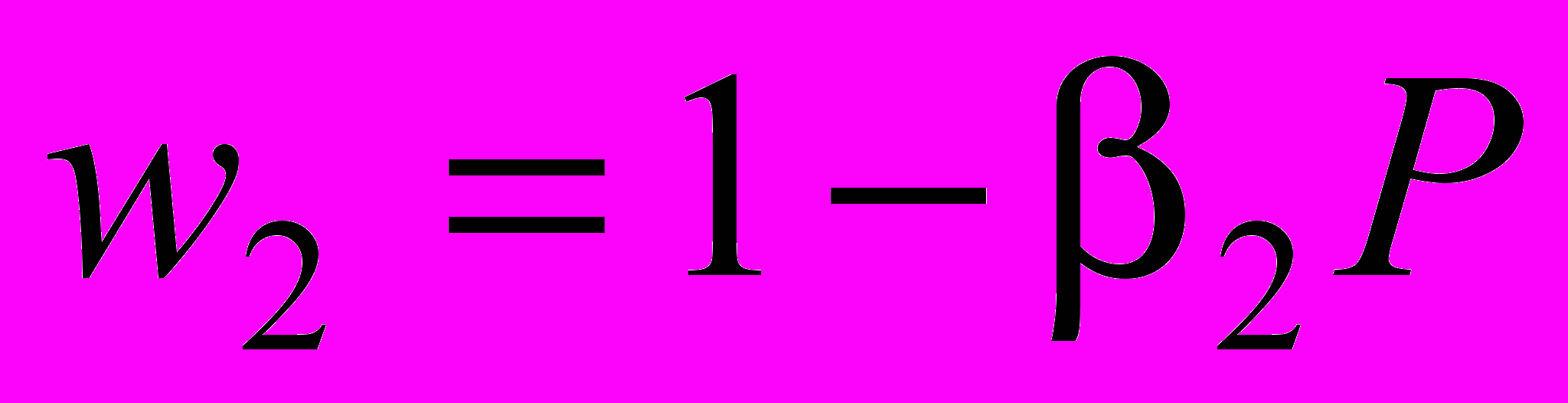 , где β1 (β1≥0) и β2 (β2≥0) – коэффициенты, описывающие интенсивность внутрипопуляционной конкуренции. Кроме того, считается, что рождается равное количество самок и самцов (δ=0.5). Замена переменных позволяет избавиться от параметра β2 и (с учетом сделанных предположений) записать модель (3) в новых переменных - «относительных» численностях:
, где β1 (β1≥0) и β2 (β2≥0) – коэффициенты, описывающие интенсивность внутрипопуляционной конкуренции. Кроме того, считается, что рождается равное количество самок и самцов (δ=0.5). Замена переменных позволяет избавиться от параметра β2 и (с учетом сделанных предположений) записать модель (3) в новых переменных - «относительных» численностях: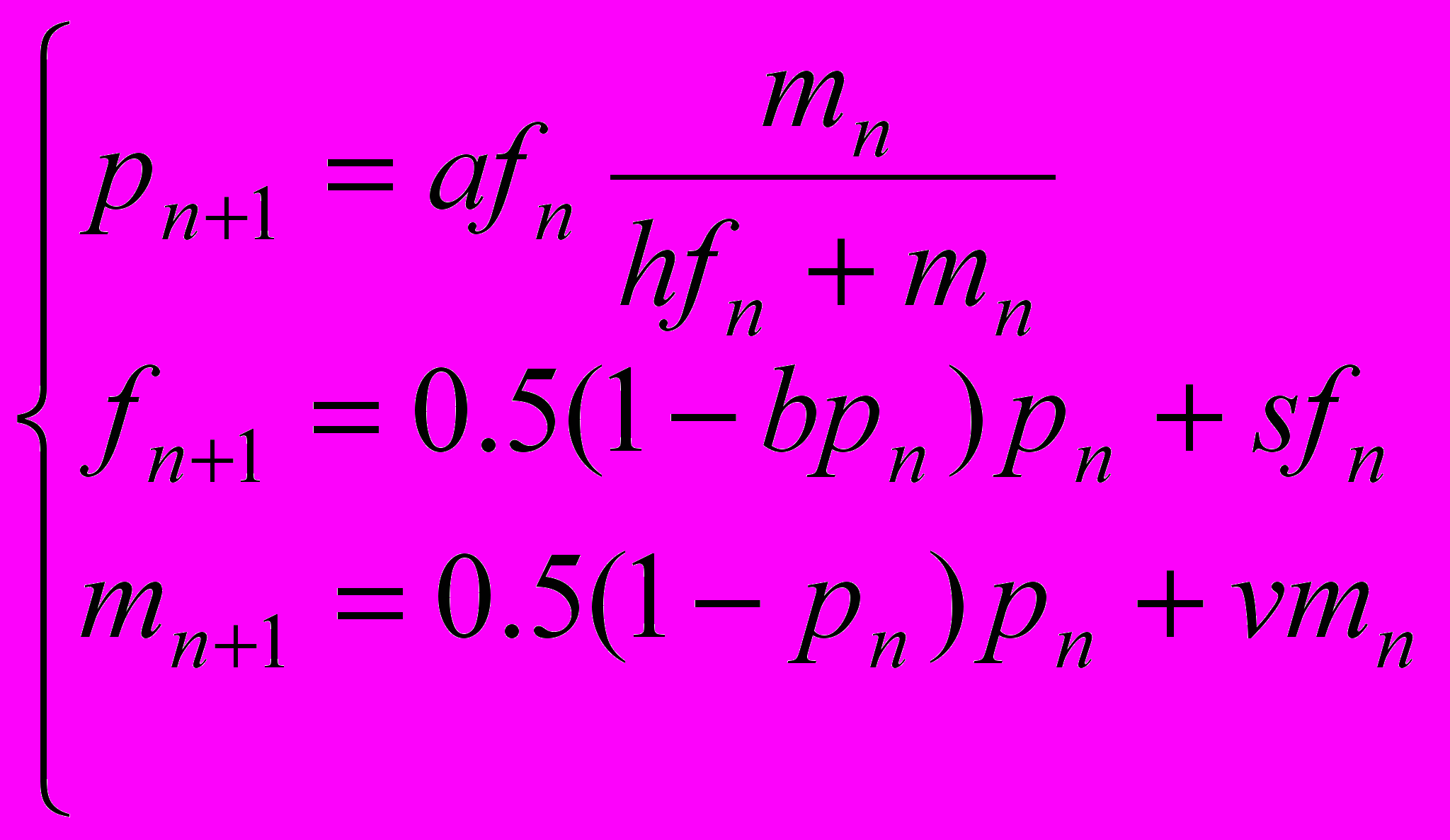 , (4)
, (4)где b= β1/ β2.
В пункте 2.2.1. показано, что система (4) имеет единственную ненулевую равновесную точку, потеря устойчивости которой происходит только при прохождении пары комплексно-сопряженных корней характеристического уравнения через единичную окружность. В результате возникают квазипериодические колебания, которые при изменении параметров системы приобретают хаотический характер.
В пунктах 2.2.2.-2.2.5. представлено исследование основных частных случаев базовой модели (4) в зависимости от различных соотношений популяционных параметров.
В 2.2.2. рассматривается случай, когда процессы выживаемости у самок и самцов как неполовозрелых, так и репродуктивного возраста не отличаются (s=v и b=1). Показано, что система (4) сводится к модели двухвозрастной популяции, подробно исследованной в работах (Фрисман, 1994; Фрисман, Скалецкая, 1994), в которых было показано, что для большой области допустимых (биологически содержательных) значений популяционных параметров характерно появление предельных множеств фазовых траекторий, являющихся странными аттракторами.
В 2.2.3. изучаются динамические режимы модели (4), когда выживаемости половозрелых самок и самцов равны (s=v), и различия в равновесных численностях полов могут быть вызваны лишь разной их выживаемостью на неполовозрелой стадии. Здесь рассматриваются следующие ситуации: 1) рост популяции регулируется только уменьшением выживаемости неполовозрелых самцов (b=0) или самок (b1=β2/β1=0, β2=0), происходящим с ростом численности младшего возрастного класса; 2) процессы выживаемости у самок и самцов как неполовозрелых, так и репродуктивного возраста, не отличаются (b=1). Показано, что увеличение репродуктивного потенциала a приводит к потере устойчивости равновесного решения системы и появлению квазипериодических колебаний. Причем, бифуркационное значение a уменьшается с ростом коэффициента выживаемости взрослых особей (s) и при больших значениях s, может оказаться даже меньше 1 (рис. 2 а).
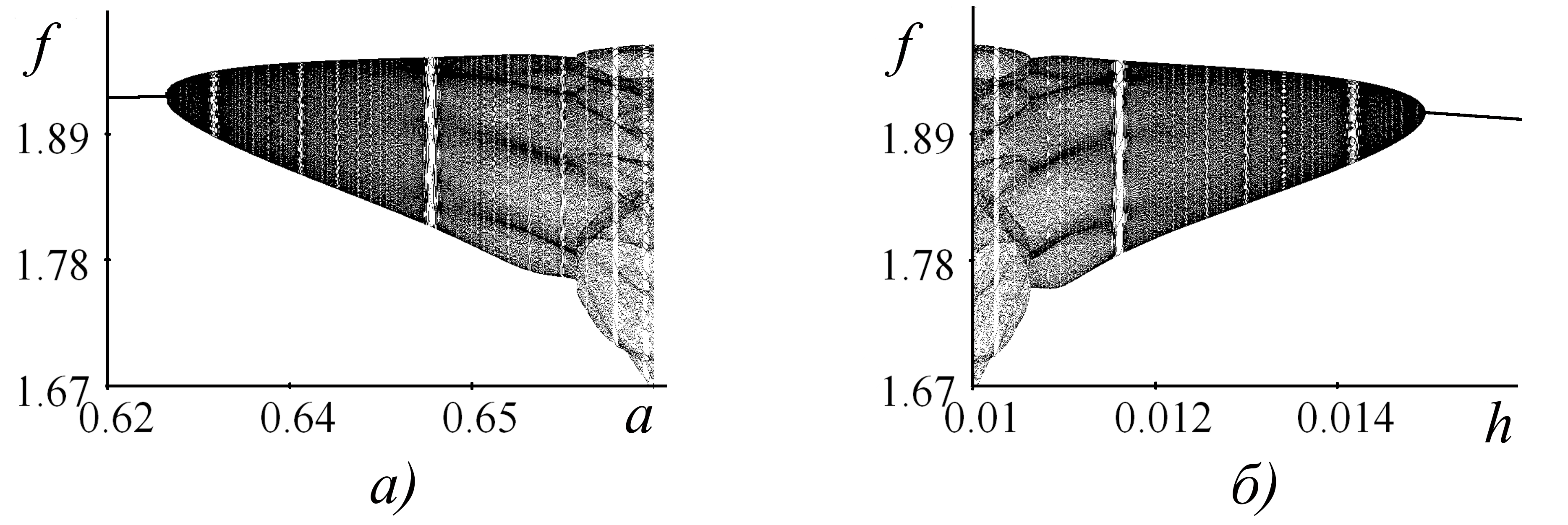
Рис. 2. Сценарии изменений предельных распределений численности самок f в аттракторах системы (4) в зависимости от величин параметров a при h=0.01 (а) и h при а=0.66 (б) при фиксированных значениях b=0, s=v=0.75. Поведения предельных распределений численности половозрелых самцов m и особей младшего возрастного класса p аналогичны
Уменьшение величины h, характеризующей зависимость рождаемости от соотношения полов (фактически, уменьшение «роли» самцов или увеличение их репродуктивных возможностей), также приводит к потере устойчивости равновесия и переходу к циклическим и хаотическим режимам (рис. 2 б).
Более детально бифуркационные переходы можно проследить по портретам аттракторов в фазовом пространстве системы (рис. 3).
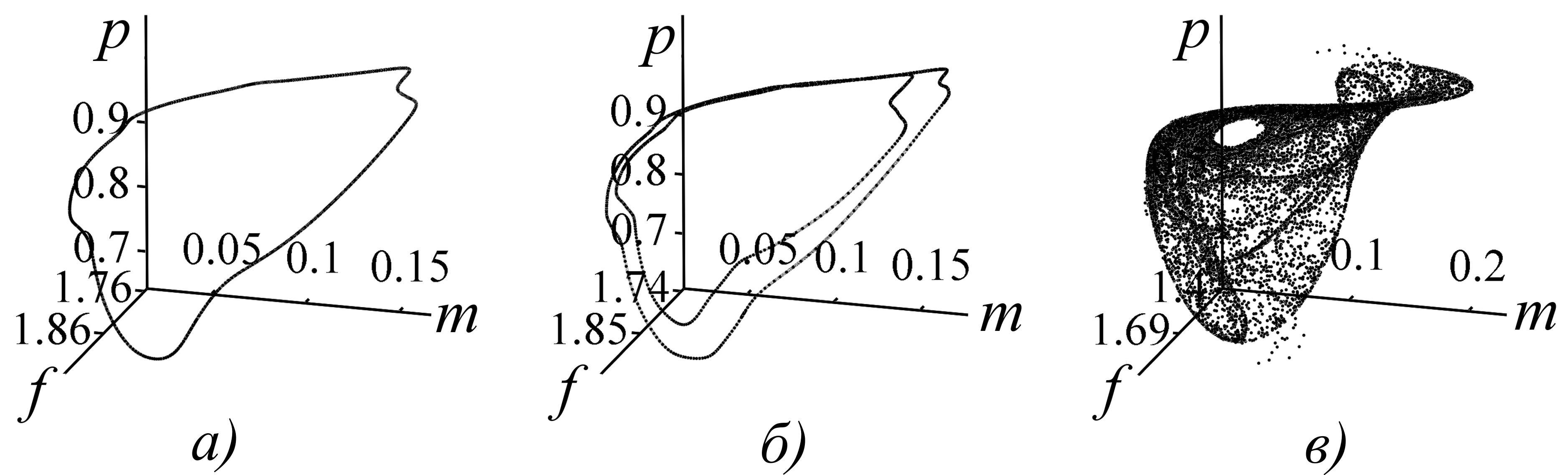
Рис. 3. Предельные траектории (аттракторы) системы (4) при b=0, h=0.01, s=0.75 и а) a=0.655, б) a=0.656, в) a=0.668
В 2.2.4. исследуется развитие двухвозрастной популяции при максимальной равновесной численности половозрелых самок (
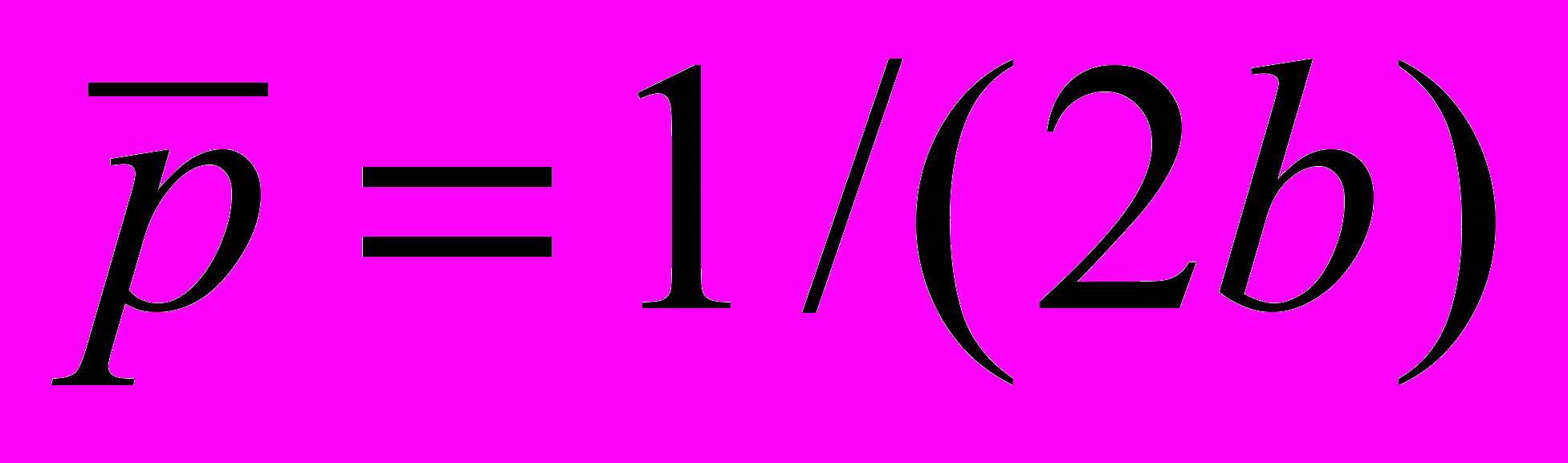 ) или самцов (
) или самцов ( ). Находятся выражения, соответствующие границам устойчивости, демонстрируются некоторые варианты аттракторов в фазовом пространстве.
). Находятся выражения, соответствующие границам устойчивости, демонстрируются некоторые варианты аттракторов в фазовом пространстве. В 2.2.5. исследуется поведение системы в случае, когда выживаемости половозрелых самок и самцов различаются (
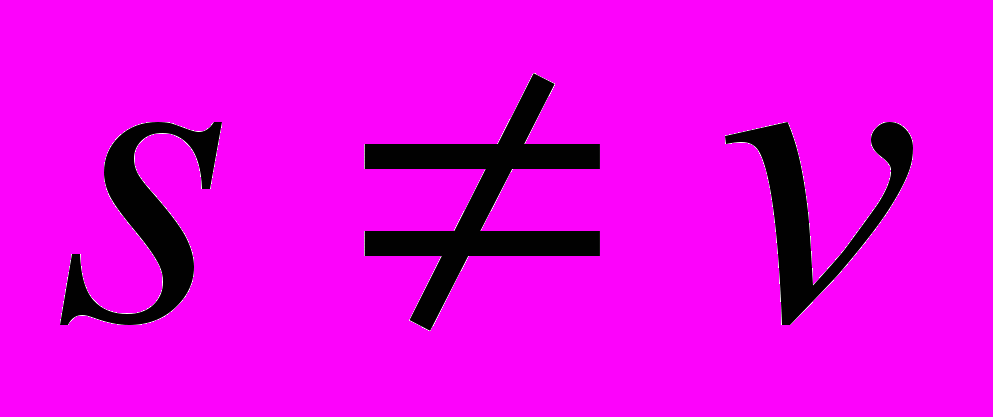 ), а выживаемости неполовозрелых особей одинаковы (
), а выживаемости неполовозрелых особей одинаковы (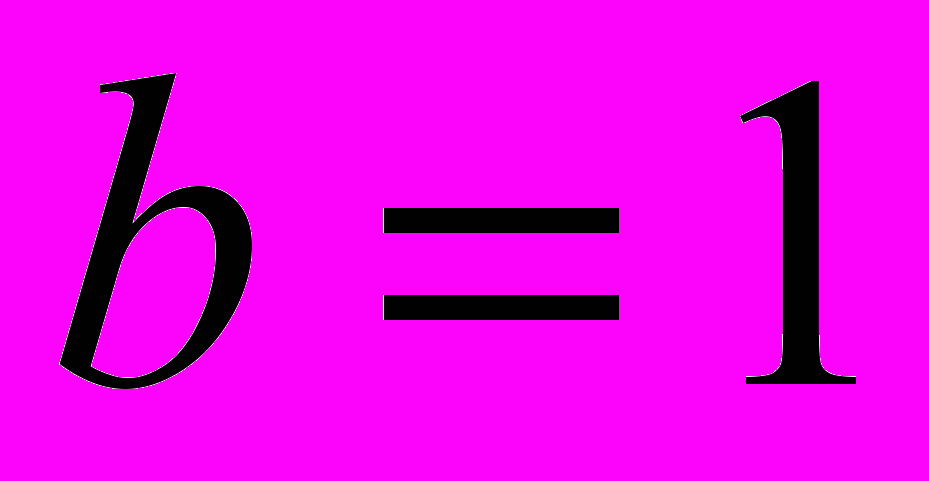 ).
). Сопоставление изображений предельных структур и значений размерности аттракторов, получаемых в случаях, когда выживаемости половозрелых самок и самцов одинаковы (рис. 4 а, б) и различны (рис. 4 в, г), позволяет заключить, что различие в коэффициентах выживаемости самцов и самок добавляет «объем» получаемым предельным траекториям и, тем самым, увеличивает размерность аттракторов.
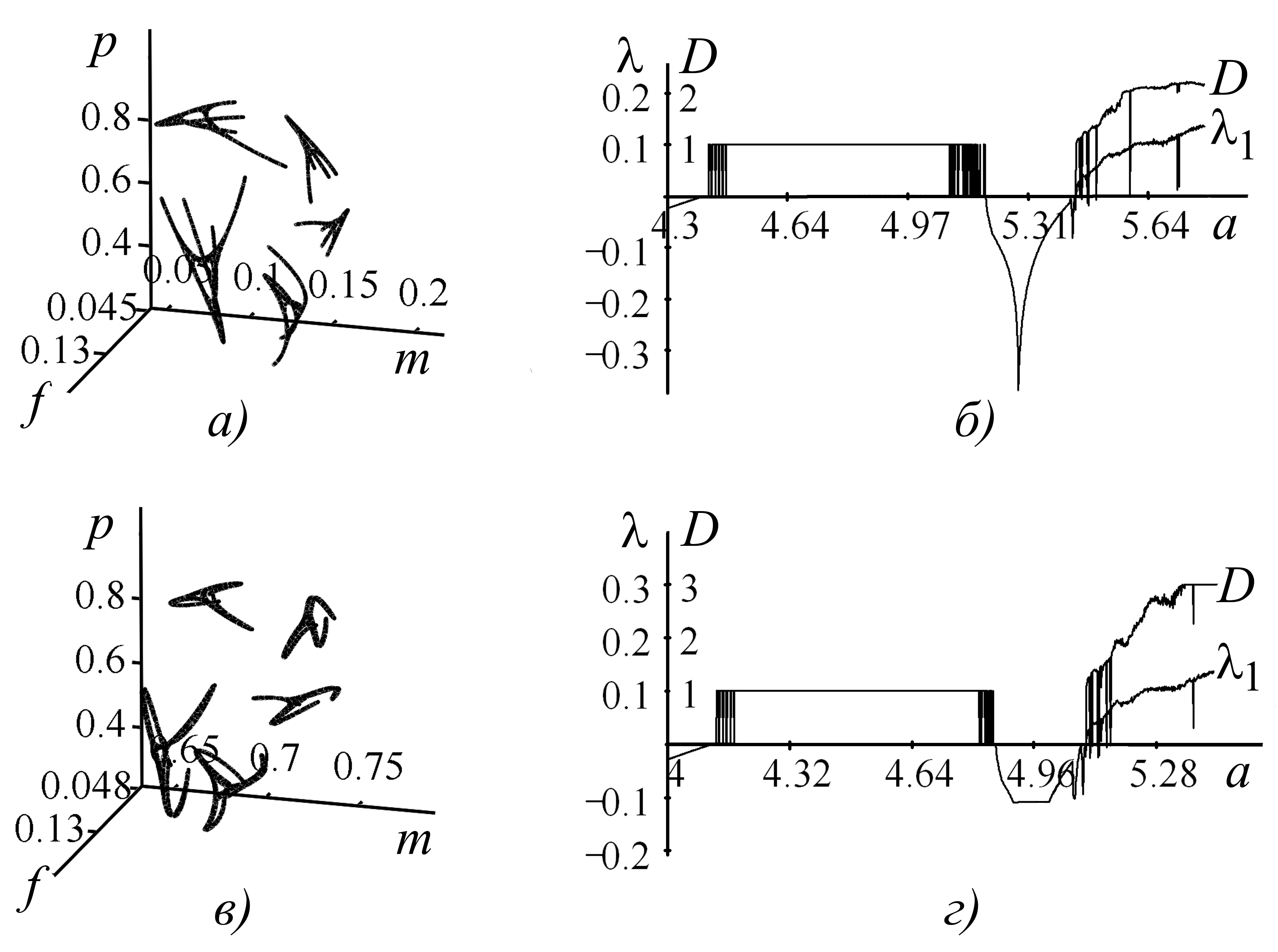
Рис. 4. Предельные траектории системы (4) при h=0.1, b=1 и a=5.503, s=v=0.5 (а); a=5.12, s=0.5, v=0.9 (в); и изменение максимального ляпуновского показателя (λ1) и размерности (D) аттрактора в зависимости от значения параметра a при s=v=0.5 (б); s=0.5, v=0.9 (г). Ляпуновские показатели вычислены по алгоритму Бенеттина, размерность аттрактора находилась по формуле Каплана-Йорка (Ланда, Неймарк, 1987)
Глава 3. Оптимизация промысла для двухвозрастной популяции
В главе 3 исследуется задача определения уровня оптимального изъятия из двухвозрастной популяции.
В параграфе § 3.1. в модель двухвозрастной популяции при плотностно - зависимом лимитировании выживаемости молоди вводится промысловое изъятие, с учетом которого система (1) принимает вид:
 , (5)
, (5)где u1 (0≤u1≤1) и u2 (0≤u2≤1) – доли изъятия неполовозрелых и половозрелых особей, соответственно.
Доли u1 и u2 при равновесном уровне изъятия обеспечивают промысел, суммарный доход от которого определяется соотношением
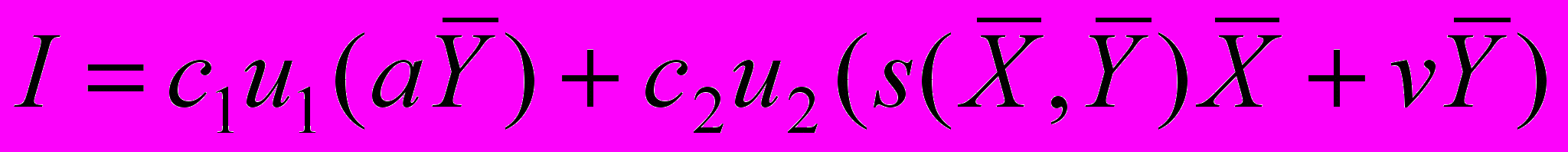 , (6)
, (6)где
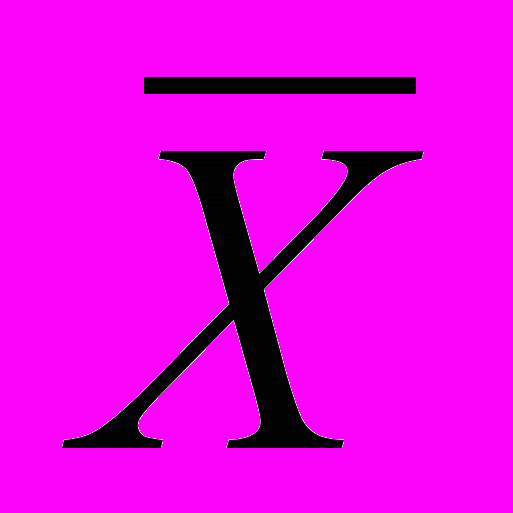 и
и 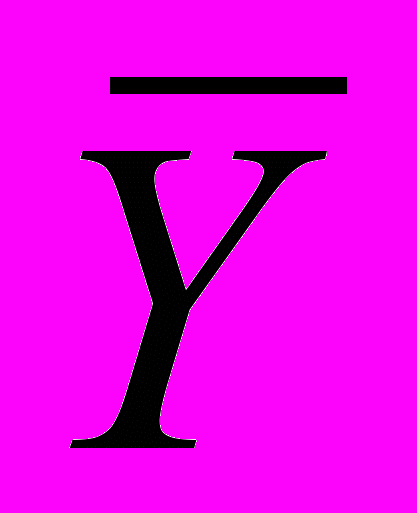 обозначают стационарные численности молоди и взрослых, c1 и c2 – среднемноголетние цены одной особи младшего и старшего возрастного класса, соответственно.
обозначают стационарные численности молоди и взрослых, c1 и c2 – среднемноголетние цены одной особи младшего и старшего возрастного класса, соответственно. Задача оптимизации промысла заключается в определении оптимальных долей изъятия и равновесных значений численности популяции, которые бы обеспечили такой равновесный промысел, который с учетом цен, давал максимальный доход от его реализации.
Поставленная задача решалась для двух видов функции выживаемости неполовозрелых особей: а)
 ; б)
; б) 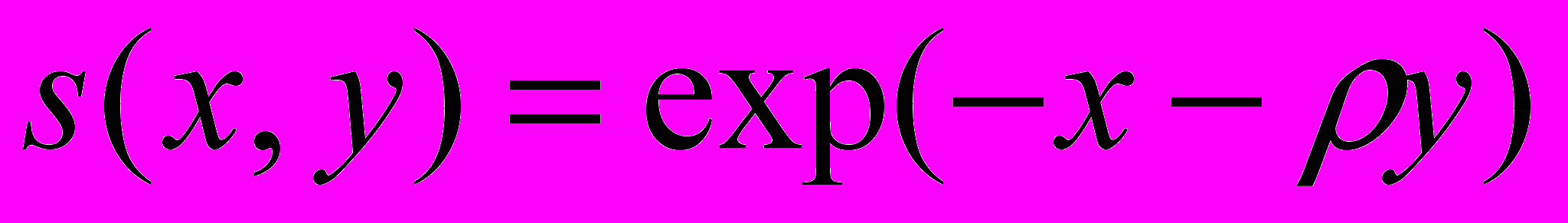 , где
, где 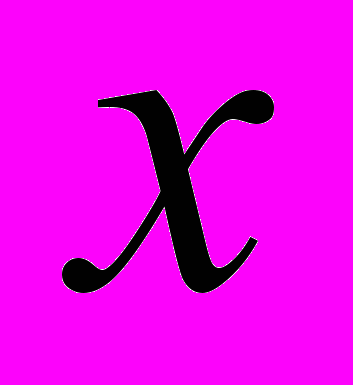 и
и 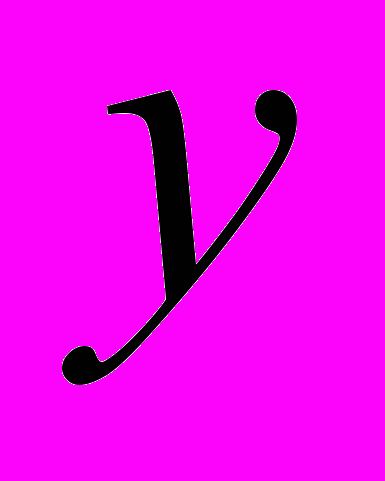 – относительные численности популяции, ρ=β/α – коэффициент интенсивности внутрипопуляционной конкуренции.
– относительные численности популяции, ρ=β/α – коэффициент интенсивности внутрипопуляционной конкуренции.В § 3.2. рассматривается задача оптимизации промысла с постоянной долей изъятия из двух возрастных классов. Показано, что равновесный доход (6) не имеет максимума внутри области {u1
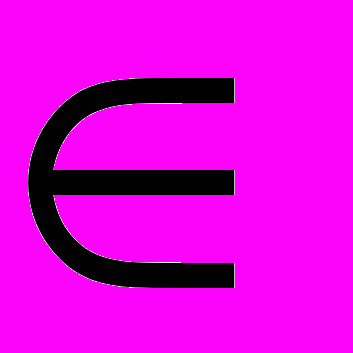 (0,1); u2
(0,1); u2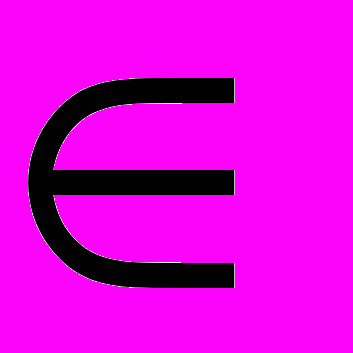 (0,1)}, поэтому одновременное изъятие особей из двух возрастных классов не является оптимальным. Максимальное значение функции дохода (6) необходимо искать на границах области {u1=0; u2
(0,1)}, поэтому одновременное изъятие особей из двух возрастных классов не является оптимальным. Максимальное значение функции дохода (6) необходимо искать на границах области {u1=0; u2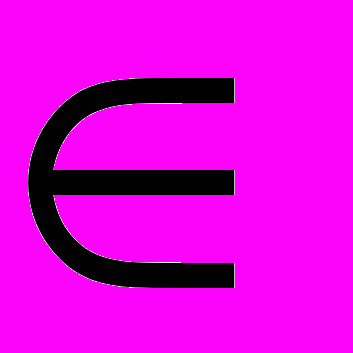 (0,1)} и {u1
(0,1)} и {u1 (0,1); u2=0)}. В связи с этим, в § 3.3. была рассмотрена задача оптимизации промысла с постоянной долей изъятия взрослых особей, а в § 3.4. – соответствующая задача для младшей возрастной группы.
(0,1); u2=0)}. В связи с этим, в § 3.3. была рассмотрена задача оптимизации промысла с постоянной долей изъятия взрослых особей, а в § 3.4. – соответствующая задача для младшей возрастной группы. В § 3.5. сопоставлены значения дохода при промысле особей младшего и старшего возрастных классов и показано, что оптимальным является изъятие из одного возрастного класса, а какого именно определяется значениями популяционных параметров и соотношением цен (рис. 5).
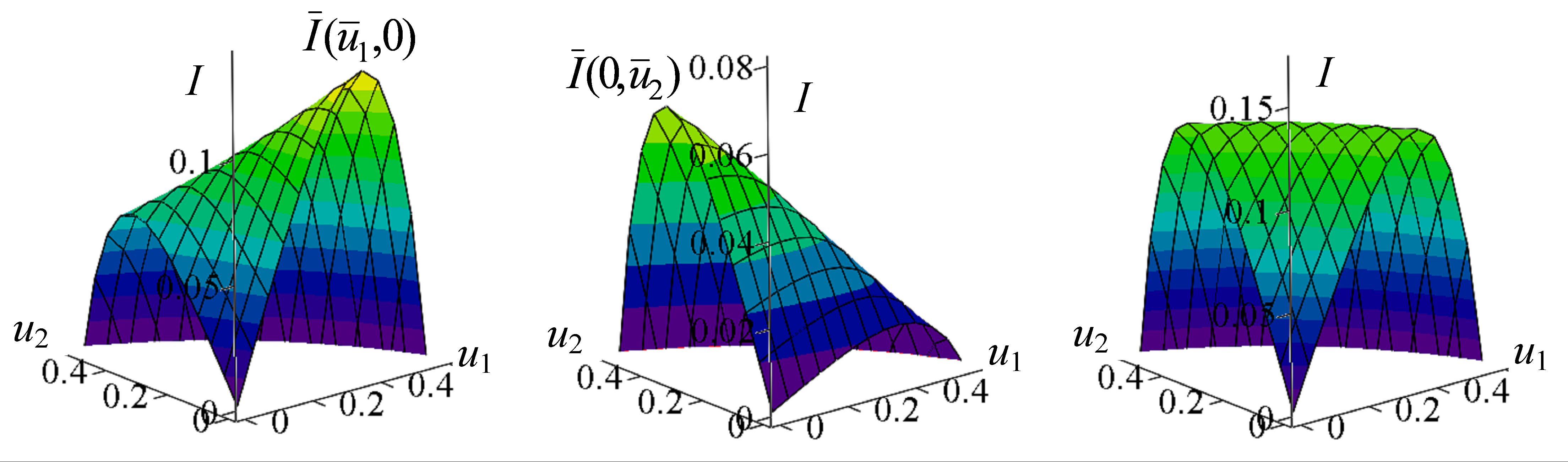 | ||
| c1=1, c2=1 | c1=0.1, c2=1 | c1=1, c2=1.988 |
Рис.5. Поверхности функции дохода в зависимости от значений цен при
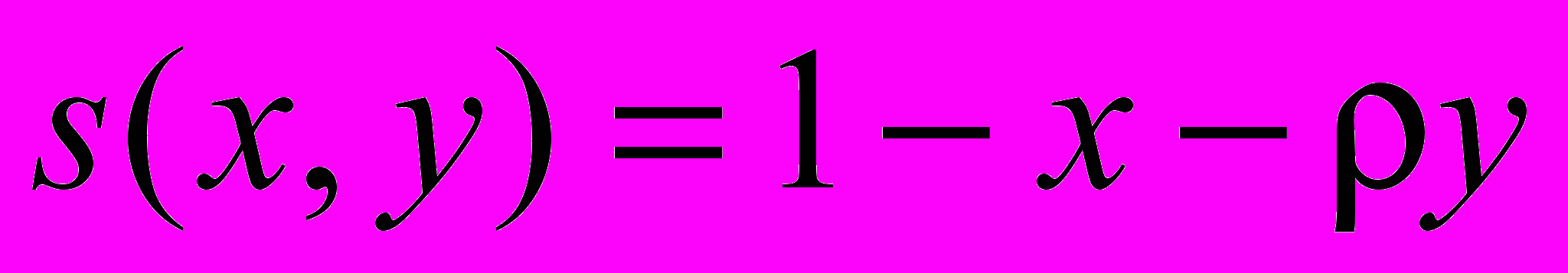 , a=1.8, v=0.2, ρ=0.5
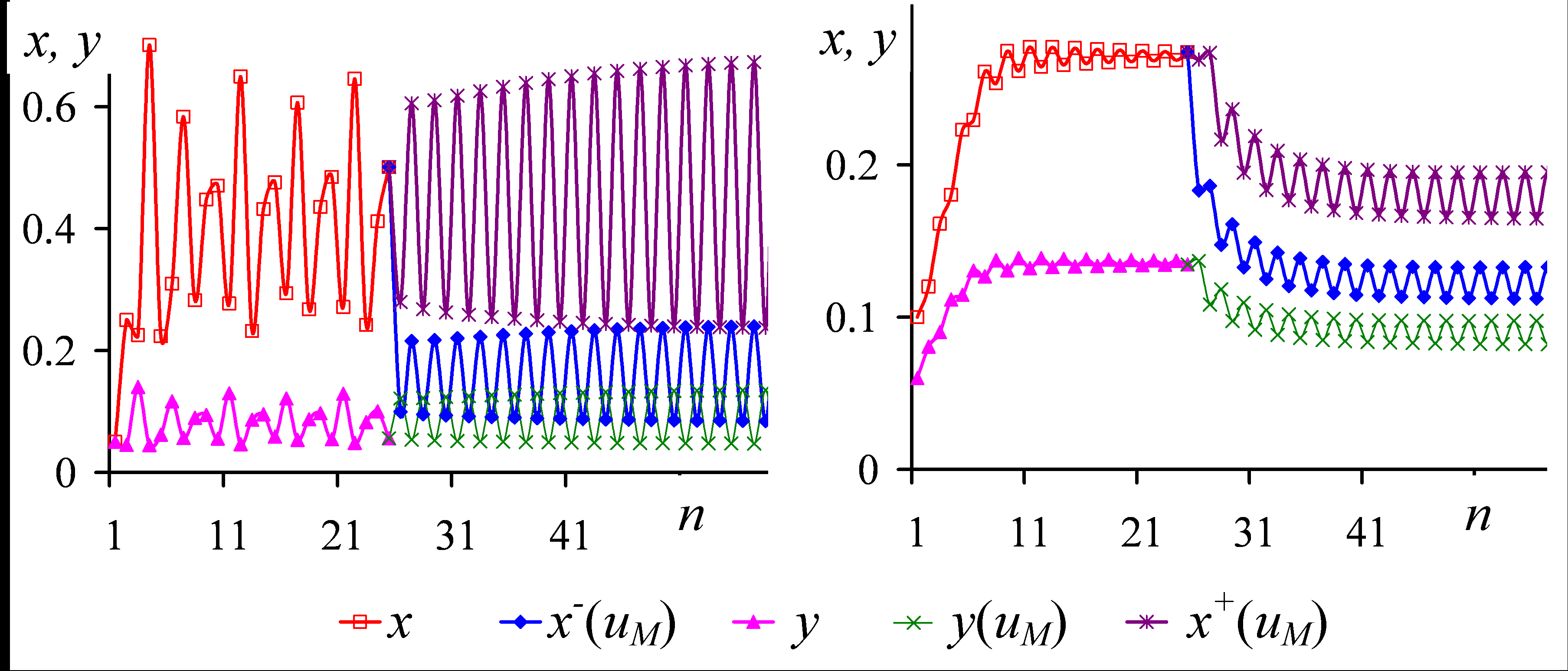
, a=1.8, v=0.2, ρ=0.5В § 3.6. проведено исследование влияния промысла с постоянной долей изъятия на динамику численности двухвозрастной популяции. Показано, что при ведении промысла с постоянной долей изъятия существует область значений популяционных параметров, при которых наблюдаются двухгодичные колебания численности. В 3.6.1 установлено, что промысловое воздействие на старший возрастной класс приводит к периодической динамике лишь в той области значений параметров, где подобная динамика наблюдается и для неэксплуатируемой популяции. Вместе с тем, как показано в 3.6.2, изъятие молоди может изменить тип динамического поведения, характерного для свободной популяции (рис. 6 а), и даже вызывать регулярные колебания численности при значениях параметров, обеспечивающих устойчивое равновесие в отсутствии промысла (рис. 6 б).
 | |
| а) | б) |
Рис. 6. Изменение численностей молоди и взрослых особей без управления (x, y), до промысла (x+(uM), y(uM)) и после промысла (x-(uM), y(uM)) с постоянной долей изъятия неполовозрелых особей uM при
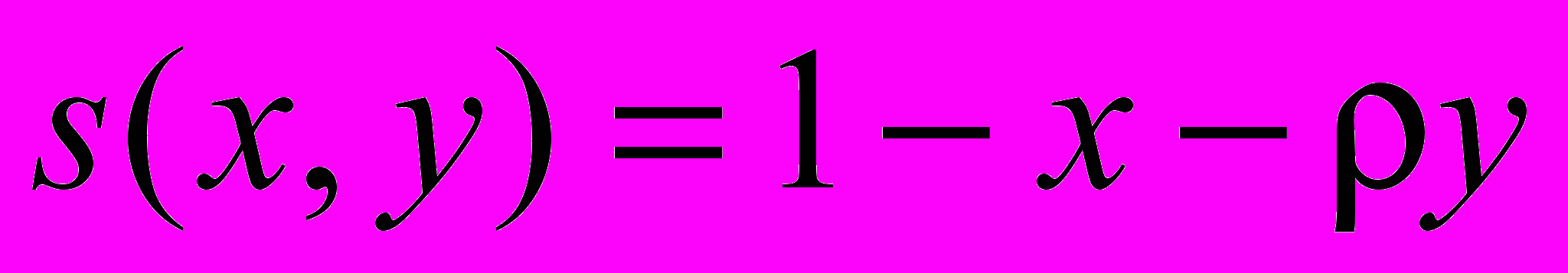 , а) a=5, ρ=5, v=0.2, x1=0.05, y1=0.05, uM =0.64; б) a=2, ρ=1.758, v=0.02, x1=0.1, y1=0.06, uM=0.32. Промысел неполовозрелых особей вводится на 26 шаге моделирования
, а) a=5, ρ=5, v=0.2, x1=0.05, y1=0.05, uM =0.64; б) a=2, ρ=1.758, v=0.02, x1=0.1, y1=0.06, uM=0.32. Промысел неполовозрелых особей вводится на 26 шаге моделированияЭта нестационарность приводит к необходимости перехода от стратегии с постоянной долей изъятия к такой стратегии, которая основана в регулярном изъятии излишка численности над значением, соответствующего величине максимального прироста популяции. В этом случае оптимальное однопараметрическое управление имеет вид (Свирежев, 1975; Скалецкая и др., 1979; Абакумов, 1994):
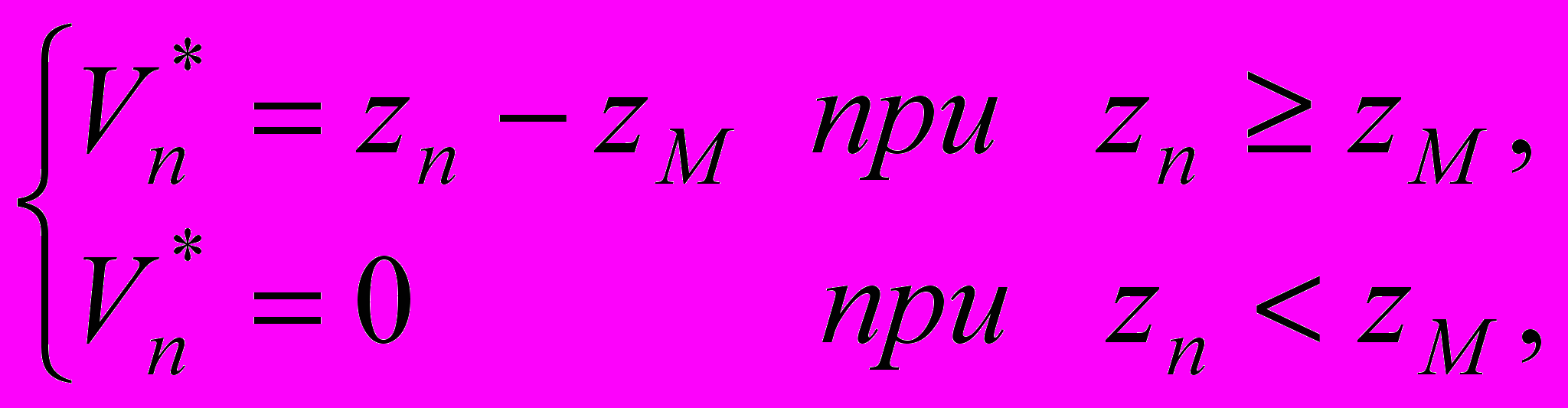 (7)
(7)где
 – количество изъятых особей в n-м году, zn – численность эксплуатируемого возрастного класса в n-м году, zM – такая численность, при которой осуществляется максимальный прирост популяции.
– количество изъятых особей в n-м году, zn – численность эксплуатируемого возрастного класса в n-м году, zM – такая численность, при которой осуществляется максимальный прирост популяции.В § 3.7. приводится решение задачи оптимизации промысла для половозрелых особей, в § 3.8. – для неполовозрелых особей на основе правила управления (7). Определены такие значения численности популяции и доли изъятия на каждом шаге управления, которые обеспечивают максимально возможный промысел за конечный промежуток времени. Показано, что в отличие от промысла с постоянной долей изъятия, такая стратегия всегда стабилизирует динамику численности двухвозрастной популяции (рис. 7).
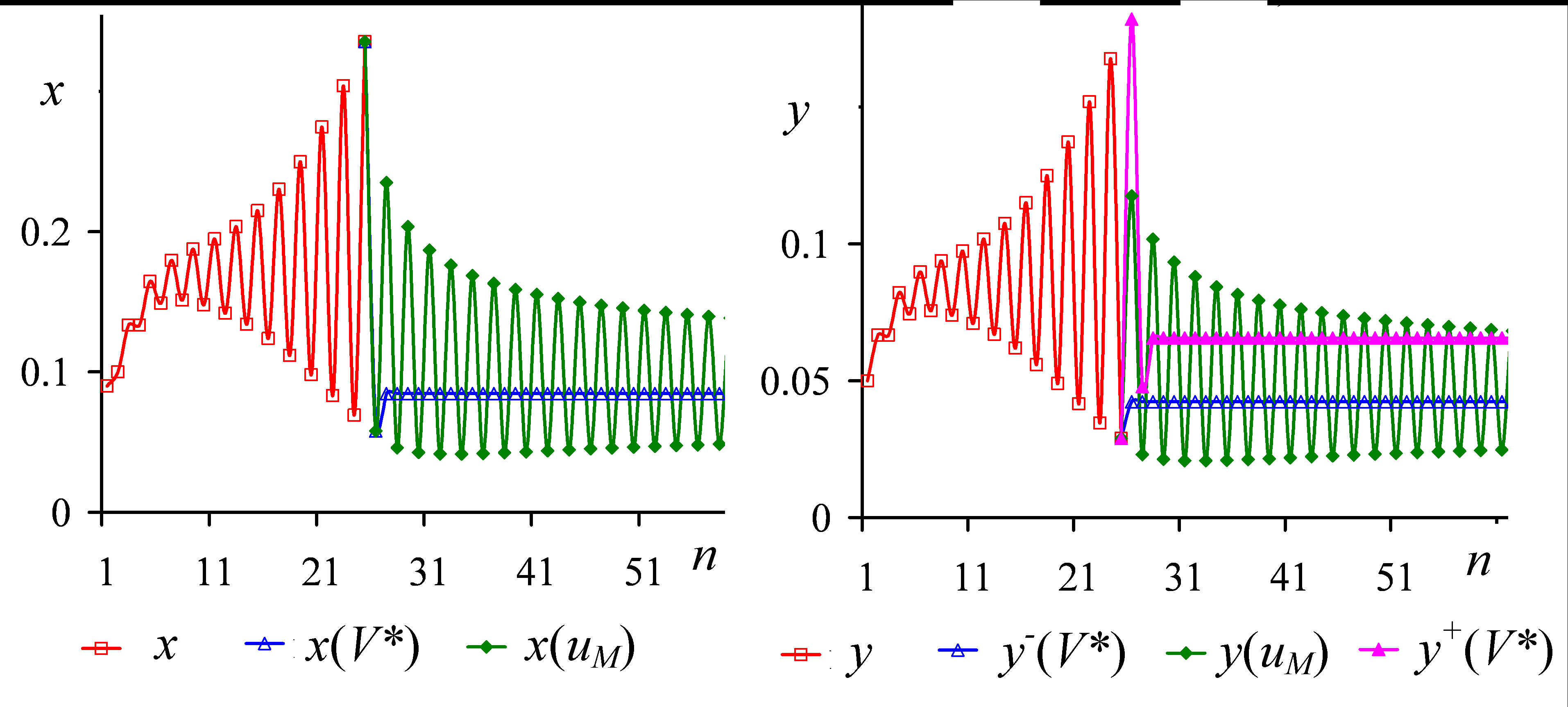
Рис. 7. Изменение численностей молоди и взрослых особей без управления (x, y), до промысла (x(V*), y+(V*)) и после промысла (x(V*), y-(V*)), (x(uM), y-(uM)) из половозрелой части популяции при
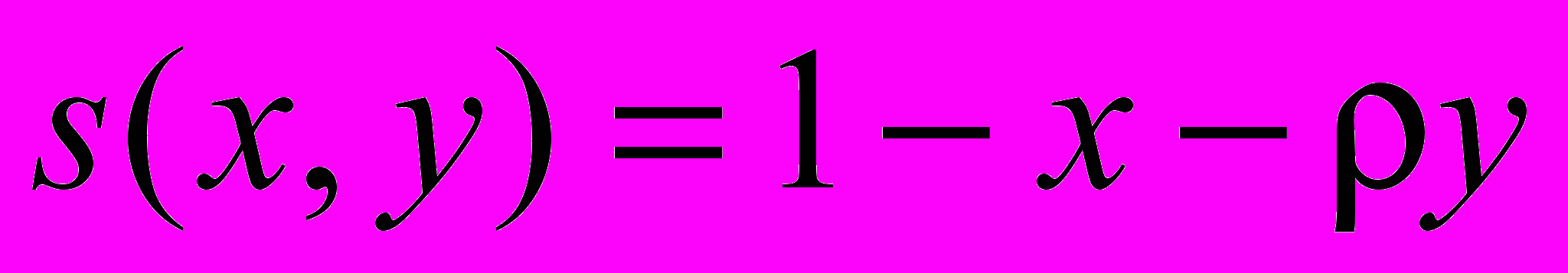 и a=2, ρ=4.5, v=0.1, x1=0.09, y1=0.05, uM=0.35. Промысел половозрелых особей вводится на 26 шаге моделирования
и a=2, ρ=4.5, v=0.1, x1=0.09, y1=0.05, uM=0.35. Промысел половозрелых особей вводится на 26 шаге моделированияВ § 3.9. рассматривается задача оптимизации промысла для популяции с возрастной и половой структурой, которая описывается моделью (4). В 3.9.1. обсуждается постановка задачи оптимального управления промыслом в стационарном режиме. В общем случае эта задача может быть решена численными методами при известных значениях популяционных параметров. В связи с этим в 3.9.2.-3.9.4. проанализированы частные случаи, когда изъятие ведется дифференцированно из одной половозрастной группы. Рассмотрено изменение величины оптимальной доли изъятия половозрелых самцов от популяционных параметров системы (коэффициентов рождаемости a (рис. 8 а), величины h, характеризующей зависимость рождаемости от соотношения полов (рис. 8 б), и выживаемости половозрелых самок s (рис. 8 в)).
 | ||
| а) h=0.011, s=0.91 | б) a=0.819, s=0.91 | в) a=0.819, h=0.011 |
Рис. 8. Зависимость оптимальной доли изъятия половозрелых самцов u3 от параметров системы: а) коэффициента рождаемости a, б) величины h, характеризующей зависимость рождаемости от соотношения полов, в) выживаемости взрослых самок s при α=0.5, β=
 , v=0.86. Изменение значений оптимальных долей изъятия неполовозрелых особей и половозрелых самок от рассмотренных параметров аналогично.
, v=0.86. Изменение значений оптимальных долей изъятия неполовозрелых особей и половозрелых самок от рассмотренных параметров аналогично.Глава 4. Применение математических моделей для описания динамики численности охотничье-промысловых животных
(на примере Еврейской автономной области)
В § 4.1. приведены результаты анализа основных тенденций изменения численности промысловых популяций и оптимизации промысла на основе одномерных моделей (моделей Бивертона – Холта, Рикера и Мальтуса). Оценка параметров моделей проведена по учетным данным следующих популяций животных: медведь, волк, лиса, выдра, соболь, колонок, лось, изюбрь, кабан, косуля, кабарга, белка, заяц.
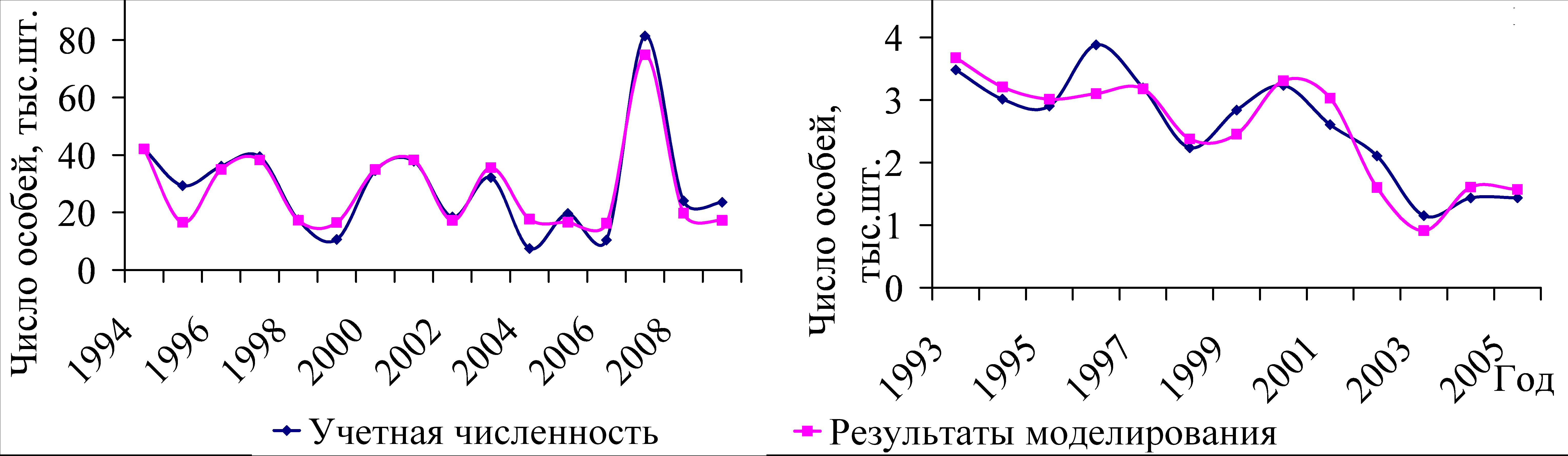
В § 4.2. на основе модифицированного варианта модели Рикера с учетом внешних факторов проведен анализ влияния факторов окружающей среды на динамику численности промысловых популяций. В частности, в пункте 4.2.1. было проанализировано влияние запасов кедра корейского на динамику численности популяции белки. В 4.2.2. представлен модельный анализ влияния высоты снежного покрова на динамику численности популяций копытных (лося, изюбря, кабана и косули). Показано, что колебания численности рассматриваемых копытных животных обусловлены негативным воздействием многоснежных зим, предшествующих размножению. На рис. 9 приведены графики учетной и модельной численности популяции белки и изюбря. Как видно из рис. 9, модель Рикера улавливает общие тенденции динамики численности и описывает основные всплески наблюдаемой численности.
 | |
| а) | б) |
Рис. 9. Данные учета и результаты моделирования динамики численности популяций а) белки в зависимости от запасов орехов кедра корейского в ЕАО, и б) изюбря в зависимости от высоты снежного покрова в госпромхозе «Облученский» ЕАО
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ РАБОТЫ:
- Показано, что тип популяционной динамики (переход к равновесным состояниям или регулярным циклам, квазипериодические или хаотические колебания) существенно зависит от соотношения параметров, характеризующих интенсивность рождаемости, выживаемость особей разных возрастных групп, и типа плотностно-зависимого лимитирования численности.
- Увеличение средней индивидуальной приспособленности особей (т.е. увеличение коэффициентов плодовитости и выживаемости) в моделях экологически лимитированных популяций может приводить к потере устойчивости и возникновению хаотических аттракторов, структура и размерность которых меняются при изменении параметров модели. Половая асимметричность коэффициентов выживаемости способствует увеличению размерности аттракторов.
- Показана возможность появления хаотических режимов динамики численности при увеличении репродуктивных потенций самцов (например, при переходе к полигамному характеру размножения и при уменьшении доли самцов, необходимой для успешного воспроизводства популяции).
- Показана возможность хаотизации популяционной динамики для видов с низкой плодовитостью, в случае, когда регуляция роста численности осуществляется путем снижения выживаемости неполовозрелых самцов с ростом численности пополнения популяции.
- Решена задача оптимизации равновесного промысла для двухвозрастной популяции при плотностном лимитировании молоди. Показано, что оптимальным является изъятие из одного возрастного класса, а какого именно определяется значениями популяционных параметров и соотношением цен. Получены аналитические формулы для расчета оптимальных равновесных долей изъятия и значений численностей, обеспечивающих максимальный прирост популяции.
- Показано, что промысел из двухвозрастной популяции с постоянной оптимальной равновесной долей изъятия при определенных значениях популяционных параметров приводит к колебаниям численности. Стабилизация динамики системы происходит при стратегии промысла, основанной в регулярном изъятии излишка численности над значением, соответствующего величине максимального прироста популяции.
- Показано, что увеличение коэффициента, характеризующего интенсивность рождаемости, и коэффициента выживаемости взрослых самок, а также уменьшение величины, характеризующей зависимость рождаемости от соотношения полов, приводят к увеличению значения оптимальных долей промыслового изъятия из трехкомпонентной популяции. Однако изъятие на максимальном уровне весьма опасно для популяции, поскольку небольшое снижение интенсивности рождаемости или выживаемости самок приводит в этом случае к быстрому снижению численности популяции вплоть до ее полного вырождения.
8. Выполнена оценка параметров динамических моделей (в том числе и модифицированных вариантов с учетом влияния внешних факторов) для описания поведения численности охотничье-промысловых видов млекопитающих, обитающих на территории Среднего Приамурья. Для каждого вида рассчитаны оптимальные в данных условиях значения численности и оптимальные квоты изъятия для территории Еврейской Автономной области.
Основные результаты и выводы настоящей диссертационной работы опубликованы. Ниже приведены основные публикации по теме диссертации.
Публикации в журналах, входящих в Перечень ВАК РФ:
- Ревуцкая, О.Л., Фрисман, Е.Я. Математическая модель динамики численности популяции с возрастной и половой структурой // Известия Самарского научного центра РАН. 2009. T.11, №1(7). С. 1588-1595.
- Фрисман, Е.Я., Ревуцкая, О.Л., Неверова, Г.П. Сложные режимы динамики численности популяции с возрастной и половой структурой // Доклады Академии наук. 2010. Т. 431, № 6. С. 844-848.
- Фрисман, Е.Я., Неверова, Г.П., Ревуцкая, О.Л., Кулаков, М.П. Режимы динамики модели двухвозрастной популяции // Изв. вузов «ПНД». 2010. Т. 18, № 2. С. 111-130.
- Фрисман, Е.Я., Ревуцкая, О.Л., Неверова, Г.П. Моделирование динамики лимитированной популяции с возрастной и половой структурой // Математическое моделирование. 2010. Т. 22, № 11. С. 65-78.
- Frisman, E.Ya., Neverova, G.P., Revutskaya, O.L. Complex Dynamics of the Population with a Simple Age Structure // Ecological Modelling. 2011. V. 222. Р. 1943-1950.
Статьи в научных сборниках и периодических научных изданиях:
- Фрисман, Е.Я., Ревуцкая, О.Л., Неверова, Г.П. Анализ популяционной динамики промысловых млекопитающих Среднего Приамурья России: математическое моделирование и оценка ресурсного потенциала // Биологические ресурсы Дальнего Востока: комплексный региональный проект ДВО РАН /под ред. Ю.Н. Журавлева. Москва: Товарищество научных изданий КМК, 2007. С.184-202.
- Ревуцкая, О.Л., Неверова, Г.П., Фрисман, Е.Я. Оценка оптимального промыслового изъятия охотничьих животных на территории Среднего Приамурья России // Региональные проблемы. 2008. № 9. С. 34-38.
- Ревуцкая, О.Л. Анализ влияния высоты снежного покрова на динамику численности диких копытных (на примере Еврейской автономной области) // Региональные проблемы. 2009. № 12. С. 8-15.
- Ревуцкая, О.Л. Анализ влияния запасов корма на динамику численности популяции белки (на примере Еврейской автономной области) // Региональные проблемы. 2010. Т. 13, № 2. С. 37-44.
Публикации в материалах научных мероприятий:
- Frisman, E. Ya., Revutskaya O. L., Neverova, G. P. Population Dynamics of Hunting Mammals in Russian Middle Priamurye: Mathematical Modeling and Estimation of Resource potential // International Union of Game Biologist XXVIII Congress, August 13-18, 2007, Uppsala (Sweden). Uppsala, 2007. P. 129.
- Revutskaya, O., Neverova, G., Frisman, E. Dynamics modes of a number in density-dependent two-age-structured model // 6th European Nonlinear Dynamics Conference (ENOC-2008), June 30–July 4, 2008, Saint-Petersburg (Russia). Saint-Petersburg, 2008. P.107.
- Revutskaya, O.L., Frisman, E.Y. Model analysis of the forage reserve and the snow depth influence on the wild boar population dynamics in the Russian Middle Priamurye // 8th International Symposium on Wild Boar and Other Suids. September 1-4, York: The Food and Environment Research Agency, UK. York, 2010. P. 28-29.
- Ревуцкая, О.Л. Определение оптимального промыслового изъятия для двухвозрастной лимитированной популяции // Доклады III международной конференции "Математическая биология и биоинформатика", 10-15 октября 2010 г. Пущино. Москва: УРАН ИМПБ РАН, 2010. С. 210-211.
- Revutskaya, O.L., Neverova, G.P., Frisman, E.Y. Dynamic modes in a discrete two-sex age-structured three-component population model // 7th European Conference on Ecological Modelling. 30 May -2 June 2011, Riva del Garda (Trento, Italy). P. 85-86.
Ревуцкая Оксана Леонидовна
Моделирование динамики численности популяции
с возрастной и половой структурой
и оптимизация промысла
Автореферат
| Подписано к печати 11.10.2011 Формат 60х84/16. | Усл. п.л. 1.2. Тираж 100. | Уч-изд л. 1.0. Заказ 34/2011 |
Издано ИКАРП ДВО РАН, г. Биробиджан, ул. Шолом-Алейхема, 4.
Отпечатано типографией Дальневосточной государственной социально-гуманитарной академии по адресу: г. Биробиджан,
ул. Широкая 70-а, к. 115, тел. 4-01-46

