Исследование сложных процессов методом дта

Вид материала

Исследование

Подобный материал:

• Лабораторный комплекс нтц-23. 000 Электрические машины Исследование силового двухобмоточного, 34.47kb.
• Журнал “Информационные технологии”, 2010г., (в печати), 44.56kb.
• Кодирование методом Хаффмана и Фано-Шеннона: демонстрация, исследование, 52.16kb.
• О новом поколении компьютерных лабораторных практикумов по электрофизике, 9.71kb.
• Конспект урока по Информатике и икт в 9 классе Тема: «Построение и исследование физических, 69.13kb.
• Кузнецова Елена Сергеевна г. Сергиев Посад 2009 г. Содержание Введение глава I. Теоретическое, 602.57kb.
• Ix международная научная конференция «химия твердого тела: монокристаллы, наноматериалы,, 81.75kb.
• Исследование переходных процессов в замкнутых нелинейных системах управления 111, 347.96kb.
• Исследование системы «пласт-скважина» методом высокочастотных фильтрационных волн давления, 150.73kb.
• «Исследование социально-экономических и политических процессов», 46.76kb.

УДК 546.175

ИССЛЕДОВАНИЕ СЛОЖНЫХ ПРОЦЕССОВ МЕТОДОМ ДТА

Клякин Г.Ф., Таранушич В.А., Хоружий И.А.

Южно-Российский государственный технический университет

г. Новочеркасск.


Большинство химических процессов, протекающих при нагревании вещества и регистрируемых при помощи дифференциально-термического анализа (ДТА), состоят из ряда параллельных и последовательных реакций, в результате наложения которых получается сложная кривая, весьма трудная для анализа. Одним из следствий наложения реакций является сдвиг температуры пиков, которая служит одним из основных параметров, фиксируемых ДТА. Другим следствием является невозможность расчета кинетических и термодинамических характеристик пиков по кривым ДТА.

Разработан метод анализа сложных кривых ДТА, записанных в системе координат температура образца – разность температур образца и эталона, в основе которого лежит моделирование кривой ДТА путем сложения моделей простых процессов.

В основе метода лежит уравнение, предложенное в работе [1] как математическая модель для описания участка кривой ДТА, характеризующегося экстремальным отклонением от базисной линии:

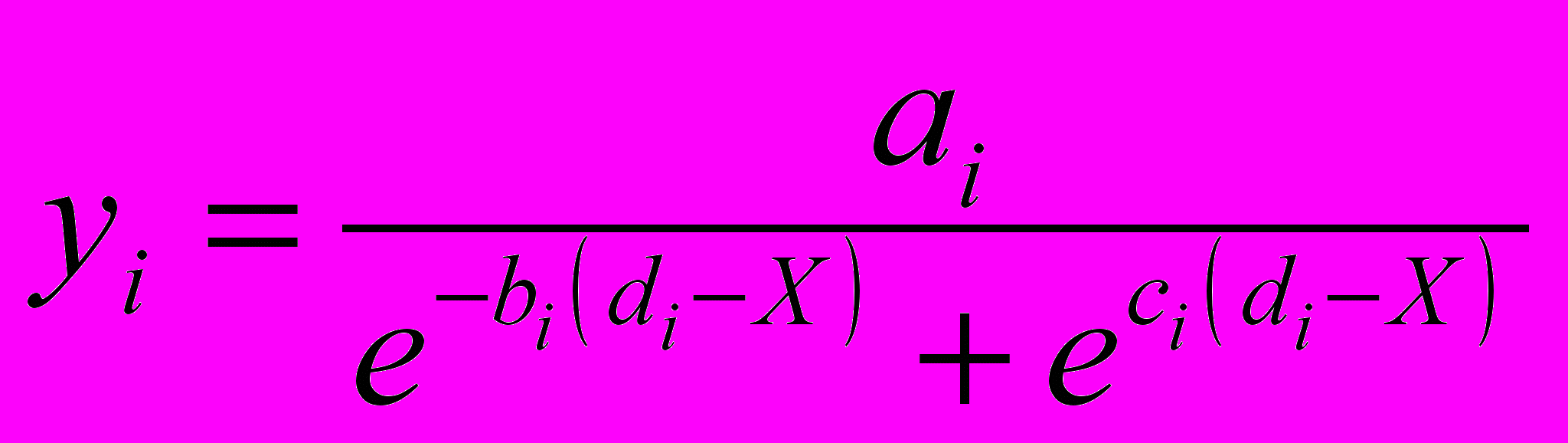(1)

где: а_i – величина, характеризующая высоту пика, b_i и с_i – величины, характеризующие форму соответственно переднего и заднего фронтов пика, d_i – величина, соответствующая положению вершины пика на оси абсцисс. Подобное уравнение применялось также для аппроксимации опытных данных, образующих прямую линию с выступом, например вязкости растворов разбавленных солей, а также теплопроводности разбавленных растворов глицерина [2].

Для описания группы процессов, протекающих при дифференциально-термическом анализе вещества, использовали следующее уравнение:

Y = y_i + y_i+1 + …y_n (2)

где i – порядковый номер простого процесса, изменяющийся от 1 до значения общего количества предполагаемых простых процессов (n).

Расчет модели осуществляли методом наименьших квадратов с использованием итерационной процедуры в среде Mathcad.

Обработка термограмм ДТА состоит из нескольких стадий:

1. Сканирование термограммы ДТА.
   
2. Проведение базисной линии.
   
3. Оцифровка выбранных участков кривой ДТА.
   
4. Визуальный подбор начальных значений коэффициентов модели.
   
5. Итерационная процедура подгонки коэффициентов модели.
   

Предлагаемым методом был исследован процесс термического разложения нитрата аммония марки ХЧ. Скорость подъема температуры составляла 5^оС/мин. при навеске около 0,1 г. Запись кривых производилась на двухкоординатном самопишущем потенциометре.

На рис. 1 в координатах температура (t, ^оС) - размер (l, мм) представлена часть термограммы ДТА нитрата аммония от плавления до полного разложения, и результат ее моделирования. Результирующая кривая модели представлена сплошной линией с расположенными на ней экспериментальными точками.



Рис.1. Модель кривой ДТА


Как следует из рисунка, процесс экзотермического разложения нитрата аммония носит двустадийный характер (кривые 2 и 3) и начинается при температуре около 220^оС на некотором расстоянии от пика плавления (кривая 1). Экзотермические реакции протекают параллельно. При температуре около 240^оС становится заметным эндотермический процесс разложения жидкой конденсированной фазы (кривая 4), при этом начинается «кипение» расплава.

Литературные данные [3] свидетельствуют о четырех основных реакциях, имеющих место при термическом разложении нитрата аммония: эндотермическая реакция распада конденсированной фазы на аммиак и азотную кислоту, экзотермические процессы взаимодействия молекул N₂O₅ и HNO₃ c ионом NH₄⁺ и протекающий только в присутствии большого избытка азотной кислоты распад N₂O₅

Энергии активации, рассчитанные по модельным кривым, для экзотермических процессов 2 и 3 соответственно равны 140 кДж/моль и 111 кДж/моль. По литературным данным [3] энергии активации процессов взаимодействия HNO₃ и N₂O₅ с ионом аммония, определенные по данным кинетических экспериментов, соответственно составляют 126 кДж/моль и 101 кДж/моль, что позволяет с большой долей вероятности идентифицировать полученные модельные эффекты.

Реакция (кривая 3) заканчивается значительно раньше реакции, моделируемой кривой 2, что можно объяснить тем, что в процессе термораспада нитрата аммония, по мере накопления воды, реакция окисления иона аммония пентоксидом азота затухает и дальнейшее тепловыделение обусловливается взаимодействием между ионом аммония и HNO₃.

Интересно отметить несовпадение температур, соответствующих вершинам пиков 2 и 4, что создает видимость прекращения реакции экзотермического распада до наступления полного израсходования вещества. Это явление может иметь место в том случае, когда в результате усиливающегося «кипения» происходит вынос реагирующих компонентов из расплава, экзотермические процессы протекают преимущественно в газовой фазе и не регистрируются термопарой.


Литература.

1. Горшков B.С., Тимашев В.В, Савельев В.Г. Методы физико-химического анализа вяжущих веществ. – М.: Высш. школа, 1981. - С. 15
   
2. Батунер Л.М., Позин М.Е. Математические методы в химической технике. – М.: Химия, 1968, - С. 733.
   
3. Манелис Г.Б., Назин Г.М., Рубцов Ю.И., Струнин В.А. Термическое разложение и горение взрывчатых веществ и порохов. – М.:Наука, 1996. с.116.