Журнал “Информационные технологии”, 2010г., (в печати)

Вид материала

Документы

Содержание Ключевые слова Постановка задачи Численный метод Petrov I. B., Kvasov I. E., Favorskaya A. V., Sannikov A. V.

Подобный материал:

• Название Предмет Направление, 921.62kb.
• Научно-методический журнал издается при участии, 1713.39kb.
• Международная конференция «Информационные технологии в образовании и науке», 86.4kb.
• Интернет-Университет Информационных Технологий, 444.14kb.
• Программа «информатика и икт (информационные и коммуникационные технологии)», 827.46kb.
• Программа «информатика и икт (информационные и коммуникационные технологии)», 443.93kb.
• Программа государственного экзамена по специальности: 230201. 65 «Информационные системы, 450.31kb.
• Межпредметные связи на урок, 42.95kb.
• Направление 230400 «Информационные системы и технологии», 20.25kb.
• V международная научно-практическая конференция www objectsystems, 108.28kb.

Журнал “Информационные технологии”, 2010г., (в печати)

УДК 519.63

И. Б. Петров, доктор физ.- мат. наук, проф., зав. каф.,
И. Е. Квасов, аспирант, А. В. Фаворская, студентка,
А. В. Санников, студент, Московский физико-технический институт (государственный университет), e-mail: petrov@mipt.ru

Компьютерное моделирование пространственных динамических процессов сеточно-характеристическим методом
на неструктурированных тетраэдральных сетках

Целью данной работы является численное моделирование сложных пространственных динамических процессов в гетерогенных средах сеточно-характеристическим методом на неструктурированных тетраэдральных сетках с использованием интерполяции высоких порядков. Данный метод имеет большую общность и пригоден для подробного исследования волновой картины.

Ключевые слова: сеточно-характеристический метод, тетраэдральные сетки, интерполяция высоких порядков, сейсмология, сейсморазведка.

Введение

В работе предложены усовершенствованные методы пространственного численного моделирования распространения волн в сложных гетерогенных средах. Эти методы применимы и для геологической среды с большим количеством полостей и трещин, расположенных без строгих закономерностей и имеющих различную форму. При такой постановке трехмерных задач оптимальным является использование неструктурированных тетраэдральных сеток.

Так как система уравнений математической модели состояния сплошной линейно-упругой среды [1] является гиперболической и требуется аккуратный расчет волновых процессов, сообразно применения именно сеточно-характеристического метода [2] с использованием интерполяции [3] высоких порядков. Примеры использования сеточно-характеристического метода с квадратичной интерполяцией с ограничителем на неструктурированных треугольных сетках для решения задач сейсморазведки можно найти в [4 – 6].

Постановка задачи

Согласно [1, 6] состояние бесконечно малого объема сплошной линейно-упругой среды подчиняется следующим уравнениям:

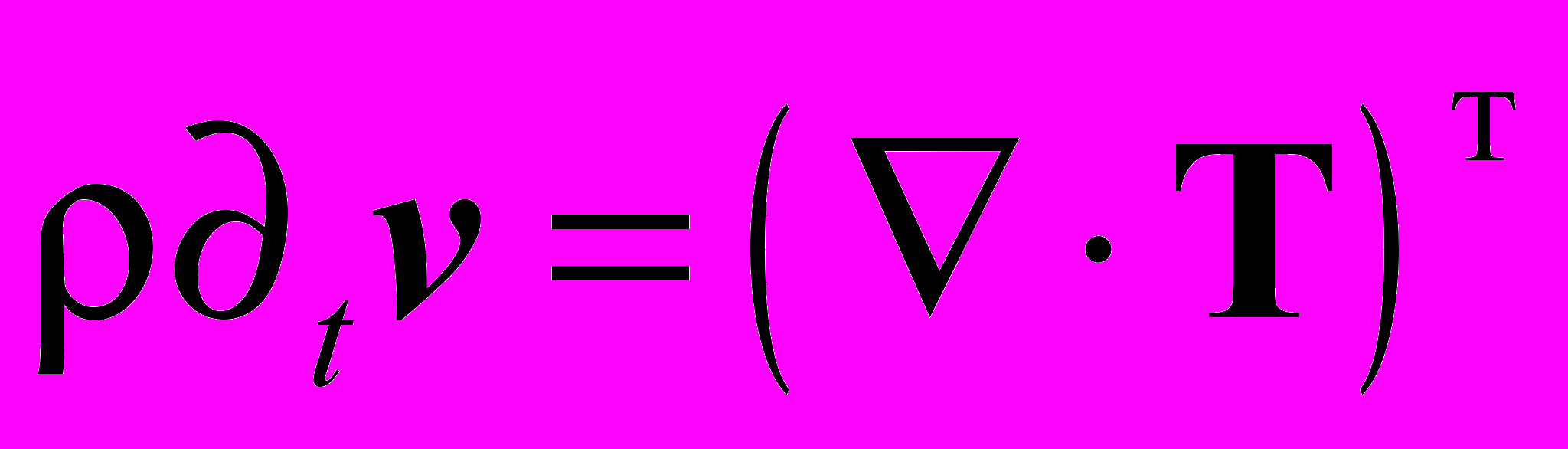, (1)

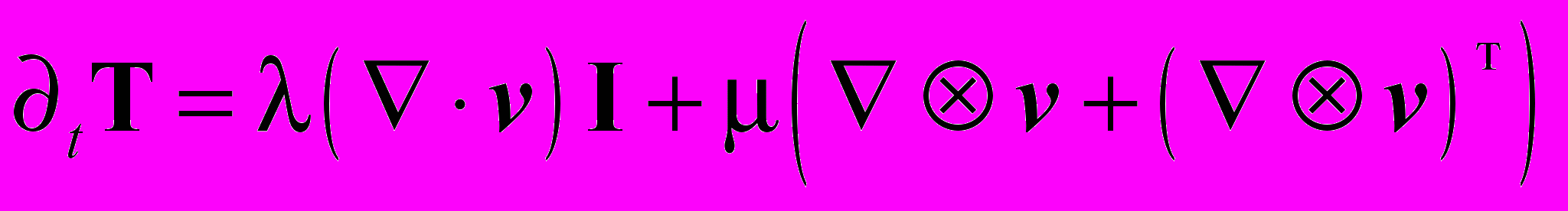. (2)

Уравнение (1) является локальным уравнением движения. В нем – плотность материала, 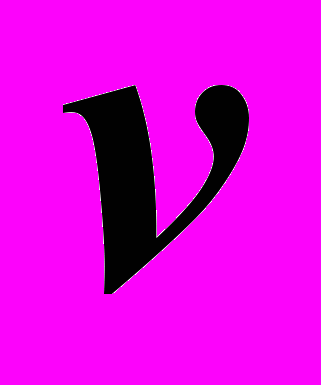– скорость движения, – тензор напряжений Коши, являющийся симметричным в силу закона парности касательных напряжений. Уравнение (2) выводится из закона Гука путем дифференцированя по времени. В нем 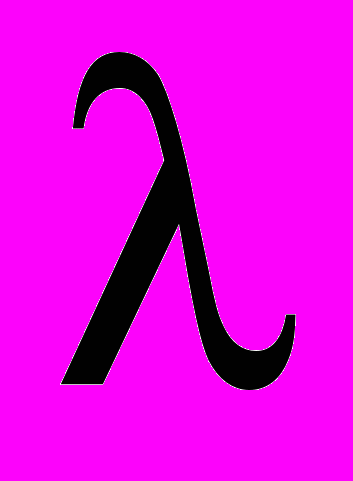, 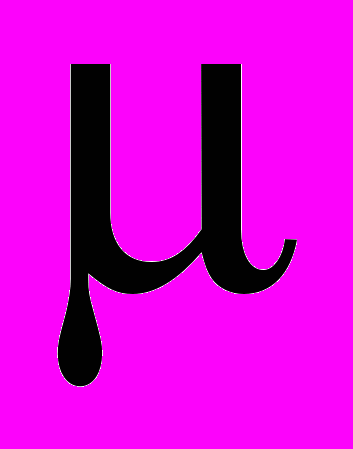– параметры Ляме, определяющие свойства упругого материала.

В (1), (2) использованы следующие обозначения:

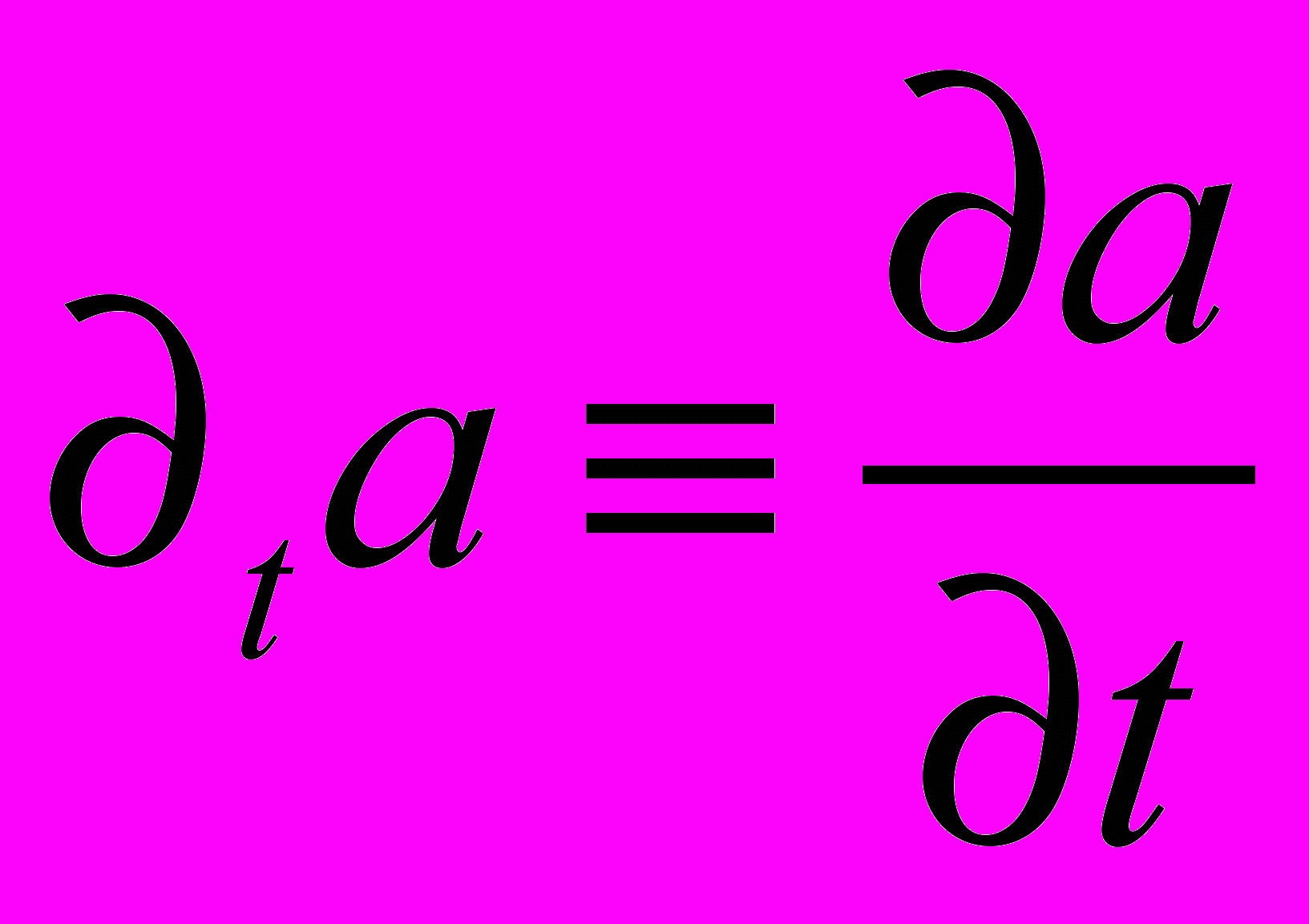– частная производная поля по ;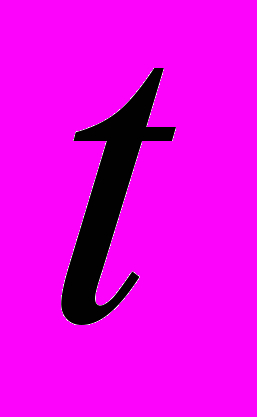

– тензорное произведение векторов и , .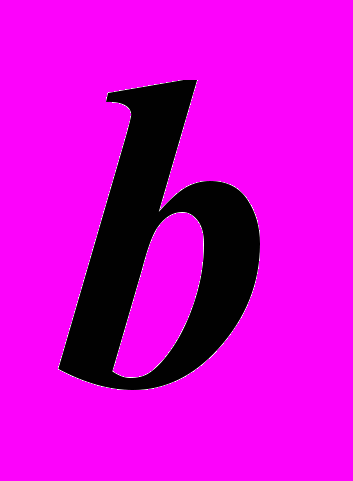

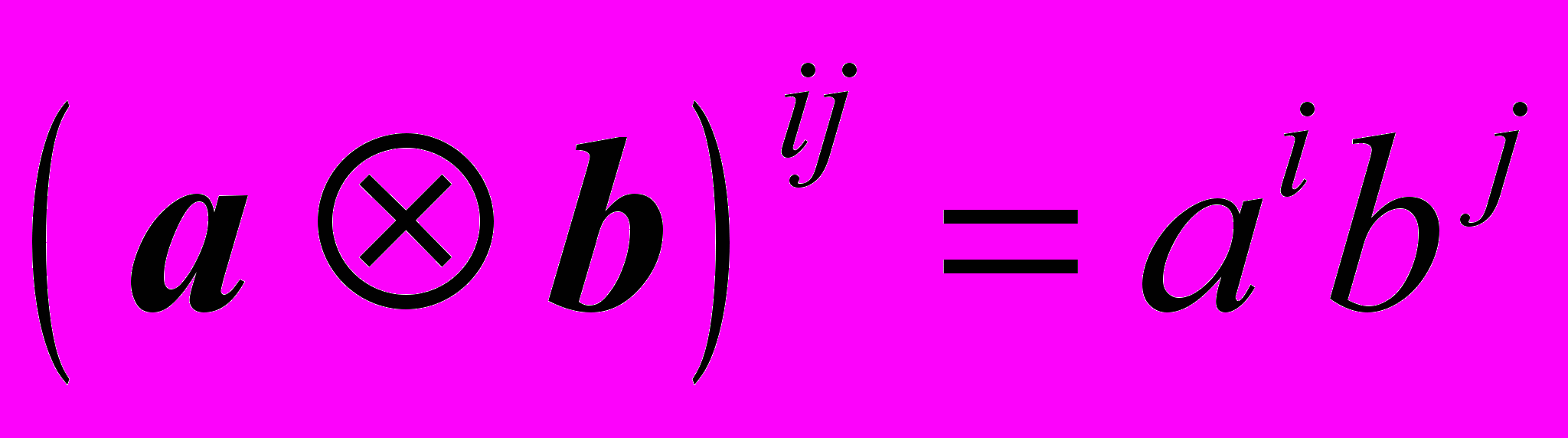Численный метод

Для численного решения системы (1), (2) используется сеточно-характеристический метод на тетраэдральных сетках, позволяющий строить корректные численные алгоритмы для расчета граничных точек и точек, лежащих на поверхностях раздела сред.

Выбираются три произвольных направления, что обеспечивает изотропность метода, и вводится новая система координат 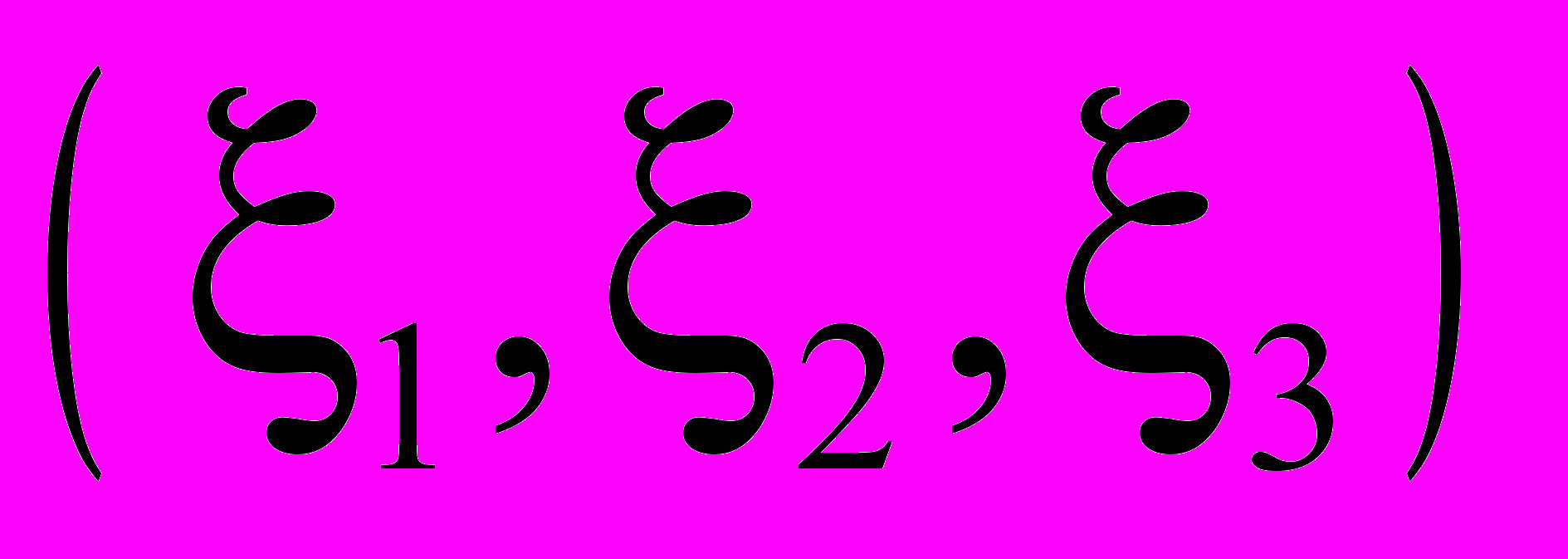. В ней систему (1), (2) можно представить в следующем виде

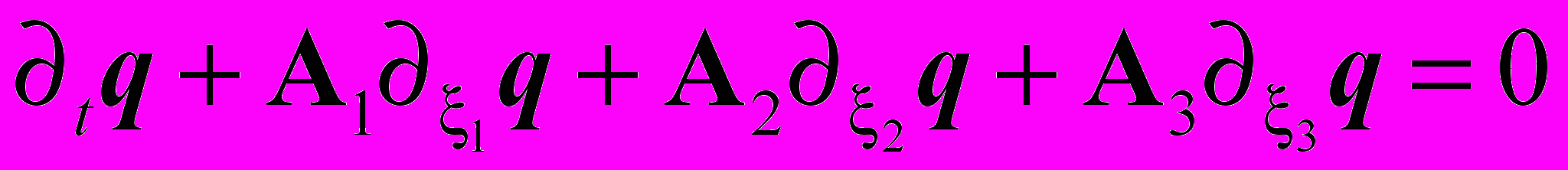(3)

В (3) под вектором понимается вектор, составленный из компонент трех скорости и шести компонент симметричного тензора напряжений.

Для каждой из трех систем вида

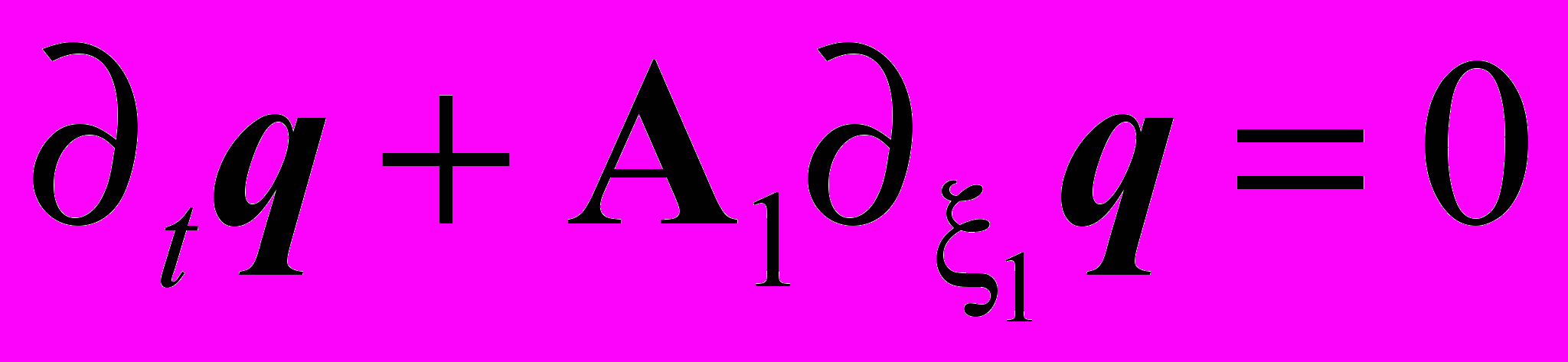(4)

справедливо следующее точное выражение

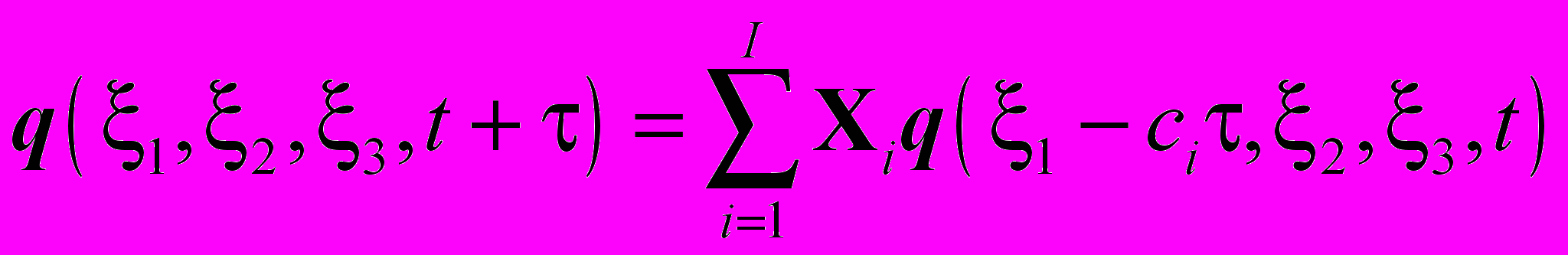(5)

где 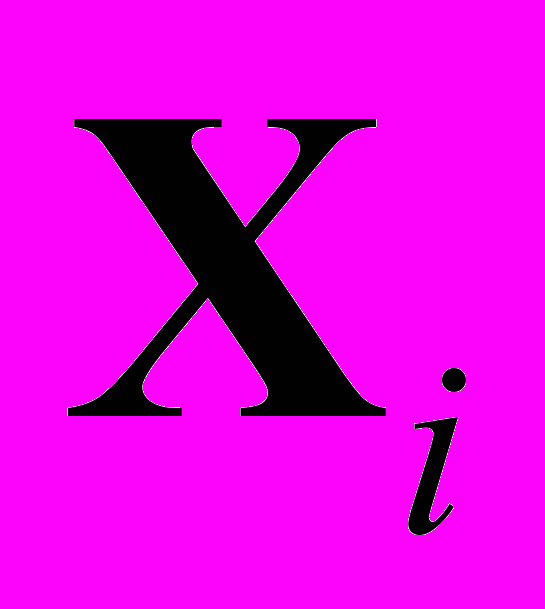– некие матрицы, выражающиеся через компоненты матрицы , 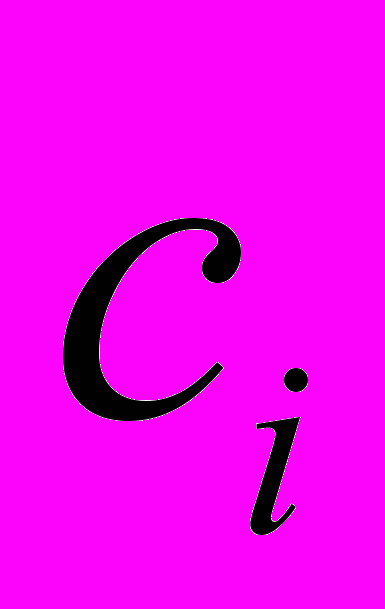– собственные числа матрицы .

Используя в (5) интерполяцию высокого порядка и последовательно применяя формулы, аналогичные (5), для каждого из направлений 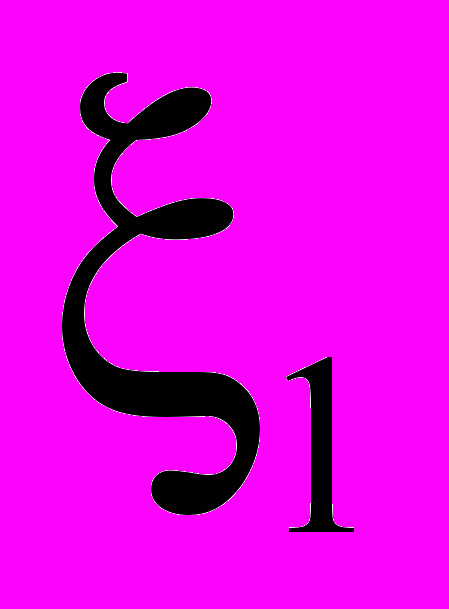, , 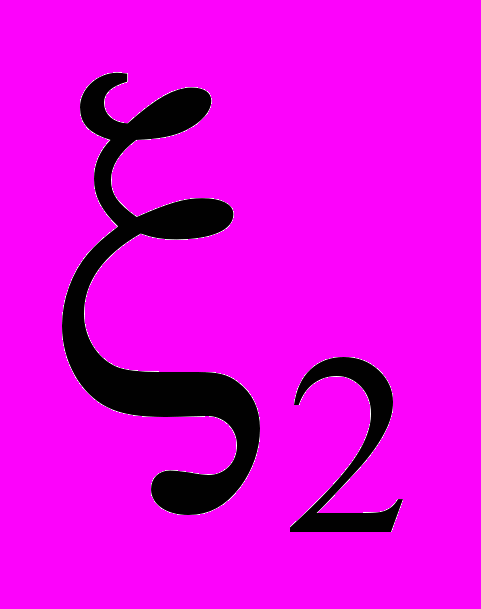, 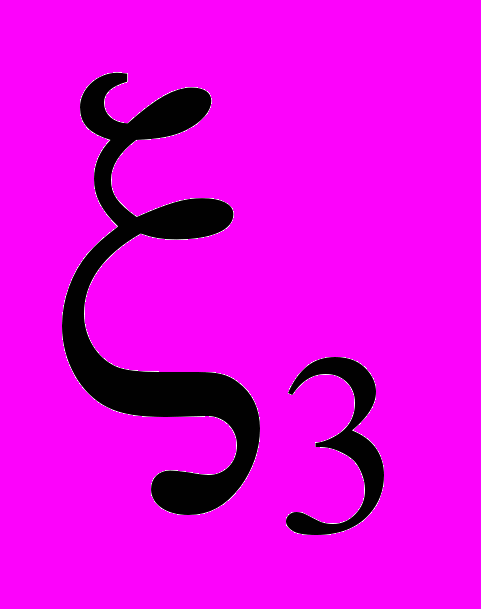получаем способ нахождения решения на следующем временном слое.

Результаты

Рассматриваются четыре задачи: моделирование торцевого удара в стенку куба, моделирование сферического взрыва в центре куба, моделирование приповерхностного сейсмического сферического взрыва в линейно-упругой среде и моделирование землетрясения в земной коре.

Во всех четырех случаях область интегрирования представляет собою куб, в котором сгенерирована тетраэдральная сетка. Использовалась интерполяция с ограничителем на основе кубической. На всех сторонах куба задано условие свободной границы.

На рис. 1 изображен результат моделирования торцевого удара в центр стенки куба, а на рис. 2 – сферического взрыва в центре куба. Сетка состоит из приблизительно 200 тысяч неразбитых на вспомогательные тетраэдров. Было сделано около 100 шагов по времени.

На рис. 3 представлен результат моделирования приповерхностного сейсмического взрыва, а на рис. 4 – результат моделирования землетрясения. Сетка состоит из приблизительно из 500 тысяч неразбитых тетраэдров. При моделировании приповерхностного взрыва было сделано 1200 шагов по времени, а при моделировании землетрясения – 700.

На всех рисунках цветом показан модуль скорости, стрелочками – ее направление. Видна картина возникающих волн: объемных сейсмических продольных и поперечных, а также поверхностных сейсмических волн.

Список использованной литературы

1. Кондауров В. И., Фортов В. Е. Основы термомеханики конденсированной среды. – М.: МФТИ, 2002.

2. Магомедов К. М., Холодов А. С. Сеточно-характеристические численные методы. – М.: Наука, 1988.

3. Петров И. Б., Лобанов А. И. Лекции по вычислительной математике. – М.: Интернет-Университет Информационных Технологий, 2006.

4. Квасов И. Е., Петров И. Б., Челноков Ф. Б. Расчет волновых процессов в неоднородных пространственных конструкциях // Сборник научных трудов МФТИ: Моделирование процессов обработки информации. – 2007. – С. 4 – 15.

5. Панкратов С. А., Мациевский Н. С., Петров И. Б. Численное моделирование деформационных динамических процессов в задачах сейсморазведки сеточно-характеристическим методом // Сборник научных трудов МФТИ: Моделирование процессов обработки информации. – 2007. – С. 30 – 37.

6. Челноков Ф. Б. Численное моделирование деформационных динамических процессов в средах со сложной структурой // Диссертация на соискание ученой степени кандидата физико-математических наук.


Petrov I. B., Kvasov I. E., Favorskaya A. V., Sannikov A. V. Computer modeling of spatial dynamic processes using grid-characteristic method on unstructured tetrahedral grids

The aim of this work is the numerical modeling to investigate complex spatial dynamic processes in heterogeneous environments with the help of grid-characteristic method on unstructured tetrahedral grids by using high-order interpolation. This method has great generality and is suitable for the detailed study of wave pattern.

Keywords: grid-characteristic method, tetrahedral grids, high-order interpolation, seismic exploration, seismology.

Список подрисуночных подписей

Рис. 1 Задача о торцевом ударе. Трехмерный случай.

Рис. 2 Задача о сферическом взрыве в центре куба. Трехмерный случай.

Рис. 3 Задача о приповерхностном сейсмическом сферическом взрыве. Трехмерный случай.

Рис. 4 Моделирование землетрясения. Трехмерный случай.


Иллюстрации




Рис. 1




Рис. 2




Рис. 3




Рис. 4