Учебная программа алгебра 7-9 классы Астана 2010

Вид материала

Программа

Содержание Учебная программа «Алгебра» для 7-9 классов общеобразовательной школы. – Астана, 2010. – 11 стр. Ii. базовое содержание учебного предмета Формулы сокращенного умножения (14 ч.). Алгебраические дроби (15 ч.). Приближенные значения (5 ч.). Частота и вероятность события (5 ч.). Квадратные корни (16 ч.). Анализ данных (4 ч.). Квадратичная функция (10 ч.) Квадратные неравенства (10 ч.). Уравнения, неравенства и их системы (16 ч.). Тригонометрические выражения (18 ч.). Прогрессии (12 ч.). Вероятность (6 ч.). к концу 8 класса Iv. особенности методической системы обучения

Подобный материал:

• Учебная программа музыка 5-6 классы Астана 2010, 211.13kb.
• Учебная программа музыка 1-4 классы, 321.24kb.
• Учебная программа география 6-9 классы Астана 2010, 359.66kb.
• Учебная программа изобразительное искусство 1-4 классы Астана 2010, 457.13kb.
• Учебная программа русская литература 5-9 классы Астана 2010, 687.44kb.
• Учебная программа география 10-11 классы общественно-гуманитарное направление, 164.75kb.
• Учебная программа география 10-11 классы естественно-математическое направление, 333.89kb.
• Учебная программа физика и астрономия 7-9 классы астана 2010, 365.06kb.
• Учебная программа Алгебра и начала анализа 10-11 классы естественно-математическое, 92.04kb.
• Приказ № от 2010 г. Рабочая программа Алгебра 8 класс Составил: учитель математики, 578.02kb.

Министерство образования и науки Республики Казахстан


Национальная академия образования имени Ы.Алтынсарина


Учебная программа


АЛГЕБРА


7-9 классы


Астана 2010


Министерство образования и науки Республики Казахстан


Национальная академия образования имени Ы.Алтынсарина


АЛГЕБРА


УЧЕБНАЯ ПРОГРАММА


для 7-9 классов общеобразовательной школы


Астана 2010


Утверждено Приказом Министра образования и науки Республики Казахстан от 09.07.2010 г. № 367.


Авторы программ: Чакликова С. Е., Алдибаева Т. А., Рустемова Н. И.

Учебная программа «Алгебра» для 7-9 классов общеобразовательной школы. – Астана, 2010. – 11 стр.

© Национальная академия образования

им.Ы.Алтынсарина, 2010


І. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА


Обучение алгебре в 7-9 классах представляет собой не завершающий, а промежуточный этап в системе математического образования каждого школьника. На базе, полученной учеником в 5-6 классах математической подготовки, строится его дальнейшее обучение.

При изучении курса алгебры учащиеся овладевают опреативными умениями и навыками, составляющими существеннное звено математического аппарата, который активно прменяется при решении как разнообразных математических, так и нематематических задач.

Курс алгебры строится вокруг четырех содержательных линий: числа и выражения, тождественные преобразования уравнения и неравенств, функций. Все эти линии развиваются в курсе не изолированно, а тесно переплетаются и взаимодействуют.

Цель: развитие математического мышления и устойчивых вычислительных умений в процессе изучения алгебры.

Основные задачи обучения алгебре:

- развитие умений выполнять арифметические действия над различными числами;

- овладение формально-оперативным алгебраическим аппаратом и умением применять его к решению практических и жизненных задач;

• формирование функционально-графических представлений для описания и анализа реальных зависимостей;
  
• ознакомление с основными способами представления и анализа статистических данных, со статистическими закономерностями в реальном мире, приобретение элементарных вероятностных представлений.
  

Учебная программа опирается на следующие основные принципы отбора содержания учебного материала и построения предмета: научности, непрерывности образования, деятельности, внутрипредметной и межпредметной интеграции, доступности, учета индивидуальных достижений учащихся.

Принцип научности предполагает создание необходимых условий для усвоения и оперирования школьниками научными терминами и понятиями в учебных ситуациях и повседневной жизни.

Принцип непрерывности обеспечивает непрерывное развитие всех содержательно-методических линий в курсах математики дошкольной подготовки, начальной, основной и старшей школы, означает преемственность между всеми уровнями образования на уровне методологии, содержания, методики и технологий обучения.

Принцип деятельности обеспечивает основу для осознанного и прочного усвоения математических понятий и способов действий. Позволяет «открывать» новые знания, посредством включения учащихся в активную учебно-познавательную деятельность, формировать самооценку и самоконтроль своих действий.

Принцип внутрипредметной интеграции обеспечивает органичное единство содержательных линий, как числа и выражения, уравнения и неравенства, функции, геометрические фигуры и измерение геометрических величин, элементы теории вероятностей и статистики, составляющих содержание математического образования.

Межпредметная интеграция позволяет формировать у учащихся целостную картину мира, помогает осознавать взаимосвязи различных учебных предметов. Важным компонентом данного принципа является обучение математическому языку как особому средству коммуникации.

Принцип доступности предполагает создание психологического комфорта в процессе изучения математики основной школы.

Принцип учета индивидуальных достижений учащихся предполагает использование заданий различного уровня трудности, самостоятельных, исследовательских и проектных работ, позволяет формировать личностно-значимые мотивы учения. У учителя есть возможность выбора оптимальных технологий обучения, учебных материалов и степени их адаптации в учебном процессе по достижению планируемых результатов, а также для организации различных видов деятельности (воспроизводящей, преобразующей, алгоритмической и творческой). Учебные материалы должны быть рассчитаны на обучающихся с разным уровнем знаний.

Принцип творчества предполагает формирование у обучающихся способности самостоятельно находить решение нестандартных, творческих, логических задач, «открывать» новые способы действий, умения создавать новое, находить нестандартные решения в жизненных ситуациях.

Объем учебной нагрузки по предмету «Алгебра» составляет:

7 класс: 2 часа в неделю, всего 68 часов;

8 класс: 2 часа в неделю, всего 68 часов;

9 класс: 2 часа в неделю, всего 68 часов.

Вариативный школьный компонент по алгебре в 7-9 классах предполагает организацию усвоения содержания программы на уровне стандарта, а также может быть направлен на углубленное изучение предмета. Углубленное изучение предмета может быть реализовано через расширение основного содержания курса алгебры в следующих направлениях: решение нестандартных и занимательных задач, задач повышенной трудности; приемы рационализации вычислений, делимость чисел; элементы теории вероятностей и статистики и др.

II. БАЗОВОЕ СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА


7 КЛ­АСС – 68 часов


Степень с натуральным и целым показателем (12 ч.). Степень с натуральным показателем и ее свойства. Функции y=x², y=x³ и их графики. Степень с целым показателем и ее свойства. Вычисления на калькуляторе степени числа и числа, обратного данному.


Одночлены и многочлены (12 ч.). Одночлен. Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители: вынесение общего множителя за скобки, способ группировки.


Формулы сокращенного умножения (14 ч.). Формулы (a-b)(a+b)=a²–b²; (a±b)²=a²±2ab+b^{2 ;} [(a±b) (a² ab+b²) = a³ ± b ³]. Применение формул сокращенного умножения к разложению многочленов на множители.


Алгебраические дроби (15 ч.). Алгебраическая дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. Преобразования рациональных алгебраических выражений. Функция y=k/x и и ее график.


Приближенные значения (5 ч.). Измерение величин. Абсолютная и относительная погрешности приближенного значения. Стандартный вид числа. Запись приближенных значений.


Частота и вероятность события (5 ч.). Случайное испытание. Случайные события. Виды случайных событий. Частота, вероятность случайного события.


Повторение. Решение задач (5 ч.).


8 КЛАСС – 68 часов


Квадратные корни (16 ч.). Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 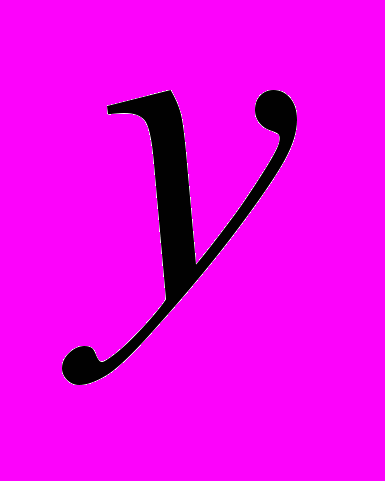=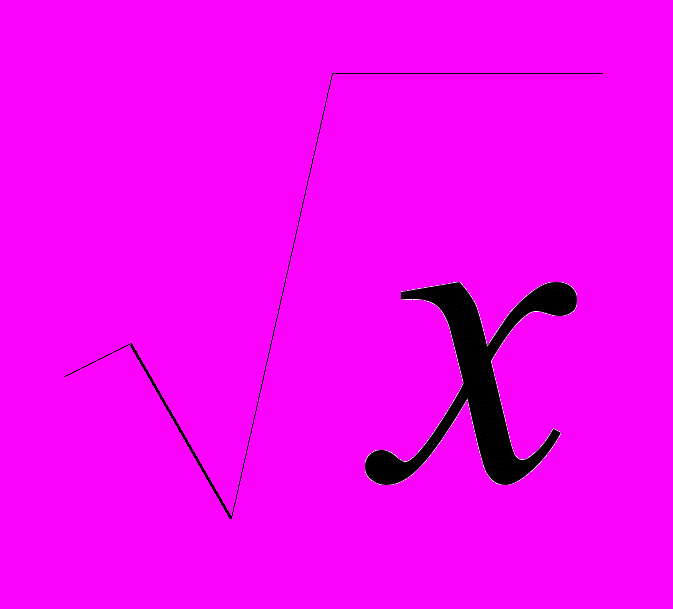, ее свойства и график.


Анализ данных (4 ч.). Группировка и анализ статистических данных. Отклонение от средней характеристики.


Квадратные уравнения (20 ч.). Квадратное уравнение и его корни. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям.


Квадратичная функция (10 ч.). Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Определение квадратичной функции. Функции у= х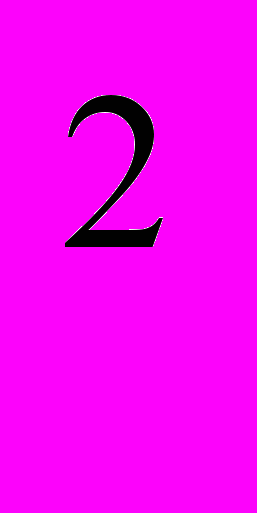, у= ах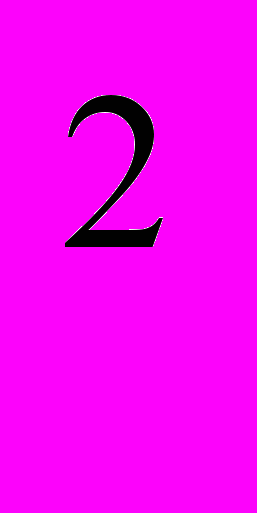, у= ах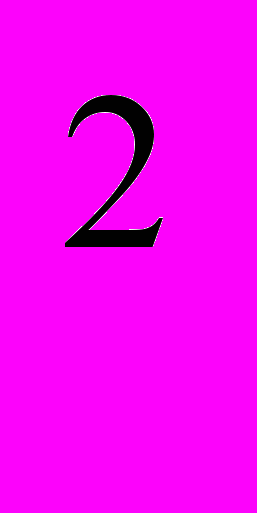+вх +с, их свойства и графики. Возрастание и убывание функции. Четные и нечетные функции. Простейшие преобразования графиков функций.


Квадратные неравенства (10 ч.). Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции.


Повторение (8 ч.).


9 КЛАСС – 68 часов


Уравнения, неравенства и их системы (16 ч.). Уравнение с двумя переменными и его график. Решение систем, содержащих одно уравнение первой, а другое второй степени. Решение текстовых задач методом составления систем. Решение систем неравенств с одной переменной.


Тригонометрические выражения (18 ч.). Радианное измерение углов. Синус, косинус, тангенс и котангенс произвольного угла. Основные тригонометрические тождества sin²х + cos²x=1, tgx=sinx/cosx, ctgx=cosx/sinx. Их применение в вычислениях и тождественных преобразованиях. Формулы приведения.


Прогрессии (12 ч.). Числовая последовательность. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов арифметической и геометрической прогрессий.


Вероятность (6 ч.). Способы нахождения вероятности. Графики реальных процессов.


Повторение (16 ч.).


ІІІ. ТРЕБОВАНИЯ К ЗНАНИЯМ, УМЕНИЯМ И НАВЫКАМ


Учащегося к концу 7 класса:

- записывает произведение одинаковых множителей в виде степени;

- упрощает числовые и буквенные выражения со степенями с натуральными показателями на основе свойств степени;

- упрощает числовые выражения со степенями с нулевым и целым отрицательным показателями на основе свойств степени;

- находит степень числа с помощью калькулятора;

- различает многочлены среди других буквенных выражений;

- находит степень данного многочлена;

- записывает многочлен с одной переменной по убывающим степеням переменной;

- находит сумму и разность двух многочленов;

- находить произведение двух многочленов;

- раскладывает многочлен на множители путем вынесения общего множителя за скобки;

- использует формулы сокращенного умножения для умножения многочленов, разложения многочлена на множители;

- различает алгебраические дроби среди других буквенных выражений;

- применяет основное свойство алгебраической дроби для сокращения дробей;

- находит сумму, разность, произведение и частное двух алгебраических дробей;

- выполняет тождественные преобразования несложных алгебраических выражений, содержащих многочлены и алгебраические дроби;

- понимает смысл основных форм записи приближенных значений (а=6,3±0,1; а6,45), производить прикидку и оценку результата вычислений;

- различает достоверные и невозможные события, приводить примеры;

- иллюстрирует понятие случайного события на конкретных примерах;

- находит в несложных случаях вероятность события.

к концу 8 класса:

- находит приближенные значения квадратных корней, используя таблицы, калькулятор;

- применяет свойства квадратных корней для упрощения числовых выражений;
- распознает уравнения второй степени с одной переменной;

- решает уравнения второй степени с одной переменной;

- решает несложные рациональные уравнения, сводящиеся к решению уравнения первой или второй степени;

- методом составления уравнения решает текстовые задачи, приводящие к несложным рациональным уравнениям;

- раскладывает квадратный трехчлен на множители;

- выделяет квадрат двучлена из квадратного трехчлена;

- строит график квадратичной функции;

- находит нули и промежутки знакопостоянства квадратичной функции;

- с помощью графика находит промежутки возрастания и убывания квадратичной функции;

- решает простейшие квадратные неравенства с одной переменной;


к концу 9 класса:

- решает несложные системы уравнений с двумя переменными (системы, в которых одно уравнение второй степени);

- решает текстовые задачи методом составления систем уравнений с двумя переменными;

- находит значения синуса, косинуса и тангенса с помощью калькулятора;

- находит значения синуса, косинуса и тангенса по заданному значению одного из них;

- применяет формулы приведения для нахождения значений синуса, косинуса и тангенса углов, сводящихся к табличным;

- выполняет преобразования несложных тригонометрических выражений, применяя основные тригонометрические тождества, формулы приведения;

- находит по заданной формуле n-ый член арифметической и геометрической прогрессии, сумму n первых членов.


IV. ОСОБЕННОСТИ МЕТОДИЧЕСКОЙ СИСТЕМЫ ОБУЧЕНИЯ

Содержание обучения распределено в соответствии с содержательными линиями курса алгебры и геометрии. Следует отметить некоторую особенность программы по алгебре 8-9 классов по сравнению с предыдущей (2000 г.). Так, тема «Показательная, логарифмическая, степенная и тригонометрические функции» из 9 класса перенесены в 10 и 11 классы, как было по традиционной программе в связи с уменьшением количества часов на алгебру в 9 классах. Формирование умений решать квадратные неравенства осуществляется с опорой на сведения о графике квадратичной функции. При наличии времени можно познакомить учащихся с решением неравенств методом интервалов. Курс алгебры 9 класса начинается с темы «Уравнения, неравенства и их системы». В этой теме завершается изучение рациональных уравнений с двумя переменными и их систем. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях.

В 8-9 классах получает дальнейшее развитие вероятностно-статистическая линия. В теме «Группировка и анализ статистических данных. Отклонение от средней характеристики» учащиеся знакомятся с анализом статистических данных, выраженных действительными числами, что имеет важное значение для обработки и анализа экспериментальных данных в курсах физики, химии, биологии. В курсе алгебры 9 класса систематизируются сведения о способах нахождения вероятности.

В 7 классе курс алгебры вводится впервые. Соответственно, дается понятие о математическом языке и модели, систематизируется понятие о координатной плоскости и координатной прямой, о масштабе, функции и их графики, свойства. Особенность курса алгебры 7-8 классов заключается в том, что здесь впервые вводятся такие понятия, как функция, алгебраическое выражение, одночлен, многочлен и т.д. Учебный материал данного курса алгебры построен так, чтобы формировать у школьников умение выполнять все арифметические действия с алгебраическими выражениями, преобразовывать их.

В программе поставлена задача развития и закрепления умений, сформированных к началу обучения в 7 классе, а также формирования новых вычислительных умений. Решение этой задачи занимает существенное место в курсе алгебры, где не обойтись без вычислений, при обработке выполнения алгоритмов тождественных преобразований, решения уравнений, неравенств, и прочих умений. Умения возводить в степень с целым показателем и извлекать квадратные корни, выполнять действия со степенями, приближенные вычисления формируются в 7-8 классах. Здесь же закладываются умения рационально организовывать вычислительный процесс, проверять правильность вычислений, производить прикидку результата.

Учащиеся в 7-8 классах осваивают те умения, которые часто используются не только при решении математических задач, но и при решении нематематических задач (в первую очередь смежных предметов). От формирования вышеназванных умений и навыков зависит успешность использования этих навыков в дальнейшем при изучении предметов естественно-математического цикла.

По теории вероятности и элементам статистики изучается частота и возможность случайных событий.

Цель обучения курсу алгебры заключается в усвоении аппарата решения уравнений и неравенств с использованием задач в качестве основного инструмента, подготовки к математическому моделированию, развитию функциональной грамотности. К концу данного цикла у учащихся должно быть сформированы навыки построения графиков функций, они должны иметь полное представление о функциях, иметь понятие о действительных числах.