Технология построения информационного и математического обеспечения систем автоматизированного управления движением судов на внутренних водных путях

Вид материала

Автореферат

Содержание Таблица 3. Транзитный грузооборот портов региона В пятой главе Таблица 4. Границы критической области для теста 2

Подобный материал:

• Математическое и информационное обеспечение мониторинга и управления движением судов, 217.22kb.
• Общая характеристика Актуальность темы исследования, 183.53kb.
• Методы построения радионавигационных полей для информационного обеспечения автоматизированных, 575.96kb.
• Типовая программа обучения судоводителей судов, поднадзорных государственной инспекции, 520.4kb.
• Санкт – Петербург, 721.71kb.
• Правила радиосвязи на внутренних водных путях российской федерации введены в действие, 652.54kb.
• Федерации решение, 81.23kb.
• Задачи и структура информационного обеспечения управления Унифицированные системы документации, 10.89kb.
• Рабочая программа итоговой государственной аттестации выпускников для специальности, 240.91kb.
• Правила радиосвязи на внутренних водных путях Российской Федерации. Департамент речного, 227.59kb.

Таблица 3. Транзитный грузооборот портов региона

Порты a-вывоз, б - ввоз		1996	1997	1998	1999
		Wтыс.т
Всего	А	2278	2048	4612	4784
	Б	1906	1607	1819	1437
Гданьск	А	354	159	2694	2841
	Б	17	49	196	203
Гдыня	А	248	158	314	207
	Б	471	334	216	1272
Щецин	А	1071	1233	1168	1264
	Б	613	667	727	670
Свиноустье	А	604	498	436	472
	Б	805	559	681	435

Стохастическая формализация динамики грузопотоков транспортного узла обусловлена необходимостью разработки математической модели продолжительности “жизненного цикла” (времени ожидания на рейде). В работе определены виды математических моделей и методы оценивания их параметров с учетом цензурирования выборок и альтернативности моделей.

В пятой главе исследованы вопросы управления информационными потоками в АСУ река-море политранспортного узла. Установлено, что использование вероятностной меры показателей эффективности работы АСУ обусловливает применение марковских моделей случайного процесса с дискретными состояниями и непрерывным временем. Показано, что процедура моделирования по этой схеме требует предварительного статистического обоснования на основе использования информационно-статистических методов. В связи с этим в работе поставлена и решена задача обнаружения “разладки” случайного пуассоновского процесса по первым наблюдениям. Задача обнаружения изменения свойств пуассоновского процесса по первым наблюдениям. Задача обнаружения изменения свойств пуассоновского процесса сформулирована как задача о различении двух статистических гипотез Н_О: разладки нет; Н₁: разладка есть.







Решение этой задачи позволило ввести две тестовые статистики

(45)

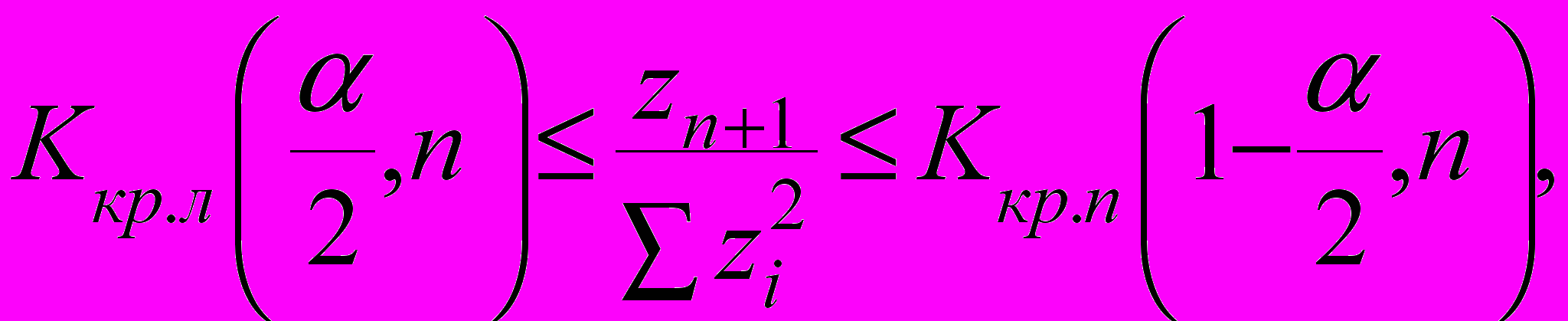(46)

где t_n – моменты появления случайного события (n=1,2,…),

z_i – стандартные нормальные случайные величины, определяемые по наблюдениям последовательности t1, t2,… tn, tn+1

Показано, что введенный в рассмотрение второй тест в силу его чувствительности к дисперсии, нормализованной случайной величины является критичным к тенденции вырождения пуассоновского потока в регулярный.

В работе определены законы распределения тестовых статистик и получены решающие правила для первого и второго тестов. Формула (45) по сути дела является решающим правилом. Границы критической области для второй тестовой статистики определялись численным методом с использованием ее закона распределения. Границы критической области для этого теста представлены в таблице 4. Введенные в рассмотрение тесты обнаружения разладки пуассоновского потока позволяют выявить момент изменения свойств случайной последовательности событий и перейти от пуассоновской модели “редких” событий к одной из ее модификаций. В качестве такой модификации в работе рассмотрено распределение Пуассона степени k, производящая функция которого имеет вид

(47)

Показано, что параметры этого распределения можно определить из следующей системы уравнений

(48)

где E[n] – математическое ожидание числа событий в единицу времени;

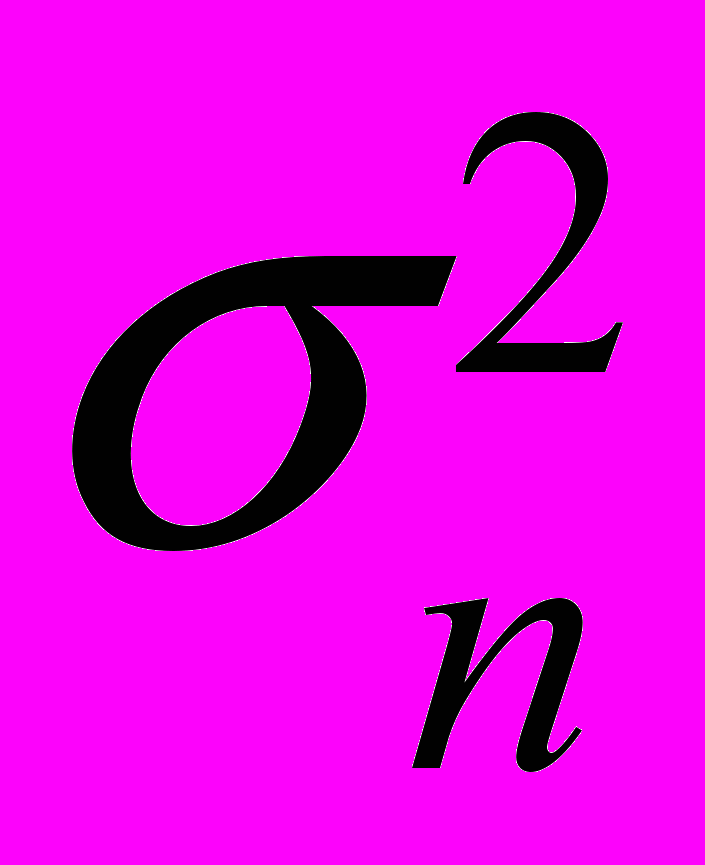–- дисперсия этой величины.

Таблица 4. Границы критической области для теста 2

n+1	β = 0,2		β = 0,3		β = 0,4
2	0,0273	51,49	0,0625	20,57	0,1153	10,79
3	0,0108	5,39	0,0251	3,07	0,0446	2,03
4	0,0068	2,36	0,0153	1,47	0,0278	1,03
5	0,0048	1,47	0,0109	0,95	0,0197	0,69
6	0,0038	1,07	0,0085	0,71	0,0155	0,52
7	0,0031	0,85	0,007	0,56	0,0128	0,42
8	0,0026	0,7	0,0058	0,47	0,0106	0,35
9	0,0023	0,6	0,0051	0,41	0,0092	0,3
10	0,002	0,53	0,0045	0,36	0,0082	0,26
11	0,0018	0,47	0,004	0,32	0,0073	0,24
12	0,0016	0,43	0,0037	0,29	0,0067	0,21
13	0,0015	0,39	0,0034	0,27	0,0059	0,18
14	0,0013	0,57	0,0031	0,24	0,0055	0,17
15	0,0012	0,34	0,0028	0,23	0,0051	0,16
16	0,0011	0,32	0,0026	0,21	0,0048	0,15

В случае непуассоновских потоков используется аппроксимация реальных потоков потоками Эрланга, что приводит к замене отдельных состояний (для которых поток событий не является пуассоновским ввиду наличия последействия) группами псевдосостояний с пуассоновскими потоками и, следовательно, экспоненциальным распределением времени перехода. Количество псевдосостояний равно порядку потока Эрланга. Достаточно детально моделировать динамику объектов и анализировать влияние вариаций потоков событий на оценку продолжительности существования системы может обеспечить метод, базирующийся на рандомизации интенсивности перехода λ и последующем осреднении вероятностей состояний систем с учетом маргинального (частного) распределения этого параметра.

С целью определения плотности маргинального распределения параметра λ формируется зависимость (интегральное уравнение Фредгольма 1 рода) с ядром, равным характеристической функции экспоненциального распределения 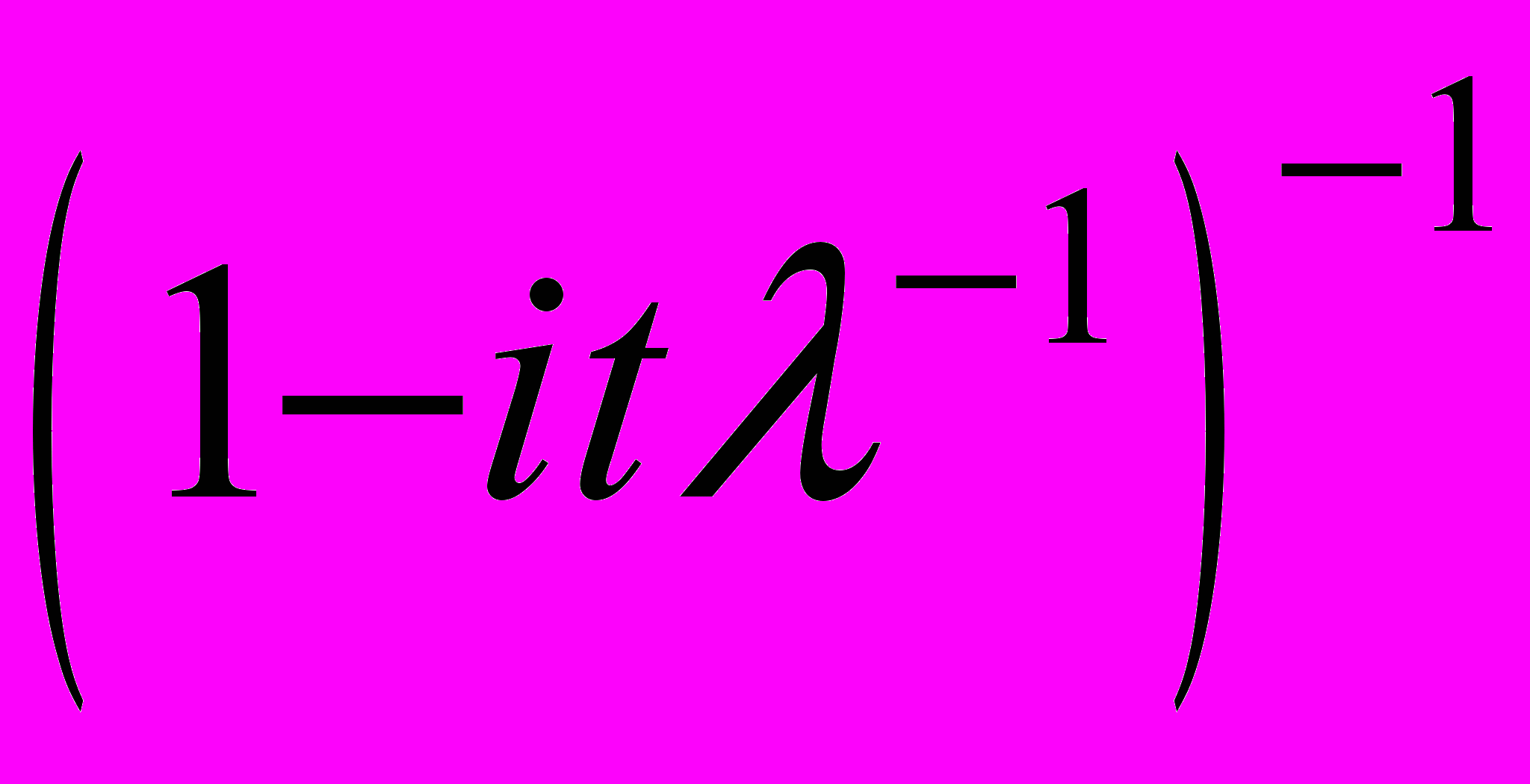и правой частью, равной характеристической функции времени возможного перехода между состояниями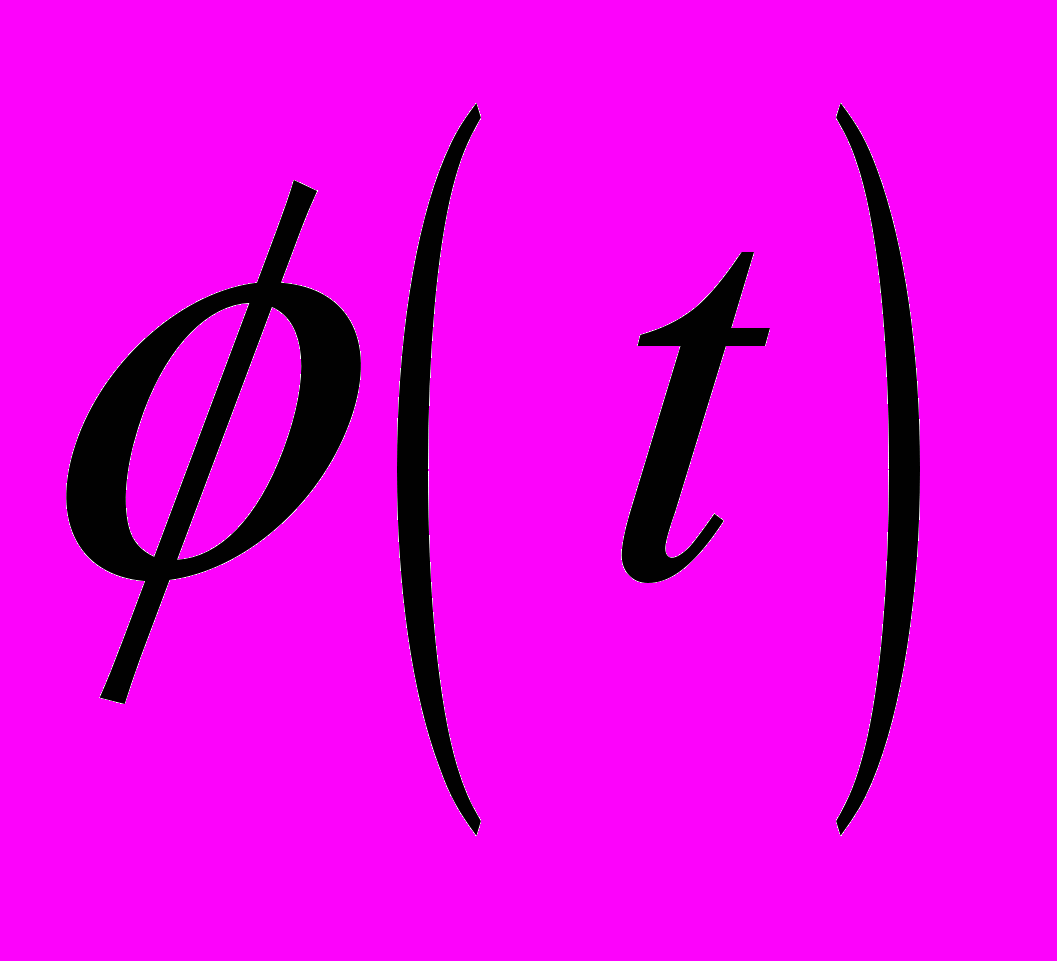

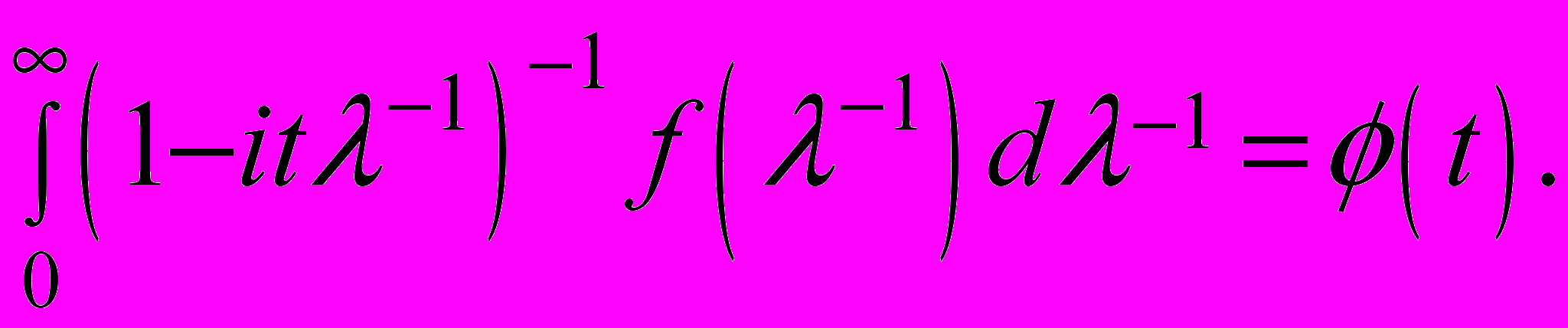(49)

Сущность предлагаемого подхода заключается в целенаправленном преобразовании потоков (непуассоновского в пуассоновской и обратно). Такое преобразование случайного потока событий связано с изменением положения точек на временной оси при сохранении их числа и сопровождается деформацией области существования потока (смещением, нестационарностью и др.) . Это обстоятельство открывает возможность построения математических моделей, описывающих эволюцию систем, для которых идеализированная схема в большинстве случаев не подходит. Естественно, что более точная аппроксимация механизма формирования случайного потока событий порождает более сложные математические модели. В работе проанализированы методы решения интегрального уравнения (48). Реализуемость методов проиллюстрирована решением ряда примеров.

Таким образом, показано, что сведение реального процесса инамики системы к процессу, допускающему построение математической модели и обеспечение соответствия показателей исходной и аппроксимирующей систем, можно добиться с помощью метода рандомизации интенсивности переходов, для которых потоки Эрланга редуцируются к потокам Пойа-Лундберга (потокам Эрланга со случайными интенсивностями переходов). Статистической эквивалентности исходной информации о времени пребывания системы в определенном состоянии можно достичь и на основе рандомизации числа псевдосостояний.

Для того, чтобы добиться статистической эквивалентности исходной информации о времени пребывания системы в определенном состоянии преобразованной случайной величины, необходимо найти закон распределения числа псевдосостояний (порядок потока Эрланга p_к). Очевидно, что такой закон распределения должен удовлетворить по определению характеристической функции следующему уравнению – дискретному аналогу уравнения (49)

(50)

где 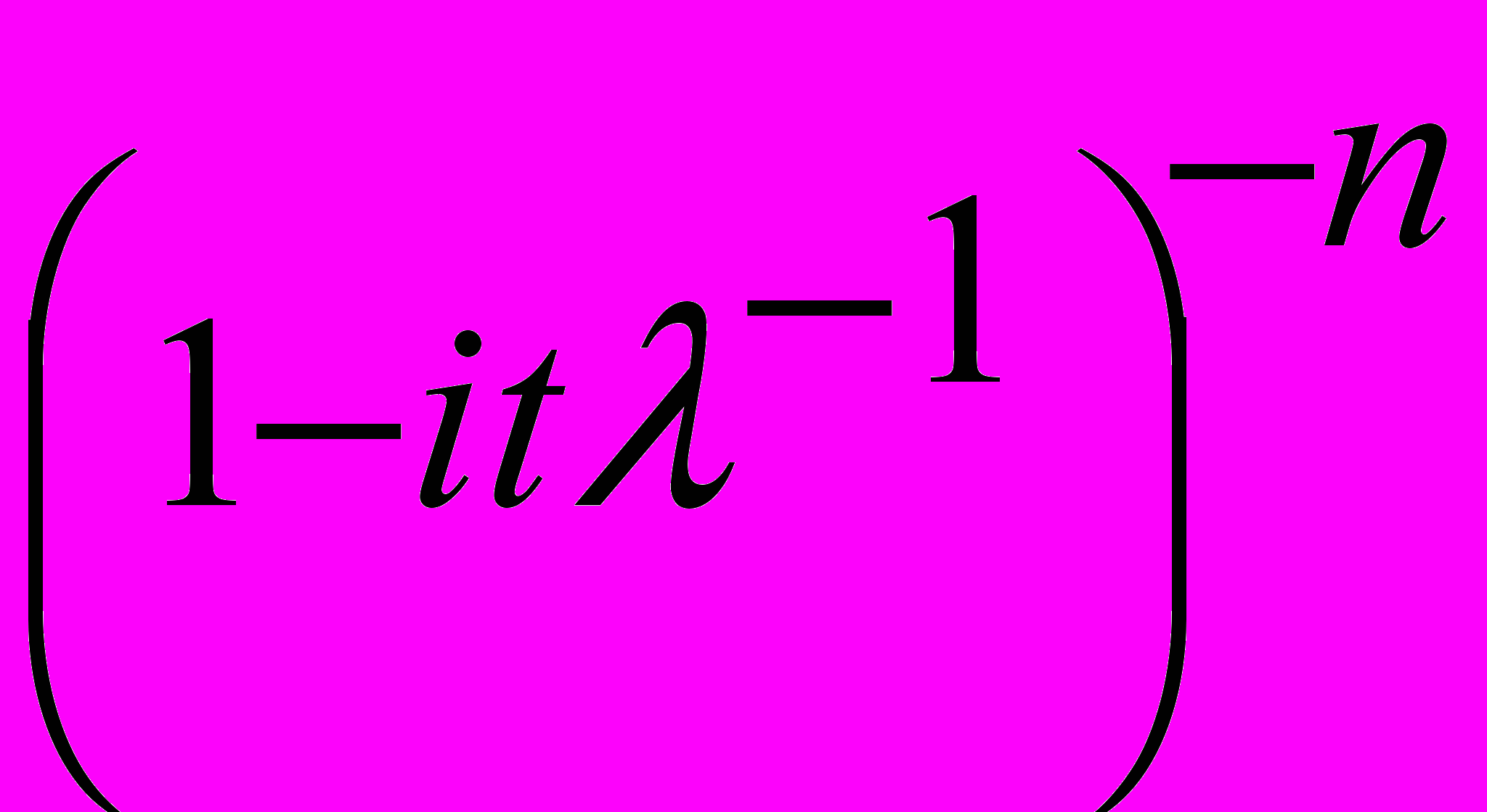–- характеристическая функция распределения Эрланга случайной величины T c целочисленным параметром формы n.

Используя метод моментов и постулируя вид закона распределения p_n, решение уравнения (50) можно приблизить с достаточно высокой степенью точности. Последовательно дифференцируя левую и правую части уравнения и используя свойства характеристических функций, можно составить следующую систему уравнений моментов

(51)

или в общем виде

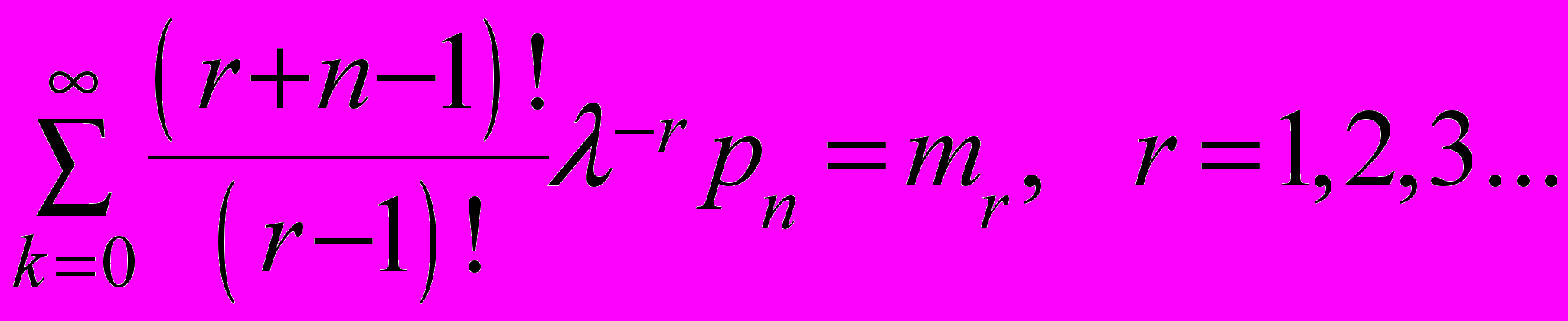(52)

Очевидно, что число используемых уравнений (51) должно определяться числом параметров закона распределения р_n. Так, например, для пуассоновского числа псевдосостояний n, определяемый закон

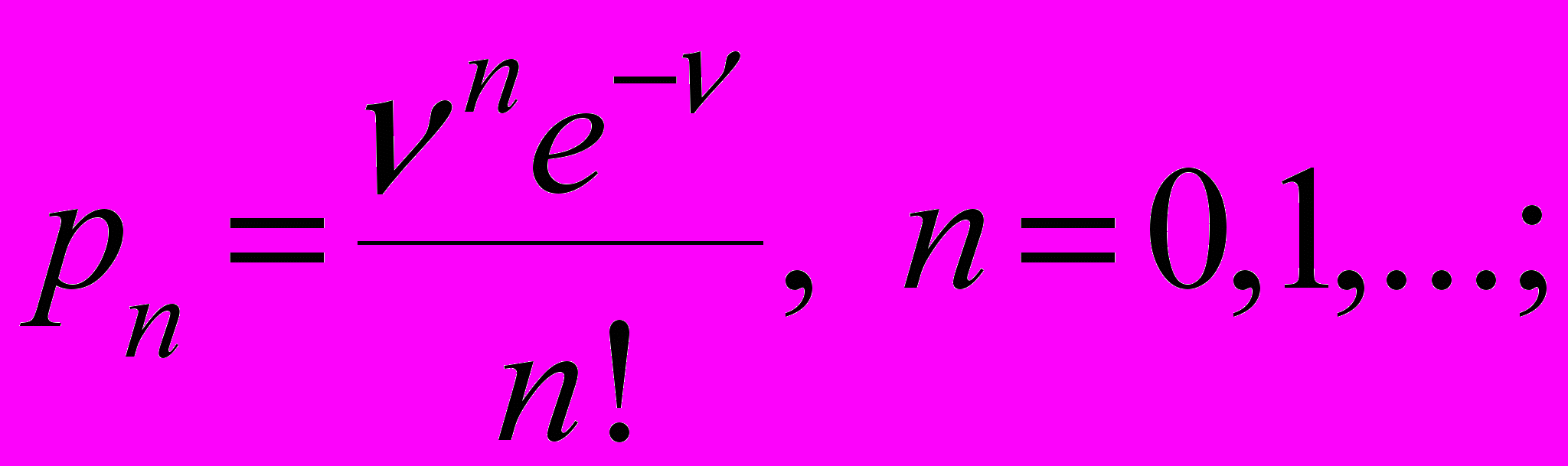(53)

где ν – среднее число псевдосостояний будет равно следующему выражению

(54)

где υ₁– коэффициент вариации;

интенсивность перехода

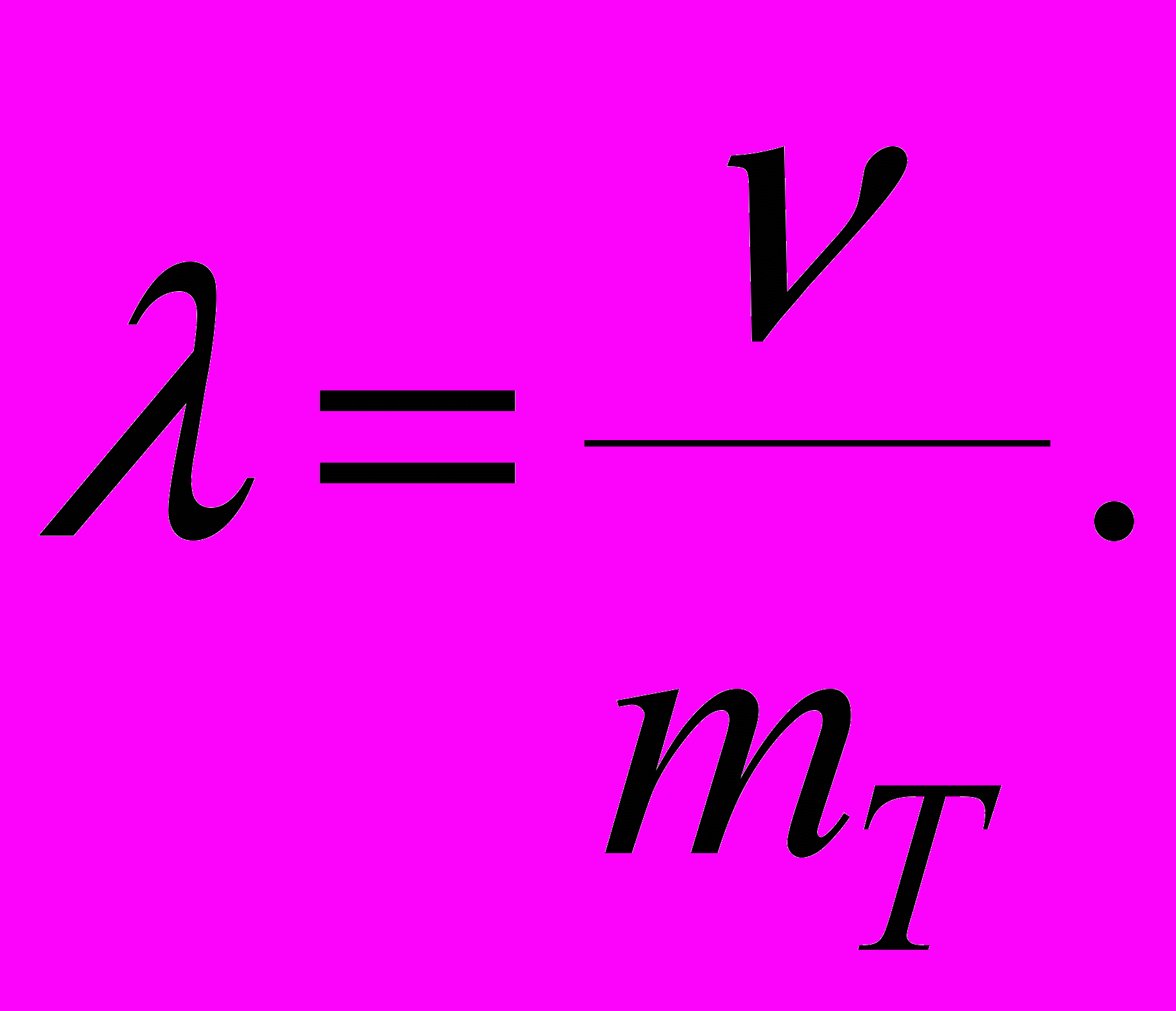(55)

В работе рассмотрена также и неэрланговская аппроксимация реальных потоков, при которой состояние, характеризующееся средним временем m_T и дисперсией времени D_T, замещается парой последовательных состояний: состоянием с детерминированным временем τ пребыванием в нем и следующем состоянием с пуассоновской интенсивностью λ потока выхода пр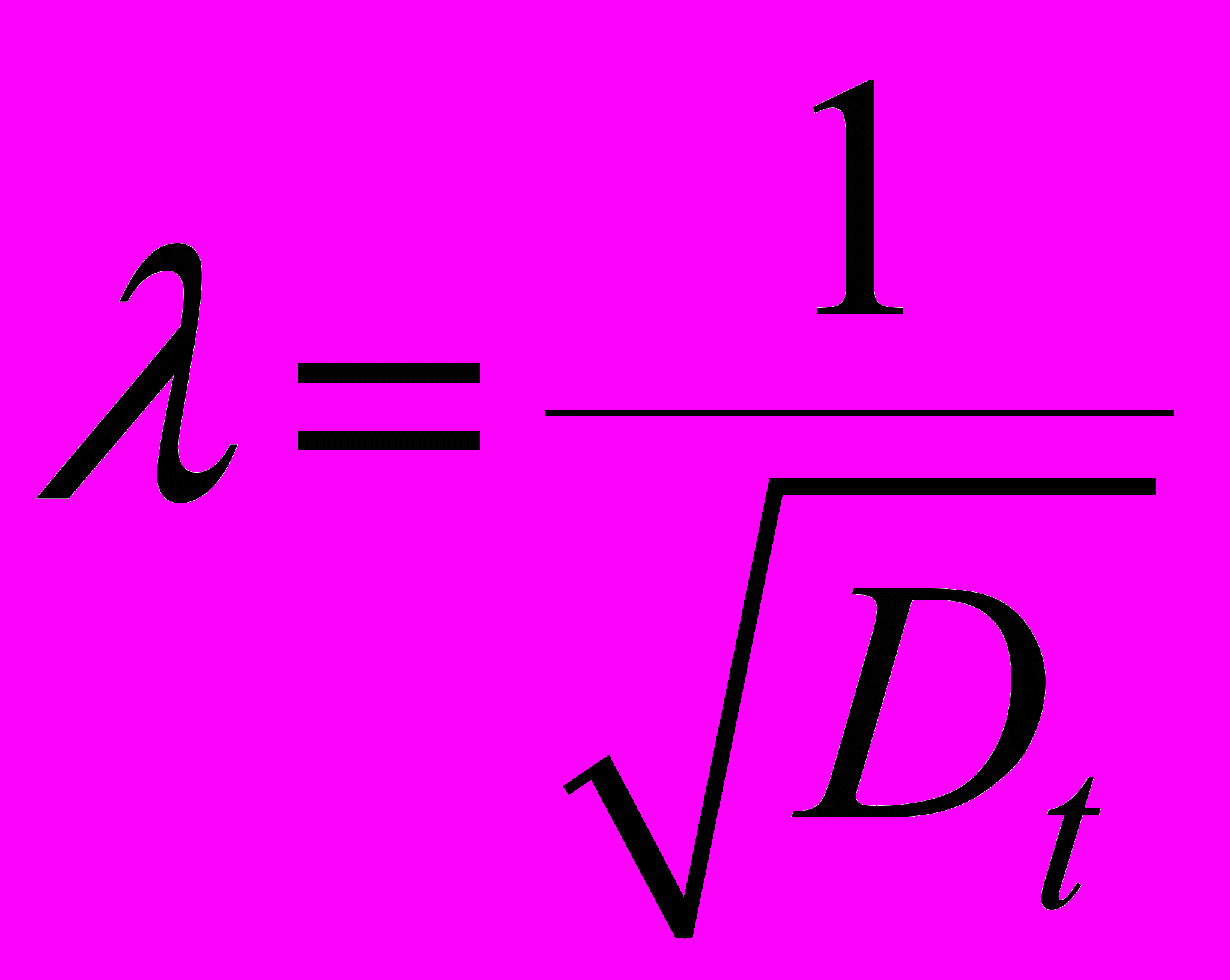и и 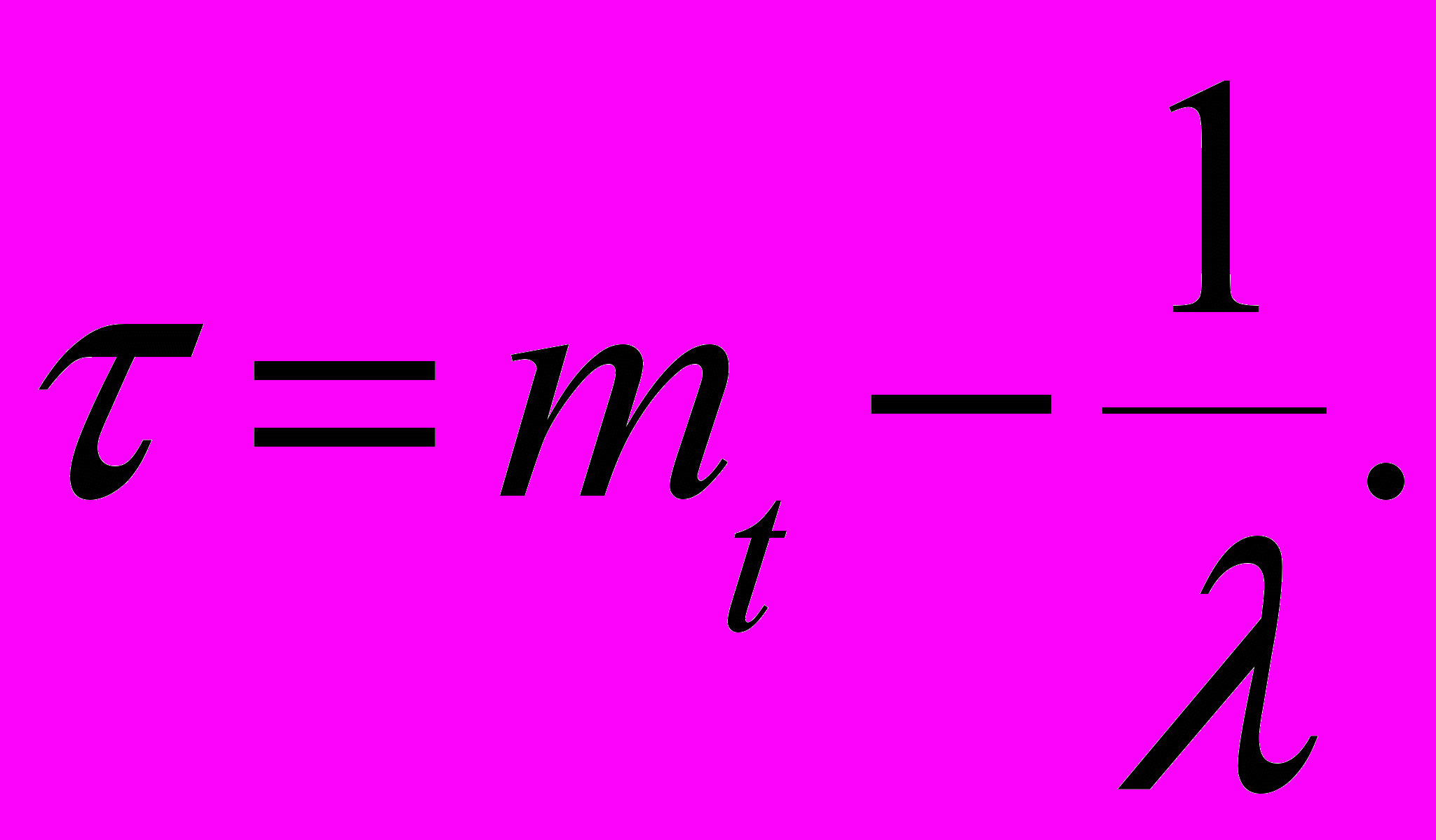Для полученной схемы бинарного замещения реального потока получено дифференциальное уравнение, основное отличие которого от уравнения Колмогорова заключается в том, что к системе уравнений динамики добавляется уравнение для вероятности состояния, соответствующего пуассоновской части замещающей пары состояний, а запаздывание τ аргумента равно разности между средним временем пуассоновского перехода и величины, обратной интенсивности пуассоновского замещения.

В связи с изложенным, поставлена и решена задача оптимизации организации управления информационными потоками в АСУ река-море политранспортного узла. Решение такой задачи представляется реализовать методом “насыщения сечений”, сущность которого заключается в использовании алгоритмов маршрутизации добавления фазы удаления и фазы регенерации. Алгоритмы решения основной задачи получены на основе основных соотношений теории массового обслуживания, использования аппарата уравнений Колмогорова, учитывающих аппроксимацию реальных потоков. Показано, что основные показатели (число сообщений в стационарном режиме, вероятность обнаружения занятости всех узлов обработки, среднее время задержки сообщения и др.), используемые для решения оптимизационной задачи, зависят от коэффициента использования канала.

Если 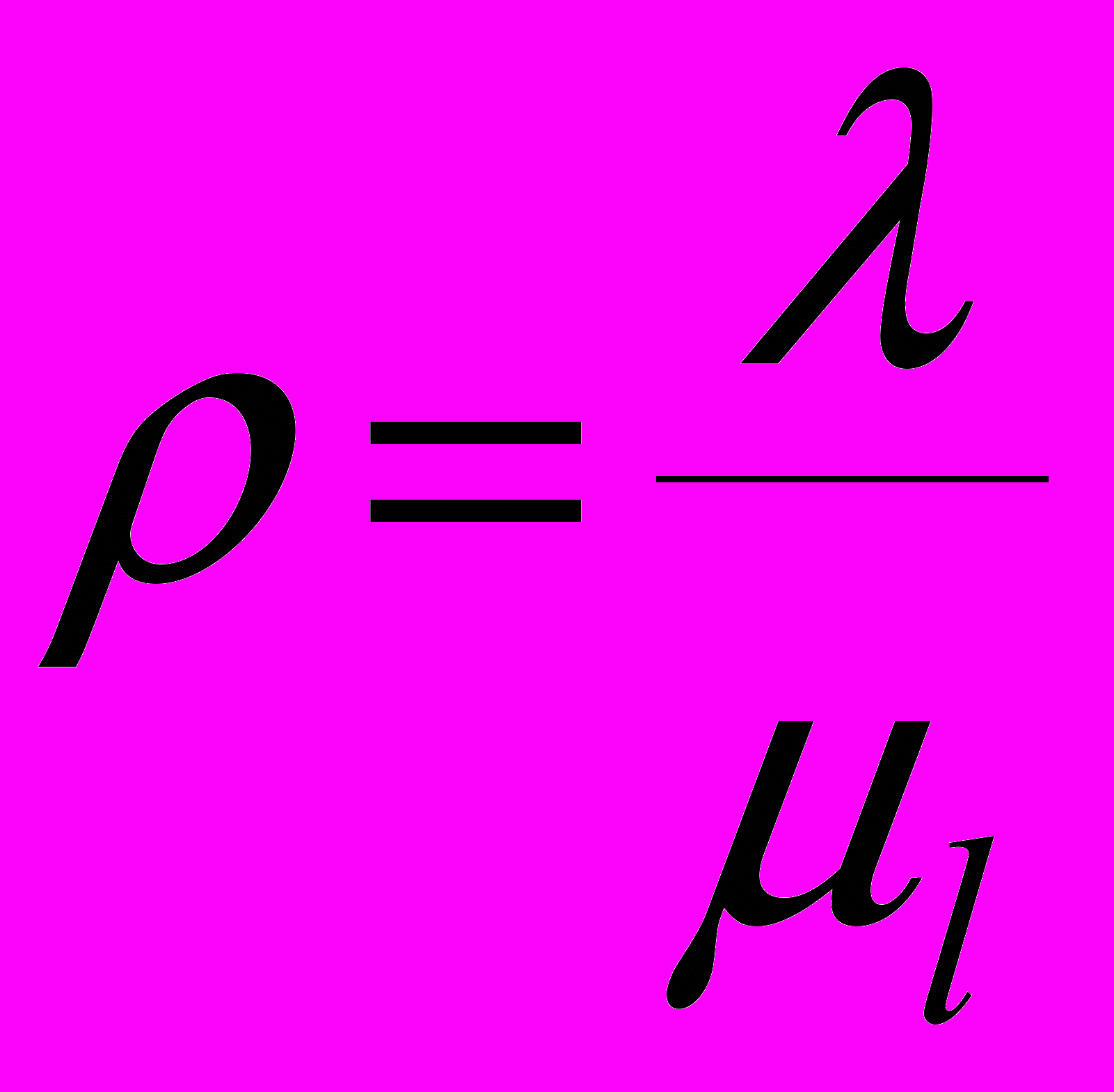– коэффициент использования канала, то λ – скорость поступления сообщения, а μ_l – интенсивность обслуживания.

В работе показано, что плотность распределения коэффициента ρ имеет вид

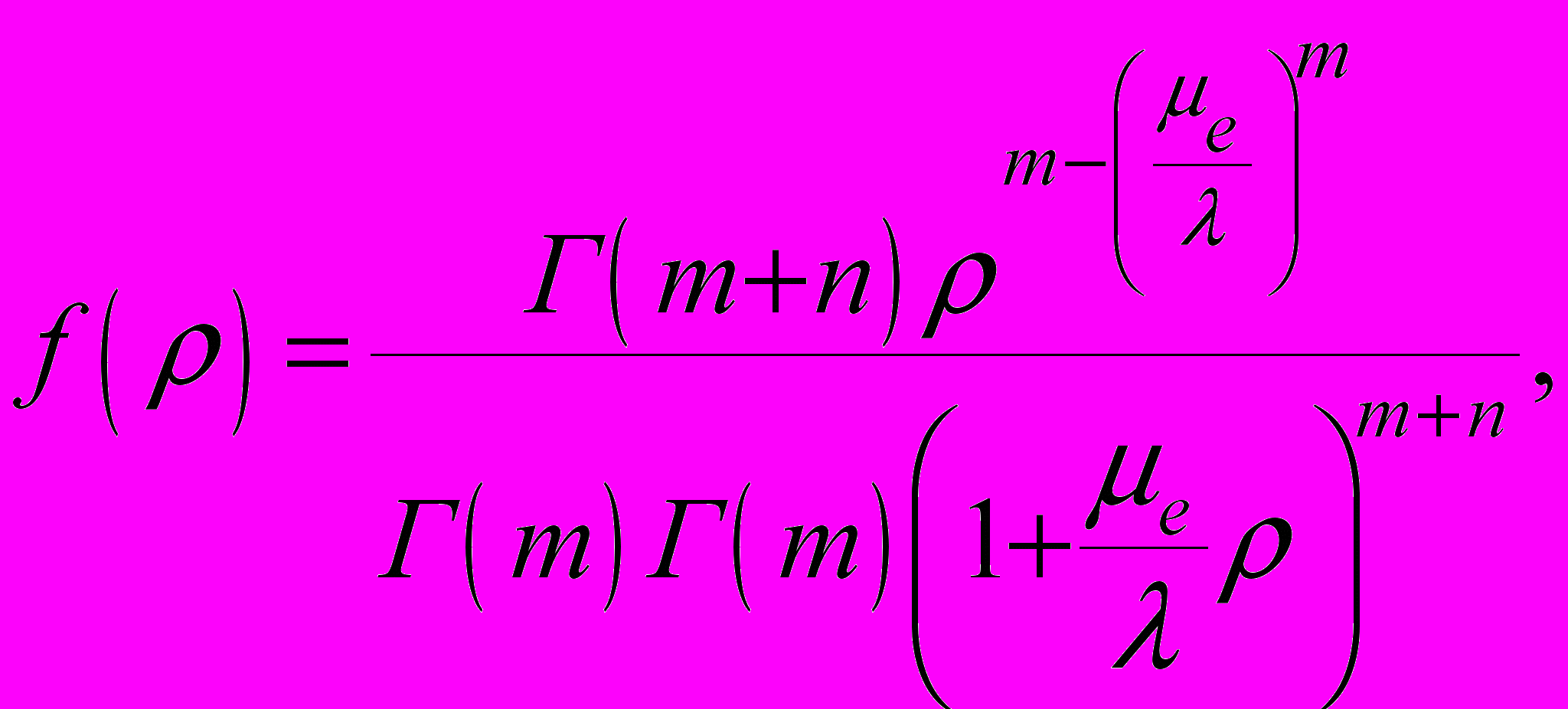(56)

и сделан вывод, что используя основные оптимальные решения, полученные на основе теории массового обслуживания, представляется целесообразным провести расчеты и анализ полученных результатов с учетом стохастичности коэффициента использования канала ρ и параметров λ и μ_l методом Монте-Карло. С этой целью в работе использовались:

- “простейший” метод;

- геометрический метод;

- метод использования существенной выборки;

- метод выделения главной части;

и разработаны с помощью метода операторных рядов эффективные алгоритмы для имитации параметров λ, μ_l и ρ.


ЗАКЛЮЧЕНИЕ


Анализ систем, методов и средств информационного и инструментально-технологического обеспечения управления речным флотом на ВВП Польши показал, что имеется достаточным резервы повышения эффективности и безопасности судоходства за счет внедрения надежной высокоточной информационной поддержки судоводителя речного или смешанного река-море плавания судна с использованием автоматизации управления движением судна и высокоточных методов проводки на всем протяжении ВВП в районе Нижней Одры (от Щецина до Одры-Хавеля) на основе развертывания в этом районе автоматизированной системы управления движением судов нового поколения.

Поэтому в работе сформулирована научно-техническая проблема, имеющая важное народно-хозяйственное значение – повышение эффективности управления судоходством на внутренних водных путях Польши на основе создания единого методологического подхода к внедрению и развитию эффективного информационного и математического обеспечения систем автоматизированного управления судов в районе Нижней Одры.

Решение этой проблемы в рамках данного научного направления позволило определить цели исследований диссертационной работы. В соответствии с ними получено теоретическое обоснование и практическая реализация системных методов, математических моделей и алгоритмов принятия решений при проектировании, использовании и оценке состояния сложной организационно-технической системы по автоматизации управления движением судов на ВВП с использованием новейших информационных технологий.

Научные результаты, полученные в работе, содержат решения по следующему кругу задач.

1. Методологию создания высокоэффективной автоматизированной системы управления движением судов на ВВП Польши в ее важнейшем регионе Нижней Одры на основе системного подхода к структурной, алгоритмической, объектно-ориентированной реализации и новых информационных технологий.

Такой подход включает:

1. Анализ состояния современной научной методологии создания и информационного обеспечения концептуальных исследований предметной области на уровне метасистемы – КРИС и РИС как основы системного подхода к вычленению исследуемых АСУДС из метасистемы и определению подходов к их структуре и критериям эффективности.
   
2. Совокупность теоретических, экспериментальных и модельно предсказательных приемов, решений, рекомендаций для обоснования тонкой структуры, топологии, информационной технологии и технических принципов построения АСУДС и ее подсистем и узлов для внутренних водных путей Польши.
   
1. Концепцию и логико-информационную модель построения АСУДС в районе водных путей и судоходства Нижней Одры как в организационном, так и технологическом аспектах.
   
2. Комплекс решений по структурно-информационному, математическому и алгоритмическому обеспечению важнейшей подсистемы мониторинга и управления в АСУДС – автоматизированной идентификационной системы, включающей в том числе методику решения многопараметрических стохастических задач, оптимизирующих топологию размещения береговых базовых станций на основании решений для оптимальной дальности по линии базовая станция – судовой транспордер АИС и зон действия базовых станций с учетом одновременного воздействия трех вероятностных факторов: свойств модели канала передачи информации, влияния заграждающего рельефа на линии БС-СТ и случайного перемещения СТ относительно БС.
   
3. Комплекс решений по моделям, математическому и алгоритмическому обеспечению оптимизации системы наблюдателей для информационного обеспечения судовых систем управления режимами движения судов на ВВП, включающий в том числе оценки параметров судовых динамических систем, алгоритмы статических фильтров Калмана и алгоритмы оценивания динамически подвижных объектов в турбулентных средах.
   
4. Комплекс решений по математическому сопровождению программно-целевого управления река-море политранспортным узлом, включающий:
   

5.1. Доказательство необходимости использования следующих математических моделей:

- статистической модели с накопителем без внутренней структуры;

- модели с накопителем по приоритетам вывоза груза;

- модели с накопителем ограниченной мощности.

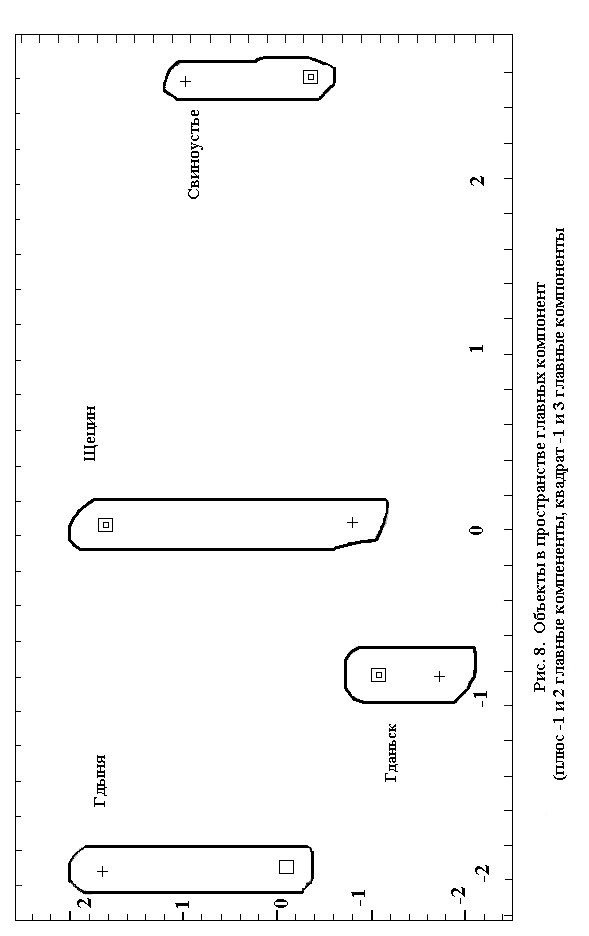
5.2. Решение задачи идентификации река-море порта по объему и номенклатуре обрабатываемых грузов методом главных компонент и кластерным анализом. С помощью указанных процедур сформирован алфавит классов портов региона, что является необходимой предпосылкой формирования современных логистических цепочек. Границы решения указанной задачи в постановочном плане могут быть в дальнейшем расширены и результаты использованы в субглобальном масштабе, что неизбежно приведет к следующей программной задаче – задаче прогнозирования грузооборотных транспортных узлов.

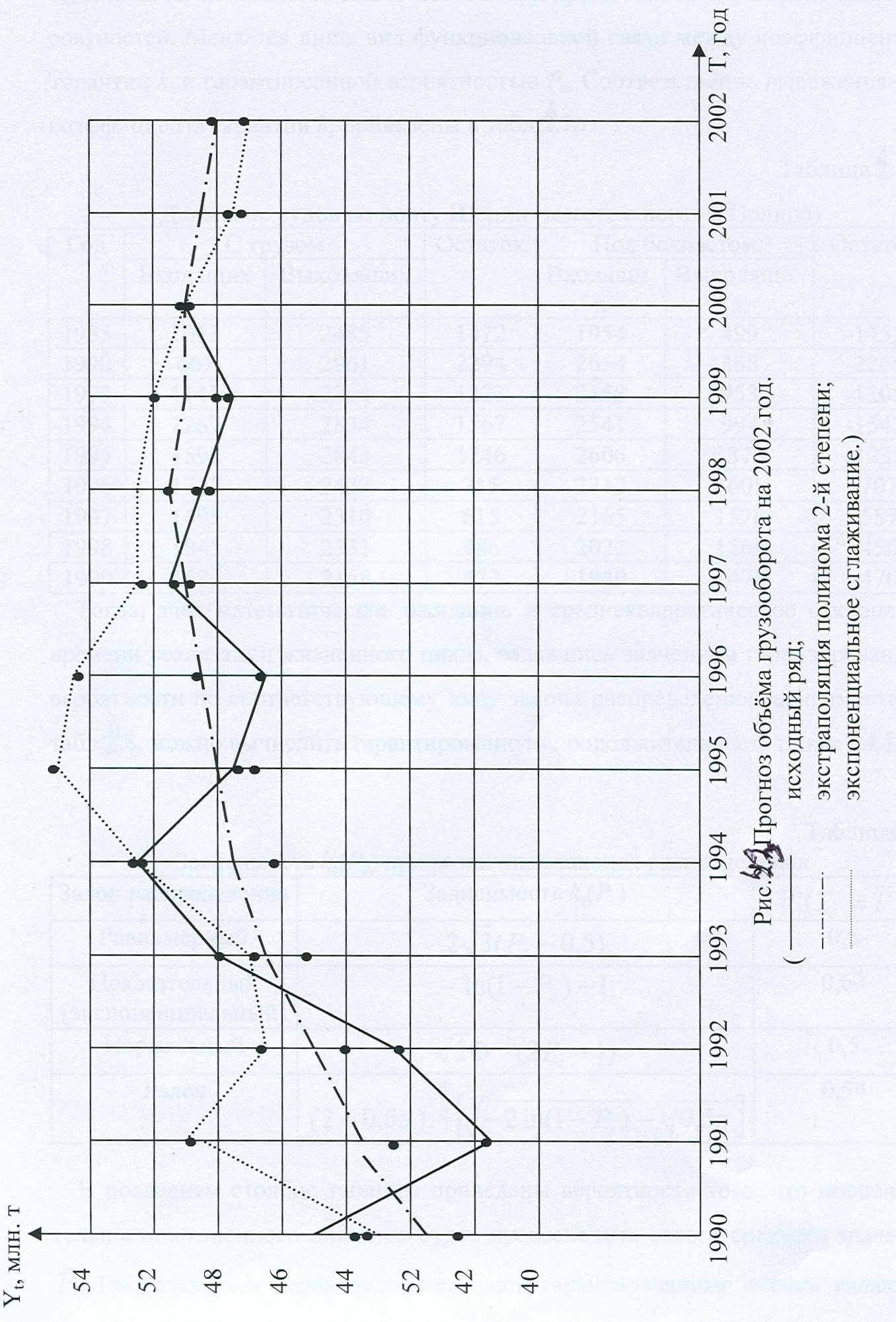
5.3 Методы экспоненциального сглаживания и экстраполяции тенденций дали согласованный на уровне 5% результата. Грузооборот река-море портов региона за последние пять лет стабилизировался, и эта тенденция будет наблюдаться и в следующую пятилетку.

6. Способы, пути и стратегию анализа информационных потоков и управления такими потоками в политранспортным узле речной АСУДС, содержащие
   
   1. Совокупность последовательных алгоритмов и статической процедуры оценки момента “разладки” пуассоновского потока в реальном масштабе времени, базирующиеся на использовании двух введенных в рассмотрение статистик.
      
   2. Математические модели потоков в транспортном узле в зависимости от исходной статистической информации, построенные на основе модели Пойа-Лундберга, моделей рандомизированных псевдосостояний и бинарных моделей замещения реального потока.
      
   3. Рекомендации и решения по управлению информационными потоками в АСУ транспортного узла на основе минимизации целевой функции с использованием алгоритмов расчета показателей качества управления методами теории массового обслуживания с последующей корректурой показателей методом Монте-Карло.
      

Полученные результаты подтвердили эффективность и практическую реализуемость системной методологии, выдвинутой в диссертации, для конструктивного построения и развития таких сложных организационно-технических информационных систем, какой является автоматизированная система управления движением судов района Нижней Одры в Польше.