Методические особенности обучения тригонометрии учащихся профильных классов 13. 00. 02 теория и методика обучения и воспитания

Вид материала

Автореферат

Содержание Основное содержание диссертации Первая глава Целевой компонент Содержательный компонент Процессуальный компонент Этап 1. Информационно-оценочный Средства обучения Этап 2. Практический Средства обучения Этап 3. Прогностический Основное содержание диссертационного исследования отражено в следующих публикациях Методические особенности обучения тригонометрии

Подобный материал:

• Взаимосвязанное обогащение синонимической лексикой родной и русской речи учащихся VI-VII, 389.12kb.
• Методика развития деятельностной компоненты медиакомпетентности учащихся старших классов, 402.96kb.
• Методика обучения решению математических задач учащихся основной школы в условиях дифференциации, 489.79kb.
• Программа вступительного экзамена в аспирантуру по курсу теория и методика обучения, 45.44kb.
• Методика интенсивного обучения иностранному языку, 9.05kb.
• Теория и методика обучения и воспитания (литература), 47.67kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 224.65kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.55kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.63kb.
• Формирование методологической компетентности будущего учителя географии средствами, 305.29kb.

Основное содержание диссертации

Во введении обосновывается актуальность темы, определяются проблема, цель, предмет и гипотеза исследования, формулируются цели и задачи исследования, показывается научная новизна, теоретическая и практическая значимость работы.

Первая глава «Дидактические основы обучения тригонометрии учащихся в условиях профильного обучения» посвящена логико-дидактическому анализу содержательно-методической линии тригонометрии в профильном курсе математики и выявлению методических особенностей обучения тригонометрии учащихся профильных классов.

В ходе анализа психолого-педагогической и методической литературы были систематизированы теоретические положения, служившие основополагающими при проведении настоящего исследования.

В исследовании в основу построения обучения тригонометрии учащихся профильных классов положен личностно-деятельностный подход к обучению, который на основе анализа исследований (В.И. Данильчук, И.С. Якиманская, Л.С. Выготский, А.Н.Леонтьев, Н.Ф. Талызина и др.), понимается нами как субъектно ориентированная организация учебной деятельности, направленная на учет интересов, склонностей и способностей учащихся, на создание условий при организации обучения в соответствии с их профессиональными интересами. Так, в условиях реализации личностного компонента в процессе обучения, на что обращают внимание В.И. Данильчук, И.С. Якиманская и др., в работе учитывались индивидуальные потребности обучающихся, осуществлялось разностороннее развитие личности каждого конкретного ученика. Таким образом, личностный компонент обеспечивает познание себя, развитие рефлексивной способности, жизненного самоопределения. В соответствии с деятельностным компонентом, раскрытым в трудах Л.С. Выготского, А.Н. Леонтьева, Н.Ф. Талызиной и др., полноценное освоение изучаемого материала было невозможно без развития у обучающихся личностных умений. При этом данный компонент был связан с формированием и развитием у учащихся разнообразных способов деятельности по освоению содержания образования.

В исследовании обосновано, что одна из серьезных проблем, с которой приходится сталкиваться преподавателям профильного курса математики, — проблема необходимости существенных различий отбора содержания модуля «Тригонометрии» для различных профилей.

Как отмечает М.Н. Скаткин, профильное обучение должно работать на обеспечение дальнейшего жизненного пути старшеклассника, его подготовку к профессиональному образованию и освоению различных социальных ролей, развитие индивидуальных особенностей и способностей, становлению активной гражданской позиции.

Профильное обучение в отличие от традиционного позволяет ученикам выбрать конкретную приоритетную область для более глубокого изучения. Поскольку выбор предполагает ряд вариантов, то переход к профильности – это, прежде всего, расширение свободы, вариативности школьного образования.

В исследовании уточнено, что при изучении математики на профильном уровне обширнее представлены следующие темы: числовые и буквенные выражения, корни и степени, логарифмы, основы тригонометрии, функции, начала математического анализа, уравнения и неравенства.

Для того чтобы развивающая функция математики была реализована в наибольшей степени, очевидно, что для каждого из выделенных профилей должна быть создана в некотором смысле «своя» математика. Отличия определяются общими целями обучения школьников в каждом профиле, а значит, и целями обучения математике, которые различны в каждом из выделенных профилей.

Как отмечают многие исследователи (Бескин Н.М., Новоселов С.И., Рыбкин Н.А.), изучение тригонометрии имеет важное значение с точки зрения профессиональной подготовки, что кроме общих целей – образовательных, воспитательных и практических, обучение тригонометрии ставит ещё специальные цели, (как уже упоминалось выше в программе по математике для средней школы).

В ходе анализа организации системы знаний при изучении разделов тригонометрии (исследователи Блох А.Я., Мокрушин Е.Л., Павленкова И.А., Чичигин В.Г.) были выявлены особенности обучения тригонометрии на профильном уровне:

• позиции деятельностного подхода – это использование на занятиях математики заданий по тригонометрии, направленных на развитие самостоятельной деятельности учащихся в ходе решения заданий связанных с практическим применением тригонометрии для каждого профиля, трансформация содержания модуля «Тригонометрия» в задачи, системы задач, практические работы;
  
• позиции содержательного подхода – это выбор значимых для каждого профиля дидактических единиц, определение возможности интеграции дидактических единиц в более крупные единицы, определение ключевых операций и понятий в значимых для профиля дидактических единицах;
  
• позиции личностно-ориентированного подхода – это учет интересов обучающихся и уровня знаний, умений в целях развития их личности при организации учебного материала.
  

В ходе исследования было установлено, что процесс проектирования содержательного модуля «Тригонометрия» представляет собой выбор различных дидактических единиц, дифференцированных по уровням и профилям обучения, трансформацию содержания модуля в задачи, системы задач, практические работы и др. для использования при организации обучения в рамках различных профилей реализуется, при соблюдении дидактических принципов научности, фундаментальности и прикладной направленности; преемственности, последовательности и системности; расширения содержания модуля в зависимости от специфики каждого профиля; наглядности, гуманитарности и поляризации.

Во второй главе «Методическая система обучения тригонометрии учащихся в условиях профильного обучения» определены целевой, содержательный и процессуальный компоненты методической системы обучения тригонометрии в классах с профильным уклоном на разных этапах процесса обучения, обобщены результаты опытно-экспериментальной работы, проведенной в рамках исследования, выявлены и экспериментально проверены педагогические условия реализации предложенной методической системы.

Методическая система обучения тригонометрии учащихся профильных классов понимается как определенная совокупность частей или компонентов обучения тригонометрии, образующих единое целое в своем взаимодействии.

Целевой компонент методической системы обучения представлен постановкой обобщенной цели и целей этапов процесса обучения; целей, реализуемых на этапах обучения, и целей блоков содержания тем учебного материала, отражающих динамику обучения тригонометрии в профильной школе на каждой фазе освоения учащимися учебного материала (при разрешении учебных ситуаций, оперативных целей, достижимых в рамках учебно-профессиональных ситуаций, при решении задач в условиях конкретного урока).

В качестве основной организационной формы учебного процесса был выбран урок, что определило содержательный и процессуальный компоненты.

Содержательный компонент методической системы обучения учащихся в условиях профильного обучения представлен трансформированным содержанием модуля «Тригонометрии» в задачи, системы задач, где в сюжете задач отражается профильная направленность, практические работы, материалы, представленные на уроках; дидактическими единицами, требующими изучения, основными математическими знаниями и умениями из соответствующей профильной области.

Например, для расширения круга задач, решаемых с помощью тригонометрии, учащимся предлагаются задачи и практические работы с профильным содержанием:

Задачи с геометрическим содержанием: (практическая): между двумя графически заданными точками А и В наметить произвольную точку, расположенную на дуге окружности известного радиуса R, но с недоступным центром (например, разметка дуги окружности закругления железного полотна)

Задачи с геодезическим содержанием: определить расстояние от доступного пункта до недоступного (например, до дерева, стоящего на другом берегу реки).

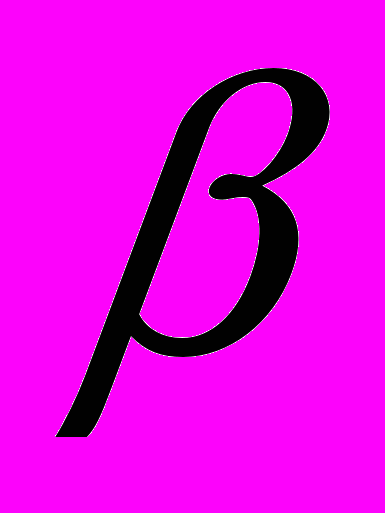Задачи с астрономическим содержанием: определить расстояние до небесного светила, зная радиус Земли R и углы и , полученные в результате астрономических наблюдений и измерений.

Задачи с физическим содержанием: данную силу разложить на две взаимно перпендикулярные составляющие силы так, чтобы одна из них составляла угол с данной силой , и определить составляющие силы.

Мы придерживаемся позиции В.М. Симонова, что выбор содержания и его представление в виде систем задач позволяют создать условия для эффективного обучения учащихся различных профилей.

В исследовании трансформация содержания модуля «Тригонометрия» в задачи, системы задач, практические работы строилась с целью усиления практической направленности образования, включения заданий, требующих исследовательских работ учащихся, направленности на профессиональную ориентацию для каждого профильного класса в специфике данного профиля в зависимости от целей изучения математики в каждом профиле.

Профиль обучения	Дидактические единицы	Основные знания и умения из математики	Знания из соответствующей профильной области
Физический	Техника триангуляции, все разделы физики: особенности распределения света, разряд конденсатора, затухающие и вынужденные колебания, колебание маятника, биение, сложение колебаний	Длина, расстояние, гармонические колебания, тригонометрические функции, синусоида	Измерение расстояние до звезд в астрономии; контролирование системы навигации спутников; техники навигации, акустики, электроники, машиностроения, кораблестроение, радиоэлектроника, тригонометрия и все разделы физики, современные способы синтезации звука, математические модели природных явлений, описание технологических процессов средствами математики
Биологический	Строение и темпы роста растений	Синусоида, полярные координаты	Фазы роста растений, изучение строения растений, медицина (включая ультразвуковое исследование и компьютерная томография), графики тригонометрических функций и их приложение в биологии
Химический	Органические и неорганические процессы	Синусоида и периодичность тригонометрических функций	Фармацевтики, тригонометрия в химии, периодические процессы в химии
Географический	Масштаб, определение длины дуги параллели или меридианы, изучение явления - приливов и отливов	Расстояние, длина, площадь, колебание, биение	Сейсмологии, метеорологии, океанологии, картографии, топографии, геодезии, простейшие задачи на местности, математические модели природных явлений
Математический	Синус, косинус, тангенс, обратные тригонометрические функции, графики тригонометрических функций, умение решать тригонометрические уравнения, гармонические колебания, производная тригонометрических функций, геометрическое приложение производной	Вычисление площадей фигур и объемов тел.	Экономики, анализ финансовых рынков, электронной техники, компьютерной графики, теории вероятности, задачи с параметрами, задачи повышенной сложности по тригонометрии, основы экономики, математическая статистика, компьютерный дизайн, описание технологических процессов средствами математики

Процессуальный компонент методической системы обучения тригонометрии учащихся профильных классов включал использование активных и интерактивных (поисковых, частично-поисковых, проблемных, проектных) методов обучения, организацию и структурирование предъявляемой информации, определение видов, форм и способов подачи учебной информации в соответствии с особенностями обучения математике учащихся классов профильного обучения.

Анализ систем учебно-предметных задач с тригонометрическим содержанием позволил выделить следующие виды:

1) предметно-познавательные (направлены на формирование у учащихся логической группы интеллектуальных умений, которые построены на основе рассмотрения ситуаций, направленных на освоение знаний соответствующего раздела модуля «Тригонометрия»);

2) практико-ориентированные (направлены на формирование у учащихся группы интеллектуальных умений, которые построены на раскрытие прикладного потенциала тригонометрии);

3) гуманитарно-ориентированные (направлены на формирование у учащихся оценочно-регулируемой группы интеллектуальных умений, которые предполагают познание мира через инструментарий тригонометрии).

В исследовании использовалась предложенная В.И. Андреевым и Г.А. Баллом типология задач:

• задачи исполнения и воспроизведения;
  
• задачи на объяснение;
  
• задачи на определение понятий;
  
• задачи с некорректно представленной информацией;
  
• задачи с явно выраженным противоречием; задачи на рецензирование;
  
• задачи на разработку алгоритмов или эвристических предписаний;
  
• задачи на переформулировку задач;
  
• конструкторские и исследовательские задачи;
  
• задачи на обнаружение противоречий и формулировку проблем;
  
• задачи на оптимизацию, решение которых стимулирует прогрессивные изменения в способах выполнения действий и уровнях сформированности интеллектуальных умений.
  

В исследовании к методам обучения тригонометрии отнесены: монологический, показательный, диалогический, эвристический, исследовательский, алгоритмический, программированный и интерактивный методы (для темы «Тригонометрические функции» – монологический, показательный, эвристический, исследовательский, интерактивные методы; для темы «Тригонометрические уравнения» – показательный, алгоритмический, программированный, интерактивный методы; для темы «Преобразование тригонометрических выражений» – диалогический, эвристический, исследовательский, интерактивный методы).

Например, задачи на доказательство и задачи с элементами исследования (в частности, практические работы и исследование тригонометрических уравнений, содержащих параметры) являлись средством развития навыков самостоятельной исследовательской работы.

В исследовании к средствам обучения, обеспечивающим обучение тригонометрии учащихся профильных классов, отнесены печатные издания учебников, учебно-методические пособия; справочники по математике и справочная математическая литература; записи на доске; учебное оборудование; аудио-, и видео, учебно-информационые материалы; речь преподавателя; электронные учебники; сетевые учебно-методические пособия; компьютерные обучающие системы, тренажеры; виртуальная реальность.

Например, в начале изучения темы «Графики тригонометрических функций» использовались компьютерные обучающие программы, позволяющие продемонстрировать свойства функции, преобразование графиков функций и практическое применение графиков тригонометрических функций.

Нами составлены методические рекомендации для отбора или конструирования учителями математических задач по тригонометрии, направленных на обучение тригонометрии учащихся классов с профильным уклоном: содержание задач должно быть разноуровневым, связанным с практической значимостью тригонометрии для каждого профиля и использованием наглядности; должны быть реализованы обобщенные способы или методы решения математических задач; необходимо согласование уровня сложности задач со степенью владения тригонометрическими знаниями и их проявлениями в профильных областях.

В работе описана организация и результаты педагогического эксперимента, проведенного с целью проверки гипотезы исследования.

Был сформирован комплекс диагностических методик: первая группа диагностических методик была направлена на исследование положительного отношения учащихся к тригонометрии (анкетирование), вторая группа диагностических методик на определение уровня (общекультурного², прикладного³, творческого⁴) обучаемости по темам тригонометрии (модифицированная методика П.И.Третьякова и И.Б.Сенновского).

Цель констатирующего этапа эксперимента заключалась в создании и проверке комплекса диагностических методик.

В констатирующем этапе эксперимента приняло участие 200 учащихся школ г. Волжского Волгоградской области.

Формирующий эксперимент позволил оценить эффективность методической системы обучения тригонометрии учащихся профильных классов. Основными этапами формирующего эксперимента стали: информационно-оценочный, практический и прогностический. В формирующем этапе эксперимента приняли участие экспериментальная группа – 50 и контрольная группа – 150 учащихся школ г. Волжского Волгоградской области. В ходе диагностирования было установлен недостаточный уровень положительного отношения к тригонометрии и в связи с этим низкий уровень обучаемости. В результате были получены следующие данные: на начало эксперимента – творческий уровень обучаемости в экспериментальных классах имели – 8 человек (16%), в контрольных классах и группах – 22 человека (15%). Учащихся с прикладным уровнем обучаемости в экспериментальных классах было 23 человека (46 %), а в контрольных – 72 человека (49%); с общекультурным уровнем: в экспериментальных классах– 19 человек (38%), а в контрольных – 56 человек (36%).

Компоненты методической системы	Этапы процесса обучения тригонометрии
Этап 1. Информационно-оценочный
Целевой	Сформировать систему тригонометрических знаний и представлений на основе межпредметных связей и знаний по элементарной математике
Процессуальный	Средства обучения: задачи: а) предметно-познавательные, ориентированные на формирование тригонометрических понятий: задачи исполнения и воспроизведения; на объяснение; на определение понятий; б) практико-ориентированные, направленные на формирование взаимосвязи тригонометрии с соответствующей профильной областью: задачи на разработку алгоритмов или эвристических предписаний; в) гуманитарно-ориентированные, направленные на приобретение первичного практического опыта по применению тригонометрии в соответствующей профильной области: конструкторские и исследовательские задачи; деловые игры.

На первом этапе обучения тригонометрии учащихся профильных классов типовыми являются занятия, построенные следующим образом: актуализация знаний; проверка домашней работы; беседа по тригонометрическим терминам или ситуациям; решение задач с тригонометрическим содержанием с четким выделением всех составных частей процесса решения: формализация (переход от реальной ситуации к построению формальной математической модели), решение «внутри математической модели» (выбор наиболее подходящего метода для решения поставленной математической задачи), интерпретация (переход к исходной ситуации, установление соответствия полученных результатов рассматриваемой ситуации из профильной области, оценка значения полученного результата для заданной ситуации из профильной области); исследовательские задания с большой степенью реальности содержания; проблемные мини-задания; рефлексия деятельности.

Например, задача с практическим содержанием: «Определить высоту телевизионного столба, стоящего на ровной местности». В ящике с песком учащиеся моделируют эту задачу и намечают возможный план работы, затем, построив соответствующий чертеж, решают задачу.

Решите уравнение 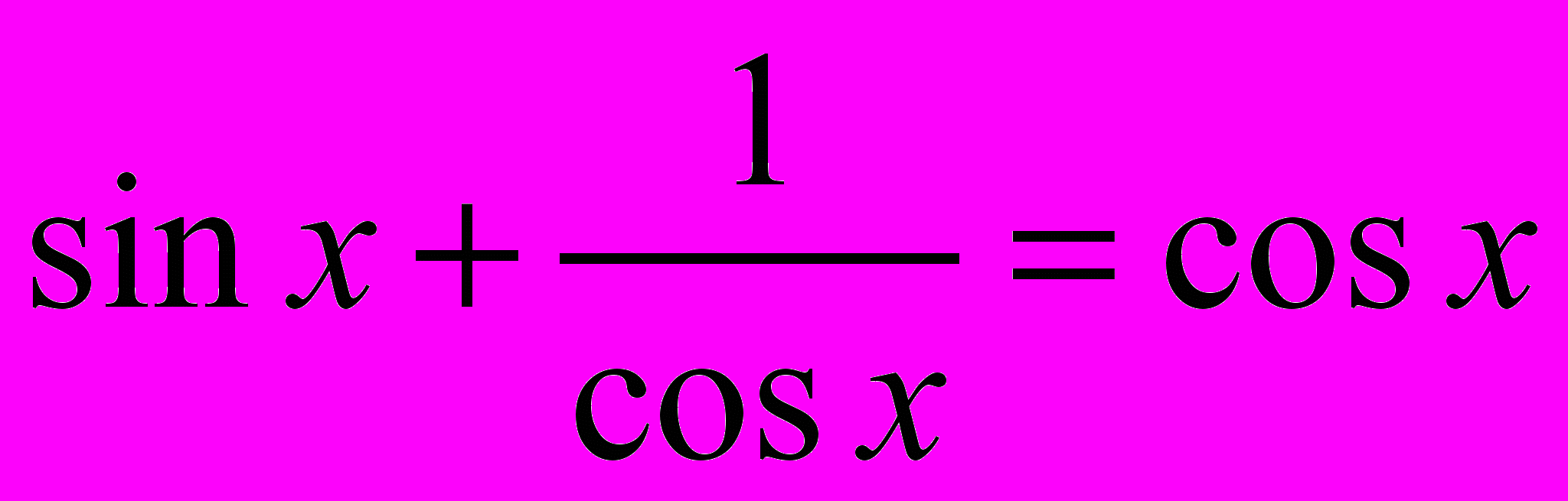. Учащиеся рассматривают все варианты решения данного уравнения и выбирают наиболее рациональное решение.

Анализ результатов показал, что при прохождении информационно-оценочного этапа эксперимента в экспериментальных классах 10 человек (20%) от общего количества учащихся изменили уровень обучаемости, причем 8 человек (16%) перешли с общекультурного уровня на прикладной, 2 человека (4%) с прикладного уровня на творческий. В контрольных классах изменили уровень обучаемости 5 человек (2%): с прикладного на творческий движения не наблюдалось, а с общекультурного на прикладной уровень перешли 5 учащихся (2%).

Этап 2. Практический
Целевой	Формирование стремления к самообразованию, совершенствованию, позитивного отношения к процессу познания, осознание своей деятельности при изучении тригонометрии
Процессуальный	Средства обучения: задачи: а) предметно-познавательные, ориентированные на приобретение первичного практического опыта исследования в области тригонометрических знаний; в) гуманитарно-ориентированные, направленные на приобретение первичного практического опыта построения исследования; имитационные игры.

Типовыми для второго этапа обучения тригонометрии учащихся профильных классов являются занятия по разрешению ситуаций с профильным содержанием, проводимые в форме беседы, исследования-соревнования (соревнование на лучшую шпаргалку) мозговой штурм, дискуссии и диспуты (по теме «Тригонометрия и физика») или игры (дидактический театр «Тригонометрические функции», «Зри в корень» по теме, математические сказки).

Например, исследования-соревнования на лучшую шпаргалку по теме «Тригонометрические функции»: перед началом задания учащимся объясняется, что необходимо конспектировать материал кратко, образно и доходчиво, отображая учебную информацию так, чтобы это было понятно всем, что нужно создать не просто шпаргалку, а произведение искусства. В центре шпаргалки предлагалось изобразить несколько главных ключевых понятий по теме, а в разные стороны провести стрелки, линии, отображающие, с какими понятиями соотносятся ваши ключевые слова. Предлагалось придумать рисунки – символы, структурные формулы. Разрешалось творить, выдумывать, пробовать, выдвигалось лишь условие: сама шпаргалка должна быть понятна любому из присутствующих. После истечения времени, отведенного на работу, работы учащихся собирались, перемешались и снова раздавались учащимся с предложением оценить творческие работы. Учащиеся по очереди рассматривали, оценивали все работы, в конце суммировались баллы и определялись победители соревнования, которые всем рассказывали о процессе составления своих шпаргалок. В заключение работы совместно разрабатывался алгоритм составления мини-конспекта.

Анализ результатов показал, что при прохождении практического этапа эксперимента в экспериментальных классах с общекультурного на прикладной перешли 8 человек (16%), с прикладного на творческий 3 человека (6%). В контрольных классах изменили уровень обучаемости 2 человека (1%) – с общекультурного уровня на прикладной, с прикладного на творческий уровень изменения не наблюдалось.

Этап 3. Прогностический
Целевой	Приобретение опыта решения практических задач из соответствующей профильной области
Процессуальный	Средства обучения: задачи: а) практико-ориентированные, направленные на формирование ценностного отношения к объектам, процессам из соответствующей профильной области: задачи с явно выраженным противоречием; задачи на рецензирование; задачи на разработку алгоритмов или эвристических предписаний; б) практико-ориентированные, направленные на применение знаний тригонометрии в профильной области: задачи на переформулировку задач; конструкторские и исследовательские задачи; задачи на обнаружение противоречий и формулировку проблем; в) гуманитарно-ориентированные, направленные на формирование ценностного отношения к объектам, процессам из соответствующей профильной области: конструкторские и исследовательские задачи; задачи на обнаружение противоречий и формулировку проблем; задачи на оптимизацию; имитационные игры.

Для третьего этапа обучения тригонометрии учащихся профильных классов типовыми являются занятия по решению математических задач и ситуаций с тригонометрическим содержанием с обращением внимания на составные части процесса решения (формализация, решение «внутри математической модели», интерпретация), на которых обязательно организуются беседы по тригонометрическим понятиям, поисковые исследовательские работы частично-поискового исследования (например, исследовательская группа учащихся, проводя экспериментальную часть работы «Конструирование системы навигации спутников и техника навигации» определила значение навигации для многих отраслей жизни, выявила важность использования и потом обратились к возможности их внедрения в профессиональной области. Это доказывает, что профессиональное знание на ступени развития ситуации исследовательской деятельности становилось частью общечеловеческих знаний), поисковые исследования с неопределенным содержанием (например, при изучении темы «Функции 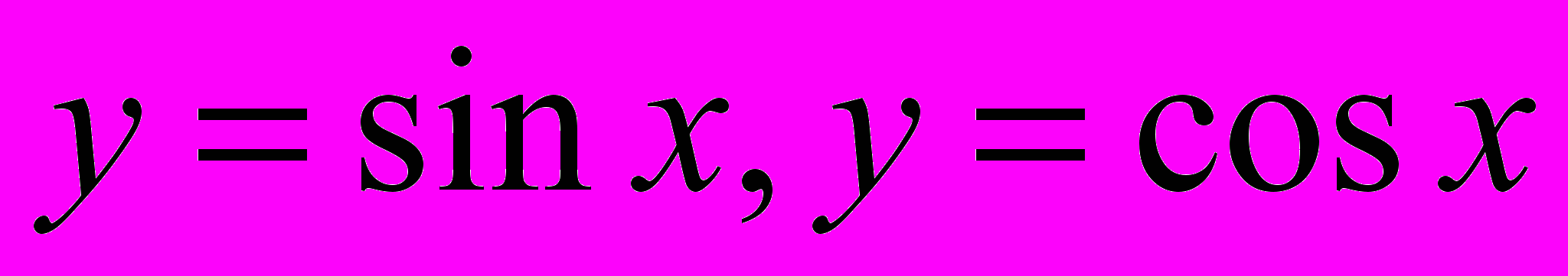, их свойства и графики» учащиеся проводили исследования по теме «Анализ финансовых рынков учащиеся: изучали литературу по предложенной теме и определяли значение графиков тригонометрических функций для анализа финансовых рынков), мозговые штурмы, дискуссии или имитационные игры.

По завершению эксперимента (прогностический этап) было выявлено, что в экспериментальных классах с общекультурного на прикладной уровень перешло 2 человека (4%), с прикладного на творческий 1 человек (2%). В контрольных классах динамика была такова: с общекультурного на творческий и с прикладного на творческий движения не наблюдалось.

По результатам мониторинга учащихся, проводимого в ходе экспериментальной работы, установлено, что произошли количественные изменения в представленности уровней обучаемости как в экспериментальной, так и контрольной группах; при этом в контрольной группе изменения незначительны.

Результаты формирующего этапа педагогического эксперимента позволили констатировать, что у учащихся экспериментальной группы наблюдалась динамика роста обучаемости (табл.1) в процессе обучения тригонометрии.

Таблицы 1. Динамика продвижения учащихся по уровням обучаемости в процессе обучения тригонометрии.

	Начало эксперимента		Информацио-нно-оценочный		Практический		Прогности-ческий		Конец эксперимента
	Экспер.	Контр.	Экспер.	Контр.	Экспер.	Контр.	Экспер.	Контр.	Экспер.	Контр.
общекуль-турный	38%	36%	36%	32%	24%	32%	14%	31%	10%	31%
прикладной	46%	49%	42%	53%	50%	53%	54%	54%	56%	54%
творческий	16%	15%	22%	15%	26%	15%	32%	15%	34%	15%

Рис. 1. Сравнение динамики продвижения по уровням обучаемости в процессе изучения тригонометрии.

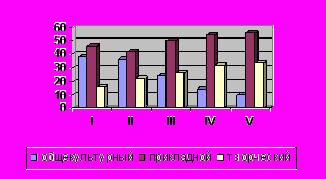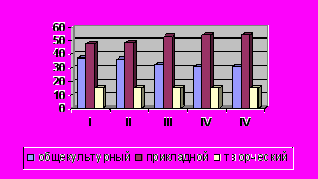Экспериментальная группа

Контрольная группа

I-начало эксперимента, II- информационно-оценочный этап, III- практический этап, IV-прогностический этап, V- конец эксперимента

Результаты диагностики (по критерию Пирсона) подтвердили эффективность разработанной методической системы обучения тригонометрии учащихся профильных классов.

Приведенные данные опытно-экспериментальной работы подтверждают гипотезу исследования.

Проведенное исследование в целом подтвердило гипотезу, что позволило в заключение работы сделать выводы, что в ходе исследования:

1) выявлены методические особенности (разноуровневость заданий по тригонометрии в зависимости от возможностей учащихся и профиля обучения; учет интересов обучающихся, уровня их знаний и умений для определения учебных целей формирования всего образовательного процесса в целях развития личности учащихся при организации учебного материала; использование на занятиях заданий, направленных на развитие самостоятельной деятельности учащихся, трансформация содержания модуля «Тригонометрия» в задачи, системы задач, практические работы) обучения тригонометрии старшеклассников в условиях профильного обучения на основе деятельностного, содержательного и личностно - ориентированного подходов;

2) спроектирован содержательный модуль «Тригонометрия» для использования в процессе обучения математике в рамках различных профилей при соблюдении дидактических принципов: научности, фундаментальности и прикладной направленности; преемственности, последовательности и системности; расширения содержания модуля в зависимости от специфики каждого профиля; наглядности, гуманитарности и поляризации;

3) разработан целевой (обобщенная цель и цели этапов процесса обучения; цели, реализуемые на этапах обучения, и цели блоков содержания тем учебного материала), содержательный (трансформированное содержание модуля «Тригонометрии») и процессуальный (активные и интерактивные методы обучения, организация и структурирование предъявляемой информации, определение видов, форм и способов подачи учебной информации) компоненты методической системы обучения тригонометрии учащихся профильных классов;

4) в ходе опытно-экспериментальной работы были выявлены педагогические условия эффективной реализации методической системы обучения тригонометрии в условиях профильного обучения на старшей ступени среднего (полного) общего образования: интерактивности, структурности, целостности, преемственности.

В рамках поставленных задач выполненное диссертационное исследование можно считать завершенным, гипотезу исследования подтвержденной. Дальнейшая разработка проблемы диссертационного исследования может идти в направлении построения методической системы обучения математике в профильных школах с учетом методических особенностей обучения.


Основное содержание диссертационного исследования отражено
в следующих публикациях:

Статья в журнале, входящем в список ВАК

1. Захарова, О.В.Промежуточный контроль по разделам тригонометрии как средство подготовки к итоговой аттестации. /Захарова О.В. //Сибирский педагогический журнал -2009.-№10.- С.264-270 (0,24 п.л.)

Статьи докладов в сборниках научных трудов
и материалов научных конференций

2. Захарова, О.В. Методические особенности обучения тригонометрии в профильной школе. /Захарова О.В. //Педагогика: семья-школа-общество: монография / [Е.Н.Абузярова, О.Ю Афанасьева, С.А.Барамзина и др.]; под ред.проф. О.И. Кирикова.-Книга 11.-Воронеж: ВГПУ, 2007.- С.351-357 (0,45 п.л.)

3. Захарова, О.В. Проектирование целевого и содержательного компонентов методической системы обучения тригонометрии учащихся профильных классов. /Захарова О.В. //Педагогика и жизнь: международный сборник научных трудов / под ред.проф. О.И. Кирикова.-Выпуск 11.-Воронеж: ВГПУ, 2009.- С.312-322 (0,57п.л.)

4. Захарова, О.В. Методическая система обучения тригонометрии - система форм организации обучения / Захарова О.В. // Образование и наука в 21 веке: Материалы IV международной научно-практической конференции 17-25 октября 2008 г./ Том 5. Педагогические науки. Психология и социология. Музыка и живопись. – София: «Бял ГРАД-БГ» 2008. – С. 34-39 (0,25 п.л.).

5. Захарова, О.В. Методы обучения тригонометрии, как компонент методической системы обучения тригонометрии в профильных классах / Захарова О.В. // Новейшие научные достижения: Материалы V международной научно-практической конференции 17-25 марта 2009 г./ Том 15. Педагогические науки.– София: «Бял ГРАД-БГ» 2009. – С. 37-40 (0,16 п.л.).

6. Захарова, О.В. Средства обучения тригонометрии, как компонент методической системы обучения тригонометрии в профильных классах / Захарова О.В. // Дни науки - 2009: Материалы V международной научно-практической конференции 27.03-05.04 2009 г./ Том 12. Педагогика. Психология и социология.– Прага: «Education and Science» 2009. – С. 15-20 (0,33 п.л.).

7. Захарова, О.В. Разноуровневые задания по тригонометрии как элемент усвоения тригонометрических знаний и умений/ Захарова О.В. // Становление современной науки-2009: Материалы V международной научно-практической конференции 27.09-05.10 2009 г./ Том 6. Педагогика. Психология и социология.– Прага: «Education and Science» 2009. – С. 79-81 (0,12 п.л.).

8. Захарова, О.В. Типология тригонометрических уравнений. /Захарова О.В. //Образование и эпоха: международный учебно- методический сборник/ под общей ред. проф. О.И. Кирикова, Ю.А. Бубнова. – Выпуск 4.-Воронеж: ВГПУ, 2008.- С.198-244 (1,35 п.л.)

9. Захарова, О.В. Требования к знаниям и умениям по тригонометрии как основа построения измерения качества математической подготовки. /Захарова О.В. // Научно- теоретический и практический журнал// Уральский научный вестник № 4 (19) //Серия: право, педагогика, история /. Республика Казахстан, Уральск: Уралнаучкнига, 2009.- С.89-92 (0,2 п.л.).

10. Захарова, О.В. Некоторые актуальные проблемы формирования содержания и организации учебной деятельности профильного обучения. /Захарова О.В. // Научно- теоретический и практический журнал// Современный научный вестник № 20 (46) //Серия: педагогика, психология / Белгород: Руснаучкнига, 2008.- С.28-39 (0,52 п.л.).

Учебно-методические работы

11. Захарова, О.В. Основные методы решения тригонометрических уравнений: учеб.-метод. пособие / О.В.Захарова. — Волгоград: Перемена, 2010. — 65 с. (1,8 п.л.).


ЗАХАРОВА Ольга Викторовна

МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ОБУЧЕНИЯ ТРИГОНОМЕТРИИ

УЧАЩИХСЯ ПРОФИЛЬНЫХ КЛАССОВ

Автореферат

диссертации на соискание ученой степени

кандидата педагогических наук


Подписано к печати 10.10.2010 г. Формат 60х84/16. Печать офс.
Бум. офс. Усл. печ. л. 1,4. Уч.-изд. л. 1,5. Тираж 110 экз. Заказ 28.

ВГПУ. Издательство «Перемена»
Типография издательства «Перемена»
400131, Волгоград, пр. им. В. И. Ленина, 27