Рые учатся устанавливать связь между комбинаторными способами решения задач на плавание и решением этих же задач с помощью составляющей топологии- теории графов
| Вид материала | Решение |
- «Применение информационный технологий в теории графов», 272.84kb.
- Утверждаю, 103.15kb.
- Утверждаю, 103.77kb.
- Графы. Решение практических задач с использованием графов (С++) Курсовая работа, 296.48kb.
- Институте Вычислительной Математики и Математической Геофизики со ран создается электронный, 47.84kb.
- "Теория графов в решении задач теории систем", 83.04kb.
- 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
- «Применение ит при решении задач теории графов», 298.34kb.
- Построение структурных сеток трёхмерных геологических сред произвольной топологии для, 27.27kb.
- Календарно-тематическое планирование элективного курса " методы решения физических, 107.87kb.
Топология, привлекает нас еще в детстве при решении головоломок и отгадывании лабиринтов, затем мы ее изучаем как научную дисциплину математики в университете, и наконец обращаемся к ней учителем математики при научно-исследовательской деятельности учащихся, пропагандируя и вовлекая, не только юных математиков, мотивированных на точные науки, но и юных спортсменов, которые учатся устанавливать связь между комбинаторными способами решения задач на плавание и решением этих же задач с помощью составляющей топологии- теории графов.
Обучая пловцов на спортивном отделении лицея, мотивированных на исследовательскую деятельность по математике, отмечая их целеустремленность и гармонию как в спорте, так и в учении, я сформировала творческую группу учеников 10-Е и 11-Е классов: Танасиенко Евгения Александровна, Михайлова Наталья Дмитриевна, Артемов Дания Андреевич, Налейкин Владимир Олегович, Яковишин Александр Дмитриевич, которые являясь участниками ИОУ по математике в 2010 году заняли 4 место в ИОУ г.Тирасполя.
Являясь ведущими спортсменами по плаванию сборной Приднестровья и Молдовы, выезжая на соревнования в различные города и страны мира, они ставят перед собой задачу не только успешно выступить на соревнованиях и добиться блестящих результатов, но и узнать новое в мире культуры, жизни общества и науки других стран и народов, изучить историю и опыт человечества по разным предметам, применить полученный опыт на практике. Так на соревнованиях в Прибалтике, группа познакомилась с историческим фактом Задача о семи мостах города Кенигсберга, являясь математической головоломкой, основана на топологических закономерностях, которые ребята исследовал изучили, проанализировали, систематизировали и представили, как исследовательскую работу: «Применение графов для решения комбинаторных задач спортивной направленности». Задачи, предложенные в работе придуманы ребятами, они понятны пловцам в их практической спортивной направленности и специфики. Изучая « Введение теорию графов», учащиеся убедились, что многие комбинаторные задачи по плаванию, в которых требуется подсчитать количество всевозможных вариантов, можно решать с помощью «графа»-рисунка, от слова grafo-пишу.
Методика применения графов доступна и наглядна, она сводится к исследуемой ситуации, применение свойств уникурсальных фигур, использование графо-дерева, использование графов в прикладных задачах, в частности, для плавания, альпинизма и других видов спорта. Работая над данной исследовательской темой перед учащимися ставятся задачи:
1.Установить связь, между комбинаторными способами решения задач на плавание и решением эти же задач с помощью графов.
2. Развить у учащихся начальные сведения о топологии , как науки.
3. Выработать и систематизировать полученный опыт учащихся решения и составления задач на спортивную направленность.
4. Пропагандировать полученные знания по составлению и решению комбинаторных задач с помощью графов.
5. Применить полученный опыт для составления новых задач и создания базы данных придуманных нами прикладных задач спортивной направленности.
Задача о 7 Мостах Кенигсберга
1). К 18 веку, через реку Прегель, протекавшую по городу Кенигсбергу ( ныне Калининграду), было построено7 мостов, которые связывали берега с двумя островами, расположенных в черте города рис.1

Рассказывают, что жители Кенингсберга хвастали, что никто не сможет осмотреть центр их города, пройдя при этом по каждому из семи мостов лишь по одному разу.
Этой задачей заинтересовались ученые разных стран, решить ее удалось в 1730г. Известному швейцарскому математику Леонардо Эйлеру, который в то время работал в Петербурге в Академии наук, и не приезжая в Кенигсберг, он решил задачу, при чем сумел найти общий метод решения аналогичных задач. Решая задачу о семи мостах, Эйлер поступил следующим образом: он изобразил точками В и С берега реки, а точками А и Д острова, а линиями- мосты, соединяющие соответствующие участки берегов и островов. В результате получилась фигура , приведенная на рис.2

. Из вершины В,С, и Д исходят по три ребра, а из Вершины А- пять ребер.
Вершины графа, из которых исходят нечетное число ребер, Эйлер назвал НЕЧЕТНЫМИ вершинами, а вершины, из которых исходят четное число ребер-ЧЕТНЫМИ. Все вершины данного графа оказались нечетными. Входе решения этой задачи, Эйлер установил следующие свойства графа:
1). Если все вершины графа четные, то его можно изобразить одним росчерком, т.е. не отрывая карандаша от бумаги.
2).Если у графа не более двух нечетных вершин, то его можно изобразить, не отрывая карандаша от бумаги.
3). Если у графа более двух нечетных вершин, то его изобразить одним росчерком нельзя, и граф не будет уникурсальным( от латинского: уни- один, курсор-росчерк).
Поскольку, у графа задачи о 7-ми мостах все вершины нечетные, то его изобразить одним росчерком нельзя, и задача о 7-ми мостах Кенигсберга решения не имеет.
Задача об осе, которая забралась в бассейн, когда пловцы на каникулах, составила Танасиенко Евгения Александровна-Мастер спорта международного класса по плаванию, участница Олимпийских юношеских игр 2010 года в Сингапуре.
Летом, когда пловцы на каникулах, бассейн на ремонте, вода в бассейне спущена, оса забралась в бассейн. В задаче спрашивается, сможет ли оса последовательно обойти все 12 ребер бассейна, не проходя дважды по одному ребру? Подпрыгивать и перелетать с места на место она не может.

У данного графа 4-ре вершины, из которых выходят по три ребра, значит, у данного графа все вершины нечетные, значит, он является не уникурсальной фигурой, поэтому оса не может обойти все ребра не перелетая, и не подпрыгивая, значит задача не имеет решения.
Учащиеся рассмотрели и проанализировали три различные ситуации в геометрии нитей, это графы, представляющие собой нить со свободными концами, либо нить со связанными концами- замкнутая нить, либо нить с узлами на концах. Число узлов- число вершин графа, число промежутков- число ребер графа, учащиеся установили закономерности нитяных ситуаций:
1 ситуация- для нитей, концы которых свободны, число Узлов меньше числа Промежутков на 1, П-У=1
2.ситуция, для нитей, концы которых связаны, замкнутая нить, число Узлов равно числу Промежутков, У=П
3.ситуация-для нитей со свободными концами с узлами на концах, число Узлов на 1 больше числа Промежутков, У-П=1.
Задача№1 на нитяную ситуацию, составил Налейкин Владимир Олегович, мастер спорта по плаванию.
Пловцы Данила, Александр, Владимир и Влад соревновались в заплыве на 200м. Сколько всего толчков о борт бассейна они совершили во время соревнования, если длина бассейна 50м.
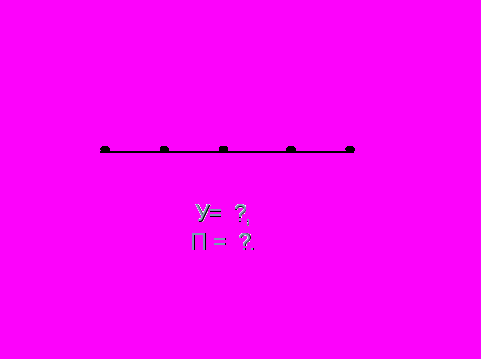
Решение: Условие задачи соответствует нитяной ситуации- нить с узлами на концах, построим граф, вершины которого узлы- число толчков о борт бассейна, ребрами обозначим- число промежутков между толчками, нитяная ситуацияправилу:У-П=1
Найдем число промежутков, т. К. длина бассейна 50м, а длина дистанции: 200м, то число промежутков равно 200:50=4, значит, П=4, по правилу данной нитяной ситуации находим число узлов ( число толчков) У=П+1=4+1=5, значит число толчков 5, т. к. пловцов 5, то 5*5=25. Ответ:25 толчков.
Задача №2 на нитяную ситуацию, составил Яковишин Александр Дмитриевич, мастер спорта по плаванию.
Условие: Команда пловцов принимает участие в соревновании по плаванию на 200м, длина бассейна 50м. Сколько пловцов участвует в эстафете, если число толчков о борт бассейна 45?

Подсчет вариантов с помощью правила произведения и графа дерева.
Граф дерево это дерево вариантов, ребра графа дерева это ветви, рисовать граф дерево полезно, когда требуется записать все существующие комбинации элементов. Дерево вариантов дает наглядное представление о том, как применяется правило произведения при подсчете комбинаций большего, чем два числа элементов.
Задача№3 на подсчет вариантов с помощью графа дерева, составил Артемов Данила Андреевич мастер спорта по плаванию.
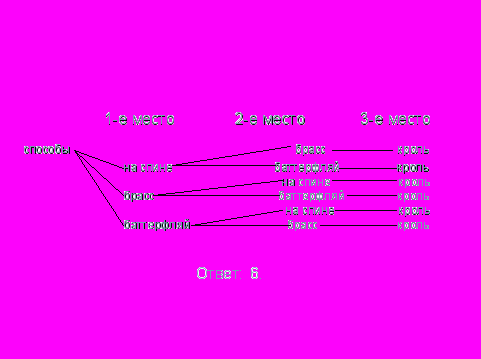
Постановка задачи: КОМПЛЕКС-это плавание поочередно всеми стилями плавания: на СПИНЕ, БРАССОМ, БАТТЕРФЛЯЙ, КРОЛЬ, как правило, комплекс заканчивается КРОЛЛЕМ. Пловцу предстоит выполнить комплекс, длина дистанции 200м, длина бассейна 50м. Сколькими способами может проплыть дистанцию пловец, если выбор стилей за ним, а закончить дистанцию надо кролем?
Построим граф-дерево, вершинами обозначим стили плавания, ребрами все связи существующих комбинаций. При выполнении комплекса пловец может начать дистанцию всеми стилями, кроме кроля, составим дерево вариантов.
Задача о психологической совместимости альпинистов, составила покорительница вершины Эльбрус в 2010 году, Михайлова Наталья Дмитриевна.
Постановка задачи: Известно, что при формировании команды альпинистов для восхождения, предусматривается их психологическая совместимость. Пусть подбирается команда-связка из трех человек: ведомый, ведущий и замыкающий. Имеется 4 кандидата на роль ведущего:А1, А2, А3, А4.
Три кандидата на роль ведомого: В1, В2, В3 и три кандидата на роль замыкающего: С1, С2, С3. Специальные испытания показали:
1). Ведущий А1 психологически совместим с ведомыми В1 , В3 и замыкающими С2, С3.
2). Ведущий А2 психологически совместим с ведомыми В1 и В2 и всеми замыкающими.
3). Ведущий А3 психологически совместим с ведомыми В1 и В2 и замыкающими С1 и С3.
4). Ведущий А4 психологически совместим со всеми ведомыми и замыкающим С2.
Кроме того, ведомый В1 психологически не совместим с замыкающим С3, ведомый В2-с замыкающим С1, ведомый В3- с замыкающим С2.
Сколькими способами при этих условиях может быть сформирована команда-связка альпинистов, состоящая из трех человек для восхождения?
Решение: Составим граф по условию данной задачи: вершинами обозначим тех или иных кандидатов( сохранив те же обозначения), в качестве ребер графа выступит совместимость кандидатов, отмеченных в условии задачи, отсутствие ребра у того или иного означает, что следующая пара людей не совместима.
Получаем 4 графа:
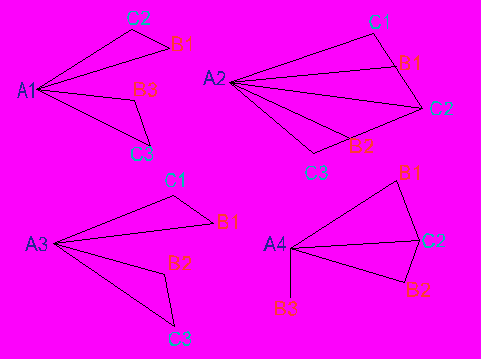
Из рисунка видно, что искомое число всевозможных команд-связок альпинистов для восхождения будет равно числу треугольников с вершинами в точках А, В, С.
Искомые сочетания альпинистов: (А1, В1,С2), (А1, В2, С3) (А2, В1, С2), (А2, В2, С2),
(А2, В2, С3), (А3, В1, С1), (А3, В2, С3), (А4, В1, С2), (А4, В2, С2).
Ответ:10.
Задача об олимпийских кольцах, составила Танасиенко Евгения Александровна

Решение: Если представит кольца в виде графа, где вершины-точки пересечения колец, а ребра, сами линии колец, то получится, что все вершины у данного графа будут четными, так как из каждой вершины графа исходит по 4-ре ребра, значит, полученная фигура-уникурсальна, и ее можно нарисовать, не отрывая карандаша от бумаги.
Лицеисты- спортсмены в результате проделанной исследовательской деятельности составили и решили более 50 прикладных задач спортивной направленности, на различные виды спорта, различные игровые ситуации; научились устанавливать связь между комбинаторными способами решения прикладных задач и их решением с помощью графов; применяют в решении прикладных задач перебор вариантов, правило произведения, факториал числа; проводят уроки-конференции для слушателей лицеистов ТОТЛ, где применяют полученные ими знания в их исследовательской деятельности в области прикладной математики и пропагандируют спорт и здоровый образ жизни.
Литература.
- Перельман Я.И. Занимательная алгебра, Москва, наука, 1973.
- Березина Л.Ю. Графы и их применение, Москва. Просвещение, 1983.
- математика в школе. Москва, 2003.
