Методические указания составлены в соответствии с новой программой и предназначены для студентов-заочников. Даны методические указания по основным разделам программы курса и выполнению контрольных работ
| Вид материала | Методические указания |
СодержаниеТаблица 37. Симплексная таблица 3 |
- Методические указания по выполнению контрольных работ ч. I общие положения, 556.66kb.
- Методические указания по выполнению контрольных работ Специальность, 638.85kb.
- Методические указания и контрольные задания для студентов-заочников Читинского лесотехнического, 346.73kb.
- Методические указания и контрольные задания по выполнению контрольных работ №№1,2 для, 473.31kb.
- Методические указания по выполнению контрольных работ для студентов заочной формы обучения, 255.7kb.
- Методические указания по выполнению контрольных работ (Группа ттз-2), 39.48kb.
- Методические указания по их выполнению по дисциплине «исследование систем управления», 134.73kb.
- Методические указания по изучению дисциплины и задания для контрольных и курсовых работ, 725.2kb.
- Методические указания и контрольные задания для студентов заочников образовательных, 369.95kb.
- Методические указания и контрольные задания для студентов- заочников, экстерната образовательных, 211.24kb.
* В столбце х2 табл. 35 все коэффициенты имеют отрицательные знаки. И этим коэффициентам в столбце свободных членов соответствуют отрицательные значения. В этом случае в качестве разрешающего можем взять коэффициент, от деления на который получим наибольшее положительное частное. При подобном подходе скорее получаем опорное решение. Поскольку такие ситуации редки, решение продолжаем обычным способом.
В табл. 3. опорное решение не получено. Продолжаем его поиск.
Берем любой из двух оставшихся отрицательных свободных членов. Например, первый - 17,6. Первый отрицательный коэффициент в его строке а11 = -1,2 не является разрешающим, так как от деления на него не получаем меньшее положительное частное.
Проверяем: a12=-0,5. Коэффициент является разрешающим. В равной мере разрешающим может быть коэффициент а22=-0,05, т. е. во второй строке, так как полученные частные одинаковы
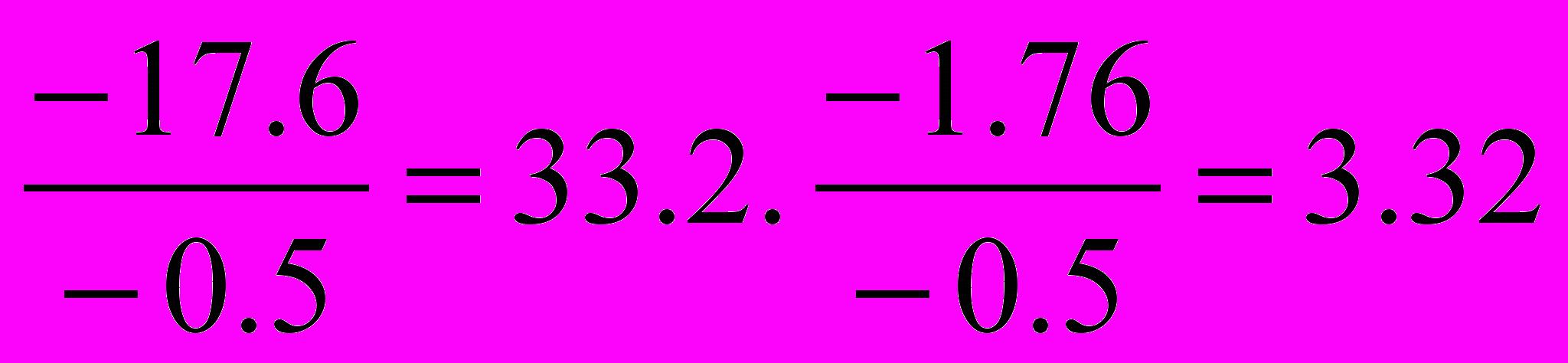
Заменяем небазисную переменную y5 базисной y1 и делаем преобразования (табл. 37).
Таблица 37.
Симплексная таблица 3
| Базисные переменные, λj | Свободные члены, bi | Небазисные | |||
| y3 | х2 | х3 | х4 | ||
у5 | 35.2 | 2.4 | -2 | 0.6 | 0.4 |
| у2 | 0 | -0.01 | -0.1 | -0.003 | 0 |
| xl | 7 | -1 | | | |
| у4 | 5 | 1 | | | |
| х2 | 45.2 | 2.4 | -2 | 0.6 | 0.4 |
| у6 | 40 | | | 1 | |
| у7 | 60 | | | | 1 |
F | 272.54 | -1.92 | -8.4 | 0.12 | 0.48 |
