Учебно-методическое пособие Основы физико-химических методов анализа. Часть фотометрия
| Вид материала | Учебно-методическое пособие |
СодержаниеГлава 3. Основы метрологии аналитического контроля 3.1. Аналитический сигнал Аналитический сигнал 3.2. Погрешности химического анализа Случайная ошибка S и относительное стандартное отклонение S Q-критерия (доверительная вероятность 0,90) Если при заданном числе определений n S, оно равняется 0,36. Делается это с той целью, чтобы при помощи критерия Стьюдента — t Систематическими ошибками Методические ошибки Ошибки, зависящие от применяемых приборов и реактивов Ошибки оперативные Ошибки индивидуальные 3.3. Измерение концентрации вещества в растворе методом градуировочного графика Выбор длины волны Выбор кюветы Построение градуировочного графика Вычисление метрологических характеристик линейного графика Вычисление параметров Вычисление метрологических характеристик результатов анализа ... Учебно-методическое пособие по курсу a handbook with resource material for the course, 711.05kb. Глава 3. Основы метрологии аналитического контроля Аналитическая методика — это сложная, многостадийная измерительная процедура. Изучением общих вопросов, связанных с измерением, обработкой и интерпретацией результатов химического анализа занимается специальный раздел аналитической химии — химическая метрология. Для методов количественного анализа особенно важна их точность. Точность метода — это собирательное название или характеристика, включающая его правильность и воспроизводимость. Когда говорят о высокой точности, то предполагают, что результаты правильные и разброс данных минимальный. Точность часто характеризуют относительной погрешностью (ошибкой) определения в процентах. Из современных методов наиболее точен кулонометрический метод, позволяющий проводить определение компонентов с погрешностью 10-3 — 10-2 %. Требования к точности анализа обычно определяется целью и задачами анализа объекта. Неоправданное требование высокой точности определения обычно удлиняет и удорожает химический анализ, приводит к необходимости использовать сложную и дорогостоящую аппаратуру. 3.1. Аналитический сигнал Для обнаружения компонента или определения его количества измеряют аналитический сигнал. В большинстве методов аналитическим сигналом служат физико-химические величины, функционально связанные с содержанием определяемого компонента, им может быть сила тока, ЭДС системы, оптическая плотность, интенсивность излучения, появление осадка, окраски, спектральной линии. В качественном анализе фиксируют появление аналитического сигнала, в количественном — измеряют его величину. Затем, используя функциональную зависимость аналитический сигнал содержание — y = f(C), рассчитывают содержание компонента. Функция y = f(C) может быть представлена в виде формулы, таблицы или графика и устанавливается опытным или расчетным путем. Аналитический сигнал является суммарной величиной полезного аналитического сигнала и аналитического сигнала фона. Аналитический сигнал фона обусловлен многими причинами, например, составом анализируемого образца, шумами измерительных приборов, чистотой реактивов и многими другими причинами. Избежать аналитического сигнала фона ни в каких случаях не удается. Необходимо максимально снизить его. Аналитический сигнал фона учитывают при проведении контрольного (холостого) опыта, в котором через все стадии химического анализа проводится проба, не содержащая определяемого компонента. Тогда, полезный сигнал будет равен разности аналитического сигнала и аналитического сигнала фона. 3.2. Погрешности химического анализаПогрешности фотометрических определений возникают вследствие неправильно проведенной химической реакции, использования грязных кювет, невоспроизводимости установки кювет в фотометрическом приборе и неточной настройкой его на оптический ноль, нестабильности работы источника сплошного излучения и оптической схемы, а также за счет погрешностей при построении градуировочного графика. По способу вычисления погрешности можно подразделить на абсолютные и относительные. Абсолютной погрешностью называется разность между результатом анализа ( 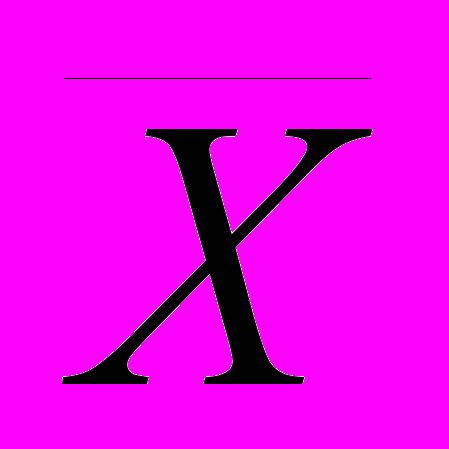 ) и истинным значением () этой величины: ) и истинным значением () этой величины: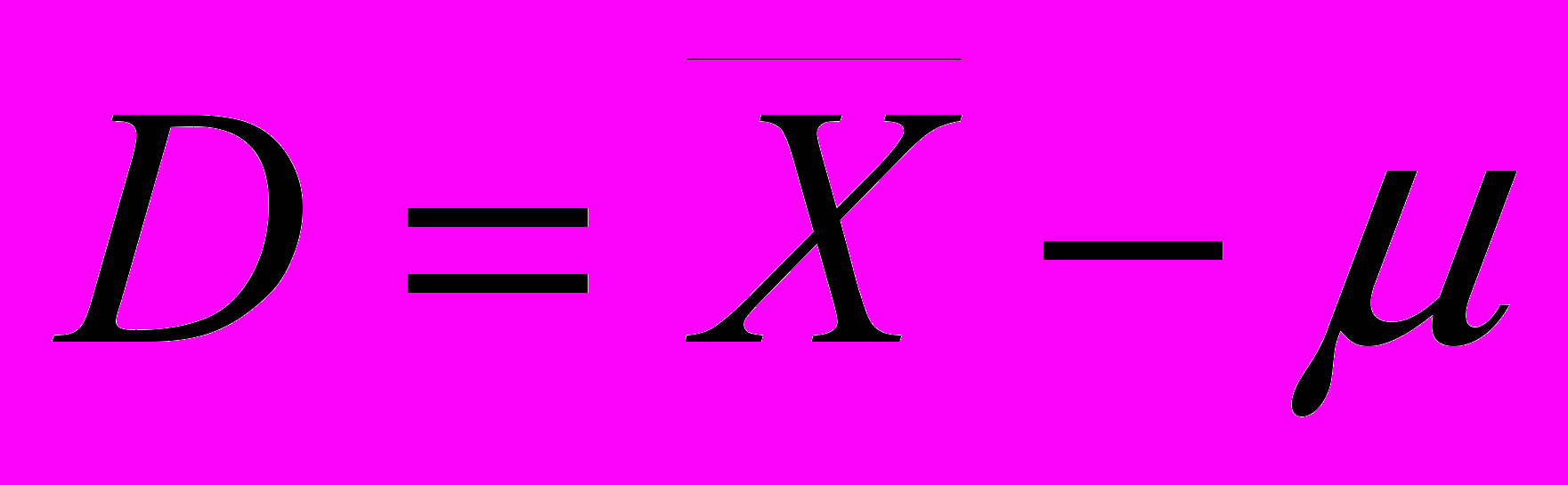 В зависимости от величины 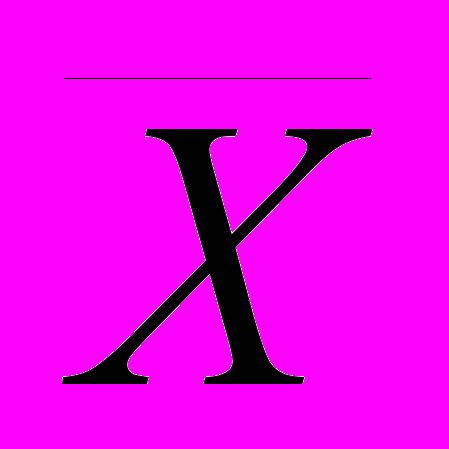 , абсолютные погрешности могут быть и положительными и отрицательными. Относительные погрешности, выраженные в процентах или в долях, знака не имеют: , абсолютные погрешности могут быть и положительными и отрицательными. Относительные погрешности, выраженные в процентах или в долях, знака не имеют: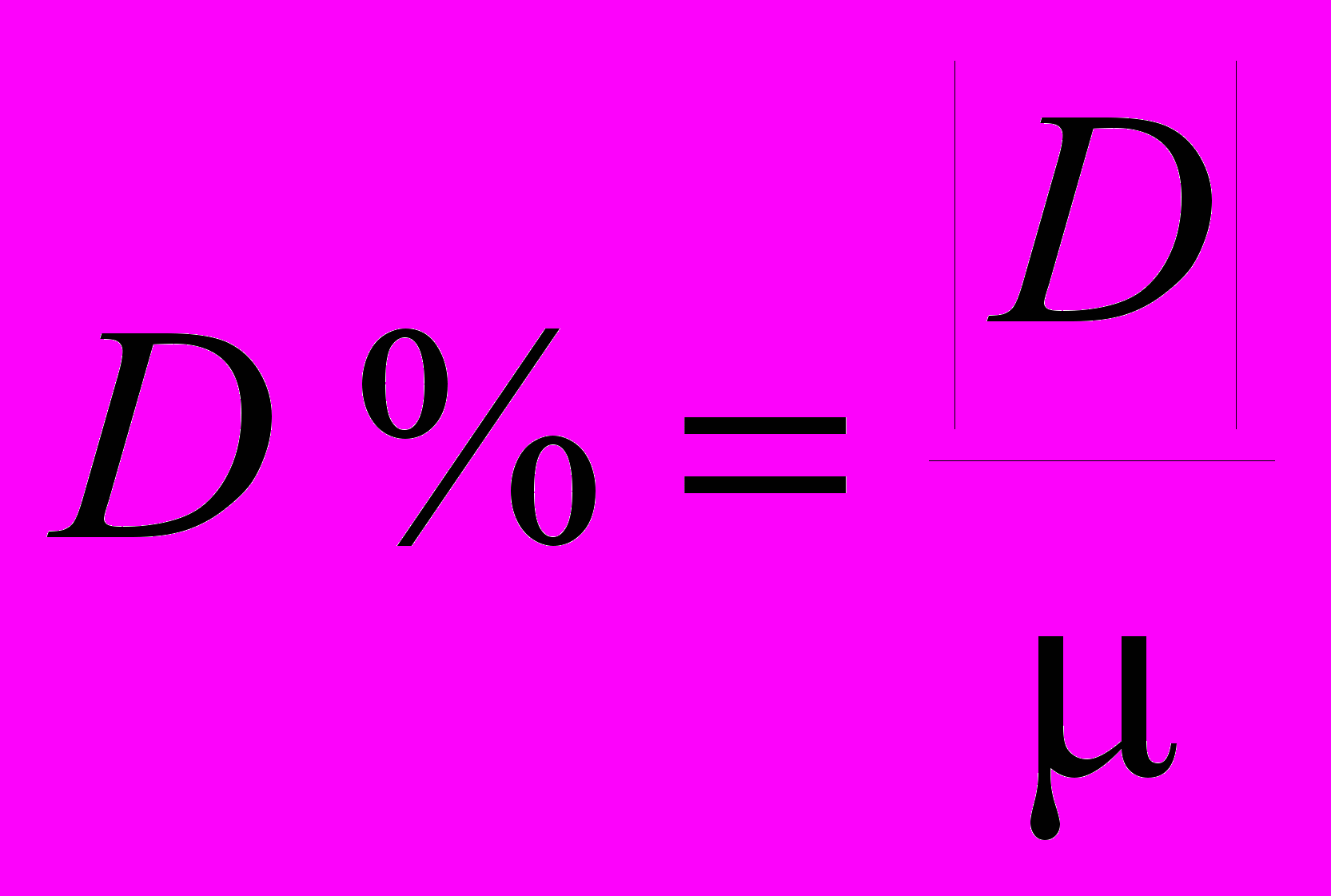 100% 100%Погрешности классифицируют по характеру причин, их вызывающих, на систематические, случайные и промахи.
Промах обычно легко обнаруживается и вызвана либо сбоем в работе прибора, либо ошибкой аналитика. Все виды погрешностей хорошо иллюстрируются на рис.2 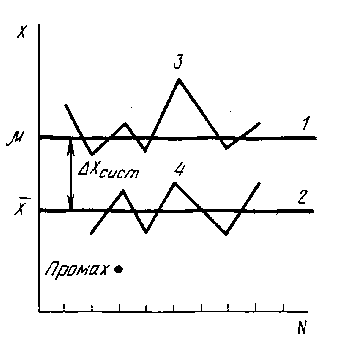 Рис.2. Систематические и случайные погрешности химического анализа Прямая 1 — систематическая и случайные погрешности отсутствуют, идеализированные результаты анализа равны истинному содержанию вещества в пробе . Прямая 2 — все измерения не содержат случайных ошибок, но имеют постоянную отрицательную систематическую погрешность х. Линия 3 полностью отсутствует систематическая погрешность. Линия 4 отражает реальную ситуацию, возникающую при измерениях: налицо и систематическая и случайная погрешности. А выпавшая точка символизирует промах. С систематическими и случайными погрешностями связаны понятия воспроизводимости и правильности. Воспроизводимость характеризует степень близости друг к другу единичных определений, рассеяния единичных определений относительно среднего. Правильность характеризует отклонение полученного результата анализа от истинного значения измеряемой величины (рис.3). 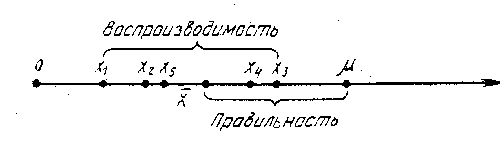 Рис.3 . Воспроизводимость и правильность химического анализа. Часто источники систематических и случайных погрешностей одни и те же. Таблица 2 Типы ошибок и частота их возникновения
Основной вклад в общую погрешность вносят методические погрешности, в которые входят - погрешности отбора пробы (60 %), - переведение пробы в удобную для анализа форму (например, сплавление и растворение), - погрешности операции концентрирования и разделения компонентов (30 %); - погрешности, обусловленные природой химической реакции, взятой в основу методики определения компонента; - инструментальные погрешности или погрешности метода измерения составляют 10 %. Случайная ошибка — одиночное значение, не выходящее за пределы установленной для данного исследуемого компонента области, но стремящееся к выходу за эти пределы. Случайные ошибки происходят при всяком измерении, и в том числе при любом аналитическом определении, как бы тщательно оно не проводилось. Наличие их сказывается в том, что при повторном определении того или иного элемента в данном образце, выполненном одним и тем же методом, дают, как правило, не одинаковые, а несколько различающиеся между собой результаты. Они обусловлены:
Случайные ошибки практически невозможно исключить совсем, но их можно значительно ограничить после оценки размера ошибки. Чем меньше величина случайных ошибок и меньше разброс индивидуальных показателей, тем лучше воспроизводимость лабораторных исследований. Случайные ошибки могут быть выявлены при постановке анализа в двух или больше параллельных пробах. Для обработки случайных ошибок применяются методы математической статистики. Обычно при проведении химического анализа одного и того же объекта стараются получить от 3 до 7 результатов. Полученный числовой ряд называется выборочной совокупностью. Дисперсия V характеризует рассеяние данных в выборочной совокупности относительно среднего: 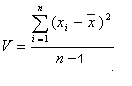 Для характеристики рассеяния результатов в выборочной совокупности используют также стандартное отклонение S и относительное стандартное отклонение Sr: 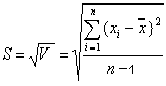 , ,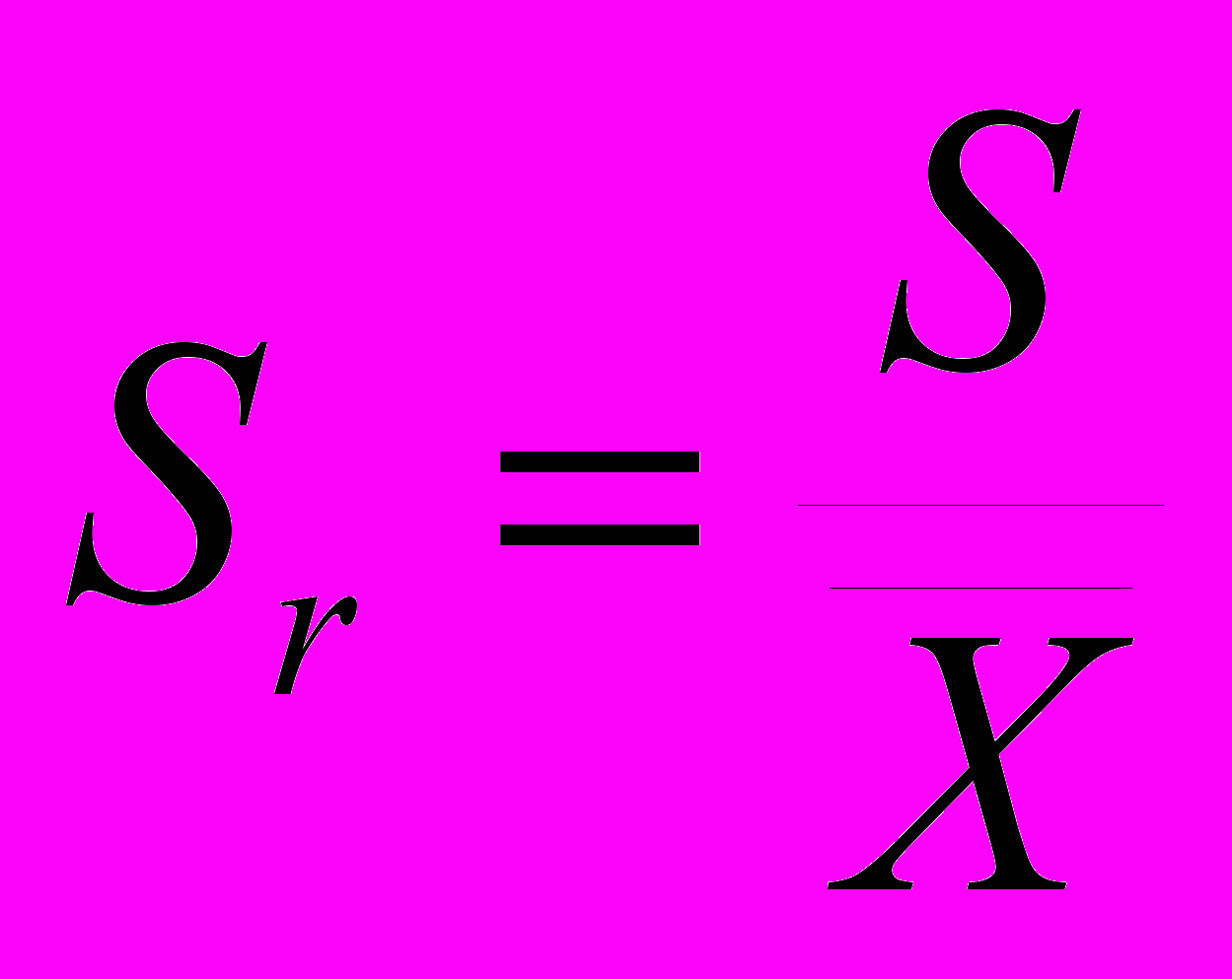 Все три величины — дисперсия, стандартное отклонение и относительное стандартное отклонение характеризуют воспроизводимость результатов химического анализа. Тест, предназначенный для сравнения среднего значения и константы, называется простым тестом Стъюдента. Но прежде чем обрабатывать данные с помощью методов математической статистики нужно исключить из совокупной выборки промахи при помощи Q-критерия (Табл.3). Таблица 3
Делается это следующим образом: рассчитывают Qэксп, равное отношению разности выпадающего результата и величины наиболее близкой к нему, к разности максимальной и минимальной величины результатов определений ( размах): 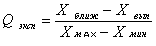 Значения Q-критерия (доверительная вероятность 0,90) Если при заданном числе определений n, Qэксп > Qкритерия, известной из табличных данных, то следует этот результат исключить из выборочной совокупности, а если Qэксп < Qкритерия, то исключать результат нельзя. Поясним эту операцию примером: при проведении химического анализа были получены следующие результаты: (мкг) 2,4; 3,2; 2,5; 2,7; 2,6; 2,5. Можно ли исключать величину 3,2мкг? Оценим Qэксп: 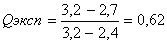 Находим по таблице Qкритерия при 6 параллельных определениях, он в данном случае равен 0,56. Значит, Qэксп > Qкритерия, и результат 3,2 мкг следует исключить. Далее из 5 результатов, образующих выборочную совокупность, находим результат анализа — средний результат: 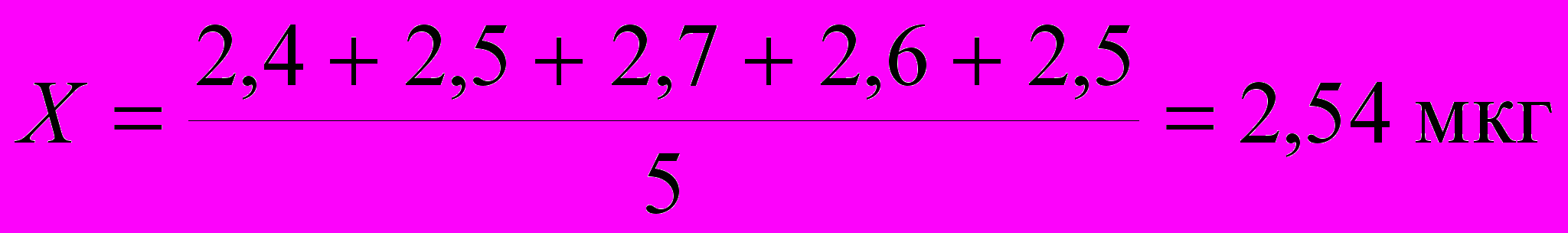 Далее рассчитываем стандартное отклонение S, оно равняется 0,36. Делается это с той целью, чтобы при помощи критерия Стьюдента — t критерия найти доверительный интервал (вероятность) того, что истинная величина будет лежать в пределах, определяемых по следующей формуле: 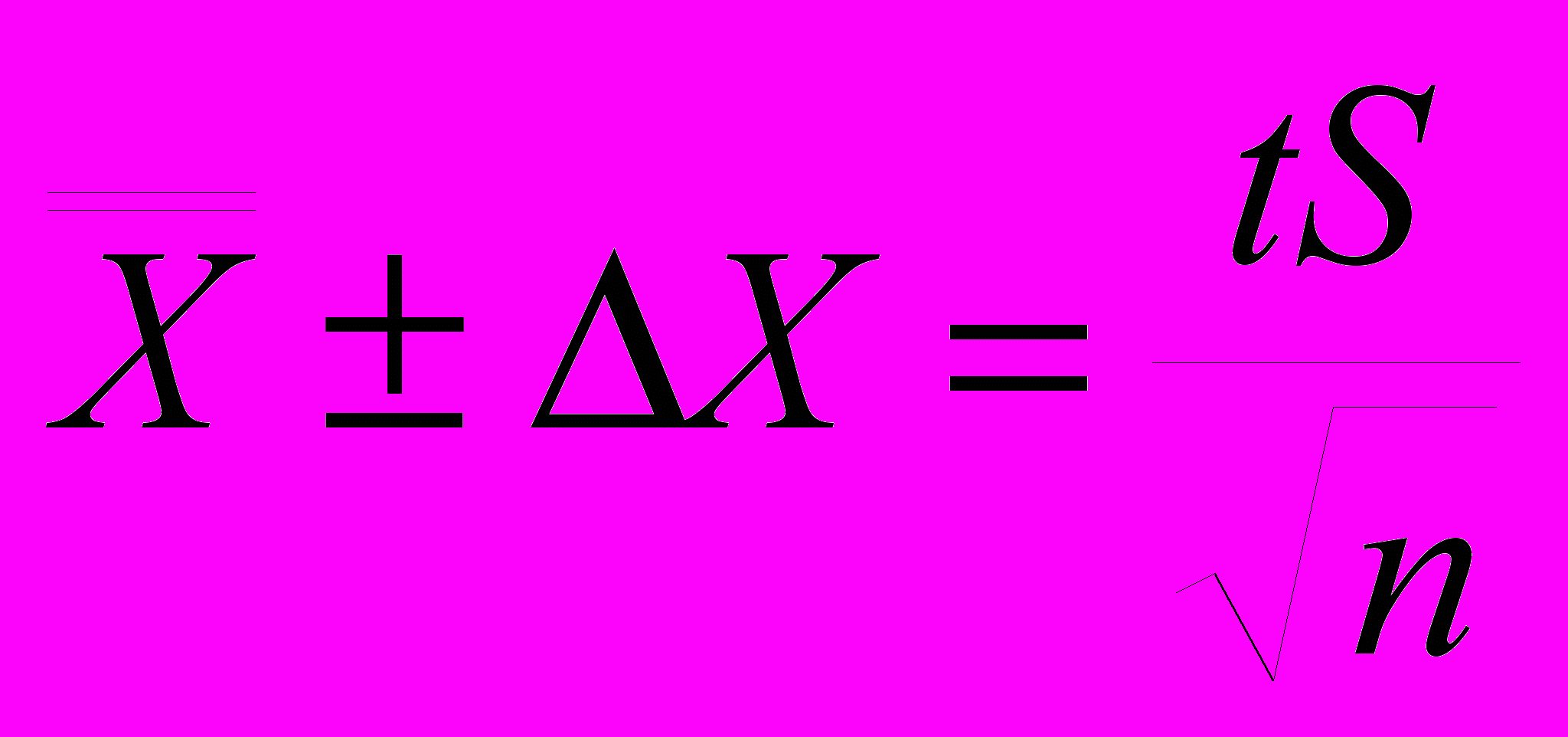 где t — критерий Стьюдента для заданной вероятности Р. Обычно доверительный интервал рассчитывают для вероятностей, равных 0,90 или 0,95. При n равной 5 величина t для Р = 0,90 и Р = 0,95 t0,90 = 2,02 и t0,95 = 2,57. Следовательно, с вероятностью Р = 0,90 истинное значение будет лежать в интервале 2,54 0,32 и с вероятностью 0,95 — 2,54 0,41 мкг. Для оценки достоверности результатов аналитических определений следует учитывать реальные возможности используемого метода или методики. Принято экспериментальные результаты и данные расчеты выражать только достоверно известными цифрами. Например, при гравиметрических методиках взвешивание на обычных аналитических весах позволяет получать результаты с точностью 0,2 мг. Если средний результат анализа содержит сотые доли миллиграмма, то это недостоверные цифры. Если эти цифры >> 5, то следует округлять их в сторону ближайшего большего числа, а если меньше 5 — просто не принимать во внимание. Таким образом, результаты гравиметрического анализа 23,67 мг следует округлить до 23,7 мг, а 35,43 до 35,4 мг. Систематическими ошибками называют погрешности, одинаковые по признаку, происходящие от определенных причин, влияющих на результаты либо в сторону увеличения, либо в сторону уменьшения его. Систематические ошибки можно предусмотреть и устранить или же ввести соответствующие поправки. Наиболее характерными систематическими ошибками являются:
Последние три вида систематических ошибок могут быть учтены и сведены до минимальных величин. Систематические ошибки повторяются при каждом измерении, так как они вызываются постоянными причинами. Поэтому они влияют на всю серию определений. Величина систематической ошибки характеризует правильность результатов анализа. Когда результаты отклоняются от истинного значения на постоянную величину, такая систематическая ошибка называется постоянной ошибкой. Она может вызываться неправильной холостой пробой, а также химической или спектральной интерференцией. Когда ошибки между измеренной и истинной концентрацией пропорциональны концентрации вещества, систематическая ошибка называется пропорциональной ошибкой. Частая причина возникновения пропорциональной ошибки — это ошибочная калибровка. Обнаружение и предупреждение систематических ошибок представляет собой сложную задачу. Систематическую погрешность проще всего выявить с помощью стандартных образцов. Такая проверка одновременно дает возможность испытать и методику, и инструмент измерения аналитического сигнала. Непременное условие применения стандартного образца в химическом анализе — это максимальная близость состава и свойств стандартного образца, и анализируемой пробы. Оценка правильности результатов анализа — проблема значительно более трудная, чем оценка воспроизводимости. Для оценки воспроизводимости нам не надо иметь ничего, кроме серии параллельных результатов измерения. Для оценки же правильности необходимо сравнение результата измерения с истинным значением. Такое значение никогда не может быть известно точно. Важнейшие способы получения информации о действительном значении содержания определяемого компонента в анализируемом образце состоят в следующем.
Существует ряд специальных приемов, которые позволяют выявить, а во многих случаях и существенно снизить систематическую погрешность. Одним из таких приемов служит способ варьирования размера пробы. В этом случае для анализа используют серию проб различного размера (например, несколько аликвот разного объема) и исследуют зависимость найденного содержания от размера пробы. Предположим, что методика анализа содержит систематическую погрешность А, которая постоянна и не зависит от размера пробы. Погрешность такого типа называется аддитивной. Ее влияние состоит в том, что она увеличивает или уменьшает измеряемое значение аналитического сигнала на одну и ту же постоянную величину. Таким образом, при наличии аддитивной систематической погрешности с увеличением объема аликвоты наблюдается закономерное изменение результата анализа — убывание либо возрастание в зависимости от знака А. Однако не всякая систематическая погрешность является аддитивной. Существуют погрешности другого типа, величина которых прямо пропорциональна размеру пробы (или содержанию определяемого компонента). Такие погрешности называются мультипликативными. Они увеличивают или (чаще) уменьшают значение аналитического сигнала в одно и то же число раз, т.е. изменяют наклон градуировочной зависимости. Очевидно, что такие систематические погрешности описанный способ выявить не может. В то же время мультипликативные систематические погрешности можно значительно уменьшить с помощью специального способа градуировки, называемого способом добавок. 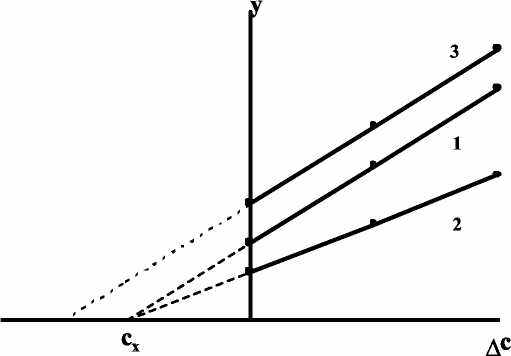 Рис. 4. Градуировка по способу добавок. 1 - систематическая погрешность отсутствует, 2 - наблюдается мультипликативная систематическая погрешность, 3- аддитивная систематическая погрешность Основная цель способа добавок — беспечение максимально точного соответствия условий градуировки и собственно определения. При использовании способа добавок эти две операции совмещаются воедино: известные содержания определяемого компонента вводят как добавки непосредственно в анализируемый раствор и представляют градуировочную функцию в виде графика зависимости аналитического сигнала от концентрации добавки Ас (рис. 4). Содержание компонента в анализируемом растворе находят путем экстраполяции полученной зависимости на нулевое (или фоновое, если оно известно) значение аналитического сигнала. Легко видеть, что в этом случае даже при наличии мультипликативной погрешности (т.е. изменении тангенса угла наклона градуировочного графика) получается правильный результат (ср. кривые 1 и 2 рис.4). В то же время аддитивную систематическую погрешность способ добавок устранить не может (кривая 3 рис.4). 3.3. Измерение концентрации вещества в растворе методом градуировочного графика Для измерения концентрации вещества в растворе необходимо предварительно выполнить ряд подготовительных операций в следующей последовательности: выбор длины волны; выбор кюветы; построение градуировочного графика для данного вещества; измерение концентрация вещества. Выбор длины волны Для достижения наименьшей погрешности в определении концентрации следует правильно выбрать длину волны, на которой будет выполняться измерение. Для этого по спектральной кривой раствора, выбрать такой участок, на котором выполняются следующие условия: - оптическая плотность имеет максимальную величину; - ход кривой примерно параллелен горизонтальной оси т. е. оптическая плотность мало зависит от длины волны. Длина волны, соответствующая этому участку, выбирается для измерения. Если для некоторых растворов второе условие не выполняется, то рабочая длина волны выбирается по первому условию. Выбор кюветы При определении концентрации вещества в растворе необходимо сделать правильный выбор кюветы. Абсолютная погрешность измерения коэффициента пропускания не превышает 0,5%. Относительная погрешность измерения оптической плотности раствора будет различной и достигает минимума при значении оптической плотности 0,4. Поэтому при работе на фотометре рекомендуется путем соответствующего выбора длины кювет работать вблизи указанного значения оптической плотности, например, в пределах от 0,2 до 0,8. При работе на приборе работайте вблизи указанного значения оптической плотности. Если раствор интенсивно окрашен (темный), пользуйтесь кюветами с малой рабочей длиной (10 мм). В случае слабо окрашенных растворов работайте с кюветами с большей рабочей длиной (50 мм). В предварительно подобранную кювету налейте раствор и измерьте его оптическую плотность, введя в ход лучей соответствующий для данного раствора светофильтр. При измерении ряда растворов кювету заполните раствором средней концентрации. Если полученное значение оптической плотности составляет примерно 0,2—0,8, то данную кювету выбирайте для работы с этим раствором. В том случае, когда это не выполняется, испробуйте кювету другой рабочей длины. Построение градуировочного графика Построение градуировочного графика проводить следующим образом. Приготовить ряд растворов данного вещества с известными концентрациями, охватывающими область возможных изменений концентраций этого вещества в исследуемом растворе. Измерить оптические плотности всех растворов и построить градуировочный график, откладывая по горизонтальной оси известные концентрации, а по вертикальной — соответствующие им значения оптической плотности, рассчитанные по методу наименьших квадратов. Следует убедиться в том, что зависимость концентрации от оптической плотности — линейная (по критерию Фишера), т. е. выражается на графике прямой линией. По градуировочной кривой (точнее по уравнению линейной регрессии) в дальнейшем определяют неизвестную концентрацию вещества в исследуемых растворах. Для этого раствор наливают в ту же кювету, для которой построена градуировочная кривая, и, включив тот же светофильтр, определяют оптическую плотность раствора. Затем находят концентрацию, соответствующую измеренному значению оптической плотности. Вычисление метрологических характеристик линейного графика Наиболее объективным и правильным является установление математической зависимости А = f (С), которую находят методом регрессионного анализа. В фотометрических методах она выражается обычно линейной и, значительно реже, параболической зависимостью. Вычисление параметров а и b. В общем случае линейная зависимость выражается уравнением: у = а + bх Значения параметров а и b вычисляют методом регрессионного анализа. Величина a, представляющая собой значение аналитического сигнала при нулевой концентрации определяемого компонента, называется фоновым значением сигнала. Она играет важную роль при оценке чувствительности методик Если имеется п взаимосвязанных пар значений (уi хi), то можно записать: 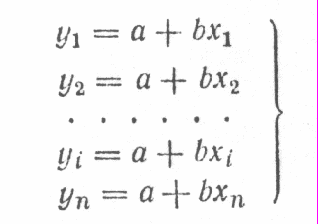 Здесь n — число измерений; хi, — известное содержание (концентрация) определяемого компонента в i-м стандартном растворе; уi — результат измерении аналитического сигнала (оптической плотности) i-го стандартного раствора. В левой части системы уравнении находятся измеренные значения уi, а в правой — вычисленные значения Yi = а + bхi. Разность между обеими величинами дает погрешность. Аналитически задача метода наименьших квадратов может быть выражена в следующей форме: SQ = 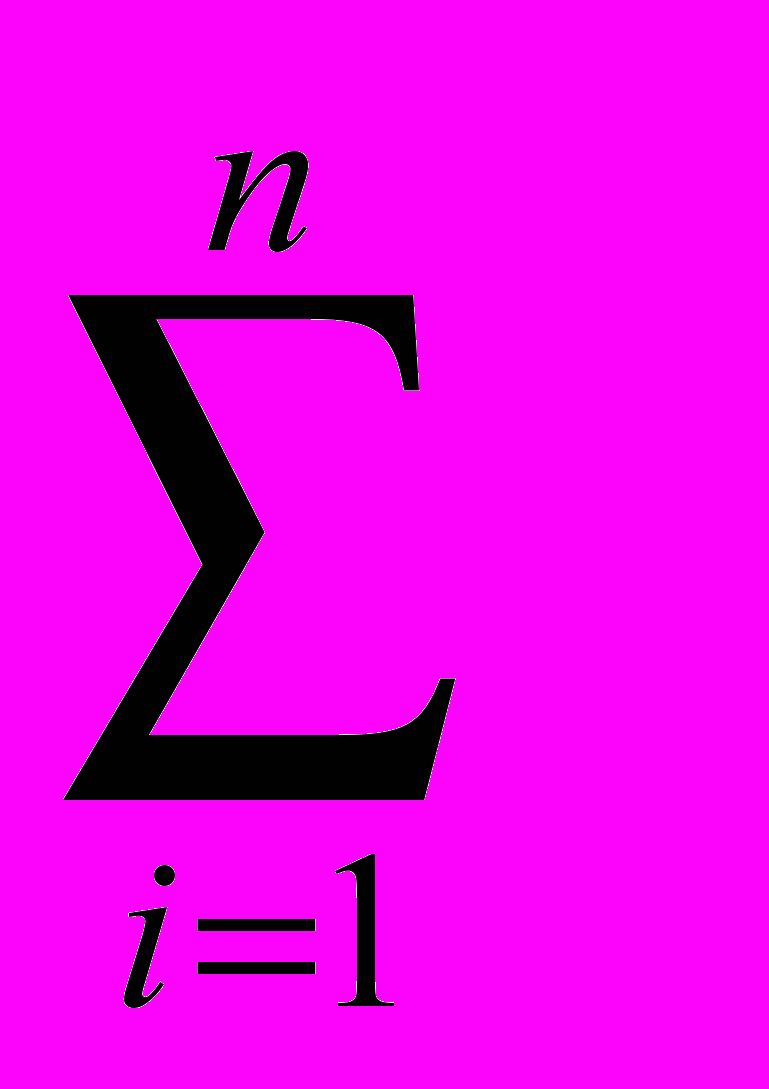 (yi – Yi)2 = (yi – Yi)2 = 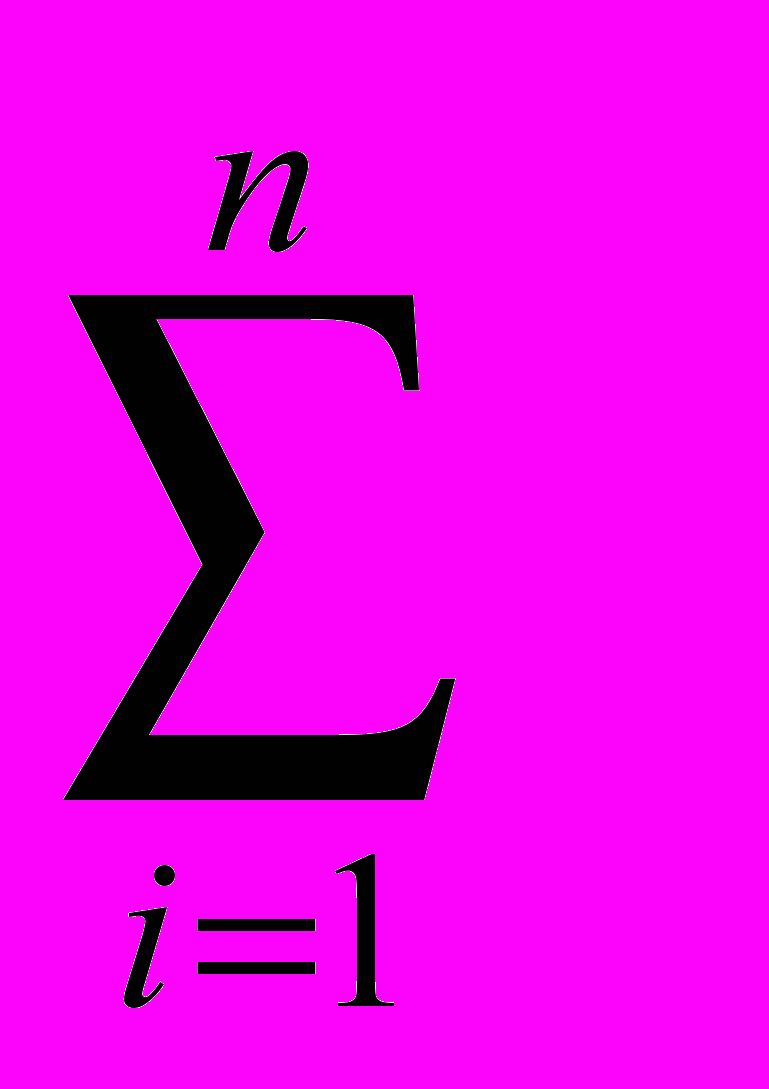 ( yi – (a + bxi)2мин ( yi – (a + bxi)2минЕсли yi – (a + bxi) = δi, тогда SQ = 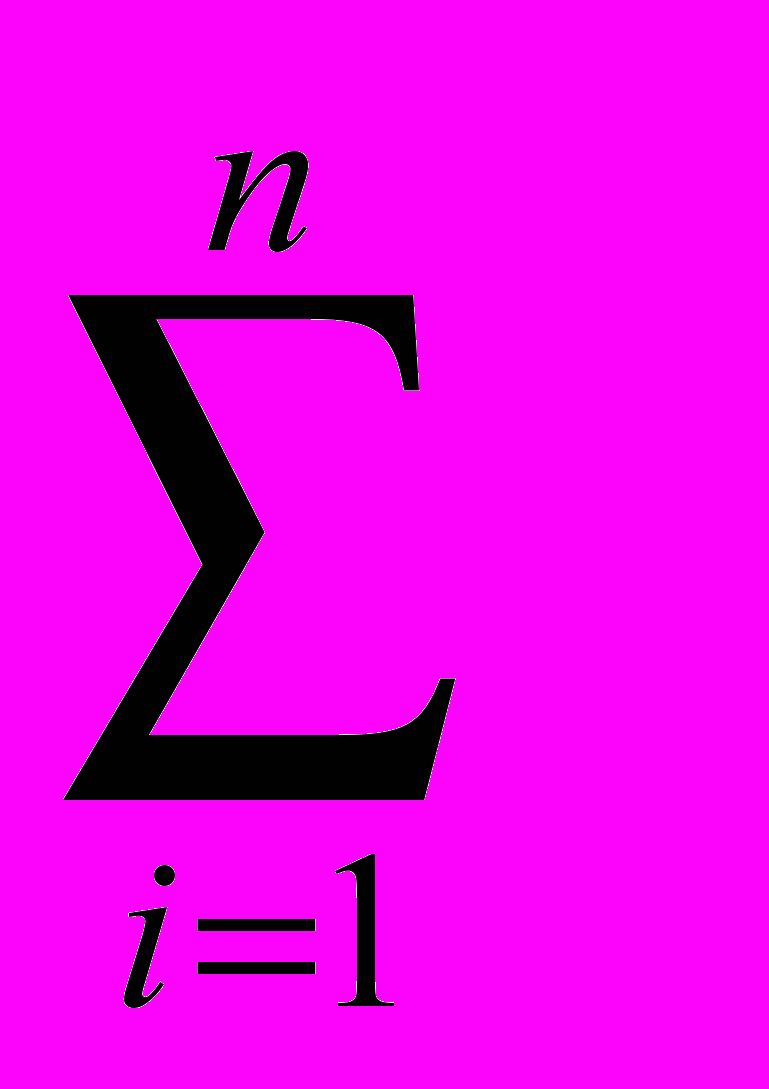 δi2, i = 1, …, n δi2, i = 1, …, nСледовательно, задача линейного регрессионного анализа (метода наименьших квадратов) состоит в том, чтобы сумма квадратов отклонений SQ экспериментальных точек (уi хi) вдоль ординаты от проведенной прямой была минимальной. Для того, чтобы найти параметры а и b, удовлетворяющие минимуму SQ, берут частные производные относительно а, затем относительно b, полученные выражения приравнивают нулю и, решая уравнения, находят; 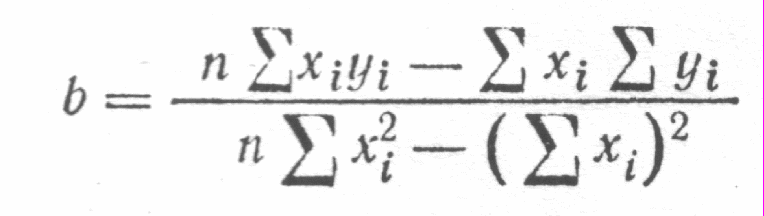 Вычисление метрологических характеристик результатов анализа После того как определена функциональная зависимость у = а + bх и рассчитаны значения а, b, Δа, Δb, по данным измерений аналитического сигнала у (оптическая плотность A) анализируемых проб рассчитывают метрологические характеристики результата анализа. Доверительный интервал результата анализа 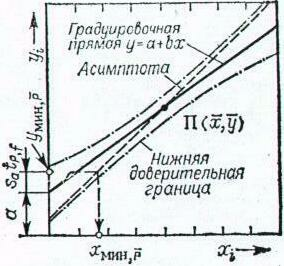 3.4. Измерение концентрации вещества в растворе методом стандартов В методе стандартов сравниваются полезные аналитические сигналы эталонного образца (уэт) с известным содержанием компонента (Сэт) и анализируемой пробы (у х); у эт = S С эт; у х = S С х, где S — коэффициент пропорциональности. Если S — известно, то С х = у х : S. Обычно применяют соотношение: у эт : у х = С эт : С х, откуда  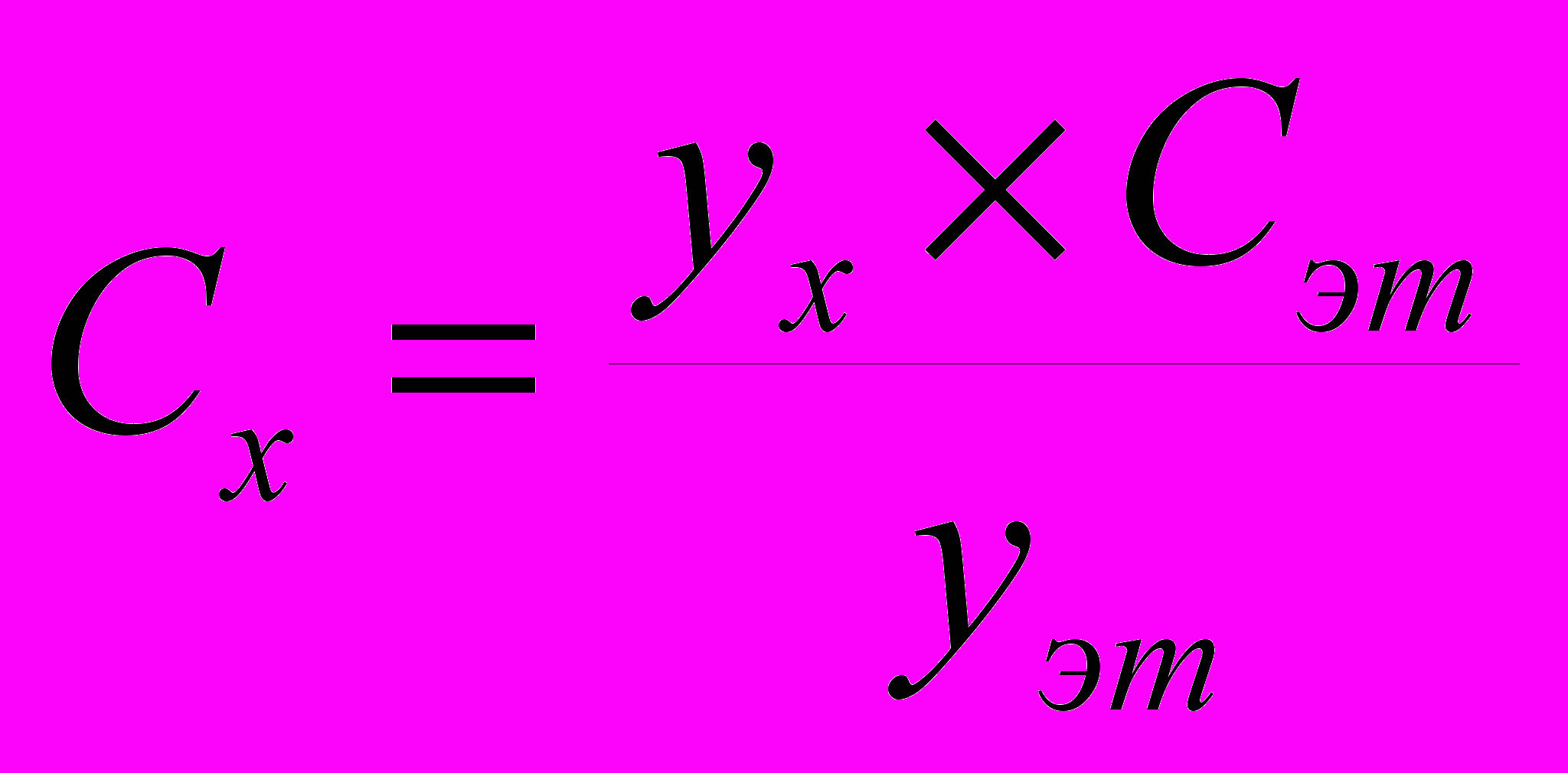 Наиболее надежные результаты получают, когда в качестве образцов сравнения используют стандартные образцы — специально приготовленные материалы, состав и свойства которых достоверно установлены и официально аттестованы специальными государственными метрологическими учреждениями. В способе ограничивающих растворов линейный (в выбранном концентрационном диапазоне) характер градуировочной функции постулируют заранее (и, при возможности, экспериментально проверяют), а стандартный раствор выбирают так, чтобы С1<Сx 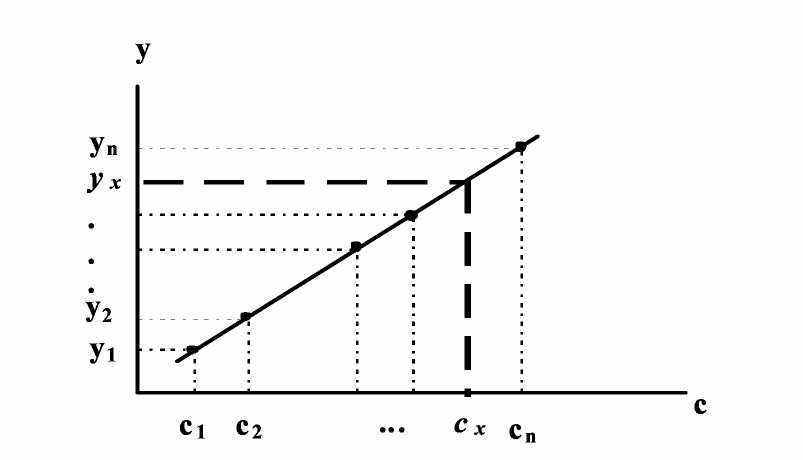 Рис. 5. Метод стандартов Легко видеть, что в этом случае  Если c1 и с2 достаточно близки к сх то способ ограничивающих растворов иногда дает более точные результаты, чем "полный" вариант способа внешних стандартов. 3.5. Измерение концентрации вещества в растворе методом добавок Если нужно учесть влияние матрицы образца, часто используют метод добавок — расчетный и графический. При определении содержания расчетным методом берут две аликвоты раствора анализируемой пробы. В одну из них вводят добавку определяемого компонента известного содержания. В обеих пробах измеряют аналитический сигнал — ух и ух+доб. Неизвестную концентрацию определяемого компонента рассчитывают по формуле: 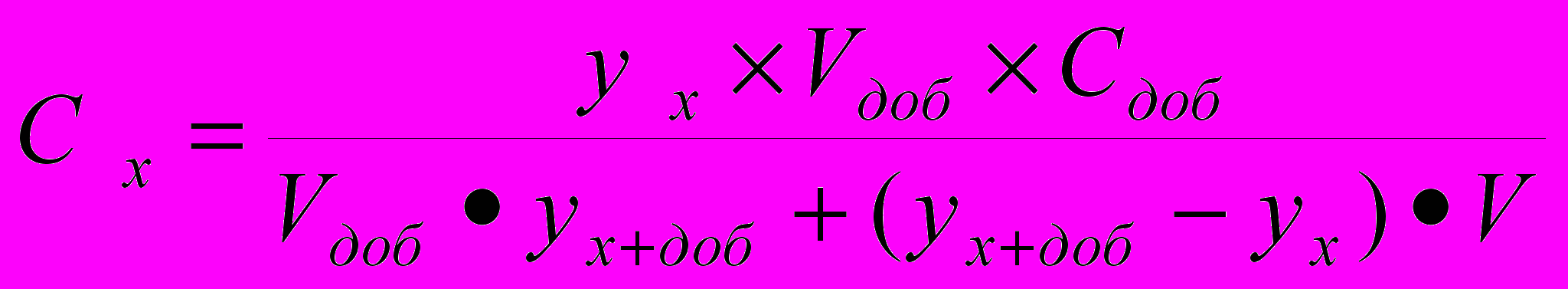 где Vдоб и Сдоб — объем и концентрация добавленного раствора определяемого компонента; V — аликвота анализируемой пробы. При определении содержания компонента графическим методом берут n аликвот анализируемой пробы: 1, 2, 3, , n. В аликвоты 2, 3,, n вводят известные, возрастающие количества определяемого компонента. Во всех аликвотах измеряют аналитический сигнал и строят график в координатах аналитический сигнал — содержание определяемого компонента, приняв за условный ноль содержание определяемого компонента в аликвоте без добавки (аликвота 1). Экстраполяция полученной прямой до пересечения с осью абсцисс дает отрезок, расположенный слева от условного нуля координат, величина которого в выбранном масштабе и единицах измерения соответствует искомому содержанию (Cх) определяемого компонента (рис.6). 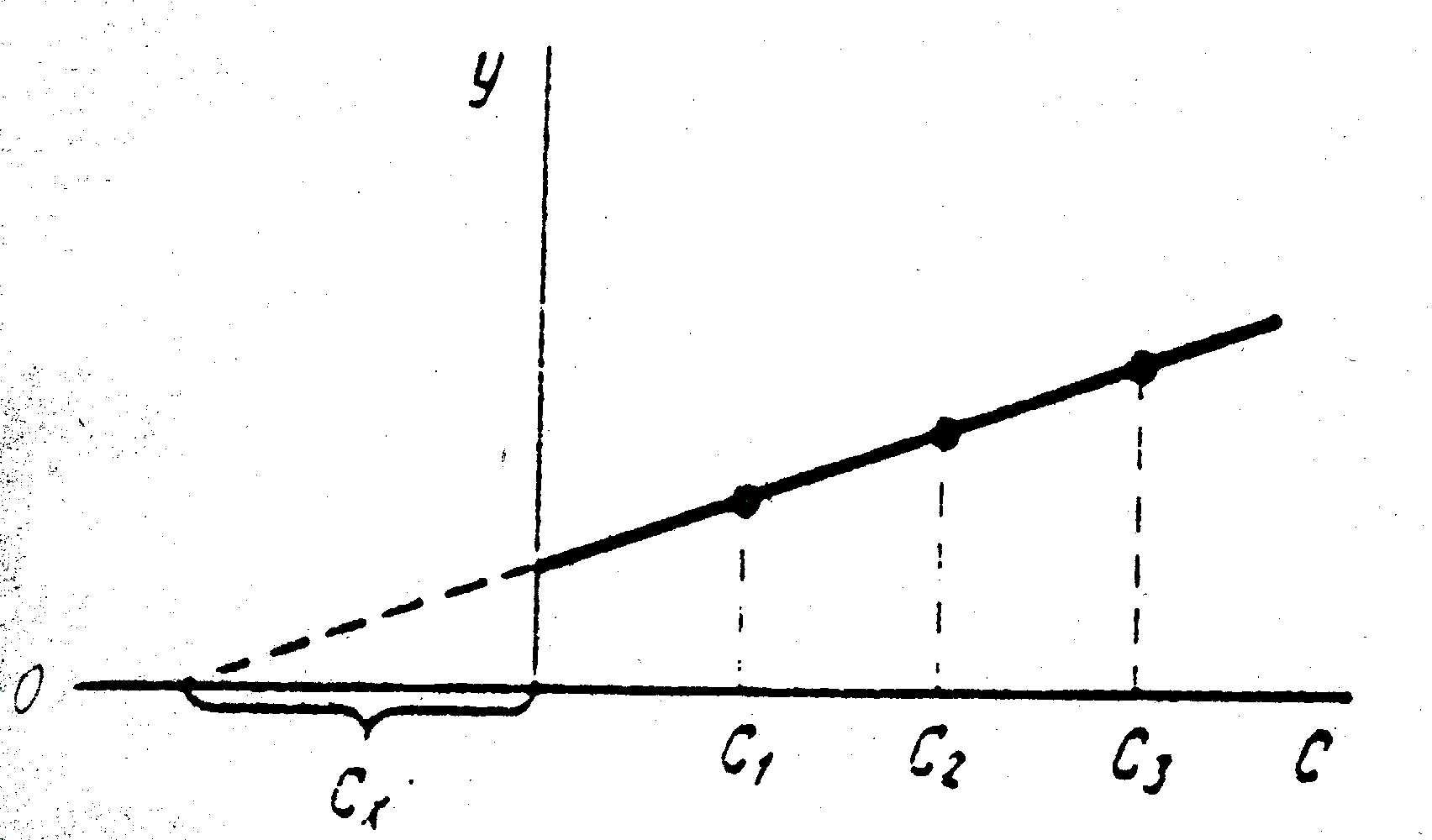 Рис.6. Метод добавок Метод стандартов и метод добавок применимы для линейной градуировочной функции. Метод градуировочного графика допускает использование как линейной, так и нелинейной функций аналитический сигнал — содержание. В последнем случае требуется большее число экспериментальных данных и результат определения содержания компонента бывает, как правило, менее точным. При проведении химического анализа обычно не ограничиваются единичным определением, а проводят, как правило, 3–5 параллельных определений для одной и той же пробы или стандартного образца в одинаковых условиях. Средний результат параллельных определений называется результатом анализа (С или 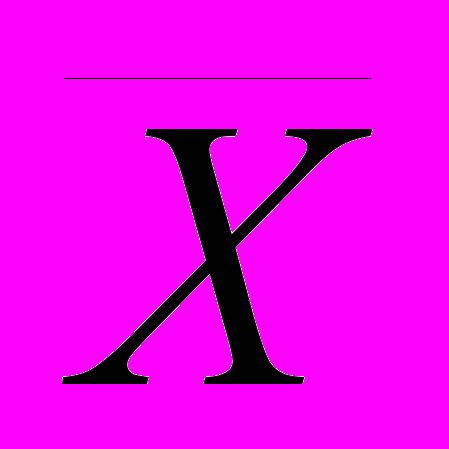 ). Отклонение результата анализа от истинного содержания определяемого вещества () в образце называют погрешностью определения. Поэтому, наряду с определением содержания вещества важна оценка достоверности результатов измерений. ). Отклонение результата анализа от истинного содержания определяемого вещества () в образце называют погрешностью определения. Поэтому, наряду с определением содержания вещества важна оценка достоверности результатов измерений.3.6. Оперативный контроль точности В качестве характеристики случайной составляющей погрешности результата анализа принимают наибольшее возможное значение среднего квадратического отклонения случайной составляющей погрешности (показатель) — σ (∆). В качестве характеристики систематической составляющей принимают границы интервала (∆сн, ∆св, Р), в которых неисключенная систематическая составляющая погрешности находится с принятой вероятностью Р. Контроль сходимости результатов параллельных определений при анализе одной пробы следует проводить по двум параллельным результатам анализа Х1 и Х2, полученным в одинаковых условиях. Считается, что методика находится в контрольном состоянии, если расхождение между параллельными определениями не превышает допускаемого, то есть выполняется условие: │ X1 – X2 │≤ d, где d — норматив контроля сходимости — значение допускаемого расхождения между параллельными определениями, приведенное в методике КХА. При выполнении данного условия среднее арифметическое значение (Х = (Х1 + Х2)/2) принимается за результат анализа. В противном случае анализ следует повторить, используя резервную пробу. Контроль сходимости следует проводить при каждом анализе. Контроль воспроизводимости. Образцами для контроля являются реальные пробы анализируемых объектов. Контроль воспроизводимости следует проводить по двум результатам анализа одной и той же пробы, полученным в разных условиях (Х1 и Х2), допускаемых методикой, например, в разные дни, разными руками, на разных приборах данного типа, с использованием разной посуды и реактивов и т.д. Методика находится в контрольном состоянии, если выполняется условие: │ X1 – X2 │≤ D, где D — норматив контроля воспроизводимости допускаемого расхождения в результате анализа пробы в различных условиях, который также должен приводится в методике КХА. В противном случае один результат или оба неверны, анализ необходимо повторить. Контроль воспроизводимости обязательно следует проводить при смене партии реактивов, посуды, после ремонта прибора и т.д. Контроль точности результатов анализа можно проводить по вариантам: 1. В первом варианте образцами для контроля точности являются пробы стандартных образцов (ГСО), по составу адекватные пробам анализируемых объектов. Если предварительно установлено, что в анализируемой пробе отсутствует определяемый компонент, то образцами для контроля точности может служить реальная проба с добавками ГСО определяемого компонента в диапазоне определяемых концентраций. Добавка делается на самой ранней стадии (до пробоподготовки). Тогда контроль точности результатов анализа можно проводить путем сравнения результатов анализа стандартного образца (образца для контроля) и аттестованным значением концентрации элемента в стандартном образце (образце для контроля). В этом случае расхождения результатов анализа (Х) стандартного образца и его аттестованного значения (Сат) не должны превышать значений К, приведенных в прописи методики анализа: │ X – Сат │≤ К где К — норматив оперативного контроля точности — значение допускаемого расхождения между результатом анализа стандартного (контрольного) образца и аттестованного значения содержания компонента в нем. ГЛАВА 4. ФОТОКОЛОРИМЕТРИЯ 4.1. Общие положения Фотоколориметрический анализ (молекулярная абсорбционная спектроскопия) относится к оптическим методам анализа. Метод основан на способности вещества поглощать электромагнитное излучение оптического диапазона, который включает ультрафиолетовую, видимую и ИК-области. Наибольшее распространение получили фотометрические методы анализа, основанные на поглощении окрашенными соединениями в видимой области спектра, т.е. в интервале длин волн 400 — 780 нм. Фотометрический метод анализа широко применяется в практике аналитического контроля. Метод имеет низкий предел обнаружения (10-5 — 10-6 М), относительная ошибка большинства определений 1 — 2 %. Поглощение квантов h электромагнитного излучения оптического диапазона молекулой или ионом обусловлено переходом электронов на орбитали с более высокой энергией. Каждая молекула обладает определенным набором возбужденных квантовых состояний, отличающихся значением энергии, поэтому интенсивно поглощаются те кванты света, энергия которых равна энергии возбуждения молекулы. Характер поглощения зависит от природы вещества, на этом основан качественный анализ. За формирование аналитического сигнала ответственными являются в основном d d*- и *- переходы. d d*- переходы характерны для аква-ионов и некоторых комплексных соединений d-элементов с неполностью заполненными d-орбиталями. *- переходы свойственны молекулам органических соединений и обеспечивают их окраску. Для количественного анализа используют зависимость светопоглощения от концентрации определяемого вещества. П 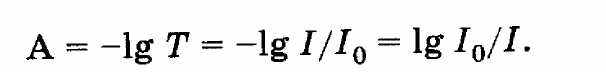 оглощение света подчиняется закону Ламберта – Бугера – Бера А = lc где А — оптическая плотность, I0 и I — интенсивности падающего и прошедшего через образец света, T — пропускание, — молярный коэффициент поглощения (экстинкиции), l — длина оптического пути (толщина поглощающего слоя) в см, c — молярная концентрация. Закон этот строго справедлив только для разбавленных растворов и в определенных условиях:
Молярный коэффициент светопоглощения характеризует чувствительность реакции и является постоянной величиной для данного окрашенного соединения. Для повышения чувствительности определения выбирают реакцию с максимальным значением (см. справочник по аналитической химии). Молярный коэффициент поглощения раствора можно рассчитать, если приготовить серию растворов с известными концентрациями веществ и измерить оптическую плотность раствора. Коэффициент линейной регрессии зависимости А = f(С) представляет собой молярный коэффициент поглощения. Спектры поглощения одного и того же вещества в координатах А - имеют одинаковый вид независимо от толщины слоя раствора или концентрации вещества в растворе и характеризуются максимумом при одной и той же длине волны, при которой и проводят все определения. Селективно подбирая длину волны, отвечающую максимуму поглощения вещества, можно исключить влияние матрицы (растворителя). Если исследуется смесь нескольких поглощающих веществ, то концентрацию каждого из них определяют, проводя измерения при длинах волн, отвечающих максимумам поглощения этих веществ Возможности современных измерительных приборов таковы, что позволяют измерять величину А от 0,02 до 3,0. Однако для получения удовлетворительных по точности результатов значения измеряемой оптической плотности должны находиться в пределах 0,2 < А < 0,8. Для проведения фотометрических исследований необходимо соблюдать ряд условий:
Все фотометрические определения проводят по единой схеме:
Измерение поглощения проводят с помощью фотоэлектроколориметров. Фотоэлектроколориметрия — анализ на основе измерения поглощения нестрого монохроматичного излучения. Цвет раствора всегда является дополнительным к цвету поглощенного излучения (табл. 1). Цвет светофильтра является дополнительным к цвету раствора и соответствует участку спектра, который этим светофильтром пропускается. Таблица 1 Наблюдаемые цвета и соответствующие им поглощенные участки спектра
Прохождение потока электромагнитной энергии через какую-либо жидкую среду сопровождается такими явлениями, как поглощение (уменьшение энергии потока), рассеяние и некоторые другие. Поток световой энергии, переносимый через единицу площади, называют интенсивностью потока световой энергии. На рис. показано изменение интенсивности потока световой энергии при прохождении света через раствор (а) и дисперсную среду (б) с толщиной поглощающего слоя L. 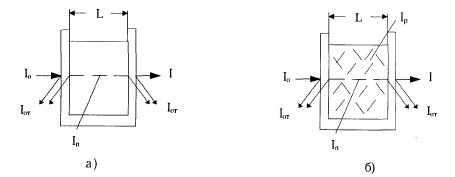 где: где:10 — интенсивность падающего потока световой энергии; 1от — интенсивность потока световой энергии, отраженной от стенки кюветы; 1п — интенсивность потока световой энергии, поглощенной окрашенным раствором; 1р — интенсивность потока световой энергии, рассеянного дисперсной средой; I — интенсивность потока световой энергии, прошедшего через слой исследуемого вещества. Если не учитывать поглощение потока световой энергии стенками кюветы, то интенсивность падающего светового потока 10 при прохождении кюветы с раствором и дисперсной средой разлагается на составляющие следующим образом: I0 = Iот + Iп + I — для раствора, I0 = Iот + Iп + Iр + I — для дисперсной среды. В фотометрии 1от, как правило, компенсируется или учитывается.
Фотометрические методы исследования базируются на способности жидких сред (растворов) поглощать и/или рассеивать, отражать электромагнитное излучение и даже излучать в результате химической реакции. 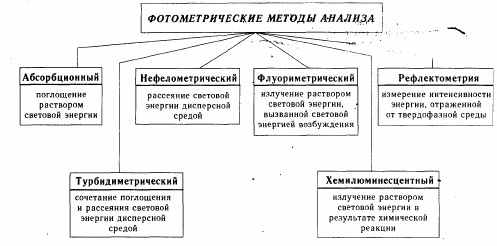 Рис.7 Классификация фотометрических методов лабораторных исследований 4.3. Измерение концентрации вещества в раствореПроводят
см.
вопросы для самоконтроля – стр.56, 66 2. Васильев В.П. Лабораторный практикум стр. 149-157 4.4. Вопросы
4.5. Задачи
=104.
 -кремнемолибденовой гетерополикислоты H4(SiMo12O40)•nH2O ( -кремнемолибденовой гетерополикислоты H4(SiMo12O40)•nH2O ( = 2,2•103 л•моль-1•см-1 при = 2,2•103 л•моль-1•см-1 при  = 400 нм), поглощение которого в кювете с l = 1,00 см отвечало бы минимальной погрешности фотометрических измерений (Аопт = 0,434)? = 400 нм), поглощение которого в кювете с l = 1,00 см отвечало бы минимальной погрешности фотометрических измерений (Аопт = 0,434)? |
