Технології навчання математиці

Вид материала

Содержание

Р Рис. 10 озв’язання.
Правило проведення знакової кривої
Розв’язання. Один із співмножників є радикалом, а тому повинно бути x
3. Розвязування алгебраїчних нерівностей за допомогою методу інтервалів.
Завдання для самостійного розв’язання

Подобный материал:

Технології навчання математиці

є не що інше, як технології

математичної діяльності.

МЕТОД ІНТЕРВАЛІВ

1. Попередні відомості

Нагадаємо, що функція у = f(x) розуміється як однозначна залежність змінної у (функція) від змінної x (незалежна змінна, або аргумент) і позначається символом у = f(x).

Сукупність значень x, для яких вираз у = f(x) має сенс або, як ще говорять, визначений, називається областю визначення функції і позначається символом D(f). Сукупність всіх значень функції називається областю її значень – позначається Е(f).

Значення аргументу х відкладаються на осі абсцис, яку ми називатимемо віссю Ох, а також числовою віссю або числовою прямою; значення функції у відкладаються на осі ординат – осі Оу.

Нагадаємо, що нулями (коренями) функції у = f(x) називаються ті значення її аргументу, для яких функція перетворюється в нуль. Наприклад, для квадратного тричлена f⁽x)=2x²+5x–3 значення х, рівні числам –3 і 0,5, є його нулями або коренями, оскільки, легко переконатися, f(–3)=0 і f(0,5)=0.

Нулі функції у = f(x) визначаються як корені відповідного рівняння f(x)=0. В нашому прикладі для функції f(x)=2x²+5x–3 відповідним є рівняння 2х² + 5х – 3 = 0, а його корені х₁= –3 і х₂= 0,5 є нулі функції.

Г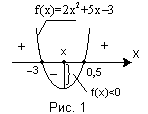еометрично нулі функції представляють собою точки осі Ох (числової прямої), в яких графік функції перетинає або торкається цієї осі.

Накресливши схематично графік квадратного тричлена f(x)=2x²+5x–3 – параболу, гілки направлені вгору, х = –3 і х = 0,5 –нулі функції, – переконуємося наочно, – або, говорять ще, візуально, – що в нулях функції графік має спільні точки з віссю Ох – перетинає вісь Ох в нашому випадку (мал. 1).

Підкреслимо ще раз, що аналітично нулі функції у = f(x) знаходяться як корені відповідного рівняння f(x)= 0.

Проміжки числової прямої, на яких функція у = f(x) має постійний знак, тобто або знак «+», або знак «–», називаються проміжками знакосталості функції.

На мал. 1 наочно видно, що всі значення f(x) для проміжку (–3; 0,5) від’ємні, тому проміжок (–3; 0,5) називають проміжком знаковід’ємності. Графік функції на цьому проміжку лежить нижче за вісь Ох і цей факт ми позначаємо значком «–» під відповідною ділянкою кривої.

Навпаки, для будь-яких значень х з проміжків (-; –3) і (0,5; +) функція додатна, і, отже, множина (–; –3)  (0,5; +) є проміжком знакододатності функції f(x). Графік функції на цій множині лежить вище за вісь Ох, що позначається відповідним значком «+» (рис.1).

Т

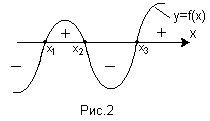аким чином, для графіка деякої функції y=f(x), зображеного, наприклад, на рис.2, для проміжків знакододатності функції частина цього графіка розташовується над віссю Ох (всі ординати f(x) тут додатні), для проміжків знаковід’ємності функції відповідна частина графіка функції лежить під віссю Ох (всі ординати функції f(x) від’ємні). Ці факти візуалізуються знаками «+» або «–», поставленими під відповідними ділянками графіка функції (рис.2).

Звернемо спеціальну увагу на те, що нулі функції – точки х₁, х₂, х₃ – не входять в проміжки її знакосталості. В цих точках функція перетворюється в нуль, а отже, не є ні додатною, ні від’ємною (нуль – беззнакове число, за визначенням).

Тепер, якщо крива, зображена на мал. 3, є графіком функції у = f(x), то по цьому графіку відразу можна сказати, що:

х

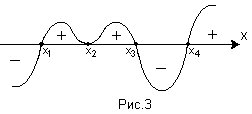₁, х₂, х_3,х₄ – нулі функції;

на проміжку (х₁; х₂)  (х₂; х₃)  (х₄; +) функція додатна, тобто f(x) >0;

на проміжку (–; –х₁)  (х₃; х₄) функція від’ємна, тобто f(x) <0.

Зверніть увагу, що в точці х₂ не відбувається зміни знака функції. В цій точці лише виконується умова f(x₂)= 0.

Н

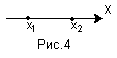агадаємо також, що з двох чисел, що зображаються точками на числовій прямій, більшим є те, яке зображене правіше розташованою точкою. Так, з двох чисел х₁, х₂(зображених точками на числовій прямій) більшим є число х₂, оскільки відповідна йому точка розташовується правіше за точку x₁(мал. 4). Але тоді різниця чисел х₂ – х₁, очевидно, додатна, тобто х₂ _–х₁ _>0, а «зворотна» різниця х₁ – х₂ у такому разі буде від’ємною: х₁ – х₂ < 0.

Назвемо точку М(х) рухомою або змінною, якщо її координата х є змінна величина.

К

оордината х, міняючись з часом, «примушує» точку М(х) міняти своє положення на числовій прямій і точка М(х) як би «рухається». В необхідних випадках напрям руху вказується стрілкою (рис.5).

Якщо в якийсь проміжок часу змінна х приймає значення х₀, то точка М приймає, як то кажуть, фіксоване положення М₀, тобто при х = х₀, М(х)= М(х₀)= M_0. При безперервній зміні координати х положення рухомої точки М(х) на числовій прямій міняється також неперервно, тобто не пропускається жодне з її можливих фіксованих положень. Надалі, якщо не буде обумовлене інше, припускатимемо тільки неперервну зміну положення рухомої точки М(х) на числовій прямій.

Нагадаємо ще, що областю визначення будь-якого многочлена є вся числова вісь, тобто множина R; графіком многочлена є неперервна крива.

Під неперервною кривою розумітимемо таку криву, яку можна накреслити, не відриваючи олівця або ручки від поверхні паперу.

Також нагадаємо, що будь-який многочлен може бути розкладений за його нулями (коренями), тобто може бути представлений у вигляді добутку простих співмножників. Наприклад, якщо многочлен f(x)= ах² + bx +с має коренями числа х₁, х₂, то його можна записати у вигляді добутку f(x)= а(х – х₁) (х – х₂), де (x – x₁), (x – x₂) – прості, тобто нерозкладні далі множники.

Взагалі многочлен n-го степеня з однією змінною х, що розглядається як функція f(x), представимо у вигляді добутку f(x)= а(x-x₁)(x-x₂).(x-x_n) Q(x). Такий добуток ми називатимемо стандартним представленням або розкладання^м многочлена (функції) на множники, якщо виконуються наступні умови:

Q(x) – додатний при всіх значеннях х з R многочлен, що не має дійсних коренів, ступінь якого парний і не перевершує n. Цей многочлен може і бути відсутній;
а – старший коефіцієнт заданого многочлена f(x), тобто коефіцієнт при х_n;
х₁, х₂., х_n – нулі (корені) функції f(x);
змінна х в кожній дужці стоїть на першому місці;
коефіцієнт перед змінною х в кожній дужці є одиниця.

2 Знакова крива

Півплощину над віссю Ох (тобто при y>0) вважатимемо додатною, півплощину під віссю Ох (при y<0) вважатимемо від’ємною. Додатна півплощина позначатиметься значком «+», а від’ємна – значком «–»; по відношенню одна до одної півплощини називатимуться суміжними.

Як попередній приклад розглянемо деякий многочлен 3-го степеня, нулями якого є числа 1, –2, 5. Згідно вищесказаному, цей многочлен можна розкласти по нулях, тобто представити у вигляді добутку f(x)= а(x – 1)(x+2)(x – 5), де а – деяке число (коефіцієнт перед х³), яке вважатимемо додатним.

Відзначимо точками на числовій прямій числа 1, –2, 5 (не в масштабі, але в порядку зростання) і візьмемо змінну точку x правіше за най правішу з отриманих «числових» точок (рис.6). Примусимо змінну точку х рухатися вліво (напрям вказаний стрілкою).

Поки рухома точка х знаходиться правіше за точку х = 5, кожна з дужок в добутку а(х+2)(х –1)(х –5) додатна. Отже, весь добуток, а значить, і функція f(x) додатні. Це означає, що на проміжку (5; +) функція знакододатна, і тому її графік розташовується над віссю Ох. Цей факт ми схемно відзначимо кривій, розташованій над числовою прямою із значком «+» (рис.6).

Коли змінна точка співпаде з точкою, що зображає число 5, отримаємо (х – 5) = (5 – 5)= = 0. І тоді весь добуток, а вслід за ним і функція f(x), перетвориться в нуль. Відповідна крива, що зображає графік функції, торкнеться осі Ох (мал. 6).

Д

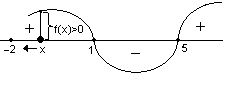
Рис. 6
алі рухома точка «заходить» в проміжок (1;5) – рис.7 – і, оскільки точка х тепер уже розташується зліва від точки, що зображає число 5, дужка (х – 5) стає від’ємною. Решта дужок в добутку як і раніше додатна, і тому весь добуток стане від’ємним: всі множники – «плюси», а один – «мінус».

К

Рис.7
рива, яку ми називатимемо знаковою, прийме вигляд, зображений на рис.7. Для проміжку (1;5) ця крива розташується під числовою прямою, що позначається знаком «–».

П

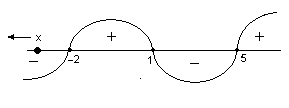
Рис. 8
ри збігу рухомої точки x з точкою x = 1 дужка (х – 1) в розкладі перетвориться в нуль, і знакова крива перетне вісь Ох в точці х = 1 знизу вверх, переходячи в додатну півплощину (мал. 7). Потім рухома точка х переходить на проміжок (–2;1), і в цьому випадку множник (х+2) стає додатним, а множники (х–1) і (х–5) – від’ємні. Тоді весь добуток матиме «один знак «плюс» і два знаки «мінус»»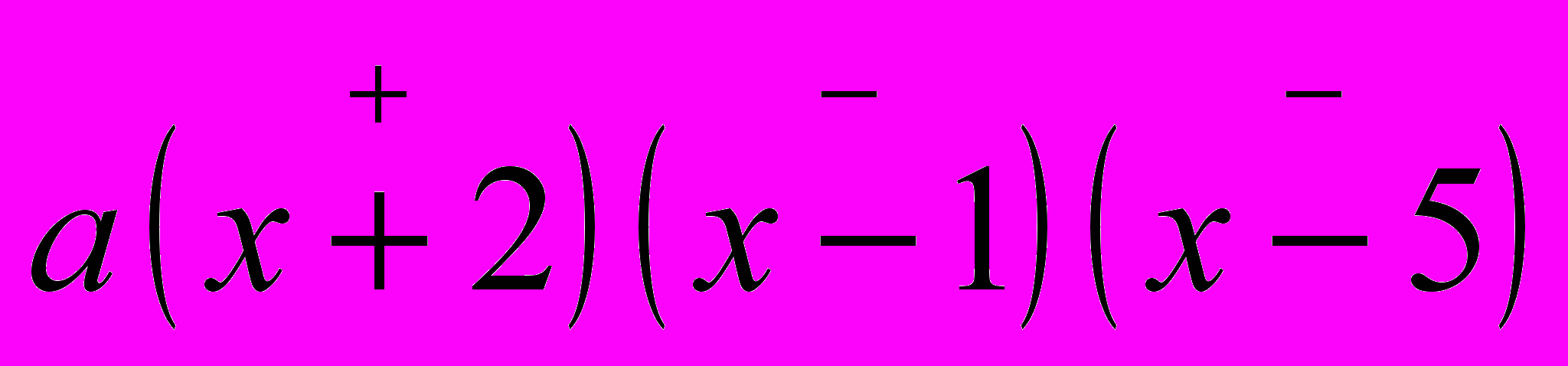. Після того, як рухома точка х переходить положення точки х = –2 (знакова крива перетинає числову вісь зверху вниз) і займає положення зліва від усіх числових точок, всі дужки стануть від’ємними, а отже, і сама функція стане від’ємною, тобто («непарний добуток «мінусів» є «мінус»»).

Побудова знакової кривої закінчена і вона прийме вигляд, зображений на рис.8.

П

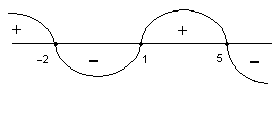
Рис. 9
ідсумуємо, що отримали. Саме, якщо число а, те, що стоїть, перед добутком, додатне, тобто «загальний знак» добутку є знак «+», то знакова крива проводиться хвилеподібним чином справа зверху через всі нулі функції на числовій прямій (рис.8).

Якщо ж число а від’ємне, тобто загальний знак добутку буде «–», і тоді всі отримані раніше знаки знакової кривої повинні змінитися на протилежні, а отже, знакова крива на рис.8 відобразиться симетрично щодо числової осі і прийме вигляд, представлений малюнком 9.

Таким чином, якщо а менше нуля, тобто загальний знак добутку є «–», знакова крива проводиться хвилеподібно через нулі функції справа знизу.

Приведемо декілька прикладів.

Приклад 1. Побудувати знакову криву для функції f(x)= 4(x – 1)(x+3)(x+2).

Р
Рис. 10
озв’язання. Очевидно, нулями функції є числа 1, –3, –2, які ми і розташуємо на числовій прямій в порядку їх зростання (рис.10). Оскільки число 4 не впливає на знак добутку, то загальний знак добутку є знак «+». Тому знакову криву проводимо справа зверху хвилеподібно через відзначені числа (рис.10).

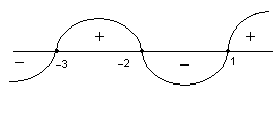
Приклад 2. Побудувати знакову криву для функції f(x)= –5(x – 0,2)(x+7).

Розв’язання. Нулі функції – числа –7 і 0,2. Загальний знак є знак «–». Отже, знакову криву проводимо хвилеподібно справа знизу (рис.11).

Рис. 11

Приклад 3. Побудувати знакову криву для функції

у =.

Розв’язання. Квадратний тричлен х² – х + 1 не має дійсних коренів і додатний.

Н

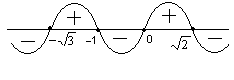
Рис. 12
асправді, його дискримінант від’ємний: D = 1 – 4 = –3 < 0 – не має коренів. А оскільки коефіцієнт при х² цього тричлена додатний («плюс одиниця»), то парабола у = х² – х + 1 при всіх х з R розташовується над віссю Ох, тобто х² – х + 1 > 0 при будь-яких значеннях х. Тому множник х² – х + 1 не робить впливу на знак всього розкладу, а отже, цей множник можна і опустити.

Далі, множник х можна представити у вигляді «дужки»: х = (х – 0) і тоді дану функцію можна записати так:

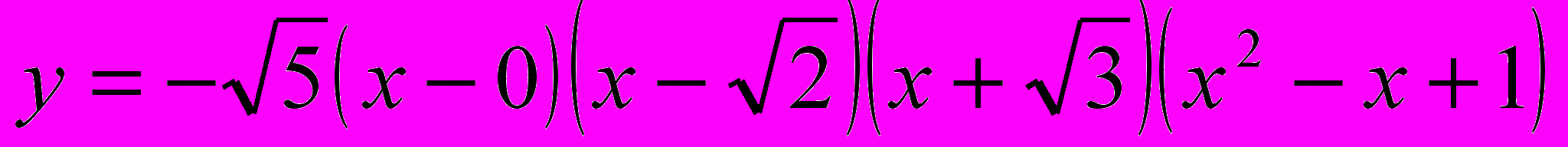
Нулями функції будуть, очевидно, числа –, –1, 0, 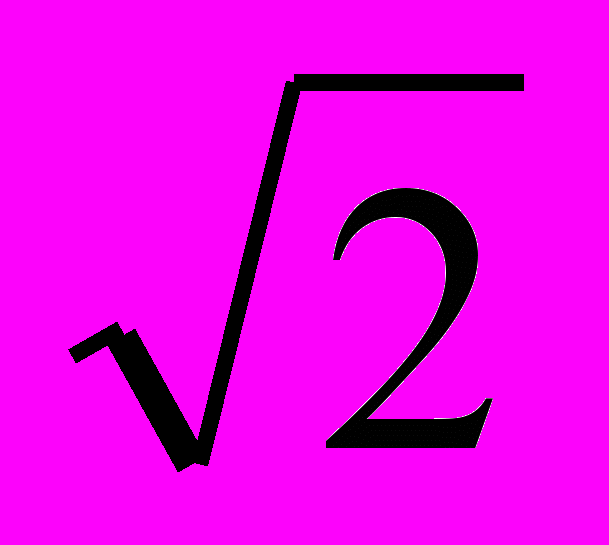і загальний знак добутку визначається знаком «мінус», що стоїть перед множником . Знакова крива проводиться справа знизу через відповідні точки числової прямої (рис.12).

По цьому малюнку можна наочно визначити нулі функції і проміжки її знакосталості. Саме:

числа, –1, 0,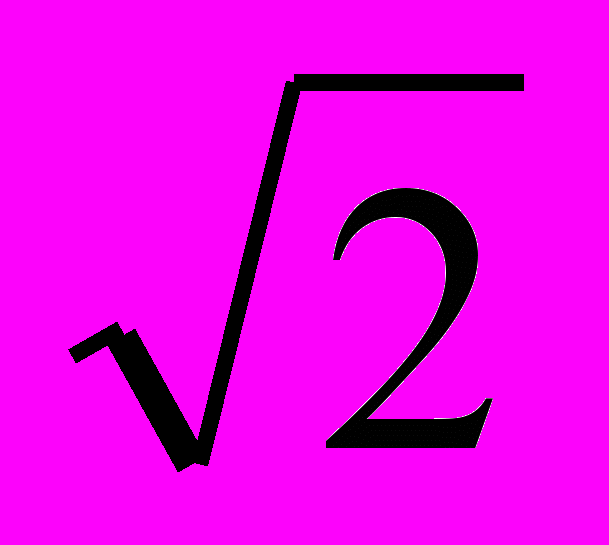 – є нулі функції;
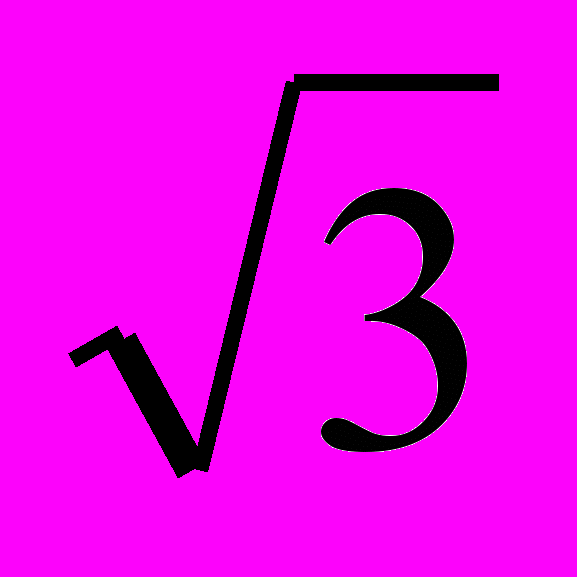(–; –1) і (0;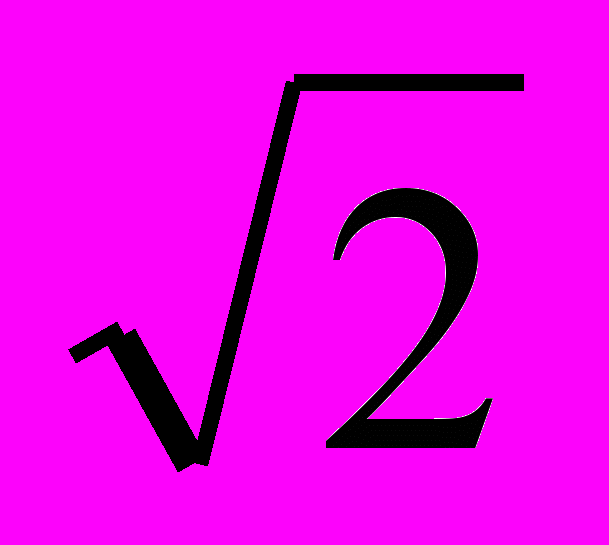) – проміжки знакододатності функції: f(x) >0;
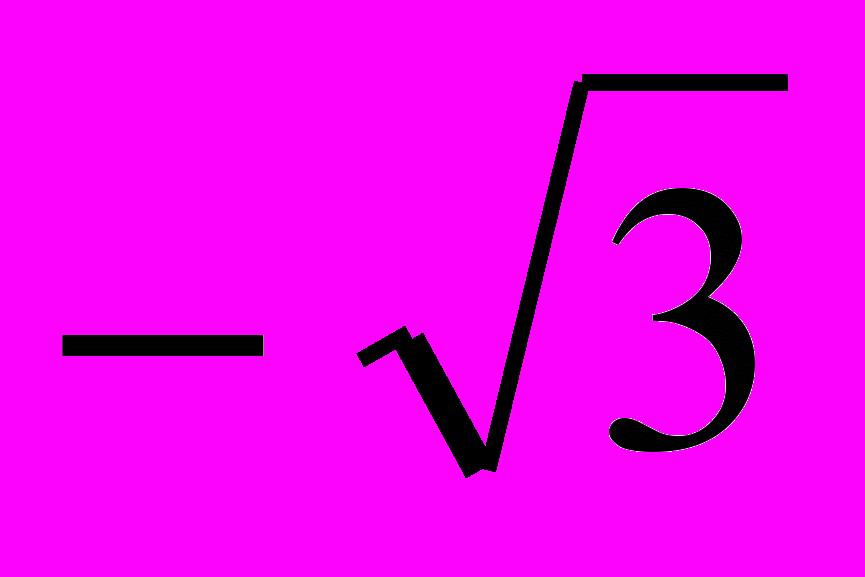(–;), (–1; 0) і (; +) – проміжки знаковід’ємності функції: f(x) <0.

Хай функція f(x) є многочлен n-го порядку, який може бути приведений до стандартного розкладу у вигляді добутку множників:

f(x)= а(x-x₁)(x-x₂)…(x-x_n) Q(x), де Q(x) – нерозкладний додатний тричлен.

Тоді справедливо

Правило проведення знакової кривої:

відкласти нулі функції x₁, х₂,…, х_n на числовій прямій в порядку їх зростання;
провести знакову криву хвилеподібно справа зверху, якщо а > 0, і справа знизу, якщо а < 0.

Зауваження. Знакова крива проводиться автоматично, тобто без підрахунків і роздумів, якщо:

розкладання многочлена стандартне, тобто в кожній дужці змінна х на першому місці і її коефіцієнт рівний 1;
обидва пункти правила виконано.

У разі, коли розклад (добуток) для f(x) не має стандартного вигляду, то відповідними перетвореннями його необхідно привести до такого.

Покажемо це на прикладах.

Приклад 4. Побудувати знакову криву для функції у = 2(7–3x)(2+x)(5x+4) і вказати проміжки її додатності.

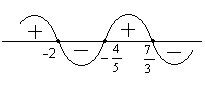Розв’язання. Перетворюючи добуток до стандартного вигляду, одержуємо: .

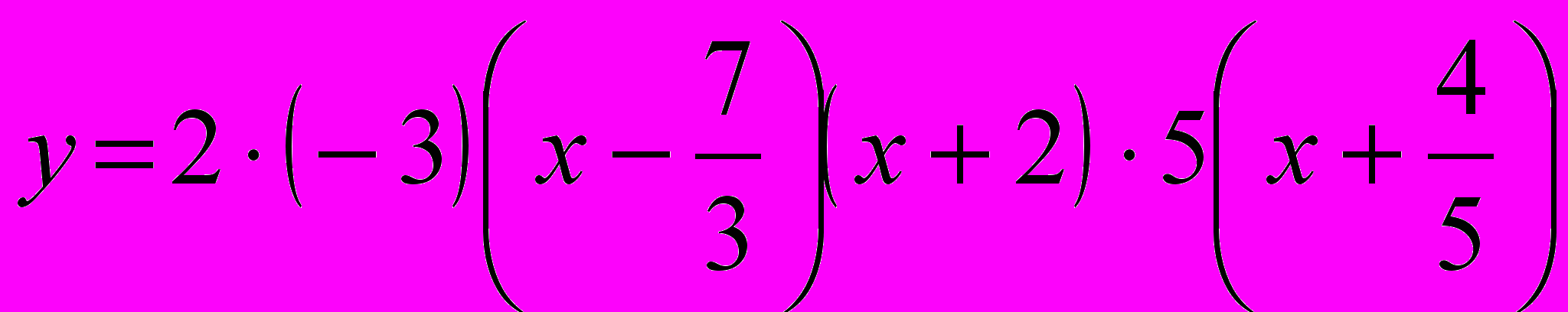П
Рис. 13
о кількості дужок , що містять змінну х, визначаємо кількість нулів функції: три дужки – три нулі. Тому «кидаємо» три точки на числову пряму, потім позначаємо їх по порядку: –2, – (мал. 13). Знакову криву проводимо знизу, оскільки загальний знак добутку є «–».

Функція невід’ємна, якщо вона або додатна (f(x) >0), або рівна нулю (f(x)=0), тобто додатність означає виконання вимоги f(x)0 (нестрога нерівність). Цим вимогам відповідають проміжки, для яких знакова крива розташовується або над віссю Ох, або торкається її.

З рис.13 видно, що задана функція невід’ємна для проміжків (–; –2] і [;].

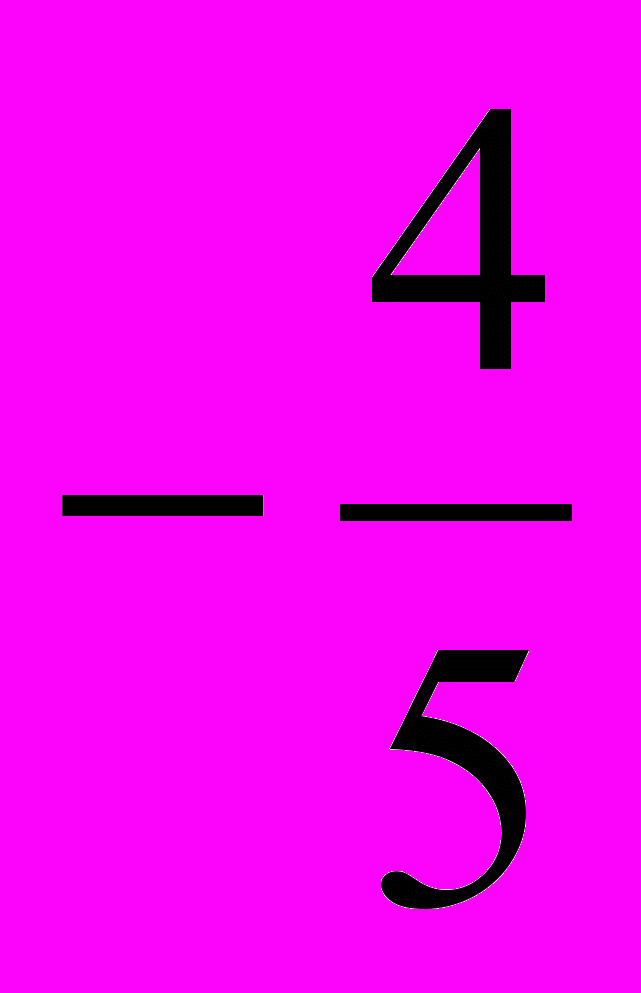Отже, f(x)0 на множині (–; –2]  [;].

Приклад 5. Побудувати знакову криву для f(x)= 2x (x+1-)(2–x)(x2–2x+3^).

Р

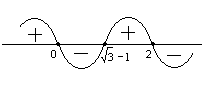озв’язання. Дискримінант тричлена x² – 2x +3 від’ємний (D₁=1–3<0), його старший коефіцієнт додатний («плюс одиниця»), а тому тричлен x² – 2x+ 3 > 0 при всіх x з R.

О
Рис. 14
пускаючи цей тричлен і пам’ятаючи, що х=х–0, (x+–1) = (x–(- 1)), (2–x) = (–1)(х–2), перепишемо дану функцію у вигляді:

f(x)= .

Відзначаємо на числовій прямій три точки: 0, –1, 2, проводимо знакову криву справа знизу (рис.14).

Умовимося зображати числові проміжки x >, x , x < b, x  b,

 x < b, < x  b,  x  b на числовій прямій графічно як вказано на рис.15 (а-h відповідно):

Рис. 15

Графічну символ-схему , що зображає проміжок х  а, називатимемо прямим кутом, а символ-схему , що зображає проміжок х > а, – округляючим кутом. Проміжок  x  b, що зображається символом, називатимемо закритим проміжком.

Приклад 6. Побудувати знакову криву для функції f(x)= 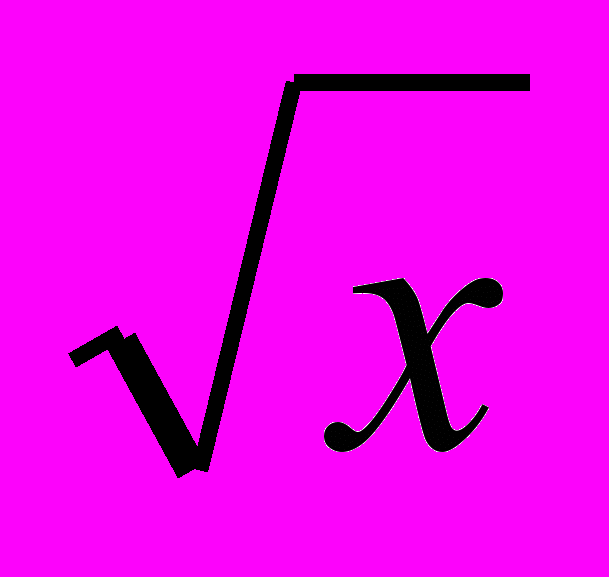(x–2)(x+5) і вказати проміжки від’ємності функції.

Розв’язання. Один із співмножників є радикалом, а тому повинно бути x  0. Отже, знакова крива повинна розглядатися в проміжку [0; +).

Д

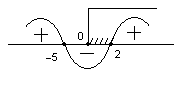ля цього проводимо знакову криву звичайним способом і розглядаємо її тільки за умови x  0, тобто відтинаємо від неї проміжок x  0 прямим кутом (рис.18).

Ф
Рис.16
ункція від’ємна в проміжку (–5; 2), але прямий кут відтинає від цього проміжку частину [0; 2) – рис.18.

Проте при х=0 f(x)=0, а нам вимагається, щоб виконувалася строга нерівність f(x) <0, тобто точка х = 0 нам не підходить.

Т.ч., функція від’ємна на проміжку (0;2).

Розглянемо тепер побудову знакової кривої для так званого алгебраїчного дробу , тобто функції вигляду 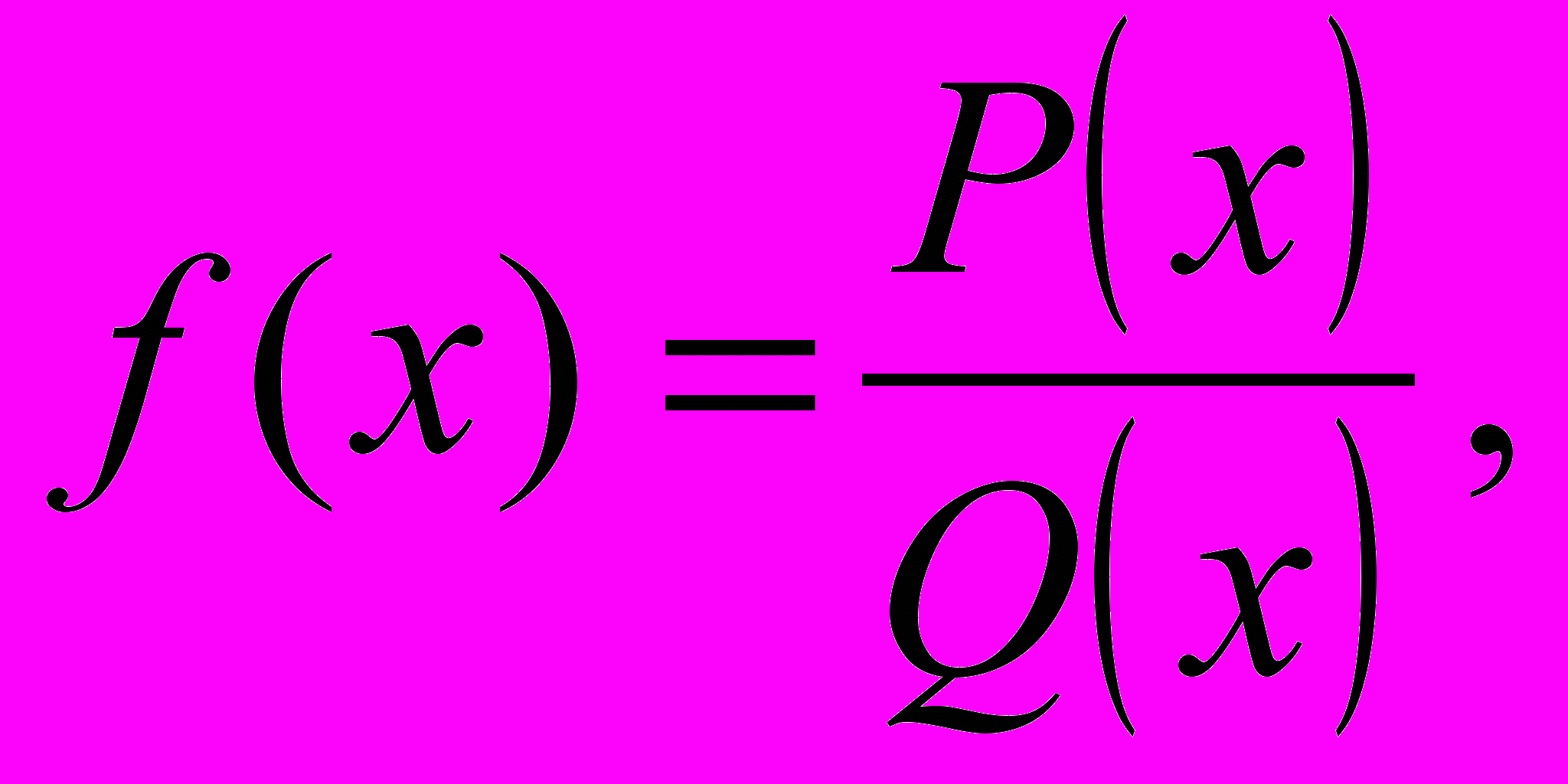де P(x) і Q(x) – деякі многочлени.

Для розуміння загального підходу розглянемо спочатку приклад.

Приклад 7. Побудувати знакову криву для функції

Розв’язання. Функція f(x) не існує, говорять ще, втрачає значення, при x = –1 і х = 3.

Значення аргументу, при яких функція не існує, назвемо полюсами функції. Т.ч., полюси функції є нулі знаменника алгебраїчного дробу..

Для нашої функції полюсами є числа x = –1 і x = 3, а нулями – числа 1 і –2.

Відзначимо нулі і полюси функції на числовій прямій і назвемо їх вузлами функції (рис.19).

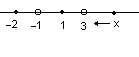
Рис. 17

Рис. 18

Оскільки в полюсах функція втрачає значення, то ці значення аргументу повинні бути виключені з розгляду. Графічно це означає, що точок x = –1 і x = 3 для нашої функції f(x) не повинне існувати, і тому ми їх “виколюємо”, тобто обводимо кружечками (рис.17).

Далі, візьмемо рухому точку х і «примусимо» її рухатися справа наліво. Тоді з урахуванням правила знаків (або того, що знаки відношення і добутку ab співпадають) побудуємо знакову криву, що проходить через вузли функції і зображену на рис.18.

Тепер уже можна перейти до узагальнення. Саме для побудови знакової кривої дробово-раціональної функції 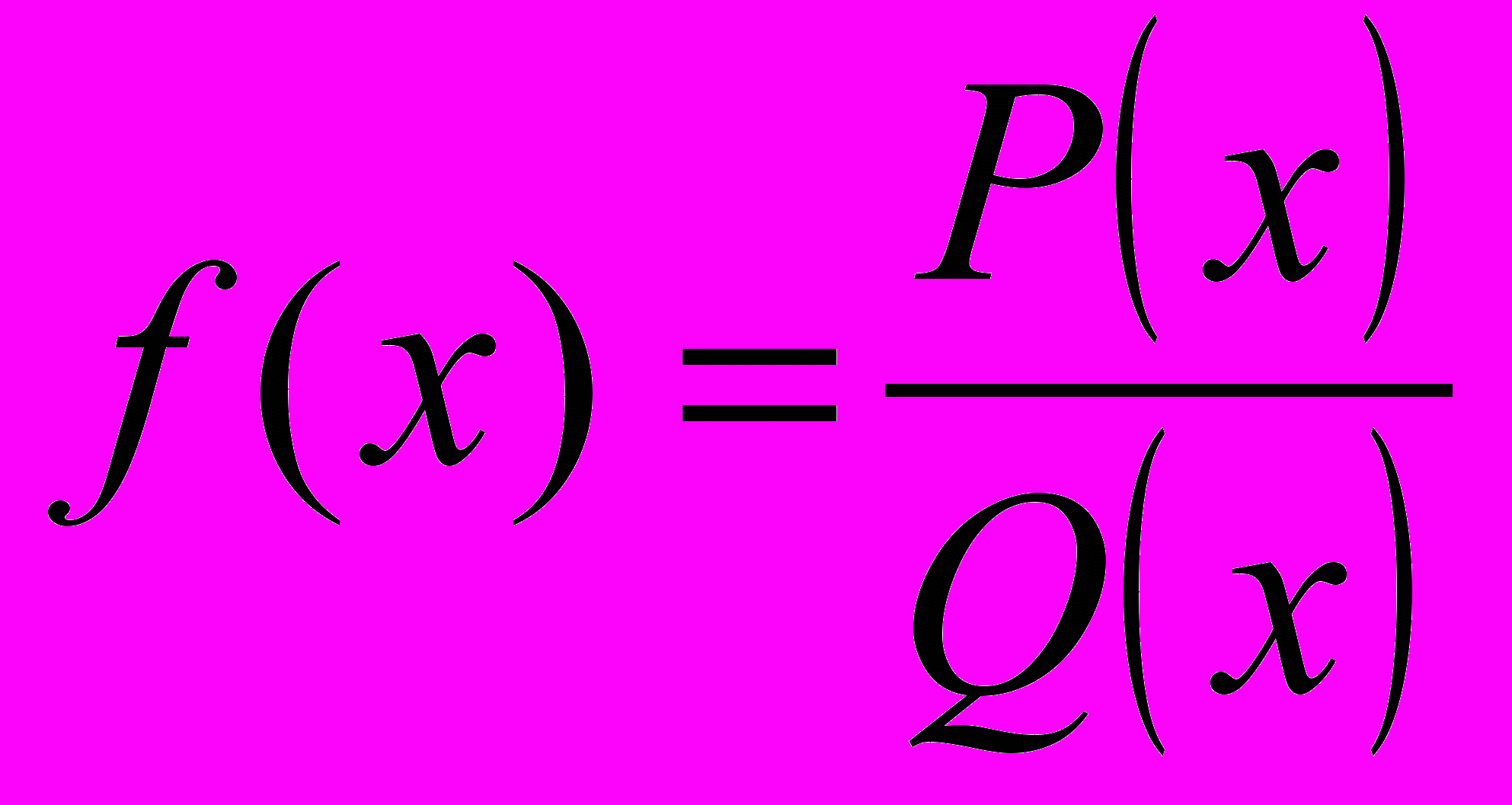необхідно:

Представити многочлени P(x) і Q(x) у вигляді їх стандартного розкладання і зобразити нулі функцій P(x) і Q(x) у вигляді точок (вузлів) на числовій прямій. При цьому, нулі знаменника – полюси функції f(x) – повинні бути виколоті, тобто обведені кружечками.
Далі залежно від загального знака відношення 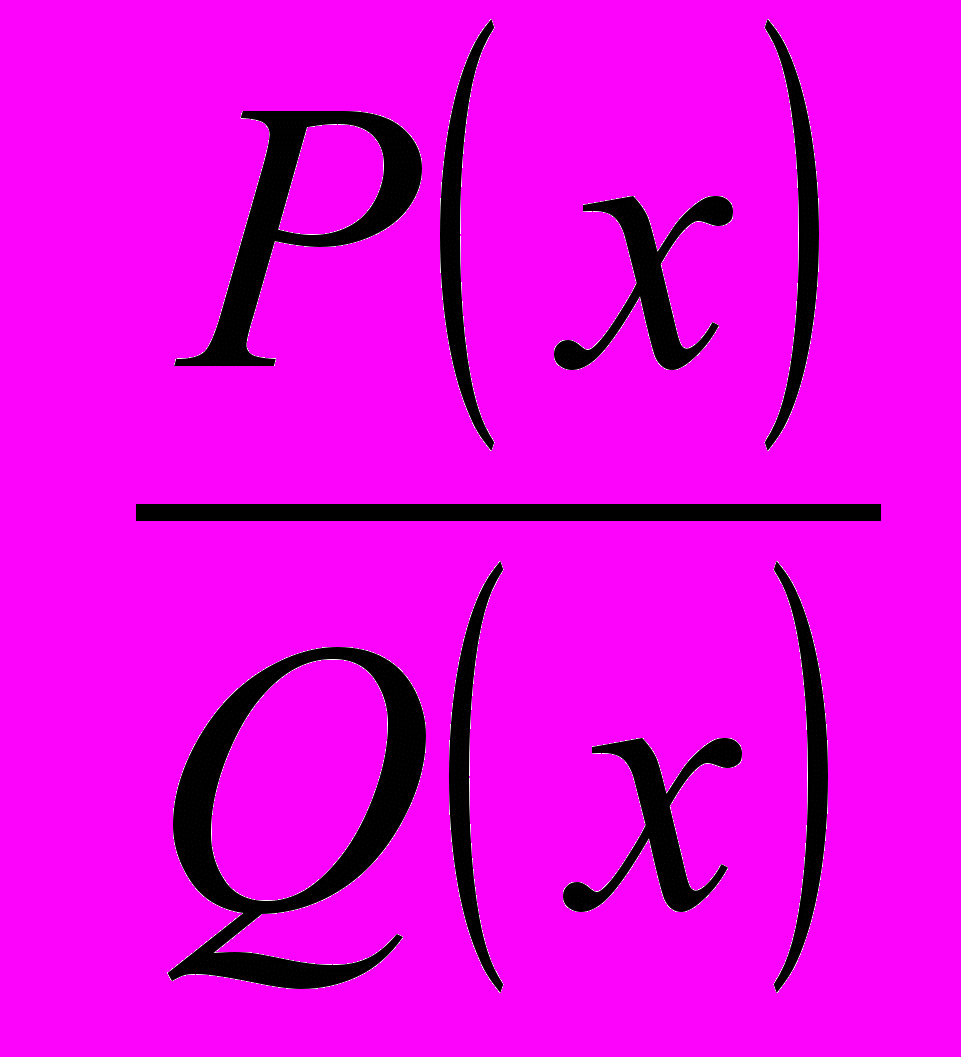провести знакову криву через вузли функції, згідно сформульованому вище правилу побудови знакової кривої.

Розглянемо ще приклади.

Приклад 8. Побудувати знакову криву для.

Розв’язання. Приведемо праву частину f(x) до стандартного вигляду і при цьому коефіцієнти, винесе з дужок запишемо попереду:

.

Як ми бачимо, нулями функції є числа

, а полюсами – числа 0,

і . Відзначивши 5 точок на числовій прямій у відповідному порядку, отримаємо вузли функції, причому її полюси повинні бути «виколоті» (рис.21).

Н

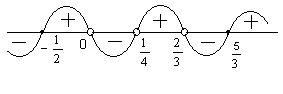
Рис. 19
е звертаючи уваги на коефіцієнти, що стоять в чисельнику і знаменнику перед дужками, (нічого з ними не роблячи, – важливі тільки їх знаки!), врахуємо тільки, що загальний знак дробу буде «+», автоматично проводимо хвилеподібну знакову криву справа зверху (рис.19).

Розглянемо дещо інший тип функцій.

Приклад 9. Функція f(x) визначається розкладанням виду f(x)= x(x–1)²(x+3)³. Побудувати знакову криву для цієї функції.

Новим моментом тут є те, що прості множники входять в добуток в деяких степенях (не лінійні). Покажемо, як в цьому випадку будується знакова крива.

Нулями функції будуть, очевидно, числа 0, 1 і –3. Відзначимо їх на числовій прямій і візьмемо рухому точку правіше за точку х = 1 (рис.20а).

Примусимо її рухатися як завжди справа наліво. Спочатку, при х >1 множники х, (х–1) і (х+3) додатні, а отже, і весь добуток додатно – знакова крива знаходиться над віссю Ох (рис.20а).

Як ми вже знаємо, у вузлах функції знакова крива або перетинає вісь Ох або торкається її, тому в точці х = 1 знакова крива торкнеться осі Ох.

Рис. 20

Після переходу рухомої точки через вузол х = 1 в проміжок (0; 1) – мал. 20б – дужка (х–1) стає від’ємною, але парний показник її степеня (число 2) «гасить» цей знак мінус: (–(x –1))² = (x–1)². Отже, ця дужка, як і дві інші, як і раніше залишається додатною, а значить, і f(x) залишається додатною. Тоді знакова крива для проміжку (0;1) залишається над віссю Ох і має знак «+» (рис.22б).

Т.ч., «парна дужка», говоритимемо, парний вузол, не дозволяє знакової кривої перейти через числову вісь в суміжну півплощину, а повертає її в ту ж півплощину, в якій вона була раніше. Образно кажучи, парний вузол «відображає» знакову криву в колишню півплощину.

Потім рухома точка х переходить через вузол х=0 в проміжок (–3;0) і оскільки множник х=(х–0) входить в добуток в непарному степені, то при цьому переході він міняє свій знак на протилежний, тобто функція f(x), а вслід за нею і знакова крива, набуває знак «–». Таким чином знакова крива переходить в суміжну від’ємну півплощину (рис.20в).

П

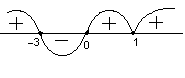ід час переходу рухомої точки через вузол х=-3, якому відповідає дужка (х+3)³, її непарний степінь не «гасить» від’ємності цієї дужки: (–(х+3))³ =–(х+3)³. Знаковакрива переходить в додатну півплощину, придбаваючи знак «+»

Н
Рис. 21
а рис. 21 представлений остаточний вид знакової кривої.

Висновок. До сформульованого раніше правила побудови знакової кривої можна додати наступне: парні вузли не пропускають знакову криву через вісь Ох в суміжну півплощину (відображають назад), непарні вузли – пропускають. Закріпимо ці поняття на прикладах.

Приклад 10. Побудувати знакову криву для f(x)= 3(2–3x)²(1–x) ³(x+1)⁴⁽5x²+4x+1).

Розв’язання. Квадратний тричлен 5x²+4x+1 завжди додатний, оскільки його дискримінант D = 4–5<0, а старший коефіцієнт – число 5 – більше нуля. Тому далі на нього не звертаємо ніякої уваги, начебто це було просто додатне число, або навіть опускаємо його.

Приводимо праву частину рівності до стандартного вигляду, виносячи з 1-й дужки множник –3 і з другої дужки – множник –1. (Пам'ятайте: перед змінною х множник повинен бути «плюс одиниця»). З урахуванням степенів цих дужок, одержуємо:

.

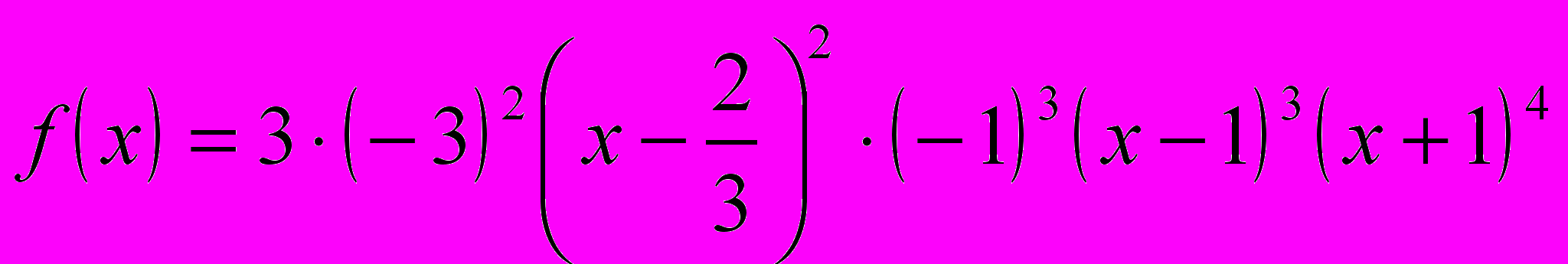Остаточно одержуємо: – задана функція f(x) представлена стандартним розкладом.

Точки –1,

і 1 відзначаємо на числовій прямій і проводимо знакову криву справа знизу, враховуючи, що парні вузли х =

і х = –1 не пропустять знакову криву через вісь Ох. Непарний вузол х=1 (дужка (х –1)³ пропускає знакову криву в суміжну півплощину. Шукана знакова крива зображена на рис.21.

Процес проведення знакової кривої, по можливості, потрібно максимально автоматизувати, тобто необхідно використовувати оптимальний алгоритм діяльності з мінімальними витратами на обдумування тих або інших дій. Для цього необхідно:

Привести задану функцію до стандартного розкладу.
По виду змінних множників визначити вузли функції, тобто сукупність її нулів і полюсів.
Розподілити ці вузли на числовій прямій по порядку і «виколоти» полюсы функції.
Визначити парні вузли функції і зробити відповідну помітку під кожним таким вузлом – буква «П».
Відповідно до загального знака розкладу провести хвилеподібну знакову криву з урахуванням парності або непарності вузлів: парні вузли не пропускають, непарні – пропускають знакову криву в суміжну півплощину.

3. Розвязування алгебраїчних нерівностей за допомогою методу інтервалів.

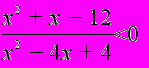
Приклад 11. Розв’язати нерівність

Р

озв’язання. Розкладемо на множники квадратні тричлени: x²+x-12=(x-3)(x+4) і x²-4x+4=(x-2)² і позначимо дріб у лівій частині нерівності через f(x). Вузлами утвореної функції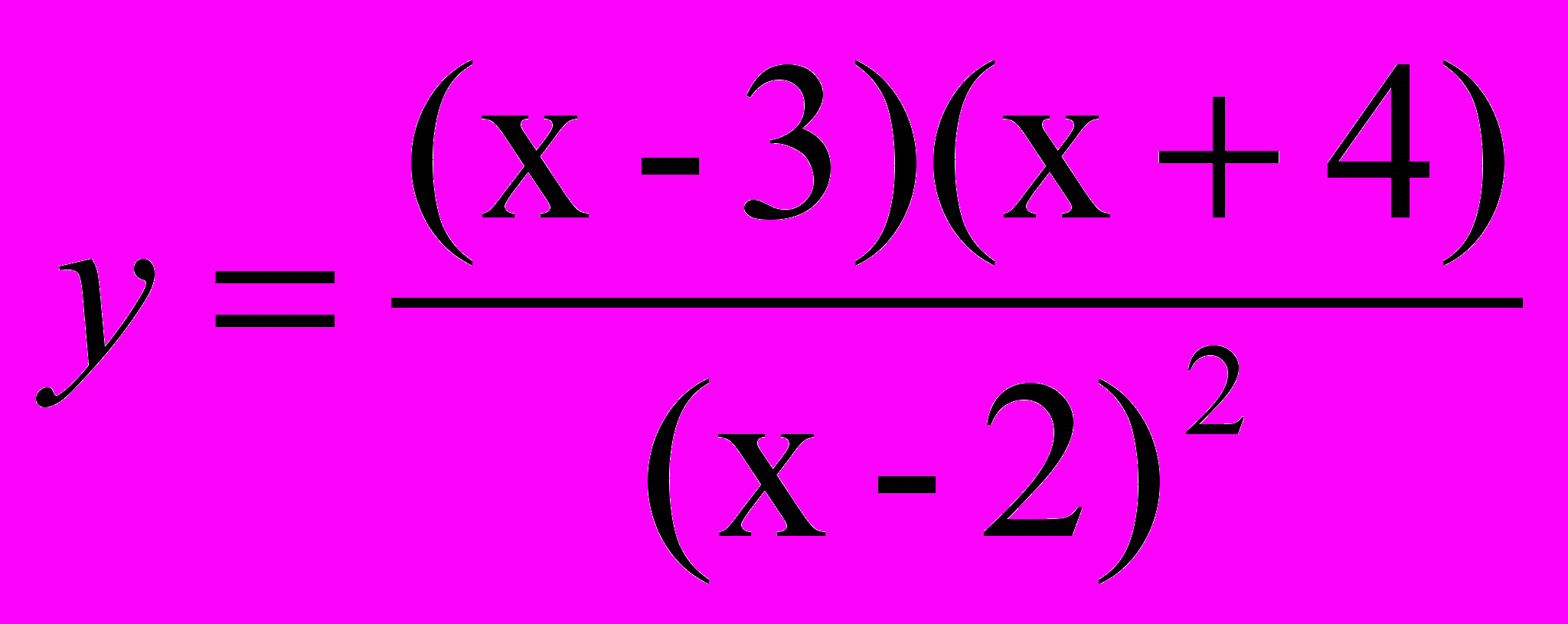

являються точки 3, -4, 2. Позначимо їх на числовій прямій у порядку зростання, виколовши полюс 2 і вказавши парність. Проведемо криву знаків з права зверху. Дана нерівність рівносильна умові f(x)<0, тому розв’язком нерівності є значення х, при яких виконується ця умова. По знаковій прямій видно, що це проміжки

[-4;2)U(2;3].

Приклад 15. Розв’язати нерівність .

Розв’язання. Алгебраїчний дріб, що стоїть в лівій частині нерівності позначимо через f(x) і побудуємо знакову криву для функції .

Вузли функції – точки 2, –3, 0, 1 – позначимо на числовій прямій в порядку зростання і виколюємо полюси – точки 0 і 1 (мал. 23 а). Функція f(x) представлена стандартним розкладанням, а тому знакову криву проводимо справа зверху (мал. 23 б).

Рис. 23

нерівність рівносильна умові f(x)  0, а отже, потрібно знайти всі значення х, для яких виконується ця умова.

По знаковій кривій визначаємо, що це проміжки [–3; 0) і (1; 2]. Об'єднання цих проміжків є розв’язанням нерівності.

Відповідь: [–3; 0)  (1; 2].

Зауваження. Розв’язанням протилежної нерівності, очевидно (див. знакову криву), є множина (–; –3)  (0; 1)  (2; +).

Зверніть увагу на те, що остання множина доповнює множину [–3; 0)(1; 2] до області допустимих значень заданої нерівності: (–; 0)  (0; 1)  (1; +). Іншими словами, якщо «складемо» (а в теорії множин говорять об'єднаємо) розв’язання початкової нерівності і нерівності їй протилежної, то отримаємо ОДЗ початкової нерівності:

[–3; 0)  (1; 2]  (–; –3)  (0; 1)  (2; +) = (–; 0)  (0; 1)  (1; +).

Завдання для самостійного розв’язання

Розв’язати нерівність:

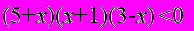
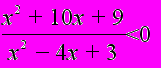
(х + 4)² (х² + 8х + 12) < 0;

(х + 4)² (х² + 8х + 12) ≤ 0;

(х - 1)² (x - 2)⁴ (х - З)³ ≥ 0;

(х - 1)² (х - 2)³ (х - З)⁴ (х - 4)⁵ ≤ 0;

(х² + 9х + 18) (х² + 4х + 5) ≥ 0;

Blog

Технології навчання математиці

Содержание

Завдання для самостійного розв’язання