Тематично-календарний план лекц І й з дисципліни „ в ищ а математика
| Вид материала | Документы |
- Тематично-календарний план лекцій для студентів IV курсу стоматологічного факультету, 207.46kb.
- Міністерство освіти І науки україни тернопільський державний технічний університет, 518.06kb.
- Про Календарний план роботи деканатів, кафедр, навчально-методичного відділу з організації, 14.05kb.
- Календарний план виконання дипломної роботи для студентів денної І заочної форм навчання, 19.26kb.
- З дисципліни «Обчислювальна математика» для студентів геологічного факультету напряму, 228.15kb.
- Календарний план спортивно-масових заходів комітету з фізичного виховання та спорту, 1859.17kb.
- Програма навчальної дисципліни "елементарна математика" Мелітополь 2010, 70.48kb.
- Програма навчальної дисципліни робоча програма навчальної дисципліни кваліфкаційні, 680.22kb.
- Календарний план уроків зарубіжної літератури, 114.81kb.
- Тематичний та календарний план передатестаційного циклу за спеціальністю "Хірургія", 73.04kb.
ТЕМАТИЧНО-КАЛЕНДАРНИЙ ПЛАН
лекцій з дисципліни „Вища математика"
І курс, I семестр _______/______навч. рік
(фармацевтичний факультет, спеціальність 7.110 201- фармація)
- Всі заняття 2-х годинні
Всього – 14 год
-
№ лекції
Теми лекції та їх зміст
Дата
Лектор
1
Елементи теорії ймовірностей.
Випадкові події і операції над ними. Класичне і статистичне визначення ймовірностей. Формула додавання і перемноження ймовірностей. Формула Байєса. Схема послідовних незалежних випробувань Бернуллі. Формула Лапласа.
2
Поняття випадкової величини (ВВ).
Дискретні і неперервні ВВ. Закон розподілу дискретних ВВ (ДВВ). Способи задання розподілу ДВВ. Неперервні ВВ(НВВ). Поняття про функцію розподілу і функцію щільності розподілу НВВ.
-„”-
3
Закони розподілу НВВ (біноміальний, Пуассона, рівномірний, нормальний, х2-розподіл, t-розподіл). Точкові та інтервальні оцінки параметрів нормально розподіленої ознаки. Поняття статистичного оцінювання. Точкове та інтервальне оцінювання. Вірогідний інтервал для математичного сподівання та для дисперсії нормально розподіленої ознаки.
-„”-
4
Граничні закони (теореми) теорії ймовірностей.
Нерівність Чебишева. Закон великих чисел: теорема Чебишева. Застосування теореми Чебишева в теорії вимірювань. Центральна гранична теорема та її прикладне значення.
-„”-
5
Статистична перевірка гіпотез (загальний розгляд статистичної перевірки гіпотез).
1. Основні поняття і термінологія.
2. Формування гіпотез про:
2.1. Узгодження емпіричного закону розподілу з теоре-
тичним (за критерієм згоди χ2).
2.2. Рівність дисперсій двох нормальних сукупностей.
2.3. Рівність центрів розподілу двох незалежних нормальних сукупностей (для рівних і нерівних дисперсій).
-„”-
6
Планування експерименту і дисперсійний аналіз.
План експерименту. Модель дисперсійного аналізу. Однофакторний дисперсійний аналіз.
-„”-
7
Однофакторний кореляційний аналіз.
Функціональний та статистичний зв'язок між ознаками. Кореляційний зв'язок. Коефіцієнт кореляції та його оцінювання (глибина - сила кореляційного зв'язку і його надійність). Однофакторний регреаійний аналіз. Оцінювання параметрів рівняння регресії методом найменших квадратів. Інтервальні оцінки параметрів лінійної регресії та лінії регресії.
-„”-
ТЕМАТИЧНО-КАЛЕНДАРНИЙ ПЛАН
лекцій з дисципліни „Вища математика"
І курс, I семестр _______/_______навч. рік
(фармацевтичний факультет, спеціальність 7.110206 - клін. фармація)
- Всі заняття 2-х годинні
Всього – 38 год
-
№
лекції
Теми лекції та їх зміст
Дата
Лектор
1
1. Введення до дисципліни „Вища математика".
2. Деякі поняття та термінологія математичного аналізу. Загальні відомості про функції. Множина і її елементи. Числові множини. Функція однієї змінної. Область визначення та область значення функції. Елементарна функція. Функція багатьох змішаних. Границя функції (числові послідовності). Теореми про границі. Неперервні функції.
2
Диференціальне числення.
Похідна і диференціальна функція, їх фізичний та геометрич-ний зміст. Похідні диференціали вищих порядків. Частинні похідні повний диференціал (першого і вищих порядків). Застосування повного диференціалу для наближених обчислень і оцінювання похибок непрямих вимірювань (загальні підходи).
-„”-
3
Інтегральне числення.
Означення і основні властивості невизначеного інтегралу. Знаходження невизначеного інтегралу безпосередньо, способом підстановки та частинами (загальні підходи).
Визначений інтеграл. (Означення основні властивості). Формула Ньютона-Лейбніца.
-„”-
4
Диференційні рівняння. Означення, загальний і частинний розв'язок. Рівняння першого порядку з відокремлюваними змінними.
-„”-
5
Математичне моделювання деяких процесів.
Моделювання диференціальними рівняннями процесів у фізиці, хімії тощо (радіоактивний розлад; поглинання іонізуючого випромінювання (з-н Бугера-Бера; розмноження бактерій; розчинення лікарської речовини з таблеток; хімічні реакції 1-го та 2-го порядків)).
-„”-
6
Елементи теорії ймовірностей.
Випадкові плоди і операції над ними. Класичне і статистичне визначення ймовірностей. Формула додавання і перемноження ймовірностей. Формула Байеса. Схема послідовних незалежних випробувань Бернуллі Формула Лапласа.
-„”-
7
Поняття випадкової величини (ВВ). Дискретні та неперервні ВВ. Закон розподілу дискретних ВВ (ДВВ). Способи задання розподілу ДВВ. Неперервні ВВ (НВВ). Поняття про функцію розподілу і функцію щільності розподілу НВВ.
-„”-
8
Закони розподілу НВВ (біномінальний*, Пуассона*, рівномі-рний*, нормальний, х2-розподіл, t-розподіл). Точкові та інтервальні оцінки параметрів нормально розподіленої ознаки.
-„”-
9
Поняття статистичного оцінювання.
Точкове та інтервальне оцінювання. Вірогідний інтервал для математичного сподівання та для дисперсії нормально розподі-леної ознаки.
-„”-
10
Граничні закони (теореми) теорії ймовірностей.
Нерівність Чебишева. Закон великих чисел: теорема Чебишева. Застосування теореми Чебишева в теорії вимірювань.
Центральна гранична теорема та її прикладне значення.
-„”-
11
Статистична перевірка гіпотез (загальний розгляд статистичної перевірки гіпотез).
2. Основні поняття і термінологія.
2. Формування гіпотез про:
2.1. Узгодження емпіричного закону розподілу з теоретичним (за критерієм згоди х2).
-„”-
12
Продовження теми лекції № 11
2.2. Рівність дисперсій двох нормальних сукупностей (за
допомогою Р - критерію).
2.3. Рівність центрів розподілу двох незалежних нормальних
сукупностей (за критеріями F, t).
-„”-
13
Планування експерименту і дисперсійний аналіз.
План експерименту. Модель дисперсійного аналізу. Однофа-кторний дисперсійний аналіз.
-„”-
14
Однофакторний кореляційний аналіз.
Функціональний та статистичний зв'язок між ознаками. Кореляційний зв'язок. Коефіцієнт кореляції та його оцінювання (глибина - сила кореляційного зв'язку і його надійність).
-„”-
15
Однофакторний регресійний аналіз.
Оцінювання параметрів рівняння регресії методом найменших квадратів. Інтервальні оцінки параметрів лінійної регресії та лінії регресії.
-„”-
16,
17
Ряди динаміки.
Класифікація часових рядів. Основні кількісні характеристики (статистики) та ланцюгові і базисні показники часового ряду і порівняння його рівнів:
- середній рівень моментного часового ряду - ряду динаміки
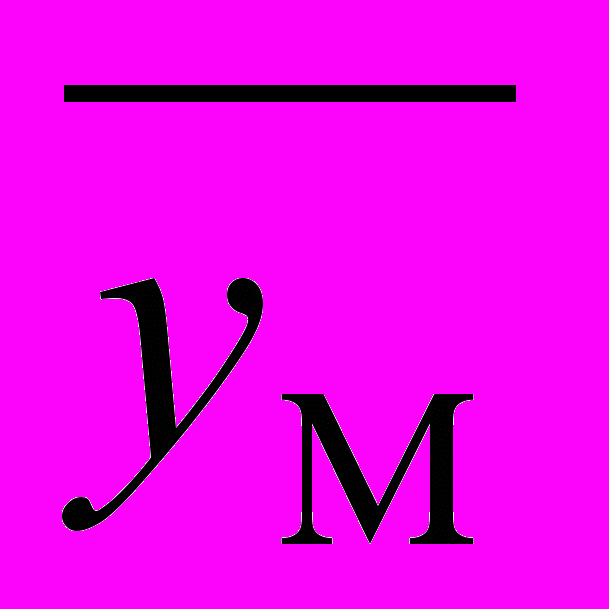 ;
;
- середній рівень інтервального ряду з рівними проміжками
часу - середнє арифметичне показника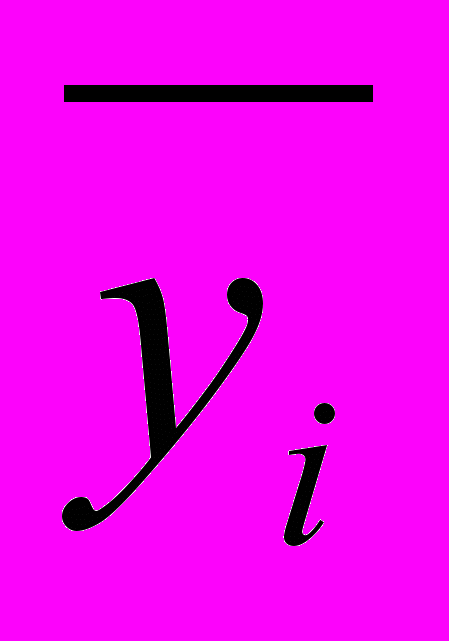 ;
;
- середньоквадратичне відхилення рівнів ряду - S;
- коефіцієнт варіації - ν;
та ланцюгові і базисні показники часового ряду і порівняння його рівнів;
- абсолютний приріст і та io - базисного) показників;
- темп росту (Кі - ланцюгового та Ко - базисного) показників;
- темп приросту ( T i - ланцюгового та Тio, - базисного) показників.
-„”-
18
Поняття про вирівнювання (відшукання рівнянь регресії) для часових рядів (тренду). Моделювання лінійного тренду.
-„”-
19
Заключна лекція.
-„”-
- середній рівень інтервального ряду з рівними проміжками
ТЕМАТИЧНО-КАЛЕНДАРНИЙ ПЛАН
практичних занять з вищої математики
І курс, I семестр / навч.року
(фармацевтичний факультет, спеціальність 7.110 206 - клін. фармація)
Всі заняття 2-х годинні
Всього – 38 год
-
№№ зан п/п
Дата заняття
Теми занять та їх зміст
1
- Введення в дисципліну „Вища математика"
Ознайомлення студентів з таким:
1.1. Мета і завдання предмету.
1.2. Особливості вивчення предмету (види занять, методика підготовки до занять).
1.3. Види кінцевого (на окремих етапах вивчення предмету) та підсумкового контролів.
2. Тема №1.* Поняття функції. Границя функції. Неперервні функції. Похідна функції. Похідні простих функцій. *Примітка: Номер теми подано відповідно до Методичних вказівок (МВ) до практичних занять з вищої
математики.
2
Тема №2. Похідні складених функцій. Похідні вищих порядків. Диференціал функції.
3
Тема №3. Дослідження функцій за допомогою похідних. Побудова графіків функцій.
4
1. Самопідготовка до контрольної роботи з тем №№ 1-3.
2. Контрольна робота №1. (теми №№1-3).
5
Тема №4. Функції багатьох змінних. Частинні похідні. Повний диференціал.
Тема №5. Наближені обчислення і оцінка похибок непрямих вимірювань за допомогою повного диференціала.
6
1. Самопідготовка до контрольної роботи з тем №№ 4,5.
2.Контрольна робота №2. (теми №№ 4-5)
7
Тема №6+№7. Невизначений інтеграл. Обчислення невизначеного інтеграла (безпосереднє, заміною змінної та по
частинах).
Тема №8. Визначений інтеграл. Обчислення площі та енергії за допомогою визначеного інтегралу.
8
Тема №9. Поняття про диференційні рівняння (ДР). ДР першого порядку з відокремлюваними змінними. Однорідні ДР
першого порядку.
9
Тема №10. 1. Закріплення знань-вмінь з тем №№ 6-9 та розв'язків типових вправ (див. Додаток в МВ). Самопідготовка
до контрольної роботи №3.
2. Контрольна робота №3 (з матеріалу тем №№ 1-9).
10
Тема №11+№12. (Набуття практичних навичок в застосуванні теорем додавання і множення ймовірностей, формул
повної ймовірності Байеса для обчислення ймовірності випадкових подій; формування знань про
способи подання закону розподілу дискретної випадкової величини (ДВВ) 1 розрахунків числових
характеристик ДВВ: М, D, σ).
11
Тема №13. Неперервні випадкові величини (НВВ) та їх числові характеристики. Приклади розподілів неперервних
випадкових величин: рівномірний, експонентний та нормальный (Гаусса). Стандартний нормальний
(нормований) розподіл.
12
1. Самопідготовка до контрольної роботи з тем №№ 11-14.
2. Контрольна робота №4 (з тем №№ 11-14).
13
Тема №14. Основні поняття математичної статистики. Генералъна та вибіркова сукупність. Вибірковий метод.
Представлення вибірки. Основні поняття про точкові оцінки характеристик (ТОХ) випадкових величин
(тлумачення, статистичний зміст, вимоги до ТОХ, застосування).
14
Тема №15. Статистична перевірка гіпотез (загальні поняття і термінологія).
Тема №16. Статистична перевірка гіпотез щодо середніх і дисперсіі незалежних нормальних генеральних сукупностей.
15
Закріплення практичних навичок з тем №15 та №16:
1. Оцінка вірогідності різниці середніх за допомогою 2 та 1 критеріїв.
2. Перевірка гіпотези про рівність генеральних дисперсій двох нормальних сукупностей за допомогою F-критерію.
3. Перевірка гіпотези про узгодження емпіричного закону розподілу F*(х) з теоретичним за допомогою критерію згоди х2.
16
Тема №17. Однофакторний дисперсійний аналіз (ОДА).
17
Тема №18. Однофакторний кореляційний (ОКА) та регресійний (ОРА) аналізи.
18
1. Самопідготовка до контрольної роботи з тем №№ 15-18.
2. Контрольна робота №5 (з тем №№ 15-18).
19
Підсумкове заняття з дисципліни „Вища математика".
1. Визначення підсумкової оцінки з практичних занять дисципліни „Вища математика" і характеристик на екзамен.
2. Одержання допуску до екзамену з дисципліни „Вища математика".
- Введення в дисципліну „Вища математика"
ТЕМАТИЧНИЙ I КАЛЕНДАРНИЙ ПЛАНИ
практичних занять з вищої математики
І курс, І семестр_______/______ навч. рік
(спеціальність 7.110201 – фармація)
Всі заняття 2-х годинні
Всього – 72 год
-
№зан п/п
Дата заняття
Вид заняття
Теми занять та їх зміст
1
семінар (С)
- Введения в дисципліну „Вища математика"
Ознайомлення студентів з таким:
1.1. Мета і завдання предмету.
1.2. Особливості вивчення предмету (види занять, методика підготовки до занять).
1.3. Види кінцевого (на окремих етапах вивчення предмету) та підсумкового контролів.
2. Тема №1. Поняття функції. Границя функцій. Неперервні функції. Похідна функції. Похідні простих функцій.
Примітка: Номер теми подано відповідно до Методичних вказівок (МВ) до практичних занять з
вищої математики.
2
практичне (П)
Тема №1. (Набуття практичних навичок).
3
С
Тема №2. Похідні складених функції. Похідні вищих порядків. Диференціал функцій.
4
П
Тема №2. (Набуття практичних навичок).
5
С
Тема №3. Дослідження функції за допомогою похідних. Побудова графіків функцій.
6
П
Тема №3. (Набуття практичних навичок).
7
П
1. Самопідготовка до контрольної роботи з тем №№ 1-3.
2. Контрольна робота №1. (теми №№1-3)
8
С
Тема №4. Функції багатьох змінних. Частинні похідні. Повний диференціал.
9
П
Тема №4. (Набуття практичних навичок).
10
С
Тема №5. Наближені обчислення і оцінка похибок непрямих вимірювань за допомогою повного диференціала.
11
П
Тема №5. (Набуття практичних навичок).
12
П
1. Самопідготовка до контрольної роботи з тем №№ 4,5.
2. Контрольна робота №2. (теми №№ 4-5)
13
С
Тема №6+№7. Невизначений інтеграл. Обчислення невизначеного інтеграла (безпосереднє, заміною змінної та по частинах).
14
П
Тема №6+№7. (Набуття практичних навичок).
15
С
Тема №8. Визначений інтеграл. Обчислення площі та енергії за допомогою визначеного інтегралу.
16
П
Тема №8. (Набуття практичних навичок).
17
С
Тема №9. Поняття про диференційні рівняння (ДР). ДР першого порядку з відокремлюваними змінними. Однорідні ДР першого порядку.
18
П
Тема №9. (Набуття практичних навичок).
19
П
Тема №10. 1. Закріплення знань-вмінь з тем №№ 6-9 та розв'язків типових вправ (див. Додаток в МВ). Самопідготовка до контрольної роботи №3.
2. Контрольна робота №3 (з матеріалу тем №№ 1-9).
20
С
Елементи теорії ймовірностей і математичної статистики.
Тема №11. Основні поняття теорії ймовірностей. Класичне та статистичне означення ймовірності. Випадкові події та операції над ними. Формули додавання і множення ймовірностей.
21
С
Тема №12. Формула повної ймовірності. Формула Байєса. Дискретні і неперервні випадкові величини та їх числові характеристики. Приклади розподілів дискретних випадкових величин: біномний, Пуасона.
22
П
Тема №11+№12. (Набуття практичних навичок в застосуванні теорем додавання і множення ймовірностей, формул повної ймовірності і Байєса для обчислення ймовірності випадкових подій; формування знань про способи подання закону розподілу дискретної випадкової величини (ДВВ) і розрахунків числових характеристик ДВВ: М, D, ).
23
С
Тема №13. Неперервні випадкові величини (НВВ) та їх числові характеристики. Приклади розподілів неперервних випадкових величин: рівномірний, експонентний та нормальний (Гаусса). Стандартний нормальний (нормований) розподіл.
24
П
Тема №13. Засвоєння понять і знань про властивості М, D, та їх обчислення; вмінь встановлення зв'язку між довільним нормальним і стандартним нормальним (нормованим) розподілами; навичок обчислення ймовірності значень НВВ за допомогою таблиць функції Лапласа.
25
П
1. Самопідготовка до контрольної роботи з тем №№ 11-14.
2. Контрольна робота №4 (з тем №№ 11-14).
26
С
Тема №14. Основні поняття математичної статистики. Генеральна та вибіркова сукупності. Вибірковий метод. Представлення вибірки. Основні поняття про точкові оцінки характеристик (ТОХ) випадкових величин (тлумачення, статистичний зміст, вимоги до ТОХ, застосування).
27
С
Тема №15. Статистична перевірка гіпотез (загальні поняття і термінологія).
28
С
Тема №16. Статистична перевірка гіпотез щодо середніх і дисперсій незалежних нормальних генеральних сукупностей.
29
П
Закріплення практичних навичок з тем №15 та №16:
1. Оцінка вірогідності різниці середніх за допомогою 2 та 1 критеріїв.
2. Перевірка гіпотези про рівність генеральних дисперсій двох нормальних сукупностей за допомогою Р-критерію.
3. Перевірка гіпотези про узгодження емпіричного закону розподілу F*(х) з теоретичним за допомогою критерію згоди 2.
30
П
Тема №17. Однофакторний дисперсійний аналіз (ОДА).
31
С
Тема №18. Однофакторні кореляційний (ОІСА) та регресійний (ОРА) аналізи.
32
П
Закріплення знань і практичних навичок з теми №18.
33
П
1. Самопідготовка до контрольної роботи з тем №№ 15-18.
2. Контрольна робота №5 (з тем №№ 15-18).
34
С
Самопідготовка з теми: „Елементи теорії масового обслуговування".
35
П
Ліквідація академзаборгованості з розділу „Математична статистика".
36
П
Підсумкове заняття з дисципліни „Вища математика".
1. Визначення підсумкової оцінки з практичних занять дисципліни „Вища математика" і характеристик на екзамен.
2. Одержання допуску до екзамену з дисципліни „Вища математика".
- Введения в дисципліну „Вища математика"
