Geum.ru

П. Е. Денисов, И. В. Измайлов, Б. Н. Пойзнер Томский государственный университет, Томск

Вид материалаДокументы
Подобный материал:
ИЗУЧЕНИЕ ВЛИЯНИЯ НАСЫЩЕНИЯ НЕЛИНЕЙНОСТИ НА (НЕ)УСТОЙЧИВОСТЬ КОЛЬЦЕВОЙ СИСТЕМЫ: МЕТОДИЧЕСКИЕ АСПЕКТЫ


П.Е. Денисов, И.В. Измайлов, Б.Н. Пойзнер

Томский государственный университет, Томск

634021, г. Томск, ул. Кулагина, д. 9, кв. 64, pavden@mail.ru

Интеграция учебного и научно-исследовательского процесса, с зачтением


Излагается опыт разработки проблемного компьютерного эксперимента по изучению влияния физических факторов (включая насыщение нелинейности1) на (не)устойчивость структурообразования в нелинейном кольцевом интерферометре.


В последние годы активно развиваются различные аспекты оптоинформатики как полидисциплинарного научного направления. Изучение теоретических основ оптоинформатики студентами предполагает создание для них специальных учебно-исследовательских контекстов. Особенностями последних, на наш взгляд, должны быть, во-первых, необходимость оперирования методами, понятиями и моделями нескольких учебных предметов, в том числе – физической и нелинейной оптики, теории систем и детерминированного хаоса (ДХ), численных методов решения дифференциальных уравнений etc. Во-вторых, учебные задания для студентов должны быть многоуровневыми и содержать проблемные задачи, требующие творческого подхода, а не только обращения к учебному материалу других дисциплин. В-третьих, содержание части проблемных задач должно коррелировать с тематикой НИР, проводимых сотрудниками кафедры, что позволило бы обновлять учебно-методический материал за счёт освоения и рутинизации исследовательских процедур.

Например, моделирование процессов структурообразования и хаотизации в нелинейном кольцевом интерферометре (НКИ) позволяет создать учебно-исследовательский контекст, требующий от студента обращения к методам, упоминавшимся выше. Отметим, что исследование различных моделей НКИ перспективно в связи с возможностью генерации в поперечном сечении лазерного пучка, циркулирующего в контуре обратной связи (КОС) ДХ2.

Режим ДХ интересен в плане его применения в коммуникационных технологиях, в частности при скрытой передаче информации. Поэтому необходимо изучение условий возникновения ДХ. Для этого нами предлагается вариант создания проблемного компьютерного эксперимента по изучению влияния физических факторов на возможность возникновения ДХ. В качестве методики исследования предлагается построение бифуркационных диаграмм (БД) и фазовых портретов, иллюстрирующих, а иногда и диагностирующих характер сложной динамики в модели процессов в НКИ.

НКИ содержит 4 зеркала (два из которых - полупрозрачные) и керровский нелинейный элемент. В КОС НКИ находится линейный элемент, осуществляющий поворот светового поля. Характер процессов в НКИ обусловливается наличием поворота поля, НС, а при заданном уровне её нелинейности – уровнем интенсивности насыщения нелинейности Is. Модель процессов в НКИ – дифференциальное уравнение, описывающее изменение нелинейного фазового набега U(r, t) в НС. Оно получено в приближении медленно меняющихся амплитуд, фаз, модуляции положения плоскости поляризации входного светового поля; медленной релаксации нелинейной части показателя преломления, а также с учётом насыщения нелинейности керровской среды (в приближении геометрической оптики):



По результатам моделирования строятся семейства БД на различных плоскостях параметров модели и фазовые портреты (рис. 1):






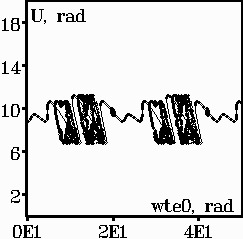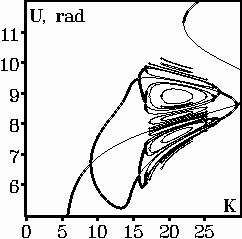а
б
в
г

Рис. 1. БД при  = /4, коэффициенте насыщения нелинейности Ks = 18 на плоскостях: нелинейный фазовый набег U – фазовая задержка te поля в КОС при K = 20, q  0.14 (а); U – параметр нелинейности K при te = 10 рад, q  0.14 (б); U – коэффициент бихроматичности q входного поля при K = 20, te = 10 рад (в). Тонкими линиями показаны неустойчивые состояния. Фазовый портрет системы при  = 2/3, q = 3, K = 13 (г)

Наличие насыщения нелинейности приводит к тому, что изменение структуры распределения решений за счёт возникновения новых ветвей и бифуркаций на плоскости U – K наблюдается в ограниченной области изменения параметра K. Дальнейший рост значения K влечёт уменьшение числа решений, и ветвь диаграммы стремится к значению U = Ks. Такое поведение ветви диаграммы наблюдается и на плоскости U – te. Представленные диаграммы на трёх различных плоскостях позволяют всесторонне исследовать бифуркационное поведение НКИ и выявить степень влияния параметров модели на бифуркационное поведение.

Анализ построенных фазовых портретов позволяет судить о типе бифуркаций, возникновение которых возможно в системе при определённых значениях параметров, а также о типе перехода к хаосу. Указанные выше аспекты обусловливают содержание возможных заданий студентам, моделирующим процессы в НКИ с учебно-исследовательскими целями. Ниже приводится ориентировочный перечень заданий:

1. При заданных параметрах НКИ и входного оптического излучения путём варьирования значений угла поворота  в заданном диапазоне добиться появления петель пространственной бистабильности на БД в нескольких плоскостях параметров (поочерёдно). Дать физическую интерпретацию результатам.

2. Убедиться в возможности появления фракталоподобных областей в структуре БД и изучить степень влияния заданного ряда параметров на их вид.

3. Для получения желаемого режима функционирования НКИ путём целенаправленного подбора параметров модели обеспечить заданное распределение (не)устойчивых состояний на БД в заданном диапазоне значений бифуркационного параметра. Провести идентификацию режима с помощью построения фазового портрета.

  1. Проблемы когерентной и нелинейной оптики / Под ред. И.П. Гурова и С.А. Козлова. СПб: СПбГИТМО, 2000. 278 с.
  2. Новые физические принципы оптической обработки информации / Под ред. С.А Ахманова, М.А Воронцова. М.: Наука, 1990. 400 с.