Geum.ru

Методические указания по определению устойчивости энергосистем

Вид материалаМетодические указания

Содержание


Примеры расчетов настроечных параметров арв
Определение максимально допустимой постоянной времени возбудителя
Подобный материал:
1   ...   5   6   7   8   9   10   11   12   13

ПРИМЕРЫ РАСЧЕТОВ НАСТРОЕЧНЫХ ПАРАМЕТРОВ АРВ

ПО УСЛОВИЯМ УСТОЙЧИВОСТИ СИНХРОННЫХ МАШИН


Пример 1.


Выбрать настроечные параметры АРВ по условию устойчивости синхронной машины, работающей в режиме холостого хода. Настроечными параметрами являются коэффициент усиления по отклонению напряжения, параметры обратной связи, охватывающей возбудитель, и коэффициент усиления по первой производной напряжения (в случае АРВ сильного действия). Учитывая постоянную времени ротора 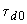, регулятора 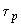и параметры обратной связи в виде эквивалентной постоянной времени возбудителя 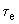, получим, используя критерий Гурвица, условие устойчивости в виде неравенства


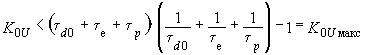. (П5.1)

Если при заданных параметрах 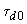, , 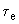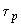значение 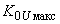, полученное по условию устойчивости, меньше значения, необходимого по условию заданной точности поддержания напряжения, то его можно увеличить либо уменьшением 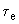(охват возбудителя отрицательной жесткой обратной связью), либо увеличением 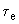(охват возбудителя отрицательной гибкой обратной связью), либо дополнительный введением регулирования по первой производной напряжения. В последнем случае значение 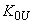ограничено неравенством


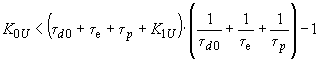. (П5.2)


Реальные коэффициенты, обеспечивающие достаточную точность поддержания напряжения (1-5%), лежат в пределах 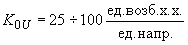. Так, например, на генераторах Братской ГЭС


, .


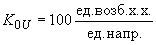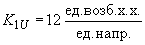Пример 2.


Построение областей устойчивости в координатах коэффициентов регулирования по производным АРВ сильного действия в простой системе производится методом 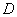-разбиения, для чего:


1) записывается характеристическое уравнение (3.12) в виде


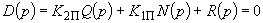, (П5.3)


где 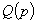, , 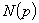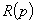- многочлены по 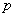[Л.12];


2) в выражение 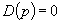подставляют 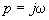, получают 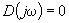и приравнивают нулю его вещественные и мнимые части


,


,


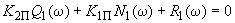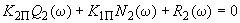где 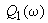, , 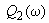, ,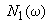, 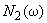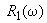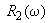- соответственно вещественные и мнимые части полиномов , , ;


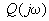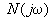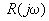3) система уравнений решается относительно 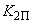и 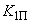, и получается параметрическое уравнение для коэффициентов регулирования по производным в форме


, ,


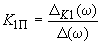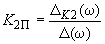где ,


, ;


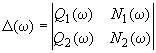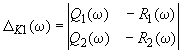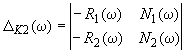4) параметру 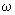даются значения от 0 до 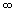, вычисляются значения 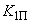и 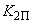, принадлежащие границам 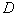-разбиения. Для выделения предполагаемой области устойчивости при изменении 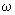от 0 до 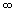граница штрихуется справа, если 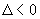, и слева, если .


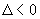Если из ранее полученного опыта неизвестно, что выделенная область устойчивости является действительно областью устойчивости, то необходимо проверить устойчивость (или число корней в правой полуплоскости) для одной точки плоскости 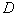-разбиения с помощью критерия Рауса или Михайлова.


Если передаточная функция регулятора возбуждения сильного действия имеет вид


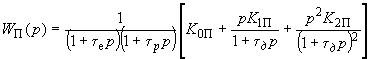, (П5.4)


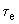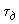то при расчетах в ручную целесообразно применять методику построения границ областей устойчивости, позволяющую учесть постоянные времени системы возбуждения и АРВ и 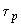без получения характеристического уравнения высокого порядка.


Расчет области устойчивости сначала ведется по параметрическим уравнениям, полученным из характеристического уравнения при 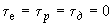, причем определяются зависимости 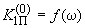, , 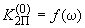отмеченные индексом "0" как коэффициенты нулевого приближения.


Затем вычисляются коэффициенты первого приближения, определяющие при изменении 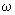от 0 до 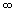новые границы области устойчивости через значения коэффициентов нулевого приближения при 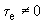, затем при 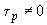и, наконец, при .


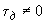Применение такой методики особенно целесообразно, если расчеты имеют целью, кроме анализа устойчивости и определения области значений настроечных параметров, также выбор конструктивных параметров системы регулирования (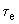, 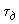и т.д.).


Современные регуляторы возбуждения, как правило, осуществляют комбинированное регулирование по отклонению тока (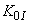) и напряжения (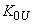), и, кроме основных параметров стабилизации, в АРВ сильного действия часто вводятся дополнительные параметры стабилизации. Для определения деформации области устойчивости в этом случае целесообразно применять графоаналитические методы, один из которых описан в приложении 6.


Разделение границы области статической устойчивости на опасную и безопасную [Л.10, 47, 48].


Работоспособность электрической системы, имеющей малый коэффициент запаса периодической устойчивости, зависит от характера границы. Вблизи опасной границы при возмущениях, превышающих некоторые, возможные в нормальных режимах значения, система становится практически неустойчивой. Нарушение безопасной границы сопровождается появлением автоколебаний тем меньшей амплитуды, чем меньше это нарушение.


При разделении границ области статической устойчивости необходимо учитывать нелинейность ограничения силового блока AРB.


Расчет для выделения опасной и безопасной границ совмещается с построением области статической устойчивости. Для этого по тем же формулам метода 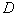-разбиения (см. пример 2) и по тем же программам повторяется расчет, но все коэффициенты регулирования АРВ (кроме 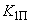, , 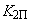в плоскости которых строится граница), приравниваются к нулю. Результат второго расчета определит в комплексной плоскости 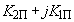для каждой частоты 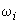вектор смещения 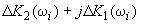, направление которого определяет характер границы. Если вектор смещения направлен внутрь области статической устойчивости, граница опасная, если наружу, то безопасная (рис.П5.1).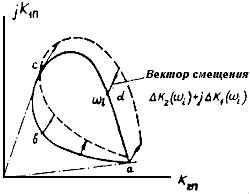





Рис.П5.1. Область статической устойчивости в координатах ,


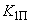При регулировании по одному параметру при условии, если коэффициент 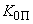мало влияет на границу области статической устойчивости, расположенную в первом квадранте, рекомендуется применять упрощенный метод выделения опасной и безопасной границ области статической устойчивости [Л.44]. Из начала координат плоскости настроечных параметров АРВ проводятся две касательные к границе области статической устойчивости. Низкочастотная часть границы 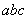опасная, часть 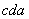. (более высокочастотная) безопасная (см. рис.П5.1).


Приложение 6

ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНО ДОПУСТИМОЙ ПОСТОЯННОЙ ВРЕМЕНИ ВОЗБУДИТЕЛЯ


Одним из мероприятий, ведущих к увеличению размеров области устойчивости, является уменьшение постоянных времени элементов системы возбуждения и регулирования. Если, например, сравнивается электромашинная и быстродействующая системы возбуждения, то нужно оценить влияние уменьшения постоянной времени 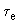силового элемента АРВ - возбудителя - на размеры области устойчивости.


Если в проекте станции уже предусмотрена быстродействующая система возбуждения асинхронных машин, то можно составить требования к постоянным времени некоторых элементов АРВ, которые в случае необходимости могут быть реализованы усовершенствованием схемы или конструкции этих элементов.


Так как изучение перечисленных мероприятий связано с проведением многочисленных однотипных расчетов, то с целью уменьшения затрачиваемого на них труда и времени целесообразно использовать специальные методы, один из которых приведен ниже. Целесообразность применения тех или иных методов следует выяснить вначале для простейшей схемы соединения выделенной станции с системой, а затем уже проверить эффективность выбранного мероприятия путем расчета в сложной системе (с помощью ЦВМ).


Методы, рекомендуемые для такого рода расчетов, основаны на сочетании графоаналитических способов и метода 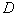-разбиения.


Чтобы выяснить, можно ли уменьшением постоянной времени возбудителя обеспечить необходимый размер области устойчивости, следует провести расчет, предположив 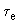=0. Если при 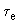=0 полученная область устойчивости больше, чем минимально необходимая, нужно определить максимально допустимую постоянную времени возбудителя. Чтобы исключить необходимость проведения серии расчетов при вариации 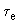, рекомендуется следующий графоаналитический метод. Запишем уравнения кривой 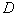-разбиения при регулировании по одному режимному параметру так


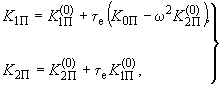(П6.1)


где 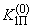, 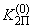- координаты области устойчивости при 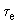=0 (рис.П6.1, а), кривая 1).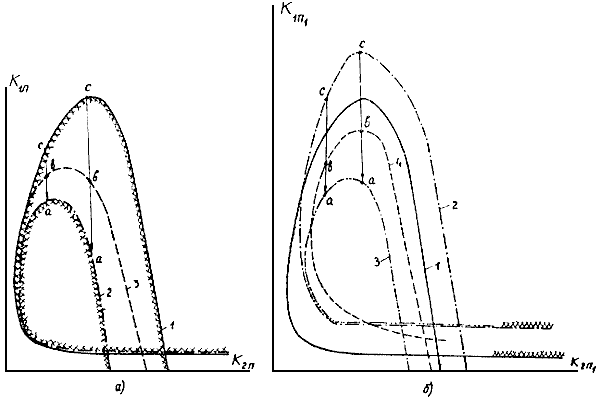





Рис.П6.1. Построение областей устойчивости для определения значения :


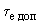а - регулирование по одному режимному параметру 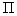; 1 - при 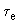=0; 2 - при ;

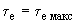3 - при 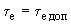; б - регулирование по нескольким режимным параметрам:

1, 2 - при 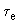=0; 3 - при 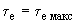; 4 - при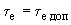


Задаемся 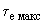максимальным значением из всех рассматриваемых вариантов схем возбуждения. В каждой точке кривой 1, соответствующей некоторому значению 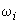, проводим вектор 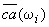, равный


.


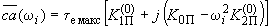Совокупность точек концов построенных векторов образует область устойчивости при 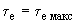(кривая 2). Исходя из желательного размера области устойчивости (условно определяемого точкой 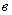на кривой 3), определим максимально допустимое значение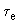


.


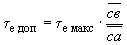При регулировании по нескольким режимным параметрам (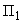, , 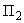...) уравнения кривой 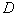-разбиения можно записать так


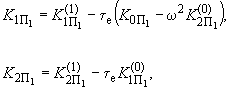(П6.2)


где 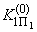, 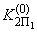- координаты области устойчивости (см. рис.П6.1, б, кривая 1) пр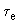и =0 и 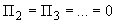; 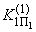, 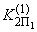- координаты области устойчивости (кривая 2) пр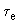и =0 и 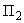, , 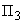+, не равных нулю.


Для определения максимально допустимого значения 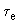поступаем так: задаемся 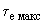и в каждой точке кривой 2 проводим вектор 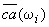, равный


.


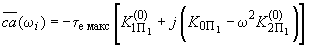Совокупность точек концов построенных векторов образует область устойчивости при 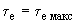(кривая 3). Исходя из желательного размера области устойчивости (условно оцениваемого точкой 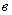на кривой 4), определим максимально допустимое значение


.


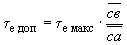Предлагаемая методика справедлива для определения максимально допустимого значения постоянной времени системы возбуждения выделенной станции при любой связи с остальной частью сложной системы. При этих расчетах постоянные времени дифференцирующих звеньев не учитываются.


Приложение 7