Курсовая работа по методике

Вид материала

Курсовая

Содержание Анализ монографии Ii. анализ опыта работы учителя Цель урока Тип урока: Урок-путешествие. Конспект урока по геометрии в 9 классе Тип урока Ход урока Урок № 1 по теме «Прогрессии» (Лекция) Ход урока Внеклассная работа по предмету

Подобный материал:

• Курсовая работа по методике преподавания математики небольшая по объему самостоятельная, 1134.75kb.
• К написанию курсовой работы по методике преподавания биологии, 74.36kb.
• Методика изучения правильных многоугольников в курсе планиметрии Курсовая работа, 313.94kb.
• Методические рекомендации по выполнению курсовых работ курсовая работа по «Общей психологии», 54.44kb.
• Курсовая работа по методике преподавания географии по теме: «Особенности применения, 222.81kb.
• Курсовая работа Социокультурные лакуны в статьях корреспондентов, 270.94kb.
• Курсовая работа, 30.27kb.
• Курсовая работа тема: Развитие международных кредитно-финансовых отношений и их влияние, 204.43kb.
• Курсовая работа+диск + защита, 29.4kb.
• Курсовая работа+диск + защита, 118.7kb.

Анализ монографии

Анализируемая монография посвящена одной из важнейших задач совершенствования системы обучения математики: развитию творческих способностей учащихся на уроках и внеклассных занятиях. Автором этой монографии «Спасибо за урок, дети!», написанной в 1988 году, является учитель-методист математики города Петербурга с 25-летним стажем работы в школе А.А. Окунев. Эта монография состоит из 20 отдельных глав, в каждой из которых рассматривается творческий подход к различным видам деятельности учителя и учащихся на уроке, которые учитель использует для обучения математике и воспитанию учащихся. Первая глава монографии называется «Поиск своего урока». В этой главе идет речь о проблеме структуры урока. О необходимости ставить перед собой сверхзадачу – тот главный стержень, вокруг которого строится весь процесс обучения. И эту задачу надо осознать самому. Отсюда и начинается творческое отношение к педагогической работе. Далее идет речь о деятельности учителя на уроке и деятельности учащихся. Главное внимание занимает вопрос «Как научить всех? Как заставить работать дома? Как управлять познавательной деятельностью учащихся? Изучая этот вопрос приходишь к выводу о том, что учитель на уроке должен поставить перед собой цель: сформировать у учащихся полную систему ориентиров для правильного выполнения действия. Теория Гальперина позволяет по-другому анализировать процесс обучения решения задач, составляя определенную систему вопросов:

1. О каких процессах идет речь в задаче.
   
2. Сколько процессов описано в условии.
   
3. Какими величинами характеризуется каждый процесс.
   

Далее составляется таблица, с помощью которой составляется уравнение для решения задачи. От логики построения урока зависит успех урока. Главное на уроке «учить». И это не одно и то же, что быть на уроке и общаться с учениками. Далее идет речь об уроке – импровизации. Так ли часто мы его проводим. Этот урок рождается тут же в классе, правда, для ребят он отличается лишь особой приподнятостью настроения учителя, его воодушевлением, азартом. Но у этого урока огромная сверхзадача: крепнет уверенность ребенка в своих силах, творческих способностях, растет авторитет в глазах товарищей, создается атмосфера радости. Урок-импровизация возможен лишь тогда, когда учитель сформировал свою систему преподавания. Эти уроки особенно удаются, когда в их основу берется принцип Выготского Л.С. Он считал, что обучение должно подталкивать, вести за собой развитие ученика, Несколько опережать его и прокладывать ему дорогу, чтобы пробудить в ребенке новые творческие силы, о которых он и не подозревает. Далее в главе идет речь об уроке – анализе контрольной работы. Раскрываются положительные и отрицательные стороны этого урока: основная трудность – управлять вниманием класса. Положительным же является то, что систематизируются знания, получаемые на предыдущих уроках, анализируются все допущенные ошибки, составляются подобные примеры и задачи тем, в которых допущено большое количество ошибок, отрабатывается алгоритм решения. Попутно развивается внимание, наблюдательность. Учитель должен быть хорошим стратегом и вовремя создавать для интеллекта детей посильные трудности, не ликвидировать все преграды на пути ребят к вершинам знаний, а планомерно создавать их, это позволит детям не только осознанно владеть школьной программой, но и продвигаться по пути формирования своей личности. Итак, подводя итог I главе можно сказать, что на уроке нет мелочей, надо уметь все предусмотреть.

Вторая глава называется «Как можно начать урок». В этой главе рассматриваются различные способы начала урока, как условия создания у школьников положительной мотивации к выполнению умственных и практических действий, которые помогут сформировать стремление к познанию, умение управлять собственной познавательной деятельностью. Решение этих проблем зависит от умения учителя овладеть вниманием учеников. Как правило, удачный вид деятельности, выбранный в начале урока – настраивает ребят на плодотворную работу в течении всех 45 минут. Вот почему особое внимание уделяется организации начала урока. На этом этапе используются те приемы активизации, которые обеспечивают подведение учащихся к осознанию необходимости усвоения нового материала или выполнение определенного задания. И чем не навязчивей действовать, тем большего результата можно достичь. Детям необходимо четко представлять, какой вид деятельности их ждет на уроке. Планируя способ включения учеников в урок, необходимо думать о создании мотивационной основы их работы, ведь именно творческие, посильные задания наиболее цепко держат внимание ребят. При этом опора на интерес и радость, которую получают дети от открытия своих способностей, поможет создать сложившуюся основу для истоков творческой деятельности. Помогает в поиске построения начала урока осознание того, что сложность, доступная для ребят, и новизна – основные причины интереса. При определении сложности задачи необходимо напомнить слова известного педагога Щацкого о том, что учение без препятствий, без трудностей вызывало бы мало интереса у школьников, ослабило бы переживание положительных эмоций, лишило бы чувства радости от преодоления трудностей. Далее перечисляются некоторые способы организации начала урока, используемые автором:

1. Предлагается задача, которая решается только с опорой на жизненный опыт ребят и их смекалку.
   
2. Дается задача на тренировку памяти, наблюдательности, на поиск закономерностей по материалу, хорошо усвоенному школьниками.
   
3. На доске записаны уравнения и ответы к ним, среди которых есть как верные, так и неверные. Предлагается проверить их.
   
4. На доске записано решение примера или задачи с традиционными, наиболее часто встречающимися ошибками. Предлагается осуществить проверку каждого логического хода решения.
   
5. Дается обычная задача с традиционным решением. Предлагается найти более короткое, рациональное решение.
   
6. На доске дан чертеж к сложной задаче и методом мозгового штурма осуществляется поиск ее решения.
   
7. На столе у каждого ученика лежит чистый лист бумаги и учитель объявляет, что в конце урока по некоторым вопросам будет проведена проверочная работа.
   
8. Урок начинается с чтения по фразам и коллективного обсуждения параграфа, предназначенного для самостоятельного изучения. Если класс оказывается в затруднении, то отвечают консультанты по этой теме.
   
9. Ребята изображают некоторую фигуру и проводят некоторую исследовательскую работу по определенному плану.
   
10. Обсуждаются различные способы решения задачи, заданной на предыдущем уроке.
    
11. Если на дом было задано творческое задание, то начинают урок с представления наиболее удачных работ.
    
12. Рассматривается некоторая математическая проблема, которая не обсуждалась в классе. Ученики намечают план поиска ее решения.
    
13. На доске выполнен чертеж к домашним задачам. По готовым чертежам обсуждается их решение.
    
14. Урок начинают «солисты». Так называют учеников, которым предстоит «защитить» решение домашних задач». Затем перечисляются те моменты, которые способствуют быстрому включению ребят в работу:
    

1. Чертеж, приготовленный заранее, его простота
   
2. Легко воспринимаемом условие задачи
   
3. Коллективное обсуждение задачи
   
4. Четкое понимание последовательности действий, направленных на поиск решения.
   

Общим во всех приведенных примерах является стремление вызвать противоречие между теми установками, шаблонами, которые у учащихся сформировались в процессе обучения, и той ситуацией, рассмотреть которую ему предлагалось.

Третья глава называется «Конструкция урока и умственное развитие школьников». В этой главе идет речь об эффективности работы учащихся на уроке в зависимости от творческой активности учащихся. Рассматривается 6 различных по конструкции уроков по теме «функция у=ах² и ее график. Отмечаются их достоинства и недостатки.

Следующая глава монографии называется «Урок алгебры в «сильном» и «слабом» классе. В данной главе подчеркиваются различия в действиях учителя и деятельности учащихся в слабом и сильном классе. Отмечается, что урок в сильном классе впечатляет умелыми ответами ребят, кажущейся легкостью работы учителя, интересным диалогом учеников и учителя, да и самих детей. Интерес к работе в слабом классе даже у профессионалов снижается: дети не сразу выдают нужный ответ, не с такой легкостью делают вычисления, от непрочности знаний появляется неуверенность в себе и поэтому говорят они тихо, как бы желая, чтобы их ответ услышал только преподаватель, но не гости. Так как движущей силой учебного процесса является противоречие между познавательными и практическими задачами и уровнем знаний, умении и умственным развитием школьников, то уроки для каждого из этих классов строятся по-разному. Успех зависит от того, насколько точно удалось определить уровень сложности задач, которые позволили бы наиболее эффективно организовать процесс обучения. Сильный класс требует меньше работы по усвоению алгоритмов решения, причем учащиеся значительно быстрее и часто самостоятельно обобщают показанные приему сразу на целый класс задач и с интересом применяют их в нешаблонных ситуациях. Слабый класс требует от учителя большой методической изощренности: умения придумать доступную форму подачи алгоритма, продумать работу по его запоминанию, обеспечить ребенку деятельность по формированию определенного умения. Тогда в серьезную интеллектуальную работу, свойственную сильному классу, включается и ученик слабого класса. Итак на каждом уроке сверхзадачей является обучение выполнению приемов обобщения и конкретизации, но в слабом классе эта работа была более конкретной. Четко выделены приемы выполнения каждой мыслительной операции и показана эта работа на ряде примеров. На уроке в сильном классе были созданы условия для того, чтобы ученик догадался, какое обобщение надо сделать. Учить догадываться – это сверхзадача урока. Следующие 2 главы посвящены проблемам геометрии: «Выход в пространство при изучении геометрии» и «Развитие геометрического видения – одна из целей двух уроков». Анализируя эти главы приходишь к выводу, что несложные задачи с выходом в пространство дают большие возможности для творчества учащихся. Такие задачи решаются более свободно, т.е. все понимают, что материал дается на вырост, он не обязателен для быстрого усвоения. Может быть это и является тем, что приковывает внимание учащихся, требует от ребят активной работы мысли, «провоцирует» их на поиск. Задачи подбирают так, чтобы их нескучно было решать и сильным ученикам. В следующих двух главах монографии «Анализ условия – первый этап решения задачи» и «Отработка умения наблюдать на уроке», автор подчеркивает необходимость анализа условия и умения наблюдать для каждого учащегося в процессе обучения математике. Далее автор рассматривает одну из важнейших проблем 4-го класса – организация деятельности 4-ро классников, способствующую интеллектуальному развитию. И констатирует, что нужны упражнения для раскрепощения мысли учеников, на проявление инициативы, смелости при поиске решения. Такими задачами по мнению автора являются задания на закрашивание части прямоугольника. Эти задания оказывают огромную помощь при введении понятия о
быкновенной дроби.

½ ½ ½ ½ ½


и т.д. (аналогично с другими дробями)

Аналогичным приемом автор пользуется при изучении действий с обыкновенными дробями. Этот прием позволяет учащимся лучше усвоить все действия с дробями. Видеть наглядно перед собой результат. Для слабых учащихся большая помощь, для сильных дает возможность высвободить время для решения более сложных задач. В главе «Обучение решению текстовых задач в 4 классе» автор еще раз обращает внимание на необходимость составления системы вопросов при решении задач и оформление зависимостей между величинами в виде таблиц. Отмечается роль в задаче таких слов как: больше, меньше, дешевле, дороже, быстрее, медленнее, выше, ниже, шире, уже и т.д. Все эти слова говорят о сравнении величин, которое можно выполнить вычитанием… Слова же «всего сделали, всего собрали, всего прошли, всего получили, общая масса» и т.д. указывают на суммирование величин. Далее дается алгоритмическое предписание. Такой способ решения задач на составление уравнений учит учеников видеть величины, вскрывать связи между ними, а это способствует формированию обобщенных видов познавательной деятельности. Большое внимание в монографии автор уделяет преподаванию геометрии. Следующая глава книги называется «Лабораторные работы по геометрическому материалу 4-5 классов. Автор предлагает для создания условий, обеспечивающих вдумчивую осмысленную работу ученика при изучении геометрического материла проводить лабораторные работы, в которых учащимся предлагается изобразить некоторую геометрическую фигуру и ответить на вопросы и высказать свою гипотезу по поводу подмеченных закономерностей. Этот способ дает возможность держать внимание всего класса и при этом способствует развитию мышления учащихся. Выполняя задания, ребята кроме того, учатся работать с чертежными инструментами. Опытным путем устанавливают свойства геометрических фигур, которые в дальнейшем будут доказаны. Факты, полученные в лабораторных работах более длительное время удерживаются в памяти и в нужный момент помогают усваивать сложный теоретический материал. Далее приводится серия лабораторных работ по темам «Отрезок», «Отрезок, луч», «Окружность», «Угол», «Треугольник», «Прямоугольник», «Параллельные отрезки» , «Перпендикулярные отрезки».

Следующая глава называется «Искусство ставить вопросы». В этой главе автор с исторической точки зрения трактует само слово «вопрос» как мыслительную форму, обеспечивающую переход от незнания к знанию. Концентрация внимания на том или ином понятии тоже требует умения задавать цепочку вопросов, позволяющих рассмотреть его со всех сторон. Изучить его во взаимосвязях с ранее изученным. Любая система вопросов регулирует деятельность учителя, направляет ее в необходимое русло. Разговор об умении ставить вопросы при чтении текста ведется не на одном уроке. И начинается в младших классах. Опыт, приобретенный в этой работе, позволит ребятам осознать, что познание истины связано с серьезным трудом, требующим большой собранности. Может быть эти уроки откроют перед ними радость познания и толчком для размышления будут вопросы, направленные на выполнение основных мыслительных операций: анализа, синтеза, сравнения, обобщения, абстрактирования. Не менее важно показать пример вопросов. Они выделяют главное – основные его закономерности, с их помощью исследуются структуры объекта, устанавливаются связи с ранее изученным. Происходит обучение правильному запоминанию и хранению информации с опорой на смысл, структуру, ассоциации. Домашнее задание тоже можно организовать серией вопросов, ответить на которые предназначено ученикам после прочтения указанного материала в учебнике. Любое исследование, любое творчество начинается с постановкой вопроса, т.е. проблемы. Хороший вопрос помогает совершенно по-новому увидеть существо дела и искать ответ новыми путями, о которых раньше никто не думал. Все это требует некоторых навыков в составлении вопросов. Ученики не умеют задавать вопросы, они привыкли на них отвечать. Значит, необходимо учить ставить вопросы. При этом сначала разумно приветствовать любые вопросы, отмечая более содержательные, постепенно приучая их к постановке вопросов. Сформировать же умение ставить вопросы – дело времени. И это предпринимается уже на изученном материале. И лучше с исследованием изображенных на чертеже фигур или графиков. И если сначала составляют вопросы по небольшому объему материала, то постепенно переходим к вопросам, требующим глубокого анализа ситуации. Следующие две главы монографии посвящены задаче, ее роли в формировании навыков исследовательской работы. Урок одной задачи как бы завершает некоторый этап обучения решению задач, поэтому его лучше провести в конце большой темы. Внимание на этом уроке концентрируется в основном на анализе приемов, которыми решается задача. Поэтому, чтобы не тратить сила на знакомство с условием нескольких задач, достаточно рассмотреть решение только одной задачи, интересной по содержанию, богатой идеями, имеющей несколько способов решения. Еще один урок + урок-бенефис. Это своего рода отчет о домашней исследовательской работе. Урок-бенефис служит цели, направленной на то, чтобы заставить слабого ученика поверить в свои силы. Одним из требований к «бенефисной» задаче является возможность увидеть несколько способов ее решения. Ведь цель таких уроков . стимулирование творческой деятельности, но для этого необходимо, чтобы у учащихся была сформирована готовность к быстрому поиску многообразных вариантов решения проблем. Далее приводятся примеры "бенефисных» задач по геометрии для 6, 7, 8 классов и способы их решения.

Следующая глава называется «О методах устной работы». Устная контрольная работа несколько отличается от традиционной контрольной. Здесь ученик как бы сам себя контролирует при помощи заданий учителя. Он сам делает выводы о степени усвоения. Учитель не видит его неудач. Поэтому устная контрольная работа чаще имеет обучающий характер. Ученик поставлен в ситуацию, когда он вынужден работать в темпе, заданном учителем, контролировать свои действия и использовать весь материал темы. Сверхзадача урока - обучить рациональным приемам работы, без которых невозможно творчество. Далее приводятся образцы устных работ для 5, 6, 7, 8 классов.

В главе один из способов организации индивидуальной работы на уроке автор ведет речь о наличии в классе второй доски, которая помогает неуверенным в своих способностях ученикам отвечать, решать задачи, а так же экономить время учителя на уроке для работы с классом. Далее идет речь о еще одной форме индивидуальной работы – зачете. Далее рассматривается методика его проведения и подготовки. Изучение материала по темам, которые завершаются зачетом, строятся так:

1. Излагается вся теория или читается лекция либо используются поисково-исследовательские методы.
   
2. Рассматривается ряд типичных задач, изучаются алгоритмы их решения.
   
3. Выписываются основные задачи, из которых складывается решение творческих задач.
   
4. Несколько уроков посвящается решению задач.
   
5. После нескольких самостоятельных работ проводится зачет.
   

Далее автор утверждает, что такая система работы позволяет более свободно и творчески строить изучение материала. Каждый ученик получает возможность работать в своем темпе, у учителя же освобождается время для индивидуальной работы. Автор отмечает положительные стороны такой системы: Материал дается целиком и воспринимается более осознанно. Высвобождается время для отработки основных алгоритмов, систематизации изученных понятий. Естественно знания становятся более прочными.

Итак, зачет – это сдвоенный урок, на котором работа строится

следующим образом:

На доске написано 2 варианта контрольной работы, в которую входят одни задачи по теме зачета. Эта контрольная рассчитана на 1 урок. Второй урок отводится для устного опроса. Устно отвечают сначала сильные ученики. Слабые же имеют возможность послушать ответ, уточнить, а так же большее время для выполнения контрольной работы. Каждый ученик получает за зачет 2 оценки: за теоретическую часть и контрольную работу. Затем описывается методика подготовки к зачету:

1. За 2 недели до зачета вывешиваются вопросы и номера основных задач.
   
2. В течении этих 2-х недель к каждому уроку задается один-два вопроса для повторения. Отвечать вызываются только сильные ученики.
   
3. На последнем уроке класс разбивается на пары и сильный ученик проверяет слабого и итог сообщает учителю.
   

Далее подчеркивается особенность зачета в 6 классе и приводятся примеры зачетов по курсу геометрии в 6 классе, 7 классе и 8 классе.

Последняя глава называется «Математические сказки», Сказки особенно нужны детям 5-6 классов. Они готовят к изучению геометрии, которая требует развитого воображения, умения обдумывать предложенную ситуацию. Кроме того, на уроке, если находится место для сказки, всегда царит хорошее настроение, а это залог продуктивной работы. Сказка помогает понять внутренний мир ребенка. Она дает возможность найти путь к сердцу ребенка. Сказка изгоняет с урока скуку, а главное учит быть добрым и справедливым. Сказка вызывает радость и интерес, а от этого зависит творчество ребенка. В заключение монографии автор, подводя итог сказанному выше, отмечает, что дидактами накоплен огромный материал, позволяющий эффективно построить учебный процесс, но беда в том, что их прекрасные проекты довольно часто не находят отражения в преподавании трудных, основных тем школьного курса. Эту работу приходится выполнять учителю самому. Способы формирования умений, описанные в данной книге, позволили автору организовать урок так, что радостно становилось на душе от внимательных глаз учеников и что самое важное на этих уроках успеха добивались самые слабые ученики.

Переходя к анализу практических рекомендаций, изложенных в монографии, следует отметить, что они являются содержательными и непременно окажут учителю математики существенную помощь. Среди рекомендаций можно выделить следующие:

1. Рекомендация состоит в том, что каждый урок должен иметь сверхзадачу, на достижение которой должна быть направлена деятельность учащихся и учителя.
   
2. Деятельностью учащихся на уроке необходимо управлять.
   
3. Учитель должен быть хорошим стратегом и вовремя создавать для интеллекта детей посильные трудности, это позволит детям не только осознанно овладеть школьной программой, но и продвинуться по пути формирования своей личности.
   
4. На уроке нет мелочей, надо уметь все предусмотреть.
   
5. Состоит в том, как можно начать урок. Перечисляется
   

15 способов начала урока, которые окажут несомненно огромную помощь не только начинающему учителю.

6. Успех урока зависит от уровня сложности задач, которые позволяют наиболее эффективно организовать процесс обучения.
   
7. Необходимость проведения лабораторно-практических занятий. Эти занятия способствуют развитию пространственного воображения учащихся, способности логически мыслить.
   
8. Необходимо учить учащихся задавать вопросы. Ценность этой рекомендации заключается в том, что учащиеся более осознанно и глубоко изучают материал, чтобы верно поставить вопрос.
   
9. Необходимость устных контрольных работ. Устные контрольные работы способствуют выработке навыков рациональных примеров работы, без которых невозможно творчество.
   
10. Необходимо с учащимися 5-6 классов сочинять сказки, т.к. сказки способствуют не только развитию воображения учащихся, но и развивают критическое мышление, создают хорошее настроение, делают детей смелее, раскрепощеннее.
    
11. Взаимоотношения учащихся и учителя должны быть добрыми, построенными на взаимоуважении.
    

В целом математическое содержание монографии способствует решению тех задач, которые ставит перед школой жизнь.

Занимаясь изучением данного вопроса, которому посвящена курсовая работа, мною проработано много статей в журнале «Математика в школе» за последние 5 лет, которые непосредственно касаются активизации познавательной деятельности, работе по устранению пробелом в знаниях, самостоятельной деятельности учащихся на уроке и т.д. И.О. Овечкина «Приемы активизации познавательной деятельности». Одной из первоначальных задач при обучении математике является выработка хорошего счета. Однако однообразие заданий в виде примеров на вычисление притупляет интерес к счету, так и урокам вообще. Поэтому у учителя необходимо должен быть арсенал различных приемов, направленных на выработку вычислительных навыков. Одним из приемов является игра «Рыбалка» . Из 4 предложенных на рыбках примерах ребята 1 варианта «вылавливают» примеры с ответом например 5, а второго – 6.

Следующий вид заданий – круговые примеры, которые позволяют ребятам осуществлять самоконтроль, а учителю облегчают проверку работ. Следующий вид заданий – направление преднамеренных ошибок в решение, восстановление частично стертых записей. Всевозможные формы кодирования ответов привлекают внимание ребят не меньше, чем интересная задача, Далее рассматривается 3 вида заданий6

1. Программированный опрос.
   
2. Рядом с примером записаны ответы, закодированные буквами, необходимо выбрать верный.
   
3. Ответы закрыты карточками. Ребята дают ответ, открывают его, перевернув карточку, прикрепляют его рядом с ответом. На обратной стороне карточки буквы, образующие слово (желательно похвалу).
   

Далее отмечается, что при устном счете со всем классом удобно использовать игры «Математическое лото», «Математическое домино», «Математические барьеры». Большой арсенал игр предлагает телевидение. Это и «Счастливый случай», и «Поле чудес», и «Звездный час».

Активизировать познавательную деятельность позволяют и ряд известных приемов и методов:

1. Групповой метод при решении задач. Работа в парах.
   
2. Различные формы работы с книгой.
   
3. Использование различных видов поощрений.
   
4. Самостоятельные работы с использованием аналогий.
   
5. Использование проблемных ситуаций.
   
6. Использование элементов историзма.
   
7. Изложение материала блоками.
   
8. Наглядность, доступность, оригинальность решений, самостоятельность в получении знаний.
   
9. Наблюдение за речью, рецензирование по схеме.
   
10. Дидактические игры, соревнования.
    

Рассмотрим некоторые из этих приемов.

Различные виды самостоятельной работы можно использовать для активизации учебной деятельности школьников, воспитания у них активности, самостоятельности мышления, умения применять знания в процессе обучения. Обучающие самостоятельные работы можно разделить на следующие виды:

а) Самостоятельная работа с предварительным разбором.

Дается подробный разбор задачи или упражнения со всеми теоретическими обоснованиями. Затем для самостоятельной работы предлагается сначала подобная задача, а затем задание с усложненным элементом.

б) Решение задач с последующей проверкой.

Ученики выполняют задание самостоятельно, затем проверяют свою работу по показываемому им образцу. При этом учитель проверяет осмысленность решения путем постановки соответствующих вопросов.

в) Многовариантные задания с готовыми ответами по типу перфокарт.

Эти работы помогают выявлению пробелов и разборку неясных ситуаций.

г) Математические диктанты с самопроверкой или взаимопроверкой.

д) Самостоятельная работа с показом. Такая работа позволяет учащимся не только увидеть способ решения, но и самостоятельно установить логические связи между увиденным и тем, что надо сделать.

е) Работа по заданному алгоритму приучает учащихся к четкому, последовательному выполнению задания.

ж) Сквозная контрольная работа. Эта работа требует хорошей методической и теоретической подготовки учителя и класса, т.к. предполагает использование большого количества задач различной степени сложности.

з) Домашняя контрольная работа.

к) Создание проблемных ситуаций.

Нет сомнения в том, что математика является основой для изучения всех предметов естественнонаучного цикла. По широте практического применения математическое образование несоизмеримо ни с какими другими видами знаний. Исторически сложились 2 стороны назначения математики: практическая и духовная. Практическая – количественная форма продуктивной деятельности, духовная – развитие мышления человека. Главным в процессе обучения является постановка перед учащимися на уроках маленьких проблем, и старание их решить. В понимании детей учитель – это компьютер, который не может ошибаться никогда, и они, обычно, слепо копируют его решение. Поэтому в процессе решения, допуская специально ошибку, можно предложить затем учащимся ее найти. В результате все самостоятельно трудятся и находят ошибку в решении. Результат – внимательность на уроках. Можно дать на дом задачу, объявив, что у учителя она не получается и предложить ее решить, обратившись за помощью к кому-либо, если сам учащийся с ней не справится. Естественно, задача решается и на следующем уроке можно увидеть не один вариант решения. Можно оставить задачу или пример, решаемый в классе, незавершенным. Ученики вынуждены его самостоятельно решать до конца. При решении задач, связанных с исследованием функций применяются сравнения и аналоги из других дисциплин, например из географии, механики, химии, биологии. Традиционные уроки надо совмещать с такими уроками, чтобы у учеников не было понятия о стандарте преподавания. На таких уроках у учеников есть желание мыслить, говорить, раскрыть себя со всех сторон. Такие проблемные ситуации можно создать практически на каждом уроке и совместно с учащимися успешно с ними справляться. Естественно, учитель всегда должен знать все новинки периодической печати, специальной литературы, иначе можно потерять уважение учеников. Но эти проблемы должны быть дифференцированы по уровню интеллекта учеников. (У.Д. Таймасканов. Дагестан).

Групповая форма подготовки у учащихся к уроку применяется

нечасто, т.к. требует особых организационных усилий, но зато дает эффект не только в обучении, но и в воспитании учащихся. В каждой группе выделяется свой лидер. От того, насколько авторитетен и серьезен будет этот ученик, зависит настрой всей группы. Учащиеся, объединенные в одну группу, привыкают работать вместе, находить общий язык, преодолевать сложности общения. Кроме того сильные учащиеся начинают чувствовать ответственность за менее подготовленных учащихся, а те в свою очередь стараются показать себя с лучшей стороны. Для групповой работы подходит далеко не каждый урок, а такой, к которому необходимо готовиться всему классу длительное время. Примерами таких уроков могут быть: уроки-семинары, уроки-решения задач. В течении нескольких дней ребята распределяют и изучают вопросы теории, обсуждаются различные способы решения задач. Длительная и кропотливая работа групп всегда должна находиться в поле зрения учителя. Не вмешиваясь в нее явным образом, учитель должен поощрять учащихся к совместной работе, развивать у них требовательность, учить видеть сильные и слабые стороны ответа. На семинаре бригадиры полностью руководят ответами своих групп. Каждый член группы изучает свою часть материала и следит за ответами в группе, дополняя или исправляя их.

Постройка системы образования обусловила необходимость изменений в структуре взаимоотношений между учителем и учеником. Реально встал вопрос о замене авторитарной педагогики, бытовавшей в школе многие десятилетия, педагогикой сотрудничества. Но было бы ошибкой полагать, что педагогика сотрудничества реализуется только через улучшение личностных взаимоотношений между учителем и учеником. Педагогика сотрудничества должна проявляться прежде всего в его учебном процессе. Именно в конструировании урока целесообразно искать ее резервы. Под педагогикой сотрудничества надо понимать составную часть научной педагогики, которая изучает такую деятельность учителя и учащегося, в ходе которой активность учащихся направляется на открытие новых фактов изучаемого предмета, на усвоение научных понятий в четкой системе, а учебный процесс организуется с привлечением максимального числа разнообразных методических средств и приемов. Для педагогики сотрудничества желательны все виды учебных занятий на уроке: индивидуальная деятельность, работа в паре, в группе, наконец, фронтальная работа. Педагогика сотрудничества приветствует и различные формы урока: лекцию, зачет, тестирование, урок-бенефис, урок «КВН», «Поле чудес» и т.д. Само построение урока, подбор материала помогает учащемуся получать знания, как бы сотрудничают с ним. Педагогика сотрудничества требует специальных упражнений, сконструированных в четкой логической последовательности. Реализовать это требование особенно удобно с помощью программированного обучения. Разработанная система программированных заданий позволяет вовлечь всех учащихся в активную творческую деятельность, способствует выявлению взаимосвязей учебного материала, повышению сознательности в обучении.

II. АНАЛИЗ ОПЫТА РАБОТЫ УЧИТЕЛЯ

Анализируемая монография и статьи применяются мною в работе учителем математики в Землянской средней школе Инжавинского района. В организации учебных занятий я использую многие приемы и методы, описанные выше.

Я, Гриднева Наталья Алексеевна – учитель математики Землянской средней школы. О профессии учителя я мечтала со школы. В школе училась отлично. Старшая сестра тоже работает учителем русского языка и литературы. Я закончила основную школу в 2000 году, поступила в Тамбовский педагогический колледж №1 им. К.Д. Ушинского. С 2002 г. совмещала учёбу в колледже и в Тамбовском государственном университете им. Г.Р. Державина. В 2002 году я поступила на заочное отделение физико-математического факультета, отделение : математика. По окончании колледжа в 2005 г., по распределению поехала в п. Землянский Инжавинского района, где второй год веду математику в 5, 9, 10, 11 классах, физику и информатику. Здесь я впервые почувствовала себя учителем, ощутила всю серьезность и важность выбранной профессии, познала радость открытий и горечь неудач. Большую часть своего времени я провожу в школе, люблю свой предмет и стремлюсь организовать учебно-воспитательный процесс так, чтобы учиться было интересно и радостно. Добиваться определенного успеха всем людям помогает трудолюбие, творческое и серьезное отношение к делу, собранность и систематическая работа над собой. Я всегда стремилась к этому.

Ведущей идеей моей работы является идея воспитания математически образованного ученика. Максимально раскрывая перед ними приложение математических знаний, передавая ученикам свою увлеченность предметом, я считаю необходимым в работе развивать математическую подготовку учащихся, полученную на предыдущей ступени обучения, а также учитывать возможность продолжения выпускниками школы образования в средних специальных учебных заведениях и высшей школе.

В моём кабинете математики есть дидактический материал для 5-11 классов, раздаточный материал, карточки коррекции знаний, карточки для индивидуальной работы, различные таблицы, графики. Почти всё сделала своими руками. В своей работе я использую приемы и технологии современного обучения. Использую зачетную систему контроля знаний, включая и тестовый контроль. В своей работе стараюсь использовать разнообразные виды самостоятельной работы. Чаще всего применяю для активизации познавательной деятельности учащихся такие приемы как дидактическая игра, работа с книгой, лекция, семинар (старшие классы), обучающая, контролируемая самостоятельные работы, тестирование, творческие работы…

Я считаю, что игровой компонент, дух творчества должны присутствовать на уроках математики в 5 классе. Тогда урок вызовет интерес, желание узнавать и работать. Так при изучении темы «Натуральные числа», «Действия с десятичными дробями» – использовала математическое лото. На уроки часто использую сказочных героев, которым нужна помощь. К обобщающим урокам ребята сочиняют сказки, составляют кроссворды и ребусы. При объяснении нового материала использую проблемный метод, при закреплении использую задания на исправление преднамеренных ошибок, деформированные задания. Для повышения интереса к предмету на уроках провожу веселые пятиминутки, разминки ума, эстафеты. Немаловажной задачей считаю обучение детей 5 класса работать с учебником. Применяется следующая методика :

1)Рассматривается учебник.

2) Изучается как расположен учебный материал.

3) Как называются пункты учебника.

4) Как пользоваться оглавлением и символикой.

5) Выделять главное.

5. Составлять план рассказа и по плану отвечать на вопросы.
   

Тема урока: «Действия с десятичными дробями»

Девиз: «Знания имей отличные по теме «Дроби десятичные».

Цель урока: Образовательные: Систематизировать знания учащихся по изученной теме.

Проверить знания учащимися правил по теме «Действия с десятичными дробями».

Проконтролировать умение учащимися выполнять действия с десятичными дробями.

Развивающие: развивать умение пользоваться правилами и обосновывать эти действия. Способствовать развитию речи учащихся.

Воспитывающие: воспитание внимания учащихся. Формирование познавательной активности.

Тип урока: Урок-путешествие.

Оборудование: Карточки с заданиями (класс разбивается на 3 группы и выбираются капитаны экипажей).

Ход урока

1. Организационный момент (проверяется наличие необходимого к уроку, наличие карточек).
   
2. Вступительное слово учителя о необходимости отправиться в путешествие по стране десятичных дробей), а всякое путешествие требует закалки, подготовки и тренировки. Проверим как мы к этому готовы.
   

а)Проверка домашнего задания, выполненного с преднамеренными ошибками: Заранее на лоске записывается учителем 1) (644,4+75,6):7,2=100; 3)(12,48-8,64):2,4=16 (1,6);

2) (3,9+13):1,3=1,3 (13) 4) (47-9,4): 4,7= 0,818

Необходимо пояснить ошибки.

б) Чтобы нас пропустили в эту страну, вы должны ответить на вопросы и выполнить устные задания (на магнитной доске на плакате изображены рисунки:











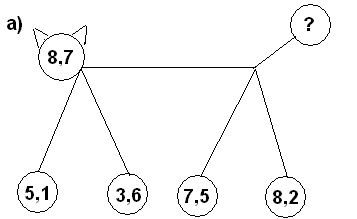
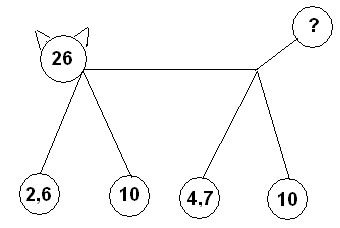
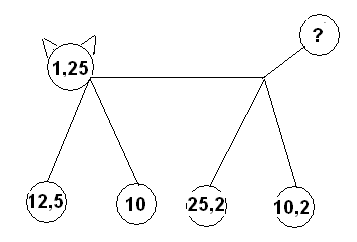
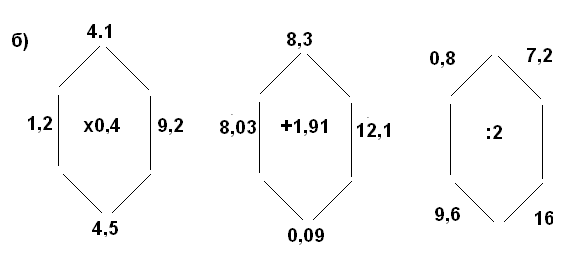
в) Дополнить каждое из чисел до 2,5 если числа даны : 1,5; 0,8; 1; 0,4 (команда, ответившая быстрее и верно, получает 1 очко).

3. Первый этап путешествия будет проходить на катере и чтобы оно прошло успешно, нужно решить задачу на определение скорости по течению и против течения ( Капитанам выдают карточки с заданиями а) Vm= 3,5 км/ч б) Vm = 3,7 км/ч

Vпр.т. =11,3 км/ч V по т = 15,7 км/ч

Vс- - ? Vс - ?

Vпо т - ? Vпр.т. - ?

в) Vпо т - 19,8 км/ч

Vc = 18 км/ч

Vm - ?

Vпр.т - ?

Пока капитаны решают задачи, все учащиеся должны приобрести билеты, а для этого выполнить задания (проверяются на обратной стороне доски)

Сравнить:

72,03 72,18 37,24 37,05

10,72 10,79 1,3 1,237

0,37 0,368 5,603 5,6

14,2 14,20 13,8 13,80


Решить уравнение

Х – 0 = 0,12 2,3 – Х = 1,5

7Х + 2,4 = 34,6 9Х + 3,9 = 31,8

Округлить до единиц (десятых)

13,87;403,524; 0,17; 38,52; 60,399; 0,52

(каждый ученик выполняет ее на месте)

4. Итак, все заняли свои места на катере, плывем против течения реки. Чтобы помочь катеру члены команд должны подбросить горючего, а для этого нужно каждому выполнить задание

(Проводится эстафета. Запись на доске).

1,4 + 1,6 = □ 3,6 + 0,4 = □ 2,8 + 1,2 = □

□ – 1,7 = □ □ – 2,4 = □ □ – 1,5 = □

□ • 1,3 = □ □ • 1,6 = □ □ • 2,5 = □

□ + 0,3 = □ □ + 0,44 = □ □ – 0,25= □

□ : 2 = □ □ : 3 = □ □ : 3 = □

□ – 0,2 = □ □ – 0,1 = □ □ – 0,4 = □

□ : 0,2 = □ □ : 0,2 = □ □ : 0,4 = □

5. Ребята, наш катер сел на мель, чтобы снять его с мели нужно решить задачу с комментированием.

а) В прямоугольнике одна из сторон равна 5,45 м, а вторая в 5 р больше. Найти площадь и периметр прямоугольника.


б) Второе задание размыло водой. Необходимо верно поставить запятую:

3 + 108 = 408 42 +7 = 112

63 – 27 =603 736 – 336 = 4

52 + 18 = 5

1. Дидактическая игра с числами (запятая перебегает с места на место, а ребята должны прочитать получившееся число). (Участвуют ребята, у которых на голове шапочка с цифрой).
   
2. Ребята, для завершения нашего путешествия вы должны выполнить самостоятельно задание. Найти значение буквенного выражения, записать ответ в строке «результат» и закрасить рисунок цветом, соответствующим данному результату.
   

(Каждый получает картинку)

1( а + в) х с : d

2 а х b : ( c + d)

3. Заключительное слово учителя:
   

Подведение итогов, оценки: Команда, набравшая 15 очков – 5, 10 очков – 4, меньше 10 очков – 3.

4. Стихотворение 0,3.
   
5. Д/з «Сочинить сказку о стране десятичных дробей».
   

Весь урок построен так, что ученики должны думать, анализировать, находить аналоги и делать соответствующие выводы. Кроме того идет работа в группах, где можно получить помощь товарища, что не запрещается, т.к. при этом идет более успешное осмысление материала. Групповая работа имеет место на многих уроках в различных вариантах: будь то пары постоянного или сменного состава или экипажи-группы. Групповая работа обязывает учащихся ответственно относиться к результатам учебного труда.


В работе с учащимися 9 класса уделяется большое внимание развитию речи учащихся. Учащиеся учатся описывать рисунок, т.е. рассказывать все, что они знают о фигуре, изображенной на рисунке. Большая роль уделяется теоретическим работам, которые способствуют более глубокому осмыслению изученного, а также лабораторным работам по геометрии.

Конспект урока по геометрии в 9 классе.

Тема урока: Прямоугольники (первый урок из обобщающего повторения за 9 кл).

Цели урока:

Обобщающие:

1. Повторить основные вопросы, связанные с понятием равнобедренного треугольника и его свойствами.
   
2. Вспомнить формулы для вычисления площадей треугольников.
   
3. Вспомнить соотношение между сторонами и углами треугольника.
   
4. Систематизировать знания учащихся по данной теме.
   

Развивающие: Способствовать развитию речи учащихся.

Учить учащихся обосновывать свои ответы.

Воспитывающие: Воспитание активного внимания;

Воспитание аккуратности при выполнении чертежей;

Формирование самостоятельности;

Развитие познавательной активности.

Тип урока: Обобщающе-повторительный.

Оборудование: Карточки с номерами 1, 2, 3

Карточки 2-х цветов с темной и светлой стороной;

Чертежи к задачам.

План урока:

1. Геометрическая перестрелка ( 5 мин.)
   
2. Описать рисунок (70 минут)
   
3. Задачи-картинки (80 минут)
   
4. Верно-неверно (13 минут)
   
5. Решение задач (20 минут)
   
6. Подведение итогов, задание на дом (2 м).
   

ХОД УРОКА:

1. Организационный момент
   
2. Повторение изученного и проверка домашнего задания.
   

а) Геометрическая перестрелка между учащимися 1 и 2 ряда. Проверка знаний основных определений и свойств.

Вопросы могут быть такими:

1. Какую геометрическую фигуру называют треугольником.
   
2. Какие треугольники называются равнобедренными.
   
3. Свойства равнобедренного треугольника.
   
4. Признак равнобедренного треугольника.
   
5. Какой треугольник называется прямоугольным.
   
6. Свойства прямоугольного треугольника.
   
7. Признаки равенства треугольников.
   
8. Медиана, биссектриса и высота треугольника.
   
9. Соответствие между сторонами и углами в треугольнике.
   
10. Равносторонний треугольник и его свойства.
    

б) Описать рисунок по чертежу (чертеж выполняется на пленке графпроектора).

Необходимо назвать как можно больше свойств фигуры, изображенной на рисунке)

(Можно назвать следующие свойства)

Р
ис.1.

1. Определение равнобедренного треугольника.
   
2. Теорема о свойстве углов равнобедренного треугольника.
   
3. Теорема о свойстве медианы равнобедренного треугольника, проведенной к основанию.
   
4. Теорема о свойстве внешнего угла треугольника
   
5. Теорема о сумме углов треугольника.
   
6. Определение внешнего угла.
   
7. Свойство биссектрисы угла.
   

Р
ис. 2.

(Можно назвать следующие свойства

1. Определение прямоугольного треугольника, название его сторон.
   
2. Признаки равенства прямоугольных треугольников.
   
3. Свойства прямоугольного треугольника (их 2)
   
4. Определение sin, cos,tg.
   
5. Теорема Пифагора.
   
6. Решения прямоугольного треугольника.
   
7. Теорема о центре окружности, описанной около треугольника.
   

Р
ис.3.

Можно сформулировать следующие свойства:

1. Определение тупоугольного треугольника.
   
2. Соотношение между сторонами и углами треугольника.
   
3. Теорема Синусов.
   
4. Теорема Косинусов.
   
5. Неравенство треугольников.
   

В) Задачи на готовых чертежах с выбором ответов (Задачи-картинки).

Выбрать верный ответ доказать истинность


1

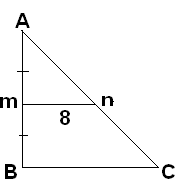
) 2)

< DBA=20° AC=10

< DBA=55° АС=100см

<
DBA=35° АС=20см

3
)

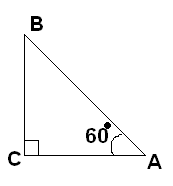
г) Верно-неверно!(Задачи на доказательство)

1. Верно ли, что теорему Пифагора можно доказать из теоремы косинусов? (Доказать)
   

Верно ли, что в любом треугольнике либо все углы острые, либо 2 острых , а один прямой или тупой?

III Решить на закрепление

а) с взаимопроверкой и последующей проверкой ответов

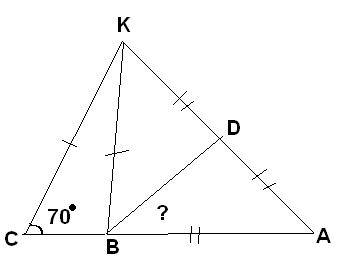
Р
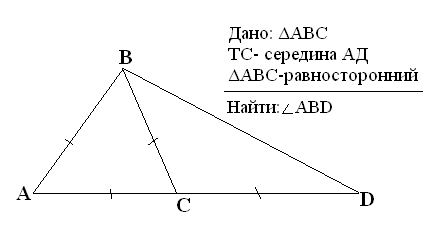
ешение:

1. Так как Δ АВС - равносторонний,=> < А=<АВС=<АСВ=60°
   
2. Так как Δ СВD - равнобедренный,=> < СBD=

б) На доске:

Р
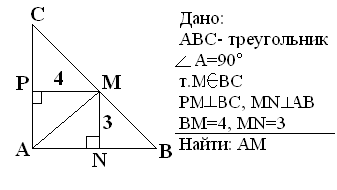
ешение: так как РМ ┴ АС, МN ┴ AB и АС ┴ АВ => PMNA- прямоугольник, АМ- диагональ, ∆AMN- прямоугольный, найдем АМ по теореме, обратной теореме Пифагора: AN² + NM²=5(см).


В работе с учащимися 10-11 классов я использую лекционно-семинарскую систему. Урок-лекция, как правило, позволяет дать материал крупными блоками. Поэтому эта система нашла свое применение при изучении тем: «Прогрессия, уравнения и неравенства», «Способы преобразования многочленов, логарифмическая, показательная функция, тригонометрические функции, тригонометрические уравнения и неравенства и др.

Урок № 1 по теме «Прогрессии» (Лекция)

Тема урока: Арифметическая и геометрическая прогрессии, формула n-ого члена арифметической и геометрической прогрессии.

Цель урока: 1. Познакомить учащихся с определением прогрессий.

2. Рассмотреть 2 вида прогрессий.
   
3. Вывести формулу n-ого члена арифметической и геометрической прогрессий.
   

Оборудование:

1. Таблица «Арифметическая и геометрическая прогрессия».
   
2. Карточки для устного счета.
   
3. Карточки для выполнения индивидуальных заданий.
   

ХОД УРОКА

1.Организационный момент (Проверяется наличие всего необходимого к уроку у учащихся, на доске).

2. Повторение изученного, контроль знаний

а)Устно повторяется тема «Последовательности».

1. Последовательность (аn) задана формулой n-ого члена
   

аn = 3n –1 Найти а1, а3, а10.

2. Задача последовательности: 1, 2, 3, 4, 5, 6,... n, ... Найдите а1, а3, аn .
   
3. Последовательность (вn) задана рекуррентным способом:
   

в1= 2 в n+1= вn + 1

Найдите первые 5 членов последовательности.

4)(аn.) а1 = 16 аn+1=1/2 аn

Найдите первые 4 члена. Каким способом задана последовательность.

5. Задана последовательность: 5, 7, 9, 11, 13, 15, 17... Назовите член последовательности, предыдущий 9; 13; 7; 11

Следующий за членом 5; 11; 9; 13

Найдите разницу между 2-м и 1-м членами, 6 и 5, 7 и 6 членами.

6. У доски проверяется домашнее задание № 338.

Выпишите первые 4 члена последовательности (вn), если:

А) в1 = 5, в n+1 = в n + 5

Решение:

А)

в1 = 5

в2 = 5 + 5 = 10

в3 = в2 + 5 = 10 + 5 = 15

в4 = в 3 + 5 = 15 + 5 = 20

вn: 5; 10; 15; 20; ...

в)

в1=5, в n+1 = вnх5

Решение:

в1=5

в2 = в1 х 5 = 5 х 5 = 25

в3 = в2 х 5= 25 х 5 = 125

в4= в3 х 5= 125 х 5= 625

(вn): 5; 25; 125; 625;...


в) Второй ряд выполняет проверочную работу по карточкам:

1. Является ли число 15 членом последовательности (аn), если аn=2n+1.
   
2. Последовательность вn=2n^2. Найти в5, в8, в30, в45.
   
3. Последовательность (аn) задана формулой: аn= n + 1/ n – 1. Найти а1 – а5.
   
4. (аn) – последовательность заданная формулой аn= 2n+3. Найти а1 – а5
   
5. Является ли число 7 членом последовательности (аn), если
   

а1= 3n-10

6)Найти первые 6 членов последовательности заданной формулой Хn=2n- 1

7) Является ли число 20 членом последовательности (аn), заданной формулой аn= n²+2n-4

8) Вычислить а2, а4, а5, а7, если известно, что последовательность а(n) имеет 1 член, равный 10, а каждый следующий на 10 больше.

III. Изучение нового материала: (Лекция)

План лекции

1. Определение прогрессий
   
2. Разность арифметической и знаменатель геометрической прогрессий
   
3. Формула n-ого члена арифметической и геометрической прогрессий
   
4. Тетрадь делится пополам. Материал рассматривается в сравнении 2-х прогрессий. Учащиеся фиксируют в тетрадях лекцию.
   

Рассмотрим 2 последовательности чисел, полученных при выполнении домашнего задания № 338

5, 10, 15, 20... 5, 25, 125, 625,...

Как получается каждый последующий член каждой последовательности?


Урок-семинар требует предварительной подготовки. Класс разбивается на несколько групп, которые получают свои задания и контролируются консультантом группы. Лекционно-семинарская система позволяет высвободить время для неоднократного повторения на уроках вопросов теории, решения задач, выработке программных умений и навыков по изученной теме. Эта система позволяет усилить практическую направленность преподавателя, активнее привлекать учащихся к работе с учебником, тем самым обеспечить более высокий уровень математической подготовки. После изучения каждой темы провожу зачеты. Контроль за уровнем изученного осуществляется в форме математических диктантов, самостоятельных работ разных видов, тестирования, программированный контроль. При изучении геометрии использую наглядные пособия, изготовленные учащимися: модель координатной плоскости, модель координатной прямой, модели многогранников, которые используются для проведения лабораторно-практических работ. Для построения графиков функций используются изготовленные шаблоны и трафареты. Все виды активизации познавательной деятельности учащиеся будут эффективны при условии доброжелательного отношения к ученику, его успехам со стороны учителя и товарищей.


ВНЕКЛАССНАЯ РАБОТА ПО ПРЕДМЕТУ


« Брейн-ринг » между сборными командами 9,10,11 классов


Цель: Развитие интереса к изучаемому предмету, расширение кругозора учащихся, развитие умений логически мыслить, четко выражать свои мысли


Оборудование: Высказывания по математике, две настольные лампы, гонг, карточки с вопросами, две скатерти, эмблемы команд, звезды для подсчета очков, черный ящик, песочные часы, призы и награды.


Ход игры: Учитель или ведущий: Сегодня мы проводим встречу на ринге. Участниками игры являются команды «Ромб, Треугольник, Квадрат».


Ученик: Ты нам, математика, даешь

Для победы трудностей закалку