Школе необходима соответствующая специальная подготовка педагогов, способных овладеть предметом, имеющим математическую природу и широчайшее прикладное значение

Вид материала

Пояснительная записка

Содержание Занятие № 4. Количество информации. Решение задач Задача № 3/4 Ответ: 7/5 Log3 - 32/15 (бит). Ответ: 7/5 Log3 - 32/15 (бит). Занятие № 5. Решение логических задач на взвешивание через энтропию и количество информации Задачи занятия Занятие № 6. Решение логических задач о лжецах через энтропию и количество информации Задачи занятия Занятие № 7. Защита творческих проектов

Подобный материал:

• Программа и количество зачетных участников соревнований и конкурсов: 13 марта, 244.61kb.
• Программа курса "Международное право" Для специальности, 260.66kb.
• Планирование работы с педагогами и родителями совместно с психологом; подготовка педагогов, 166.16kb.
• Программа дисциплины дпп. Дс. 01 История риторики Цели и задачи дисциплины Курс «История, 214.83kb.
• Нп «сибирская ассоциация консультантов», 161.33kb.
• Как правильно подготовить ребенка к школе. Первый класс, или Как подготовить ребенка, 93.78kb.
• Ответы на вопросы: Каково значение и место системы обеспечения безопасности в деятельности, 35.06kb.
• Учебное пособие Учебный центр «Блокпост» Ступак А. А., Шеблов В. А. Тактико-специальная, 1944.16kb.
• Vi международная научная школа-конференция «Фундаментальное и прикладное материаловедение», 99.7kb.
• Viii международная научная школа-конференция «Фундаментальное и прикладное материаловедение», 93.5kb.

Занятие № 4. Количество информации. Решение задач

Цель занятия: Введение понятия количества информации для решения задач.

Задачи занятия:

• Ввести новые понятия и формулы: количество информации, ориентированный граф, свойства количества информации;
  
• Разобрать типовые задачи на количество информации;
  
• Провести интерпретацию информации через энтропию;
  
• Доказать ряд свойств количества информации;
  

План занятия:

1. Введение понятия количества информации;
   
2. Введение ориентированного графа для решения соответствующих задач;
   
3. Решение задач
   

Ход занятия: Основные задачи, которые ставил перед собой К. Шеннон в середине XX в. при создании направления, в последующие годы получившего название «теория информации», были связаны с чисто техническими вопросами электросвязи и радиосвязи. Работы Шеннона оказали большое стимулирующее влияние на исследования, относящиеся к передаче и сохранению какой бы то ни было информации в природе и технике. За количество меры информации события А принимается величина I (А) = log[Р(A)]^-1= - log[Р(A)]. Информацию сложного опыта можно измерить числом, которое называется количеством информации об опыте β, содержащемся в опыте α: I(α, β )=Н(β) – Н(β /α ).

К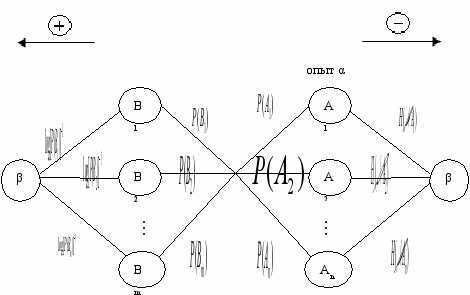оличество информации : I(α, β) показывает, насколько осуществление опыта α уменьшает

неопределенность

опыта β.


Количество информации предлагается находить на ориентированном графе, позволяющем найти Н(β) и Н(β/α), при этом считаем, что Н(β) – энтропия опыта β без влияния других опытов, Н(β/α) – энтропия опыта β при осуществлении опыта α. граф – авторское изобретение ректора ЯГПУ им. К.Д. Ушинского В. В. Афанасьева. Задача 1/4. В урне два белых и два черных шара. Опыт β состоит в извлечении из урны двух шаров, а опыт α – предварительном извлечении из той же урны (без возвращения) одного шара. Найти количество информации об опыте β, содержащейся в опыте α.

Решение. Построим ориентированный граф опытов α и β






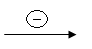
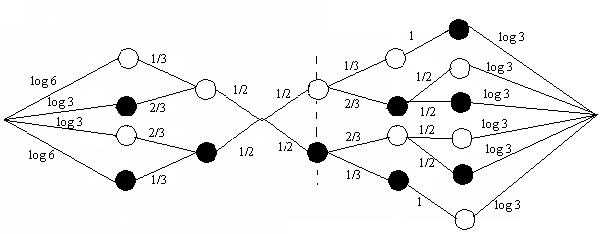
опыт α







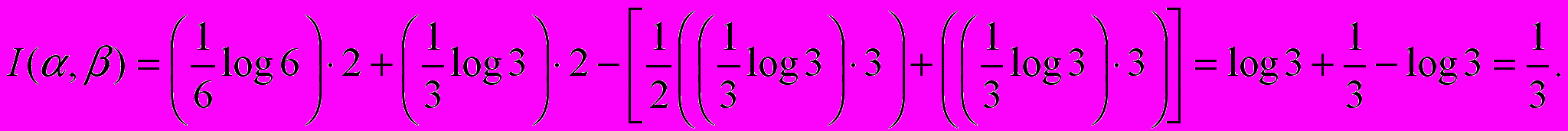
Задача № 2/4. Найти количество информации при вынимании козырной карты из 16 карт с картинками, содержащейся в предварительно извлеченной одной карте.

Решение: Пусть опыт β = {извлечение карты из 16 с картинками}, а опыт α = {предварительное извлечение одной карты}. Для вычисления 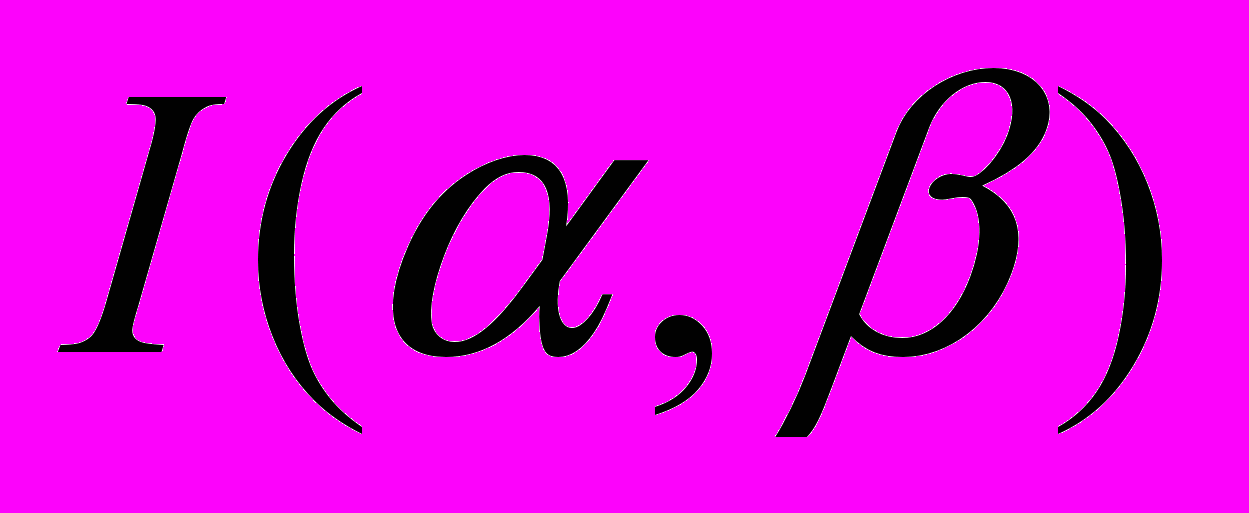используем ориентированный граф.



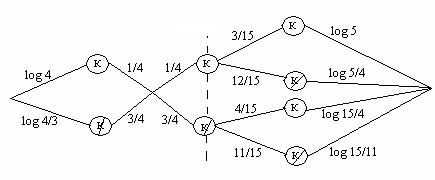
опыт α




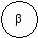
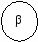
Н(β) = 1\4 Log4 + 3\4 Log4/3 = 1 \2 + 3\2 – 3\4 Log3 = 2 - 3\4 Log3 (бит);

Н(β/α)=1\4*3/15* Log5 + 1\4 *12/15Log5/4 + 3\4 * 4/15 * Log15/4 + 3\4 *11/15* Log15/11 =

1\20* Log5 + 1\5*(Log5 – Log4+Log5 + Log3– Log4) + 11\20*(Log5 + Log3– Log11) =

Log 5 + 3/4 Log 3 – 11\ 20 Log 11 – 4\5(бит).

I(α,β) =2-3\4Log3-Log 5-3/4Log3 + 11\20Log11 + 4\5 = 14\5 –3/2Log3 - Log5+ 11\20 Log11 (бит).

Ответ: 14\5 –3/2Log3 - Log5+ 11\20 Log11 (бит).

Таким образом, понятно, что граф (ориентированный граф) является не только наглядным сопровождением решения, но и точной схемой решения, дающего безошибочный ответ. Рассмотрим свойства количества информации

Свойства количества информации

1. 0 ≤I(β/α) ≤ Н(β)
   
2. I(α,β) = Н(α) + Н(β) - Н(α*β),
   
3. I(α,β) = I(β,α)
   
4. I(α,β,γ) ≥I(α,β), где α,β,γ- три произвольных опыта
   

Доказательство

2. I(α,β) = Н(α) + Н(β) - Н(α*β)

Учитывая, что Н(α*β) = Н(α) + Н(β/α) и I(α, β )=Н(β) – Н(β /α ) = Н(β) + Н(α) – Н(α*β).

3. I(α,β) = I(β,α)

Учитывая, что Н(α*β) = Н(α) + Н(β/α) =Н(β*α) = Н(β) + Н(α/β)

I(α, β )=Н(β) – Н(β /α ) = Н(α) - Н(α/β) = I(β,α)


Задача 2/4. В задаче 1/4 поменяем местами очередность проведения опытов и 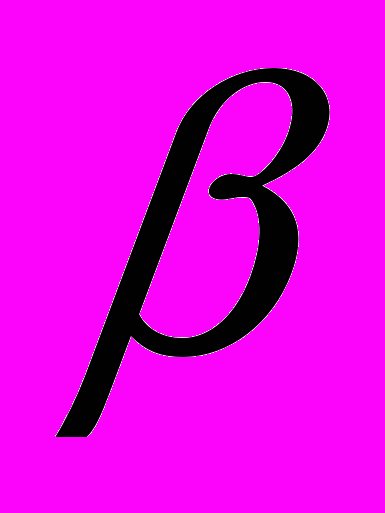. Найти количество информации об опыте , содержащемся в опыте .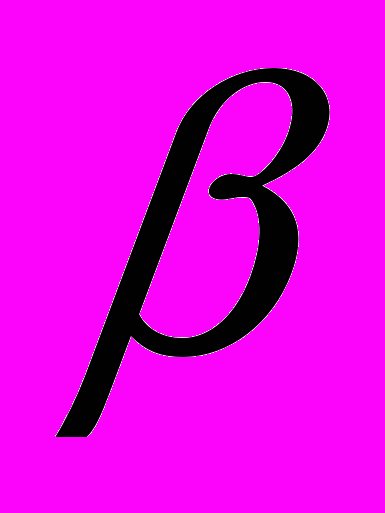

Решение. 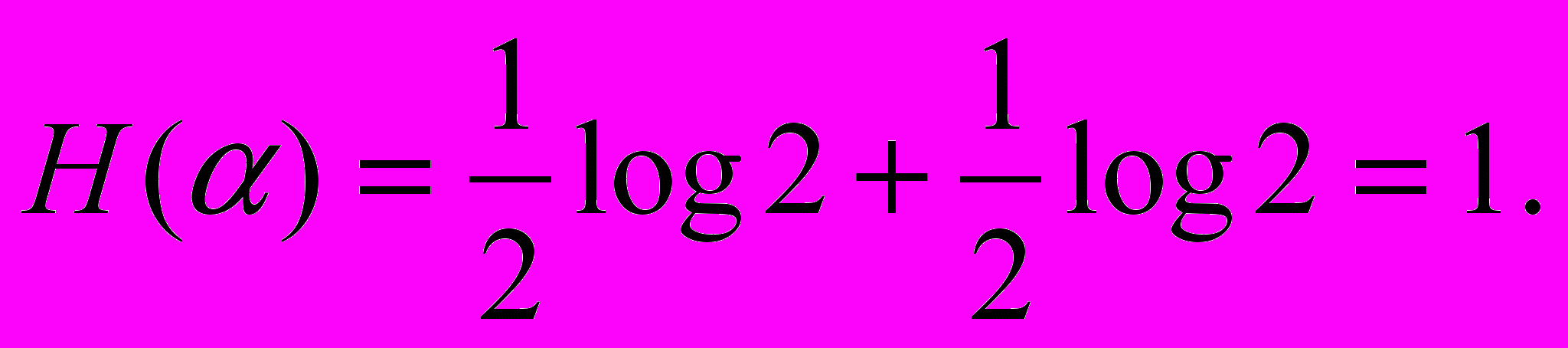Найдем условную энтропию 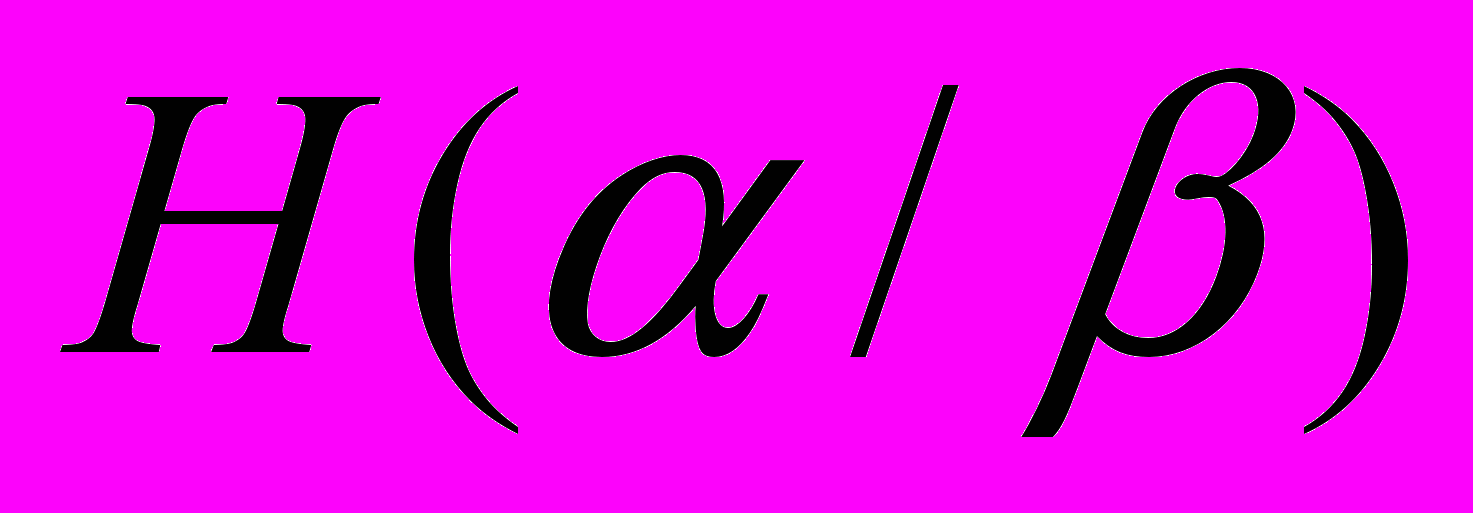по графу


опыт β








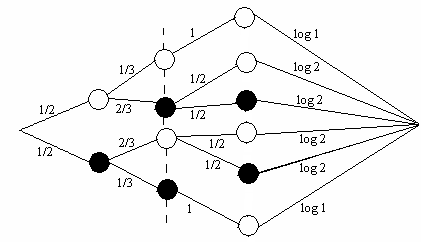
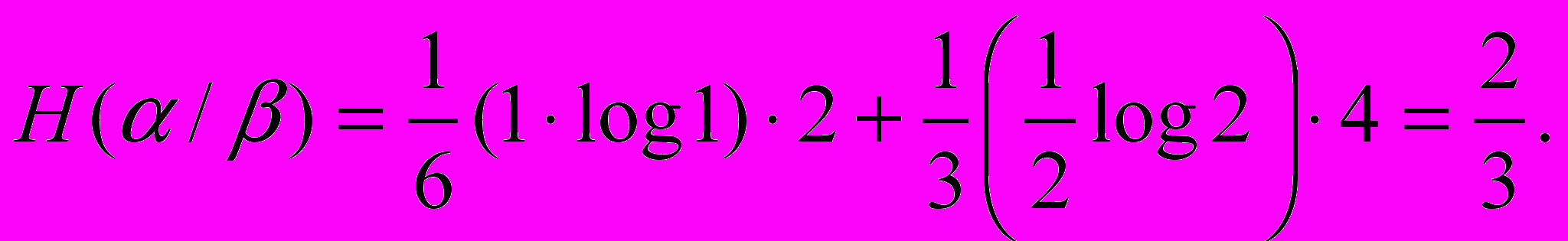
Отсюда

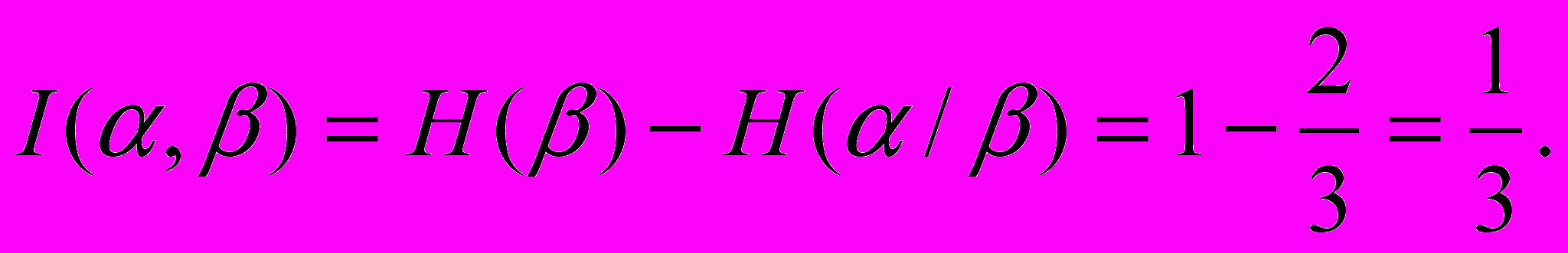
Эти две задачи (1/4 и 2/4) иллюстрируют свойство 3. количества информации.

Задача № 3/4 В урне находятся один белый и два черных шара. Найдите количество информации об извлечении шара, содержащейся в предварительном извлечении одного шара.

Решение: Для вычисления I(α,β) построим ориентированный граф.

α = {предварительный шар}

β = {изъятие шара }



2/3

1/3

Log3/2

Log3



2/3

1/3

1/2

1/2

2/2

0/2

Log2

Log2

Log1

Log2

β

β/α

Н(β /α )


Н(β)


I(α, β )=Н(β) – Н(β /α ).

Н(β) = 2\3 Log3/2+ 1\3 Log3 =Log3 – 2/3(бит);

Н(β/α)=2\3*1/2* Log2 + 2\3 *1/2Log2 + 1\3*2/2 * Log1 = 1/3 +1/3 +0 = 2/3 (бит).

I(α,β) = Log3 – 2/3 – 2/3 = Log3 – 4/3бит).

Ответ: Log3 – 4/3(бит).


Задача 4/4. В урне находятся 2 белых и 4 черных шара. Опыт β состоит в вытаскивании 2 шаров с предварительным вытаскиванием одного. Найти количество информации об опыте β в опыте α.

Р
2/5
ешение: П остроим ориентированный граф:




опыт α


4/6

2/6

4/5

1/5

3/5

2/5

Log15/4

Log15/4


Log15


Log5/2


Н(β)


4/6

2/6

3/5

1/5

4/5

3/4

2/4

2/4

1/4

3/4

-----

4/4

Log10/3

Log10/3

Log10/3

Log5

Log5/3

-------

Log5




I(α, β )=Н(β) – Н(β /α ).

Н(β) = 2(4\15Log15/4) + 2\5Log5/2 + 1/15Log15= Log5 + 3/5 Log3 – 22/15 (бит);

Н(β/α)=4\6*(3* 3\10Log10/3+ 1\10Log10) + 2\6(2*1/5Log5 + 3/5 Log5/3) =

= Log5 - 4\5Log3 + 2/3 (бит).

I(α,β) = Log5 + 3/5 Log3 – 22/15 - Log5 + 4\5Log3 - 2/3 = 7/5 Log3 - 32/15 (бит).

Ответ: 7/5 Log3 - 32/15 (бит).


Задача № 5/4. В урне находятся 2 белых и 4 черных шара. Опыт β состоит в предварительном вытаскивании 2 шаров с последующим вытаскиванием одного α . Найти количество информации об опыте α в опыте β .


Решение:

I(β,α )=Н(α) – Н(α/ β).

Н(α) = 4\6Log6/4 + 2\6Log6/2 = Log3 – 2/3 (бит);


Построим ориентированный граф:

опыт β


2/5

3/4

Log4/3


Н(α)


3/5

1/5

4/5

1/4

2/4

2/4

1/4

3/4

-----

4/4

Log 4

Log4/2

Log4/2

Log4

Log4/3

-------

Log1


Log 3/2

Log 3


4/6

4/6


2/6

2/6

Н(α/β)= 4\15*(3/4Log4/3+ 1\4Log4) + 2\5 (2*1/2Log2) + 4\15*(1/4Log4+ 3\4Log4/3) =

= - 2\5Log3 + 22/15 (бит).

I(α,β) = Log3 – 2/3 + 2\5Log3 - 22/15 = 7/5 Log3 - 32/15 (бит).

Ответ: 7/5 Log3 - 32/15 (бит).

Вывод: сравнивая результаты 2 последних задач, получили подтверждение свойства 3 количества информации.

Домашнее задание:

№ 1. найдите количество информации при вынимании козырной карты из колоды в 52 карты, содержащейся в предварительно извлеченной одной карте.

№ 2. предлагается угадать карту, наудачу вынутую из колоды в 36 карт. Какое количество информации получит угадывающий, если дополнительно сообщить:

а) масть вынутой карты;

б) что вынутая карта оказалась тузом.

Занятие № 5. Решение логических задач на взвешивание через энтропию и количество информации

Цель занятия: разобрать оптимальный способ решения логических задач на взвешивание через формулы энтропии и количества информации.

Задачи занятия:

• Ввести типологию задач на взвешивание, решаемых методом энтропии и количества информации;
  
• Осуществить переход от решения задач через графы к решению через формулы энтропии и количества информации;
  
• Отработать общий алгоритм решения задач на взвешивание в зависимости от исходных условий.
  

Ход занятия:

1. Предложенные для занятия задачи, классифицировать по какому–либо признаку. Свое решение обосновать.
   
2. Разобрать решение задачи на угадывание одной фальшивой монеты из 9, если известно, легче она или тяжелее; если неизвестно легче она или тяжелее;
   
3. Провести решение оставшихся задач через понятие энтропии и количества информации;
   
4. Домашнее задание: составить кодовые деревья для каждой решенной задачи.
   

Занятие № 6. Решение логических задач о лжецах через энтропию и количество информации

Цель занятия: разобрать оптимальный способ решения логических задач о лжецах через формулы энтропии и количества информации.

Задачи занятия:

• Ввести типологию логических задач о лжецах, решаемых методом энтропии и количества информации;
  
• Осуществить переход от решения задач через графы к решению через формулы энтропии и количества информации;
  
• Отработать общий алгоритм решения логических задач о лжецах в зависимости от исходных условий.
  

Ход занятия:

1. Предложенные для занятия задачи, классифицировать по какому–либо признаку. Свое решение обосновать.
   
2. Найти отличительные черты для выделения задач о лжецах из многообразия других задач;
   
3. Разобрать решение задач с использованием энтропии и двоичной системы счисления;
   
4. Провести решение оставшихся задач через понятие энтропии и количества информации;
   
5. Провести иллюстрацию решения логических задач о лжецах на кодовом дереве;
   
6. Домашнее задание: составить кодовые деревья для каждой решенной задачи.
   

Задачи для решения берутся из Главы II § 8.

Занятие № 7. Защита творческих проектов

Цель: обобщение изученного материала, формирование творческой математической индивидуальности учащихся.

Идея: На первом занятии учащимся предлагаются формы творческих заданий по изучаемой теме:

• Реферат
  
• Web – сайт
  
• Компьютерная презентация
  
• Составление опорной таблицы и опорных конспектов модуля
  
• Решебник домашних задач с приведением дополнительных;
  

На данном занятии происходит творческая защита – представление выбранной формы с конкретным содержанием по теме изучаемого модуля.

В течение работы над освоением данного модуля, учащиеся изучают дополнительную литературу, консультируются с учителем, и выполняют свое задание. Реферат, решебник и составление опорных конспектов предполагают индивидуальную работу, составление сайта и презентации предполагает коллективную работу и требует специальных навыков в данной технологии.