Школе необходима соответствующая специальная подготовка педагогов, способных овладеть предметом, имеющим математическую природу и широчайшее прикладное значение

Вид материала

Содержание

Занятие № 2. Энтропия по Шеннону. Свойства энтропии
Задачи занятия
Общая мера неопределенности опыта есть сумма мер неопределенностей отдельных исходов: -p(А
Задача №1/2.
Домашнее задание

Подобный материал:

1 2 3 4 5

Занятие № 2. Энтропия по Шеннону. Свойства энтропии

Цели занятия:

Продолжить усвоение понятия энтропия и ее свойств через введение формулы Клода Шенона

Задачи занятия:

Создать проблемную ситуацию невозможности решить задачу с помощью формулы Хартли;
Ввести формулу Клода Шеннона;
Рассмотреть анализ условий задач табличным и графическим методами;
Ввести алгоритм решения задач на сравнение неопределенностей событий;
Свойства энтропии;
Провести тренинг сравнения степеней неопределенности событий.

Методика проведения занятия: Лекция с элементами диалога;

План занятия:

Переход от формулы опытов с равновероятными исходами к опытам с неравновероятными исходами;
Понятие энтропии в общем случае;
Решение задач 1 / 2 - 4 / 2
Домашнее задание

Ход занятия: Итак, пусть опыт имеет k равновероятных исходов, тогда общая неопределенность опыта равна logk. Каждый отдельный исход, имеющий вероятность 1\k, вносит неопределенность, равную 1\k logk, а учитывая рассмотренные ранее формулы, имеем 1\ k logk = -1\ k log1\k. Так рассуждал Джон Хартли, который не учел возможность неравновероятных исходов. Ошибочность точки зрения Хартли была показана Клодом Шенноном, американским математиком и инженером, который предложил принять в качестве меры неопределенности опыта α с возможными исходами А_1,А_2,… А_kвеличину

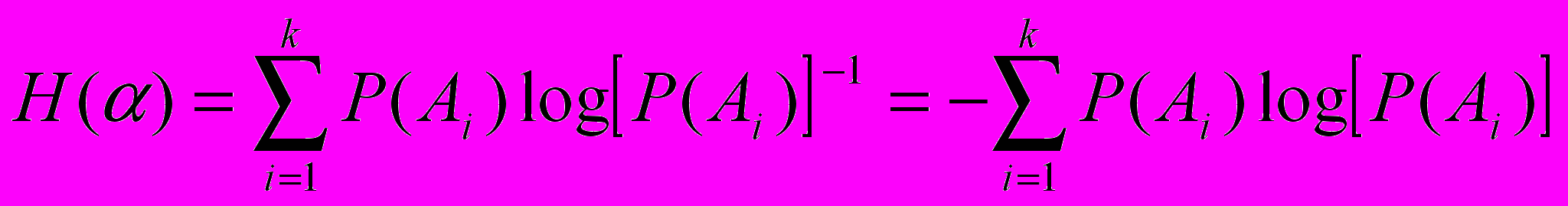
Исходы опыта	А₁	А₂	А₃	А_k
Вероятности	p(А₁)	p(А₂)	p(А₃)	p(А_k)
Мера неопр.	-p(А₁) log p(А₁)	-p(А₂) log p(А₂)	-p(А₃) log p(А₃)	-p(А_k) log p(А_k)

Общая мера неопределенности опыта есть сумма мер неопределенностей отдельных исходов: -p(А₁) log p(А₁) - p(А₂) log p(А₂) - p(А₃) log p(А₃) … -p(А_k) log p(А_k) = Н (α), что называется энтропией опыта α.

Рассмотрим все сказанное выше на задачах.

Задача №1/2.

Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5 черных и 5 красных; вторая содержит 16 шаров: 4 белых, 4 черных и 8 красных во второй. Из каждой урны вытаскивают по одному шару. Исход какого из этих двух опытов следует считать более неопределенным?

Решение:

Первый опыт связан с первой корзиной:

Цвет вынутого шара	белый	черный	красный
Вероятность	1\2	1\4	1\4
Энтропия (неопределенность)	-1\2 log 1\2	-1\4 log 1\4	-1\4 log 1\4

Неопределенность данного опыта, или энтропия равна:

Н (α)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита

Второй опыт связан со второй корзиной:

Цвет вынутого шара	белый	черный	красный
Вероятность	1\4	1\4	1\2
Энтропия (неопределенность)	-1\4 log 1\4	-1\4 log 1\4	-1\2 log 1\2

Неопределенность данного опыта, или энтропия равна:

Н (β)= -1\2 log 1\2 - 1\4 log 1\4 - 1\4 log 1\4 = 1\2 +1\2 +1\2 = 3\2 бита

Ответ: опыты одинаково неопределенны.

Изобразить решение задачи графически, вписать в пунктирные рамки соответствующие значения

.

белый

черный

α

красный

вероятность=1 неопределенность=3\2

белый

черный

β

красный

вероятность=1 неопределенность=3\2

Задача №2/2.

Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из урны, в которой находятся 2 белых и 3 черных шара?

Решение: построим графическую модель опыта

Р=2\4
Р=2\5 Р=3\5

Р=1\4

Р=3\4

Р=2\4

Р=3\10

Р=3\10

Р=3\10

Р=2\5 * 1\4 =1\10

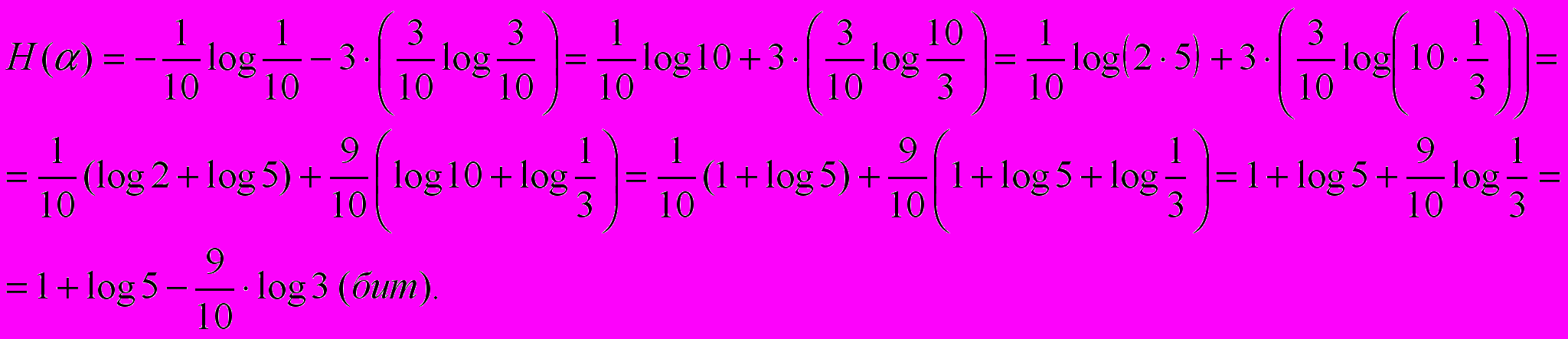
Ответ:

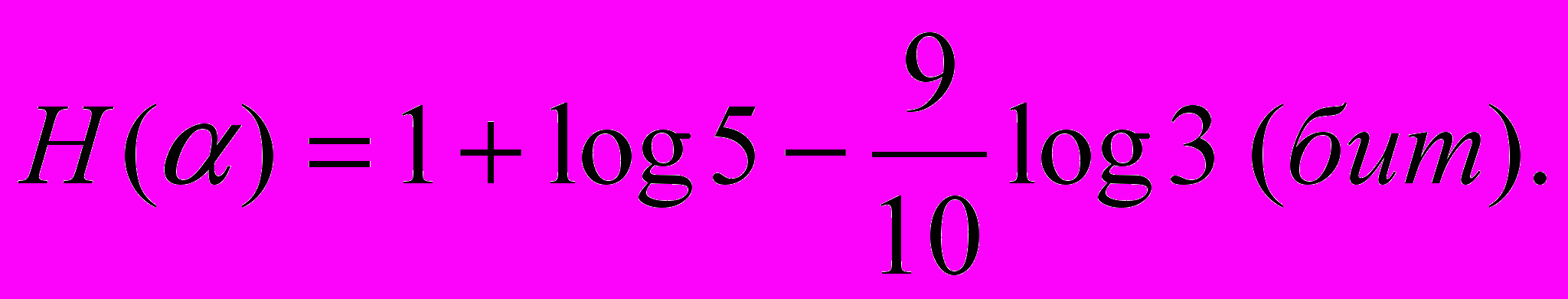
Задача №3/2.

Из многолетних наблюдений за погодой на определенной территории известно, что 15 июня вероятность осадков равна 0,4; а 15 ноября вероятность осадков равна 0,8. Какой из прогнозов является более неопределенным?

Решение:

15 июня

Погода	Осадки	Отсутствие осадков
Вероятность	0,4	0,6
Неопределенность	-0,4 log0,4	-0,6 log0,6

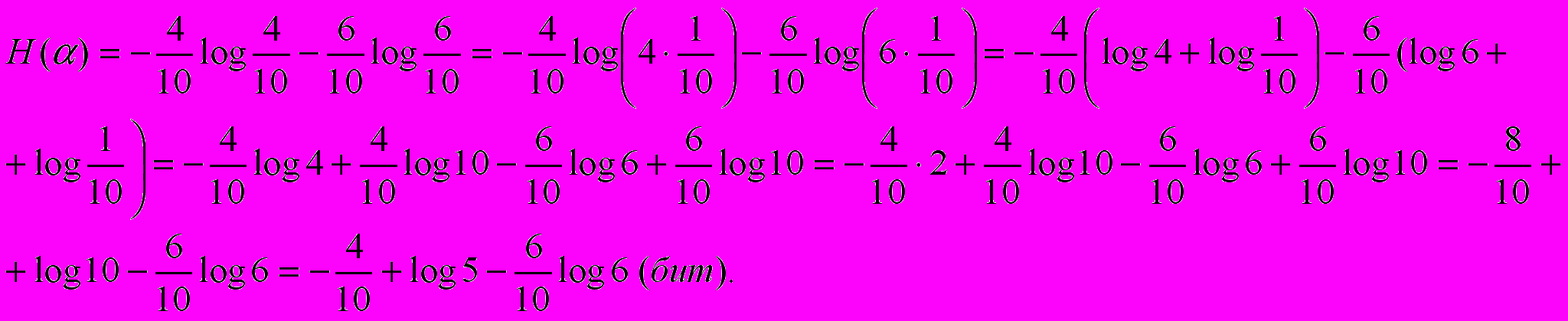
15 ноября

Погода	Осадки	Отсутствие осадков
Вероятность	0,8	0,2
Неопределенность	-0,8 log0,8	-0,2 log0,2

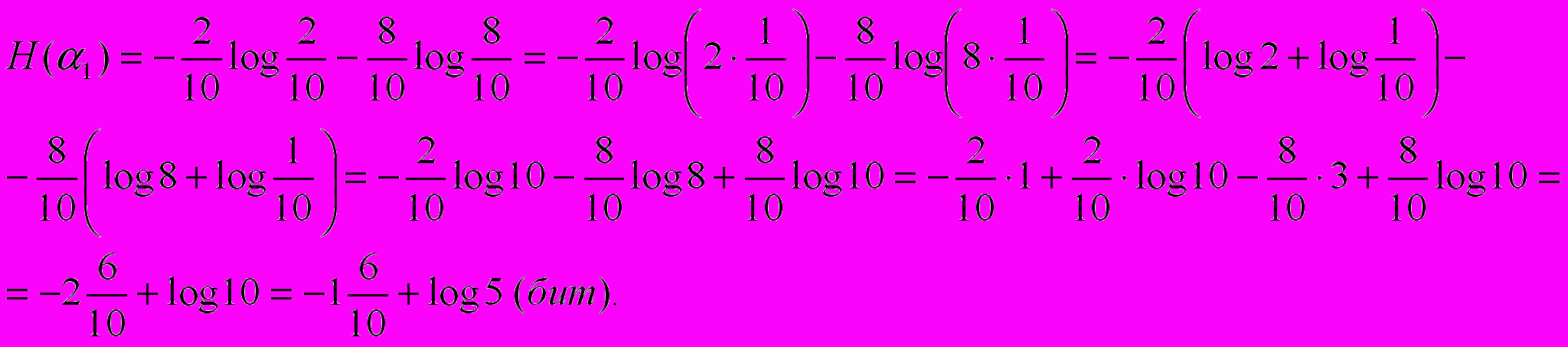
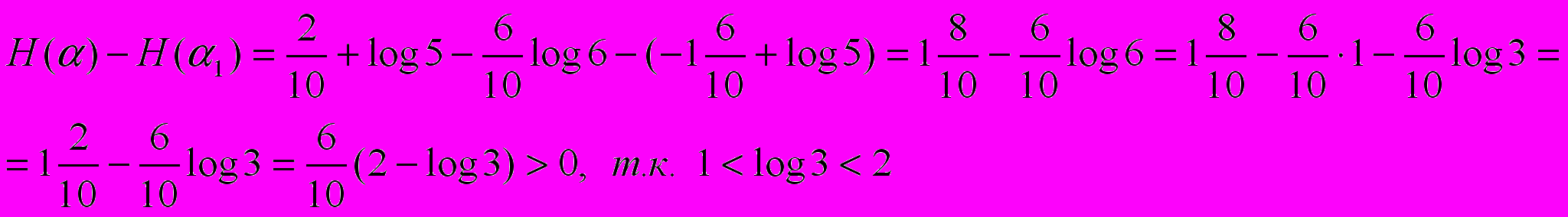
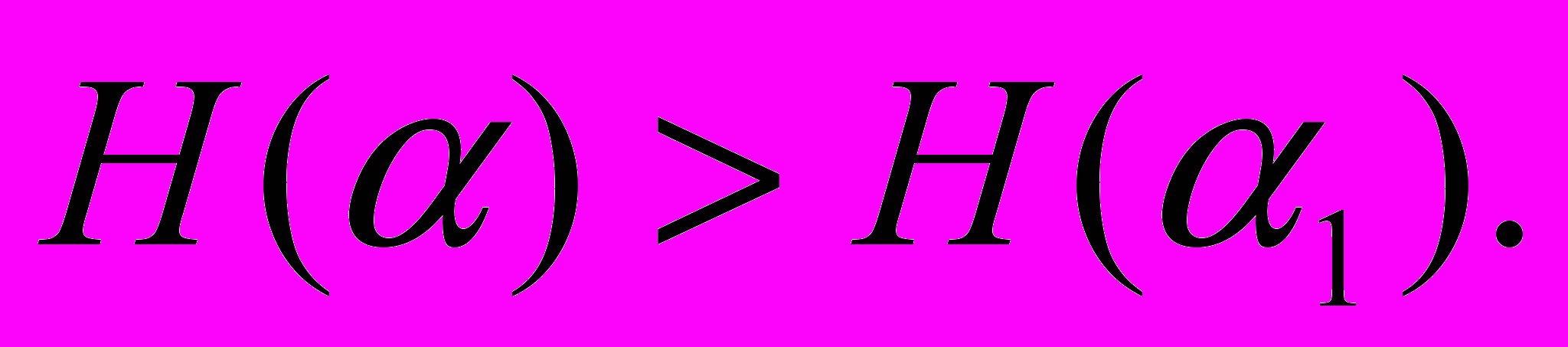
Ответ: Прогноз на15 июня является более неопределенным

Задача №4/2. (Немного изменяем условие задачи №3/2: уточним вероятности возможных осадков. Можно сначала учащихся попросить высказать гипотезы относительно ответа)

Из многолетних наблюдений за погодой на определенной территории известно, что 15 июня вероятность осадков равна 0,4; а 15 ноября вероятность осадков равна 0,8, причем вероятность дождя равна 0,48,а вероятность снега 0,32. На какое число прогноз погоды является более неопределенным?

Решение:

15 июня (без изменений)

Погода	Осадки	Отсутствие осадков
Вероятность	0,4	0,6
Неопределенность	-0,4 log0,4	-0,6 log0,6

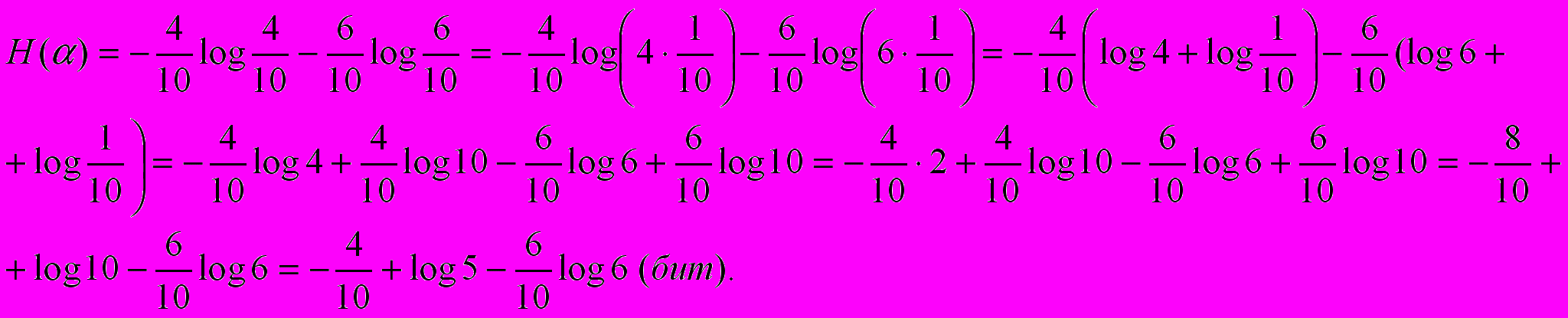
15 ноября (с уточнением вероятностей видов осадков)

Погода	Дождь	Снег	Отсутствие осадков
Вероятность	0,48	0,32	0,2
Неопределенность	-0,48 log0,48	-0,32 log0,32	-0,2 log0,2

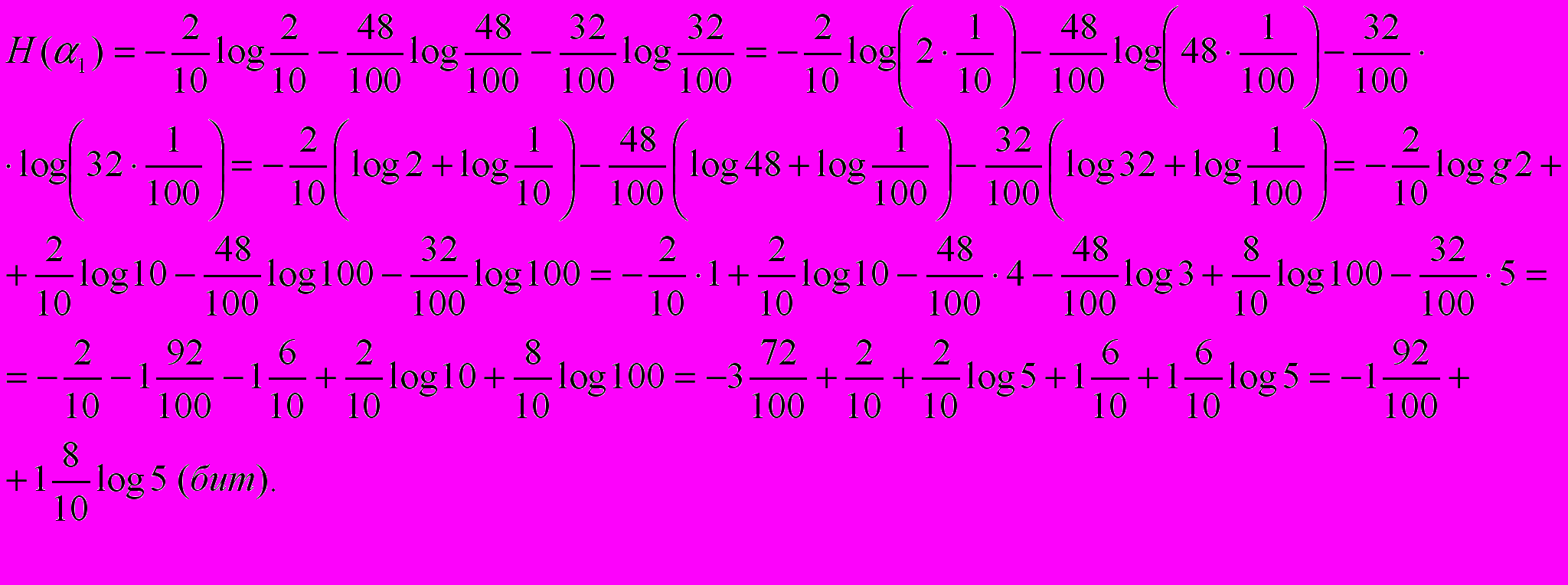
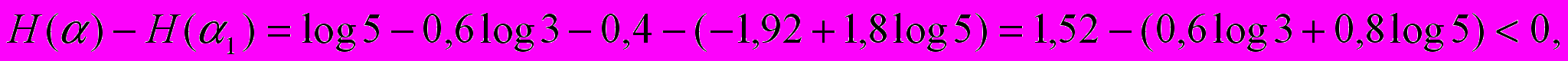
т.к. 1
2
2,2< 0,6 * log3+ 0,8 log5<3,2

Н (α) < Н (α₁).

Ответ: Прогноз на15 ноября с уточнением вероятностей видов осадков является более неопределенным.

Домашнее задание

№1. Найдите степень неопределенности извлечения 2 шаров из урны, содержащей один белый, 2 черных и три красных шара.

№2. Одна урна содержит 1 белый и 2 черных шара, а другая 2 белых и 3 черных. В каком случае угадывание цвета вынутого шара более предсказуемо?

№3. в первой урне 2 белых и 4 черных шара, а во второй – 3 белых и 3 черных. Из каждой урны вынимают по 2 шара. Исход какого из этих 2 опытов менее предсказуем?

Blog

Содержание

Занятие № 2. Энтропия по Шеннону. Свойства энтропии