Geum.ru

Школе необходима соответствующая специальная подготовка педагогов, способных овладеть предметом, имеющим математическую природу и широчайшее прикладное значение

Вид материалаПояснительная записка

Содержание


Занятие № 1. Случайные события. Мера их неопределенности. Формула Хартли
II. Понятие ЭНТРОПИИ
Задача № 1/1.
Задачи на угадывание. Решение с помощью формулы Хартли.
Задача № 2/1.
Ключевой вопрос занятия
Отвечающий дает ответы «да» или «нет»
Отвечающий дает ответы «да» или «нет»
Подобный материал:
1   2   3   4   5

Занятие № 1. Случайные события. Мера их неопределенности. Формула Хартли


Цели занятия:
  • Вспомнить понятие случайных событий;
  • Ввести понятие энтропии, ее свойства;
  • Ввести формулу Хартли, рассмотреть условия применения ее при решении задач на угадывание;

Задачи занятия:
  • Научиться среди предложенных событий выбирать неопределенные;
  • Установить соответствие между вероятностью события и его неопределенностью;
  • Научиться подсчитывать энтропию события по формуле Хартли;
  • Отработать метод половинного деления для решения задач на угадывание;
  • Разобрать алгоритм решения задач на угадывание с применением понятия энтропии

Методика организации занятия:
  • Лекция с элементами диалога;
  • Дискуссия относительно выдвигаемых гипотез;
  • Игровые ситуации по содержанию задач;
  • Работа в микрогруппах, аргументация доказательства конкретной точки зрения.

План занятия:
  1. Лекция – диалог «Вероятность – характеристика случайных событий»
  2. Упражнение № 1. Неопределенные события, их характеристика.
  3. Понятие энтропии по Хартли. Задача 1/1.
  4. Решение задачи 2 \1, Решение задач на угадывание 3/1 – 11/1

Ход занятия: I. В рамках курса «Теория вероятностей и математическая статистика» введен алгоритм определения вероятности того или иного события. Необходимо вспомнить, как называется событие, вероятность наступления которого отлична от 1. (Случайное). Обратить внимание на то, что название отражает характер наступления события (Неизвестно, наступит оно или нет), подобрать слово – синоним к состоянию неизвестности (неопределенность).





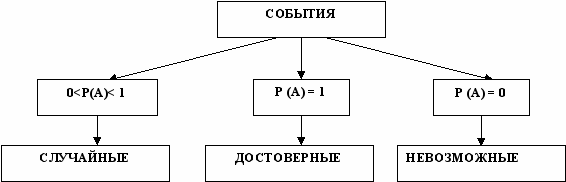
Предметом дальнейшего изучения будут случайные (неопределенные) события.

Упражнение № 1.
  1. Первый встречный человек мужского пола.
  2. За понедельником будет вторник.
  3. За контрольную работу можно получить «отлично».
  4. К телефону из пяти членов семьи подойдет младший сын.
  5. После 31 января наступит 1 февраля.
  6. После лета буде зима.
  7. Каждый из 15 учеников, посещающих данные занятия, поступит на математическую специальность.
  8. В лотерее победит билет с номером 777777.
  9. Подброшенная монетка упадет гербом вверх.
  10. На подброшенном кубике выпадет шесть очков.
  11. Из выбираемых наугад карточек с цифрами выберем карточку с цифрой 5.

Задания: среди 11 событий
  1. Указать достоверные (2,5)
  2. Указать невозможные (6)
  3. Указать неопределенные. (1, 3,4,6,7,8,9,10)
  4. Среди неопределенных указать те, которые имеют 2 равновозможных исхода (1,9)
  5. Неопределенные события расставить в порядке возрастания числа равновероятных исходов (№ 1,9-2; № 3-4; №4-5; № 10-6; № 11-10; № 7-15; № 8-число проданных билетов)
  6. Назвать событие более неопределенное. (№ 8)
  7. Назвать событие менее неопределенное. (№ 1,9)
  8. Учитывая задания № 6 и № 7, установить зависимость степени неопределенности от числа равновероятных исходов. (Чем больше равновероятных исходов, тем больше степень неопределенности)
  9. Сделать тот же вывод, используя понятие вероятности. (Чем меньше вероятность, тем больше степень неопределенности).

Таким образом, степень неопределенности – есть еще одна характеристика случайного события, которую назвали энтропией. (Н(α)). За единицу энтропии принимается неопределенность, содержащаяся в опыте, имеющем два равновероятностных исхода. Единица измерения, учитывая двоичную систему исчисления, - бит.

II. Понятие ЭНТРОПИИ

Пусть опыт α меет k равновозможных исходов. От этого числа зависит и значение вероятности одного из них Р(А)=1/k, и значение энтропии. Но как ее подсчитать, пока неизвестно. Этому и посвящена основная часть занятия.
  • Если k=1, то f(k) = 0 (неопределенности нет)
  • f(k) – возрастающая, т.к. чем больше равновозможных исходов, тем больше степень неопределенности.
  • Рассмотрим сложный опыт αβ, где опыт α имеет k равновозможных исхода, а β – m равновозможных исхода. Очевидно, что неопределенность сложного опыта αβ будет складываться из неопределенностей каждого опыта в отдельности. т.е. f(km) = f (k) + f(m)

Сопоставляя полученную информацию с имеющими знаниями функциональных зависимостей, получаем, что f (k) – есть логарифмическая зависимость: log2k или logk

Заметим, что выбор основания системы логарифмов здесь несуществен, так как в силу известной формулы 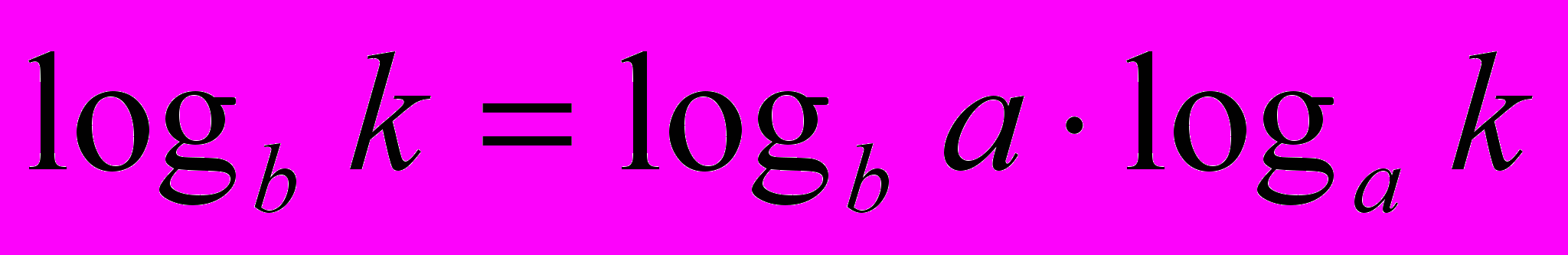переход от одной системы логарифмов к другой сводится лишь к умножению функции 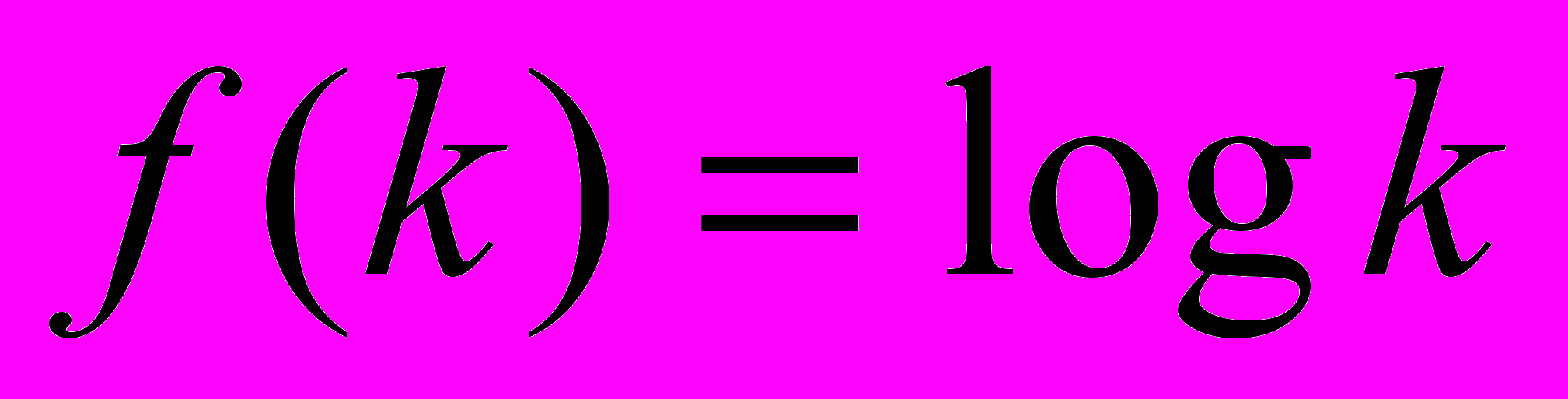на постоянный множитель (модуль перехода 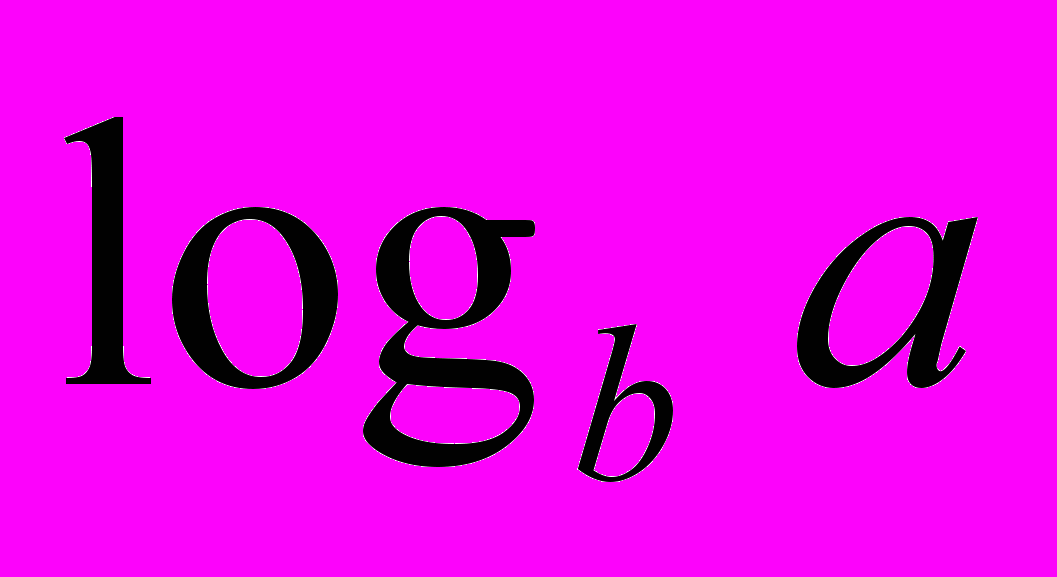), т. е. рав­носилен простому изменению единицы измерения степени неопределенности. В конкретных примерах «меры степени неопределенности» обычно используют логарифмы при основании два. Это означает, что за единицу измерения степени неопределенности здесь принимается неопределен­ность, содержащаяся в опыте, имеющем два равновероят­ных исхода (например, в опыте, состоящем в подбрасывании монеты и выяснении того, какая сторона ее оказалась сверху, или в выяснении ответа «да» или «нет» на вопрос, по поводу которого мы с равными основаниями можем ожидать, что ответ будет утвердительным или отрицатель­ным). Такая единица измерения неопределенности назы­вается двоичной единицей или битом1. В дальнейшем будем все время пользоваться двоичными единицами (битами); таким об­разом, запись log k (где мы, как правило, не будем указы­вать основания системы логарифмов) будет обычно озна­чать log2k. Заметим, что ничего не изменилось бы, если бы мы использовали более привычные десятичные логарифмы; это лишь означало бы, что единицу степени неопределенности опыта, имеющего 10 равновероятных исходов. Таким является, например, опыт, состоящий в извлечении шара из урны с десятью перенумерованными шарами, или опыт по отгадыванию одной цифры, если любая из десяти цифр имеет одинаковую вероятность быть загаданной. Эта последняя единица степени неопределенности (которую называют десятичной единицей или дитом) примерно в 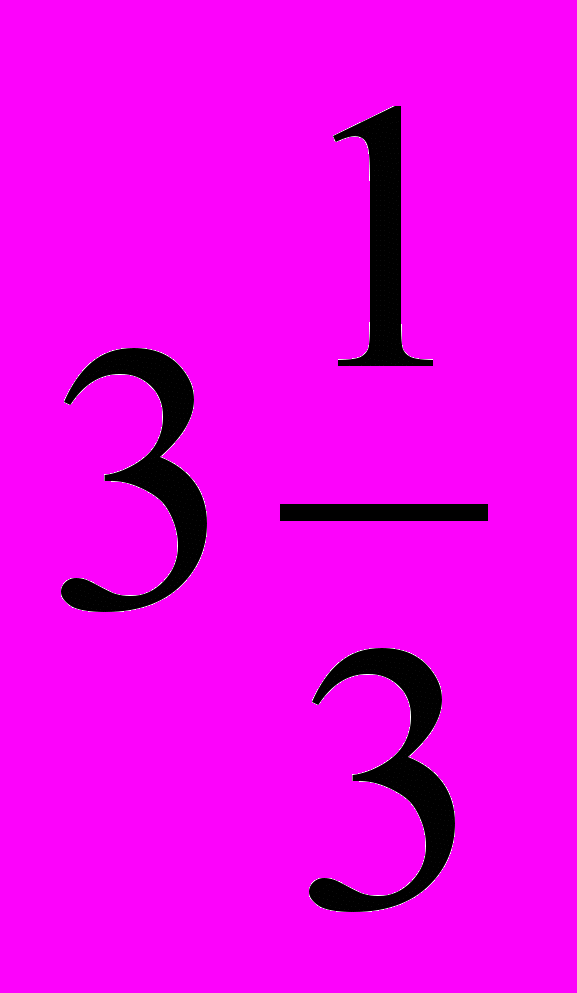раза больше двоичной единицы (так как ).

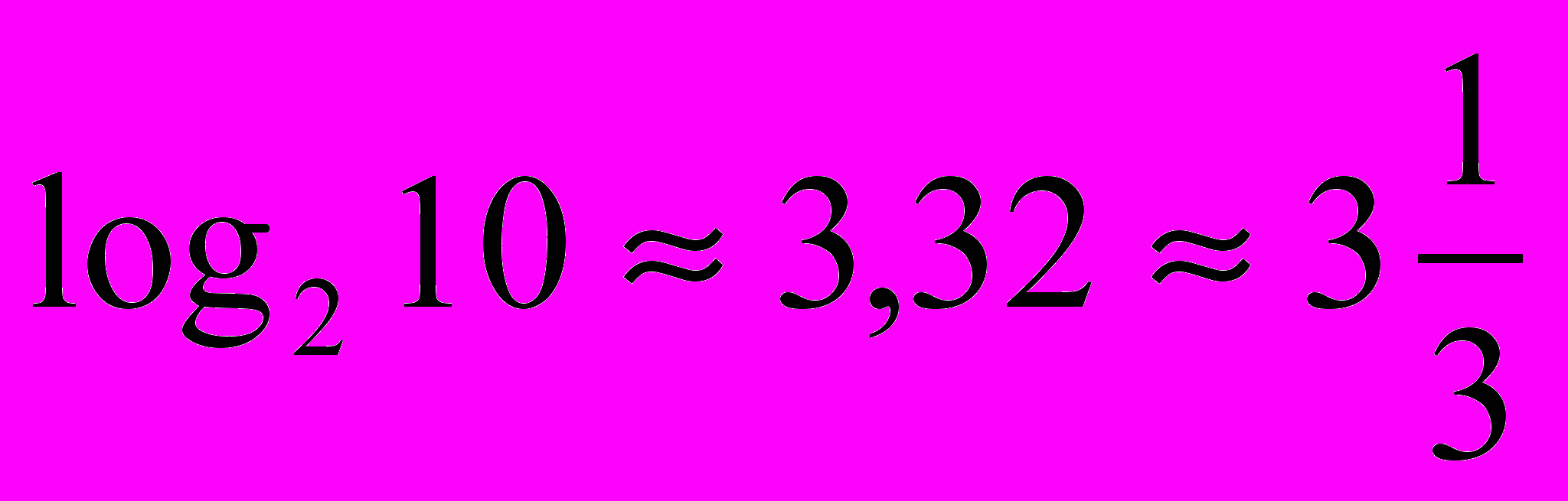Учтем, что logk = -1/k log 1/k

Именно такой подход к определению степени неопределенности опыта лежит в основе идеи американского инженера-связиста Хартли (1928). Пусть опыт α меет k равновозможных исходов. 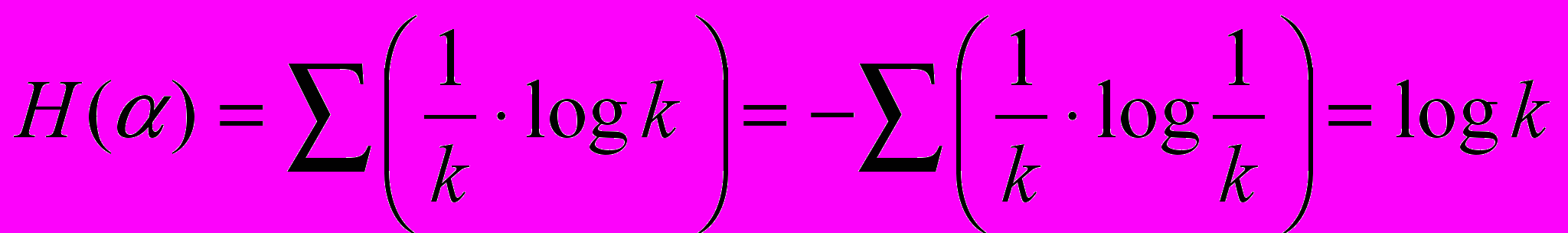. Этой формулой удобно пользоваться, когда исходы равновероятны.

Задача № 1/1. Что имеет большую степень неопределенности угадывание месяца или дня недели рождения случайно встреченного человека.

Решение: Так как месяц рождения имеет 12 равновероятных исходов, а день недели имеет 7 равновероятных исхода, то степень неопределенности угадывания месяца рождения больше, чем угадывание дня недели.

Задачи на угадывание. Решение с помощью формулы Хартли.

Характерной особенностью задач на угадывание, в которых можно применить понятие энтропии, является наличие условия: на вопросы при угадывании отвечающий говорит «да» или «нет». Исходы равновероятны, значит уместно применять формулу Хартли.

Задача № 2/1. Какую степень неопределенности имеет угадывание месяца рождения случайно встреченного человека.

Решение:

Методические рекомендации: Так как месяц рождения имеет 12 равновероятных исходов, то воспользуемся формулой Хартли: Н(α) = log k = log12 = 2 + log 3.

Ответ: 2 + log 3.

Ключевой вопрос занятия: Сколько вопросов следует задать, чтобы быстрее отгадать конкретный месяц? Отвечающий говорит «да» или «нет».

Интересно выслушать предположения относительно ответа на задачу 2/1.

Так как неопределенность данного опыта равна 2 + log 3, а число вопросов – целое, то для полного снятия неопределнности требуется число вопросов – ближайшее целое число, превышающее (или совпадающее, если Н(α) целое) с Н(α), т.е. n ≥ Н(α) = log k.

Решение задачи №2/1:

n ≥ Н(α) = log k

3<2+log3 <4; 2+log 3≈ 3,24, Значит, вопросов должно быть 4.

Ответ: 4.

Предложить вариант системы вопросов. Например,
  1. В первой половине года? (Да)
  2. В первой половине выбранной половины? (Да)
  3. Это средний из трех месяц? (Нет)
  4. Это первый из трех месяц? (Нет) Значит, третий месяц сезона.

Рассмотреть алгоритм рассуждений при формировании группы вопросов. Обратить внимание на то, что сначала делим на две группы, затем еще раз на две, и лишь затем на три, формулируя вопросы для максимального снятия неопределенности.(метод половинного деления)

Далее группа разбивается на 3 микрогруппы, каждая получает свою задачу. В течение 5 минут проводят решение, которое затем предлагается всей группе.


Задача № 3 / 1
Задача № 4 /1
Задача № 5 / 1

Сколько вопросов необхо-димо задать, чтобы отга-дать задуманное собесед-ником целое положитель-ное число, не превыша-ющее 10.

Отвечающий дает ответы «да» или «нет»
Сколько вопросов необхо-димо задать, чтобы отга-дать задуманное собесед-ником целое положитель-ное число, не превыша-ющее 100.

Отвечающий дает ответы «да» или «нет»
Сколько вопросов необхо-димо задать, чтобы отга-дать задуманное собесед-ником целое положитель-ное число, не превыша-ющее 1000.

Отвечающий дает ответы «да» или «нет»

Решение:

n ≥ Н(α) = log k;

log 10 = log 2+ log 5 ≈

1+ 2,32 = 3,32


n=4
n ≥ Н(α) = log k;

log 100= log 4 + 2 log 5 ≈ 2+2*2,32 = 6,64


n=7
n ≥ Н(α) = log k;

log 1000 = log 8 + log 125 = log 8 + 3 log 5 ≈ 3+3*2,32 = 9,96

n=10

Далее можно проиграть задачи в конкретной ситуации, предложив группе загадать число в соответствии с условием задачи, а другой провести систему вопросов. Так по цепочке каждую микрогруппу поставить в разную позицию: спрашивающего и загадывающего. Если группа выходит за пределы контрольного показателя, то подключается другая группа. Вопросы при этом фиксируются. Необходимо обсудить вопрос о том, что количество вопросов может быть и меньше (удачный частный случай), но это нельзя считать общим решением задачи.

Метод, применяемый при составлении системы вопросов, называется методом половинного деления: вопросы ставить так, чтобы число элементов исследуемого множества уменьшалось вдвое или почти вдвое.

Далее группа делится на 5 микрогрупп, каждая получает свою задачу, на предположение ответа, решение и обсуждение (проигрывание системы вопросов) которой отводится 10 минут, после чего проходит защита своего решения. На доске плакат. Сразу после прочтения задачи, группа заполняет столбец гипотезы, затем решает и сверяет свою математическую интуицию. Курсивом указано то, что появляется после работы групп. (таблица)

№
Содержание
Гипотеза

Решение

6/1
Человек живет в пятиэтажном доме с четырьмя подъездами и четырьмя квартирами на каждом этаже. За какое наименьшее число вопросов можно определить точно номер квартиры, если на все вопросы человек будет отвечать «Да» или «Нет»?



Число квартир = 80

n ≥ Н(α) = log k;

log80= log 16 + log5 ≈ 4+2,32 = 6,32

n=7

№
Содержание
Гипотеза

Решение

7/1
За сколько вопросов, на которые отвечают «Да» или «Нет», можно угадать дату рождения конкретного человека?



Дней в году 365

n ≥ Н(α) = log k;

log365 = log73 + log 5 ≈ 6,19+2,32 = 8,51

n=9

8/1
За сколько вопросов, на которые отвечают «Да» или «Нет», можно угадать номер шестизначного телефона?



Учитывая знания по комбинаторике, получаем, что всего шестизначных номеров 9*105

n ≥ Н(α) = log k;

log(9*105)= log9 + 5log10 ≈ 2log3 + 5log2+5 log5= 2*1,24 +5+5*2,32=19,8

n=20

9/1
За сколько вопросов, на которые отвечают «Да» или «Нет», можно отгадать одного из загаданных учащихся группы из 27 человек?



n ≥ Н(α) = log k;

log27= log33 =3 log3 ≈ 3*1,24 =3,72

n=4

10/1
За сколько вопросов, на которые отвечают «Да» или «Нет», можно отгадать одного из загаданных учащихся группы из 32 человек?



n ≥ Н(α) = log k;

log32= log25 =5 log2= 5

n=5

11/1
Одна из составных частей бензинового двигателя имеет форму валика, для измерения толщины которого используется стальная лента с 15 шаблонными отверстиями от 10 мм до 10,56 через каждые 0,04 мм. Калибровка калика заключается во вкладывании валика в отверстия контрольного стенда. За какое наименьшее число испытаний обязательно удастся найти диаметр валика? (знание данного метода позволит автослесарю работать эффективнее)



n ≥ Н(α) = log k;

log15= log3+ log5≈

1,24 + 2,32=3,56

n=4


Итог решения задач на угадывание:
  • Если исходы каждого отдельного испытания равновероятны, то для решения задачи оптимально применить формулу Хартли;
  • Задачи на угадывание при ответах «Да», «Нет» решаются методом половинного деления, что позволяет определить оптимальную систему вопросов;
  • Наименьшее число вопросов – ближайшее натуральное число, при округлении дробного значения - с избытком, т.е. n ≥ Н(α) = log k;

Домашнее задание: придумать 2-3 задачи на данный метод, оформить для банка упражнений.