Тема Принципы и методы прогнозирования
| Вид материала | Документы |
СодержаниеТема 8. Прогнозирование на основе экспертных оценок |
- 2 Альтернативы прогнозированию, 641.92kb.
- Рабочая программа дисциплины «Методы социально-экономического прогнозирования» Рекомендуется, 142.86kb.
- Курс «Методы прогнозирования и оценки мпи» (для гин) Лекция, 100.16kb.
- 3 глава теоретические основы макроэкономического планирования и прогнозирования, 1661.1kb.
- Федеральное агентство по образованию, 55.51kb.
- Тема 2: Методология прогнозирования и макроэкономического планирования, 109.99kb.
- Программа учебной дисциплины «экономическое прогнозирование» для аспирантов, обучающихся, 180.42kb.
- Методические указания для студентов по дисциплине патофизиология, 1054.3kb.
- Темы рефератов (контрольная работа) Статистический анализ факторов роста валового внутреннего, 33.94kb.
- С целью изучения, формулирования выводов, принятия решений и прогнозирования, 231.79kb.
Тема 8. Прогнозирование на основе экспертных оценок
Экспертные оценки используются в случае отсутствия информации об исследуемом явлении или ее недостаточной достоверности. Индивидуальная оценка эксперта выражает его стремление выразить какое-либо свойство или признак в виде числа. Предполагается, что правильно обработанное коллективное мнение экспертов более достоверно и надежно, чем индивидуальные мнения экспертов, и что истинная величина изучаемого явления находится внутри диапазона оценок групп экспертов.
Надежность экспертных оценок определяется в первую очередь подбором специалистов-экспертов, их информированностью в изучаемых проблемах, а также возможностью математической и статистической обработки полученной информации.
Статистический подход к подбору экспертов состоит в проверке эрудиции и аналитических способностей экспертов путем заполнения специальных анкет, а также проверки точности их прошлых оценок.
Проведение экспертного анализа основывается на ранговых экспертных оценках, которыми называют оценки признаков объектов, получаемые на основе устанавливаемого экспертом предпочтения одного объекта над другим с точки зрения изучаемого качества и выражающиеся в виде чисел натурального ряда (рангов), присвоенных отдельным объектам. Они есть лишь символы, указывающие положение каждого объекта в построенном ряду предпочтения по отношению к другим объектам. Поэтому расчетные операции, выполняемые с ранговыми оценками, отличатся от операций, которые выполняются над натуральными числами.
Основными задачами статистической обработки ранговых оценок являются:
- определение характеристик положения исследуемого объекта в общем ряду ранжировок;
- характеристика взаимосвязи (близости) двух ранжировок, построенных различными экспертами;
- согласованность групп ранжировок: выделение еретиков - несостоятельных экспертов и школ - подгрупп экспертов с единым мнением о проблеме;
- определение показателей обобщенного мнения
- ранжировки наилучшим образом согласованной с полученными индивидуальными экспертными ранжировками (агрегирование объектов);
- выделение лидера.
Исходная информация для процедуры обработки экспертных оценок, как правило, представляется в виде матрицы:
r

 11 r12 ... r1n
11 r12 ... r1nr21 r22 ... r2n
... ... ... ...
rm1 rm2 ... rmn|
где m - количество исследуемых объектов;
n - количество экспертов;
r - ранг присвоенный i-ому объекту j-ым экспертом. Ограничение - обязательное отсутствие связных рангов - недопускаются одинаковые ранги поставленные одним экспертом разным объектам.
Статистическая обработка ранговых экспертных оценок осуществляется в виде следующей последовательности этапов:
1. Характеристики положения объекта.
1.1. Частота присвоения объекту А ранга 1:
Число экспертов, присвоивших объекту А ранг 1
P= --------------------------------------------------------------
Общее число экспертов
1.2. Частота присвоения объекту А ранга не более r:
Число экспертов, присвоивших объекту А ранг от 1 до r
P= -----------------------------------------------------------------------
Общее число экспертов
1.3. Модальный ранг - ранг, присвоенный объекту наибольшим числом экспертов.
2. Характеристика взаимосвязи - коэффициент ранговой корреляции Спирмена:
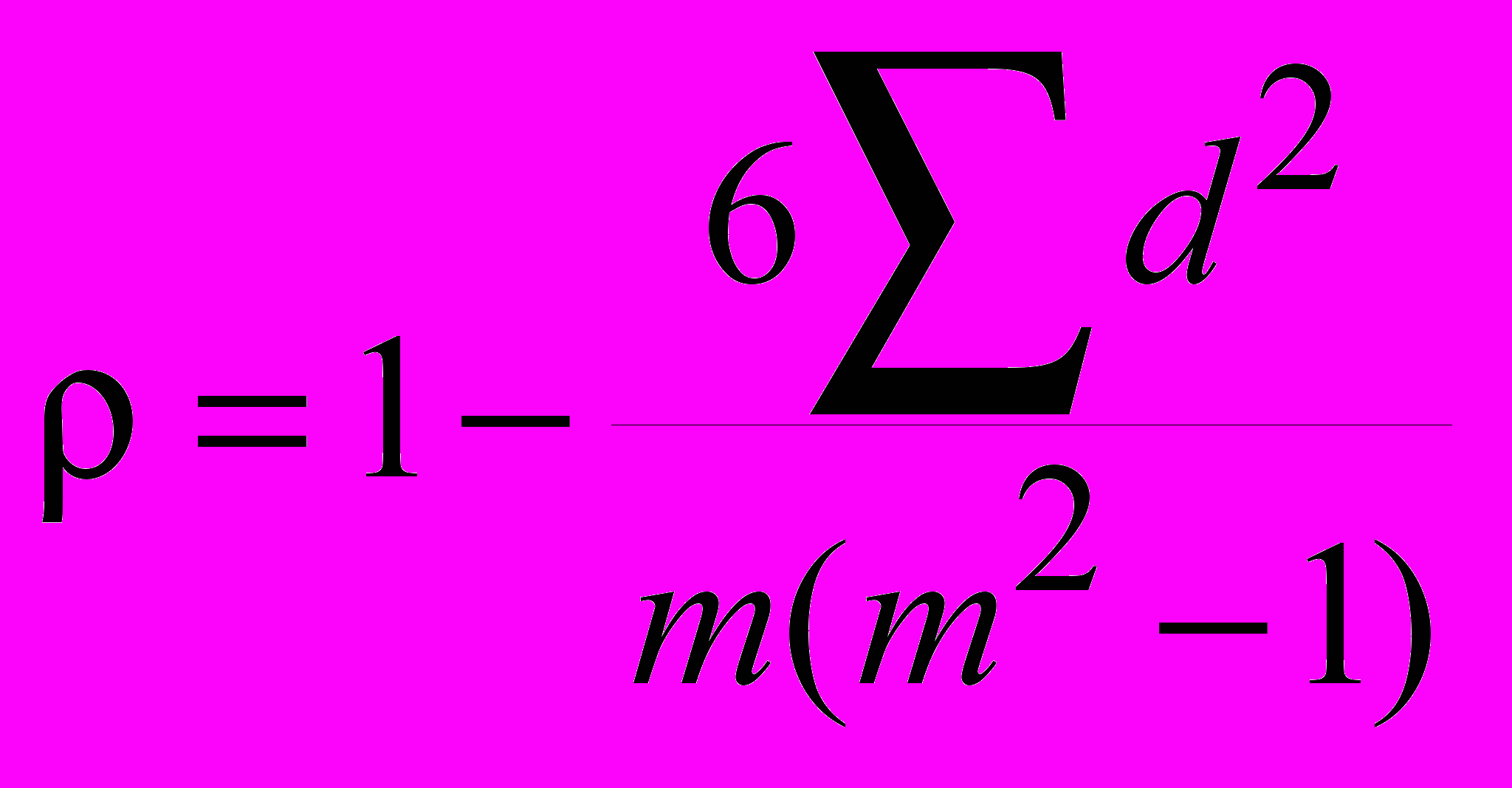
где d - разница рангов, присвоенных каждому отдельному объекту в двух ранжировках.
Значение коэффициента ранговой корреляции меняется в диапазоне [-1;+1]. Значения близкие к +1 говорят о значительной близости мнений экспертов; близкие к 0 - отсутствие связи; близкие к -1 - щ наличии обратной связи.
3. Согласованность индивидуальных ранжировок - коэффициент конкордации:
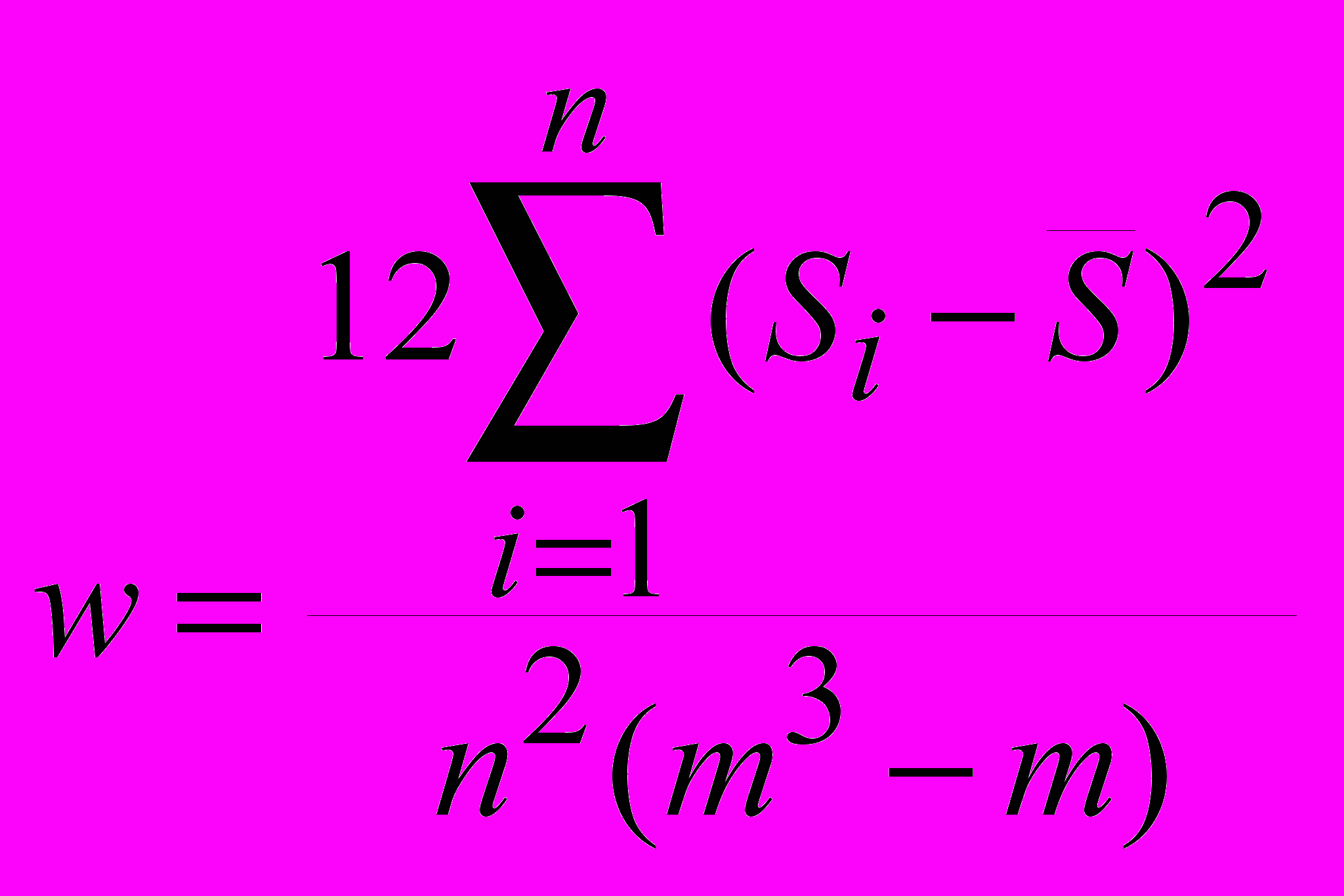
где Si - сумма рангов, полученных данным объектом во всех ранжировках;
S - средняя сумма рангов, полученных одним объектом.
Коэффициент конкордации меняется в пределах от 0 - полная несогласованность, до 1 - полная согласованность. Он применяется для сравнения согласованности экспертных ранжировок. При этом согласованность в группе экспертов считается высокой, если w>= 0.75.
В случае, если w<0.75, для повышения достоверности результатов прогноза, полученного по методу экспертных оценок, необходимо или расширение группы экспертов, или включение в нее более квалифицированных специалистов вместо менее квалифицированных.
4. Агрегация объектов. На основании матрицы модальных рангов (п.1.3.) может быть получена обобщенная ранжировка - ранжировка признаков, наиболее соответствующая полученным экспертным оценкам. По каждой строке матрица модальных рангов выбирается номер элемента с наибольшим значением. Этот номер является наиболее предпочтительным рангом для данного объекта (строки).
5. Выделение лидера. Эксперт j является лидером группы экспертов, если количество совпадений рангов, выставленных им по результатам проведенной экспертизы, и обобщенных рангов, полученных в п. 4. максимально. Эксперты имеющие наименьшее число совпадений, признаются неквалифицированными.
Применение метода ранговых экспертных оценок проиллюстрируем на примере. Пусть имеются сведения пяти экспертов о семи изучаемых объектах.
1 2 2 2 2
6 6 6 6 6
3 3 7 7 7
5 5 5 5 3
2 1 1 1 1
7 7 3 3 5
4 4 4 4 4
Решение
1.1. Частота присвоения объекту А ранга 1:
Частота присвоения объекту 1 ранга 1 0.200
Частота присвоения объекту 2 ранга 1 0.000
Частота присвоения объекту 3 ранга 1 0.000
Частота присвоения объекту 4 ранга 1 0.000
Частота присвоения объекту 5 ранга 1 0.800
Частота присвоения объекту 6 ранга 1 0.000
Частота присвоения объекту 7 ранга 1 0.000
1.2. Частота присвоения объекту А ранга не более r=3:
Частота присвоения объекту 1 ранга не более 3 1.000
Частота присвоения объекту 2 ранга не более 3 0.000
Частота присвоения объекту 3 ранга не более 3 0.400
Частота присвоения объекту 4 ранга не более 3 0.200
Частота присвоения объекту 5 ранга не более 3 1.000
Частота присвоения объекту 6 ранга не более 3 0.400
Частота присвоения объекту 7 ранга не более 3 0.000
1.3. Модальные ранги
1 4 0 0 0 0 0
0 0 0 0 0 5 0
0 0 2 0 0 0 3
0 0 1 0 4 0 0
4 1 0 0 0 0 0
0 0 2 0 1 0 2
0 0 0 5 0 0 0
2. Коэффициенты ранговой корреляции Спирмэна
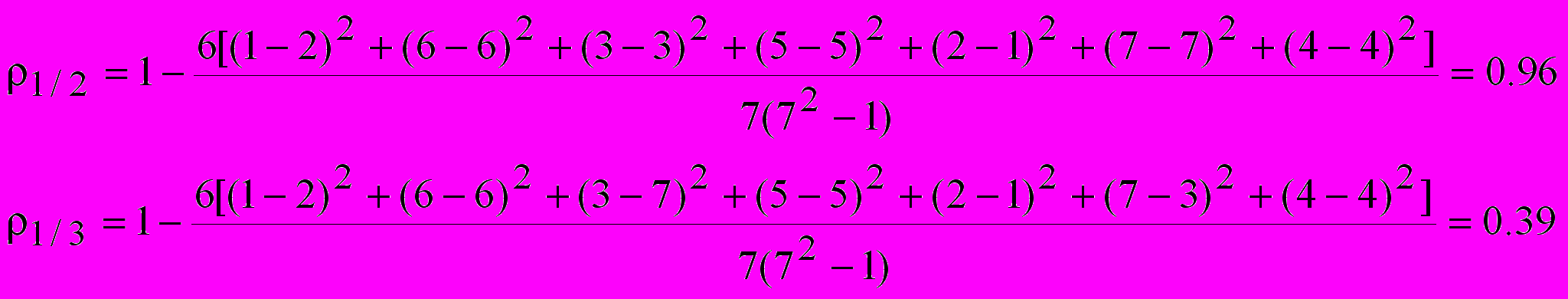
. . .
1.00 0.96 0.39 0.39 0.54
0.96 1.00 0.43 0.43 0.57
0.39 0.43 1.00 1.00 0.86
0.39 0.43 1.00 1.00 0.86
0.54 0.57 0.86 0.86 1.00
3. Согласованность мнений экспертов Расчет коэффициента конкордации
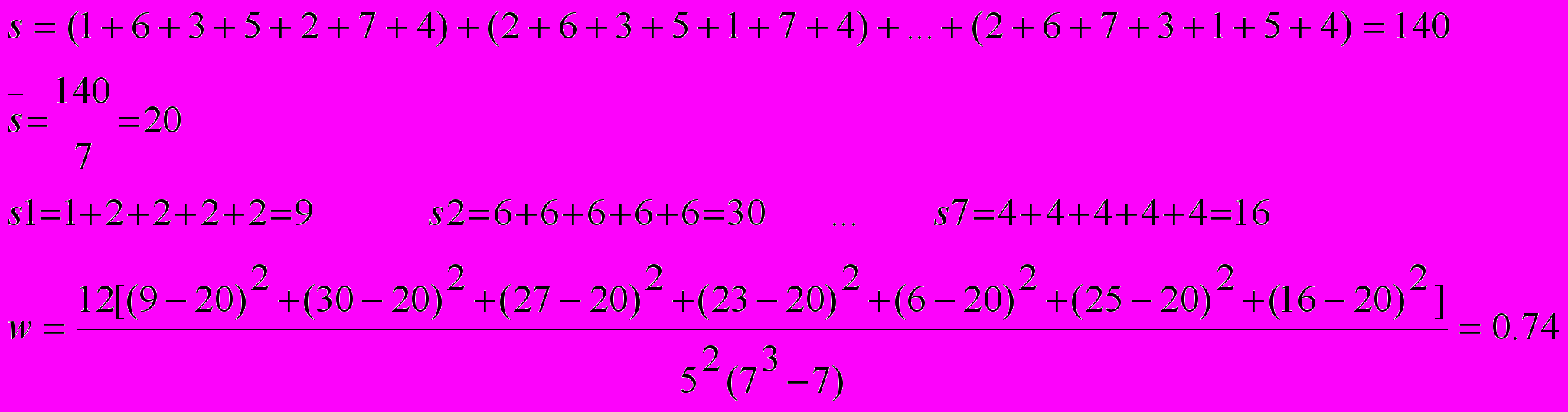
4. Агрегация объектов - определение наиболее представительной ранжировки
1 4 0 0 0 0 0 2
0 0 0 0 0 5 0 6
0 0 2 0 0 0 3 7
0 0 1 0 4 0 0 5
4 1 0 0 0 0 0 1
0 0 2 0 1 0 2 3
0 0 0 5 0 0 0 4
5. Выделение лидера
Эксперт 1 совпадения 4
Эксперт 2 совпадения 6
Эксперт 3 совпадения 6
Эксперт 4 совпадения 6
Эксперт 5 совпадения 5
Наиболее квалифицированы эксперты 2,3,4, неквалифицирован эксперт 1.
