Тема Принципы и методы прогнозирования
| Вид материала | Документы |
- 2 Альтернативы прогнозированию, 641.92kb.
- Рабочая программа дисциплины «Методы социально-экономического прогнозирования» Рекомендуется, 142.86kb.
- Курс «Методы прогнозирования и оценки мпи» (для гин) Лекция, 100.16kb.
- 3 глава теоретические основы макроэкономического планирования и прогнозирования, 1661.1kb.
- Федеральное агентство по образованию, 55.51kb.
- Тема 2: Методология прогнозирования и макроэкономического планирования, 109.99kb.
- Программа учебной дисциплины «экономическое прогнозирование» для аспирантов, обучающихся, 180.42kb.
- Методические указания для студентов по дисциплине патофизиология, 1054.3kb.
- Темы рефератов (контрольная работа) Статистический анализ факторов роста валового внутреннего, 33.94kb.
- С целью изучения, формулирования выводов, принятия решений и прогнозирования, 231.79kb.
Тема 4. Метод экспоненциального сглаживания
Сущность метода экспоненциального сглаживания заключается в том, что временной ряд сглаживается с помощью взвешенной скользящей средней, в которой веса подчиняются экспоненциальному закону распределения, в отличии от скользящей средней, использующей одинаковые веса для всех наблюдаемых значений. Взвешенная скользящая средняя с экспоненциально распределенными весами характеризует значение процесса на конце интервала сглаживания, т.е. является средней характеристикой последних уровней ряда. Именно это свойство используется для прогнозирования.
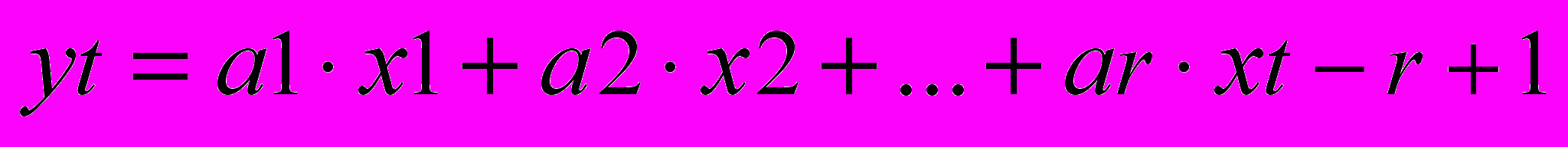 (7)
(7)при a1>a2>…>ar a1+a2+…+ar=1. В частности выбираются такие коэффициенты
a2=(1-)a1, a3=(1-)a2, a4=(1-)a3, где =const.
На основании этого имеем следующую рекурентную формулу для определения экспоненциальной средней:
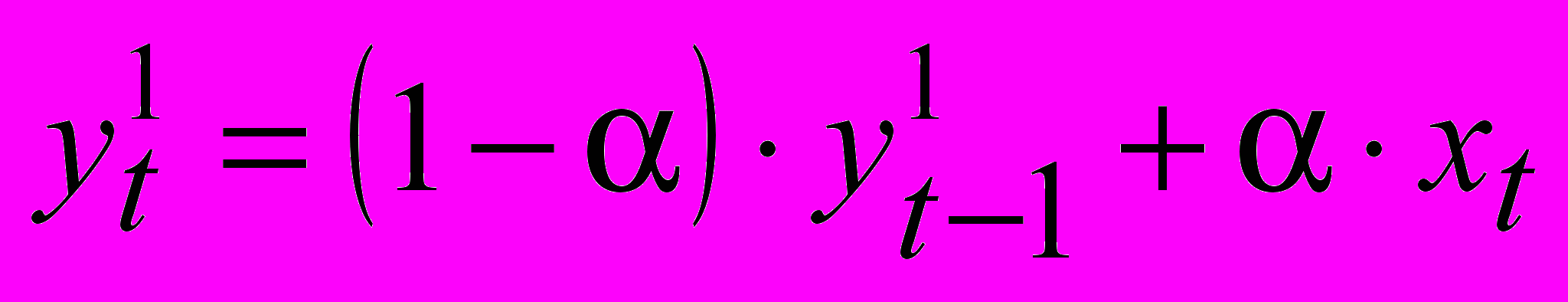 (8)
(8)В случае повторного применения формулы:
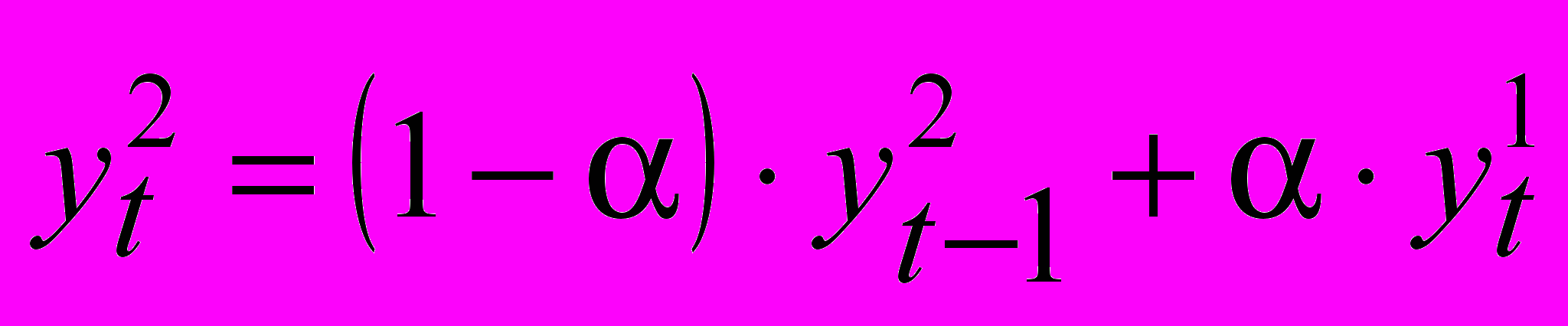 (9)
(9)В общем случае имеем
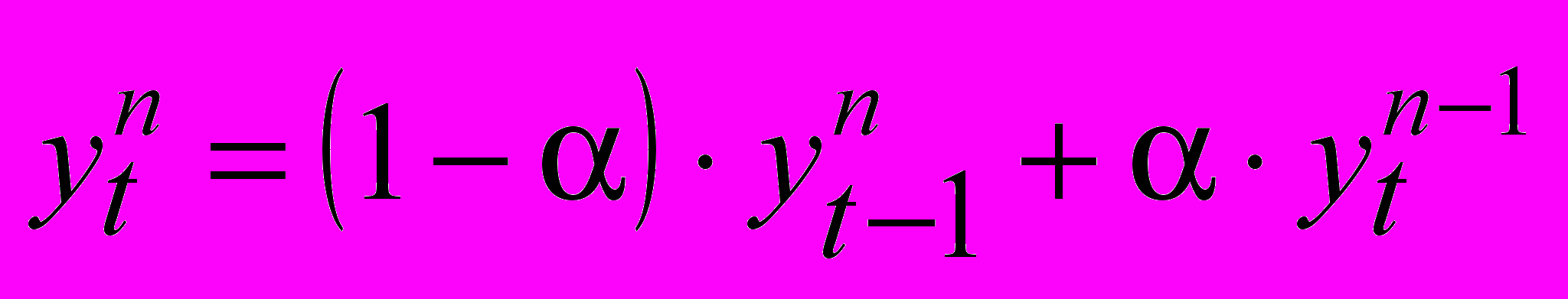 (10)
(10)Предположим, что исходный ряд описывается полиномом
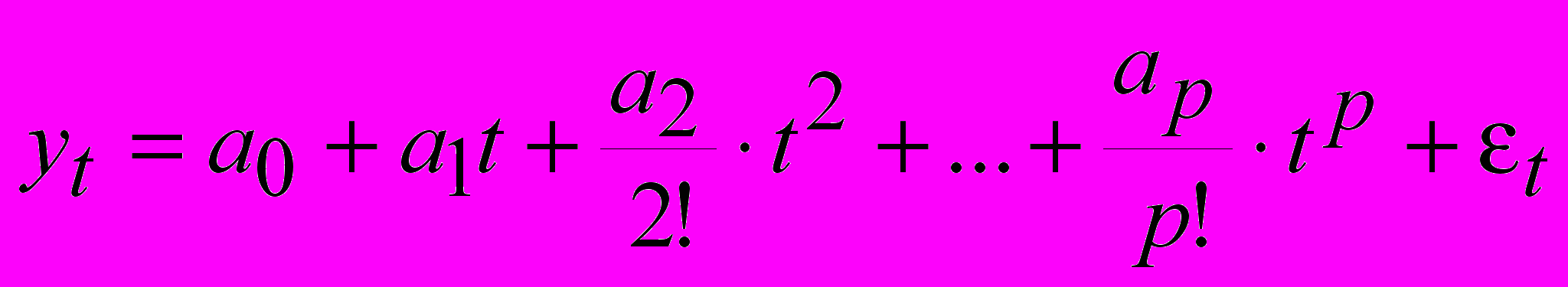 (11)
(11)который в последствии можно использовать для расчета прогноза.
Пусть ряд описывается полиномом второго порядка
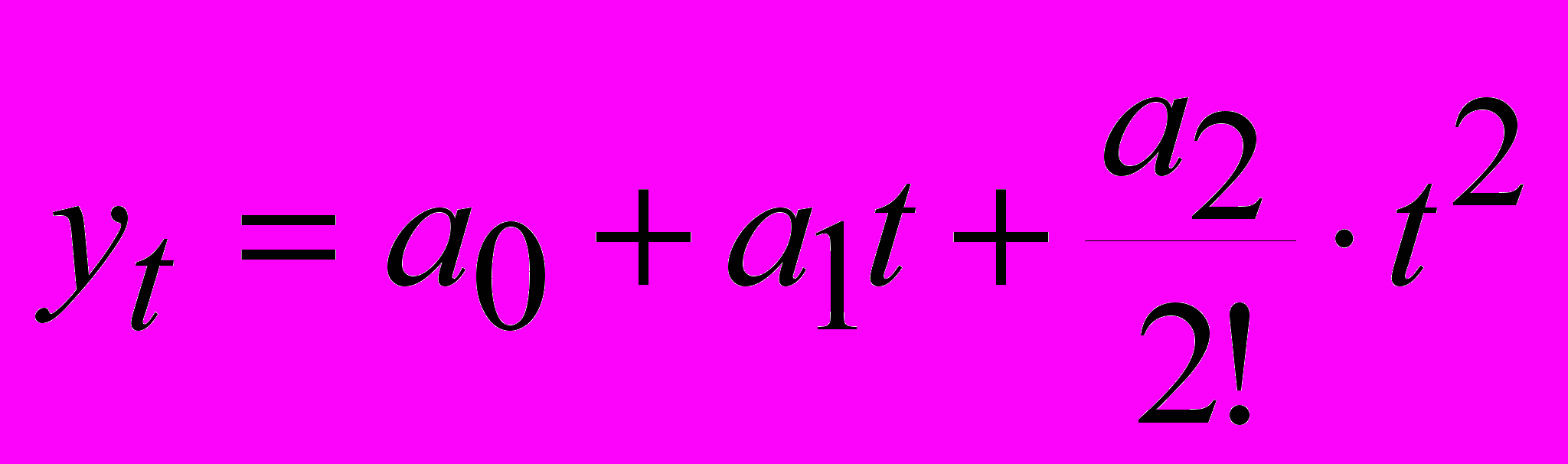 (12)
(12)Для того, чтобы выразить коэффициенты полинома a0, a1, a2 через экспоненциальные средние на основании теоремы Брауна-Майера получаем систему уравнений:
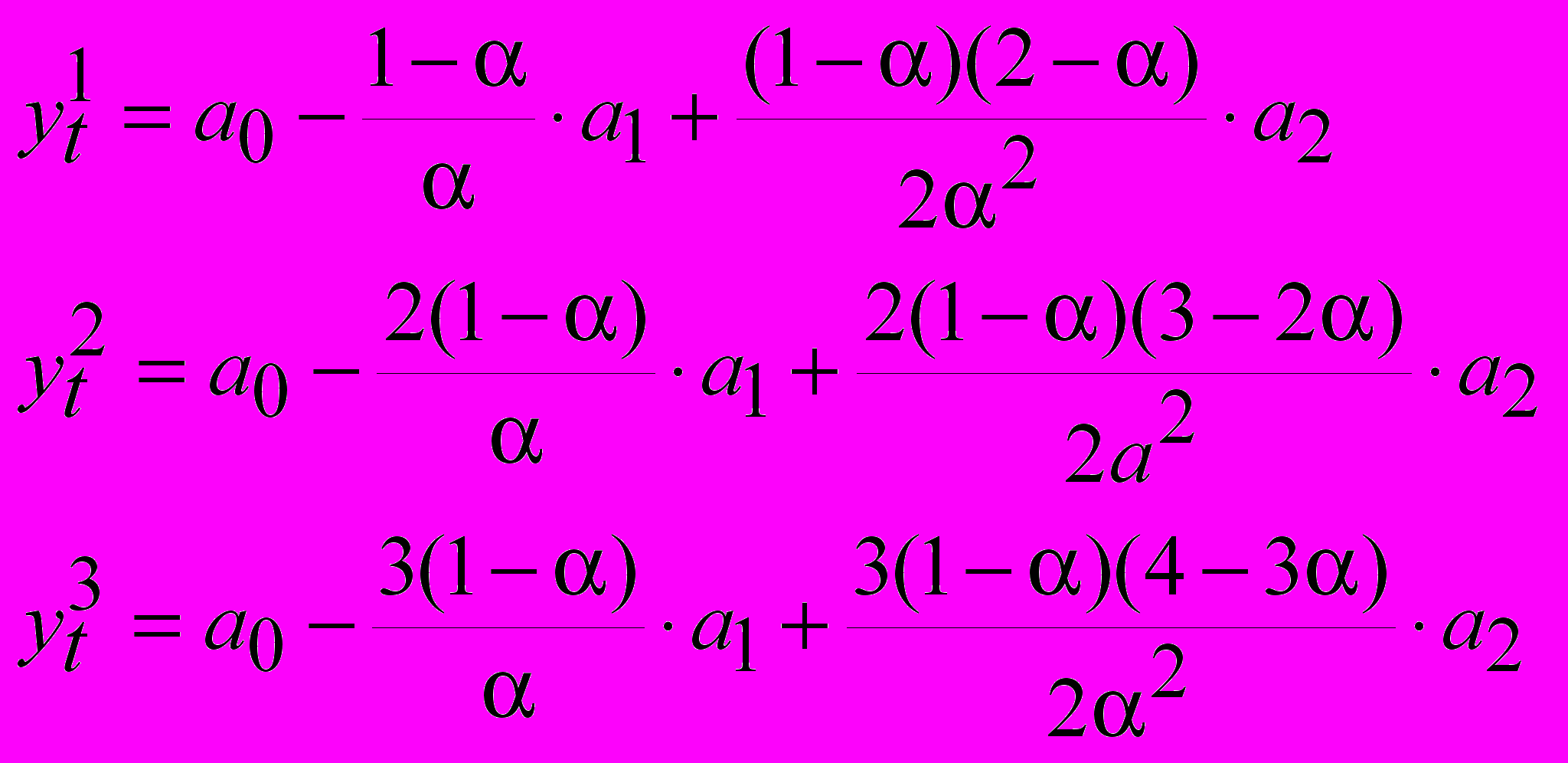 (13)
(13)Откуда получаем
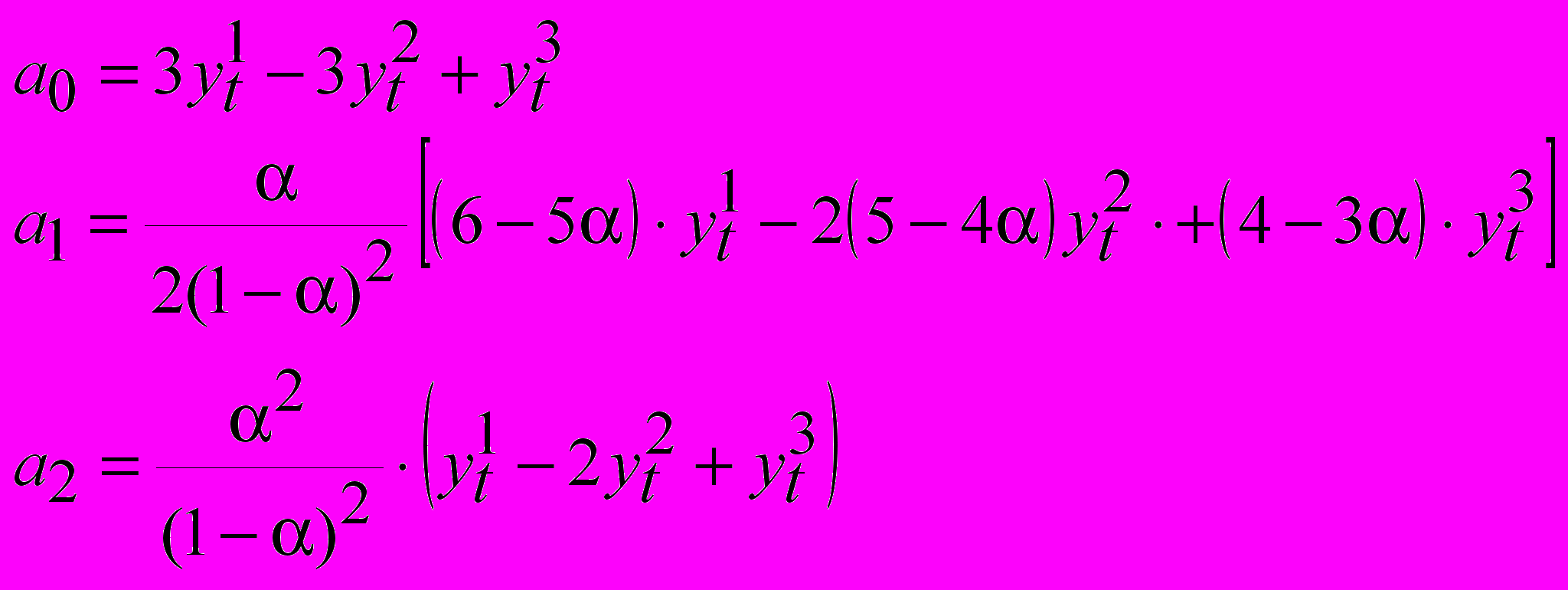 (14)
(14)Прогноз на n периодов осуществляется по формуле
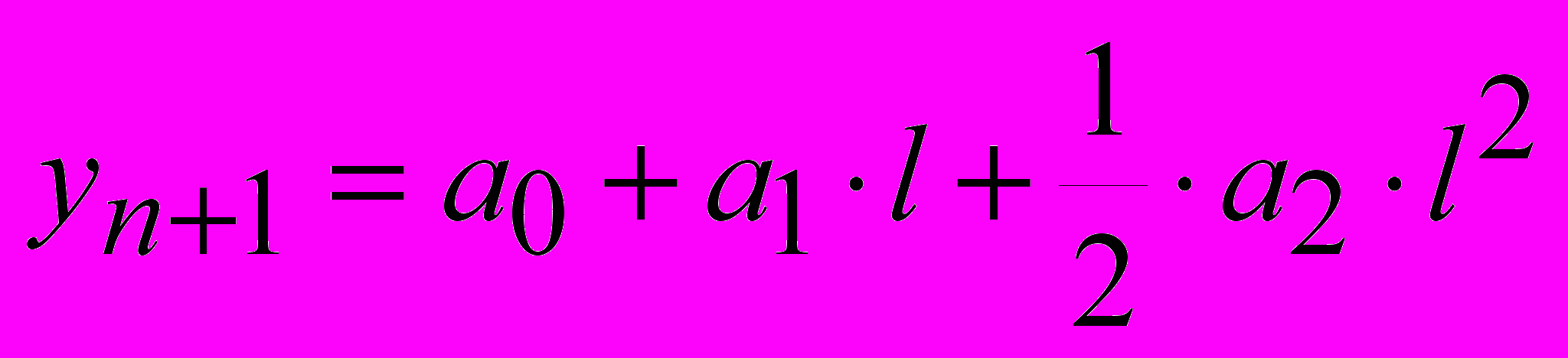
Алгоритм экспоненциального сглаживания рассмотрим на примере. Пусть имеется временной ряд из 12 наблюдений x, значения которого представлены в виде таблицы 5. (=0.6)
Таблица 5.
| | xt | yt1 | yt2 | yt3 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 82.3 | 82.3 | 82.3 | 82.3 | 0.482.3+0.675.4=78.2 |
| 2 | 75.4 | 78.2 | 79.8 | 80.8 | 0.482.3+0.678.2=79.8 |
| 3 | 83.7 | 81.5 | 80.8 | 80.8 | 0.482.3+0.679.8=80.8 |
| 4 | 82.9 | 82.3 | 81.7 | 81.4 | … |
| 5 | 89.8 | 86.8 | 84.8 | 83.4 | 0.478.2+0.683.7=81.5 |
| 6 | 86.0 | 86.3 | 85.7 | 84.8 | 0.479.8+0.681.5=80.8 |
| 7 | 77.2 | 80.9 | 82.8 | 83.6 | 0.480.8+0.680.8=80.8 |
| 8 | 79.5 | 80.0 | 81.1 | 82.1 | … |
| 9 | 81.0 | 80.6 | 80.8 | 81.3 | … |
| 10 | 72.3 | 75.6 | 77.7 | 72.2 | 0.474.4+0.683.3=79.1 |
| 11 | 73.6 | 74.4 | 75.7 | 77.1 | 0.475.7+0.679.7=78.1 |
| 12 | 83.3 | 79.7 | 78.1 | 77.7 | 0.477.1+0.678.1=77.7 |
а0=379.7-378.1+77.1=82.54
0.6
а1=------------[(6-50.6)79.7-2(5-40.6) 78.1+(4-30.6) 77.7]=7.33
2(1-0.6)2
0.62
a2=-----------(79.7-278.1+77.7)=2.68
(1-0.6)2
На основании рассчитанных коэффициентов ai получаем прогнозную модель. На ее основании для значений параметра t строим прогнозные значения:
| T | 1 | 2 | 3 | 4 | 5 |
| Y | 91.2 | 102.5 | 116.6 | 133.3 | 152.7 |
Важнейшую роль в методе экспоненциального сглаживания играет выбор оптимального параметра сглаживания , т.к. именно он определяет оценки коэффициентов модели, а, следовательно, и результаты прогноза.
В зависимости от величины прогнозные оценки по-разному учитывают влияние изменения значения исходного ряда наблюдений: чем больше , тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убывает. При малых прогнозные оценки параметров модели учитывают все наблюдения, при этом уменьшение влияния более «старой» информации происходит медленно.
Тема 5. Адаптивное прогнозирование
Упрощенная модель экспоненциального сглаживания
Для составления прогноза (особенно краткосрочного) на основе временного ряда н при отсутствии или несущественности данных за прошедший период применяется метод экспоненциального сглаживания. Получаемый при этом прогноз является теоретически устойчивым. Вместе с тем его чувствительность к изменениям можно регулировать выбором коэффициента отклика , вводимого ниже.
Пусть требуется предсказать сбыт за (t+1)-й месяц на основании данных о сбыте за r прошедших месяцев Xi(i=t—г+1,... ,t). На первый взгляд решение состоит в том, чтобы взять в качестве прогнозируемой величины среднее значение
mt=(xt-r+1+…+xt)/r
Однако оценка mt, как правило, не годится, так как Xt+1 зависит в большей степени от Xt, чем от Xt-1, в большей степени от Xt-1, чем от Xt-2, и т. д. Поэтому разумнее в качестве прогнозируемой величины брать взвешенное среднее
Yt=a1Xt+ a2Xt-1+ …+arXt-r+1
где a1>a2> …>ar и a1+a2+ …+ar =1. В частности, можyо выбирать экспоненциальные весовые коэффициенты: a2= (1—)a1; a3== (1—)a2,...., где a—константа. Для больших r из условия нормировки получаем: a1=, a2=(1-). При этом
yt=(1-)yt-1+xt=yt-1+(xt-yt-1)=yt-1+et
где et — погрешность, т. е. разность между предсказанным и фактическим показателями в текущий момент t.
Допустив, что х является входом, а прогноз у—выходом некоторой управляемой системы, можно по виду передаточной функции доказать, что при <1 процесс на выходе i/i будет устойчивым. Когда система идеально устойчива, т. е. не подвержена никаким флуктуациям во времени, коэффициент отклика равен нулю; при больших флуктуациях для отслеживания процесса следует увеличивать почти до 1.
Прогноз на начальный период иногда приходится лишь угадывать; в последующие периоды прогноз вычисляется с учетом погрешности, имевшей .место в предшествующий период. Значение коэффициента отклика обычно выбирается субъективно н сохраняется постоянным в течение длительного времени, если только значения погрешности не получаются слишком большими.
Применение экспоненциального сглаживания в адаптивном прогнозировании
Метод экспоненциального сглаживания разработан для частного случая, когда сведения о динамических изменениях показателя отсутствуют и для принятия решений требуется хотя бы грубый краткосрочный прогноз. Если прогнозируемый показатель подвержен значительным флуктуациям, то данный метод позволяет отслеживать уже происшедшие изменения. Поэтому целесообразно так обобщить этот метод, чтобы коэффициент отклика изменялся со временем.
. Метод Тригга и Личй. Тригг и Лич предложили 'метод следящих сигналов для обновления значения коэффициента отклика в .каждый момент времени [21]. Этот .'метод благодаря своей простоте 'получил широкое распространение. Его можно назвать двухэтапным сглаживанием. На первом этапе происходит сглаживание погрешности с произвольным коэффициентом отклика и определяется сглаженная погрешность e(t) в момент t
et=et+(1-)et-1
а среднее абсолютное отклонение mt; в момент t удовлетворяет соотношению
mt=et+(1-)mt-1
Параметр et=et+(1-)et-1 берут обычно в интервале 0,1—0,3. По определению следящий сигнал Tt в момент t равен отношению сглаженной погрешности к среднему абсолютному отклонению:
T=et/mt
В качестве нового значения в формулу подставляют
t=|Tt|
Если погрешность et имеет нормальное распределение с нулевым средним и дисперсией 2, то можно показать, что математическое ожидание mt=0,4. Математическое ожидание следящего сигнала равно коэффициенту отклика только в отдельных случаях, тем не менее оценка хорошо зарекомендовала себя на практике.
Метод динамической регрессии*.
Этот метод был предложен для обновления значений . Искомая оценка для в момет t получается при минимизации суммы квадратов погрешностей за предыдущие периоды. В результате
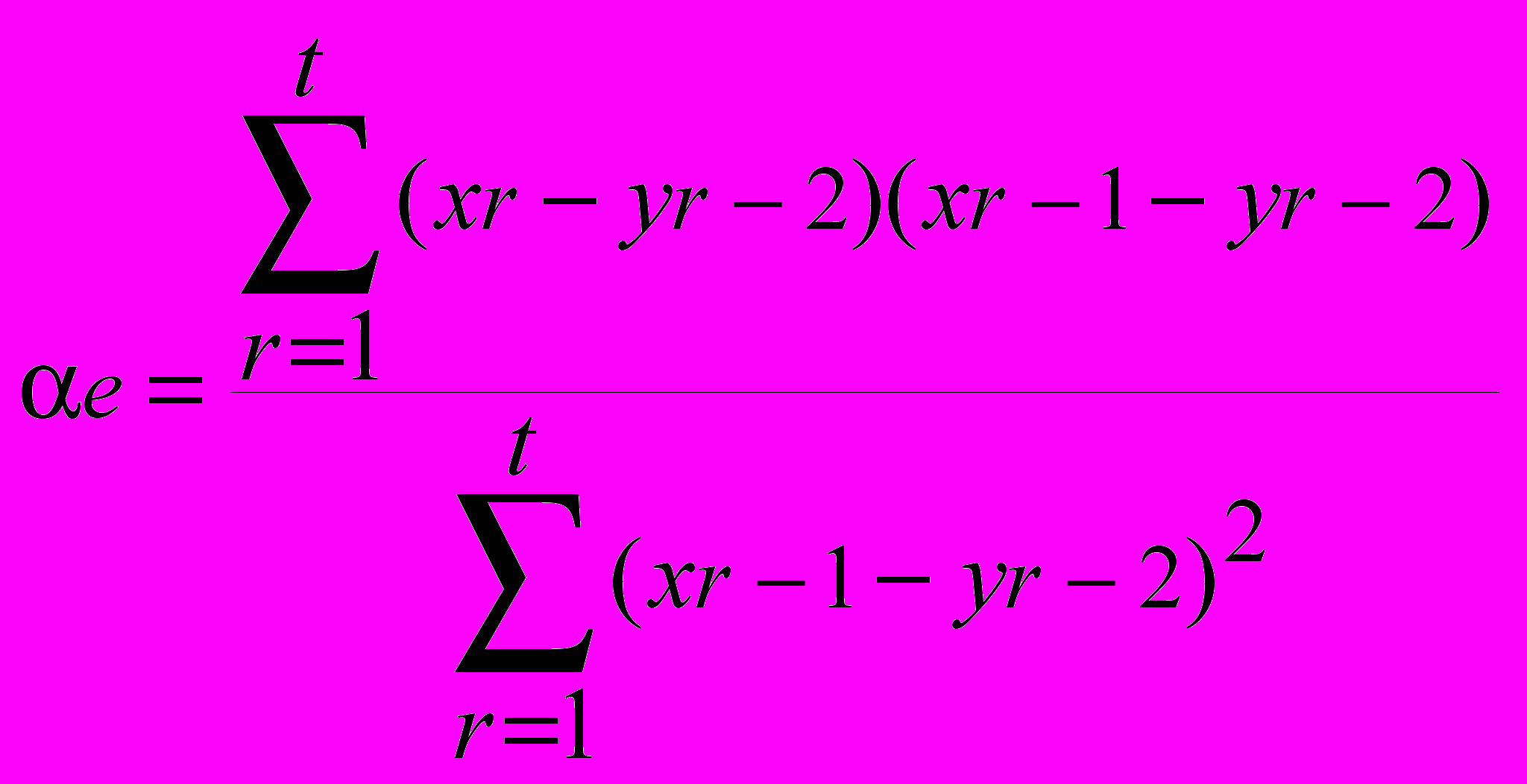
По существу речь идет о регрессии величины dr=xr—yr-2 по величине er-1=xr-1-yr-1, иначе говоря, о регрессии погрешности прогноза на два периода вперед по погрешности прогноза на один период вперед. Линейное уравнение регрессии имеет вид
dr= er-1
В данном случае коэффициент пропорциональности обновляется по мере накопления информации, поэтому метод назван методом динамической регрессии. После вычисления по формуле прогноз yt на (t+1)-u период получается из соотношения
yt= yt-1+ er
Тема 6. Многофакторные прогнозные модели
В предшествующем разделе были рассмотрены примеры прогнозирования на основе однофакторной параметрической зависимости. Однако опыт прогнозирования показывает, что применение однопараметрических зависимостей в экономическом прогнозировании не всегда обеспечивает получение предъявленных требований и точности к прогнозам и объективности зависимостей в прогнозных моделях.
Наиболее характерные многопараметрические зависимости, используемые в практике экономического прогнозирования имеет следующий вид:
- Линейные
y=A0+A1x1+A2x2+…+Anxn (45)
где А0 – свободный член многопараметрической модели;
А1, А2, Аn - регрессионные коэффициенты, отражающие степень влияния соответствующих параметров (факторов) X1, X2, Xn;
n – количество параметров (факторов), рассматриваемых в модели.
- Степенная
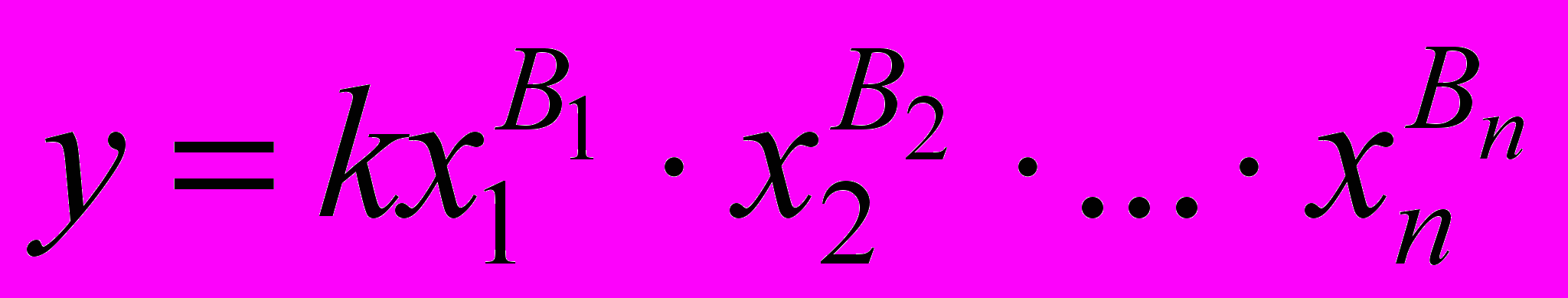 (46)
(46)- где к – постоянный коэффициент многопараметрической регрессионной модели;
В1,В2,В3…Вn – постоянные показатели степени при соответствующих факторах (параметрах), включаемых в данную модель.
Практическое решение задачи успешного построения многопараметрических прогнозных моделей возможно лишь при последовательном выполнении взаимосвязанных стадий:
Стадия 1. Вырабатывается первоначальная гипотеза о наборе факторов, влияющих на результативность показателя у на основе профессионального (логического) анализа. При этом первоначально может быть отобрано большое количество факторов, чтобы в дальнейшем, в процессе корреляционного анализа, можно было ограничиться только теми, которые лучше всего характеризуют существенные изменения моделируемого показателя.
Стадия 2. Сбор исходных данных. На этой довольно трудоемкой стадии решается вопрос о необходимости получения (сбора) исходных данных о рассматриваемом прогнозном объекте. Эти сведения можно получить на базе накопленной ранее информации, которая может быть получена из данных первичного учета действующих организаций. Результаты этой стадии являются основой для построения многопараметрических прогнозных моделей.
Стадия 3. Разрабатывается сводная таблица, которая включает в себя столбцы значений полученных исходных данных расчета, необходимых для вычисления параметров прогнозной модели (табл. 15)
Таблица 15.
Макет таблицы для определения линейной многопараметрической модели
| № п/п | y | x1 | … | xn | y2 | x12 | … | xn2 | yx1 | … | yxn | x1x2 | … | xn1xn2 |
| 1 | | | | | | | | | | | | | | |
| 2 | | | | | | | | | | | | | | |
| … | | | | | | | | | | | | | | |
| m i=1 | | | | | | | | | | | | | | |
Стадия 4. Рассчитываем по данным сводной таблицы (см. табл. 15) основные статистические характеристики:
среднее значение рассматриваемых факторов и результирующего показателя по формулам:
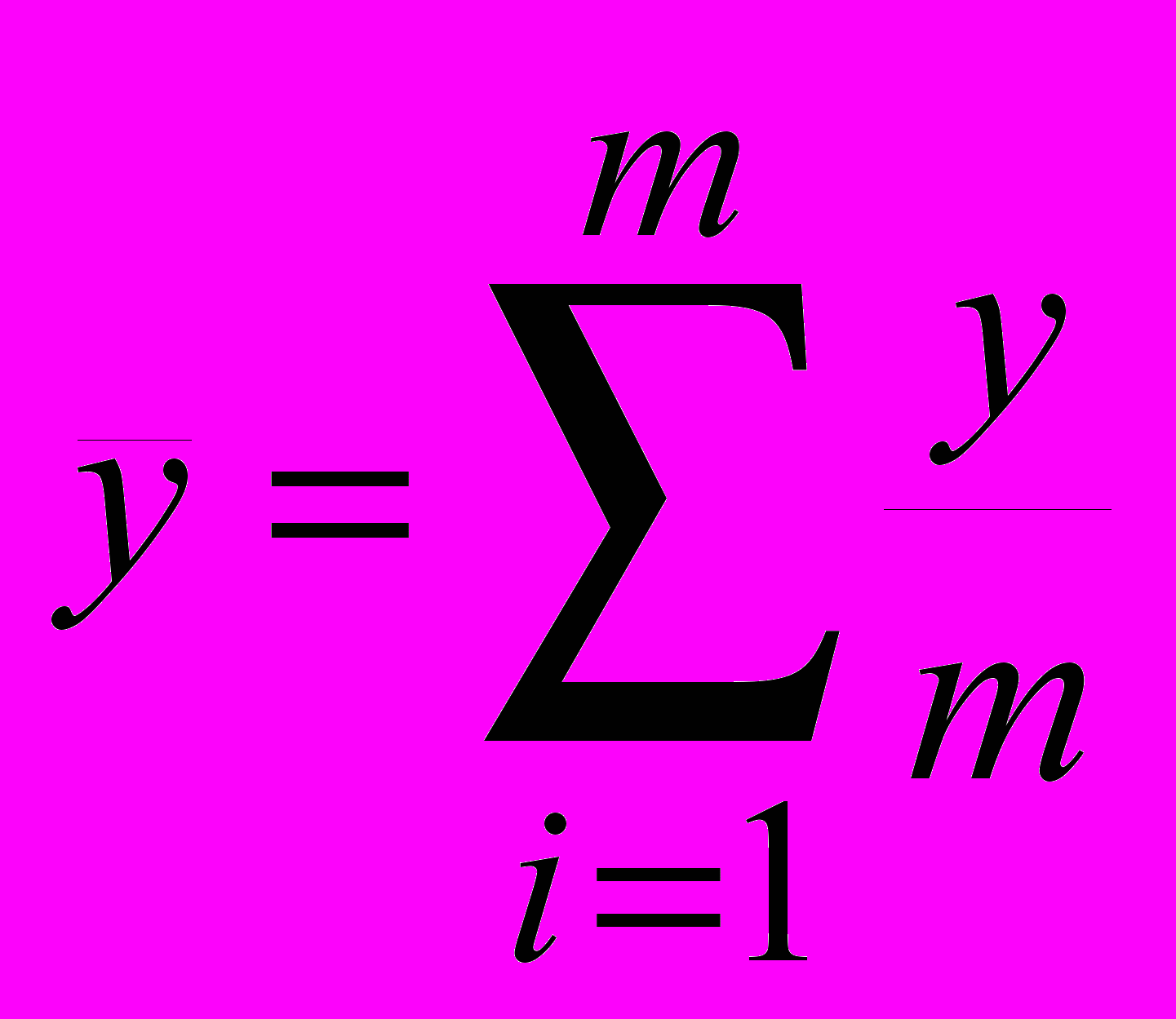 (47)
(47)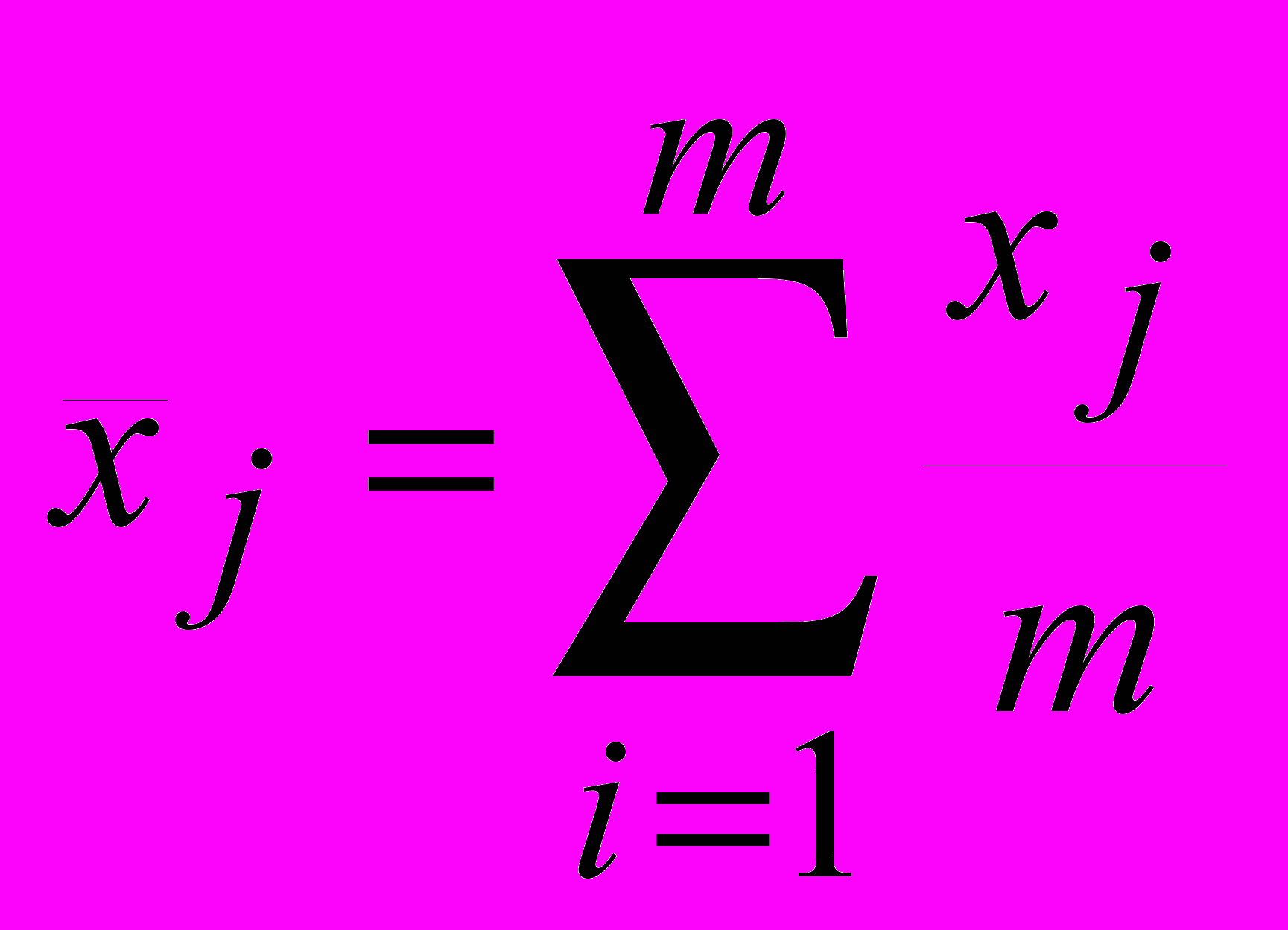 (48)
(48)где m – количество имеющихся исходных данных.
среднее квадратическое отклонение по формулам:
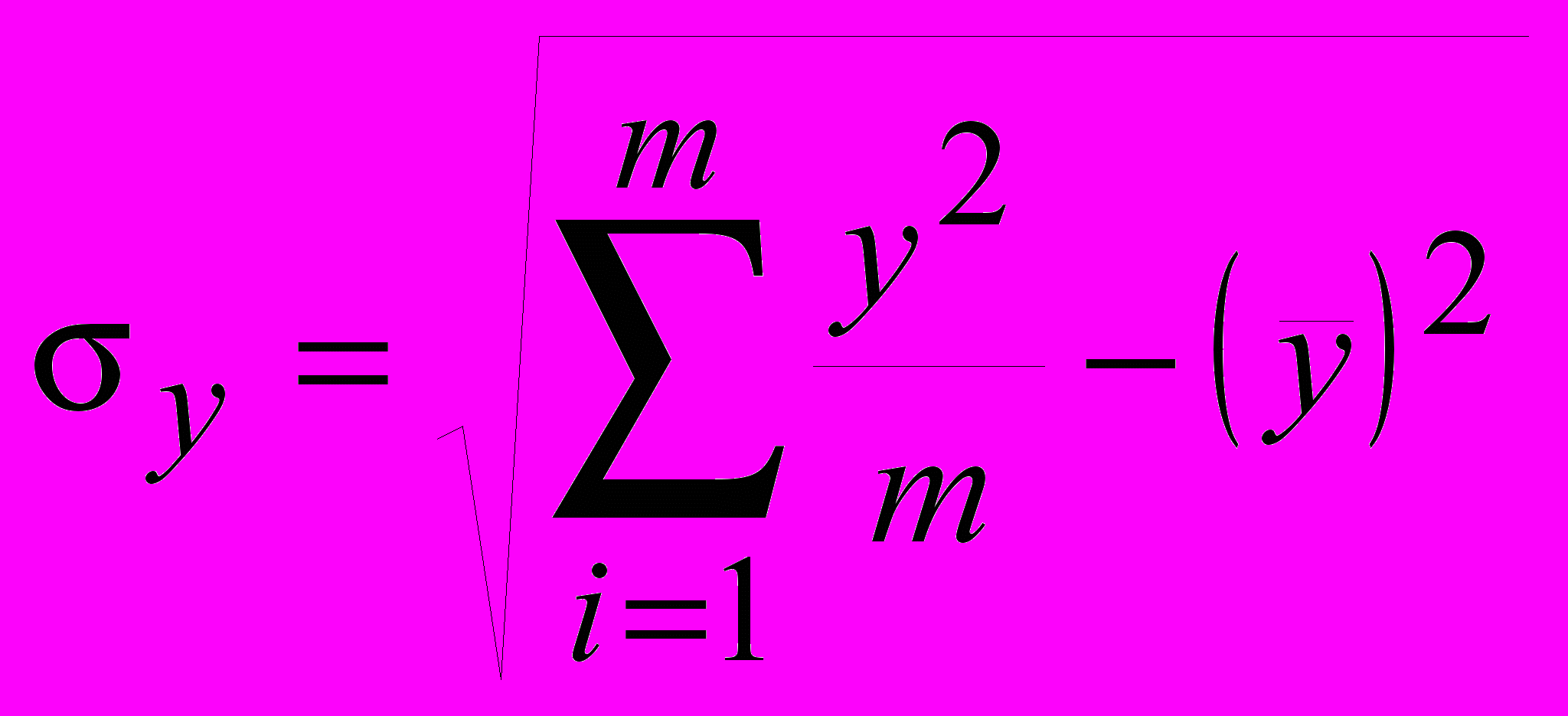 (49)
(49)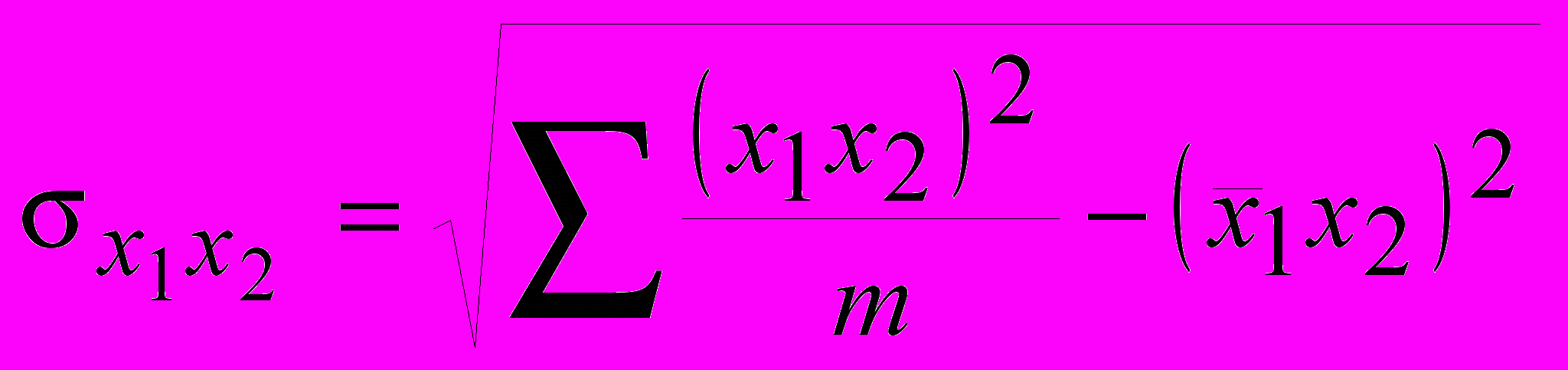 (50)
(50)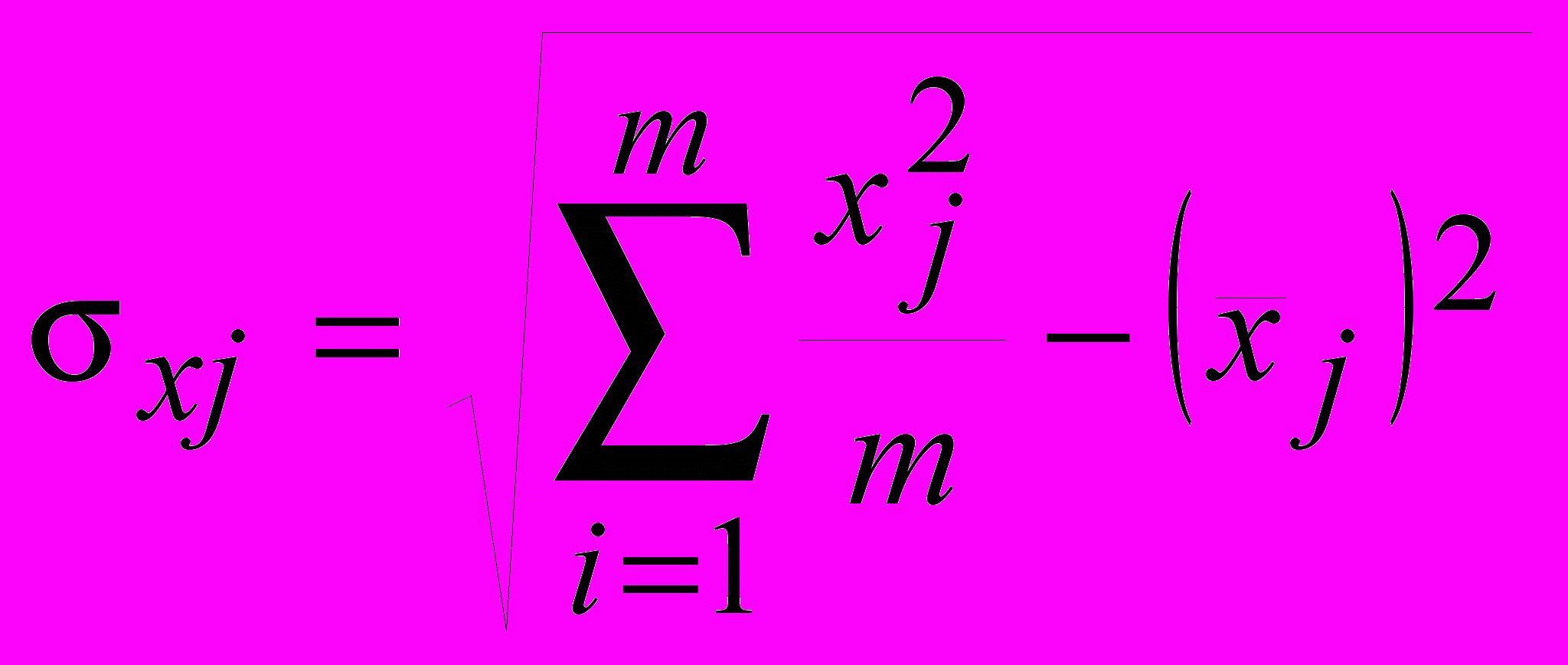 (51)
(51)коэффициенты парной корреляции по формулам:
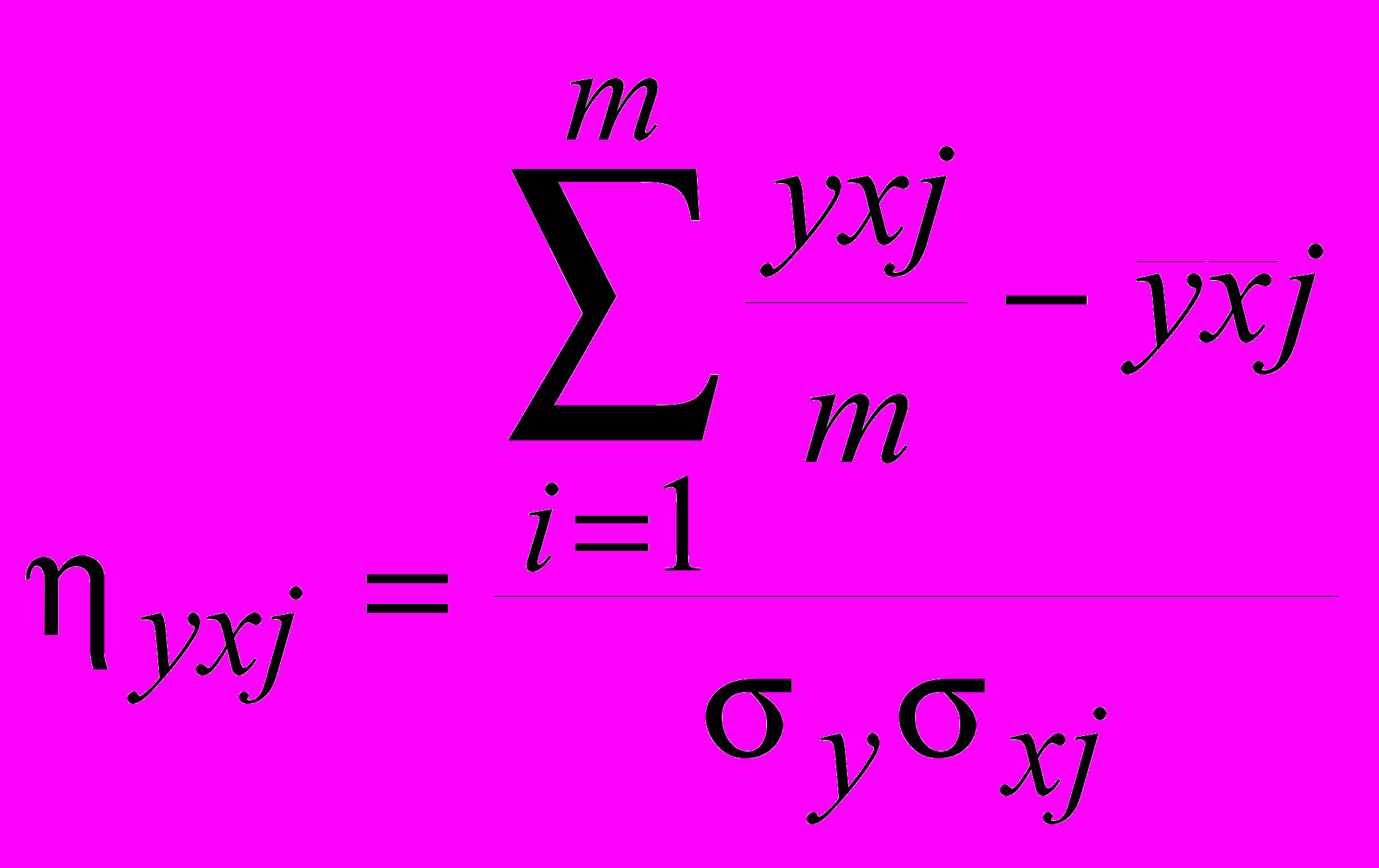 (52)
(52)надежность вычисления коэффициентов парной корреляции определяется по формуле:
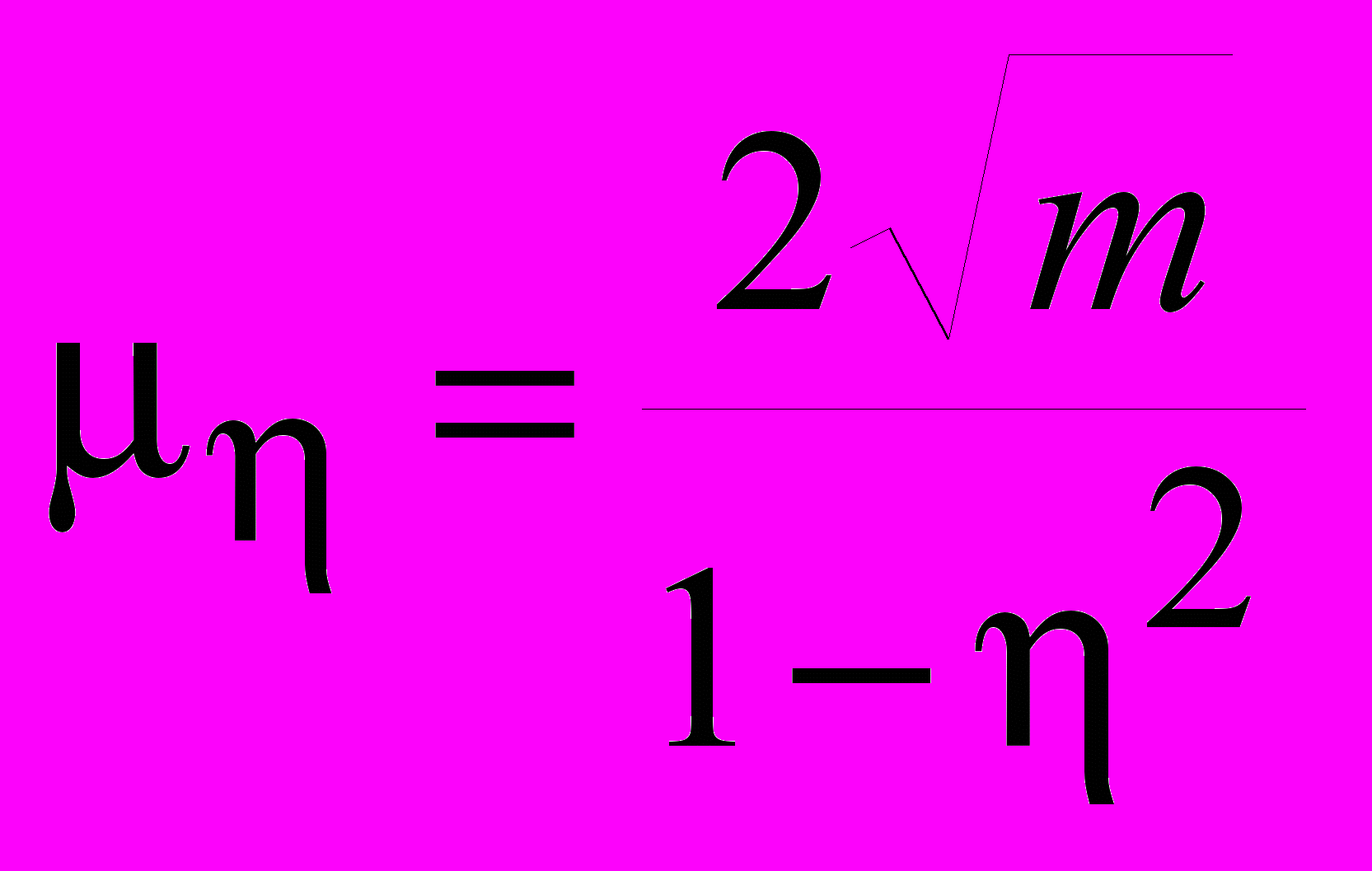 (53)
(53)Стадия 5. По результатам вычисления коэффициентов парной корреляции составляется матрица (см. табл. 16).
Таблица 16. Матрица коэффициентов парной корреляции
| – | y | x1 | x2 | … | xn |
| y | – | yx2 | yx2 | … | yxn |
| x1 | yx1 | – | x1x2 | … | x1xn |
| x2 | yx2 | x1x2 | – | … | x2xn |
| … | … | … | … | … | … |
| … | … | … | … | … | … |
| xn | yxn | xnx1 | xnx2 | … | – |
На основе оценки значимости коэффициентов парной корреляции, приведенных в табл. 16, выделяются факторы, наиболее сильно влияющие на результирующий показатель. При этом также учитывается, что в многопараметрической регрессионной модели не должны одновременно включаться факторы, находящиеся между собой в строгой функциональной зависимости (включается один из них - более важный по влиянию). По отобранным факторам составляется система уравнений:
yx1=1+yx22+…+yxnn
yx2=x1x21+2+…+x2xnn (54)
…
yxn=x1xn1+x2xni+…+n
Решение этой системы (как правило, методом Гаусса) позволяет получить стандартизованные коэффициенты искомой модели j.
Стадия 7. На данной стадии определяются :
регрессионные коэффициенты прогнозной модели по формуле:
aj=jy
или (55)
aj=xj
свободный член регрессионной модели:
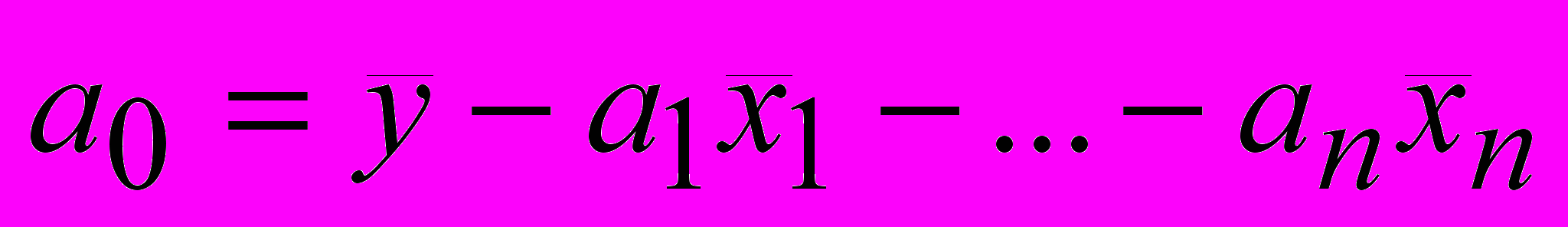 (56)
(56)коэффициент множественной корреляции:
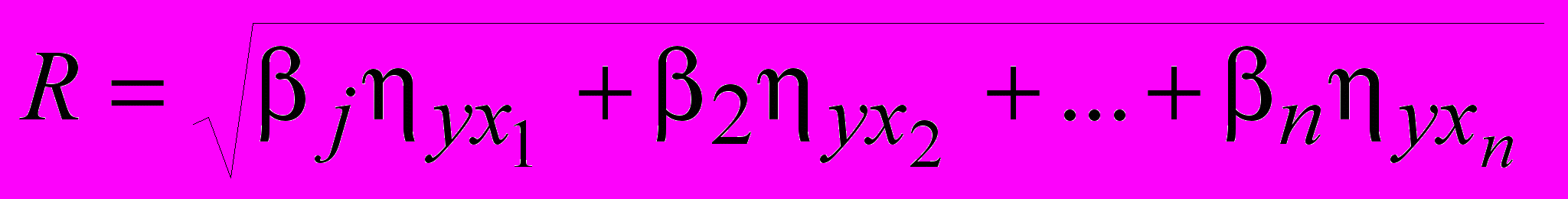 (57)
(57)где
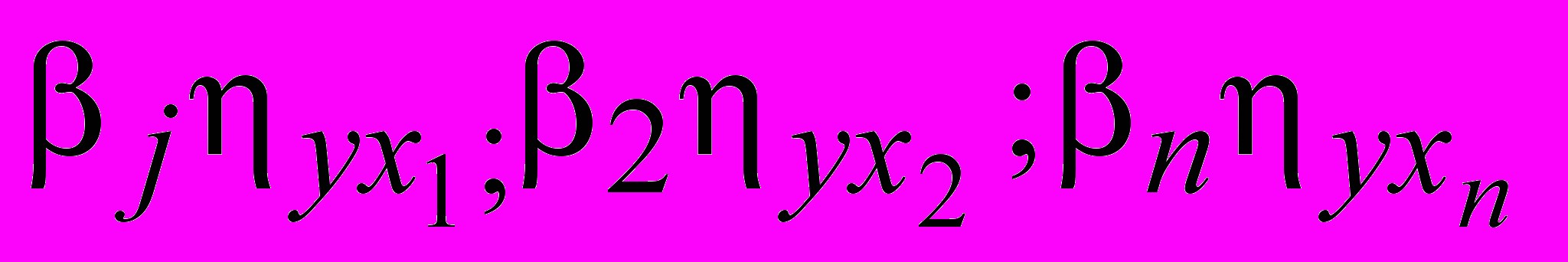 – коэффициенты частной детерминации, показывающие какая доля результирующего показателя приходится на соответствующий фактор, учтенный в регрессионной модели.
– коэффициенты частной детерминации, показывающие какая доля результирующего показателя приходится на соответствующий фактор, учтенный в регрессионной модели.Рассчитанный на основе небольшого числа наблюдений коэффициент множественной корреляции имеет свойство преувеличивать действительную тесноту связи. Эта погрешность увеличивается с ростом числа факторов, включаемых в прогнозную модель. Для устранения погрешности коэффициент множественной корреляции необходимо корректировать. Его уточненная форма имеет вид:
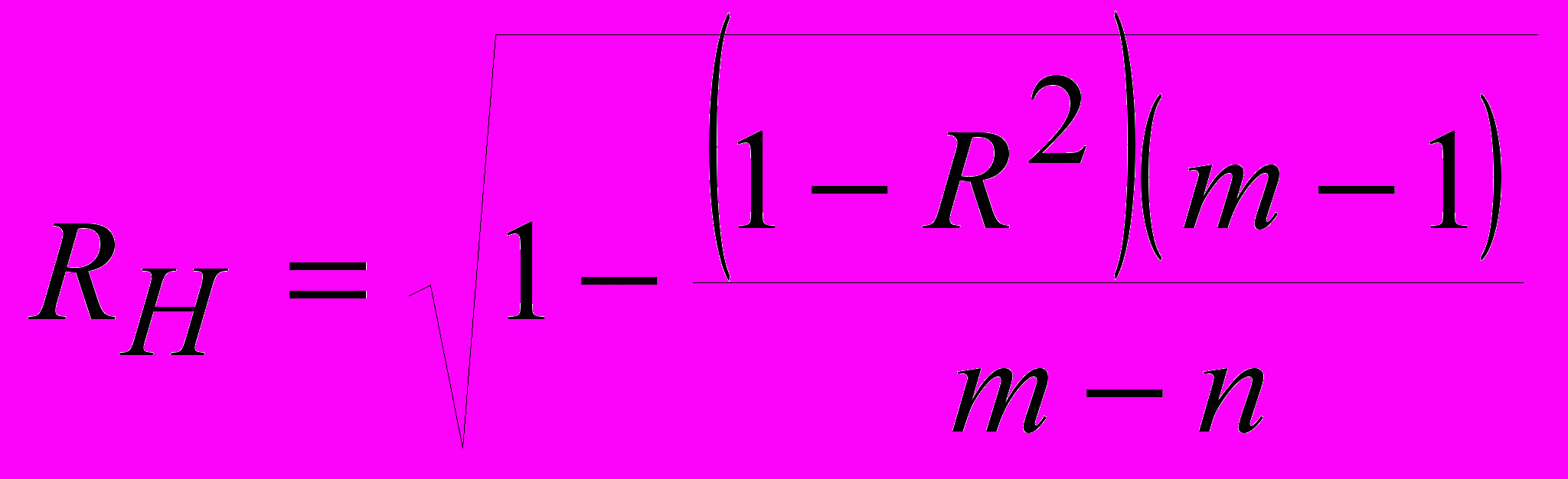 (58)
(58)Его надежность определяется как
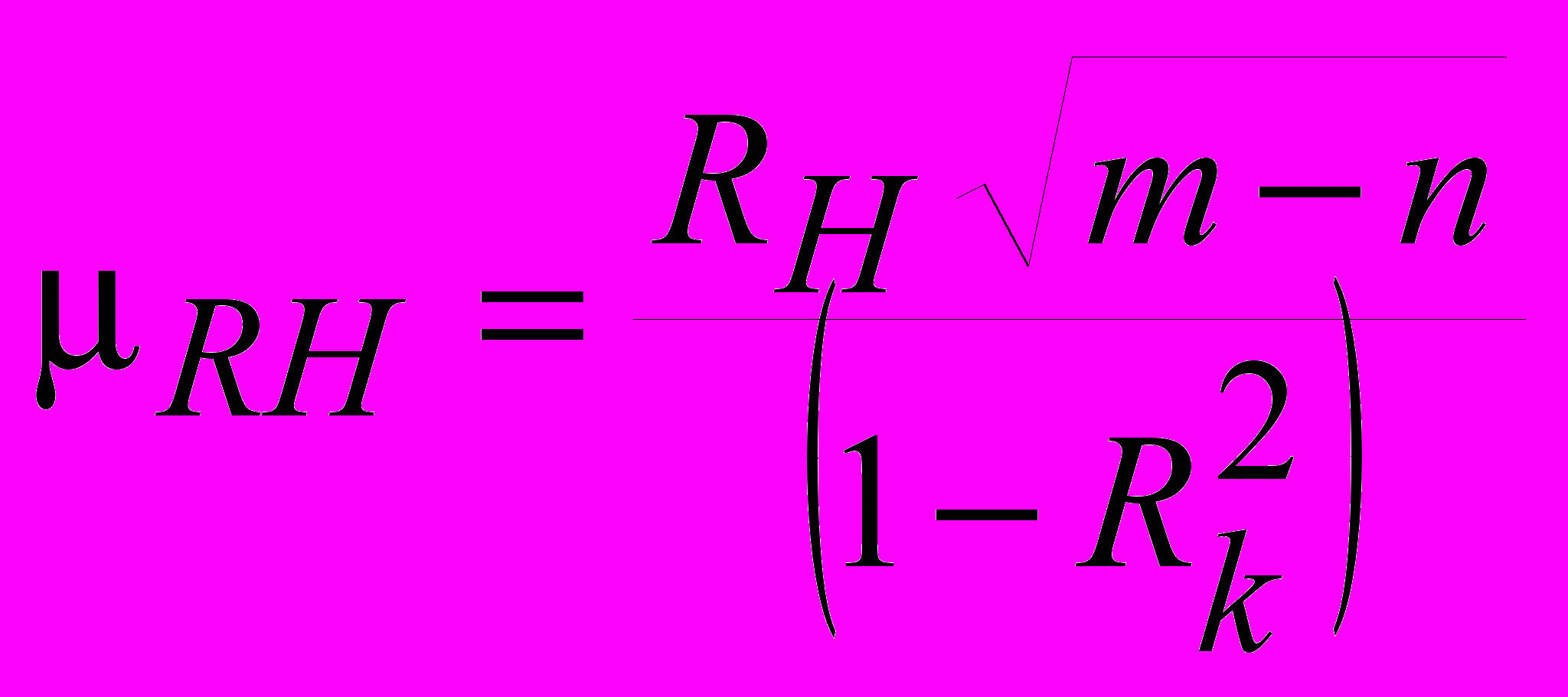 (59)
(59)Принято считать, если RH2, то с вероятностью равной 0.95, а в случае RH3, равной 0.99, можно считать значимость величины полученного коэффициента множественной корреляции.
Стадия 8.На каждой стадии решается вопрос, можно ли использовать разработанную модель для всей генеральной совокупности или она не представляет практической ценности. С этой целью определяются доверительные пределы, %:
коэффициентов парной корреляции, которые показывают степень их устойчивости по формуле:
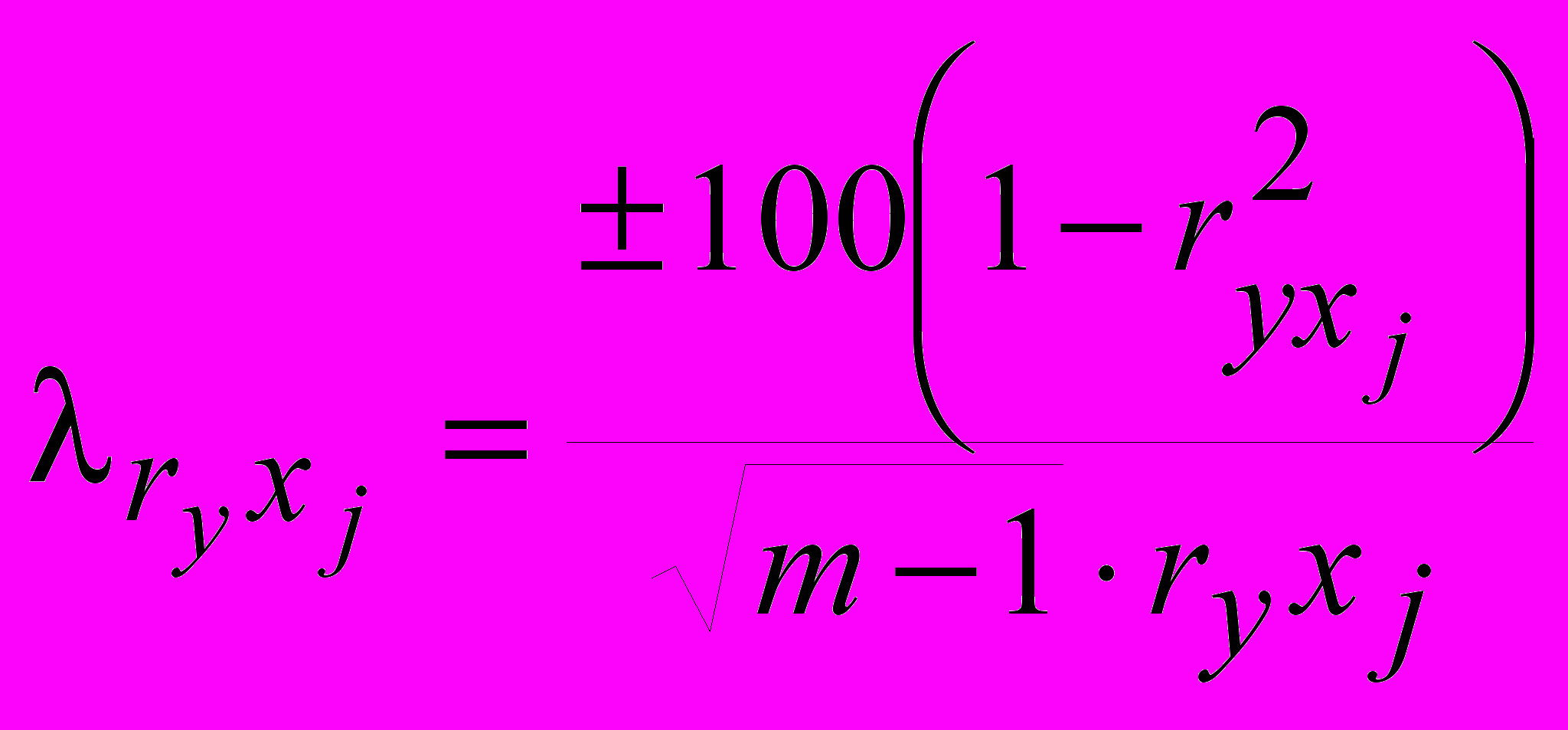 (60)
(60)расчетного значения результирующего показателя, являющегося критерием, позволяющим сделать вывод о возможности использования разработанной модели не только для данных, на основании которых эта модель рассчитана, но и для всей совокупности по формуле:
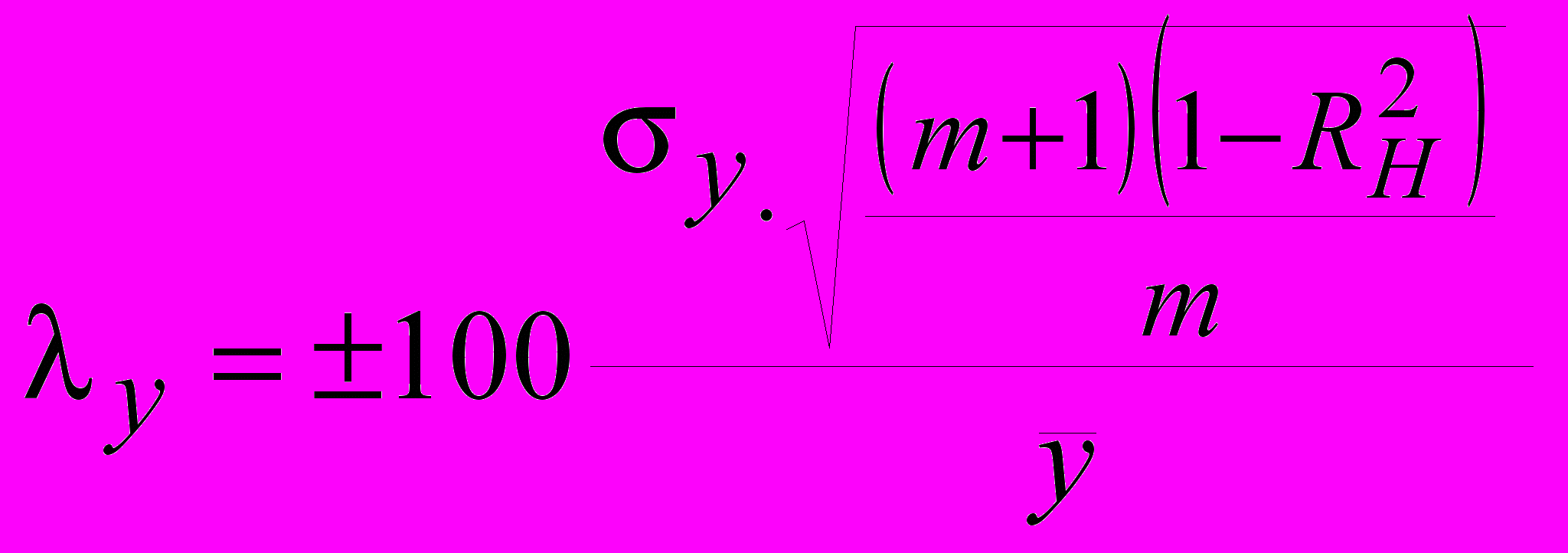
Статистическая оценка результатов построения прогнозных моделей выполняется только для тех моделей, которые строятся не на данных генеральной совокупности, а на основе выбранного метода.
Стадия 9. Определение прогнозного смысла построения моделей осуществляется с помощью вычисления коэффициента эластичности, показывающего влияние разноименных факторов в соизмеримых единицах процентах. Коэффициент эластичности указывает, на сколько процентов в среднем изменяется результирующий показатель при изменении j-го фактора на каждый процент и фиксированном уровне остальных факторов, рассматриваемых в модели. Этот коэффициент для линейной многопараметрической зависимости определяется по формуле: