Geum.ru

Задача. Задано фігуру складної форми. Обчислити її площ

Вид материалаЗадача

Содержание


Задача. Задано фігуру складної форми. Обчислити її площ
Блок-схема алгоритму
Подобный материал:
КРАСИЛІВСЬКИЙ НВК «ЗОШ І – ІІІ СТУПЕНІВ №5 ТА ГІМНАЗІЯ»


методична розробка

задачі з програмування для теми

«Цикли»




Метод Монте-Карло


Роботу виконав: Габельчук Юрій Петрович,

вчитель інформатики

Красилівського НВК «ЗОШ І-ІІІ ст. №5 та гімназія»


Красилів – 2006

Метод Монте-Карло


Щоб у вас не склалось враження, що математичні моделі потрібно будувати тільки для розв’язування задач, далеких від математики, побудуємо її для математичної задачі. Одна з таких задач – обчислення площ. Звичайно, для най простіших фігур площини (прямокутників, многокутників, кругів) обчислення площі не складає труднощів: потрібно у відомі формули підставити вхідні дані. А як же поступати, коли фігура складної форми?


Задача. Задано фігуру складної форми. Обчислити її площу.


Можна запропонувати різні моделі для цієї задачі. Наприклад, нас в молодших класах вчили використовувати палетку: на фігуру накладається прозорий папір в клітинку (палетка), і підраховується кількість квадратиків, що попали на фігуру. В цій моделі за замовчуванням мається на увазі, що чим дрібніші будуть клітинки, тим точніший буде результат, незалежно від того, яким чином накладати палетку на фігуру.

Можна придумати і «фізичну» модель: скопіювати фігуру на картон, акуратно вирізати її, зважити і поділити її масу на масу одиничного квадрату з того ж картону.

В 11 класі ви ознайомитесь ще з одним способом знаходження площ фігур: за допомогою інтегралів.

Однак, за всіма цими моделями досить важко скласти алгоритм, а потім програму для комп’ютера.

Як бачите, і для розв’язку математичних задач можна будувати різні математичні моделі. Математичні моделі життєвих задач – це «мости» між життям і математикою. Наприклад, метод координат дає змогу створювати алгоритмічні моделі геометричних об’єктів.

Математична модель, яку ми зараз побудуємо, може здатись вам неочікуваною, але вона дає змогу дуже ефективно використовувати ЕОМ для розв’язання задач на знаходження площ, об’ємів і т. ін.

Помістимо задану фігуру в квадрат. Будемо навмання (як кажуть математики, випадковим чином) «кидати» точки в цей квадрат. Природно припускати, що чим більша площа фігури, тим частіше в неї будуть попадати точки. Уявіть собі квадратний дворик і на ньому дитячу площадку. Кожному зрозуміло, що під час снігопаду кількість сніжинок, що потрапили на дитячу площадку, пропорційна її площі. Таким чином, можна зробити припущення: при більшій кількості точок, наугад вибраних всередині квадрату, частка точок, що містяться в даній фігурі, наближено рівна відношенню площі цієї фігури до площі квадрата.

Такий метод наближеного знаходження площ фігур має назву метод Монте-Карло (за назвою міста, де розміщена знаменита рулетка, котру можна розглядати як «генератор» випадкових чисел).

Нескладно визначити, що в нашій моделі – початкові данні, а що – результат. Позначимо нашу фігуру буквою F. Вхідними даними є сторона a квадрата, що містить фігуру F, і кількість точок N, котрі ми будемо випадковим чином вибирати всередині квадрату. Результатом є площа S фігури F. Якщо через М позначити число тих, навмання вибраних точок, котрі містяться у фігурі F, то площа S наближено рівна a2M/N. Зрозуміло, що зв’язків між вхідними даними і результатом слід віднести і математичні співвідношення, які дають можливість визначити, чи потрапила вибрана точка в фігуру F.

Ці співвідношення будуть розрізняти моделі, побудовані для різних фігур. Значить, фактично ми описали не одну модель, а швидше – деякий спосіб отримання моделей. Для кожної фігури буде своя модель.

Давайте розглянемо модель для наближеного обчислення площі круга радіусу R. Формула площі круга вам відома: 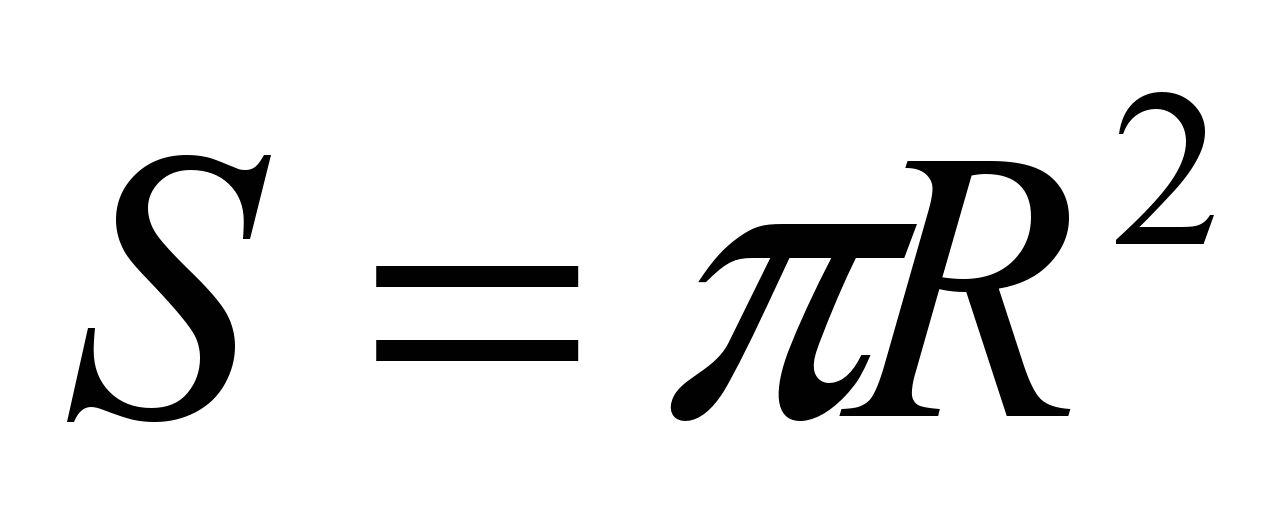. Перевіримо її за допомогою комп’ютера!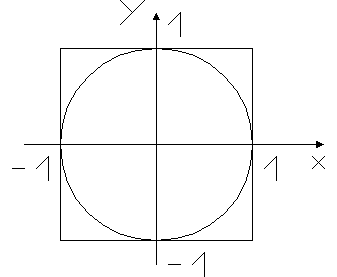

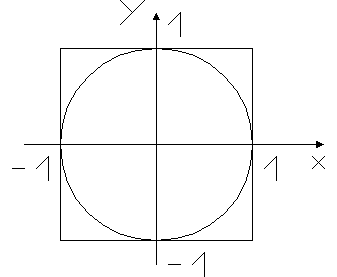Нехай, для певності, R=1. На рисунку зображено круг радіусом 1, обмежений квадратом зі стороною а=2. Таким чином, фігура F – це круг одиничного радіусу. Вибрати точку – це значить задати її координати: числа x та y. Точка належить квадрату, якщо 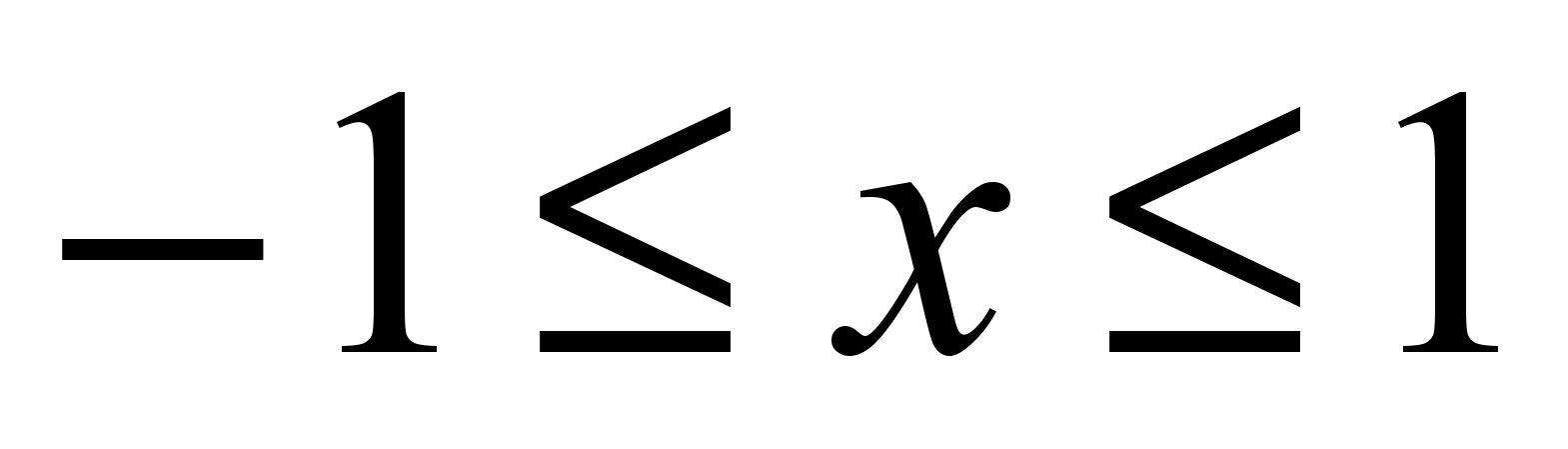і 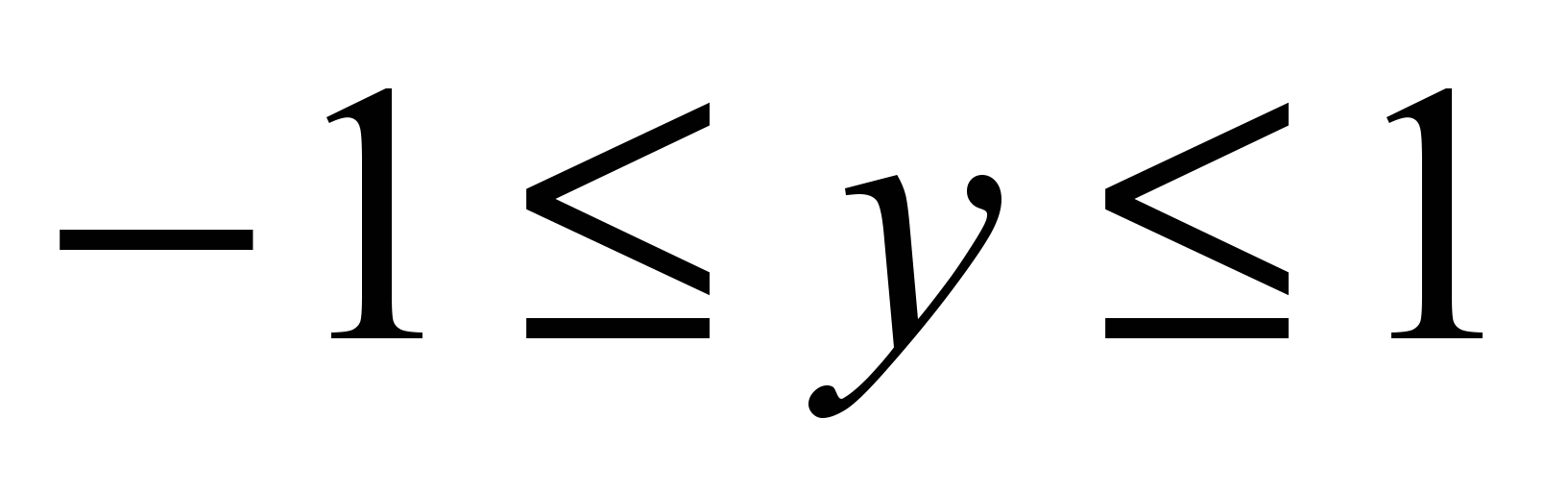. Якщо 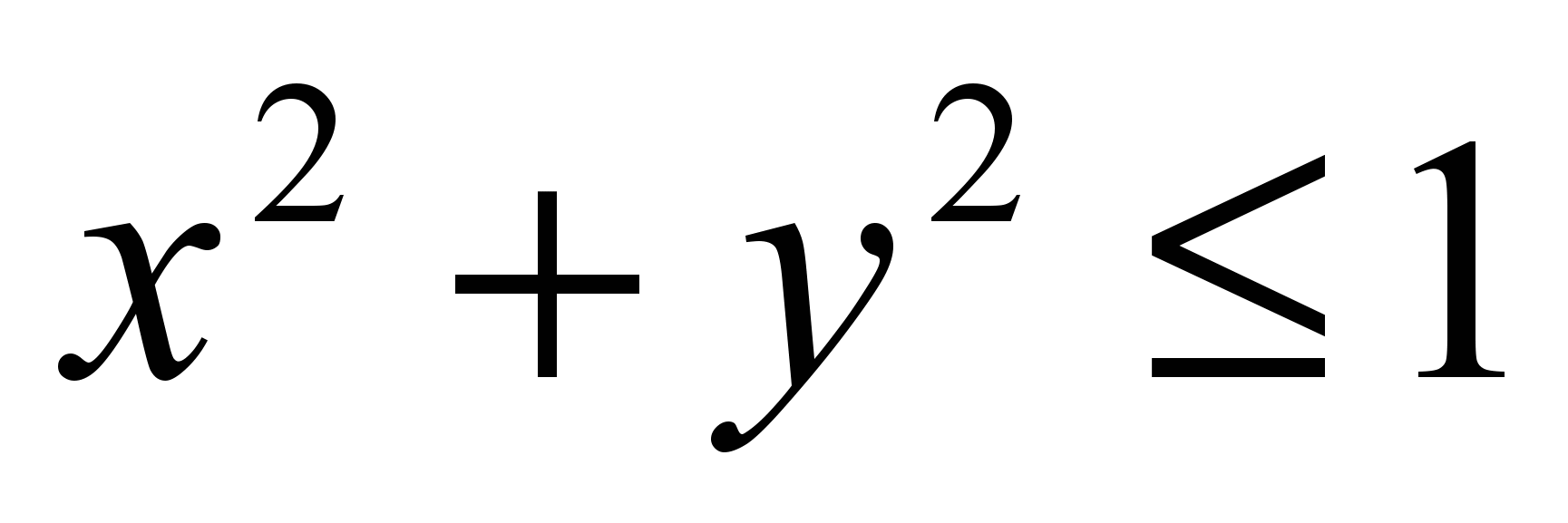, то точка попадає в круг F, інакше вона по за межами круга. Це і є математичні співвідношення, що дають змогу для кожної точки визначити, чи належить вона F.

Математична модель обчислення площі круга побудована. Приступимо до складання алгоритму розв’язку даної задачі. Випадкові числа будемо генерувати на Паскалі за допомогою стандартної функції Random, яка повертає дійсні числа з проміжку [0; 1). Вибирати точки будемо тільки в першій чверті (квадранті) координатної площини. Це на ймовірність попадання їх у круг не вплине, тому що частка площі, яку займає круг у квадраті однакова в усіх чотирьох менших квадратах, на які розбивають наш квадрат координатні осі.

Блок-схема алгоритму:



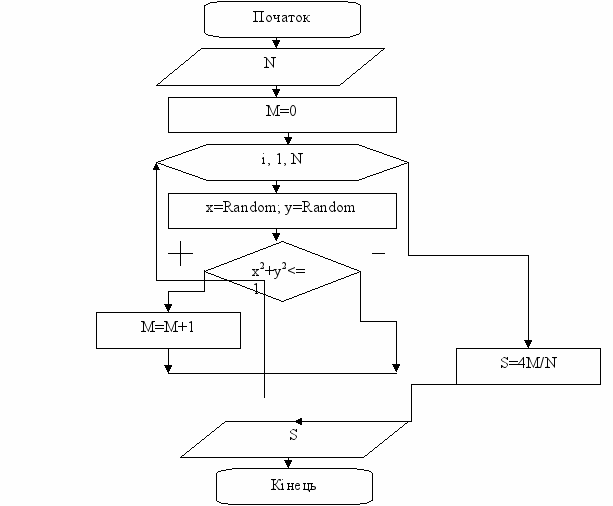
Програма на мові Паскаль:

Program Monte_Carlo;

Var i, N, M: integer;

x, y, S: real;

Begin

Write(‘Введіть кількість точок ‘); Readln(N);

M:=0;

for i:=1 to N do

begin

x:=Random; y:=Random;

if x*x+y*y<=1 then M:=M+1

end;

S:=4*M/N;

Writeln(‘S=’, S)

End.


Результат роботи програми:

Введіть кількість точок 10000

S=3.1476


Запускаючи програму на виконання, пам’ятайте що кількість точок N повинна бути достатньо великою – не менше 300. У автора результат вийшов S=3.1476 (від точного значення π цей результат відділяють менше 6 тисячних). А який результат получився у вас?

Чи не правда, незвичайне питання? Раніше таке питання не виникало, через те що результат виконання програми завжли був однаковий при однакових вхідних даних. Вибрана математична модель для знаходження площ відрізняється від попередніх тим, що в ній використовуються випадкові числа (такі моделі називаються ймовірнісними). Через те й результати получаються різними.

Можливо, де-хто засумнівався: а чи можна за допомогою ймовірносних моделей отримувати хоча б трохи достовірні результати? На подібні запитання відповідає спеціальний розділ математики – теорія ймовірності. Можете не хвилюватись, математиками доведено, що метод Монте-Карло можна застосовувати для обчислення площ.


Габельчук Юрій Петрович, учитель інформатики Красилівського НВК «ЗОШ І-ІІІ ст. №5 та гімназія»